Abstract
Rapid adjustments occur after initial perturbation of an external climate driver (e.g., CO2) and involve changes in, e.g. atmospheric temperature, water vapour and clouds, independent of sea surface temperature changes. Knowledge of such adjustments is necessary to estimate effective radiative forcing (ERF), a useful indicator of surface temperature change, and to understand global precipitation changes due to different drivers. Yet, rapid adjustments have not previously been analysed in any detail for certain compounds, including halocarbons and N2O. Here we use several global climate models combined with radiative kernel calculations to show that individual rapid adjustment terms due to CFC-11, CFC-12 and N2O are substantial, but that the resulting flux changes approximately cancel at the top-of-atmosphere due to compensating effects. Our results further indicate that radiative forcing (which includes stratospheric temperature adjustment) is a reasonable approximation for ERF. These CFCs lead to a larger increase in precipitation per kelvin surface temperature change (2.2 ± 0.3% K−1) compared to other well-mixed greenhouse gases (1.4 ± 0.3% K−1 for CO2). This is largely due to rapid upper tropospheric warming and cloud adjustments, which lead to enhanced atmospheric radiative cooling (and hence a precipitation increase) and partly compensate increased atmospheric radiative heating (i.e. which is associated with a precipitation decrease) from the instantaneous perturbation.
Similar content being viewed by others
Ozone-depleting halocarbons and nitrous oxide (N2O) are well-mixed greenhouse gases that have contributed substantially to radiative forcing (RF) since pre-industrial time, by 0.33 ± 0.03 W m−2 (0.18 ± 0.17 W m−2 when including stratospheric ozone depletion) and 0.17 ± 0.03 W m−2, respectively1. A substantial contribution to global warming and Arctic sea-ice loss in the latter half of the 20th century was recently attributed to ozone-depleting substances2,3. Atmospheric lifetimes of chlorofluorocarbons (CFCs), an important group of ozone-depleting halocarbons, are typically several decades or centuries4. Their impact on climate will therefore remain strong for many years to come despite regulations of halocarbon emissions through the Montreal Protocol signed in 1987.
Most halocarbons, such as CFC-12, have their main infrared absorption bands at different spectral wavelengths compared to the two main anthropogenic greenhouse gases CO2 and methane (CH4), in the so-called atmospheric window region around 800–1200 cm−1 where the RF efficiency is strong5,6. The main infrared absorption bands of N2O partly overlap with CH4, but an important difference is that CH4 has more significant shortwave (SW) absorption bands7,8. Although these factors may imply that the climate effects of halocarbons and N2O differ from those of CO2 and CH4, relatively little is known about the details of short and long-term responses of halocarbons and N2O on climate.
While numerous studies exist on radiative transfer modelling of halocarbons, only a few studies have performed global climate model (GCM) experiments to investigate the climate effects of halocarbons separately. Hansen et al.9,10 found that the surface temperature response to a large forcing of CFCs and N2O had very similar geographical patterns as the response to CO2 and CH4 forcing. The efficacies (i.e. the warming per unit RF) for CFCs were, however, around 30% larger than for CO2, but close to unity for CFCs and N2O when rapid adjustments were accounted for, as also found in a recent multi-model study11. Forster and Joshi12 investigated halocarbon contributions to atmospheric temperature change and found a significant warming at the tropical tropopause; e.g. this led to a ~6% weaker surface warming per unit forcing for CFC-12 compared to CO2.
In the 5th Assessment Report (AR5) of the Intergovernmental Panel on Climate Change (IPCC), RF was diagnosed as effective radiative forcing (ERF), which includes instantaneous radiative forcing (IRF) and rapid adjustments including stratospheric temperature adjustment1,13,14. These fast responses occur on timescales of days to months, before most of the changes in the global-mean and annual-mean surface temperature occur. ERF is shown to be a better indicator for surface temperature change than the earlier RF definition (RF which includes stratospheric temperature adjustment), and rapid adjustments have recently been quantified for some of the most important climate drivers15,16. However, for halocarbons and N2O, contributions of different rapid adjustment terms remain largely unknown, with the exception of stratospheric temperature adjustment which can be estimated in radiative transfer models17.
The fast responses are typically investigated with GCMs using fixed sea surface temperatures (SSTs) and the total response is normally studied using coupled atmosphere–ocean GCMs. The slow (feedback) response is the difference between the total and fast response. In terms of global mean precipitation, an increase of 2–3% per kelvin global mean surface warming is found for the slow response, independent of the climate drivers studied (CO2, CH4, solar irradiance, black carbon and sulphate)18, but rapid adjustment processes lead to differences in the total precipitation response between drivers15,19. Further, one modelling study has indicated that CFCs would have had a strong impact on the hydrological cycle without the Montreal Protocol20.
Here, our focus is to explore how halocarbons and N2O, some of the most important anthropogenic greenhouse gases, influence climate on various time scales by using a range of GCMs. A main aim is to quantify ERF of these compounds and to determine their impact on the hydrological cycle. The climate effects of these gases through stratospheric ozone depletion is beyond the scope of this study but covered elsewhere (see ref. 4 and references therein), and rapid adjustments due to ozone changes (in both the troposphere and stratosphere) have recently been quantified21. Experiments are performed within the Precipitation Driver and Response Model Intercomparison Project (PDRMIP)22, where a main focus is on how different climate drivers affect various components of the climate system, and the hydrological cycle in particular, on both short and long time scales. PDRMIP studies have been used to better understand results from the more complex Coupled Model Intercomparison Project phase 5 (CMIP5)23 simulations for the historical period19,24,25, where several climate drivers are perturbed at the same time; similarly, PDRMIP results can be used to explain results from the new generation CMIP6 model simulations26, which will serve as input to the upcoming 6th Assessment Report of IPCC.
Results presented here involve GCM simulations of perturbations in CFC-11 (named “CFC11×8”), CFC-12 (“CFC12×9”), and N2O concentrations (named “N2O×3”) (where the multiplier indicates the approximate size of the imposed perturbation—see “Methods” for exact factors and how the experiments are constructed) and complement the core PDRMIP experiments CO2×2, CH4×3, solar irradiance + 2% (Sol + 2%), black carbon×10 (BC×10) and sulphate×5 (Sul×5).
Results
Changes in temperature, humidity and clouds
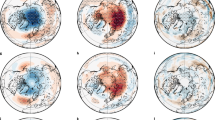
Figure 1 shows vertical profiles of temperature, humidity and cloud changes for the three experiments (CFC11×8, CFC12×9 and N2O×3) and compared to some of the most relevant core experiments (CO2×2, CH4×3, Sol + 2%) (see Supplementary Fig. 1 for results for individual models). On a short timescale, the very different profiles of temperature change between the CFCs and the other climate drivers is evident (Fig. 1a). For CFC11×8 and CFC12×9, there is only a weak temperature increase in the lower and middle troposphere while there is strong warming in the upper troposphere and lower stratosphere (UTLS) region. A strong warming in the UTLS due to halocarbons was also found by Forster and Joshi12, using a fixed dynamical heating model, and occurs partly because halocarbons tend to absorb weakly in a spectral region where there is little overlap with other gases. The temperature increase for CFCs in the lower stratosphere is in strong contrast to the well-known cooling due to increased CO2; this results from the increased emission exceeding increased absorption of upwelling radiation from the troposphere, as the saturation of the CO2 bands means most of the upwelling radiation originates from the cold upper troposphere. Zonal mean temperature plots indicate, however, a lower stratospheric cooling over Antarctica also for CFC12×9 (Supplementary Fig. 2), and this is evident in 7 out of 8 models (not shown). The balance between increased absorption of upwelling radiation from the troposphere and increased emission from the stratosphere will be quite different over Antarctica, and hence the height of transition from warming to cooling can be expected to be at lower CFC concentrations. For N2O×3, the temperature change profile is similar to CH4×3 except for a cooling at low pressures. However, the inter-model differences are large for N2O×3 (even disagreeing in the sign in the UTLS region), while the CFC temperature change profiles show much less model diversity (Supplementary Fig. 1a).
a–c Fast and d–f slow changes in a, d temperature (K), b, e specific humidity (kg kg−1) and c, f clouds (%) for individual drivers in CFC11×8, CFC12×9, N2O×3, CO2×2, CH4×3, Sol + 2% (see “Methods” for exact definition of experiments). The fast response in a–c is divided by the IRF (W m−2) and the slow response in d–f is divided by the near-surface temperature change (K) induced by each driver.
The changes to the vertical profile of specific humidity after the rapid adjustments is different for the CFCs than for the other climate drivers (Fig. 1b), mainly due to the weaker temperature increase in the lower troposphere which leads to a smaller increase in saturation vapour pressure compared to e.g., CO2×2. The local minimum in the change in specific humidity at around 800 hPa is intriguing and appears in 7 out of 8 models for CFC12×9 (Supplementary Fig. 1b). Further investigation indicates that this is at least partly due to increased descent in the sub-tropics (Supplementary Fig. 2). While this is also the case for CO2×2, increased specific humidity at high northern latitudes, which is related to strong temperature increase there, more than compensates the decrease in specific humidity in the sub-tropics, and the local minimum is therefore not evident in the global mean specific humidity change profile for CO2×2.
The fast response for clouds shows some important differences between CFCs and the other climate drivers (Fig. 1c). While the decrease in clouds around 800 hPa is evident for all drivers shown, CFC11×8 and CFC12×9 show a relatively strong decrease in high clouds (pressures less than ≈400 hPa) that is evident in all models (Supplementary Fig. 1c), likely due to the temperature increase at this height, as opposed to the temperature decrease and cloud cover increase for CO2×2. The N2O×3 profile is similar to CH4×3 for both specific humidity and cloud changes (Fig. 1b, c).
The slow response in temperature, specific humidity and clouds has been normalized by the near-surface temperature change induced by each climate driver, to account for the effect of the different sizes of the IRF for the various perturbations (Fig. 1d–f). Differences between the drivers are relatively small, and the differences that exist, such as the weaker temperature increase in the upper troposphere for CFC11x8 and N2Ox3 compared to CFC12x9, partly reflects that not all models have performed all experiments (Supplementary Fig. 1d–f).
Rapid adjustments at the top-of-atmosphere
By applying radiative kernels, the ERF, as diagnosed by radiative fluxes in the GCMs’ fixed SST experiments, can be split into IRF and different rapid adjustment terms (see “Methods” section). The actual IRF from each GCM is normally not available and is calculated here based on the kernel method. The IRF has, however, been calculated in the HadGEM2 model by applying a double radiation call, and the IRF estimates at the top-of-atmosphere (TOA) based on the kernel method show good agreement (within 5% difference) with the double call calculation (Supplementary Table 1). When isolating shortwave radiation rapid adjustments from the net radiation (SW + longwave (LW)), the kernel method can be evaluated because the shortwave contribution to IRF is zero or very small for the CFCs and N2O. This occurs because SW absorption for these species is not included in the radiation schemes of the models, or, in the case of N2O, its weak SW absorption is only included in some of the models. Hence, the sum of the rapid adjustment terms should ideally equal the ERF in the shortwave, and for most models there is relatively good agreement with <0.2 W m−2 difference (Supplementary Figs. 3 and 4) (see also Smith et al.16 and Myhre et al.15 for evaluation of the kernels).
Figure 2 shows the decomposition of ERF (at TOA) and atmospheric radiative cooling (see Supplementary Figs. 3 and 4 for results for individual models and kernel methods). The surface temperature rapid adjustment term (Ts) is non-zero because the fixed SST simulations include a small land surface warming. The IRF derived using the kernel method is in excellent agreement with detailed line-by-line (LBL) radiative transfer model calculations for CFC-12 but is ~25% too high for CFC-11 and ~10% too high for N2O, possibly because of differences in the underlying spectroscopic data, or the way gaseous overlap is handled in GCM radiation codes. At TOA, the individual rapid adjustment terms for CFC11×8 and CFC12×9 show some similarity to CH4×3 (see Fig. 3 in ref. 16), e.g. with a relatively strong negative tropospheric temperature adjustment that is nearly offset by the positive water vapour adjustment (Fig. 2a). The CFCs show some differences to CH4×3, however, with a negative stratospheric temperature adjustment term and more positive cloud term for the CFCs. Note that the stratospheric temperature adjustment term for the CFCs would be positive rather than negative if evaluated at the tropopause, which is common for RF17 (ERF is evaluated at TOA). The stratospheric temperature adjustment for CFC12×9 using the kernel method is a 4.2% decrease of the IRF, somewhat smaller than the 5.5% decrease obtained by using LBL calculations.
a Instantaneous radiative forcing (IRF), individual rapid adjustments, sum of rapid adjustments (RA) (derived using radiative kernels) and effective radiative forcing (ERF) at TOA and b contribution to atmospheric radiative cooling (dQ) from instantaneous perturbation (Inst.) and rapid adjustments (derived using radiative kernels). Line-by-line calculations are included as white dots. Note that atmospheric radiative cooling is associated with increased fast precipitation according to Eq. (1). The different rapid adjustment terms are surface temperature (Ts), tropospheric temperature (Ttrop), stratospheric temperature (Tstrat), water vapour (WV), albedo (α) and clouds. Bars show multi-model and multi-kernel global and annual means while error bars show uncertainties represented by the standard deviation, weighting each model and kernel method equally. The perturbation factors in CFC11×8, CFC12×9, N2O×3 are approximate; see “Methods” section for exact definition of experiments. Tabulated values are in Supplementary Tables 2–3.
Results for CFC11×8 and CFC12×9 differ slightly (Fig. 2a), partly reflecting that a different set of models has done each experiment, but also because one of the models (NCAR-CESM1-CAM4) shows a different sign of the total rapid adjustment between the two experiments (Supplementary Fig. 3c, f). Further inspection indicates that the different sign is due to differences in the vertical profile of temperature and cloud changes between CFC11×8 and CFC12×9 (Supplementary Fig. 5). Nevertheless, as for CH4×3, the individual rapid adjustment terms approximately cancel, and the total rapid adjustment is not robustly different from zero for either of the CFC perturbations. For N2O×3 at TOA, the rapid adjustment terms are similar to the CFCs except for the stratospheric temperature adjustment which has a different sign (Fig. 2a) because most models show cooler temperatures in the stratosphere in N2O×3 (Supplementary Fig. 1a). This leads to the ERF becoming slightly higher than IRF for N2O×3, but the total rapid adjustments are still not robustly different from zero. However, for all three perturbations, some individual model/kernel combinations (e.g. ECHAM-HAM with the Oslo kernel for CFC11×8) show total rapid adjustments that have sizeable values, in either positive or negative direction (Supplementary Fig. 3c, f). The inter-model and inter-kernel spread are mainly dominated by differences in the cloud adjustment term and this should be investigated further in future studies. We emphasize that radiative changes due to the chemical effect of these gases on ozone are not investigated here and would lead to additional fast feedbacks.
Interestingly, the cloud rapid adjustment term for all of CFC11×8, CFC12×9 and N2O×3 is positive (Fig. 2a) while their profiles of cloud changes are somewhat similar to Sol + 2% (Fig. 1c), which has a negative cloud rapid adjustment term16. This is at least partly due to the stronger decrease in low clouds (around 800–900 hPa) for the CFCs and N2O×3 compared to Sol + 2%, because low clouds generally have a net cooling effect due to increased albedo.
Atmospheric rapid adjustments and implications for precipitation
Precipitation changes (dP) are constrained by the atmospheric energy budget
where L is the latent heat of vaporization, dQ is net atmospheric radiative cooling and dSH is the change in surface sensible heat fluxes24. Figure 2b shows atmospheric cooling calculated as differences in radiative fluxes at TOA and surface, and thus positive values represent precipitation increase and negative values represent precipitation decrease. The instantaneous perturbation flux changes (which are analogous to IRF at TOA but instead for the atmosphere) estimated using the kernel method are in good agreement with LBL calculations, and the effect of stratospheric temperature adjustment is only slightly underestimated (−11% vs. −12% of the instantaneous perturbation for the kernel method and LBL, respectively).
In contrast to TOA, the sum of rapid adjustments for the atmosphere is significant and robustly different from zero for all of CFC11×8, CFC12×9 and N2O×3 (Fig. 2b). While the negative instantaneous perturbation values contribute to decreased precipitation, this is partly counteracted by the positive rapid adjustment terms so that dQ is around 60% of the instantaneous perturbation for CFC11×8 and CFC12×9. This is in stark contrast to the CO2×2 experiment, where the total rapid adjustments have the same sign and approximately the same magnitude as the instantaneous perturbation (see Fig. 2 in ref. 15). The two main reasons for these differences are that the stratospheric temperature adjustment is weakly positive for the CFCs (it is strongly negative for CO2×2), and that the cloud adjustment is strongly positive for the CFCs (it is weakly negative for CO2×2). Both factors can be linked to the vertical profiles of temperature and cloud changes where differences between CFCs and CO2×2 are large in the upper troposphere and lower stratosphere (Fig. 1a, c). Different temperature responses in the middle and lower troposphere are also likely to contribute; as evident by the structure of radiative kernels (e.g. Fig. 5 in ref. 27), atmospheric cooling is particularly sensitive to temperature change in the boundary layer. Interestingly, the rapid adjustment terms, and particularly the strong cloud adjustment, for CFCs are similar to the adjustment terms for the strongly absorbing black carbon aerosol (Fig. 2b vs. BC×10 in Fig. 1 of ref. 15). However, it should be noted that the radiative cooling, and likely the individual rapid adjustment terms, depend on the altitude profile of the added BC28. For N2O×3, the opposite sign of the stratospheric temperature adjustment compared to the CFCs causes dQ to be only 20% smaller than the instantaneous perturbation, and again this is similar to CH4×3. The sensible heat term (dSH) is small compared to dQ for both CFC11×8 and CFC12×9, but has a non-negligible contribution to the precipitation change for N2O×3 (Supplementary Table 3).
Figure 3 gives a visual summary of the results of Fig. 2 and compares them to other important climate drivers (presented in refs 15,16). It combines information on how rapid adjustments influence surface temperature change (through ERF) and precipitation change (through atmospheric radiative cooling). All three experiments, CFC11×8, CFC12×9 and N2O×3, show a small and uncertain positive total rapid adjustment at TOA, but a strongly positive total rapid adjustment on the atmospheric radiative cooling. The total rapid adjustments for the CFCs and N2O are quite similar to CH4, being small at TOA and showing enhanced atmospheric radiative cooling. While enhanced atmospheric radiative cooling is also found for BC and solar changes, the effect of CO2 is quite dissimilar due to reduced atmospheric radiative cooling.
All values are normalized to the IRF at TOA for each driver and are therefore unitless. Markers show multi-model and multi-kernel global and annual means while error bars show uncertainties represented by the standard deviation across the different models. Numbers for the core experiments are from Myhre et al.15 (their Tables S1 and S2). The perturbation factors in CFC11×8, CFC12×9, N2O×3 are approximate; see “Methods” section for exact definition of experiments.
Hydrological cycle
The hydrological sensitivity (HS) is the relative change in precipitation per degree kelvin surface temperature change due to forcing by a climate driver. Figure 4 shows the global- and annual mean precipitation change and hydrological sensitivity for individual drivers. The precipitation change associated strictly with surface temperature change (i.e. the slow change) differs more between models than between drivers, but the model diversity is much smaller when normalizing by the surface temperature change to obtain the slow HS (Fig. 4a, b). For the CFC12×9 experiment the relative standard deviation, representing the spread between models, is 36% and 12% for slow precipitation change and slow HS, respectively (Supplementary Table 4). When averaged across the models, the slow HS is similar between climate drivers and in the range 2.5–2.8% K−1 (Fig. 4c; grey bars). These results therefore confirm that an earlier finding, that the slow HS is independent of climate drivers18,19, applies also when including CFC-11, CFC-12 and N2O.
Fast (light coloured bars), slow (grey bars) and total (dark coloured bars) changes in global- and annual-mean a precipitation (%) and b–c hydrological sensitivity (% K−1) for CFC11×8, CFC12×9 and N2O×3 for a–b individual models and c as multi-model means compared to other key climate drivers. Error bars show the standard deviation representing inter-model uncertainty. The perturbation factors in CFC11×8, CFC12×9, N2O×3 are approximate; see “Methods” section for exact definition of experiments. Tabulated values are in Supplementary Table 4.
The apparent HS, which is the precipitation change from both fast and slow responses divided by the surface temperature change, derived solely from the coupled atmosphere–ocean GCM simulations, shows much larger differences between drivers (Fig. 4c; coloured bars). CFC11×8 and CFC12×9 have larger apparent HS than any of the other greenhouse gases (CO2×2, CH4×3, N2O×3) and is more similar to Sol + 2%. This is due to the small offset by the negative fast precipitation response for the CFCs (Fig. 4a). This can again be explained by the total rapid adjustment contributing to atmospheric cooling (i.e. larger dQ in Eq. (1)) (Fig. 2b). For N2O×3, the apparent HS is smaller than for the CFCs and similar to CH4×3 (Fig. 4c).
Discussion
Although IPCC AR5 adopted the ERF terminology, the ERF was assumed to be the same (albeit with a larger uncertainty) as RF (which only includes stratospheric temperature adjustment) for, among others, halocarbons and N2O, due to lack of studies investigating rapid adjustments of these compounds1. With the exception of stratospheric temperature adjustment, GCM calculations are needed to quantify individual rapid adjustment terms. Our results, using a range of GCMs combined with radiative kernel calculations, show that rapid adjustments at TOA for CFCs and N2O are substantial, but unlike CO2, their sum is not significantly different from zero due to compensating effects. However, individual models and kernels show significant differences and the causes need to be examined in future work. The stratospheric temperature adjustment term estimated here is relatively small (around 5% of the IRF), confirmed also by LBL calculations for CFC-12, indicating that the assumption made in AR5 that ERF was equal to RF is approximately valid.
In the case of rapid adjustments for halocarbons, it is, however, difficult to generalize because this group of compounds consists of a range of different gases with a wide variety of lifetimes (and thereby atmospheric distributions) and spectral absorption features6, which can, for example, lead to quite different stratospheric temperature adjustment17. Limitations related to the GCMs’ radiation schemes29,30 and the small number of halocarbon gases normally included in the GCMs, make it challenging to quantify rapid adjustments for a range of individual halocarbon gases; also the perturbations necessary to generate significant signals in GCMs are much larger than expected changes, and so this requires assumptions about the linearity of the rapid responses to the size of perturbation. However, the two CFC compounds investigated here are currently amongst the most abundant halocarbons in the atmosphere31, and we find good agreement between forcings calculated using radiative kernels and using an LBL code. Future studies should investigate rapid adjustment for CFC replacement compounds, such as hydrochlorofluorocarbons (HCFCs) and hydrofluorocarbons (HFCs), for which atmospheric concentrations are still rising. Specifically, HCFC-22 and HFC-134a have recently become the 2nd and 4th most abundant greenhouse gases, respectively, among those with only anthropogenic sources31. Better knowledge of the ERF of these compounds could potentially lead to improved estimates of policy-relevant metrics, such as global warming potentials (GWPs), which are currently based on RF and not ERF32.
We find that the apparent (fast + slow) hydrological sensitivity is larger for the CFCs compared to other well-mixed greenhouse gases. The slow hydrological sensitivity is approximately the same across drivers, and fast atmospheric processes explain the differences. The atmospheric energy budget shows that total rapid adjustments lead to atmospheric cooling, largely due to cloud changes and strong upper tropospheric heating. These rapid adjustments counteract the fast precipitation decrease from the instantaneous perturbation, somewhat similarly to what has been shown for black carbon15. For N2O, the total rapid adjustment term relative to the instantaneous perturbation is smaller, and the apparent HS is more similar to what is found for other well-mixed greenhouse gases.
Methods
Climate models and experiments
We use global climate model results from PDRMIP22, and specifically from the eight models that have performed one or more of the CFC-11, CFC-12, and N2O phase 2 experiments: MIROC-SPRINTARS (all), HadGEM2 (all), HadGEM3 (CFC-12), NorESM1 (CFC-12, N2O), NCAR-CESM1-CAM5 (CFC-12), ECHAM-HAM (all), GISS-E2-R (CFC-12) and NCAR-CESM1-CAM4 (all). The models have been described in earlier publications11,22.
The perturbation simulations have been compared to a BASE simulation representative of year 2000 conditions (year 1850 for HadGEM2). In the CFC-11 and CFC-12 experiments, the volume mixing ratio of CFC-11 and CFC-12 has been separately increased from a BASE mixing ratio of 653.45 and 535 ppt, respectively, to 5 ppb, and these experiments are named CFC11×8 (rounded from 7.652) and CFC12×9 (rounded from 9.346). The CFC-11 mixing ratio in BASE is higher than observed because it accounts also for halocarbon gases other than CFC-11 and CFC-12. The vertical distribution of CFCs is unchanged from what is default in each model, where some are constant and some assume a generic vertical profile. In addition, the perturbations on CFC-11 and CFC-12 are far higher than total expected perturbations of halocarbons. The choice of amplitude of the different experiments is a trade-off between ensuring a significant signal from relatively short GCM runs, of which we consider an IRF of at least 1 W m−2 is needed, and at the same time reducing potential non-linearities by choosing concentrations that do not deviate too much from realistic abundances. Although the IRF for each experiment differ, we have in most cases normalized the results by the IRF for the fast response and the surface temperature change for the slow response; this makes the results more comparable across different experiments. Indirect effects of CFCs through stratospheric ozone depletion are not included in these simulations. HadGEM2 uses a pre-industrial BASE experiment with zero abundance of CFC-11 and CFC-12, and in the perturbation simulations the mixing ratios have been increased to 4346 and 4465 ppt, respectively, in order to approximate the same RF perturbation as in the other models by using the formulas in Myhre et al.33.
In the N2O experiment, the mixing ratio is increased from a BASE value of 316 ppb to 1 ppm in the perturbation experiment, named N2O×3 (rounded from 3.165). Again, the perturbation is larger than expected, in order to ensure a significant signal. Indirect effects of N2O through stratospheric ozone depletion are not included in these simulations. In HadGEM2, mixing ratios of 276.4 and 915 ppb were used in BASE and the N2O experiment, respectively.
Two types of simulations have been performed; one with fixed monthly sea-surface temperatures (SST) for at least 15 years, and one with coupled atmosphere–ocean for at least 100 years. Two models, ECHAM-HAM and NCAR-CESM1-CAM4, used slab ocean instead of full ocean in the coupled simulations. As in previous PDRMIP studies, we analyse years 6–15 in the fixed SST simulations and the last 50 years of the coupled atmosphere–ocean simulations. Fast changes denote the results from the fixed SST simulations while slow changes are diagnosed by subtracting the fast changes from the total changes, and the total changes are the results from the coupled simulations.
Radiative kernels
The radiative kernel technique34 has been used to calculate individual rapid adjustments, and their contribution to ERF and atmospheric radiative cooling; the technique is also used to diagnose the IRF in models without a double radiation call (see Eq. (1) in Smith et al.16). The kernels describe how the TOA and surface radiative fluxes respond to a small perturbation in surface temperature, atmospheric temperature, water vapour, surface albedo and clouds. A further separation of the rapid adjustment due to atmospheric temperature into contributions from tropospheric and stratospheric temperature has been done assuming a tropopause defined at 100 hPa at the equator and linearly increasing with latitude to 300 hPa at the poles34. We use seven sets of radiative kernels to quantify rapid adjustments at TOA and six for the atmosphere. The radiative kernels have been derived from the Oslo radiative transfer model15, and the radiative transfer models and base states of various GCMs, including HadGEM216, GFDL34, CESM35, ECHAM636, BMRC34 and CCSM4 (TOA only)37. Like Smith et al.16, we find these six GCM radiative kernels closely agree, and present the results as averages and standard deviations across these radiative kernels (Supplementary Figs. 3 and 4). For the Oslo kernel, water vapour and cloud adjustments were computed using a variant of the partial radiative perturbation method38. Cloud adjustments for the remaining kernels were estimated using the difference between all-sky and clear-sky kernel decompositions15,16.
Line-by-line calculations
Offline radiative transfer calculations have been carried out using the Oslo line-by-line model using the same version and same atmospheres as in Shine and Myhre17. The vertical profiles are given in Myhre et al.39 and the tropopause height is defined at levels 11 and 15 for tropical and extra-tropical profiles, respectively.
Data availability
The PDRMIP model results are available at http://cicero.uio.no/en/PDRMIP/.
References
Myhre, G. et al. In Climate change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker, T. F. et al.) Ch. 8, 659–740 (Cambridge University Press, 2013).
Polvani, L. M., Previdi, M., England, M. R., Chiodo, G. & Smith, K. L. Substantial twentieth-century Arctic warming caused by ozone-depleting substances. Nat. Clim. Chang. 10, 130–133 (2020).
Polvani, L. M. & Bellomo, K. The key role of ozone-depleting substances in weakening the walker circulation in the second half of the twentieth century. J. Clim. 32, 1411–1418 (2019).
WMO. Scientific Assessment of Ozone Depletion: 2018. Global Ozone Research and Monitoring Project—Report No. 58, 588 (World Meteorological Organization, Geneva, 2019).
Ramanathan, V. Greenhouse effect due to chlorofluorocarbons—climatic implications. Science 190, 50–51 (1975).
Hodnebrog, Ø. et al. Global warming potentials and radiative efficiencies of halocarbons and related compounds: a comprehensive review. Rev. Geophys. 51, 300–378 (2013).
Etminan, M., Myhre, G., Highwood, E. J. & Shine, K. P. Radiative forcing of carbon dioxide, methane, and nitrous oxide: a significant revision of the methane radiative forcing. Geophys. Res. Lett. 43, 12614–12623 (2016).
Collins, W. D., Feldman, D. R., Kuo, C. & Nguyen, N. H. Large regional shortwave forcing by anthropogenic methane informed by Jovian observations. Sci. Adv. 4, 9 (2018).
Hansen, J., Sato, M. & Ruedy, R. Radiative forcing and climate response. J. Geophys. Res.—Atmos. 102, 6831–6864 (1997).
Hansen, J. et al. Efficacy of climate forcings. J. Geophys. Res.-Atmos. 110, D18104 (2005).
Richardson, T. B. et al. Efficacy of climate forcings in PDRMIP models. J. Geophys. Res.—Atmos. 124, 12824–12844 (2019).
Forster, P. M. & Joshi, M. The role of halocarbons in the climate change of the troposphere and stratosphere. Clim. Change 71, 249–266 (2005).
Boucher, O. et al. in Climate Change 2013: the physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker, T.F. et al.) Ch. 7, 571–658 (Cambridge University Press, 2013).
Sherwood, S. C. et al. Adjustments in the forcing-feedback framework for understanding climate change. Bull. Am. Meteorol. Soc. 96, 217–228 (2015).
Myhre, G. et al. Quantifying the importance of rapid adjustments for global precipitation changes. Geophys. Res. Lett. 45, 11399–11405 (2018).
Smith, C. J. et al. Understanding rapid adjustments to diverse forcing agents. Geophys. Res. Lett. 45, 12023–12031 (2018).
Shine, K. P. & Myhre, G. The spectral nature of stratospheric temperature adjustment and its application to halocarbon radiative forcing. J. Adv. Model. Earth Syst. 12, 16 (2020).
Samset, B. H. et al. Weak hydrological sensitivity to temperature change over land, independent of climate forcing. npj Clim. Atmos. Sci. 1, 3 (2018).
Richardson, T. B. et al. Drivers of precipitation change: an energetic understanding. J. Clim. 31, 9641–9657 (2018).
Wu, Y. T., Polvani, L. M. & Seager, R. The importance of the Montreal protocol in protecting Earth’s hydroclimate. J. Clim. 26, 4049–4068 (2013).
Skeie, R. B. et al. Historical total ozone radiative forcing derived from CMIP6 simulations. Npj Clim. Atmos. Sci. 3, 10 (2020).
Myhre, G. et al. PDRMIP a precipitation driver and response model intercomparison project-protocol and preliminary results. Bull. Am. Meteorol. Soc. 98, 1185–1198 (2017).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498 (2011).
Myhre, G. et al. Sensible heat has significantly affected the global hydrological cycle over the historical period. Nat. Commun. 9, 1922 (2018).
Hodnebrog, Ø. et al. Water vapour adjustments and responses differ between climate drivers. Atmos. Chem. Phys. 19, 12887–12899 (2019).
Eyring, V. et al. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016).
Kramer, R. J., Matus, A. V., Soden, B. J. & L’Ecuyer, T. S. Observation-based radiative kernels from CloudSat/CALIPSO. J. Geophys. Res.—Atmos. 124, 5431–5444 (2019).
Ming, Y., Ramaswamy, V. & Persad, G. Two opposing effects of absorbing aerosols on global-mean precipitation. Geophys. Res. Lett. 37, L13701 (2010).
Collins, W. D. et al. Radiative forcing by well-mixed greenhouse gases: estimates from climate models in the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4). J. Geophys. Res.—Atmos. 111, D14317 (2006).
Soden, B. J., Collins, W. D. & Feldman, D. R. Reducing uncertainties in climate models implementing accurate calculations of radiative forcing can improve climate projections. Science 361, 326–327 (2018).
WMO/GAW. WMO Greenhouse Gas Bulletin. Number 15, 25 November 2019. https://library.wmo.int/doc_num.php?explnum_id=10100 (2019).
Hodnebrog, Ø. et al. Updated global warming potentials and radiative efficiencies of halocarbons and other weak atmospheric absorbers. Rev. Geophys. 58, e2019RG000691 (2020).
Myhre, G., Highwood, E. J., Shine, K. P. & Stordal, F. New estimates of radiative forcing due to well mixed greenhouse gases. Geophys. Res. Lett. 25, 2715–2718 (1998).
Soden, B. J. et al. Quantifying climate feedbacks using radiative kernels. J. Clim. 21, 3504–3520 (2008).
Pendergrass, A. G., Conley, A. & Vitt, F. M. Surface and top-of-atmosphere radiative feedback kernels for CESM-CAM5. Earth Syst. Sci. Data 10, 317–324 (2018).
Block, K. & Mauritsen, T. Forcing and feedback in the MPI-ESM-LR coupled model under abruptly quadrupled CO2. J. Adv. Model. Earth Syst. 5, 676–691 (2013).
Shell, K. M., Kiehl, J. T. & Shields, C. A. Using the radiative kernel technique to calculate climate feedbacks in NCAR’s Community Atmospheric Model. J. Clim. 21, 2269–2282 (2008).
Colman, R. A. & McAvaney, B. J. A study of general circulation model climate feedbacks determined from perturbed sea surface temperature experiments. J. Geophys. Res.—Atmos. 102, 19383–19402 (1997).
Myhre, G., Stordal, F., Gausemel, I., Nielsen, C. J. & Mahieu, E. Line-by-line calculations of thermal infrared radiation representative for global condition: CFC-12 as an example. J. Quant. Spectrosc. Radiat. Transf. 97, 317–331 (2006).
Acknowledgements
Ø.H., G.M., T.A. and C.J.S. were funded by the European Union’s Horizon 2020 Research and Innovation Programme under Grant Agreement 820829 (CONSTRAIN). Ø.H., G.M. and B.H.S. were also funded through the Norwegian Research Council project NAPEX (grant no. 229778) and acknowledge resources from Notur/NorStore (NN9188K/NS9042K). R.J.K. acknowledges support from an appointment to the NASA Postdoctoral Programme administered by Universities Space Research Association. T.A. was also supported by the Met Office Hadley Centre Climate Programme funded by Department for Business, Energy and Industrial Strategy (BEIS) and Department for Environment, Food and Rural Affairs (Defra). A.K. and D.O. were supported by the Research Council of Norway (grant nos. 229771, 285003 and 285013) and by Notur/NorStore (NN2345K and NS2345K). C.J.S. was also supported by a NERC/IIASA Collaborative Research Fellowship (NE/T009381/1). T.T. was supported by the Environment Research and Technology Development Fund (JPMEERF20202F01) and the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Number JP19H05669. We thank Lorenzo M. Polvani and two anonymous reviewers for many helpful suggestions.
Author information
Authors and Affiliations
Contributions
Ø.H. led the work with the analysis and wrote the paper, with particular input from G.M. and K.P.S. G.M. had the original idea. R.J.K. and G.M. did radiative kernel calculations. G.F., D.S., T.A., C.J.S., M.K., A.V., J.M., B.H.S., Ø.H., A.K., D.O., J.-F.L. and T.T. did GCM simulations. G.M. did LBL calculations. All authors gave input in the writing process.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hodnebrog, Ø., Myhre, G., Kramer, R.J. et al. The effect of rapid adjustments to halocarbons and N2O on radiative forcing. npj Clim Atmos Sci 3, 43 (2020). https://doi.org/10.1038/s41612-020-00150-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-020-00150-x