Abstract
Global mean precipitation is expected to increase with increasing temperatures, a process which is fairly well understood. In contrast, local precipitation changes, which are key for society and ecosystems, demonstrate a large spread in predictions by climate models, can be of both signs and have much larger magnitude than the global mean change. Previously, two top-down approaches to constrain precipitation changes were proposed, using either the atmospheric water or energy budget. Here, using an ensemble of 27 climate models, we study the relative importance of these two budgetary constraints and present analysis of the spatial scales at which they hold. We show that specific geographical locations are more constrained by either one of the budgets and that the combination of water and energy budgets provides a significantly stronger constraint on the spatial scale of precipitation changes under anthropogenic climate change (on average about 3000 km, above which changes in precipitation approach the global mean change). These results could also provide an objective way to define the scale of ‘regional’ climate change.
Similar content being viewed by others
Introduction
Improving our understanding of the response of the hydrological cycle to climate change is key to effective adaptation strategies—and remains a major scientific challenge. As the global mean temperature increases with changing climate, the global mean precipitation rate is predicted to increase by about 1–3% K−1. This rate of increase in precipitation is slower than the rate of increase in humidity in the atmosphere due to thermodynamic considerations (which is predicted to be ~7% K−1 from the Clausius–Clapeyron relation). The slower rate of precipitation increase compared to the humidity increase is due to energetic constraints1,2,3,4, i.e. the ability of the atmosphere to radiatively cool, and must impose a decrease in convective mass fluxes1. Compared to the global mean response, regional changes in precipitation remain poorly understood5. At what scale do precipitation changes transition from global (or large-scale) to regional precipitation changes values? We note that previously ‘regional’ and ‘global’ has generally not been objectively defined in this context.
Any global or local precipitation change is constrained by both the atmospheric energy budget4,6,7 and the atmospheric water budget8,9. The atmospheric energy budget forces any global mean precipitation increase (which increases the latent heat release) to be balanced by an increase in the radiative cooling of the atmosphere and/or by a decrease in the surface sensible heat flux. Locally, the increased latent heating could be compensated by changes in the divergence of dry static energy6,10,11, which was shown to exhibit contrasting behaviour for tropical and extra-tropical perturbations12. A similar argument could be presented for the atmospheric water budget, i.e. globally, any increase in precipitation must be accompanied by a similar increase in evaporation. Again, local precipitation changes could be compensated by changes in the divergence of water vapour8. Changes in the divergence of water vapour could be induced by either changes in atmospheric circulation, driving changes in air mass divergence (referred to as the dynamical contribution), or by changes in the water vapour capacity, driving changes in the divergence of water vapour, even for a given air mass divergence (referred to as the thermodynamically contribution13). The latter is expected to follow the Clausius–Clapeyron relation.
On long time-scales (for which atmospheric storage terms can be neglected), the vertically integrated energy and water budgets are given, respectively, by:
where P is the precipitation, E is the evaporation and div(s) and div(qv) are the divergence of dry static energy (s) and water vapour (qv), respectively (all in units of W m−2). Q is the sum of the surface sensible heat flux (QSH) and the atmospheric radiative heating (QR) due to radiative shortwave (SW) and longwave (LW) fluxes (F). QR can be expressed as the difference between the top of the atmosphere (TOA) and the surface (SFC) fluxes as follows:
where LW fluxes are positive upward and SW fluxes are positive downward.
Recent research has demonstrated that under our current climate conditions the atmospheric water and energy budgets are locally closed on scales of the order of 4000–5000 km8,14. That means that, based on observations in the tropics, once averaged over ~5000 km P ≅ Q and the atmosphere is close to radiative-convective equilibrium14. In addition, based both on climate model and reanalysis data-sets it was shown that a similar averaging scale (~4000 km) is required to close the water budget (i.e. P ≅ E)8. Beyond these scales, the divergence terms become inefficient in compensating the energy/water imbalance.
Shifting our perspective from the current climate to a changing climate, Eqs. (1) and (2) become:
where δ represents the difference between a future climate and the current climate. Previous work demonstrated that the correlation between δ\({\it{P}}\) and δE8 and between δ\({\it{P}}\) and δQ6 increase with the spatial scale of averaging and becomes larger than 0.5 for a scale of a few 1000 km. This again demonstrates that the ability of divergence to compensate for changes in precipitation decrease with the spatial scale. Once the divergence terms become inefficient, the precipitation changes approach the global mean change, which is known to be relatively small (compared to local precipitation changes—1–3% K−1)1,2,3. However, precipitation changes on regional scales, for which the divergence terms remain efficient, could be much larger than the global mean. Hence, identifying the ‘break-down’ scale between these two regimes can help in understanding and predicting future changes in precipitation. A priori, the decrease of efficiency of divergence with averaging scale does not have to be similar for the water and energy budgets. In addition, at different geographical locations the relative magnitude of the two divergence terms could change. Thus, it is possible that the characteristic spatial scale of changes in precipitation under global warming is constrained by a combination of the atmospheric energy and water budgets with a changing relative importance between them. We note that the relative role of the different budgets has not been quantified before. The aim of this study is to examine the differences and commonalities between the water8 and energy6 budgets control on precipitation and their role in determining the spatial scale of changes in precipitation under climate change. We demonstrate that combining the water and energy budget constraints results in improved predictions of the scale of precipitation changes.
Results
Energy and water budgets control on precipitation
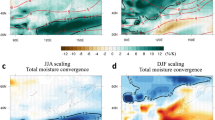
Figure 1 presents the multi-model mean divergence terms of both the water and the energy budgets, averaged over different spatial scales. In the tropics the two divergence terms are strongly anti-correlated and show the same spatial structure (please note that div(qv) is presented with a minus sign to be consistent with Eqs. (1) and (2). The multi-model mean spatial correlation between −div(qv) and div(s) in the tropics (−30° to 30°) is 0.94 (see Supplementary Fig. S1, for the zonal mean behaviour of all models). The high correlation in the tropics demonstrates that any convergence of water vapour that generate precipitation will be accompanied by production and divergence of dry static energy. The opposite is true in the sub-tropics where there is a net divergence of water vapour and a net convergence of dry static energy. Moving poleward, div(s) becomes negative and large (in absolute magnitude), while −div(qv) becomes positive and small. At high latitudes, there is a net convergence of both water vapour and dry static energy as both are being advected from lower latitudes by eddies. However, as the amount of water vapour decreases with the decrease in temperatures towards the poles, the convergence of water vapour decreases from the mid-latitudes storm tracks to the poles. In contrast, the dry static energy convergence increases pole-wards. The zonal mean divergence terms of water vapour and dry static energy reflect the meridional advection of moist static energy15. We note that at the native resolution (upper row) the divergent terms appear small at many locations especially over land; however, they are not negligible compared to the local precipitation (see Supplementary Fig. S2 presenting the normalised divergent terms).
Multi-model mean divergence of water vapour (−div(qv), left column a–e—presented with a minus sign to be consistent with Eq. (1), calculated as the precipitation minus evaporation) and of dry static energy (div(s), right column f–j—calculated as the precipitation plus the atmospheric radiative terms plus the surface sensible heat flux), at different spatial scales. The top row (a, f) shows the native model resolution, subsequent rows are averaged over a circle centred at each grid point with the given radius indicated in the title.
Averaging the water vapour and dry static energy divergence terms over increasingly larger scales (Fig. 1), we note that the spatial pattern becomes weaker and almost completely vanish at 3000 km. This weakening of the spatial pattern occurs on smaller scales for the water budget (c.f. Dagan et al.8) than for the energy budget.
Following Dagan et al.8 in Fig. 2a, b we present the length scales L for which the water budget and the energy budget are locally closed to within 10%, respectively (LWB(10%), LEB(10%)), i.e.:
for the water budget and
for the energy budget.
The CMIP5 multi-model mean: a scale [km] for which the water budget is closed to within 10% i.e., |(P − E)|/P < 0.1— LWB (10%). b scale [km] for which the energy budget is closed to within 10% i.e., |(P + Q)|/P < 0.1—LEB (10%). c regions in which each scale is larger than the other (in blue regions in which LWB (10%) > LEB (10%), while in white regions in which LWB (10%) < LEB (10%)). d combined scale of closure composed of the smaller scale between LWB (10%) and LEB (10%).
LWB and LEB exhibit similar spatial features such as evident at the eastern parts of the subtropical oceans and a sharp transition around ±40°8. These patterns emerge due to the fact that at a centre of a region of negative/positive −div(qv) or div(s) (such as the eastern parts of the subtropical oceans) the required averaging scale for closure of the relevant budget is larger. In addition, at high latitudes beyond 40°, the averaging scale required to close both the water budget and the energy budgets is large due to the large role of advection of water and energy from lower latitudes.
On average LEB > LWB due to the larger variance in E compared to Q, which more effectively counteract the large variance in P (see Supplementary Fig. S3). However, at different regions the ratio between LEB and LWB changes (Fig. 2c). For example, at high latitudes LEB > LWB everywhere, while at mid-latitudes (around ±40°) LEB is generally smaller than LWB over the oceans but less so over land (for which almost at all latitudes LEB > LWB). Over the tropical oceans we note a difference between the Atlantic and the eastern part of the Pacific, for which LEB < LWB, and the west Pacific and the Indian ocean for which LEB > LWB. For the latter, the existence of the warm pool and associated cloud cover releases a significant amount of latent heat by precipitation, which cannot be compensated locally by the relatively small radiative term.
Although both budgets are contributing to constrain precipitation, we expect that the smaller scale between LEB and LWB (locally) would be the limiting factor and will determine the spatial scales of changes in precipitation in future climate. Hence, we combine LEB and LWB to a single scale (LEB+WB), which is: LEB+WB = min(LEB, LWB) (Fig. 2d).
As was shown in Dagan et al.8, the average scale required for closure of the water budget depends on the definition of closure, or to within what percentage P is close to E. The same is true for the energy budget (Fig. 3). A stricter closure requires larger scale of averaging for both the water and the energy budgets. We also note that for both budgets the scale for closure in the tropics is smaller than the global mean scale. This is again due to the large contribution of advection of water vapour and dry static energy from low to high latitudes. In addition, on the global mean LEB > LWB for all the levels of closure. As expected, the combined scale, LEB+WB, has a smaller mean for all the levels of closure (as it is defined as the minimum of LEB and LWB for each location, Fig. 3). We note that the mean values of LEB and LWB presented here based on climate models are consistent with previous estimates based on observations8,14.
The multi-model mean spatial scale for local water budget closure (LWB—for which precipitation roughly equals evaporation), energy budget closure (LEB—for which precipitation roughly equals the sum of the atmospheric radiative heating rate and surface sensible heat flux), the combined water and energy budget scale (LWB+EB) and the scale of changes in precipitation (LδP) as a function of the degree of closure or relative precipitation change. As all quantities are normalised locally by historical P (Eqs. 6–8), the x-axis represents a similar amount of water for all. The global mean and the tropical mean are presented for each scale. The vertical lines represent the standard deviation of the 27 different CMIP5 models.
The average scale of precipitation changes under climate change (LδP) is also presented in Fig. 3. The scale of precipitation changes is calculated as the scale for which the relative precipitation changes (as absolute value) is smaller than a given value, R:
for R in the range of 7.5–15%. We note that the level of imbalance in the different budgets for a given closure threshold is similar (in terms of water amount) to the magnitude of the relative precipitation change R, as all are normalised by the (same) local historical precipitation (Eqs. 6–8).
Figure 3 demonstrates that the combined scale LWB+EB is more similar to (but slightly larger than) LδP than either LEB or LWB separately. This is also demonstrated in Fig. 4 which presents the multi-model mean LδP vs. LEB, LWB and LWB+EB for different levels of closure. Figure 4 demonstrates that LEB is much larger than LδP for all levels of closure. The same is true for LWB but to a lesser extent, and the combined scale (LWB+EB) is the closest to LδP. These results demonstrate that combination of water and energy budgets provides a better constraint on the scale of precipitation changes under climate change (2500–3000 km for a 10% combined budget imbalance or relative precipitation change). Above this scale, precipitation changes approach the global mean change (usually on the order of a few percent), while below it they could be substantially larger.
The multi-model mean spatial scale for local water budget closure (LWB—for which precipitation roughly equals evaporation), energy budget closure (LEB—for which precipitation roughly equals the sum of the atmospheric radiative heating rate and surface sensible heat flux), and the combined water and energy budgets scale (LWB+EB) vs. the scale of changes in precipitation (LδP – y-axis). The size of the dots represents the level of closure or relative precipitation change from 15% (the largest dots) to 7.5% (the smallest dots) in increments of −2.5%. The black dotted line represents the 1:1 line.
Discussion
Global mean precipitation changes due to global warming are predicted to be relatively small1,2,3 (1–3% K−1) compared to the rate of increase in atmospheric water vapour (~7% K−1). Any global mean precipitation change must be consistent with both the atmospheric energy and water budgets, meaning that precipitation must change such that the atmospheric energy and water budgets remains in balance4,7,8,9,16,17. Local precipitation changes could be compensated for by divergence of water vapour or dry static energy10,11 and hence could be much larger than the global mean change. Previous studies have accounted for the changes in the divergence term of the energy budget to understand precipitation changes due to different drivers10,11. However, these divergence terms are expected to become less efficient with increasing scales and must vanish on the global scale. While both the energy and water budget constraints on precipitation are well studied individually8,10,11,16,17, their relative importance for different regions has not been well evaluated. In addition, the spatial scales at which each constraint holds has not been thoroughly quantified. Hence, most previous studies made arbitrary definitions of ‘regional’ vs. ‘large-scale’ precipitation change.
Using 27 CMIP5 models we identify the scale for which the divergence terms become inefficient and above which the changes in precipitation are expected to approach the global mean change to be about 2500–3000 km. This could provide an objective way to define the scale of ‘regional’ climate change. We note that a shift in the precipitation spatial pattern under climate change (such as a shift in the location of the inter-tropical convergence zone or a widening of the Hadley cells) could also be interpreted as a shift in the water and energy divergence terms. For example, in the tropics the scale of closure of the different budgets is roughly determined by the scale of the Hadley cells (averaging the sub-tropical net evaporation/radiative cooling regions with the net precipitation regions of the deep tropics—Fig. 1). Hence, the future predicted widening of the Hadley cell18 is expected to enlarge the budget closure scales. However, we note that the Hadley cell is expected to widen by about 100–200 km18, while the scale of closure of the different budgets is at the order of 4000–5000 km. Hence, we do not expect this widening to significantly affect our results. This can also be seen from Dagan et al.8, which showed that the scale of closure of the water budget is not expected to change significantly in future climate compared to the inter-model spread. In addition, we note that the change in the mean location of the inter-tropical convergence zone due to aerosol forcing is expected to occur on much smaller scales19 than the closure scales presented here.
Here we show that the characteristic scale of precipitation changes under anthropogenic climate change is better constrained by a combination of the water and energy budgets than by each one separately. This demonstrates that combining the water and energy budget perspective will improve our understanding of the drivers behind, and the scale of septation of, local and large-scale precipitation changes.
Methods
CMIP5 data
The analysis is based on data from 27 CMIP5 (phase 5 of the Coupled Model Intercomparison Project20) models (listed in Supplementary Table 1) for the following two protocols: historical and RCP8.5 (Representative Concentration Pathway 8.521—a scenario with relatively fast increase in greenhouse gasses concentrations) simulations. From the historical runs we average the data over the last 20 years of the 20th century, while from the RCP8.5 runs we average the data over the last 20 years of the 21st century. Changes in precipitation (δP) are determined based on the difference between the RCP8.5 and the historical runs. All data are remapped to T63 resolution (about 1.8°). The divergence terms (of either the water or the energy budget) are calculated as the residual of the other terms. We note that, in climate models, the water and energy budget constraints (Eqs. (4) and (5)) hold to the degree the models conserve water/energy22,23,24. However, small ‘leaks’ of water or energy from the models are not expected to significantly affect the results presented here.
Data availability
All CMIP5 model data are available at: https://cmip.llnl.gov/cmip5/data_portal.html.
Code availability
Any codes used in the paper available upon request from: guy.dagan@physics.ox.ac.uk.
References
Held, I. M. & Soden, B. J. Robust responses of the hydrological cycle to global warming. J. Clim. 19, 5686–5699 (2006).
Andrews, T. & Forster, P. M. The transient response of global-mean precipitation to increasing carbon dioxide levels. Environ. Res. Lett. 5, 025212 (2010).
Andrews, T., Forster, P. M., Boucher, O., Bellouin, N. & Jones, A. Precipitation, radiative forcing and global temperature change. Geophys. Res. Lett. 37, 14 (2010).
Allen, M. R. & Ingram, W. J. Constraints on future changes in climate and the hydrologic cycle. Nature 419, 224–232 (2002).
Knutti, R. & Sedláček, J. Robustness and uncertainties in the new CMIP5 climate model projections. Nat. Clim. Change 3, 369 (2013).
Muller, C. & O’Gorman, P. An energetic perspective on the regional response of precipitation to climate change. Nat. Clim. Change 1, 266 (2011).
Myhre, G. et al. PDRMIP: a precipitation driver and response model intercomparison project—protocol and preliminary results. Bull. Am. Meteor. Soc. 98, 1185–1198 (2017).
Dagan, G., Stier, P. & Watson‐Parris, D. Analysis of the atmospheric water budget for elucidating the spatial scale of precipitation changes under climate change. Geophys. Res. Lett. 46, 10504–10511 (2019a).
Thomas, C. M., Dong, B. & Haines, K. Inverse modeling of global and regional energy and water cycle fluxes using earth observation data. J. Clim. 33, 1707–1723 (2020).
Richardson, T. et al. Drivers of precipitation change: an energetic understanding. J. Clim. 31, 9641–9657 (2018).
Liu, L. et al. A PDRMIP Multimodel Study on the impacts of regional aerosol forcings on global and regional precipitation. J. Clim. 31, 4429–4447 (2018).
Dagan, G., Stier, P. & Watson‐Parris, D. Contrasting response of precipitation to aerosol perturbation in the tropics and extra‐tropics explained by energy budget considerations. Geophys. Res. Lett. 46, 7828–7837 (2019b).
Mitchell, J., Wilson, C. & Cunnington, W. On CO2 climate sensitivity and model dependence of results. Q. J. R. Meteorol. Soc. 113, 293–322 (1987).
Jakob, C., Singh, M. & Jungandreas, L. Radiative convective equilibrium and organized convection: an observational perspective. J. Geophys. Res. 124, 5418–5430 (2019).
Armour, K. C., Siler, N., Donohoe, A. & Roe, G. H. Meridional atmospheric heat transport constrained by energetics and mediated by large-scale diffusion. J. Clim. 32, 3655–3680 (2019).
O’Gorman, P. A., Allan, R. P., Byrne, M. P. & Previdi, M. Energetic constraints on precipitation under climate change. Surv. Geophys. 33, 585–608 (2012).
Pendergrass, A. G. & Hartmann, D. L. The atmospheric energy constraint on global-mean precipitation change. J. Clim. 27, 757–768 (2014).
Hu, Y., Tao, L. & Liu, J. Poleward expansion of the Hadley circulation in CMIP5 simulations. Adv. Atmos. Sci. 30, 790–795 (2013).
Acosta Navarro, J. C. et al. Future response of temperature and precipitation to reduced aerosol emissions as compared with increased greenhouse gas concentrations. J. Clim. 30, 939–954 (2017).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An overview of CMIP5 and the experiment design. Bull. Am. Meteor. Soc. 93, 485–498 (2012).
Riahi, K. et al. RCP 8.5—a scenario of comparatively high greenhouse gas emissions. Clim. Change 109, 33 (2011).
Liepert, B. G. & Previdi, M. Inter-model variability and biases of the global water cycle in CMIP3 coupled climate models. Environ. Res. Lett. 7, 014006 (2012).
Hobbs, W., Palmer, M. D. & Monselesan, D. An energy conservation analysis of ocean drift in the CMIP5 global coupled models. J. Clim. 29, 1639–1653 (2016).
Loeb, N. G. et al. Observational constraints on atmospheric and oceanic cross-equatorial heat transports: revisiting the precipitation asymmetry problem in climate models. Clim. Dyn. 46, 3239–3257 (2016).
Acknowledgements
This research was supported by the European Research Council (ERC) project constRaining the EffeCts of Aerosols on Precipitation (RECAP) under the European Union’s Horizon 2020 research and innovation programme with grant agreement No 724602. PS also acknowledges support by the Alexander von Humboldt Foundation. We acknowledge the WCRP’s Working Group on Coupled Modeling, which is responsible for CMIP, and we thank the climate modeling groups (listed in Supplementary Table S1) for producing and making available their model output: https://cmip.llnl.gov/cmip5/data_portal.html.
Author information
Authors and Affiliations
Contributions
G.D. carried out the analyses presented. P.S. assisted with the design and interpretation of the analyses. G.D. prepared the manuscript with contributions from P.S.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dagan, G., Stier, P. Constraint on precipitation response to climate change by combination of atmospheric energy and water budgets. npj Clim Atmos Sci 3, 34 (2020). https://doi.org/10.1038/s41612-020-00137-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-020-00137-8
This article is cited by
-
Multifaceted aerosol effects on precipitation
Nature Geoscience (2024)
-
Sea surface warming patterns drive hydrological sensitivity uncertainties
Nature Climate Change (2023)
-
Boundary conditions representation can determine simulated aerosol effects on convective cloud fields
Communications Earth & Environment (2022)