Abstract
Lightning discharges in the atmosphere owe their existence to the combination of complex dynamic and microphysical processes. Knowledge discovery and data mining methods can be used for seeking characteristics of data and their teleconnections in complex data clusters. We have used machine learning techniques to successfully hindcast nearby and distant lightning hazards by looking at single-site observations of meteorological parameters. We developed a four-parameter model based on four commonly available surface weather variables (air pressure at station level (QFE), air temperature, relative humidity, and wind speed). The produced warnings are validated using the data from lightning location systems. Evaluation results show that the model has statistically considerable predictive skill for lead times up to 30 min. Furthermore, the importance of the input parameters fits with the broad physical understanding of surface processes driving thunderstorms (e.g., the surface temperature and the relative humidity will be important factors for the instability and moisture availability of the thunderstorm environment). The model also improves upon three competitive baselines for generating lightning warnings: (i) a simple but objective baseline forecast, based on the persistence method, (ii) the widely-used method based on a threshold of the vertical electrostatic field magnitude at ground level, and, finally (iii) a scheme based on CAPE threshold. Apart from discussing the prediction skill of the model, data mining techniques are also used to compare the patterns of data distribution, both spatially and temporally among the stations. The results encourage further analysis on how mining techniques could contribute to further our understanding of lightning dependencies on atmospheric parameters.
Similar content being viewed by others
Introduction
Lightning is responsible for human injuries and fatalities, the death of livestock, and house and forest fires.1,2,3 It is also a major source of electromagnetic interference and damage to electronic circuits, buildings, and other exposed man-made structures such as transmission lines, wind turbines and photovoltaics. Based on the reports for 1023 fatalities associated with natural hazard processes in Switzerland during the period from 1946 to 2015, more than 16% of the cases were caused by lightning, making it the second most frequent cause of loss of life among the natural hazards in Switzerland.4 Furthermore, lightning is reported to have an adverse impact on the aviation industry due to hazard to outdoor ramp operations, such as aircraft fueling, baggage handling, food service, and tug operations. In space centers, lightning is also a danger to fuel crews, ground operations and rocket launch operations.5,6 Lightning is also a major cause of damage to wind turbines, one of the fastest growing sectors of renewable energy production, causing transient surges and overvoltages in the power grid, inducing interference in control systems and, most importantly, causing significant damage to the blades and other wind turbine components.7,8 The consequences of these events can be very costly due to energy production losses, extra maintenance costs, or even loss of operating equipment.9
Given its noteworthy socioeconomic impact, appreciable attention has been given to accurate lightning prediction.
The widely accepted mechanism for charging in the thunderstorms is the non-inductive mechanism.10,11 In this mechanism, charge separation occurs when ice crystals and graupel particles collide in the presence of supercooled liquid water. Charge is transferred between the different types of particles and then the particles separate by weight under the influence of gravity and convective motions. Several past studies have reported on observational findings regarding how charge structures relate to different lightning types over a wide range of convective regimes. For example, analyzing nine distinct mesoscale regions of severe storms, Carey and Buffalo12 found significant and systematic differences in the mesoscale environments of positive and negative storms. They hypothesized that the mesoscale environment indirectly influences CG lightning polarity by directly controlling the storm structure, dynamics, and microphysics, which in turn control storm electrification and ground flash polarity. Since lightning involves complex interactions between many atmospheric and in-cloud processes, it is unsurprising that research into that phenomenon continues to generate a wide range of approaches for its prediction. Many studies have implemented sophisticated electrification physics within cloud-resolving numerical models.13,14,15,16,17 For example, Fierro et al.18 implemented an explicit electrification and lightning forecast module within the Weather Research and Forecasting (WRF) Model which includes in-cloud, non-inductive, and inductive collisional charging, an explicit elliptic solution of the 3D component of the ambient electric field, and two discharge parameterizations.19 On the other hand, some studies employ a simpler and practical approach of parameterization to allow for useful lightning forecasts without the need for adding electrification subroutines to cloud-resolving models.20,21,22,23,24,25 For example, Lynn et al.26 implemented a dynamic forecast scheme for both cloud-to-ground (CG) and intracloud (IC) lightning flashes based on the electrical potential energy parameter derived from the WRF cloud-resolving model. More recently, Tippett et al.27 used the product of convective available potential energy (CAPE) and precipitation rate as a proxy to predict cloud-to-ground (CG) lightning over the United States. The prediction scheme showed significant skill for lead times up to 15 days for predicting the number of flashes and their spatial extent as well as the lightning/no lightning maps.
Apart from lightning diagnostic schemes producing bulk flash metrics such as average lightning activity with useful skill up to several days forecast, some studies have focused on assessment of the lightning threat in the very near future and providing early warning by nowcasting individual flashes and/or the onset of lightning within the storm. Lightning warning systems in parks, sport complexes, schools, local government buildings, airports, space centers, etc. benefit from the output of such lightning nowcasting schemes to give decision-makers enough time to make take the necessary safety precautions for staff and visitors, stop lightning-sensitive operations, and protect equipment. For example, Mecikalski et al.28 introduced an integrated 0–1 h first-flash lightning nowcasting scheme. By merging the satellite and radar systems with numerical models, the lightning forecast is made 30–45 min before rainfall occurs. Chambra et al.29 implemented a cloud-to-ground (CG) lightning probability and binary occurrence or non-occurrence forecast in 20-km grid boxes for 2-h periods over the continental United States. This lightning guidance product is provided in the framework of the Localized Aviation MOS Program (LAMP) and it is issued at hourly intervals. Recently, Meng et al.30 developed an early lightning warning system by integrating observational data from radar, satellites, lightning detection systems, ground electric instruments and sounding instruments with synoptic pattern forecasting products, and numerical simulation of the electrification and discharge model. The system is able to provide lightning activity potential and warning products for the upcoming 0–1 h. Seroka et al.31 used radar-derived parameters, namely the isothermal reflectivity and Vertically Integrated Ice (VII), as the proxy to nowcast lighting over the Kennedy Space Center. Despite several different approaches applied to the important problem of lightning nowcasting and early warning generation, the complex processes and large number of parameters involved in the problem lends themselves to the potential application of a machine learning approach.
Knowledge Discovery in Databases (KDD) is an interdisciplinary area focusing on the process of discovering meaningful correlations, patterns, trends, and on extracting useful knowledge by mining large amounts of data.32 KDD has become a powerful tool for turning data into useful, task-oriented knowledge in a wide variety of fields such as business intelligence, marketing or genetics and it has contributed to several of the most recent breakthroughs.32,33,34,35,36,37 In atmospheric science, enormous proliferation of databases from remote sensing platforms and global-scale earth system models provides a large flow of data.38 The availability of very large volumes of such data has provided great opportunities for the big data-spun revolution to happen in atmospheric science.38 Machine learning algorithms such as KDD techniques could give computers the ability to learn a skill (such as making predictions) from sets of archived data and to apply the skill on new data. While conventional algorithms depend on developers entering reams of regulations and principles,39 forecasters and researchers have mixed machine learning with atmospheric science aiming towards improving the communities’ prediction skills for multiple weather-related phenomena at different scales.40 For example, Manzato et al.41 presented a neural network ensemble forecast for hail in Northeastern Italy. Gagne et al.42 used machine learning models to predict the probability of a storm producing hail and the radar-estimated hail size distribution parameters for each forecast storm. Herman et al.43 explored the internals of some regression and tree-based models and what physical and statistical insights they reveal about forecasting extreme precipitation from a global, convection-parameterized model. Lagerquist et al.42 described a machine learning system that forecasts the probability of damaging straight-line wind for each storm cell in the continental United States. Karstens et al.44 developed a human–machine mix for forecasting severe convective events. As an application in lightning nowcasting and early warning systems, this paper examines how the mining of basic atmospheric datasets can be used to explore correlation patterns between lightning incidence and atmospheric data and, thus, for nowcasting of lightning activity. To achieve this, a machine-learning-based model is trained to nowcast whether or not there would be any lightning incidence inside a specific region up to 30 min in advance, given the real-time measured values of four meteorological parameters which are relevant to the mechanisms of electric charge generation in thunderstorms,10,45,46 namely the air pressure at station level (QFE), the air temperature 2 m above ground, the relative humidity, and the wind speed.
Although the selected meteorological parameters do not necessarily represent upper level meteorology within the thunderstorm charging zone, they are indicators of low-level factors involved in thunderstorms. In addition, they can also be more reliably and continuously measured than many upper-atmosphere parameters that could be more closely linked to lightning generation.
Some lightning predictive schemes use operational radars and satellites to detect storm initiation and development, perhaps also aided by Convective-Allowing Models, and can provide calibrated thunder guidance up to at least a day in advance. For example, the High-Resolution Ensemble Forecast (HREF) Calibrated Thunder guidance produces probabilities that represent the likelihood of at least one cloud-to-ground (CG) lightning strike within 12 miles (20 km) of a point location over a 4-h forecast period.47 This guidance generates forecasts over the Continental United States using a rolling 4-h window out to 48 h. Using commonly available surface data makes the warning system in this study independent of external sources of data such as numerical model outputs, satellite and radar. In this regard, the proposed approach could benefit the current lightning predictive schemes. Two potential contributions are: (i) While satellites can provide broad nowcasting information for people, the ML approach provides an opportunity for much more localized forecasting and alerts, and this could be facilitated for users through a web interface where they can upload their own data. Furthermore, the method can provide information in areas where radars are not present, where weather forecaster resources are limited, or where nowcasting is not in operation, for instance in isolated areas in low-income countries in Asia, South America, and Africa.48 In fact, the method can be applied to any weather station (with extended data records to ensure appropriate training samples) to give localized forecasting, independent of the availability of other resources. (ii) The input data are not subjected to the typical scan cycles, limited forecast steps, or processing and post-processing delays. Indeed, the predictors used are commonly available in real time and they have high temporal resolutions. Given this, the proposed ML model is able to provide early lightning warnings with short lead-time ranges (0–30 min), as opposed to methods that have forecast periods measured in hours. Such warnings could contribute to the reduction of air traffic congestion at airports and to the decrease in disruptions to energy generation from wind turbines farms.
In supervised learning, algorithms are designed to learn from a given dataset with an already known output (training set). After the learning phase, predictions are made on new datasets (testing sets). In this study, we implemented the proposed nowcasting scheme using data from 12 meteorological stations in Switzerland between 2006 and 2017 (see Table S1 for the list of the selected stations). The stations were selected based on two criteria, namely (i) the availability of both meteorological and lightning activity data during the study period, and (ii) the fact that they are well distributed among different ranges of altitude and terrain topographies. Among the stations, six are located in an urban area inside cities with altitudes ranging between 273 and 776 m above sea level and one is the weather station at the Geneva airport. Five out of the 12 stations are located in mountainous regions with 3 of them having an altitude of more than 1000 m above sea level. A common feature of the stations in Switzerland is the presence of nearby topography, which increases the probability of storms being initiated near them. While this makes the results presented here directly relevant to locations that experience topographically induced thunderstorms, further work is needed to evaluate the skill of the approach in environments with different triggering mechanisms.
At each of these single-site meteorological stations, we first formed a tabular database with each row containing the observations during a specific time window with a granularity of 10-min. In each row, the corresponding meteorological measurements are used as the predictors (also called features) and the recorded lightning activity is used as the response. Once the database was formed, pattern recognition and data mining algorithms were employed to identify regularities between predictors and responses using a portion of the data which, as mentioned above, is called the training set. The model could then use the explored correlations for nowcasting the long-range lightning threat (within a circular area of 30 km radius around the meteorological station) for the unseen cases (testing set). The model predictions and observations are then compared to evaluate the model’s prediction skill. The evaluation results are presented by means of four common indices in forecasting rare events described in Table 1, namely the Probability of Detection (POD), False Alarm Ratio (FAR), Critical Success Index (CSI), and Heidke Skill Score (HSS).
Detailed information on the data acquisition, database formation, training and testing procedures, performance evaluation process, and the selection and generation of the applied machine learning algorithm in this study are presented in Methods.
Results
Machine Learning Model performance for long-range lightning activity at 12 stations in Switzerland
The database consists of the observations of four meteorological parameters with a granularity of 10 min recorded at 12 selected meteorological stations in Switzerland over a time period ranging from 2006 to 2017. In order to see how far in advance the lightning alarms could be generated, three ranges for lead time were investigated: (i) 0–10 min, which corresponds to imminent lightning activity, (ii) 10–20 min, and (iii) 20–30 min. At each station, the data are labeled according to the presence or absence of long-range lightning activity (within 30 km distance from the station) and with respect to the three aforementioned lead-time ranges to form Subsets 1–12 (see Table S3 for the list of studied subsets and Methods for the description of the data gathering).
The list of stations with their geographical information is presented in Table S1. Among the selected stations, the Säntis and Monte San Salvatore stations have been of great interest for lightning studies in the literature.49,50,51,52 The atmospheric data at these two stations were gathered in Subsets 1 and 2. Figure 1 shows the visualization of the data at the Säntis and Monte San Salvatore stations (Subsets 1 and 2, respectively) for the 0–10 minute lead-time range where the inter-relation between the considered parameters is illustrated. A recorded observation at the start of a 10-min interval is labeled according to long-range lightning activity in that interval as either a ‘lighting-inactive’ sample (without any long-range lightning activity) or a ‘lighting-active’ sample (with at least one long-range lightning activity recorded). Figure 1 shows the probability density estimates of the surface pressure and surface temperature for lighting-inactive and lighting-active samples in Subsets 1 and 2 using a kernel smoothing function. Although the visualized data suggest the existence of different distribution patterns among the two classes, they seem to be mixed together at both stations, which makes it difficult to explicitly extract any classification criteria. Alternatively, the developed machine learning model (the ML model) is used to recognize the patterns. The machine success is evaluated in two ways: (i) By measuring how accurately it can classify the data into two distinct classes (lighting-inactive or lighting-active), and, (ii) by investigating how it can improve upon three competitive baselines, namely the persistence forecasting method, the electrostatic field method, and a scheme based on CAPE threshold.
Probability density estimates of the surface pressure and surface temperature for lighting-inactive and lighting-active samples in Subsets 1 and 2 using a kernel smoothing function. The Subsets 1 and 2 include observations of four meteorological parameters respectively at Säntis and Monte San Salvatore stations from 2006 up to 2017 with the granularity of 10 min. The corresponding lead-time range is 0–10 min. Thus, a recorded observation at the start of a 10-min interval is labeled according to lightning activity in that interval as either a ‘lighting-inactive’ sample (without any long-range lightning activity) or a ‘lighting-active’ sample (with at least one long-range lightning activity recorded)
To generate forecasts based on the data, the PERSISTENCE model assumes that in every 10-min interval, the forecast is the same as the observation in the previous interval. So, if there was lightning in the previous 10-min period, then, according to the PERSISTENCE model, there will be lightning in the next period too. The persistence forecast represents a realistic and applicable competitive option against the ML model, since the preceding lightning activity is continuously stored by lightning location systems around the world. If one wanted to predict whether there will be lightning in the next 10-min interval based on the PERSISTENCE model, it would be possible to check the online lightning and thunderstorm detection networks and see if there was any lightning activity recorded in the previous time interval. Note that the prediction for the second and third lead-time ranges was carried out using the observed lightning in the 10-min interval prior to the forecast time, which is the same interval that was used to forecast for the 0–10 min lead time.
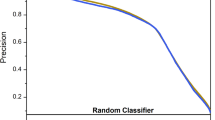
Electrostatic field readings have shown to be affected both before and during the thunderstorm due to the approaching charge centers, their rearrangement inside the thunderclouds, as well as cloud electrification and rearrangement of space charge in the atmosphere.53 Some previous studies have used these variations to forecast approaching lightning activity.53,54,55 The electrostatic field method (the E-FIELD model) used in this study is based on detecting when the vertical electrostatic field (E(z)) exceeds a specific threshold to issue the warning. The corresponding threshold used by the E-FIELD model for each subset and lead time is defined in a way that the CSI is maximized. The choice of CSI as the optimization criterion is mainly based on its inherent consideration of both, POD and FAR and, hence, it is suitable when a trade-off between these two is desired. Among the selected stations, the Säntis station was the only one equipped for vertical electrostatic field measurements. These data were available from August 2016 to July 2018. Hence, the performance results for the E-FIELD model are presented in Fig. 2 only for the Säntis station and from August 2016 to December 2017 to also match with the time period of this study.
Evaluation of the skill of warnings of long-range lightning activity for three ranges of lead times at a, b, c Säntis (Subset 1) and a′, b′, c′ Monte San Salvatore (Subset 2) station. The results from ML model are shown as solid black columns, results from PERSISTENT model are shown as columns filled with dot patterns, results from CAPE model are shown as columns filled with vertical lines, and results from E-FIELD model are shown as solid gray columns (POD: Probability of Detection, FAR: False Alarm Ratio, CSI: Critical Success Index, HSS: Heidke Skill Score)
Not having direct measurements of the electrostatic field at stations other than the Säntis, we considered a CAPE model in addition to the PERSISTENCE model as the competitive schemes for the proposed ML model. The CAPE model uses a threshold of Convective Available Potential Energy (CAPE) to assess the risk of lightning. Assessing the level of CAPE which is well understood to be reflective of environments favorable to the development of lightning,22,24,56 the CAPE model would be a more objective comparative scheme. Similar to the E-FIELD model, the corresponding threshold for each subset and lead time is defined in a way that the CSI is maximized. The CAPE model’s performance has been found to have low sensitivity to the selected threshold. For example, at the Säntis and Monte San Salvatore stations, the CSI changed respectively less than 7.5 and 5% for a ± 30% change in the threshold value at each of the lead time ranges. As mentioned in the Data Section, in this study, the CAPE data are retrieved from the ERA5 hourly reanalysis data on single levels provided by the European Centre for Medium-Range Weather Forecasts (ECMWF). The temporal resolution of the available CAPE data was originally 1 h. To make it consistent with the granularity of the meteorological parameters, which is 10 min, one possibility was to interpolate the data for missing 10-min time frames. While this interpolation would increase the number of available samples to be used by the CAPE Model, it might also negatively affect its performance skill due to possible inaccurate interpolation of samples for this highly variable and hard to measure parameter. Consequently, the CAPE model was only tested on the 10-min intervals for which the CAPE data were originally available without any temporal interpolation.
The performance results for the ML model and the three baselines are presented in Fig. 2 for the Säntis and Monte San Salvatore stations. The four selected evaluation metrics shown in the figure are introduced in the Methods section and a summary is given in Table 1. Based on the results at both stations, the ML model has consistently higher scores than the three competitive models for all three lead-time ranges. The results from Fig. 1 show clear differences in both the absolute recorded values and the distribution patterns of data at the two stations. However, the performance results for the ML model at the two stations in Fig. 2 exhibit similar evaluation results. In other words, although the atmospheric data for both, lighting-inactive and lighting-active classes have different ranges of values and are distributed differently at the two stations, the ML model was able to learn from the local patterns and predict with reasonable accuracy at both stations. Indeed, the results for the POD index at both stations reveal that more than 71% of the lighting-active samples are classified accurately.
It is worth noting that the accuracy of classification is not only important as a measure of prediction skill but it also accounts for how successful the ML model is in finding the complex correlations in the data. Low accuracy in the model does not necessarily imply that there is no correlation in the data since the low accuracy might be attributable to deficiencies in the model. High model performance, in contrast, is an indication of a strong correlation pattern between the predictors and the response and also of the capability of the model to recognize such patterns.
Using the feature reduction method, the impact of excluding individual variables from the ML model input was investigated on each metric for the two subsets. The sensitivity is calculated using the following equation,
where S is the sensitivity of each one of the four metrics to a specific feature, mwo and mw are, respectively, the values of the metric with and without the feature included in the ML model. A positive value for S means that the associated index would increase if that feature is not included in the study. If the majority of the indices show positive sensitivity to a particular feature, one could get better results if the feature is excluded from the predictors list. Looking at the sensitivity results for the long-range activity and for the three investigated ranges of lead time, no such feature could be found. This suggests that the best result is the one with all meteorological variables included.
The results in Fig. 2a–c for the CAPE model show a similar performance for all three lead-time ranges compared to the ones for the E-FIELD model. Both models show low POD and very high FAR values at all three lead-time ranges. On the other hand, the results shown in Fig. 2a, for example, indicate a good prediction skill for the PERSISTENCE model for the imminent threat warning. This noticeable lack of skill for the E-FIELD model at such lead time ranges has already been reported in the literature. For example, Aranguren et al.54 analyzed the skill of a lightning warning system based on the measurement of the electrostatic field in Northeastern Spain. Using a threshold-based lightning warning system, the FAR was around 90%, and the POD was between 10 and 70% based on the low and high threshold levels. Analyzing 7 storms, they also reported that the best achieved lead time for the forecast was <6.5 minutes.
The results in Fig. 2 show how the model’s nowcasting skill changes when a longer forecast time is required. This is important to give sufficient time for the safety actions to be undertaken. Comparing results in Fig. 2a′, c′ shows that the PERSISTENCE model is more sensitive to the increase of lead time compared to the CAPE and the ML models. The results from the PERSISTENCE model show 12% drops in each, POD, CSI, and HSS, and a 12% increase in FAR compared to the 0–10 min lead time, whereas the performance of the CAPE and the ML models is not affected by an increase in the lead time. In other words, the results in Fig. 2 suggest that, although looking at the preceding lightning activity records (i.e. what is done by the PERSISTENCE model) is good enough to warn for the very near future lightning threat (0–10 minute lead time), this would not be reliable in most of the applications where longer forecast times are needed. On the other hand, the ML model ensures that the accuracy of its warnings up to 30 minutes in advance will be maintained.
While nowcasting rare events, special emphasis needs to be given to the no-event cases, which dominate the dataset. Since no-event instances represent the majority of the samples, lacking the skill to correctly classify them would lead to a large number of false alarms. According to the results for FAR in all subsets of Fig. 2, the ML model is seen to perform much better than the other models concerning the correct rejection of no-events.
Although the sensitivity analysis described in Eq. 1 gives insights into each predictor’s importance in the ML model performance, its value often varies from one metric to the other, which makes it difficult to rank the predictors in the sense of their overall importance. To bridge the gap, the predictors importance estimates calculated by the ML model could be used to rank the predictors. As explained in Methods, the learning process was done by growing an ensemble of decision trees. To grow each of these trees, the ML model starts from the root and creates decision nodes and branches by calculating the split gains. The model would then be able to estimate the predictor importance by summing the changes in the risk due to splits on every predictor and dividing the sum by the number of branch nodes. The predictors importance associated with each split is computed as the difference between the risk for the parent node and the total risk for the two children.57 To compare the predictor rankings due to their importance at different stations, the importance estimate of each predictor is computed relative to the sum of the estimates for all predictors in that study, calculated as
where impi is the absolute value of the importance estimate for predictor i. These predictors importance estimates are reported in Fig. 3 for studies at each station. All statistics and results presented in this figure are presented for a lead time of 0–10 min. One should note here that the predictors importance does not relate to the model accuracy and it just relates to the importance of each predictor in making a prediction, not whether or not the prediction is accurate.
Predictors importance estimates for long-range lightning activities. The result includes both studies at individual stations and over all stations. The data from individual stations are standardized according to their local mean and deviation before they are included in the overall study. The presented results correspond to the lead time of 0–10 min
The result in Fig. 3 indicates that at most of the stations, for the prediction of the long-range lightning activity, the variation of the surface pressure, relative humidity, and surface temperature were more important than the wind speed. The dependence of the long-range model performance on these parameters can be explained as follows: the impact of the surface temperature can be attributed to the fact that anomalously high local temperatures are more likely to be associated with instability. This parameter could also be important due to the arrival of the gust front (cooler temperatures), or higher CAPE at the meso-scale. High relative humidity suggests a higher chance of having sufficient moisture supply to generate deep convection, as well as being related to instability of the environment. The surface pressure identifies local troughs propagating through. Alternatively, the increases or decreases of pressure perturbations could be associated with the propagation of a gust front. Results indicate that the wind speed was also found to be useful by the classifier. In the long-range, it might be important due to the fact that large organized systems may induce strong winds far from the charging regions of the storms. The fact that the predictors importance estimates change from one station to the other might indicate that the models for individual stations may offer new insights into the relevant processes locally.
Distribution patterns of data among different stations
As stated in the Introduction, the involved stations are selected from regions with different topographies and altitudes. In order to see how these differences affect the distribution patterns of data among the stations, the probability density functions (PDFs) of each parameter in the lighting-active class for all 12 stations are compared in Fig. 4. The PDFs are plotted using each of the data Subsets 3–14 and with a lead time of 0–10 min. The reason for choosing these data subsets is that each one of them includes data from an individual station and it has the same temporal coverage as the others (2006–2017). The choice of a lead time range of 0–10 minutes accounts for the imminent lightning activity at each interval. One should note here that in order for the results to be comparable between stations, the data in the subsets were standardized. The standardizing function shifts the mean of each predictor to zero and scales the predictors by their standard deviations. The distribution patterns of the lighting-active samples for all 12 stations are also visually illustrated in Figs S1–S4. Looking at the PDF plots and the distribution patterns for all stations suggests the existence of two groups: (i) Group A, including 10 stations with their altitude lower than 1050 m above sea level, and (ii) Group B, which includes the remaining two stations with higher altitudes (Säntis and La Dôle). Figure 4 shows that the probability density of surface pressure and relative humidity are different in the stations belonging to Group A and Group B. These differences in the densities can be clearly seen in the distribution patterns shown in Figs S1–S4, where the lighting-active class data in Group B are clustered around higher pressure and higher relative humidity when compared to Group A. Looking at Table S1, one can find the potential reason for this difference in the patterns. Säntis and La Dôle are the sites with the highest elevations in the dataset and are approximately 2000 m and 1100 m higher than the bulk of the other sites. The altitude differences have a considerable effect on pressure, temperature and wind speed and, therefore, we have performed a more detailed investigation on these sites.
Comparison of probability density functions (PDFs) of each parameter in lighting-active class samples of Group A and Group B. The corresponding lead-time range is 0–10 min. For the sake of comparison, the parameters values at each station are standardized based on the local mean and standard deviation values. The standardizing function puts mean of each parameter at zero and scales the parameters by their standard deviations
To better understand these differences, the principle component analysis (PCA) is used to explain the distribution patterns of individual features in different subsets. PCA is a data mining tool that transforms a number of interrelated variables into a new set of uncorrelated variables called principle components (PCs), while retaining as much as possible of the variation that exists in the original data.58,59 The first principal component retains most of the variations in the data, and each succeeding component accounts for as much of the remaining variability as possible. The Singular Value Decomposition (SVD) algorithm is used to perform the PCA analysis on data from individual stations (Subsets 1–12). At each station, the first two Principal Components (PC1 and PC2) are kept. Figure S5 shows the percentage of total variance explained by each of these two leading PCs. Furthermore, the contribution of each original variable to each principal component is defined by sets of coefficients. Figure 5 shows the loadings of each variable on the first two components (PC1 and PC2) for all 12 stations. In each subplot, the two stations with the highest distance from the center of the main cluster are defined using cluster analysis and marked as red dots. Looking at the four subplots, it can be seen that, in all cases, black and red dots correspond exactly to stations of Groups A and B, respectively. In other words, Group B stations show quite different PC1 and PC2 coefficients in all variables compared to Group A. The results suggest different patterns of distribution between the two groups and they confirm what was visually concluded earlier from Fig. 4, Figs S1–S4.
The contribution of individual variables to the first and second principle components for all 12 stations during 2006–2017. In each subplot, data for two stations with the largest distance from the cluster center are annotated in red and the rest are presented in black. The corresponding lead-time range is 0–10 min
Change of distribution patterns over time
Further analysis of the data showed that these pattern variations are not limited to geographical characteristics. Mining the data for all stations on an annual basis using PCA reveals that patterns of distribution for stations belonging to Group B have changed widely from year to year while Group A stations exhibited only a slight change. In this regard, each of the Subsets 1 to 12 was split into 12 segments, each assembling the data for one year between 2006 and 2017. Then, the PC1 and PC2 coefficients were plotted and the differences in feature contributions were observed from year to year. Figure 6 presents the results for one representative station of each group, namely Zurich from Group A and Säntis from Group B for a lead-time range of 0–10 min. The results for the other two lead-time ranges are presented in Fig. S6.
The contribution of individual variables to the first and second principle components from 2006 to 2017 for a Zurich station (as an example of Group A) and b Säntis station (as an example of Group B). In each subplot, the horizontal axis is the coefficients for PC1 and vertical axis is coefficients for PC2. The corresponding lead-time range is 0–10 min
Discussion
Early warning systems are useful to help prevent effects of lightning strikes to critical infrastructure, sensitive equipment or systems, and outdoor facilities. Taking advantage of both, the large amount of available data for meteorological parameters and advances in data mining and knowledge discovery, we used KDD techniques to investigate the correlation between lightning and selected meteorological parameters and thus warn against the risk of long-range lightning activity. To do that, the machine was programmed to automatically extract and learn hidden regulations inside previously labeled data in order to predict the labels for unseen data. These regulations could be any information in the data that the machine could use during the training process to learn a target function that best maps the input variables to the output. The evaluation results for 12 locations in Switzerland revealed that, by looking at values for four principle meteorological parameters, the ML model was able to warn with a reasonable accuracy of future lightning activity up to 30 min in advance and in an area of 30 km around the observation point.
For each station, the ML model has been set up to predict lightning activity in three future forecast times: (i) the interval from the present to 10 min into the future which corresponds to imminent lightning activity, (ii) the interval between 10 and 20 min into the future, and (iii) the interval between 20 and 30 min into the future. These lead-time ranges are likely shorter than the lifetime of many thunderstorms, organized systems, or isolated storms. This implies that the ML model is looking at the changes in the local surface conditions leading to the occurrence of lightning within the storm life cycle, and this applies to any kind of storm. Given the fact that isolated storms (short-lived, topographically, and diurnally forced) and propagating organized storms (longer-lived) can both lead to lightning, a strength of the ML model is that it is capable of accounting for different situations leading to lightning generation, with the caveat that the different situations need to be discernible in the input data.
As discussed in the Methods section, the main challenge in developing the appropriate predictive scheme was the high imbalance seen between lighting-inactive and lighting-active classes. The situation gets even worse when the lead time is increased. This high level of imbalance not only highlights the need for special techniques in developing the machine learning algorithm, but also requires specific considerations for model performance evaluation. For the considered lightning prediction application, the cost of misclassifying lightning-inactive samples is much less than that for lighting-active ones. The average of PODs for the studied local subsets showed that more than 76% of the long-range lightning threats were correctly predicted by the ML model up to 30 min in advance.
Unlike some lightning warning systems that are based on data from lightning detection networks,55,60 the ML model provides a tool for building lightning nowcasting schemes without using nearby or preceding lightning data as the precursor of the imminent threat. In other words, it does not rely on the first detection of the lightning for generating the warnings. Instead, it uses the lightning location systems’ data for labeling the archived data and thus training the model with historical data. Once trained, the model does not need such data to predict lightning occurrence risk in future time windows.
Compared to other conventional warning techniques, the machine learning approach also offers automatic extraction of regulations and it does not require advanced background knowledge about the predicted task. Although the ML model eliminates the need for manually adjusting the thresholds or prediction criteria due to automatic detection of regulations, it is susceptible to changes that might occur in the environment and that may affect the extracted rules by the model during the training process. For example, an increase in the number of tall buildings nearby and weather and climate changes might alter the dependencies found by the model between predictors and response. On the other hand, the ML model could be readily updated to the new situation with the required periodicity using new achieved data.
Although some vulnerable sites such as airports and space centers need to warn for total lightning activity (both CG and IC flashes), being able to split the warnings for each type of flash would, in general, be a desirable feature in an early lightning warning system. The ML model presented in this study does not differentiate between the various types of lightning flashes. The reason is that the available data from lightning location systems used to train the ML model have no distinction between cloud-to-ground (CG) and intra-cloud (IC) flashes. However, one could evaluate the skill of warnings for different types of lightning activities by training the model separately using data from each flash type. The application of the method to the task of forecasting different types of lightning is beyond the scope of this work and will be dealt with in future research.
Although no data were available for direct comparison with other state of the art lightning warning approaches based on radar or satellite, their performance results are reported in the literature. For example, Seroka et al.31 investigated the use of optimized radar-derived predictors along with IC flashes to predict CG lightning over the Kennedy Space Center. The values obtained for POD, FAR, CSI and the average lead-time for the two leading predictors of CG flashes were, respectively, 78%, 35%, 55%, and 2.4 min for IC as the predictor, and 78%, 46%, 47%, and 6.4 min for a radar reflectivity value of 25 dBZ at −20 °C as the predictor. Taking advantage of the wide range of input data including radar and satellite observations, ground measurements of the electric field, data from lightning location systems, sounding instruments with synoptic pattern forecasting products and a two-dimensional charge-discharge model, Meng et al.61 made an integrated system to predict lightning within the upcoming 0–60 min. The nowcasting system gives the probability of lightning occurrence in grids of 1 km × 1 km and in 15-min lead-time steps. The probabilities above 25% lead to early warnings. The verification results for the issued warnings during 16 thunderstorms in Beijing and the surrounding area show that the mean values for the POD score drop from 49 to 37%, the FAR score increases from 67 to 77% and the CSI score decreases from 24 to 16% while coming from the minimum (0–15 min) to the maximum lead-time range (45–60 min).
The primary goal of this study was to examine the effectiveness of using single-site meteorological observations to train machine learning algorithms for nowcasting lightning and warning against the lightning threat. Secondarily, data mining techniques were used to further investigation of possible geographical and temporal dependencies in the data.
Explaining the reasoning behind the machine decisions to humans can be difficult because they often do not make use of the same intermediate abstractions that humans use.62 This kind of issues, in turn, could be addressed by the interpretable machine learning. Interpreting machine learning aims to increase the model transparency and thus make it more useful and trustable by giving explanations for model predictions. For example, applying interpretation techniques could reveal an explanation of the hidden trends found by the ML model once it is implemented at stations in different climate zones. Comparing the basis for model prediction in different stations would shed light on whether there are different regulations that correlate meteorological parameters to lightning activity or not. Such kind of findings would be obviously more valuable when more relevant atmospheric parameters to lightning initiation available in satellite and radar data are used as the predictors. This would enable the machine learning approach to better contribute to a further understanding of lightning and atmospheric interactions.
The use of surface measurements as input data in this study does not put any limitation on other relevant parameters to be used by the ML model. Large amounts of atmospheric data are available from numerical model outputs, atmospheric soundings, satellite and radar observations. Given this and also the fact that lightning activity is now readily detected with high spatiotemporal resolution by means of space-borne instruments and ground-based lightning location systems, an extensive amount of work is in progress by the authors to apply the machine learning approach to provide lightning predictive schemes (i) capable of estimating the flash rates as well as the lightning threat itself, (ii) with large spatial coverage, and (iii) with good skill for lead times up to 24 h. However, for the first-stage research presented in this study, we restricted our efforts to the selection of surface data since we wanted the scheme to be easy to implement and widely applicable to a variety of vulnerable sites. In fact, the idea behind the choice of input variables for this early warning scheme in this study was to use types of predictors that are commonly available, that have a high temporal resolution, and that are easy and fast to retrieve in real time.
Rapid increases in total lightning activity have been demonstrated to be a precursor for the occurrence of severe weather at the ground.63 As a potential application, the proposed ML model could be trained to provide an early indication of severe weather events other than lightning at short time scales. Such a model could be evaluated alongside the lightning jump algorithm.64
Even though we have not used real time data in this study, the selected meteorological parameters are available from Personal Weather Stations (PWS) with refresh rates of <2 s. Being small, precise, and easy to install and operate, individuals often own these devices and upload the data to an online platform aiming to improve weather forecasting.65,66 Given the fact that these sensors measure all four predictors needed by the ML model, it could be easily integrated into these devices. In this regard, PWSs would be converted to an accurate early lightning warning system at any arbitrary point of interest while keeping their main functionality as weather stations.
Methods
Data gathering
The dataset used in the ML model consists of data used as predictors, namely available meteorological data (air pressure, air temperature, relative humidity, and wind speed) and lightning activity data as the response. Vertical electrostatic field data measured by the E-field mill device at one of the stations and Convective Available Potential Energy (CAPE) are also gathered and used as predictors and competitive baselines in this study.
The spatial and temporal coverage of the study was set according to the availability of both atmospheric and lightning data. Furthermore, and considering the effects of the terrain topography and topological effects on the lightning incidence,51 the stations were selected to be properly distributed among different ranges of altitude and terrain topographies. The time interval of the study was set to 2006 to 2017 (12 years) and 12 stations in Switzerland were selected. Note that the vertical electrostatic field data were only available at the Säntis station from August 2016 to July 2018. In order to use these data, the time coverage at that station was therefore extended up to July 2018. More information about the selected stations is presented in Table S1. The used data are described in what follows.
In this study, data on surface air pressure at station level (QFE), air temperature 2 m above the ground, relative air humidity, and wind speed were obtained from the Swiss Federal Office of Meteorology and Climatology (MeteoSwiss) online database and they were measured by the automatic monitoring network of MeteoSwiss (SwissMetNet). SwissMetNet now comprises 160 measurement sites equipped with high-precision measurement instruments and state-of-the-art communication technology. The measurement instruments and respective sources of errors are listed in Table S4. All devices in SwissMetNet comply with the standards of the Word Meteorological Organization (WMO) regarding location selection, measurement height, and the degree of measurement precision.67 The measurement data from each station are automatically transmitted to the MeteoSwiss central database, where various quality assurance checks are performed. In the MeteoSwiss data warehouse, measurement data are processed and systematically reviewed on a continuous basis. Measurement gaps are filled, additional parameters are calculated and corrections are made.68 The pre-processing stages applied to the measurement values from the station to the end user are illustrated in SwissMetNet user guides.68,69
The minimum available granularity level of meteorological data in SwissMetNet is 10 min. As a result, the time period of the study is quantized into 10-min intervals. For each interval, the observation records at the starting point are assigned to the predictor fields in the database.
Raw surface data contain numerous unrelated trends that are likely to reduce the ability of the model to find useful regulations. Hence, removing seasonal and diurnal dependencies would help more useful meteorological signals to stand out. Note that two different de-trending algorithms were tested. However, they were not used since they were shown not to provide any gain in the prediction performance.
The data from lightning location systems are used to first train the ML model and then to validate the accuracy of lightning warnings that it generates as well as the competitive base lines. MeteoSwiss receives lightning localization data from the Météorage company to detect and locate lightning discharges.70 Météorage is a part of the European Cooperation for Lightning Detection (EUCLID), which is a network of Lightning Location Systems (LLS) operating in western Europe. Detailed information on the EUCLID network can be found in Azadifar et al.71 and Schulz et al.72 The average flash detection efficiency for the used datasets in this study is reported to be 95% for cloud-to-ground (CG) flashes and 45% for intra-cloud (IC) flashes.73 The system measures in real time the angle of incidence and the arrival times of the radiation fields at a network of ground-based measurement stations using LS7001 sensors from Vaisala.74 The signals are received in the low frequency (LF) band (1–350 kHz).74 The accuracy of the locations mainly depends on the uncertainty of the arrival time measurements, the background noise level in the operating frequency band, and the number and positions of the stations used to obtain each solution. The arrival times are measured independently at each station using an accurate time base provided by a GPS receiver.75 The system then combines the data received from all stations to provide a detailed analysis of individual flashes with 100 ms accuracy for the time of strike. It also provides the shape and size of the ellipse that can be said to contain the location of the strike with a 90% level of confidence.76 In 2017, the median accuracy of detections was reported to be 100 m in Western Europe.74 In this study, we do not aim to warn for each individual flash, but to warn of the risk of having lightning activity within a 10-min interval (aka a dichotomous decision basis). Thus, we do not explicitly import the time stamp and location of each individual recorded flash into the model. Instead, we look at total lightning activity in each 10-min interval for which we have the meteorological observations available. To do that, based on the distance of each recorded flash from each MeteoSwiss station, the flashes were labeled as long-range lightning activity if they had occurred within an area of radius 30 km surrounding the station. The lightning activity corresponding to each 10-min interval in the database was assigned to “Yes” (lighting-active class) if at least one flash was recorded in that interval and in the selected area around the station, otherwise it was assigned to “No” (lighting-inactive class). This labeling method also enables us to give lead times to the generated warnings. To do that, the data from preceding observations of meteorological parameters should be used to make the prediction for the following intervals.
CAPE data are retrieved from the ERA5 hourly reanalysis data on single levels provided by the European Centre for Medium-Range Weather Forecasts (ECMWF).77 ERA5 is the fifth major global reanalysis produced by ECMWF where, every 12 h, observations from across the world are combined with the previously generated forecast to produce the most accurate state of the atmosphere at a given point in time. Reanalysis estimations are made at each grid point around the globe over a long period of time with regular time steps and always using the same format. The provision of such estimates makes reanalysis data convenient to work with in this study, especially since we need the data to be uniformly estimated during 12 years. The horizontal resolution of ERA5 data is 0.25° × 0.25° and the temporal resolution is 1 hour. According to the ECMWF parameter database,78 CAPE is calculated by considering parcels of air departing at different model levels below the 350 hPa level. The maximum CAPE produced by the different parcels is the value retained. The calculation of this assumes: (i) that the parcel of air does not mix with surrounding air; (ii) that ascent is pseudo-adiabatic (all condensed water falls out), and (iii) other simplifications related to the mixed-phase condensational heating.
It can be seen that the spatial resolution roughly matches with the considered long-range activity (30 km) but the locations of the 12 meteorological stations do not necessarily match with the center of the grid for which the reanalysis data are available. In this regard, at each station, the data from 9 neighbor grids imported from the ERA5 are used to interpolate the value of CAPE for the area of interest corresponding to long-range activity in this study, i.e. 30 km surrounding each station. In addition, the temporal resolution of 1 h for the reanalysis data does not match with the one from meteorological data (i.e. 10 min). Hence, in addition to the data with the original resolution of 1 h, another version of data is generated where the missing values for 10-min steps are linearly interpolated. Both versions of data are used in the study and the findings are reported in Results.
Among the selected stations, the Säntis tower was the only one equipped with vertical electrostatic field measurements. The mountain summit has been used as a meteorology station since 1881. In the 1950s, the site was selected for the installation of an 18-m tall radio and TV transmitting antenna that was erected at its summit in 1955 and was replaced by a taller, 84-m tower in 1976. That tower was itself replaced in 1997 by the current tower, which is 124 m tall. Since 2010, this tower is instrumented for lightning current measurements using advanced equipment including remote monitoring and control capabilities.79,80,81 An EFM-100C RS485 BOLTEK E-field mill has been installed since 15 July 2016 to measure the vertical electrostatic field in the immediate vicinity of the Säntis tower. This electro-mechanical device measures the amplitude of the vertical static electric field (E(z)) at the installation point. The distance between the installed field mill and the tower base is about 20 m. The system is set to record the field continuously with a sampling time of 50 ms. The highest range of electric field that can be recorded is ±20 kV/m.82
The Electric Field Mill (EFM) sensor not being located over a perfect flat ground, the electric field measurements could be affected by the environment. In addition to that, the surrounding objects such as buildings and tall objects could partially shield the electric field which would consequently affect the measured electrostatic field values. Hence, a correction factor, k, was considered to correct the measured values due to these possible sources of error. In this study, the correction factor was determined by comparing the measured values of the vertical electrostatic field with simulated results obtained using COMSOL Multiphysics software for fair weather. The simulation model incorporates the exact terrain topography at the mounting location of the sensor. The modified data are then used as predictor by the E-FIELD model to provide a competitive baseline for the ML model. The value corresponding to the maximum recorded amplitude of the vertical electrostatic field during each 10-min interval was considered and assigned to the electrostatic field parameter for the corresponding interval in the database.
Once the database was formed, we partitioned the data at each station into two parts: (i) Data Part 1, including the first four years of data (from 2006 to the end of 2009) and (ii) Data Part 2, including the data for the remaining 8 years (from 2010 to the end of 2017). We then used the first part to do the model search and tune the model and its hyperparameters (Stage #1), and withheld the second part to do the final evaluation (including both training and testing) using the information derived during the first stage (Stage #2). Doing this greatly decreases the risk of overfitting since the data used for the final performance evaluation (Data Part 2) remained independent from the part that was used for model search and tuning processes (Data Part 1). What follows describes the model selection, generation, tuning, training, and testing procedures.
Stage #1: model selection, generation, and tuning
All gathered data subsets in this study are featured as high dimensional and multivariant datasets. In Fig. 7, the data subset 6 using a parallel coordinates plot can be visualized. The plot maps each row of data as a line. The orange lines correspond to the lighting-active class and the blue lines are the data from the lighting-inactive class. Looking at the distribution of these two classes in each of the coordinates, the plot shows that the two classes are highly mixed in all coordinates and no explicit distinction could be found. Similar high complexity was found as well in other data subsets summarized in Table S3. Further to this complexity, after labeling each piece of data using the aforementioned procedure in Data gathering section, the two classes turned out to be highly imbalanced at all stations. The imbalance was expected since lightning-active periods throughout the year are rare compared to periods devoid of lightning. Due to this high imbalance seen in the data, an extensive model search process was carried out to choose the most appropriate machine learning classification model based on Data Part #1 at each station. To do this, the TPOT Python Automated Machine Learning tool83 was used (i) to choose the best-fit model, and (ii) to tune the hyperparameters of the model at each station. When applied to a certain dataset, the AutoML approaches automatically explore lots of possible machine learning pipelines and build the one with competitive classification accuracy for that specific task.84 The results drawn from separate runs at each of the stations and for each of the three lead-time ranges indicated that the best performance would be achieved using the XGBoost algorithm. XGBoost30,85 stands for “Extreme Gradient Boosting” and it is a variant of the gradient boosting machine which uses a more regularized model formalization to control overfitting.
Parallel coordinates plot from data subset 10. The mean of each predictor is set to zero and the predictors are scaled by their standard deviations. Each line represents a recorded observation at the start of a 10-min interval and is labeled according to lightning activity in that interval as either blue (without any long-range lightning activity) or orange (with at least one long-range lightning activity recorded)
To do the classification, the XGBoost algorithm generates an ensemble learner out of individual classification trees using a scalable tree boosting system. Ensemble learners use multiple learning algorithms to obtain better predictive performance than could be obtained from any of the constituent learning algorithms alone called weak learners.86,87 Weak learner is an algorithm that generates classifiers that can merely do better than random guessing. In order to design an ensemble system, three questions need to be answered: (i) How will the individual classifiers (base classifiers) be generated? (ii) What is the number of ensemble members? and (iii) what is the ensemble aggregation method? What follows briefly describes the framework for ensemble learning used in this study.
In this study, we used classification trees as the weak learners. Classification trees are decision trees which predict a response following the decisions in the tree from the root node down to the leaf nodes where the responses are. Figure 8 shows an individual decision tree made by the model at an arbitrary iteration number. The flow of data points is split at each node based on the condition at each internal node. Each data point flows to one of the leaves following the direction on each node. When a data point reaches a leaf, a weight is assigned to it as the prediction score. The predictive algorithm would then combine the prediction scores that each data point gains from the ensemble members to make the final decision about the class to which it belongs, whether lighting-active or lighting-inactive. For ease of presentation, the maximum depth of the tree is limited to 3 in Fig. 8. In the real training, however, the parameters are tuned using hyperparameter tuning skills.
Sample of a decision tree grown by the ML model in the ensemble classifier. In this example, the maximum depth of the tree is set to 3 and subset 1 is used as the training set. The prediction score at each leaf would be assigned to its associated observations. The model then combines the prediction scores for each sample to predict its class as whether lightning active or lightning-inactive
Boosting is a machine learning ensemble algorithm that is based on the idea that a weak learner can be turned into a strong learner that generates a classifier that is arbitrarily well-correlated with the true classification. Most boosting algorithms consist of iteratively learning weak classifiers and adding them to a final strong classifier. At each iteration, the algorithm attempts to construct a new model that corrects the errors of its predecessor. Hence, the next weak learner will learn from an updated version of residual errors.
The XGBoost algorithm is called gradient boosting since the objective function is optimized using the gradient descent algorithm before each new model is added. The objective function consists of two terms: The loss function, which is put as a measure of the predictive power, and the regularization factor, which controls the complexity of the model which helps to avoid overfitting. At each iteration, the algorithm needs to solve two key problems: (i) How to define the structure of the next weak learner (decision tree) in the ensemble so that it improves the overall prediction skill, and (ii) how to assign the prediction scores to the leaves. The algorithm uses gradient descent to solve these two problems. To build a tree, the algorithm greedily enumerates the features and finds the best splitting point by calculating the split gains. After each split, it assigns the weight to the two new leaves grown on the tree. This process continues repeatedly until the maximum depth is reached. The algorithm then starts pruning the tree backwards and removes nodes with a negative gain.
More information about the XGBoost algorithm including the definition and calculation of the loss function, regularization function, and split gain can be found in Chen and Guestrin85 and Chen and He.30
For each subset of the data, some hyperparameters of the model such as the number of trees or iterations in the ensemble (number of learners), the rate at which the gradient boosting learns (learning rate), and the depth of the tree (maximum depth), were optimally selected using both manual and AutoML approaches.
In the manual approach, the model was first initialized with a set of hyperparameters. Second, using 4-fold cross validation,88 we repeatedly split Data Part 1 at each station into four folds (groups) in a way that each group contains the data from a specific year. The XGBoost model was fitted on the data from 3 years (training set) and evaluated on the data from the remaining one year (validation set). This process is repeated until each group (each year of data) had been assigned once as the validation set. At the end, the results from all four runs were summarized to give the overall classification skill. The hyperparameters of the model at each station were tuned in order to improve the summarized cross validation scores. The AutoML approaches, in turn, do an intelligent search inside the hyperparameter space sweeping a broad range of possible combinations to find the optimized set of parameters that perform best on the given data (Data Part 1 at each station).84
Given the large temporal coverage and high temporal resolution of the gathered data, it is common that the data contains noise and outliers due to for instance to measurement errors. Removing the noise and outliers allows the learning algorithm to learn more accurate classification criteria and helps to provide better evaluation of the classification quality. We took advantage of the ML model evaluation results in Data Part 1 to find the conditions when the model has poor performance by looking at a random number of the misclassified instances. We then identified criteria that could explain these conditions and used them to identify samples in Data Part 2 with similar conditions to those of the outliers in Data Part 1. These samples were then removed from Data Part 2 with the presumption that the ML model would have no skill under those conditions. As a result of this filtering process, at some of the stations, a small portion of data (the size varied between 4 and 6% of the total data at each station) remained un-fitted and, hence, excluded from the final training and testing procedure based on Data Part 2. It is worth noting that the criteria to identify and filter the outliers on final evaluation were derived based on Data Part 1 and the filtering was done before the training and testing procedure based on Data Part 2. One should also note here that since this filtering process starts with selecting a random number of the misclassified samples in Data Part 1, different executions may lead to different results. More work is underway to optimize this process and to make it fully automatic.
Stage #2: training and testing procedure
As mentioned in the previous section (Stage #1), to do the final evaluation, the predictive ML model was trained and tested based on Data Part 2. To do this, at each station, Data Part 2 was split into different groups in such a way that each group contained the data from an individual year. As a result, each observation in the dataset was assigned to an individual group and remained there for the duration of the training and testing process. For each unique group, the group was held out from the dataset as the test set and the training was done using the remaining groups as the training set. The XGBoost model with the hyperparameters already optimized based on Data Part 1 was then fitted on the training set and evaluated on the test set. The prediction results on the test set were evaluated using the evaluation metrics. The process continued until each individual group had been taken once as the test set. The evaluation results were combined over the rounds to summarize the model prediction skill. This validation method is similar to the k-fold cross validation whereas the folds are forced to be the data from individual years and are not randomly selected from the shuffled data. This splitting method would help to eliminate the leakage of correlated samples from the training set into the test set due to the high temporal correlation of lightning data. The proposed approach in Stages #1 and #2 is summarized in Fig. 9.
In order to provide lead to the warnings, the observational data for meteorological parameters for a given 10-min interval was used to do the prediction for the following intervals. To achieve this, instead of feeding the model with the labels of the same interval, the labels for the following intervals should be used. Given the fact that both the meteorological and lightning data were imported into the database with the granularity of ten minutes, the lead times would also be quantized in 10-min ranges. For example, if the model is fed with the lightning labels corresponding to the same interval as the one for the meteorological data, then the lead time for the warnings would be 0–10 minutes, which corresponds to an imminent warning. However, if, instead, the lightning labels for the next interval were used, then the lead time of the prediction would be 10–20 minutes.
Model evaluation metrics
Even in high activity regions, lightning strikes are rare. It is important for the nowcasting scheme to correctly predict non-lightning events (lightning-inactive samples) which numerically dominate lightning events. However, while a low false alarm rate is desirable, it is not indicative of predictive skill when true alarms are rare. In other words, in imbalanced databases, neither the overall accuracy nor the false alarm rate may be able to correctly evaluate the significance with which the prediction scheme performs better than chance.89 To bridge the gap, a couple of metrics to measure the skill in rare event forecasting are suggested in the literature which are mainly based on the values of the contingency table.90 A sample of a contingency table for the two-class prediction scheme is given in Table S2. The rows and columns correspond, respectively, to the observed and predicted alternatives. Giving a customized definition for the case of lightning prediction studied in this paper, for example, hit is the total number of times that at least one lightning activity (either CG or IC) occurred in a specific area in a specific time frame as it was correctly predicted by the predictive scheme. The specific area corresponds to the areas within the circular distance of radius 30 km (based on the adopted definition for long-range activity) around each of the 12 stations and the specific time frames are 10-min time windows defined according to the desired lead time. Similarly, correct rejection denotes the total number of times that the predictive model responds that lightning will not occur when it indeed did not occur. The Miss parameter gives the number of cases that the predictive scheme actually misses the occurred events and False Alarm gives the number of cases when the model would predict lightning when it did not occur. Based on the four described entries in the contingency matrix, a couple of performance parameters are adapted and defined in Table 1.
Probability of Detection (POD) is defined as the ratio of the hits to the total number of observed events (lighting-active samples). This parameter shows how the prediction scheme was able to correctly predict the rare events (lighting-active samples). However, it does not provide any information on how the model performs in the majority of cases where no lightning has actually occurred. The False Alarm Ratio (FAR) indicates the fraction of lightning alarms issued by the model that were actually false. The Critical Success Index (CSI) is sensitive to both POD and FAR since it penalizes both misses and false alarms. It can be also regarded as a measurement of accuracy when correct rejections are removed from consideration assuming that they are less important. Therefore, it concentrates on the fraction of hits to the total number of both forecast and missed events.
The Heidke Skill Score (HSS) is also used to evaluate the performance of the model. The score ranges from −∞ for no skill to 1 for perfect skill and it measures the performance of the prediction scheme after eliminating the correct predictions that would have been achieved purely by random chance. The Heidke Skill Score (HSS) is known to be usable in forecasting rare events since it gives credit to the correct rejections in a controlled way so that the false alarms are also considered. It is also known to take into account the correct random forecasts of both event and non-event cases.90 The performances of the ML model and the competitive models are evaluated using the aforementioned metrics.
Data availability
The data for the meteorological parameters and lighting activity are available for users in the field of teaching and research from: https://gate.meteoswiss.ch/idaweb/login.do. The data for CAPE can be retrieved from: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab = form. The electrostatic field data are available upon request from the corresponding author.
Code availability
The codes relevant to this paper are available upon request from the corresponding author.
References
Cooper, M. A. & Holle, R. L. Current Global Estimates of Lightning Fatalities and Injuries. 65–73 (Springer, Cham, 2019). https://doi.org/10.1007/978-3-319-77563-0_6.
Holle, R. L. Annual rates of lightning fatalities by country. in 20th International Lightning Detection Conference 2425, (2008).
Cerveny, R. S. et al. WMO assessment of weather and climate mortality extremes: lightning, tropical cyclones, tornadoes, and hail. Weather. Clim. Soc. 9, 487–497 (2017).
Badoux, A., Andres, N., Techel, F. & Hegg, C. Natural hazard fatalities in Switzerland from 1946 to 2015. Nat. Hazards Earth Syst. Sci. 16, 2747–2768 (2016).
Watson, A. I., López, R. E., Holle, R. L. & Daugherty, J. R. The relationship of lightning to surface convergence at kennedy space center: a preliminary study. Weather Forecast. 2, 140–157 (1987).
Watson, A. I., Holle, R. L., López, R. E., Ortiz, R. & Nicholson, J. R. Surface wind convergence as a short-term predictor of cloud-to-ground lightning at kennedy space center. Weather Forecast. 6, 49–64 (1991).
Uadiale, S., Urban, E., Carvel, R., Lange, D. & Rein, G. Overview of problems and solutions in fire protection engineering of wind turbines. Fire Saf. Sci. 11, 983–995 (2014).
Yokoyama, S., Honjo, N., Yasuda, Y. & Yamamoto, K. Causes of wind turbine blade damages due to lightning and future research target to get better protection measures. in 2014 International Conference on Lightning Protection (ICLP) 823–830 (IEEE, 2014).
Braam, H. et al. Lightning Damage of OWECS Part 3: ‘Case Studies’. (Energieonderzoek Centrum Nederland (ECN), Petten, 2002).
Reynolds, S. E., Brook, M. & Gourley, M. F. Thunderstorm charge separation. J. Meteorol. 14, 426–436 (1957).
Saunders, C. P. R., Bax-norman, H., Emersic, C., Avila, E. E. & Castellano, N. E. Laboratory studies of the effect of cloud conditions on graupel/crystal charge transfer in thunderstorm electrification. Q. J. R. Meteorol. Soc. 132, 2653–2673 (2006).
Carey, L. D., Buffalo, K. M., Carey, L. D. & Buffalo, K. M. Environmental control of cloud-to-ground lightning polarity in severe storms. Mon. Weather Rev. 135, 1327–1353 (2007).
MacGorman, D. R., Straka, J. M. & Ziegler, C. L. A lightning parameterization for numerical cloud models. J. Appl. Meteorol. 40, 459–478 (2001).
Mansell, E. R., MacGorman, D. R., Ziegler, C. L. & Straka, J. M. Simulated three-dimensional branched lightning in a numerical thunderstorm model. J. Geophys. Res. Atmos. 107, ACL 2-1–ACL 2-12 (2002).
Mansell, E. R., MacGorman, D. R., Ziegler, C. L. & Straka, J. M. Charge structure and lightning sensitivity in a simulated multicell thunderstorm. J. Geophys. Res. D Atmos. 110, 1–24 (2005).
Fierro, A. O., Mansell, E. R., MacGorman, D. R. & Ziegler, C. L. The implementation of an explicit charging and discharge lightning scheme within the WRF-ARW model: benchmark simulations of a continental squall line, a tropical cyclone, and a winter storm. Mon. Weather Rev. 141, 2390–2415 (2013).
Helsdon, J., Wojcik, W. & Farley, R. An examination of thunderstorm-charging mechanisms using a two-dimensional storm electrification model. J. Geophys. Res. 106, 1165–1192 (2001).
Fierro, A. O. et al. The implementation of an explicit charging and discharge lightning scheme within the WRF-ARW model: benchmark simulations of a continental squall line, a tropical cyclone, and a winter storm. Mon. Weather Rev. 141, 2390–2415 (2013).
Fierro, A. O., Mansell, E. R., Ziegler, C. L. & Macgorman, D. R. Explicit electrification and lightning forecast implemented within the WRF-ARW model. In XV International Conference on Atmospheric Electricity (2014).
Field, P. R., Roberts, M. J. & Wilkinson, J. M. Simulated lightning in a convection permitting global model. J. Geophys. Res. Atmos. 123, 9370–9377 (2018).
Dowdy, A. J. Seasonal forecasting of lightning and thunderstorm activity in tropical and temperate regions of the world. Sci. Rep. 6, 20874 (2016).
Romps, D. M. et al. CAPE times P explains lightning over land but not the land‐ocean contrast. Geophys. Res. Lett. 45, 12,623–12,630 (2018).
Bates, B. C., Dowdy, A. J. & Chandler, R. E. Lightning prediction for australia using multivariate analyses of large-scale atmospheric variables. J. Appl. Meteorol. Climatol. 57, 525–534 (2018).
Lopez, P. A lightning parameterization for the ECMWF integrated forecasting system. Mon. Weather Rev. 144, 3057–3075 (2016).
Price, C. & Rind, D. A simple lightning parameterization for calculating global lightning distributions. J. Geophys. Res. Atmos. 97, 9919–9933 (1992).
Lynn, B. H. et al. Predicting cloud-to-ground and intracloud lightning in weather forecast models. Weather Forecast. 27, 1470–1488 (2012).
Tippett, M. K. & Koshak, W. J. A baseline for the predictability of U.S. cloud‐to‐ground lightning. Geophys. Res. Lett. 45, 10,719–10,728 (2018).
Mecikalski, J., Jewett, C., Carey, L., Zavodsky, B. & Stano, G. An integrated 0-1 h first-flash lightning nowcasting, lightning amount and lightning jump warning capability. In 7th Conference on the Meteorological Applications of Lightning Data.
Charba, J. P. & Samplatsky, F. G. Operational 2-h thunderstorm guidance forecasts to 24 h on a 20-km grid. in Preprints, 23rd Conf. on Weather Analysis and Forecasting/19th Conf. on Numerical Weather Prediction, Omaha, NE, Amer. Meteor. Soc. B 17, (2009).
Chen, T. & He, T. Higgs boson discovery with boosted trees. in HEPML’14 Proceedings of the 2014 International Conference on High-Energy Physics and Machine Learning 42, 69–80 (2015).
Seroka, G. N., Orville, R. E. & Schumacher, C. Radar nowcasting of total lightning over the kennedy space center. Weather Forecast. 27, 189–204 (2012).
Sumathi, S. & Sivanandam, S. N. Introduction to Data Mining and its Applications. (Springer, 2006).
Libbrecht, M. W. & Stafford Noble, W. Machine learning applications in genetics and genomics. Nat. Rev. Genet. 16, 321–322 (2015).
Alpaydin, E. Introduction to Machine Learning. (MIT press, 2014).
Perlich, C., Dalessandro, B., Raeder, T., Stitelman, O. & Provost, F. Machine learning for targeted display advertising: transfer learning in action. Mach. Learn. 95, 103–127 (2014).
Jordan, M. I. & Mitchell, T. M. Machine learning: trends, perspectives, and prospects. Science 349, 255–260 (2015).
Kerepesi, C., Daróczy, B., Sturm, Á., Vellai, T. & Benczúr, A. Prediction and characterization of human ageing-related proteins by using machine learning. Sci. Rep. 8, 4094 (2018).
Bracco, A., Falasca, F., Nenes, A., Fountalis, I. & Dovrolis, C. Advancing climate science with knowledge-discovery through data mining. npj Clim. Atmos. Sci. 1, 20174 (2018).
Jones, N. How machine learning could help to improve climate forecasts. Nature 548, 379–380 (2017).
McGovern, A. et al. Using artificial intelligence to improve real-time decision-making for high-impact weather. Bull. Am. Meteorol. Soc. 98, 2073–2090 (2017).
Manzato, A. Hail in Northeast Italy: a neural network ensemble forecast using sounding-derived indices. Weather Forecast. 28, 3–28 (2013).
Lagerquist, R., McGovern, A. & Smith, T. Machine learning for real-time prediction of damaging straight-line convective wind. Weather Forecast. 32, 2175–2193 (2017).
Herman, G. R. & Schumacher, R. S. “Dendrology” in numerical weather prediction: what random forests and logistic regression tell us about forecasting extreme precipitation. Mon. Weather Rev. 146, 1785–1812 (2018).
Karstens, C. D. et al. Development of a human–machine mix for forecasting severe convective events. Weather Forecast. 33, 715–737 (2018).
Latham, J., Petersen, W. A., Deierling, W. & Christian, H. J. Field identification of a unique globally dominant mechanism of thunderstorm electrification. Q. J. R. Meteorol. Soc. 133, 1453–1457 (2007).
Cooray, V. Interaction of Lightning Flashes with the Earth’s Atmosphere. in An Introduction to Lightning 341–358 (Springer Netherlands, 2015). https://doi.org/10.1007/978-94-017-8938-7_19.
Jirak, I. L., Melick, C. J. & Weiss, S. J. Combining probabilistic ensemble information from the environment with simulated storm attributes to generate calibrated probabilities of severe weather hazards. in Preprints, 27th Conf. Severe Local Storms (2014).
African Centres for Lightning and Electromagnetics Network: Home. Available at: https://aclenet.org/. (Accessed on 5 Aug 2019).
Berger, K. Novel observations on lightning discharges: results of research on mount san salvatore. J. Franklin Inst. 283, 478–525 (1967).
Li, D. et al. On Lightning Electromagnetic Field Propagation Along an Irregular Terrain. IEEE Trans. Electromagn. Compatibility 58, 161–171 (2016).
Smorgonskiy, A., Rachidi, F., Rubinstein, M., Diendorfer, G. & Schulz, W. On the proportion of upward flashes to lightning research towers. Atmos. Res. 129 – 130, 110–116 (2013).
Mostajabi, A. et al. LMA observation of upward flashes at säntis tower: preliminary results. in Joint IEEE International Symposium on Electromagnetic Compatibility & Asia-Pacific Symposium on Electromagnetic Compatibility 2–5 (2018).
Antonio da Silva Ferro, M., Yamasaki, J., Roberto Pimentel, D. M., Pinheiro Naccarato, K. & Magalhães Fares Saba,M. Lightning risk warnings based on atmospheric electric field measurements in Brazil. J. Aerosp.Technol. Manag. 3, 301–310 (2011).
Aranguren, D. et al. On the lightning hazard warning using electrostatic field: Analysis of summer thunderstorms in Spain. J. Electrostat. 67, 507–512 (2009).
Murphy, M. J., Demetriades, N. W. S. & Cummins, K. L. Probabilistic early warning of cloud-to-ground lightning at an airport. in 16th Conference on Probability and Statistics in the Atmospheric Sciences, 126–131 (2000).
Dewan, A., Ongee, E. T., Rafiuddin, M., Rahman, M. M. & Mahmood, R. Lightning activity associated with precipitation and CAPE over Bangladesh. Int. J. Climatol. 38, 1649–1660 (2018).
Mathworks. (2019). Least-Squares Fitting: User’s Guide (R2019a). https://ch.mathworks.com/help/curvefit/least-squares-fitting.html. (Accessed on 17 May 2019).
Jolliffe, I. T. Principal Components in Regression Analysis. (Springer-Verlag, New York, 1986). https://doi.org/10.1007/978-1-4757-1904-8.
Richman, M. B. Rotation of principal components. J. Climatol. 6, 293–335 (1986).
Karagiannidis, A., Lagouvardos, K. & Kotroni, V. The use of lightning data and Meteosat infrared imagery for the nowcasting of lightning activity. Atmos. Res. 168, 57–69 (2016).
Meng, Q., Yao, W. & Xu, L. Development of lightning nowcasting and warning technique and its application. Adv. Meteorol. 2019, 1–9 (2019).
Brynjolfsson, E. & Mitchell, T. What can machine learning do? Workforce implications. Science 358, 1530–1534 (2017).
Schultz, C. J. et al. Preliminary development and evaluation of lightning jump algorithms for the real-time detection of severe weather. J. Appl. Meteorol. Climatol. 48, 2543–2563 (2009).
Smith, M. R. & Martinez, T. Improving classification accuracy by identifying and removing instances that should be misclassified. in The 2011 International Joint Conference on Neural Networks 2690–2697 (IEEE, 2011). https://doi.org/10.1109/IJCNN.2011.6033571.
Met Office WOW - Home Page. http://wow.metoffice.gov.uk/. (Accessed on 20 Feb 2019).
Personal Weather Station Network | Weather Underground. https://www.wunderground.com/weatherstation/overview.asp. (Accessed on 20 Feb 2019).
Certification of monitoring stations - MeteoSwiss. https://www.meteoswiss.admin.ch/home/measurement-and-forecasting-systems/land-based-stations/automatisches-messnetz/certification-of-monitoring-stations.html. (Accessed on 22 Feb 2019).
Data preparation - MeteoSwiss. https://www.meteoswiss.admin.ch/home/measurement-and-forecasting-systems/datenmanagement/data-preparation.html. (Accessed on 22 Feb 2019).
The measurement values journey from the station to the customers - MeteoSwiss. https://www.meteoswiss.admin.ch/content/dam/meteoswiss/de/Mess-und-Prognosesysteme/Datenmanagement/doc/DWH_Weg_der_Daten_v1_0.pdf. (Accessed on 22 Feb 2019).
Lightning detection network - MeteoSwiss. https://www.meteoswiss.admin.ch/home/measurement-and-forecasting-systems/atmosphere/lightning-detection-network.html. (Accessed on 11 July 2018).
Azadifar, M. et al. Evaluation of the performance characteristics of the European Lightning Detection Network EUCLID in the Alps region for upward negative flashes using direct measurements at the instrumented Säntis Tower. J. Geophys. Res. Atmos. (2016). https://doi.org/10.1002/2015JD024259.
Schulz, W., Diendorfer, G., Pedeboy, S. & Poelman, D. R. The European lightning location system EUCLID – Part 1: performance analysis and validation. Nat. Hazards Earth Syst. Sci. 16, 595–605 (2016).
Lightning detection network. (2016). http://www.meteoswiss.admin.ch/home/measurement-and-forecasting-systems/atmosphere/lightning-detection-network.html.
Our European detection network | Météorage. https://www.meteorage.com/who-are-we/our-european-detection-network. (Accessed on 4 Mar 2019).
Mostajabi, A. et al. LMA observation of upward flashes at Säntis Tower: Preliminary results. in 2018 IEEE International Symposium on Electromagnetic Compatibility and 2018 IEEE Asia-Pacific Symposium on Electromagnetic Compatibility (EMC/APEMC) 399–402 (IEEE, 2018). https://doi.org/10.1109/ISEMC.2018.8393808.
Measurement instruments - MeteoSwiss. https://www.meteoswiss.admin.ch/home/measurement-and-forecasting-systems/land-based-stations/automatisches-messnetz/measurement-instruments.html. (Accessed on 24 Feb 2019).
Copernicus Climate Change Service (C3S) (2017): ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate. Copernicus Climate Change Service Climate Data Store (CDS). https://confluence.ecmwf.int/display/CKB/ERA5+data+documentation#ERA5datadocumentation-HowtociteERA5. (Accessed on 21 Feb 2019).
ECMWF | Parameter details. https://apps.ecmwf.int/codes/grib/param-db/?id=59. (Accessed on 22 July 2019).
Romero, C. et al. A system for the measurements of lightning currents at the Säntis Tower. Electr. Power Syst. Res. 82, 34–43 (2012).
Romero, C., Rachidi, F., Rubinstein, M. & Paolone, M. Lightning currents measured on the Säntis Tower: a summary of the results obtained in 2010 and 2011. in 2013 IEEE International Symposium on Electromagnetic Compatibility 825–828 (2013). https://doi.org/10.1109/ISEMC.2013.6670524.
Azadifar, M. et al. An Update on the instrumentation of the säntis tower in switzerland for lightning current measurements and obtained results. in CIGRE Int. Colloquium on Lightning and Power Systems (2014).
Azadifar, M. Characteristics of Upward Lightning Flashes. 7988, (Swiss Institute of Technology (EPFL), 2017).
Olson, R. S., Urbanowicz, R. J., Andrews, P. C., Lavender, N. A. & Moore, J. H. Automating biomedical data science through tree-based pipeline optimization. in European Conference on the Applications of Evolutionary Computation 123–137 (Springer, 2016).
Olson, R. S. et al. Automating biomedical data science through tree-based pipeline optimization. in European Conference on the Applications of Evolutionary Computation 123–137 (Springer, Cham, 2016). https://doi.org/10.1007/978-3-319-31204-0_9.
Chen, T. & Guestrin, C. XGBoost: a scalable tree boosting system. in KDD ’16 Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 785–794 (2016). https://doi.org/10.1145/2939672.2939785.
Polikar, R. Ensemble based systems in decision making. Circuits Syst. Mag. IEEE 6, 21–45 (2006).
Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 33, 1–39 (2010).
Casella, G., Fienberg, S. & Olkin, I. An Introduction to statistical learning with Applications in R. in Springer Texts in Statistics (Springer, New York, 2013).
Brodersen, K. H., Ong, C. S., Stephan, K. E. & Buhmann, J. M. The Balanced Accuracy and Its Posterior Distribution. in 2010 20th International Conference on Pattern Recognition 3121–3124 (IEEE, 2010). https://doi.org/10.1109/ICPR.2010.764.
Doswell, C. A., Davies-Jones, R. & Keller, D. L. On summary measures of skill in rare event forecasting based on contingency tables. Weather Forecast. 5, 576–585 (1990).
Acknowledgements
This work was supported in part by the Swiss National Science Foundation (Project No. 200020_175594) and the European Union’s Horizon 2020 research and innovation program under grant agreement No 737033-LLR. The atmospheric and parts of lightning activity data have been provided by the Swiss Federal Office of Meteorology and Climatology (MeteoSwiss). We thank the ECMWF and the Copernicus Climate Change (C3S) programme for providing the ERA5 reanalysis data.
Author information
Authors and Affiliations
Contributions
A.M. conceived the study, developed the model, and ran the classifications. D.L.F. advised on interpreting the results and model evaluation strategies. M.R. and F.R. supervised the study and contributed to the results analysis. A.M. led the manuscript preparation with contribution from D.L.F.; all co-authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mostajabi, A., Finney, D.L., Rubinstein, M. et al. Nowcasting lightning occurrence from commonly available meteorological parameters using machine learning techniques. npj Clim Atmos Sci 2, 41 (2019). https://doi.org/10.1038/s41612-019-0098-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-019-0098-0
This article is cited by
-
Hybrid AI-enhanced lightning flash prediction in the medium-range forecast horizon
Nature Communications (2024)
-
An automated technique and decision support system for lightning early warning
International Journal of Environmental Science and Technology (2024)
-
Lightning nowcasting with aerosol-informed machine learning and satellite-enriched dataset
npj Climate and Atmospheric Science (2023)
-
Classification of precipitation types in Poland using machine learning and threshold temperature methods
Scientific Reports (2023)
-
Convective Storm VIL and Lightning Nowcasting Using Satellite and Weather Radar Measurements Based on Multi-Task Learning Models
Advances in Atmospheric Sciences (2023)