Abstract
There is a growing need for skilful predictions of climate up to a decade ahead. Decadal climate predictions show high skill for surface temperature, but confidence in forecasts of precipitation and atmospheric circulation is much lower. Recent advances in seasonal and annual prediction show that the signal-to-noise ratio can be too small in climate models, requiring a very large ensemble to extract the predictable signal. Here, we reassess decadal prediction skill using a much larger ensemble than previously available, and reveal significant skill for precipitation over land and atmospheric circulation, in addition to surface temperature. We further propose a more powerful approach than used previously to evaluate the benefit of initialisation with observations, improving our understanding of the sources of skill. Our results show that decadal climate is more predictable than previously thought and will aid society to prepare for, and adapt to, ongoing climate variability and change.
Similar content being viewed by others
Introduction
Human society and natural ecosystems are vulnerable to climate variability and change,1 which impacts food security, freshwater availability, spread of pests and diseases, heat waves, droughts, floods, cyclones, wildfires, energy supply and demand, transport, migration and conflict. There is, therefore, an urgent, and growing, need for climate information2,3,4 to inform the World Meteorological Organisation’s Global Framework for Climate Services5 and support the United Nations Sustainable Development Goals6 and the Sendai framework for disaster risk reduction.7
For climate information to be useful it should be credible.8,9 Many planners are particularly interested in the coming decade,10 and there is an increasing need for decadal climate predictions.4,11 An important advantage of decadal climate predictions compared to centennial climate projections is that their credibility can be assessed by performing retrospective forecasts (also known as hindcasts) of the historical period and comparing them against subsequent observations. Although previous assessments have shown high skill in decadal forecasts of surface temperature, confidence in predictions of precipitation and atmospheric circulation, which are vital for many climate impacts, is much lower.4,12,13,14,15,16,17 However, recent developments in seasonal forecasting have highlighted the need for very large ensembles to achieve skilful predictions especially for precipitation and atmospheric circulation.18,19,20,21,22,23 Here we take advantage of these developments to reassess decadal prediction skill using a larger multi-model ensemble than was previously available. We also propose a new approach for identifying the sources of skill in order to gain further confidence in forecasts.
Results
The signal-to-noise paradox
Although individual weather events cannot be predicted more than a couple of weeks ahead, slowly varying predictable components of the climate system, including ocean variability and changes in radiative forcing from greenhouse gases, aerosols and solar variations, influence the frequency, duration and intensity of weather events over the coming seasons to years. Hence some aspects of climate, for example, multi-year atmospheric circulation changes,24,25 the frequency of extreme weather events26 and total amounts of rainfall,27 are potentially predictable over the coming decade. Such forecasts will not be perfectly deterministic because uncertainties are inevitable due to the chaotic nature of the atmosphere, and errors will be introduced by imperfect climate models and imperfect knowledge of the initial state of the climate system. Taking the mean of an ensemble of forecasts reduces these uncertainties, since the different ensemble members sample different realisations of chaotic variability and, to some extent, uncertainties in the initial conditions and model formulation if different climate models are included. Ensemble averaging reduces the unpredictable noise to reveal the predictable signal in the models. The level of skill, and hence the usefulness of forecasts, depends on the magnitude of the predictable signal relative to the unpredictable noise (the signal-to-noise ratio).28
Recent studies of seasonal and annual forecasts have revealed that the signal-to-noise ratio can be far larger in observations than in climate models.18,19,20,21,23,29 This results in the surprising situation, referred to as the signal-to-noise paradox,20,21,30 where a climate model can predict the real world better than itself despite being an imperfect representation of the real world and a perfect representation of itself. Although this highlights a clear deficiency in climate models it also provides an opportunity to create skilful forecasts even with imperfect models by taking the mean of a very large ensemble in order to extract the predictable signal. Where the model signal-to-noise ratio is too small, the number of ensemble members needed to remove the noise and extract the signal will be larger than it would be if the signal-to-noise ratio were correct, and the amplitude of the resulting model predictable signal will be too small. Nevertheless, the ensemble mean signal may be highly skilful if it correlates with the observed variability, and its magnitude can be adjusted in a post-processing step to produce realistic forecasts.19,29,31,32
If the signal-to-noise paradox applies to decadal predictions then previous studies12,13,14,15,16,17 may have underestimated the skill. This is because the ensemble size may have been too small to remove the noise, or the skill measure used may have penalised errors in the magnitude of the predicted signal which could potentially be corrected before issuing forecasts. Indeed, averaging over many hindcast start dates to increase the ensemble size shows that decadal predictions capture many aspects of observed changes associated with large variations in the north Atlantic,33,34 and recent results with a large ensemble from one model show significant skill for predicting rainfall over land in some regions.35 We, therefore, reassess decadal prediction skill using a larger ensemble than was previously available, and focussing on anomaly correlation which is insensitive to errors in the magnitude of variability. In order to reduce modelling and initial condition uncertainties, we use multi-model hindcasts that start every year from 1960 to 2005 from the 5th Coupled Model Intercomparison Project (CMIP536) supplemented by three additional state-of-the-art decadal predictions systems to provide a total of 71 ensemble members from seven different climate models (Table 1, Methods). For the reasons above, we assess the correlation skill of the ensemble mean, for near-surface temperature, precipitation and mean sea level pressure. We average over forecast years 2–9 in order to avoid seasonal to annual predictability and focus specifically on decadal timescales (see Methods).
We illustrate our approach by first considering the North Atlantic Oscillation (NAO) for which seasonal to annual forecasts are clearly affected by the signal-to-noise paradox.18,19,20,23,29 The observed time-series of annual 8-year running mean NAO (black curve in Fig. 1a) is characterised by an increase from the 1960s reaching a peak for the period 1988–1994 (trend = 0.87 hPa/decade, p < 0.01) and a decrease thereafter (trend = −0.77 hPa/decade, p < 0.01). The model forecasts (red curve in Fig. 1a) also show an increase from the 1960s peaking for the period 1988–1994 (trend = 0.13 hPa/decade, p < 0.01), though the decrease thereafter is not significant (trend = −0.02 hPa/decade, p = 0.62). The agreement between the timing of observed and forecast variability results in a highly significant correlation skill (Fig. 1a inset, correlation r = 0.49, p = 0.02 allowing for autocorrelation in the time-series, see Methods). However, the model forecasts underestimate the observed amplitude of variability (note the different axes for the observations and models in Fig. 1a), and skill measured by the mean-squared-skill-score (MSSS14) is positive but not significant (MSSS = 0.17, p = 0.30).
The signal-to-noise paradox. a Time series of observed (black curve with red/blue shading showing positive/negative values) and model ensemble mean (years 2–9, red curve) 8-year running mean annual NAO index. Note different scales for observations (± 2hPa, left axis) and model ((± 0.4hPa, right axis). Inset shows the skill measured by MSSS and anomaly correlation (circles show the skill of the ensemble mean, whiskers show the 5–95% uncertainty range, see Methods). Straight lines show trends before and after the observed peak. b Anomaly correlation as a function of ensemble size for model ensemble mean forecasts of the observations (red curve with 5–95% confidence interval shaded, see Methods) and for model ensemble forecasts of an independent ensemble member (blue curve, averaged over all possible combinations). c–e The ratio of predictable components (RPC19) between observations and models for year 2–9 forecasts of near-surface temperature, precipitation and mean sea level pressure. RPC values significantly greater than one are stippled (crosses and circles show 90 and 95% confidence intervals, respectively). The NAO is calculated20 as the difference in pressure between two small boxes located around the Azores ([28–20°W, 36–40°N]) and Iceland ([25–16°W, 63–70N°])
The discrepancy in significance between correlation and MSSS skill measures arises because the modelled signal-to-noise ratio is too small: the models capture the phase of observed variability reasonably well but MSSS is sensitive to errors in the amplitude. This is confirmed in Fig. 1b which shows that the correlation is far higher for predicting the observations (red curve) than for predicting an individual model member (blue curve). Hence the predictable fraction of the total variability is larger in the real world than in the models. This behaviour is also found in seasonal and annual forecasts,18,20,23 and shows that the signal-to-noise paradox also applies to decadal forecasts of the NAO. Note also that the correlation increases slowly with ensemble size (red curve) confirming the need for large ensembles to obtain robust estimates of skill. Indeed, even with 71 members the forecasts are noisy (showing large inter-annual variability in overlapping 8 year periods, Fig. 1a red curve) and the correlation is still increasing, suggesting that higher skill would be achieved with an even larger ensemble. Indeed, a simple theoretical fit18,37 suggests the correlation could exceed 0.6 for an infinite ensemble.
The signal-to-noise paradox can be quantified by computing the ratio of predictable components (RPC) between observations and models.19,29,30 Since the correlation squared is the fraction of variance that is predictable, the RPC can be computed as the correlation skill for predicting the observations divided by the average correlation skill for predicting individual model members (where the square root has been taken for convenience). The expected value of the rpc should equal one for a perfect forecasting system; values greater than one are symptomatic of the signal-to-noise paradox where the real world is more predictable than models. The RPC for decadal predictions of the NAO is 6, compared to 2 or 3 for seasonal and annual timescales.19,20,23 Although some of this difference might arise from our use of a multi-model ensemble, our results clearly highlight the need for large ensembles to obtain robust estimates of skill. This conclusion is further strengthened by maps of RPC for temperature, precipitation and pressure (Fig. 1c–e) which show that the signal-to-noise paradox is widespread in decadal predictions, and generally larger for precipitation and pressure than for temperature.
Assessing the impact of initialisation
Decadal variations in climate can occur through internal variability of the climate system (the atmosphere, oceans, land and cryosphere), but they are also influenced by radiative changes from external factors, including greenhouse gases, aerosols (volcanic and anthropogenic) and solar variability.38 Climate projections39 aim to simulate the response to external factors, but cannot predict internal variability because the modelled internal variability is not aligned, on average, with that of the real world. In contrast, decadal predictions are initialised with observations of the ocean and the atmosphere, thereby aligning internal variability with reality and enabling some aspects of internal variability to be predicted. It is important to note that initialisation may also improve the response to external factors where these leave fingerprints, especially in the ocean, that are imperfectly simulated by models but can be corrected with observations. For example, if the NAO response to solar variability and/or volcanic eruptions is too weak in model simulations30 then their impacts on the ocean circulation will likely be too weak. Initialisation with observations would correct these fingerprints thereby improving skill. Hence, differences between initialised predictions and uninitialized simulations cannot necessarily be attributed to internal variability. Nevertheless, assessing the impact of initialisation provides valuable information on whether skill is dominated by external factors or whether internal variability could be playing a role, thereby highlighting the most important factors to be considered in order to reduce uncertainties in forecasts.
Previous studies have found fairly limited improvements from initialisation, mainly in the North Atlantic with little impact over land.12,13,14,15,17,24 However, the methods for comparing skill were not optimal resulting in a lack of power in the significance test and an underestimation of the impact of initialisation. The power of a significance test is defined as the probability that it will correctly detect a real signal, and depends largely on the size of the signal being tested,40,41,42 referred to as the effect size. Previous studies have assessed simple differences (or ratios) of skill, but this approach does not maximise the effect size when part of the skill is common to both sets of forecasts. For example, the global warming trend can lead to high anomaly correlations for both initialised forecasts and uninitialized simulations, with very little difference between them and hence a small effect size and low power of the significance test (see example below). This common signal introduces a bias that is not taken into account in standard significance tests and diminishes their power.43,44 In order to increase the effect size we directly test whether initialisation predicts any of the observed variability that is not already captured by the uninitialized simulations. Specifically, we create residual forecast and observed time-series by removing, via linear regression, the uninitialized ensemble mean from the initialised and observed time-series respectively. We then test whether these residuals are significantly correlated (see Methods, noting the adjustment needed to avoid introducing a bias). By construction, the residuals contain the variability in the observations and initialised predictions that is independent of the uninitialized simulations. Hence, their correlation is potentially much larger than the difference in correlation between initialised and uninitialized forecasts that contain common signals. By increasing the effect size our approach provides a more powerful assessment of the impact of initialisation, as demonstrated below.
We illustrate our approach with predictions of boreal summer (JJA, the average of June, July and August over forecast years 2–9) temperature in the sub-polar North Atlantic (SPNA). For the whole year this region shows a robust benefit from initialisation,45 but this is less clear for JJA (Fig. 2a). Both initialised and uninitialized forecasts capture the overall warming trend and are highly correlated with the observations (r = 0.98 and 0.95, respectively) but the benefit of initialisation is not detected by the difference in correlation which is small and not significant (Fig. 2a inset, r = 0.03, p = 0.29). However, observations and initialised forecasts are cooler than the uninitialized simulations in the late 1960s to early 1990s and warmer in other periods resulting in a significant correlation between residuals (Fig. 2b, r = 0.69, p = 0.05) and a clear improvement from initialisation. Furthermore, expanding our analysis to the whole globe shows that the enhanced power obtained by testing residuals reveals significant benefits from initialisation in many regions that are not seen by a simple difference in correlations (compare Fig. 2c, d), including over land in western Europe, western Africa and the Middle East.
The impact of initialisation. a Time series of observed (black curve) and initialised model ensemble mean (years 2–9, red curve) 8-year running mean boreal summer (JJA) sub-polar North Atlantic (SPNA) temperature. Ensemble mean uninitialized simulations are also shown (blue curve), and times when the observations are warmer/cooler than these are highlighted with red/blue shading. Inset shows the impact of initialisation measured by the difference in anomaly correlation. (b) As (a) but for the residual after linearly removing the ensemble mean uninitialized simulation from the observations and initialised forecasts (see Methods). Inset shows the impact of initialisation measured by the correlation between residuals. In both insets, circles show the ensemble mean, whiskers show the 5–95% uncertainty range (see Methods). c Global maps of the impact of initialisation measured by the difference between initialised and uninitialized correlation skill for years 2–9 JJA near-surface temperature. d As (c) but measured by the correlation between residuals. Stippling in (c) and (d) highlights significant values (crosses and circles show 90 and 95% confidence intervals, respectively), and green boxes show the SPNA region (60-10°W, 50–65°N)
Robust skill of decadal predictions
We now provide new estimates of decadal prediction skill together with the impact of initialisation (Fig. 3). The impact of initialisation depends on both the skill of predicting the residuals and the fraction of the total variability that they represent. We, therefore, rescale the correlation between residuals (see Methods) and present the impact of initialisation as the ratio of predicted signal arising from initialisation divided by the total predicted signal (Fig. 3b, d, f).
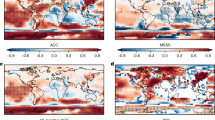
Robust skill of decadal predictions. a Correlation between year 2–9 initialised ensemble mean forecasts and observations for near-surface temperature. b The impact of initialisation computed as the ratio of predicted signal arising from initialisation divided by the total predicted signal (where positive/negative values show improved/reduced skill, see Methods). c, d As (a, b) but for precipitation. e, f As (a, b) but for mean sea level pressure. Stippling shows where correlations with observations (a, c, e) and of residuals (b, d, f) are significant (crosses and circles show 90 and 95% confidence intervals, respectively)
Our results provide robust evidence of decadal prediction skill for precipitation and pressure in addition to temperature (Fig. 3a, c, e). Temperature shows high skill almost everywhere, the main exceptions being the north-east Pacific and parts of the Southern Ocean. Precipitation shows reasonable skill (r > 0.6) in the Sahel and in a broad band across northern Europe and Eurasia, with lower but significant skill in parts of North and South America and the Maritime Continent. Pressure is also significantly skilful in most regions, the main exceptions being the eastern South Atlantic and western Indian Oceans, Africa and parts of Eurasia and the Southern Ocean.
In agreement with previous studies,12,13,14,15,17,24 temperature skill is particularly improved by initialisation in the SPNA and the Drake Passage region (Fig. 3b). However, we also find significant improvements over the western Indian Ocean, tropical and eastern Atlantic, and land regions including Europe, the Middle East and Africa. Initialisation significantly improves precipitation skill over the Sahel and western Amazon (Fig. 3d), but contributes little to the band of skill across northern Europe and Eurasia. Sea level pressure is mainly improved by initialisation in the North Atlantic (including both the Iceland and Azores nodes of the NAO, Fig. 1), north-east Europe and parts of the Southern Ocean (Fig. 3f). A detrimental impact of initialisation in the eastern South Atlantic and western Indian Oceans and northern Africa warrants further investigation given the significant improvement in temperature skill in these regions, suggesting that the relationship between surface temperature and atmospheric circulation anomalies is not simulated correctly by the initialised hindcasts.46
Regional predictions
Having established significant skill for decadal predictions of temperature, precipitation and pressure, we now investigate their ability to predict regional patterns. A key goal is to predict decadal variability in the Atlantic and Pacific, referred to here as Atlantic Multidecadal Variability (AMV, also known as the Atlantic Multidecadal Oscillation, AMO) and Pacific Decadal Variability (PDV, also referred to as the Pacific Decadal Oscillation, PDO, or the Interdecadal Pacific Oscillation, IPO). AMV switched from cool to warm conditions around 1995,45 with some evidence for a recent return to cool conditions.47,48,49 PDV switched to warm conditions around 1976, back to cool conditions around 1998, with some evidence for recent warm conditions.50 AMV (PDV) was warm (cool) during 1998–2014 and cool (warm) during 1978–1994 such that the difference between these periods summarises many aspects of decadal predictions, including predictions of AMV, PDV, greenhouse gas warming, and associated climate impacts. As noted above, the magnitude of forecast anomalies must be adjusted if the signal-to-noise ratio is incorrect. Although several objective methods have been proposed19,29,31,32 further work is needed to establish the best approach. We, therefore, follow the previous studies18,20,21 and simply compare forecasts and observations using standardised anomalies (Fig. 4).
Predicting regional patterns. a Composite difference between initialised year 2–9 temperature forecasts verifying during the periods 1998–2014 and 1978–1994. b As (a) but for the verifying observations. (c, d) As (a, b) but for precipitation. (e, f) As (a, b) but for mean sea level pressure. For each 8-year mean forecast period (years 2–9), observed and ensemble mean forecast anomalies were standardised at each grid point by dividing by their respective standard deviations before making composites. For temperature only, we first remove the global average from each grid point before standardising in order to accentuate regional patterns that are more likely to drive circulation changes than would globally uniform warming. Units are standard deviations of 8-year means. Stippling shows where the predictions and observations are significantly different (95% confidence)
Temperature differences between these periods are dominated by the global warming trend, which masks regional differences related to atmospheric circulation anomalies. To highlight regional patterns we remove the global average temperature from each 8 year period before computing temperature differences (Fig. 4a, b). This clearly highlights enhanced Arctic warming and greater warming over land than sea, which are robust patterns expected with global warming39,51,52,53 and are well captured by the predictions. The decadal predictions also capture the warm AMV, especially in the SPNA consistent with previous studies,54,55,56,57 although the relative warming in the tropical Atlantic is not captured. A negative PDV pattern is evident in the observations, seen as relatively cool conditions in the eastern tropical Pacific surrounded by a horse-shoe of warming to the west, north and south. The decadal predictions show some aspects of this pattern in the north Pacific but relative warming in the west and south Pacific is not captured. The PDV pattern is only partially simulated, and further work is needed to reconcile generally low skill for predicting PDV58,59 with an apparent ability to predict phase transitions.60 Both predictions and observations show relatively cool conditions over most of the Southern Ocean and Antarctica, but the observed warming west of the Antarctic Peninsula is not captured by the predictions which instead show warming further east.
Decadal predictions capture many aspects of the observed precipitation changes (Fig. 4c, d) including wetter conditions in the Sahel, north-west South America, the Maritime Continent and across northern Europe and Eurasia, and drier conditions in South America and south-west USA. Many of these changes in land precipitation appear to be part of large scale patterns extending over the ocean, including a northward shift of the Atlantic Intertropical Convergence Zone (ITCZ) consistent with warm AMV27,47,57,61,62 and an expansion of the Hadley circulation63 which is expected as climate warms.64 However, drier conditions in parts of Asia, the Middle East and East Africa are not captured by the predictions.
Predicted changes in pressure are clearly anti-correlated with temperature suggesting a heat low response to greater warming (hence lower pressure) over land than ocean (Fig. 4a, e). This pattern is also evident in the observations (Fig. 4f), especially over the Pacific and North and South America. However, in contrast to the predictions, observed pressure increased in the SPNA, Europe, Asia and northern Africa, and reduced in the Indian Ocean. The predictions also do not capture low pressure in the western Pacific where warming is underestimated. Reduced pressure over the Southern Ocean is seen in both predictions and observations, consistent with an increase in the Southern Annular Mode driven by increased greenhouse gases and reduced Antarctic ozone,65 although the predictions are zonal and do not capture regions of low pressure to the west of Africa and Australia. The ridge of high pressure extending north-east from the Caribbean is captured, along with reduced pressure in the subtropical North Atlantic consistent with a northward shift of the ITCZ.
Discussion
Our results show that the signal-to-noise paradox, in which the small predictable signal in climate model ensembles is inconsistent with their high level of agreement with observations, is widespread in multi-model decadal predictions, especially for precipitation and mean sea level pressure. This highlights a clear deficiency in climate models that urgently needs to be addressed. However, it also provides an opportunity to make skilful forecasts with existing models by extracting the signal from the mean of a very large ensemble and adjusting its variance. Using a larger multi-model ensemble than was previously available we demonstrate significant decadal prediction skill for precipitation and atmospheric circulation in addition to surface temperature.
Understanding the sources of skill is important for reducing uncertainties in forecasts. We propose a new approach for diagnosing the impact of initialisation that is more powerful than those used previously. This reveals significant benefits of initialisation including for temperature over Europe, Sahel rainfall, and north Atlantic pressure. However, the overall patterns of skill for temperature, precipitation and pressure are largely captured by the uninitialized simulations (compare Figs. 3a, c, e and 5), and improvements from initialisation generally occur in regions where the uninitialized simulations already have some skill. This could arise because: (1) improved skill arises from predicting internal variability in regions where there is an externally forced response; (2) externally forced skill in these regions is largely incidental66 and skill in initialised predictions arises mainly from internal variability; (3) the variability is predominantly externally forced and improved skill arises from correcting the modelled response to external factors. The first situation is particularly expected where there is a long term trend driven by slow variations in greenhouse gases. However, uninitialized simulations also capture aspects of the variability around the linear trend (Fig. 5b, d, f), highlighting the need for improved understanding of the roles of other external factors, including solar variations67,68,69 and volcanic70,71,72,73 and anthropogenic aerosols.74,75,76,77,78,79,80
Role of external forcing. a Correlation between ensemble mean uninitialized simulations and observations for near-surface temperature. b As (a) but after linearly detrending both observations and simulations. c, d As (a, b) but for precipitation. e, f As (a, b) but for mean sea level pressure. Correlations are computed for the same 8 year periods used to assess the initialised predictions (Fig. 3). Stippling in (a, c, e) shows where initialised predictions are more skilful, and in (b, d, f) where correlations are significant (crosses and circles show 90 and 95% confidence intervals, respectively)
We show that decadal predictions are able to capture many aspects of regional changes, including precipitation over land and atmospheric circulation in addition to surface temperature. There are also several differences between the forecasts and observations, and further work is needed to assess whether these are due to internal variability that was not predicted, incorrect responses to external factors or artefacts of initialisation. Nevertheless, the levels of skill are encouraging overall and support the recent establishment of operational decadal climate predictions endorsed by the World Meteorological Organization (WMO), building on the informal forecast exchange that has been running since 2010.81 The Decadal Climate Prediction Project17 contribution to CMIP6 will also provide ongoing forecasts with improved models and an even larger multi-model ensemble than used here. The World Climate Research Program (WCRP) Grand Challenge on Near Term Climate Prediction recently set out the case for operational decadal predictions4 including an Annual to Decadal Climate Update to be produced each year as an important first step towards operational services. Such information promises to benefit society by informing preparedness for, and adaptation to, near-term climate variability and change.
Methods
Observations and models
Near-surface temperature observations are computed as the average from HadCRUT4,82 NASA-GISS83 and NCDC.84 Precipitation observations are taken from GPCC85 and mean sea level pressure from HadSLP2.86 We assess a large multi-model ensemble (71 members, Table 1) of decadal predictions from seven forecast centres using hindcasts starting each year from 1960 to 2005 following the Coupled Model Intercomparison Project phase 5 (CMIP5) protocol.36 To assess the impact of initialisation we compare with an ensemble of uninitialized simulations (up to 56 members) that use the same climate models. We create ensemble means by taking the unweighted average of all ensemble members and assess rolling 8-year means defined by calendar years 2 to 9 from each start date of the initialised predictions. The forecasting systems start between 1st of November and January each year, giving a lead time of at least a year before the assessed forecast period to focus on decadal timescales and avoid skill arising from seasonal to annual variability. Both observations and models were interpolated to a 5° longitude by 5° latitude grid before comparison.
Impact of initialisation
We decompose the observed (o) and ensemble mean initialised forecast (f) anomaly time-series as
where \(\hat o\) and \(\hat f\) are the components that can be linearly explained by regression with the ensemble mean of the uninitialized simulations
where u is the uninitialized ensemble mean, σu, σf and σo are the standard deviations of u, f and o, and rou and rfu are the correlations between o and u and between f and u respectively.
The residuals o′ and f′ represent the variability that cannot be captured by the uninitialized simulations and their correlation (r′, also referred to as the partial correlation87) measures the impact of initialisation. Because the skill of f and u can be dominated by a common component (such as the global warming trend), r′ is potentially much greater than the difference in skill, thereby increasing the effect size and increasing the power of the test.40,41,42
It is important to note that errors in estimates of \(\hat o\) and \(\hat f\) arising from a finite ensemble size of u can produce a positive bias in r′. An unbiased estimate can be obtained by using independent estimates of u to obtain \(\hat o\) and \(\hat f\) separately. We do this by dividing the uninitialized ensemble into two independent halves and then estimate the bias by comparing biased and unbiased estimates of r′. This process is repeated using the block bootstrap approach describe below, from which we compute the median bias. We find the bias to be small (of order 10%) and remove it from the values computed for the full ensemble. Hence, our approach extends that used previously to compare seasonal forecasts from different models.87
The residuals could be highly correlated but represent only a small fraction of the predictable signal. We, therefore, present the impact of initialisation as the ratio of the predicted signal arising from initialisation divided by the total predicted signal, computed as \(\frac{{r\prime \sigma _o^\prime }}{{r\sigma _o}}\) where r is the total skill (the correlation between f and o), and \(\sigma _o^\prime\) is the standard deviation of o′.
Significance
For a given set of validation cases, we test for values that are unlikely to be accounted for by uncertainties arising from a finite ensemble size (E) and a finite number of validation points (T). This is achieved using a non-parametric block bootstrap approach,14,88 in which an additional 1000 hindcasts (or pairs of hindcasts for assessing skill differences) are created as follows:
-
1.
Randomly sample with replacement T validation cases. In order to take autocorrelation into account this is done in blocks of 5 consecutive cases.
-
2.
For each of these, randomly sample with replacement E ensemble members.
-
3.
Compute the required statistic for the ensemble mean (e.g., correlation, difference in correlation, partial correlation, RPC).
-
4.
Repeat from (1) 1000 times to create a probability distribution (PDF).
-
5.
Obtain the significance level based on a 2-tailed test of the hypothesis that skill (or skill difference) is zero, or RPC is one.
For skill as a function of ensemble size (Fig. 1b) we randomly sample without replacement to obtain the required number of ensemble members, and compute the average from 1000 repetitions. Uncertainties (pink shading) are computed based on single members since the samples are not independent for larger ensembles leading to an underestimated ranges.
Uncertainties in composite differences (Fig. 4) are computed using a standard t-test of the difference between two means.
Data availability
The datasets analysed during the current study are available from the corresponding author on reasonable request.
Code availability
The code used during the current study is available from the corresponding author on reasonable request.
Change history
03 April 2020
A Correction to this paper has been published: https://doi.org/10.1038/s41612-020-0118-0
References
IPCC. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (Cambridge University Press, 2014).
Goddard, L. From science to service. Science 353, 1366–1367 (2016).
Trenberth, K. E., Marquis, M. & Zebiak, S. The vital need for a climate information system. Nat. Clim. Change 6, 1057–1059 (2016).
Kushnir, Y. et al. Towards operational predictions of the near-term climate. Nat. Clim. Change 9, 94–101 (2019).
Hewitt, C., Mason, S. & Walland, D. The global framework for climate services. Nat. Clim. Change 2, 831–832 (2012).
U. N. General Assembly. Transforming our world: the 2030 agenda for sustainable development, Available from http://www.refworld.org/docid/57b6e3e44.html (2015).
for Disaster Reduction), U. U. N. I. S. Sendai framework for disaster risk reduction 2015–2030, http://www.wcdrr.org/uploads/Sendai_Framework_for_Disaster_Risk_Reduction_2015-2030.pdf (2015).
Lemos, M. C., Kirchhoff, C. J. & Ramprasad, V. Narrowing the climate information usability gap. Nat. Clim. Change 2, 789–794 (2012).
Mehta, V. et al. Decadal climate information needs of stakeholders for decision support in water and agriculture production sectors: A case study in the Missouri River Basin. Weather Clim. Soc. 5, 27–42 (2013).
Brasseur, G. P. & Gallardo, L. Climate services: lessons learned and future prospects. Earth’s Future 4, 79–89 (2016).
Xu, Y., Ramanathan, V. & Victor, D. G. Global warming will happen faster than we think. Nature 564, 30–32 (2018).
Kirtman, B. et al. Near-term climate change: Projections and predictability. In Stocker, T. F. et al. (eds.) Climate Change 2013: The Physical Science Basis. Contribution of Working Group I. to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (Cambridge University Press, 2013).
Doblas-Reyes, F. J. et al. Initialized near-term regional climate change prediction. Nat. Commun. 4, 1715 (2013).
Goddard, L. et al. A verification framework for interannual-to-decadal predictions experiments. Clim. Dyn. 40, 245–272 (2013).
Meehl, G. A. et al. Decadal climate prediction: An update from the trenches. Bull. Am. Meteorol. Soc. 95, 243–267 (2014).
Bellucci, A. et al. An assessment of a multi-model ensemble of decadal climate predictions. Clim. Dyn. 44, 2787–2806 (2014).
Boer, G. J. et al. The Decadal Climate Prediction Project (DCPP) contribution to CMIP6. Geosci. Model Dev. 9, 3751–3777 (2016).
Scaife, A. A. et al. Skillful long-range prediction of european and north american winters. Geophys. Res. Lett. 41, 2514–2519 (2014).
Eade, R. et al. Do seasonal-to-decadal climate predictions underestimate the predictability of the real world? Geophys. Res. Lett. 41, 5620–5628 (2014).
Dunstone, N. J. et al. Skilful predictions of the winter North Atlantic Oscillation one year ahead. Nature Geosci. 9, 809–815 (2016).
Dunstone, N. J. et al. Skilful seasonal predictions of summer European rainfall. Geophys. Res. Lett. 45, 3246–3254 (2018).
Athanasiadis, P. J. et al. A multisystem view of wintertime NAO seasonal predictions. J. Clim. 30, 1461–1475 (2017).
Baker, L. H., Shaffrey, L. C., Sutton, R. T., Weisheimer, A. & Scaife, A. A. An intercomparison of skill and over/underconfidence of the wintertime North Atlantic Oscillation in multi-model seasonal forecasts. Geophys. Res. Lett. 45, 7808–7817 (2018).
Smith, D. M. et al. Skilful climate model predictions of multi-year north Atlantic hurricane frequency. Nat. Geosci. 3, 846–849 (2010).
Monerie, P.-A., Robson, J., Dong, B. & Dunstone, N. A role of the Atlantic Ocean in predicting summer surface air temperature over North East Asia? Clim. Dyn 51, 473–491 (2018).
Eade, R., Hamilton, E., Smith, D. M., Graham, R. J. & Scaife, A. A. Forecasting the number of extreme daily events out to a decade ahead. J. Geophys. Res. 117, D21110 (2012).
Sheen, K. L. et al. Skilful prediction of Sahel summer rainfall on inter-annual and multi-year timescales. Nat. Commun. 8, 14966 (2017).
Kumar, A. Finite samples and uncertainty estimates for skill measures for seasonal prediction. Mon. Weather Rev. 137, 2622–2631 (2009).
Siegert, S. et al. A Bayesian framework for verification and recalibration of ensemble forecasts: How uncertain is NAO predictability? J. Clim. 29, 995–1012 (2016).
Scaife, A. A. & Smith, D. M. A signal-to-noise paradox in climate science. npj Climate and Atmospheric Science 1, 28 (2018).
Sansom, P. G., Ferro, C. A. T., Stephenson, D. B., Goddard, L. & Mason, S. J. Best practices for post-processing ensemble climate forecasts, part I: selecting appropriate recalibration methods. J. Clim. 29, 7247–7264 (2016).
Boer, G. J., Kharin, V. V. & Merryfield, W. J. Differences in potential and actual skill in a decadal prediction experiment. Clim. Dyn. https://link.springer.com/article/10.1007/s00382-018-4533-4 (2018).
Robson, J. I., Sutton, R. T. & Smith, D. M. Predictable climate impacts of the decadal changes in the ocean in the 1990s. J. Clim. 26, 6329–6339 (2013).
Robson, J. I., Sutton, R. T. & Smith, D. M. Decadal predictions of the cooling and freshening of the North Atlantic in the 1960s and the role of the ocean circulation. Clim. Dyn. 42, 2353–2365 (2014).
Yeager, S. G. et al. Predicting near-term changes in the earth system: A large ensemble of initialized decadal prediction simulations using the Community Earth System Model. Bull. Am. Meteorol. Soc. 99, 1867–1886 (2018).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498 (2012).
Murphy, J. M. Assessment of the practical utility of extended range ensemble forecasts. Q. J. R. Meteorol. Soc. 116, 89–125 (1990).
Cassou, C. et al. Decadal climate variability and predictability: challenges and opportunities. Bull. Am. Meteorol. Soc. 99, 479–490 (2018).
Collins, M. et al. Long-term climate change: Projections, commitments and irreversibility. In Stocker, T. F. et al. (eds.) Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 1029–1136 (Cambridge University Press, 2013).
Cohen, J. Statistical power analysis for the behavioral sciences. 2nd ed (Lawrence Erlbaum, New Jersey, 1988).
Murphy, K., Myors, B. & Wolach, A. Statistical Power Analysis (Routledge, New York, 2014).
Sienz, F., Müller, W. A. & Pohlmann, H. Ensemble size impact on the decadal predictive skill assessment. Meteorol. Z. 25, 645–655 (2016).
DelSole, T. & Tippett, M. K. Comparing forecast skill. Mon. Weather Rev. 142, 4658–4678 (2014).
Siegert, S., Bellprat, O., Ménégoz, M., Stephenson, D. B. & Doblas-Reyes, F. J. Detecting improvements in forecast correlation skill: Statistical testing and power analysis. Mon. Weather Rev. 145, 437–450 (2017).
Yeager, S. G. & Robson, J. I. Recent progress in understanding and predicting Atlantic decadal climate variability. Curr. Clim. Change Rep. 3, 112–127 (2017).
Wang, B. et al. Fundamental challenge in simulation and prediction of summer monsoon rainfall. Geophys. Res. Lett. 32, L15711 (2005).
Hermanson, L. et al. Forecast cooling of the Atlantic subpolar gyre and associated impacts. Geophys. Res. Lett. 41, 5167–5174 (2014).
Robson, J., Ortega, P. & Sutton, R. A reversal of climatic trends in the North Atlantic since 2005. Nat. Geosci. 9, 513–517 (2016).
Frajka-Williams, E., Beaulieu, C. & Duchez, A. Emerging negative atlantic multidecadal oscillation index in spite of warm subtropics. Sci. Rep. 7, 11224, https://www.nature.com/articles/s41598-017-11046-x (2017).
Newman, M. et al. The Pacific decadal oscillation, revisited. J. Clim. 29, 4399–4427 (2016).
Sutton, R. T., Dong, B. & Gregory, J. M. Land/sea warming ratio in response to climate change: IPCC AR4 model results and comparison with observations. Geophys. Res. Lett. 34, L02701 (2007).
Joshi, M. M., Gregory, J. M., Webb, M. J., Sexton, D. M. H. & Johns, T. C. Mechanisms for the land/sea warming contrast exhibited by simulations of climate change. Clim. Dyn. 30, 455–465 (2008).
Screen, J. A. & Simmonds, I. The central role of diminishing sea ice in recent arctic temperature amplification. Nature 464, 1334–1337 (2010).
Robson, J. I., Sutton, R. T. & Smith, D. M. Initialized decadal predictions of the rapid warming of the North Atlantic ocean in the mid 1990s. Geophys. Res. Lett. 39, L19713 (2012).
Yeager, S., Karspeck, A., Danabasoglu, G., Tribbia, J. & Teng, H. A decadal prediction case study: Late 20th century North Atlantic ocean heat content. J. Clim. 25, 5173–5189 (2012).
Msadek, R. et al. Predicting a decadal shift in North Atlantic climate variability using the GFDL forecast system. J. Clim. 27, 6472–6496 (2014).
García-Serrano, J., Guemas, V. & Doblas-Reyes, F. J. Added-value from initialization in predictions of Atlantic multi-decadal variability. Clim. Dyn. 44, 2539 (2015).
Kim, H.-M., Webster, P. J. & Curry, J. A. Evaluation of short-term climate change prediction in multi-model CMIP5 decadal hindcasts. Geophys. Res. Lett. 39, L10701 (2012).
Lienert, F. & Doblas-Reyes, F. Decadal prediction of interannual tropical and north Pacific sea surface temperature. J. Geophys. Res. 118, 5913–5922 (2013).
Meehl, G. A., Hu, A. & Teng, H. Initialized decadal prediction for transition to positive phase of the Interdecadal Pacific Oscillation. Nat. Commun. 7, 11718 (2016).
Zhang, R. & Delwoth, T. L. Impact of Atlantic multidecadal oscillations on India/Sahel rainfall and Atlantic hurricanes. Geophys. Res. Lett. 33, L17712 (2006).
Knight, J. R., Folland, C. K. & Scaife, A. A. Climate impacts of the atlantic multidecadal oscillation. Geophys. Res. Lett. 33, L17706 (2006).
Fu, Q., Johanson, C. M., Wallace, J. M. & Reichler, T. Enhanced mid-latitude tropospheric warming in satellite measurements. Science 312, 1179 (2006).
Lu, J., Vecchi, G. A. & Reichler, T. Expansion of the Hadley cell under global warming. Geophys. Res. Lett. 34, L06805 (2007).
Thompson, D. W. J. et al. Signatures of the Antarctic ozone hole in Southern Hemisphere surface climate change. Nat. Geosci. 4, 741–749 (2011).
Kim, W. M., Yeager, S. G. & Danabasoglu, G. Key role of internal ocean dynamics in Atlantic multidecadal variability during the last half century. Geophys. Res. Lett. 45, 13449–13457 (2018).
Ineson, S. et al. Solar forcing of winter climate variability in the Northern Hemisphere. Nat. Geosci. 4, 753–757 (2011).
Gray, L. et al. A lagged response to the 11-year solar cycle in observed winter Atlantic/European weather patterns. J. Geophys. Res. 118, 1–16 (2013).
Thieblemont, R., Matthes, K., Omrani, N.-E., Kodera, K. & Hansen, F. Solar forcing synchronizes decadal North Atlantic climate variability. Nat. Commun. 6, 8268 (2015).
Stenchikov, G. et al. Volcanic signals in oceans. J. Geophys. Res. 114, D16104 (2009).
Ottera, O. H., Bentsen, M., Drange, H. & Suo, L. External forcing as a metronome for Atlantic multidecadal variability. Nat. Geosci. 3, 688–694 (2010).
Swingedouw, D. et al. Bidecadal North Atlantic ocean circulation variability controlled by timing of volcanic eruptions. Nat. Commun. 6, 6545 (2015).
Zanchettin, D. Aerosol and solar irradiance effects on decadal climate variability and predictability. Curr. Clim. Change Rep. 3, 150–162 (2017).
Bollasina, M. A., Ming, Y. & Ramaswamy, V. Anthropogenic aerosols and the weakening of the South Asian summer monsoon. Science 334, 502–505 (2011).
Booth, B. B. B., Dunstone, N. J., Halloran, P. R., Andrews, T. & Bellouin, N. Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability. Nature 484, 228–232 (2012).
Cheng, W., Chiang, J. C. H. & Zhang, D. Atlantic meridional overturning circulation (AMOC) in CMIP5 models: RCP and historical simulations. J. Clim. 26, 7187–7197 (2013).
Bellucci, A. et al. Advancements in decadal climate predictability: the role of non-oceanic drivers. Rev. Geophys. 53, 165–202 (2015).
Acosta Navarro, J. C. et al. Amplification of Arctic warming by past air pollution reductions in europe. Nat. Geosci. 9, 277–281 (2016).
Smith, D. M. et al. Role of volcanic and anthropogenic aerosols in recent slowdown in global surface warming. Nat. Clim. Change 6, 936–940 (2016).
Giannini, A. & Kaplan, A. The role of aerosols and greenhouse gases in Sahel drought and recovery. Clim. Change 152, 449–466 (2018).
Smith, D. M. et al. Real-time multi-model decadal climate predictions. Clim. Dyn. 41, 2875–2888 (2013).
Morice, C. P., Kennedy, J. J., Rayner, N. A. & Jones, P. D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set. J. Geophys. Res. 117, D08101 (2012).
Hansen, J., Ruedy, R., Sato, M. & Lo, K. Global surface temperature change. Rev. Geophys. 48, https://agupubs.onlinelibrary.wiley.com/doi/10.1029/2010RG000345 (2010).
Karl, T. R. et al. Possible artifacts of data biases in the recent global surface warming hiatus. Science 348, 1469–1472 (2015).
Schneider, U. et al. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 115, 15–40 (2014).
Allan, R. J. & Ansell, T. J. A new globally complete monthly historical gridded mean sea level pressure data set (HadSLP2): 1850–2003. J. Clim. 19, 5816–5842 (2006).
DelSole, T., Nattala, J. & Tippett, M. K. Skill improvement from increased ensemble size and model diversity. Geophys. Res. Lett. 41, 7331–7342 (2014).
Wilks, D. S. Statistical methods in the atmospheric sciences, vol. 100 of International geophysics series 3rd edn (Academic Press, 2011).
Ménégoz, M., Bilbao, R., Bellprat, O., Guemas, V. & Doblas-Reyes, F. J. Forecasting the climate response to volcanic eruptions: prediction skill related to stratospheric aerosol forcing. Environ. Res. Lett. 13, 064022 (2018).
Doblas-Reyes, F. J. et al. Using EC-Earth for climate prediction research. In ECMWF Newsletter (ECMWF, 2018).
Kharin, V. V., Boer, G. J., Merryfield, W. J., Scinocca, J. F. & Lee, W.-S. Statistical adjustment of decadal predictions in a changing climate. Geophys. Res. Lett. 39, L19705 (2012).
Yang, X. et al. A predictable amo-like pattern in GFDLś fully-coupled ensemble initialization and decadal forecasting system. J. Clim. 26, 650–661 (2013).
Smith, D., Eade, R. & Pohlmann, H. A comparison of full-field and anomaly initialization for seasonal to decadal climate prediction. Clim. Dyn. 41, 3325–3338 (2013).
Chikamoto, Y. et al. An overview of decadal climate predictability in a multi-model ensemble by climate model MIROC. Clim. Dyn. 40, 1201–1222 (2012).
Mochizuki, T. et al. Decadal prediction using a recent series of MIROC global climate models. J. Meteorol. Soc. Jpn 90, 373–383 (2012).
Pohlmann, H. et al. Improved forecast skill in the tropics in the new MiKlip decadal climate predictions. Geophys. Res. Lett. 40, 5798–5802 (2013).
Acknowledgements
D.M.S., A.A.S., N.J.D., L.H. and R.E. were supported by the Met Office Hadley Centre Climate Programme funded by BEIS and Defra and by the European Commission Horizon 2020 EUCP project (GA 776613). L.P.C. was supported by the Spanish MINECO HIATUS (CGL2015-70353-R) project. F.J.D.R. was supported by the H2020 EUCP (GA 776613) and the Spanish MINECO CLINSA (CGL2017-85791-R) projects. W.A.M. and H.P. were supported by the German Ministry of Education and Research (BMBF) under the project MiKlip (grant 01LP1519A). The NCAR contribution was supported by the US National Oceanic and Atmospheric Administration (NOAA) Climate Program Office under Climate Variability and Predictability Program Grant NA13OAR4310138 and by the US National Science Foundation (NSF) Collaborative Research EaSM2 Grant OCE-1243015. The NCAR contribution is also based upon work supported by NCAR, which is a major facility sponsored by the US NSF under Cooperative Agreement No. 1852977. The Community Earth System Model Decadal Prediction Large Ensemble (CESM-DPLE) was generated using computational resources provided by the US National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US Department of Energy under Contract DE-AC02-05CH11231, as well as by an Accelerated Scientific Discovery grant for Cheyenne (https://doi.org/10.5065/D6RX99HX) that was awarded by NCAR’s Computational and Information System Laboratory.
Author information
Authors and Affiliations
Contributions
D.M.S. led the analysis with help from R.E., A.A.S. and T.M.DS. D.M.S. led the writing with comments from all authors. All authors except T.M.DS. created the data.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Smith, D.M., Eade, R., Scaife, A.A. et al. Robust skill of decadal climate predictions. npj Clim Atmos Sci 2, 13 (2019). https://doi.org/10.1038/s41612-019-0071-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-019-0071-y
This article is cited by
-
Wide range of possible trajectories of North Atlantic climate in a warming world
Nature Communications (2024)
-
Near-term temperature extremes in Iran using the decadal climate prediction project (DCPP)
Stochastic Environmental Research and Risk Assessment (2024)
-
SPEEDY-NEMO: performance and applications of a fully-coupled intermediate-complexity climate model
Climate Dynamics (2024)
-
Decadal prediction of Northeast Asian winter precipitation with CMIP6 models
Climate Dynamics (2024)
-
Causal oceanic feedbacks onto the winter NAO
Climate Dynamics (2024)