Abstract
Statistical inference of causal interactions and synchronization between dynamical phenomena evolving on different temporal scales is of vital importance for better understanding and prediction of natural complex systems such as the Earth’s climate. This article introduces and applies information theory diagnostics to phase and amplitude time series of different oscillatory components of observed data that characterizes El Niño/Southern Oscillation. A suite of significant interactions between processes operating on different time scales is detected and shown to be important for emergence of extreme events. The mechanisms of these nonlinear interactions are further studied in conceptual low-order and state-of-the-art dynamical, as well as statistical climate models. Observed and simulated interactions exhibit substantial discrepancies, whose understanding may be the key to an improved prediction of ENSO. Moreover, the statistical framework applied here is suitable for inference of cross-scale interactions in human brain dynamics and other complex systems.
Similar content being viewed by others
Introduction
A better understanding of dynamics in complex systems, such as the Earth’s climate or human brain, is one of the key challenges for contemporary science and society. A large amount of experimental data requires new mathematical and computational approaches. Natural complex systems vary on many temporal and spatial scales, often exhibiting recurring patterns and quasi-oscillatory phenomena. Data-driven approaches to detection and recognition of relationships between subsystems in complex systems have recently become an area of active study in a range of scientific fields. For example, thinking about the climate system as of a complex network of interacting subsystems1 presents a new paradigm that brings out new data analysis methods helping to detect, describe and predict atmospheric phenomena.2 A crucial step in constructing climate networks is the inference of network links between climate subsystems.3 Directed causal links determine which subsystems influence other subsystems, and their identification would thus uncover the drivers of atmospheric phenomena. A succinct formalized description of causal relationships and synchronizations in complex systems could significantly improve our understanding of such systems, which would in turn promote the development of better schemes to predict their evolution. Here, we investigate complex, multiple time-scale interactions in the El Niño/Southern Oscillation system in the equatorial Pacific.
El Niño/Southern Oscillation (ENSO hereafter) is a well known coupled ocean–atmosphere phenomenon, which manifests as a quasi-periodic fluctuation in sea-surface temperature (El Niño) and air pressure of the overlying atmosphere (Southern Oscillation) across the equatorial Pacific Ocean. It is comprised of two phases, with the warm phase, known as El Niño, being accompanied by a high surface pressure, and the cool phase, La Niña, being accompanied by a low surface pressure in the tropical western Pacific. Although the exact causes for initiating warm or cool ENSO events are not fully understood, the two components of ENSO—sea-surface temperature and atmospheric pressure—are strongly related. ENSO is one of the dominant contributors to the world’s interannual climate variability.4 Furthermore, strong ENSO events exert a large influence on the global atmospheric circulation5 via associated teleconnections,6 thus leading to significant socio-economic impacts. An important aspect of ENSO extreme events is that their positive phase, El Niño, exhibits larger magnitude than their negative phase, La Niña.7,8 This suggests that, at least to some extent, ENSO dynamics involve nonlinear processes.4,9
ENSO events occur irregularly, with a 2–7 year span between them, but have a well defined spatial pattern and seasonal dependence, with the start of development in boreal summer and a peak in boreal winter.10 The individual events generally evolve on a time scale of about two years.5,11 The mechanisms for this biennial variability of ENSO are not fully understood either, although it was previously suggested that it is due to year-to-year alternations between “weak” and “strong” annual cycles in the Indian ocean and western Pacific sector,12 with possible global repercussions.13 While the total energy associated with the biennial component of ENSO signal is not that large compared with the background variability, advanced spectral analyses of various ENSO indices14 do identify distinctive quasi-quadriennial and quasi-biennial signals in the equatorial Pacific. In summary, ENSO is known to centrally involve processes on three distinct time scales, namely the ones associated with the annual cycle (AC), quasi-biennial (QB) processes, and low-frequency (LF) interannual processes.15,16,17
Statistical inference of causal relationships within climate data has recently become an area of active research.18,19,20,21 Typically, a causal relation is sought between pairs of different variables or different modes of atmospheric variability. By contrast, Paluš22,23 suggested an approach—which we will follow in the present study—to examine the complexity of climatic interactions by identifying causal relations between processes operating on different time scales within a single climatic time series. In this study, we apply this technique (see Methods) to discern multi-scale interactions and causality in ENSO, as represented by the NINO3.4 index (spatial average of sea-surface temperatures over a box of 5°S–5°N and 170°–120°W), in observations and climate model simulations. Our results uncover intricate causal relationships between AC, QB, and LF components of ENSO, and point to a much larger than previously implied role of QB variability in ENSO dynamics.
Results
Interactions in the observed ENSO
We examined synchronization and causal interactions in the NINO3.4 time series for the quasi-oscillatory modes with periods ranging from 5 to 96 months. We are looking for the observed interactions characterized by causality estimate exceeding the 95th percentile of the distribution of this quantity for the surrogate data samples (Fig. 1), where the surrogate time series were generated using a Monte Carlo method,24 yielding synthetic time series with the same spectrum, but void of any cross-scale interactions (see Methods for further details).
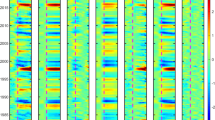
Cross-scale phase synchronization (a), phase–phase causality (b), and phase–amplitude causality (c) in the observed NINO3.4 time series. The phase synchronization is a symmetrical relation, hence the plot is symmetric, while causality plots are shown with the period of the driver (master) time series on the x-axis and driven (slave) time series on the y-axis. Shown are (positive) significance-level deviations from the 95th percentile of the k-nearest neighbor estimates of (conditional) mutual information, tested using 500 Fourier transform surrogates (see Methods)
There are three pairs of modes that exhibit phase synchronization (a process by which two or more cyclic signals tend to oscillate with a repeating sequence of relative phase angles) (Fig. 1a). The quasi-biennial (QB) modes (periods of 1.8–2.1 year), which tend to peak in winter (not shown), are indeed synchronized with the annual cycle (AC) as well as with the so-called combination tones (CT; periods approximately 9 and 14 months). The combination tones result from the interaction of AC with low-frequency (LF) ENSO modes of periods 4–6 yr (see, for example, Stein et al.25 or Stuecker et al.26). Furthermore, the AC and CT modes with periods of 8–9 months are themselves phase locked. Finally, the LF modes with periods 5–6 yr and QB modes with periods 2–3 year also exhibit phase synchronization. These results reconfirm an important role of the annual cycle in ENSO dynamics, with strong ENSO events peaking in boreal winter,10,27 and point to the link between QB and LF modes, which may be responsible for extreme ENSO events14,15,16 (see below); thus, our synchronization analysis brings out known ENSO properties consistent with previous research.
On the other hand, the phase–phase causality diagnostics (Fig. 1b) provides an additional—this time new—information that complements the phase synchronization results and addresses the causes of these synchronizations by elucidating important directed connections between the LF, QB, and AC/CT ENSO modes. This analysis identifies a member of the pair of modes (time series) that is a skillful precursor of the other member in predictive context. For example, the phase of LF modes affects that of the AC/CT modes, which means that the “shape” of the annual cycle depends on whether the LF mode (periods of 4–6 year) is in its extreme warm or extreme cold phase.
Furthermore, the phase of the AC mode is a skillful precursor for the phase of QB modes with the periods of 1.8–2.1 year, while the phase of QB modes with the periods of 2–3-year dictates in part the phase of the CT modes (periods of 12–16 months).
The only pronounced phase–amplitude causality link (Fig. 1c) is the one between the phase of the LF ENSO mode (periods of 5–6 year) and the amplitude of QB modes (periods of 1.8–2.1 year).
Our analysis thus identifies the three fundamental time scales in ENSO dynamics—AC, QB, and LF—consistent with previous work,15,16,17 but offers further details on the interaction between these modes. Some of the interactions we identified rigorously here have been previously theorized to exist, but, to the best of our knowledge, were never detected in a data-driven way. Based on our results, it is natural to consider the AC and CT processes in combination to define the quasi-annual (QA) variability. The QB modes can be divided into two—‘‘faster’’ and ‘‘slower’’—sub-ranges, with the periods of 1.8–2.1 year and 2–3 year, respectively. Similarly, the LF processes can be divided into the ones associated with 4–5-year and 5–6-year periods.
We observe a pronounced connection between the (phase of) the slower LF mode and both the phase and amplitude of the faster QB mode. In particular, the slower LF mode affects the phase of the QA mode, and, therefore—indirectly—the phase of the faster QB mode, which tends to be affected by and phase-synchronized with the QA mode; the slow LF mode also directly affects the amplitude of the faster QB mode. The connections between the phase of slow LF mode and the phase of QA mode important in the causal sequence above are both direct and indirect. In the latter indirect case, the connection works through the phase synchronization between the slow LF mode and the slow QB mode and subsequent causal effect of the latter on the phase of the QA mode. The faster LF modes add to the picture by also affecting the phase of the QA mode, and, therefore, indirectly, the phase of the faster QB mode.
Consequences of causal connections
One of the main findings of our study is the apparent importance, in ENSO dynamics, of the LF phase → QA phase → QB phase causal linkages, as well as LF phase → QB amplitude causal linkages. To illustrate these causal connections further, we utilized an approach of conditional composites, in which we first identified three distinct phases (by dividing the span between maximum and minimum values into three bins) of the low-frequency (LF) ENSO component: LF−, LF0 and LF+; and subsequently computed the composites (mean values) of any variable of interest over the data points associated with these three phases.
Figure 2 visualizes the response of the AC frequency to changes in the phase of the LF ENSO variability, thus illustrating the LF phase → QA phase causal linkage. Here, we composited the instantaneous frequencies of the annual cycle computed as the slope of the continuous 12-month-long snippets of the AC-phase time series via the robust regression. These results are presented in the form of histograms and suggest that the positive phase of the LF cycle speeds up the annual cycle (thus shortens its period and increases its frequency), while the negative period of LF cycle causes the AC period to become longer than a year. Not surprisingly, the annual cycles associated with neutral LF0 conditions, as well as climatological annual cycles, have the average period of exactly 1 year.
Histograms of instantaneous frequencies of the NINO3.4 annual cycle. Top: unconditioned (using all data); bottom: histograms conditioned on the phase of the low-frequency (LF) ENSO mode. The black horizontal line marks exactly 1 year period, and also given are respective means ± one standard deviation of instantaneous frequencies for all four panels
In fact, not only the effective frequency, but also the entire shape of the annual cycle changes depending on the phase of the LF ENSO mode. Figure 3 shows conditional composites of the annual cycle associated with the LF−, LF0, and LF+ phases of the low-frequency ENSO cycle; these composites were computed by averaging the raw NINO3.4 data associated with a given phase of LF variability for each month. The neutral LF conditions correspond with the seasonal cycle of NINO3.4 temperatures that is close to climatological seasonal cycle. The latter cycle is not purely harmonic, and is characterized by relatively fast warming between January and May and a slower cooling afterwards. The annual cycle conditioned on LF− phase has the same general character, but is on average colder than the climatological AC. The annual cycle associated with the LF+ phase of interannual ENSO signal is, of course, warmer on average due to El Niño-type conditions, but also has a very different, more harmonic shape, with September-through-December warming absent from the LF−, LF0, and climatological annual cycles. Also shown in Fig. 3 are the NINO3.4 time series during two extreme El Niño events (namely, 1982/83 and 1997/98 events). Note how a very strong biennial ENSO signal during those years completely masks any visible AC variability that may be present in the NINO3.4 time series at that time. An episodic character of such pronounced biennial extreme events makes it difficult to associate the QB ENSO variability with alterations between weak and strong annual cycles, as was suggested previously.12 We argued that such extreme ENSO events arise due to synchronization between a suite of different QB modes, which are individually characterized by a relatively small variance.
We hypothesize here that these ‘‘internal’’ QB synchronizations arise due to causal interactions represented by the QA phase → QB phase causal linkage identified by our conditional mutual information analysis. This linkage is further illustrated, albeit indirectly, in Fig. S2 in the Supplementary Material, which shows that the composite annual cycles associated with QB–, QB0, and QB+ phases of QB variability closely match those associated with LF−, LF0, and LF+ phases, respectively, consistent with LF phase → QA phase → QB phase-directed connections.
Moreover, Fig. S3 in the Supplementary Material identifies clear growth in the amplitude of the BC and QB variability as the low-frequency phase changes from La Niña (LF−) to El Niño (LF+) conditions, consistent with the LF phase → QB amplitude causal interaction. On the other hand, the changes in the amplitude of AC conditioned on the LF phases are non-monotonic and somewhat less pronounced compared to those in BC and QB amplitudes.
The interactions identified above are instrumental in setting up extreme ENSO events (Fig. 4). In particular, during all of the strong El Niño events of years 72/73, 82/83, and 97/98, the QA, QB, and LF modes were characterized by synchronous pronounced maxima. Note, however, that strictly speaking, the synchronization with LF mode is not really necessary for an extreme ENSO event to materialize, since the ‘‘peak’’ of this mode spans a good part of the year (for example, the peak of LF mode did not really occur in winter 1982/83, but the LF wintertime ‘‘background’’ during that time was still abnormally warm), while the amplitude of the QA mode is, in general, small, so that this mode does not contribute much directly to the magnitude of a given event. Instead, what appears to be essential for an extreme ENSO to occur is the synchronization of multiple QB modes with each other. We believe that this ‘‘internal’’ QB synchronization is what has been picked up by our conditional mutual information analysis in the form of LF → QA → QB phase connections and also LF phase → QB amplitude connections (since synchronization of phases of different QB modes should automatically result in a large-amplitude event.) By contrast, during a moderate El Niño of 87/88, the LF, QB, and QA modes exhibited phase shifts, with lower-frequency modes leading the higher-frequency modes (in particular a suite of QB modes) instead of being ‘‘stacked’’ on top of one another, thus limiting the magnitude of this event. Notably, strong La Niña events do not seem to be associated with the minimum of the LF mode, but instead occur during near-neutral LF conditions when the minima of the QA modes and the minima of the whole range of QB modes synchronize. Thus, in both El Niño and La Niña cases, the behavior of the QB modes has a vital control on the magnitude of the ENSO events.
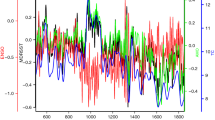
Top: wavelet reconstructions of the observed NINO3.4 index (1970–1999): reconstruction of the annual (black), quasi-biennial (for a range of periods from 18 to 30 months, with 2 month step; shades of blue to green) and 5-year ENSO cycles (red). All of these reconstructions were computed via continuous complex wavelet transform (CCWT) as Ap(t) cos ϕp(t), for the corresponding central wavelet periods p. Bottom: the full observed normalized NINO3.4 index. The years of strong El Niño and La Niña events are marked with the red and blue shading, respectively
Interactions in CMIP5 models
The Coupled Model Intercomparison Project Phase 5 (CMIP5)28 is a framework for coordinated climate change experiments providing global circulation model (GCM) outputs from various modeling groups. We analyzed time series of the sea-surface temperature obtained from the individual runs of CMIP5 models and compared the simulated NINO3.4 characteristics with the observed characteristics (Fig. 5). To start with, we measured the similarity between the observed and simulated wavelet spectra29 using root-mean-square distance and Pearson correlation coefficient, with zero distance and unit correlation coefficient indicating the perfect match. The ensemble-mean values of these two measures for individual CMIP5 models are shown in the first two columns of Fig. 5. The models exhibit great variations in their ability to match the observed NINO3.4 spectra, with correlation coefficients ranging from 0.2 to 0.8 and rms distances from 30 to 120; furthermore, there are also substantial sampling variations in the NINO3.4 spectra from multiple runs of a single model (not shown). This means that the ENSO tends to exhibit different epochs of sampling variability in models, in which its strength, spectrum and other properties may vary significantly.30
Measures of similarity between various characteristics of the observed and CMIP5 simulated NINO3.4 time series. Shown are ensemble averages of these characteristics over multiple runs of individual models (see the model acronyms on the left). The first two columns compare the observed and simulated wavelet spectra, using the root-mean-square (rms) distance and Pearson correlation, both computed in the frequency space. Next three pairs of columns display measures of similarity between the observed and simulated interaction maps analogous to the observed maps of Fig. 1, namely the phase synchronization, phase–phase causality and phase–amplitude causality maps. Each pair presents two distinct similarity measures: the Pearson correlation (corr) in the phase space of the corresponding map, as well as the Adjusted Rand Index (ARI; see text)
Similarly to the wavelet spectra, the synchronization and causality maps (see examples in Fig. 6 analogous to the observed maps of Fig. 1), vary considerably from model to model (Fig. 5, right columns), as well as between individual runs of a single model (see Supplementary Excel Table). We compared the observed and simulated maps using, once again, the standard Pearson correlation coefficient, as well as the so-called Adjusted Rand Index (ARI), which is especially well suited to measure the similarity of clustered data.31 Both measures were computed for the pairs of interaction maps (observation vs. individual simulation) filled with ones or zeros depending on whether the significant interaction between the processes of different time scales was identified or not (so the colored areas of maps in Figs. 1 and 6 would be filled with ones, and white areas—with zeros); hereafter, we will call the maps so constructed the thresholded binary maps.
The same as in Fig. 1, but for the individual simulations of CMIP5 models that best match the observed structures: phase synchronization in CanESM model (a); phase–phase causality in CCSM4 model (b); and phase–amplitude causality in CSIRO-mk360 model (c)
The above similarity measures averaged over the ensembles of individual model simulations (Fig. 5, right columns) are in fact fairly low. For phase synchronization, the highest similarity was detected in the CanESM2 model, at the 0.24 level. The phase synchronization map for the best run of the CanESM2 model (Fig. 6a) indicates synchronization between the processes with the same time scales as in the observed data (Fig. 1a), that is, between the LF, QB, and AC/CT modes. This, however, is more of an exception than a rule, as the time scales of significant phase synchronization in most of the runs do not match the observed time scales.
The similarity levels between phase–phase causality maps from observations and model simulations are about the same as for phase synchronization maps, with maximum ensemble-mean correlation of 0.23 obtained for the CCSM4 model. The causality map for the best run of this model (Fig. 6b) is correlated with the observed map (Fig. 1b) at the 0.41 level, and captures correctly the observed LF–QA, LF–QB, and QA–QB connections. Note that the best matches to the observed maps in terms of phase synchronization and phase–phase causality come from individual simulations of different models, meaning that neither model run was able to capture the entirety of the observed interactions. Finally, no model was able to capture the observed phase–amplitude causal connection between the LF and QB modes (Fig. 1c). The highest ensemble-mean correlation between the observed and simulated maps is only 0.03 (MRI-CGCM3), with the highest correlation of 0.1 for one of the CSIRO-mk360 simulations (the corresponding causality map is shown in Fig. 6c). The phase-synchronization and phase–phase causality maps for the latter run are, however, inferior to those from other models in terms of their similarity to the observed maps (not shown).
To summarize, the CMIP5 models exhibit great sampling variations in the simulated ENSO characteristics. Some of the simulations do exhibit certain aspects of interactions between the processes of different time scales, which match the observed interactions. However, no single simulation is able to reproduce the entire sequence of causal connections inferred from the observed data.
Interactions in conceptual and statistical models
The same interactions were also sought in a conceptual, low-dimensional dynamical model (parametric recharge oscillator: PRO25), as well as in the empirical stochastic (EMR) model of Pacific sea-surface temperatures due to Kondrashov et al.,32 which were both used to produce synthetic NINO3.4 time series. The results for both models are presented in the Supplementary Material. In a nutshell, the PRO dynamical model fails to reproduce any of the observed causal interactions (Supplementary Figs. S4 and S5), whereas the EMR statistical model does offer promising results, especially with regards to reproducing the observed LF → QA → QB phase causality (Supplementary Fig. S6). Some of the initial analyses suggest that the QB modes in the EMR model are inherently present in the algebraic structure of this model’s deterministic propagator, but are strongly influenced by the feedbacks that involve state-dependent (multiplicative) noise (Supplementary Fig. S7).
Discussion
In this study, we examined causal interactions between different oscillatory modes comprising ENSO variability, using the tools of information theory.22,23 These tools enabled us to uncover an intricate network of interactions underlying the observed ENSO variability. In particular, we showed that the (phase of) low-frequency (LF), interannual ENSO mode directly affects the amplitude of QB variability. It also indirectly affects the phase of QB variability, via the intermediate causal connection with the phase of the annual cycle (AC) and its combination tones (CT) associated with the LF mode.33 The AC/CT modes combined constitute the quasi-annual (QA) variability (changes in the shape of the annual cycle). The above LF → QA → QB phase interactions and LF phase → QB amplitude interactions result in intermittent synchronizations among different QB modes that occur preferentially during certain phases of the LF mode, thus leading to extreme (biennial) ENSO events (Fig. 4). This allows multiple QB modes, which are normally de-synchronized and are thus associated with small overall energy, to occasionally produce a signal with the amplitude exceeding those of QA and LF cycles. One of the key messages from our work is to suggest a much more important role of the quasi-biennial (QB) modes in ENSO dynamics than, perhaps, thought previously.
The three important time scales—QA, QB, and LF—detected by our independent analysis of ENSO interactions have been identified in previous studies as well.15,16,17 Our results on synchronization of QB and QA modes are also consistent with previous work.25,34 However, the novelty of our work, aside from applying an original methodology to analyze climate data, is in obtaining a new compact description of the causal interactions instrumental in ENSO dynamics. The causal connection between the phase of the LF variability and that of the QA variability—that is, changes in the shape of the annual cycle depending on the state of the LF ENSO mode—is conceptually similar to the effect of low-frequency component of North Atlantic Oscillation variability on the annual cycle of surface temperature over Europe.35 A mechanistic explanation of the QA → QB phase causality remains elusive, with possible hints from empirical modeling (see below).
A growing number of studies identified and analyzed decadal and longer time scale variability in ENSO.36,37,38,39,40,41,42 A major theme in the studies of decadal ENSO variability is the existence of distinct epochs exhibiting a different character (frequencies, magnitudes, teleconnections) of ENSO and, presumably, distinct dynamical mechanisms underlying the ENSO variability30,41,42,43,44,45 during these epochs. It seem likely, therefore, that these dynamics could alter dominant causal interactions in the ENSO system, leading to decadal variations in its cross-scale coupling. In the present work, however, we had to restrict the range of the time scales considered to sub-decadal variability due to a limited length (120 years) of the available ENSO time series, which precludes robust detection of causal connections on decadal and longer time scales.
The observed ENSO interactions are poorly represented in the historical simulations of CMIP5 climate models, which exhibit large sampling variations in ENSO spectra and causality maps, both from model to model and among different runs of a single model. Some of the model simulations match time scales or select causality characteristics of the observed ENSO variability, but no single simulation is able to reproduce the full picture of the observed interactions. The ENSO variability in long pre-industrial control runs of CMIP5-type models is known to exhibit multidecadal epochs characterized by different ENSO behavior.30 Hence, there is still a possibility that the models possess correct ENSO dynamics, but the sample of 89 twentieth-century simulations considered here was simply not large enough to generate the ENSO epoch that would match the observed epoch. Analyses of long pre-industrial runs are needed in order to address this issue. However, the experiments with an empirical stochastic ENSO model of Kondrashov et al.32 suggest that the chances of reproducing the observed ENSO behavior in ensemble simulations of the twentieth century climate are much higher than the CMIP5 ensemble results. This implies that CMIP5 models do indeed misrepresent ENSO dynamics. The same conclusion holds for the conceptual parametric recharge oscillator model of Stein et al.,25 which also fails to capture the observed cross-scale causal relationships in ENSO. By contrast, the success of the empirical ENSO model in reproducing the essential phase interactions among LF, QA, and QB modes allows one to address, in a mechanistic fashion, the dynamics of these interactions, with initial indications pointing to the importance of both deterministic dynamics and state-dependent (multiplicative) noise in controlling the QB variability.
Thus, neither conceptual nor state-of-the-art dynamical climate models studied here were able to mimic the structure of the observed ENSO interactions, while the empirical models considered did quite a bit better. Understanding the discrepancies between the observed interactions and the interactions simulated by the dynamical models—especially with respect to their ability to model the QB modes—may be the key to an improved ENSO prediction. On a broader scale, the framework we used here is applicable to analyzing phenomena across a wide range of disciplines—for example, in neuroscience, where cross-frequency phase–amplitude coupling has recently been observed in electrophysiological signals reflecting the brain dynamics. This cross-frequency coupling enriches the cooperative behavior of neuronal networks and apparently plays an important functional role in neuronal computation, communication, and learning.46
Methods
We analyzed monthly NINO3.4 sea-surface temperature data47 with the temporal span of 1900–2010, as well as the simulated NINO3.4 time series extracted from 89 historic simulations of 15 different global climate models (see Table S1 in Supplementary Material) participating in the CMIP5 intercomparison project.28 Both observed and modeled NINO3.4 time series were centered to zero mean before entering the analysis.
Following Paluš,22,23 we studied interactions between the processes dominated by different time scales using the phase dynamics approach.48 In particular, we first applied, to the NINO3.4 time series, the complex continuous wavelet transform (CCWT) with Morlet mother wavelet29 and obtained time-dependent complex wavelet coefficients ψp(t) for a given central period p, from which we extracted the instantaneous phase, ϕp(t), and amplitude, Ap(t), time series. Subsequently, we computed the (conditional) mutual information I49 and applied a randomization procedure24 to establish a statistical significance of the results. The methods are in detail described in the Supplementary Material. The Supplementary Material moreover discusses possible artefacts of our method and their control and robustness analyses of our results.
Data availability
All data used in this study are publicly available at the respective sites listed in the references. All scripts used in this study are written in Python and are publicly available at the github.com profile of N.J. at https://github.com/jajcayn/enso_cmi.
References
Tsonis, A. A. & Roebber, P. J. The architecture of the climate network. Phys. A 333, 497–504 (2004).
Havlin, S. et al. Challenges in network science: Applications to infrastructures, climate, social systems and economics. Eur. Phys. J. Spec. Top. 214, 273–293 (2012).
Paluš, M., Hartman, D., Hlinka, J. & Vejmelka, M. Discerning connectivity from dynamics in climate networks. Nonlinear Proc. Geoph. 18, 751–763 (2011).
Neelin, J. D. et al. ENSO theory. J. Geophys. Res. Oceans 103, 14261–14290 (1998).
Trenberth, K. E. et al. Progress during TOGA in understanding and modeling global teleconnections associated with tropical sea surface temperatures. J. Geophys. Res. Oceans 103, 14291–14324 (1998).
Alexander, M. A. et al. The atmospheric bridge: The inuence of ENSO teleconnections on air-sea interaction over the global oceans. J. Clim. 15, 2205–2231 (2002).
Burgers, G. & Stephenson, D. B. The normality of El Niño. Geophys. Res. Lett. 26, 1027–1039 (1999).
Sardeshmukh, P. D., Compo, G. P. & Penland, C. Changes of probability associated with El Nino. J. Clim. 13, 4268–4286 (2000).
Ghil, M. & Robertson, A. W. Solving problems with GCMs: General circulation models and their role in the climate modeling hierarchy. Int. Geophys. 70, 285–325 (2001).
Larkin, N. K. & Harrison, D. E. ENSO warm (El Niño) and cold (La Niña) event life cycles: Ocean surface anomaly patterns, their symmetries, asymmetries, and implications. J. Clim. 15, 1118–1140 (2002).
Barnett, T. P. Variations in near-global sea level pressure: Another view. J. Clim. 1, 225–230 (1988).
Meehl, G. A. The annual cycle and interannual variability in the tropical Pacific and Indian Ocean regions. Mon. Weather Rev. 115, 27–50 (1987).
Lau, K. -M. & Sheu, P. J. Annual cycle, quasi-biennial oscillation, and southern oscillation in global precipitation. J. Geophys. Res. Atmos 93, 10975–10988 (1988).
Jiang, N., Neelin, J. D. & Ghil, M. Quasi-quadrennial and quasi-biennial variability in the equatorial Pacific. Clim. Dynam. 12, 101–112 (1995).
Barnett, T. P. The interaction of multiple time scales in the tropical climate system. J. Clim. 4, 269–285 (1991).
Kim, K. -Y. Investigation of ENSO variability using cyclostationary EOFs of observational data. Meteorol. Atmos. Phys. 81, 149–168 (2002).
Yeo, S. -R. & Kim, K. -Y. Global warming, low-frequency variability, and biennial oscillation: an attempt to understand the physical mechanisms driving major ENSO events. Clim. Dynam. 43, 771–786 (2014).
Ebert-Uphoff, I. & Deng, Y. Causal discovery for climate research using graphical models. J. Clim. 25, 5648–5665 (2012).
Runge, J. et al. Identifying causal gateways and mediators in complex spatio-temporal systems. Nat. Comm. 6, 8502 (2015).
van Nes, E. H. et al. Causal feedbacks in climate change. Nat. Clim. Change 5, 445–448 (2015).
Hannart, A., Pearl, J., Otto, F. E. L., Naveau, P. & Ghil, M. Causal counterfactual theory for the attribution of weather and climate-related events. B. Am. Meteorol. Soc. 97, 99–110 (2016).
Paluš, M. Multiscale atmospheric dynamics: cross-frequency phase-amplitude coupling in the air temperature. Phys. Rev. Lett. 112, 078702 (2014).
Paluš, M. Cross-scale interactions and information transfer. Entropy 16, 5263–5289 (2014).
Paluš, M. From nonlinearity to causality: statistical testing and inference of physical mechanisms underlying complex dynamics. Conte. Phys. 48, 307–348 (2007).
Stein, K., Timmermann, A., Schneider, N., Jin, F. -F. & Stuecker, M. F. ENSO seasonal synchronization theory. J. Clim. 27, 5285–5310 (2014).
Stuecker, M. F., Timmermann, A., Jin, F.-F., McGregor, S. & Ren, H. -L. A combination mode of the annual cycle and the El Niño/Southern Oscillation. Nat. Geosci. 6, 540–544 (2013).
Torrence, C. & Webster, P. J. The annual cycle of persistence in the El Niño/Southern Oscillation. Q. J. Roy. Meteor. Soc. 124, 1985–2004 (1998).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An overview of CMIP5 and the experiment design. B. Am. Meteorol. Soc. 93, 485 (2012).
Torrence, C. & Compo, G. P. A practical guide to wavelet analysis. B. Am. Meteorol. Soc. 79, 61–78 (1998).
Wittenberg, A. T. Are historical records sufficient to constrain ENSO simulations? Geophys. Res. Lett. 36(12), L12702 (2009).
Hubert, L. & Arabie, P. Comparing partitions. J. Classif. 2, 193–218 (1985).
Kondrashov, D., Kravtsov, S., Robertson, A. W. & Ghil, M. A hierarchy of data based ENSO models. J. Clim. 18, 4425–4444 (2005).
Stuecker, M. F., Jin, F. -F., Timmermann, A. & McGregor, S. Combination Mode Dynamics of the Anomalous Northwest Pacific Anticyclone. J. Clim. 28, 1093–1111 (2015).
Rasmusson, E. M., Wang, X. & Ropelewski, C. F. The biennial component of ENSO variability. J. Mar. Syst. 1, 71–96 (1990).
Palus, M., Novotn, D. & Tichavsky, P. Shifts of seasons at the European mid latitudes: Natural fluctuations correlated with the North Atlantic Oscillation. Geophys. Res. Lett. 32, L12805 (2005).
Latif, M., Kleeman, R. & Eckert, C. Greenhouse warming, decadal variability, or El Niño? An attempt to understand the anomalous 1990s. J. Clim. 10, 2221–2239 (1997).
Gershunov, A. & Barnett, T. P. Interdecadal modulation of ENSO teleconnections. Bull. Am. Meteorol. Soc. 79, 2715–2725 (1998).
Wang, X., Wang, D. & Zhou, W. Decadal variability of twentieth-century El Niño and La Niña occurrence from observations and IPCC AR4 coupled models. Geophys. Res. Lett. 36, L11701 (2009).
Okumura, Y. M., Sun, T. & Wu, X. Asymmetric modulation of El Niño and La Niña and the linkage to tropical Pacific decadal variability. J. Clim. 30, 4705–4733 (2017).
Duan, W. & Mu, M. Investigating decadal variability of El Niño-Southern Oscillation asymmetry by conditional nonlinear optimal perturbation. J. Geophys. Res. Oceans 111, C07015 (2006).
Sullivan, A. et al. Robust contribution of decadal anomalies to the frequency of central-Pacific El Niño. Sci. Rep. 6, 38540 (2016).
Ruprich-Robert, Y. et al. Assessing the climate impacts of the observed Atlantic multi decadal variability using the GFDL CM2. 1 and NCAR CESM1 global coupled models. J. Clim. 30, 2785–2810 (2017).
Vecchi, G. A. & Wittenberg, A. T. El Niño and our future climate: where do we stand?. Wires.: Clim. Change 1, 260–270 (2010).
Moy, C. M., Seltzer, G. O., Rodbell, D. T. & Anderson, D. M. Variability of El Niño/Southern Oscillation activity at millennial timescales during the Holocene epoch. Nature 420, 162 (2002).
Chen, C., Cane, M. A., Wittenberg, A. T. & Chen, D. ENSO in the CMIP5 simulations: life cycles, diversity, and responses to climate change. J. Clim. 30, 775–801 (2017).
Canolty, R. T. & Knight, R. T. The functional role of cross-frequency coupling. Trends Cogn. Sci. 14, 506–515 (2010).
Rayner, N. A. et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 108, 4407 (2003). Data retrieved from https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Data/nino34.long.data.
Pikovsky, A., Rosenblum, M. & Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences, Vol. 12 (Cambridge University Press, Cambridge, UK, 2003).
Paluš, M. & Vejmelka, M. Directionality of coupling from bivariate time series: How to avoid false causalities and missed connections. Phys. Rev. E 75, 056211 (2007).
Acknowledgements
We acknowledge the World Climate Research Program’s Working Group on Coupled Modeling, which is responsible for CMIP, and we thank the climate modeling groups for producing and making available their model output. The U.S. Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support for CMIP project and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals. Lastly, we would like to thank two anonymous reviewers whose insightful comments and questions helped us to strengthen and clarify the manuscript. This study was supported by the Ministry of Education, Youth and Sports of the Czech Republic within the Program KONTAKT II, project LH14001 (N.J. and M.P.), by NSF grants OCE-1243158 (S.K.), AGS-1408897 (S.K. and A.A.T.), DBI-1667584 and DEB-1655203 (G.S.), as well as by the Ministry of Education and Science of the Russian Federation (project #14.W03.31.0006) and Russian Science Foundation (project #14-50-00095) (S.K.), and finally with Lenfest Ocean Program grant 00028335 (G.S.) and DoD–Strategic Environmental Research and Development Program 15 RC-2509 (G.S.).
Author information
Authors and Affiliations
Contributions
N.J. and M.P. designed the study, N.J. and S.K. prepared the data and carried out the analysis, S.K. provided the empirical model, N.J. and S.K. prepared the manuscript. All authors discussed the results and contributed to editing the manuscript. A.A.T. and M.P. supervised the study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jajcay, N., Kravtsov, S., Sugihara, G. et al. Synchronization and causality across time scales in El Niño Southern Oscillation. npj Clim Atmos Sci 1, 33 (2018). https://doi.org/10.1038/s41612-018-0043-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-018-0043-7
This article is cited by
-
An Anomalous Decline of the Spring Bloom Chlorophyll Concentration in the Central Pacific is an Early Indicator of El Niño
Journal of the Indian Society of Remote Sensing (2024)
-
Amplitude modulation of relative humidity by wind in Northeast China: the formation of variance annual cycle in relative humidity
Climate Dynamics (2022)
-
El Niño Modoki can be mostly predicted more than 10 years ahead of time
Scientific Reports (2021)
-
Impact of rainfall variability on crop yields and its relationship with sea surface temperature in northern Ethiopian Highlands
Arabian Journal of Geosciences (2021)
-
Systematic identification of causal relations in high-dimensional chaotic systems: application to stratosphere-troposphere coupling
Climate Dynamics (2020)