Abstract
Urban parks can effectively reduce surface temperatures, which is an important strategic approach to reducing the urban heat island effect. Quantifying the cooling effect of urban parks and identifying their main internal influencing factors is important for improving the urban thermal environment, achieving maximum cooling benefits, and improving urban sustainability. In this study, we extracted data frobut this is often unrealisticm 28 urban parks in Zhengzhou, China. We combined multivariate data, such as Landsat 8 data, to retrieve the land surface temperature (LST), extract the park interior landscape, and quantify the cooling effect using three cooling indices: park cooling distance (L∆max), temperature difference magnitude (∆Tmax), and temperature gradient (Gtemp). Furthermore, the relationship between the internal landscape characteristics of the park and the average LST and cooling indices of the park was analyzed. The results showed that different buffer ranges affect the LST-distance fitting results of urban parks, and a 300-m buffer zone is the optimal fitting interval. However, specific parks should be analyzed to select the optimal buffer range and reduce the cooling index calculation errors. Additionally, the mean values of LST, ∆Tmax, L∆max, and Gtemp for the 28 parks in Zhengzhou were 34.11, 3.22 °C, 194.02 m, and 1.78 °C/hm, respectively. Park perimeter (PP), park area, internal green area (GA), and landscape shape index (LSI) were both significantly correlated with ∆Tmax and the main factors associated with maintaining a low LST in parks. L∆max was mainly affected by the GA, LSI, and perimeter-area ratio, whereas Gtemp was positively correlated with PP. Finally, the threshold value of efficiency for parks in Zhengzhou was 0.83 ha, and comprehensive parks showed optimal cooling in every aspect.
Similar content being viewed by others
Introduction
Increasing urbanization and unstable global climate change have exacerbated the urban heat island (UHI) effect, with urban areas tending to be warmer than the surrounding suburbs (Lin et al., 2015; Lai et al., 2018; Xin et al., 2022; Yuan et al., 2022). The UHI effect can further lead to many adverse effects such as air pollution, additional energy consumption, and urban heat waves (Lowe 2016; Leal Filho et al., 2018; Mika et al., 2018; Zhou et al., 2017; Yang et al., 2020; Wang, 2022). This phenomenon can also directly or indirectly affect the health of urban inhabitants and the sustainable development of cities (He, 2018; Yao et al., 2022b; Wang et al., 2022d). To tackle this challenge, a significant amount of research and experimentation has been performed, and solutions, such as rational planning of blue-green areas, the use of innovative mitigation materials, and the adoption of green roofs and cool pavements, have been proposed (Yang et al., 2017; Gunawardena et al., 2017; Santamouris and Yun, 2020; Wang et al., 2022c, 2021). Among these many mitigation measures, urban blue-green space has proven to be a potential solution because of its inherent environmental, ecological, and social benefits (Yan et al., 2021; Sanusi and Jalil, 2021). Urban parks, an important component of urban blue-green space, not only provide values such as recreation, humidification, and air purification but also create park cooling effects (PCEs) in cities, where urban parks are cooler than the surrounding urbanized areas (Gao et al., 2022; Yang et al., 2022; Xie and Li, 2020; Wang et al., 2022b).
To study PCEs, field measurements, remote sensing, and GIS analysis are commonly used (Yu et al., 2020a; Fu et al., 2022; Şimşek et al., 2022). Field measurements primarily use small sensors to monitor meteorology in and around the urban parks at specific times or for long periods to study the spatiotemporal characteristics of the environmental thermal fields in and around the urban parks and their influencing factors (Yang et al., 2016; Yan et al., 2018). Traditional field measurement methods are time-consuming and labor-intensive and hardly reflect the overall situation of park cooling islands (PCIs). Compared with on-site measurement, remote sensing data can provide detailed land use/land cover information owing to its low cost and time advantages (Zhou et al., 2019; Wang et al., 2022b). Remote sensing combined with GIS analysis has become the mainstream method for PCEs. Researchers have used Landsat TM, QuickBird, IKONOS, and ASTER satellites to acquire surface temperature inversion data (Cao et al., 2010; Zhu et al., 2021; Aram et al., 2019). Based on surface temperature data, researchers have used different metrics successively to calculate the urban PCI. Park cooling intensity and distance are the two most commonly measured indicators that represent the temperature difference of the park, a certain range of environment, and the maximum distance the park cooling intensity can be achieved (Liao et al., 2021; Shah et al., 2021a; Gao et al., 2022). Subsequently, the park cooling gradient and area based on the deformation of the two emerged (Peng et al., 2021; Du et al., 2022; Yao et al., 2022a). Yu et al. (2017, 2021) introduced a threshold value of efficiency (TVoE) from the “Law of Diminishing Marginal Utility” in economics to represent the threshold at which a green space or park can achieve the cooling effect.
According to relevant studies, the land surface temperature (LST) of urban parks can differ from that of their surroundings in summer by 1–2 or 4–8 °C (Zhu et al., 2021; Algretawee, 2022). Furthermore, park size, scale, shape, and complexity affect the PCI effect and vary widely across climate zones (Geng et al., 2022; Zhou et al., 2022; Wang et al., 2022a). Researchers have conducted a large number of studies in quantifying the PCEs, identifying the main influencing factors, determining the optimal areas for the cooling effect, and rationalizing the planning and design of urban parks (Yu et al., 2017, 2020b, 2021; Zhu et al., 2021; Yao et al., 2022a; Du et al., 2022).
In actual planning and construction, urban parks are often built independently of their surroundings. Therefore, how to plan the interior of urban parks to alleviate UHIs is particularly critical. Few studies have calculated the PCE by excluding surrounding disturbances and exploring the correlation between the internal park landscape and PCE.
This study is based on Google Earth’s historical high-resolution imagery and Landsat 8 satellite image data for 28 parks within Zhengzhou city. Our objectives are (1) to quantify the effect of cold islands in these 28 parks using three cooling indices: ∆Tmax, L∆max, and Gtemp; (2) to identify the main internal park influences that affect park LST and cooling indices; and (3) to calculate the TVoE of urban parks in Zhengzhou and propose optimization recommendations based on the internal park perspective. Our study provides a new perspective on PCEs from the internal park landscape and offers insights into the planning and construction of future urban parks to mitigate the UHI effect.
Data and methods
Study area
Zhengzhou is located at 112°42’–114°14’ E, 34°16’–34°58’ N. It has a temperate continental monsoon climate with long, dry, and cold winters and relatively hot summers. It has typical thermal environmental problems and faces serious heat island problems in summer (Zhao et al., 2018; Li et al., 2019, 2020). The hottest month in Zhengzhou is July, with an average maximum temperature of 33.8 °C. Zhengzhou gave vital attention to the construction of urban parks and proposed a construction plan of “300 m to see the green, 500 m to see the garden”. There are 986 parks in Zhengzhou, with the built-up green space rate reaching 35.84% and a parkland area per capita of 13 m².
Data collection and processing
Selection of parks
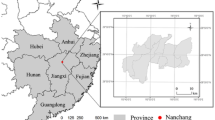
In this study, 28 urban parks with an average area of 14.75 ha (1.25–50.22 ha) in Zhengzhou City were selected (Fig. 1). The principles of park selection were as follows: (1) each park area was larger than 1 ha, and the areas were not equal; (2) the parks were located at a certain distance from each other, and their buffer zones did not overlap; and (3) the parks were located in the urban core area. The source of the park boundary data was Baidu Map (https://map.baidu.com/), and the park boundaries were further rectified by combining Google Earth’s historical high-resolution image data. Following the Zhengzhou Urban Green Space System Plan (2013–2030), the sample parks were classified into community parks (area > 0.5 ha, n = 8), theme parks (area > 5 ha, n = 10), and comprehensive parks (area > 10 ha, n = 10).
LST retrieval
A Landsat 8 image was collected on July 7, 2019, at 11:01 a.m. GMT. It was downloaded from the Geospatial Data Cloud Website (https://www.gscloud.cn/). Then, we adopted the mono-window algorithm (Qin et al., 2001) to retrieve the LST. The equations are as follows:
where Ts, T10, and Ta represent the LST, brightness temperature on the sensor, and mean atmospheric temperature, respectively, all units are in K; α and β are reference coefficients (when LST ranges from 0–70 °C, α = −67.355351, β = 0.458606); C2 and D2 are intermediate variables derived from surface emissivity; ε and ω represent the surface emissivity and atmospheric transmittance of T10, respectively. Finally, we converted the LST units from K to °C.
Buffer creation and calculation of PCI metrics
Combining previous studies and considering the resolution of Landsat 8 images, a buffer zone analysis of 600 m was generated for the parks by selecting 30 m as the interval (Peng et al., 2021). Relevant studies have shown that green spaces and water bodies around parks enhance their cooling effect (Cheng et al., 2015; Wu et al., 2021a). Thus, the disturbance areas around each park were identified, and the buffer polygons of each park were obtained by eliminating the influencing areas containing larger green belts and water bodies within the buffer zones.
First, the average LST was calculated for each park and buffer ring. Then, LST versus distance curves were plotted. Finally, different park cooling curves were fitted with 300-m and 600-m buffer zone widths using a polynomial fit to derive the most accurate fitting relationship.
In this study, PCE intensity was described by three metrics: park cooling distance (L∆max), temperature difference magnitude (∆Tmax), and temperature gradient (Gtemp) (Qiu and Jia, 2020; Chen et al., 2022). As shown in Fig. 2, the PCI was determined by the first peak of the inflection point of the LST fitted curve. The first inflection point peak was chosen where the slope of the LST fitting curve changed sharply or reached a relatively stable level (Wu et al., 2021b). ∆Tmax (°C) was the difference in the vertical coordinate values between the first turning point and average park temperature. L∆max (m) was the difference of the horizontal coordinate values between the two points. Gtemp (°C/hm) was the average temperature difference per unit ∆Tmax.
where TF is the temperature at the peak at the first turning point of the cubic polynomial fit curve, and TP is the average surface temperature inside the park.
Selection of main influencing factors
In this study, the 28 sample parks were well constructed and in good vegetation growth condition. We extracted the green areas, impervious surfaces, and water areas within the parks (Fig. 3) by visually interpreting the Google historical imagery and calibrating them with Tianditu vector map (https://www.tianditu.gov.cn). The kappa coefficient was 0.87, which fulfills the need of the study. The calculation of the landscape pattern was completed by VecLI software (Yao et al., 2022c).
We selected 13 indicators (Table 1) from four aspects: park geometry, landscape composition, landscape configuration, and remote sensing index. the effects of these indicators on park LST, ∆Tmax, L∆max, and Gtemp were analyzed.
Calculation of TVoE
The TVoE calculation method proposed by Yu et al. (2017) was used, based on a logarithmic fit curve of ∆Tmax versus park area. The TVoE is reached when the slope of the curve is 1. Before reaching the TVoE, the PCE increases significantly as the park area increases, whereas it does not increase significantly past the threshold. The TVoE was calculated in Origin 2022.
Statistical analysis
The relationship between park average LST and PCI metrics and the main influencing factors was evaluated using Pearson correlation analysis. The work was done on SPSS 26.0 software. We adopted a logarithmic function to describe the relationship between park area and LST and between park area and ∆Tmax (Yao et al., 2022a; Wang et al., 2022b).
Results
Results of land surface temperature inversion
The results of the LST inversion were classified into seven classes using the standard deviation classification method (Table 2). The LST of Zhengzhou City (Fig. 4) ranged from 20.98–52.95 °C, with an average of 35.85 °C. From a spatial perspective, the low-temperature zone (<34.42 °C) in Zhengzhou was located in blue-green spaces such as rivers, lakes, reservoirs, southern woodlands, and urban parks. The middle-temperature zone was widespread in the city. The medium-high temperature zone was located in the midwestern area of the city, as well as in the southeast. Sub-high and high-temperature zones were located in densely populated residential and commercial areas, as well as areas such as railway stations, airports, and factories.
LST, ∆T max, L ∆max, and G temp
The results and average values of LST and PCI three cooling indices, ∆Tmax, L∆max, and Gtemp, for the 28 urban parks are presented in Fig. 5. The average LST for these parks ranged from 31.84 to 36.12 °C. The average value was 34.11 °C. The average LST of 26 of these parks was below that of Zhengzhou City, and only the average LSTs of parks 4 and 5 were higher than that of Zhengzhou City, but they still had ∆Tmax values of 0.73 and 2.04. This indicates that the average LSTs of the 28 selected urban parks were below than that of the surrounding urban built-up areas, forming a PCI. The range of ∆Tmax was between 0.73 and 5.98 °C. The range of L∆max was between 51.89 and 415.02 m. The range of Gtemp was between 0.73 and 4.07 °C/hm. The average values of ∆Tmax, L∆max, and Gtemp are 3.22 °C, 194.02 m, and 1.78 °C/hm.
In order to explore the differences in LST, ∆Tmax, L∆max, and Gtemp between different types of parks, we classified the parks into three types according to their social attributes and found significant differences between them (Fig. 6). The mean LST was lower in comprehensive parks, followed by that in theme parks and community parks, with mean values of 34.88, 34.00, and 33.62 °C, respectively. The mean ∆Tmax was higher in comprehensive parks (2.38 °C), followed by that in theme parks (3.26 °C) and finally that in community parks (3.85 °C). L∆max and Gtemp followed the same trend as ∆Tmax, with L∆max mean values of 155.89 m, 190.14 m, 228.40 m for comprehensive, theme, and community parks, respectively, and Gtemp mean values of 1.48 °C/hm, 1.89 °C/hm, 1.90 °C/hm, respectively. Overall, comprehensive parks had the lowest LST and the largest cooling index.
Correlation of influencing factors with the thermal environment inside the park
We conducted a Pearson correlation analysis between a total of 13 indices and the mean LST of the park from four perspectives: park geometry, internal landscape composition, landscape configuration, and remote sensing indices (Table 3).
In terms of park geometric morphology, the correlation coefficients of park mean LST with park perimeter (PP) and park area (PA) were −0.577 and −0.546; while the correlation coefficient with the perimeter-area ratio (PPAR) was 0.641. This indicates that a larger park area and perimeter can result in a lower LST. As the shape of the park becomes more complex, the PPAR becomes larger, and the LST of the park increases. In terms of landscape composition within the park, the mean LST of the park was negatively correlated with both green areas (GA) and water-body areas (WA). This indicates that more green space and water-body areas in the park lower the LST of the park. Furthermore, in the park landscape configuration, the mean LST of the park is negatively correlated with the Shannon Diversity Index (SHDI) at the 0.05 level, and positively correlated with the landscape shape index (LSI) at the 0.01 level. This indicates that in the park, the more complex the spatial diversity of the park, the higher the average LST, and the more complex the landscape, the lower the average LST. In terms of remote sensing indices, the normalized difference vegetation index (NDVI), modified normalized difference water index (MNDWI), and park LST did not show a significant correlation.
In addition, the statistical regression analysis of park area and mean LST of the park is shown in Fig. 7. The results showed a negative logarithmic relationship between park area and mean LST (R² = 0.3752, p < 0.01). This demonstrates the potential impact of the park area on cooling.
Correlation between influencing factors and PCI
Figure 8 shows the correlation results of L∆max, ∆Tmax, and Gtemp and their influencing factors. In terms of park geometry, the PCI was significantly influenced by the PA and PP. In this study, PA and PP were positively correlated with ∆Tmax and Gtemp, and PPAR was negatively correlated with ∆Tmax and L∆max. Among them, L∆max was significantly by PPAR (p < 0.05), ∆Tmax was significantly by PA, PP, and PPAR (p < 0.01), and Gtemp was significantly by PP (p < 0.05). In the landscape configuration of the park, GA was significant at the p < 0.05 and p < 0.01 levels with L∆max (0.405) and ∆Tmax (0.626), respectively. WA was positively but not significantly correlated with L∆max, ∆Tmax, and Gtemp. Although 15 of the 28 urban parks have water bodies, the percentage and extent of water-body areas in these 15 parks are limited (6 parks have a water-body areas ratio > 10%, and 10 parks have a water-body areas > 1 ha). PI was negatively correlated with L∆max and ∆Tmax and positively correlated with Gtemp, but neither was significant. In the park landscape configuration, only LSI showed a significant positive correlation with L∆max (0.389) and ∆Tmax (0.611) at the p < 0.05 and p < 0.01 levels, respectively, for the six landscape level indices. This indicates that complex and diverse landscape configurations within the park can achieve better cooling effects. No significant correlations were found between NDVI and MNDWI with L∆max, ∆Tmax, and Gtemp on the remote sensing indices. Figure 9 shows the logarithmic and linear relationship between ∆Tmax and PA and PP, respectively.
Threshold value of efficiency (TVoE)
According to the logarithmic fitting curve of ∆Tmax to PA (y = 0.8284 ln(x) + 1.4030 R² = 0.3407), the TVoE of Zhengzhou City Park was estimated to be 0.83 ha (Fig. 9). This is of great significance for local park planning and construction, indicating that planners can design smaller spaces to achieve the best cooling effect.
Discussion
Effect of buffer zone extent on the PCI
Although the calculations for the PCEs were performed by creating buffers for thermal images, the rules for buffer creation vary. The difference in the range of buffers can have a different effect on the results. Previous studies have built buffers based on the range of park width multiples (Wang et al., 2022b), and have used ranges of 300, 600, 750, and 900 m (Yan et al., 2021; Shah et al., 2021b; Du et al., 2022; Yao et al., 2022b). In addition, the step size of the buffer varies; several are based on the resolution of the image as a step, which considers the image characteristics (Geng et al., 2022), while others use the width of the park as a step size, which considered the morphological characteristics of the park.
Therefore, a combination of image resolution and park size was considered. We used a buffer zone step of 30 m to establish two levels of buffer zones, 300 and 600 m, and excluded large areas of green belt and water bodies from the buffer zones. We analyzed the LST distance between different buffers (Fig. 10). The comparative analysis showed that: (1) the cubic polynomial fits R² for the buffer at the 300 m range were all larger than those in the 600 m range, agreeing with the findings of Peng et al. (2021) and Tian et al. (2023). (2) Moreover, we found that when L∆max was larger than 300 m (parks 13, 21, and 23), a better fitting relationship could not be obtained for the 300-m buffer at that time because the fitting curve for parks 12 and 23 had no downward turning point, and the LST scatter points for park 21 were all rising while the curves showed an inflection point. For these parks, a buffer of 600 m was used instead. (3) When the mean LST difference between the park and the first circle buffer was large, the fitting result R² was small (parks 12, 18, 24, 25, 26, and 28). This is caused by the presence of large water-body areas within the park and thus the sharp change in surface temperature with the surrounding urban land resulting in the inaccuracy of ∆Tmax and L∆max. To obtain better fitting results, the average LST of the park was masked and fitted again. At this time, the description of the fitted curve was more consistent with the actual characteristics and had a higher R² value, which further reduced the error. In summary, the buffering methodology and the choice of buffer zone extent established in this study for the measurement of urban PCIs can be used as a reference for the selection of other related studies in the future.
LST, PCI, and influencing factors
The results of our study showed that 26 of the 28 urban parks had a lower average LST than the average in Zhengzhou. Additionally, all 28 parks had positive PCI indicators, meaning all 28 parks had a cooling effect. We found that the park area and perimeter are important factors affecting the average LST of the park; larger park areas and longer perimeters correlated with lower park LST. In addition, we found that the perimeter-to-area ratio had a stronger effect on LST than the area and perimeter of the park. Normally, urban parks are integrated areas consisting of three types of landscape: green space, water-body areas, and impervious surfaces. Of these, the first two types are the main sources of cooling in the PCEs. Blue-green spaces in the park can reduce LST through shading and evapotranspiration, and high specific heat capacity and evaporation. These findings are consistent with previous studies (Wu et al., 2020; Tan et al., 2021). At the park landscape level, park mean LST was negatively correlated with LSI, while SHDI was positively correlated. Thus, in the limited and precious urban parkland, we can further reduce the park’s LST by increasing the complexity of the park’s internal landscape to obtain a better cooling effect.
In this study, three PCI metrics, L∆max, ∆Tmax, and Gtemp, were used to quantitatively assess the cooling effectiveness of 28 urban parks in Zhengzhou. Our findings suggested that urban parks can be a great strategy for reducing the temperature in cities, thus mitigating the UHI effect. The main factors affecting L∆max were PPAR, GA, and LSI; the main factors affecting ∆Tmax were GA, LSI, PP, PA, and PPAR; and the main factor affecting Gtemp was PP. NDVI, MNDWI, and park cooling index had no significant correlation, which may be due to the small number of sample parks and small area of park water bodies.
Implications for urban park planning
Urban parks are important blue-green infrastructures in cities that not only provide leisure and recreational space for inhabitants (Sun et al., 2019) but are also an important sustainable initiative to mitigate UHIs. In urban areas where land is expensive, rational planning of urban parks and maximizing their cooling effect is a top priority. Cooling in urban parks is a non-linear process similar to a logarithmic function (Peng et al., 2021). The construction of urban parks with a TVoE approach jointly considers the cooling effect and size of parks to obtain optimal benefits. When enough space and budget are available, comprehensive parks are the best option because they have the lowest LST and large ∆Tmax and L∆max, but this is often unrealistic for complex urban areas. Community parks with lower costs and close to the TVoE can provide a substantial ∆Tmax gain. Yu et al. (2021) proposed an idealized urban thermal security pattern model based on threshold size and cooling distance. In urban park planning, a network of urban parks of varying sizes—large, medium, and small—contributes more to mitigating UHIs than a single isolated park. Therefore, planners also need to focus on connecting urban parks on a network to achieve an overall regional cooling of the city (Sun et al., 2018). Moreover, the construction of more urban parks should be accompanied by a focus on landscaping their interior, e.g., designing parks with simple shapes, increasing the area of internal green space, creating water-friendly spaces, and increasing the fragmentation of the internal landscape. Our findings provide a strong basis for the planning of urban parks.
Limitations and prospect
There are some limitations in this study. First, the data used were limited in their temporal and spatial resolution, so the results of the study are only able to reflect the PCEs at the moment of satellite collection. In future research, higher resolution and more comprehensive time-series methods should be used to study the PCEs in-depth, such as unmanned aerial vehicle remote sensing, ECOSTRESS (Liu et al., 2022), and microclimate modeling (Wu et al., 2016). Second, the influencing factors explored in this study were limited; more in-depth factors such as humidity (Yan et al., 2023), 3D urban landscape patterns (Han et al., 2023), and landscape connectivity should be investigated. Third, the PCEs should be investigated against different background climates (Geng et al., 2022), extreme high temperatures and heat waves (Han et al., 2020), and the social value of urban development and parks (Xiao et al., 2023) in order to maximize the sustainability of the city and the quality of life and well-being of its inhabitants.
Conclusions
In this study, the cooling effect of 28 urban parks in Zhengzhou City was measured using three indices: ∆Tmax, L∆max, Gtemp. By analyzing multiple indicators of the internal landscape of the parks using the LST and these three indices, we drew the following conclusions: The 28 urban parks in Zhengzhou had a significant cooling effect. The mean values of ∆Tmax, L∆max, and Gtemp were 3.22 °C, 194.02 m, and 1.78 °C/hm, respectively. The different buffer ranges affected the results of the cubic polynomial fit, with the 300 m buffer R² outperforming that of the 600 m buffer; however, specific parks should be analyzed separately to calculate the most accurate park cooling index. PP, LSI, PA, GA, and WA are vital features that strongly and negatively affect the average park LST. In contrast, PPAR and SHDI were positively correlated with park LST. L∆max was positively correlated with GA and LSI. ∆Tmax was positively correlated with GA, LSI, PP, and PA. L∆max and ∆Tmax were negatively correlated with PPAR. Gtemp was positively correlated with PP. For Zhengzhou City, the most effective park size for improving the urban thermal environment was 0.83 ha. In terms of their cooling effect, comprehensive parks were more efficient than theme parks, followed by community parks. Our findings provide a new reference for the planning, construction, and landscape configuration within local parks to mitigate the UHI effect.
Data availability
The original datasets used in the study are included in the article, further inquiries can be directed to the corresponding author.
References
Algretawee H (2022) The effect of graduated urban park size on park cooling island and distance relative to land surface temperature (LST). Urban Clim 45:101255. https://doi.org/10.1016/j.uclim.2022.101255
Aram F, Higueras García E, Solgi E, Mansournia S (2019) Urban green space cooling effect in cities. Heliyon 5:e01339. https://doi.org/10.1016/j.heliyon.2019.e01339
Cao X, Onishi A, Chen J, Imura H (2010) Quantifying the cool island intensity of urban parks using ASTER and IKONOS data. Landsc Urban Plan 96:224–231. https://doi.org/10.1016/j.landurbplan.2010.03.008
Chen M, Jia W, Yan L et al. (2022) Quantification and mapping cooling effect and its accessibility of urban parks in an extreme heat event in a megacity. J Clean Prod 334:130252. https://doi.org/10.1016/j.jclepro.2021.130252
Cheng X, Wei B, Chen G et al. (2015) Influence of Park Size and Its Surrounding Urban Landscape Patterns on the Park Cooling Effect. J Urban Plan Dev 141:A4014002. https://doi.org/10.1061/(ASCE)UP.1943-5444.0000256
Du C, Jia W, Chen M et al. (2022) How can urban parks be planned to maximize cooling effect in hot extremes? Linking maximum and accumulative perspectives. J Environ Manage 317:115346. https://doi.org/10.1016/j.jenvman.2022.115346
Fu J, Wang Y, Zhou D, Cao S-J (2022) Impact of Urban Park Design on Microclimate in Cold Regions using newly developped prediction method. Sustain Cities Soc 80:103781. https://doi.org/10.1016/j.scs.2022.103781
Gao Z, Zaitchik BF, Hou Y, Chen W (2022) Toward park design optimization to mitigate the urban heat Island: Assessment of the cooling effect in five U.S. cities. Sustain Cities Soc 81:103870. https://doi.org/10.1016/j.scs.2022.103870
Geng X, Yu Z, Zhang D et al. (2022) The influence of local background climate on the dominant factors and threshold-size of the cooling effect of urban parks. Sci Total Environ 823:153806. https://doi.org/10.1016/j.scitotenv.2022.153806
Gunawardena KR, Wells MJ, Kershaw T (2017) Utilising green and bluespace to mitigate urban heat island intensity. Sci Total Environ 584–585:1040–1055. https://doi.org/10.1016/j.scitotenv.2017.01.158
Han D, Xu X, Qiao Z et al. (2023) The roles of surrounding 2D/3D landscapes in park cooling effect: Analysis from extreme hot and normal weather perspectives. Build Environ 231:110053. https://doi.org/10.1016/j.buildenv.2023.110053
Han D, Yang X, Cai H, Xu X (2020) Impacts of Neighboring Buildings on the Cold Island Effect of Central Parks: A Case Study of Beijing, China. Sustainability 12:9499. https://doi.org/10.3390/su12229499
He B-J (2018) Potentials of meteorological characteristics and synoptic conditions to mitigate urban heat island effects. Urban Clim 24:26–33. https://doi.org/10.1016/j.uclim.2018.01.004
Lai J, Zhan W, Huang F et al. (2018) Identification of typical diurnal patterns for clear-sky climatology of surface urban heat islands. Remote Sens Environ 217:203–220. https://doi.org/10.1016/j.rse.2018.08.021
Leal Filho W, Echevarria Icaza L, Neht A et al. (2018) Coping with the impacts of urban heat islands. A literature based study on understanding urban heat vulnerability and the need for resilience in cities in a global climate change context. J Clean Prod 171:1140–1149. https://doi.org/10.1016/j.jclepro.2017.10.086
Li H, Wang G, Tian G, Jombach S (2019) Mapping and assessment of the urban heat island in Zhengzhou city. Proceedings of the Fábos Conference on Landscape and Greenway Planning 6:13. https://doi.org/10.7275/5d37-w405
Li H, Wang G, Tian G, Jombach S (2020) Mapping and analyzing the park cooling effect on urban heat island in an expanding city: a case study in Zhengzhou City, China. Land 9:57. https://doi.org/10.3390/land9020057
Liao W, Cai Z, Feng Y et al. (2021) A simple and easy method to quantify the cool island intensity of urban greenspace. Urban For Urban Green 62:127173. https://doi.org/10.1016/j.ufug.2021.127173
Lin W, Yu T, Chang X et al. (2015) Calculating cooling extents of green parks using remote sensing: Method and test. Landsc Urban Plan 134:66–75. https://doi.org/10.1016/j.landurbplan.2014.10.012
Liu Y, Xu X, Wang F et al. (2022) Exploring the cooling effect of urban parks based on the ECOSTRESS land surface temperature. Front Ecol Evol 10:1031517. https://doi.org/10.3389/fevo.2022.1031517
Lowe SA (2016) An energy and mortality impact assessment of the urban heat island in the US. Environ Impact Assess Rev 56:139–144. https://doi.org/10.1016/j.eiar.2015.10.004
Mika J, Forgo P, Lakatos L et al. (2018) Impact of 1.5 K global warming on urban air pollution and heat island with outlook on human health effects. Curr Opin Environ Sustain 30:151–159. https://doi.org/10.1016/j.cosust.2018.05.013
Peng J, Dan Y, Qiao R et al. (2021) How to quantify the cooling effect of urban parks? Linking maximum and accumulation perspectives. Remote Sens Environ 252:112135. https://doi.org/10.1016/j.rse.2020.112135
Qin Z, Karnieli A, Berliner P (2001) A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int J Remote Sens 22:3719–3746. https://doi.org/10.1080/01431160010006971
Qiu K, Jia B (2020) The roles of landscape both inside the park and the surroundings in park cooling effect. Sustain Cities Soc 52:101864. https://doi.org/10.1016/j.scs.2019.101864
Santamouris M, Yun GY (2020) Recent development and research priorities on cool and super cool materials to mitigate urban heat island. Renew Energy 161:792–807. https://doi.org/10.1016/j.renene.2020.07.109
Sanusi R, Jalil M (2021) Blue-Green infrastructure determines the microclimate mitigation potential targeted for urban cooling. IOP Conf Ser Earth Environ Sci 918:012010. https://doi.org/10.1088/1755-1315/918/1/012010
Shah A, Garg A, Mishra V (2021a) Quantifying the local cooling effects of urban green spaces: Evidence from Bengaluru, India. Landsc Urban Plan 209:104043. https://doi.org/10.1016/j.landurbplan.2021.104043
Shah A, Garg A, Mishra V (2021b) Quantifying the local cooling effects of urban green spaces: Evidence from Bengaluru, India. Landsc Urban Plan 209:104043. https://doi.org/10.1016/j.landurbplan.2021.104043
Şimşek ÇK, Serter G, Ödül H (2022) A study on the cooling capacities of urban parks and their interactions with the surrounding urban patterns. Appl Spat Anal Policy. https://doi.org/10.1007/s12061-022-09452-4
Sun R, Li F, Chen L (2019) A demand index for recreational ecosystem services associated with urban parks in Beijing, China. J Environ Manage 251:109612. https://doi.org/10.1016/j.jenvman.2019.109612
Sun R, Xie W, Chen L (2018) A landscape connectivity model to quantify contributions of heat sources and sinks in urban regions. Landsc Urban Plan 178:43–50. https://doi.org/10.1016/j.landurbplan.2018.05.015
Tan X, Sun X, Huang C et al. (2021) Comparison of cooling effect between green space and water body. Sustain Cities Soc 67:102711. https://doi.org/10.1016/j.scs.2021.102711
Tian P, Li J, Pu R et al. (2023) Assessing the cold island effect of urban parks in metropolitan cores: a case study of Hangzhou, China. Environ Sci Pollut Res 30:80931–80944. https://doi.org/10.1007/s11356-023-28088-6
Wang C, Ren Z, Dong Y et al. (2022a) Efficient cooling of cities at global scale using urban green space to mitigate urban heat island effects in different climatic regions. Urban For Urban Green 74:127635. https://doi.org/10.1016/j.ufug.2022.127635
Wang C, Wang Z-H, Kaloush KE, Shacat J (2021) Cool pavements for urban heat island mitigation: A synthetic review. Renew Sustain Energy Rev 146:111171. https://doi.org/10.1016/j.rser.2021.111171
Wang T, Tu H, Min B et al. (2022b) The mitigation effect of park landscape on thermal environment in Shanghai City based on remote sensing retrieval method. Int J Environ Res Public Health 19:2949. https://doi.org/10.3390/ijerph19052949
Wang X, Li H, Sodoudi S (2022c) The effectiveness of cool and green roofs in mitigating urban heat island and improving human thermal comfort. Build Environ 217:109082. https://doi.org/10.1016/j.buildenv.2022.109082
Wang Y, Chang Q, Fan P, Shi X (2022d) From urban greenspace to health behaviors: an ecosystem services-mediated perspective. Environ Res 213:113664. https://doi.org/10.1016/j.envres.2022.113664
Wang Z-H (2022) Reconceptualizing urban heat island: Beyond the urban-rural dichotomy. Sustain Cities Soc 77:103581. https://doi.org/10.1016/j.scs.2021.103581
Wu C, Li J, Wang C et al. (2021a) Estimating the cooling effect of pocket green space in high density urban areas in Shanghai, China. Front Environ Sci 9:657969. https://doi.org/10.3389/fenvs.2021.657969
Wu J, Li C, Zhang X et al. (2020) Seasonal variations and main influencing factors of the water cooling islands effect in Shenzhen. Ecol Indic 117:106699. https://doi.org/10.1016/j.ecolind.2020.106699
Wu S, Yang H, Luo P et al. (2021b) The effects of the cooling efficiency of urban wetlands in an inland megacity: a case study of Chengdu, Southwest China. Build Environ 204:108128. https://doi.org/10.1016/j.buildenv.2021.108128
Wu Z, Kong F, Wang Y et al. (2016) The impact of greenspace on thermal comfort in a residential quarter of Beijing, China. Int J Environ Res Public Health 13:1217. https://doi.org/10.3390/ijerph13121217
Xiao Y, Piao Y, Wei W et al. (2023) A comprehensive framework of cooling effect-accessibility-urban development to assessing and planning park cooling services. Sustain Cities Soc 98:104817. https://doi.org/10.1016/j.scs.2023.104817
Xie Q, Li J (2020) Detecting the cool island effect of urban parks in Wuhan: a city on rivers. Int J Environ Res Public Health 18:132. https://doi.org/10.3390/ijerph18010132
Xin J, Yang J, Wang L et al. (2022) Seasonal differences in the dominant factors of surface urban heat islands along the urban-rural gradient. Front Environ Sci 10:974811. https://doi.org/10.3389/fenvs.2022.974811
Yan H, Wu F, Dong L (2018) Influence of a large urban park on the local urban thermal environment. Sci Total Environ 622–623:882–891. https://doi.org/10.1016/j.scitotenv.2017.11.327
Yan L, Jia W, Zhao S (2021) The cooling effect of urban green spaces in metacities: a case study of Beijing, China’s capital. Remote Sens 13:4601. https://doi.org/10.3390/rs13224601
Yan M, Chen L, Leng S, Sun R (2023) Effects of local background climate on urban vegetation cooling and humidification: Variations and thresholds. Urban For Urban Green 80:127840. https://doi.org/10.1016/j.ufug.2023.127840
Yang J, Guo R, Li D et al. (2022) Interval-thresholding effect of cooling and recreational services of urban parks in metropolises. Sustain Cities Soc 79:103684. https://doi.org/10.1016/j.scs.2022.103684
Yang J, Sun J, Ge Q, Li X (2017) Assessing the impacts of urbanization-associated green space on urban land surface temperature: a case study of Dalian, China. Urban For Urban Green 22:1–10. https://doi.org/10.1016/j.ufug.2017.01.002
Yang P, Xiao Z-N, Ye M-S (2016) Cooling effect of urban parks and their relationship with urban heat islands. Atmospheric Ocean Sci Lett 9:298–305. https://doi.org/10.1080/16742834.2016.1191316
Yang X, Peng LLH, Jiang Z et al. (2020) Impact of urban heat island on energy demand in buildings: Local climate zones in Nanjing. Appl Energy 260:114279. https://doi.org/10.1016/j.apenergy.2019.114279
Yao X, Yu K, Zeng X et al. (2022a) How can urban parks be planned to mitigate urban heat island effect in “Furnace cities”? An accumulation perspective. J Clean Prod 330:129852. https://doi.org/10.1016/j.jclepro.2021.129852
Yao X, Zhu Z, Zeng X et al. (2022b) Linking maximum-impact and cumulative-impact indices to quantify the cooling effect of waterbodies in a subtropical city: a seasonal perspective. Sustain Cities Soc 82:103902. https://doi.org/10.1016/j.scs.2022.103902
Yao Y, Cheng T, Sun Z et al. (2022c) VecLI: A framework for calculating vector landscape indices considering landscape fragmentation. Environ Model Softw 149:105325. https://doi.org/10.1016/j.envsoft.2022.105325
Yu Z, Fryd O, Sun R et al. (2021) Where and how to cool? An idealized urban thermal security pattern model. Landsc Ecol 36:2165–2174. https://doi.org/10.1007/s10980-020-00982-1
Yu Z, Guo X, Jørgensen G, Vejre H (2017) How can urban green spaces be planned for climate adaptation in subtropical cities? Ecol Indic 82:152–162. https://doi.org/10.1016/j.ecolind.2017.07.002
Yu Z, Yang G, Zuo S et al. (2020a) Critical review on the cooling effect of urban blue-green space: A threshold-size perspective. Urban For Urban Green 49:126630. https://doi.org/10.1016/j.ufug.2020.126630
Yu Z, Yang G, Zuo S et al. (2020b) Critical review on the cooling effect of urban blue-green space: A threshold-size perspective. Urban For Urban Green 49:126630. https://doi.org/10.1016/j.ufug.2020.126630
Yuan Y, Li C, Geng X, et al. (2022) Natural-anthropogenic environment interactively causes the surface urban heat island intensity variations in global climate zones. Environ Int 107574. https://doi.org/10.1016/j.envint.2022.107574
Zhao H, Zhang H, Miao C et al. (2018) Linking heat source–sink landscape patterns with analysis of urban heat islands: study on the fast-growing Zhengzhou City in Central China. Remote Sens 10:1268. https://doi.org/10.3390/rs10081268
Zhou W, Shen X, Cao F, Sun Y (2019) Effects of area and shape of greenspace on urban cooling in Nanjing, China. J Urban Plan Dev 145:04019016. https://doi.org/10.1061/(ASCE)UP.1943-5444.0000520
Zhou Y, Zhao H, Mao S et al. (2022) Studies on urban park cooling effects and their driving factors in China: Considering 276 cities under different climate zones. Build Environ 222:109441. https://doi.org/10.1016/j.buildenv.2022.109441
Zhou Y, Zhuang Z, Yang F et al. (2017) Urban morphology on heat island and building energy consumption. Procedia Eng 205:2401–2406. https://doi.org/10.1016/j.proeng.2017.09.862
Zhu W, Sun J, Yang C et al. (2021) How to measure the urban park cooling island? A perspective of absolute and relative indicators using remote sensing and buffer analysis. Remote Sens 13:3154. https://doi.org/10.3390/rs13163154
Acknowledgements
This research study was supported by the Basic Scientific Research Project (Key Project) of the Education Department of Liaoning Province (grant no. LJKZ0964), National Natural Science Foundation of China (grant no’s 41771178, 42030409), the Fundamental Research Funds for the Central Universities (grant no. N2111003).
Author information
Authors and Affiliations
Contributions
JY: contributed to all aspects of this work. XC: wrote the main manuscript text, conducted the experiment, and analyzed the data. YZ: writing—review and editing, Supervision. XX: writing—review and editing, supervision. J (Cecilia) X: writing—review and editing, supervision.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
This article does not contain any studies with human participants performed by any of the authors. Ethical approval was not relevant.
Informed consent
This article does not contain any studies with human participants performed by any of the authors. Informed consent was not relevant.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cai, X., Yang, J., Zhang, Y. et al. Cooling island effect in urban parks from the perspective of internal park landscape. Humanit Soc Sci Commun 10, 674 (2023). https://doi.org/10.1057/s41599-023-02209-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-023-02209-5
This article is cited by
-
Urban growth scenario projection using heuristic cellular automata in arid areas considering the drought impact
Journal of Arid Land (2024)
-
Exploring diurnal and seasonal variabilities in surface urban heat island intensity in the Guangdong-Hong Kong-Macao Greater Bay Area
Journal of Geographical Sciences (2024)