Abstract
Diversity drives both biological and artificial evolution. A prevalent assumption in cultural evolution is that the generation of novel features is an inherent property of a subset of the population (e.g., experts). In contrast, diversity—the fraction of objects in the corpus that are unique—exhibits complex collective dynamics such as oscillations that cannot be simply reduced to individual attributes. Here, we explore how a popular cultural domain can rapidly expand to the point where it exceeds the supply of subject-specific experts and the balance favours imitation over invention. At this point, we expect diversity to decrease and information redundancy to increase as ideas are increasingly copied rather than invented. We test our model predictions on three case studies: early personal computers and home consoles, social media posts, and cryptocurrencies. Each example exhibits a relatively abrupt departure from standard diffusion models during the exponential increase in the number of imitators. We attribute this transition to the “dilution of expertise.” Our model recreates observed patterns of diversity, complexity and artifact trait distributions, as well as the collective boom-and-bust dynamics of innovation.
Similar content being viewed by others
Introduction
"No one goes there anymore, it’s too crowded”—a quote attributed to American baseball player Yogi Berra—captures a familiar sentiment when a trend becomes mainstream (Bentley and O’Brien, 2017). In the early, formative phase of a future trend, there is a high level of interest, creativity, and specialized expert knowledge among a small population of inventors (Rogers, 2010; Gladwell, 2006). As the trend becomes more widely adopted, the balance of invention versus imitation may tilt towards imitation: the copying of ideas through social-learning, rather than invention, i.e., the creation of new ideas. The change in this balance could occur when the popularizing trend extends beyond the population of experts, or people with enough specialized knowledge to make substantial changes to the trend.
These “expert” communities are often small compared to the mainstream. Fashion designers, for example, are much fewer than those who buy and sell clothes. The pioneers in Fortran programming and the original Internet in the 1970s are vastly outnumbered by users of computers and Internet in subsequent decades. Certain intellectual trends of philosophers or management scientists often become “mainstreamed” years later, via oft-repeated “buzzwords” of workplaces or political discourse. It may be that such a transition—when the imitation of new ideas outpaces the capacity of the expert community to feed in fresh ideas—could be a root cause of stagnant genres of popular culture, bloated bureaucracy, and the phenomenon known as “the death of expertise” (Nichols, 2017).
This issue connects to the literatures of cultural evolution, social economics, social-learning theory, complexity theory, and ecology. While each field employs concepts for the balance of imitation and invention, the terminologies can be inconsistent. Joseph Schumpeter (Schumpeter et al., 1939) defined innovation as the copying of unique inventions, whereas Frank Bass (Bass, 1969) used innovation to describe invention and adoption to describe the copying. The social-learning literature sometimes uses producers versus scroungers (Mesoudi, 2008), and the complexity science and business literature may use exploitation versus exploration (Axelrod and Cohen, 2008). Fortunately, all of these refer to the same distinction between the invention of something new versus the copying of those inventions. For this study, we will call the agents who invent new things experts and those who copy/adopt those inventions to be imitators.
Common to all these theories is that the balance of experts versus imitators is a crucial measure. Invention by experts produces new ideas, and imitation diffuses those ideas into the wider population. While population and community sizes vary, what matters is the proportion: if the majority are imitators rather than inventors, then ideas or technologies will persist through time. If the majority are experts, then there will be high turnover (Bentley et al., 2021; Eriksson et al., 2010). In fast-changing environments, it helps to have more expertise to adapt quickly, as too much imitation would allow outdated ideas to persist.
Invention is high in popular culture—a novelty-driven system (Vaesen and Houkes, 2021; Leroi et al., 2020; Lambert et al., 2020)—sustained by a high ratio of experts producing novelty for imitators to diffuse. Popular culture and trends change so fast that novelty in itself may be valued, as observed for video games (Montfort and Bogost, 2009), the cryptocurrency market (Park et al., 2020; ElBahrawy et al., 2017), and internet memes (Coscia, 2014, 2017). Elements of popular culture—video games, new stories, memes or jokes—often experience marginal returns, where the attraction declines with repeated use or repetition.
As the relative proportion of expertise needs to be high to generate so much novelty, we propose that the supply of experts cannot always keep up with the exponential increase in imitators during a fashion or fad (Rogers, 2010; Bass, 1969; Henrich, 2001; Bentley and Ormerod, 2009). Our hypothesis is that fashions that undergo a “boom-and-bust” dynamic —exponential growth in the number of products followed by a rapid decline—will exhibit a change when the ratio of experts to imitators abruptly declines: there is not enough specialized expertise to supply new inventions to the genre. We call this the “dilution” of expertise as opposed to its “death” (Nichols, 2017) because expertise still exists but is no longer abundant enough to maintain the same ratio versus imitation. Simple diffusion models (Bass, 1969; Henrich, 2001; Bentley et al., 2012), which describe the boom and bust cycle of fashions, replicate the number of adoptions for a single entity. These models typically rely on a fixed ratio of experts to imitators. Here, we explore how that expertise/imitation ratio decreases as a result of exponential growth in popularity in the first part of the diffusion curve. For this we employ a simple multi-component model of cultural production, which can connect the dynamics of diversity to the mechanistic generative processes of invention vs imitation. Ideas and technologies are complex systems (Buskell et al., 2019) encapsulating multiple elements, some of which may be well established, whereas others are perhaps used for the first time. Evolved products made entirely of novel elements are extremely unlikely (Dawkins, 1997), implying that new products are simply refinement and recombination of existing variants (Kandler and Laland, 2009).
We explore these effects in contemporary case studies of explosive trends from different decades: early personal computers and home consoles, Reddit posts, and cryptocurrencies. We characterize each case using established metrics of lexical diversity, information density, and structural complexity. We find evidence for a consistent increase in redundancy coupled with a decrease in information density and complexity in all case studies. Finally, we discuss the implications of this study for theories of the diffusion of information, social-learning, and cumulative cultural evolution.
Datasets
Our datasets include three boom-and-bust case studies, plus three additional case studies as controls, from different decades. The boom-and-bust examples are Atari 2600 video games in the 1980s, cryptocurrency documentation in the 2010s, and a Reddit r/Punpatrol posts, which began as a subreddit in 2018. As a control in each case, we use a contemporary dataset written in the same language and with similar purpose, structure and media. Atari 2600 is contrasted to Commodore Vic-20, an early home computer, which produced games in the same machine language and run in the same chipset. Cryptocurrency documentation in the form of white papers is compared to the evolution of scientific publications in the field of optics, both texts in English communicating mostly technical information in pdf documents structured in standardized sections. We also compare two Reddit communities or subreddits (r/PunPatrol and r/Politics), these are posts in topic-driven discussions incorporating english but also memetic communications. This amounts to six datasets of technological and cultural change.
We downloaded a collection of video game ROM cartridges for the Atari 2600 and Commodore Vic-20 from the websites www.atarimania.com and www.tosecdev.org, respectively. A custom reverse-engineering process recovered the set of assembly source codes from binary codes stored in N = 738 ROM files (see Supplementary Materials). Cryptocurrency “white papers” from the period 2009–2020 were collected from various online sources (whitepaperdatabase.com, allcryptowhitepapers.com, whitepaper.io) and dated according to their document production date when available or their first transaction otherwise. Presumably, many more cryptocurrency projects have existed, but documentation in the form of a parseable file could be found only for the N = ∑N(t) = 1383 included in this study. Bit strings were extracted from the pdf files from using the Textract library for Python. As a negative control for the cryptocurrency dataset, scientific publications from the period 1980–2020 listed by PubMed with the keyword “optics” were downloaded from their respective publication web resources. Pdf file processing was carried out as described for cryptocurrency white papers.
Reddit posts were retrieved using the Python Reddit API wrapper (PRAW) from their respective subreddits (r/PunPatrol and r/Politics). In these datasets, cultural products are N = ∑N(t) = 10761 collated posts and comments using a depth-first strategy, accumulated over a period of ≈330 days. All English bit strings were processed using the natural-language toolkit for Python (NLTK), and synsets were elaborated using the WordNet synonym sets by replacing each non stop-word with its most frequent synonym in the Brown corpus.
Overall, the datasets are of a diverse character (machine codes, text, and memes; see Fig. 1a), and they span time-scales ranging from days to years. Each case study involves a hierarchical structure of sentences formed of symbols (Fig. 1a) that can be represented as a three-layered multilayered network (Solé et al., 2002). Each layer represents a different type of element: product, sentence, and symbol (see Fig. 1b). Interactions between elements in adjacent levels are represented as a bipartite network (Fig. 1c).
a Many cultural artifacts have internal hierarchies that are formed by combining components or symbols (words, codes) into mesoscale structures (sentences), which then produce cultural goods or artifacts, i.e., video game cartridges, technical documentation, and social media memes (see text). b Formal representation of the hierarchical organization of cultural and technological knowledge: a product (blue) is a series of sentences (green) formed by words/symbols (yellow). c Bipartite network obtained from the sentence and symbol layer, each black filled square indicates when a symbol appears in a given sentence.
Bipartite network representation of cultural products
The linear sequence of natural or artificial symbols were transformed into a bipartite network B = (V, W, E) of symbols and sentences (see Fig. 1c). In a bipartite network, there is an edge (vi, wj) ∈ E if the symbol wj ∈ W appears in the sentence vi ∈ V. Using this data structure, we visualized how elementary ideas relate to each other and how complex the generative process of cultural products could be.
For natural-language texts, we separated the content by phrases, eliminated stop words using the Natural Language Toolkit Python library (NLTK) version 3.6.1 (Bird et al., 2009), and reduced it to semantically related words. This last step of the process was carried out using the WordNet synonym sets database (Miller, 1995; Ruiz-Casado et al., 2005), substituting each word by its most commonly used synonym using the Brown corpus and custom Python code. By collapsing the synonym space, we ensure that cultural products are represented by their relevant component ideas instead of considering different synonyms as culturally different elements. This approach has been previously used to more accurately quantify the cognitive extent of science (Milojevic, 2015) and provide a network evolution model of concepts in innovations (Iacopini et al., 2018).
At the most basic level, writing a video game consists in defining a sequence of 8-bit (byte) numbers encoding graphics, sound or instructions. For convenience, these machine codes have an equivalent lexicographic representation in a high-level assembly (Leventhal, 1986) language that follows a simple artificial grammar. This high-level representation allows for a natural partitioning of sentences and symbols, as well as a network reconstruction of their associations (see Supplementary Materials).
Methods
A dynamic model of cultural production
We used a modified Polya urn model (Mahmoud, 2008), following Tria et al. (Tria et al., 2014). This model represents the processes of invention and imitation as a sequential random sampling process from a common pool \({{{\mathcal{U}}}}\) of components, which reflect the collective know-how about basic ideas or technologies that facilitate new cultural production (see Fig. 2a). In this model, q and μ denote rates of imitation and expert invention, respectively, whereas x(t) and y(t) reflect the numbers of experts and imitators, respectively. Within this framework, cultural products are generated by assembling and recombining (Kandler and Laland, 2009; Lewis and Laland, 2012; Boyd et al., 2013) these basic ideas or technologies into larger cultural products of arbitrary length. During the sampling process, creators can encounter previously used components or new components (Fig. 2a light and dark boxes, respectively), corresponding to the processes of imitation and expert invention, respectively. Previously unused elements are attainable with the current shared knowledge. When a component is used for the first time, a quantity, 1 + μ, of different new elements is introduced in the urn, representing inventions adjacent to the ones just discovered, ready to be found by further sampling. Whenever a component is chosen, this signals its value to other creators, increasing, by amount q, the number of copies within the urn, and thus the likelihood that it will be used in the future.
We simulate the process of cultural production using the Polya urn model. a At each time step t, an agent inspects the urn \({{{{\mathcal{U}}}}}_{t}\) and must decide between copying a pre-existing symbol (\({w}_{2}\in {{{\mathcal{P}}}}\), top) or introducing a symbol that has never been used before (\({w}_{5}\notin {{{\mathcal{P}}}}\), bottom). In each case, q copies of the chosen symbol are introduced in the urn \({{{{\mathcal{U}}}}}_{t+1}\) while inventions (at bottom) trigger 1 + μ other novelties (i.e., new symbols w6 and w7). b A population of experts x(t) and imitators y(t) is used as dynamic substrate for the urn exploration and reinforcement parameters (μ and q). These populations of agents are in turn coupled to the number of cultural products N(t) = x(t) + y(t), assuming for the sake of simplicity that each agent produces one artifact per unit of time. Agents can switch strategies with some given probabilities (δx and δy). In both cases, the expected population growth (2p(t) − 1) is a function of product novelty p(t) at time t (see Supplementary Materials).
To capture boom-and-bust dynamics, we have slightly modified the traditional Polya urn model by linking the urn parameters (q and μ) to a population of creators that fall into two categories: experts, x(t), and imitators y(t). Collectively, the population creates new cultural products, N(t), in an urn sampling process. For simplicity, we assume that each agent creates a single cultural artifact per unit of time: N(t) = x(t) + y(t). When the population of experts, x(t), increases, the number of new elements introduced into the common pool of knowledge also increases (i.e., μ is equal to the size of the population of experts). Similarly, a growing population of imitators enhances the processes of reinforcement, increasing q proportionately (i.e., q is equal to the size of the population of imitators). The population of imitators and experts can dynamically change following two main mechanisms (see Supplementary Materials). First, our agents are flexible creators (Miu et al., 2020): imitators can switch into experts and vice versa with rates δy and δx, respectively, as shown in Fig. 2b. Secondly, the overall population of creators grows and shrinks according to the expectation of success (Hirshleifer and Plotkin, 2021; MacKenzie, 1993; Van Lente and Rip, 1998; Kriechbaum et al., 2021), which is determined by the capacity of the system to produce novel cultural artifacts (i.e., containing new components). The probability p(t) that at least one novel component has been found corresponds to the dynamics of success in an ideal uniform search (Doncieux et al., 2019):
where C is the product size, and Ω(t) is the probability of sampling a new component at time t (see Supplementary Materials). The capacity for sustained innovation relates to the concept of open-endedness in cultural evolution, where the supply of new forms and components overcomes the limitations imposed by selection or reinforcement of cultural norms that promote stasis (Taylor et al., 2016).
Prediction of multi-scale diversity
We characterize cultural product diversity using three independent metrics: lexical diversity, information density, and product structural complexity. The Polya urn model of cultural production described above may predict cultural histories and, as a result, benchmarks for the evolution of these metrics under diverse situations of imitation and innovation. These metrics, as well as their boundaries and predicted behavior, are detailed in the following.
Assessment of lexical diversity
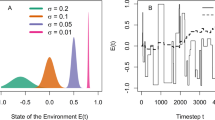
Lexical diversity measures the ratio of unique words (tokens) in a document to the total number of words in the document. We can estimate lexical diversity through the exponent of the Zipf’s law (b), where the frequency of a word, f(r), is predicted by its rank, r, in the frequency table as f(r) ≈ r−b. Lexical diversity becomes larger as the exponent b becomes smaller. However, linguistic studies have shown that natural texts display two different exponents in the rank-frequency distribution (Ferrer i Cancho and Solé, 2001; Gerlach and Altmann, 2013), corresponding to a kernel lexicon present in all communications, and another domain-specific lexicon at high ranks reflecting the topic and semantics of the communication (Piantadosi, 2014). In order to capture the topic-specific Zipf’s law exponent b, a numerical fit of the tail of symbol frequency distribution (the last 1.5 orders of magnitude in rank) was carried out. The fit was produced using standard functions from the Numpy library for Python. The Polya urn model predicts that f(r) ~ r−q/μ (Fig. 3a), where q and μ are the rates of imitation and expertise, respectively (Tria et al., 2014).
a Rank-frequency distribution of components follows a power-law f(R) ~ R−α with an exponent α ≈ q/μ. Cultural products generated by urns with higher levels of imitation have steeper frequency rank distributions and so are less diversified. b When there is more imitation, synthetic histories become more compressible. We illustrate how the information density ρ(n) increases when additional symbols are gathered for different values of q and μ. The solid line indicates the average information density in synthetic cultural histories, \(\rho\), while the shaded region contains one standard deviation of the sample. c The plot of average log-transformed structural complexity (NBDM) as a function of the ratio q/μ demonstrates how imitation results in simpler networks. Solid line marks the average complexity for 10 replicates of each pair, q ∈ [1, 40], μ ∈ [1, 40], plotted with logarithmic binning for the q/μ ratio. Shaded area represents 1 standard deviation of the sample. In each panel, simulated data comprise 10 independent synthetic cultural histories of 1000 products each, using different values of the urn parameters (q, μ) and the video game Pac-Man as a template.
Compression-based measures of information density
Information density quantifies symbol sequence redundancy, or the amount to which repeated and organized symbol sequences may be reduced without losing information. Information density is calculated using an universal compression algorithm, Lempel-Ziv-Welch (LZW) that builds a word dictionary from the data stream being compressed (Ziv and Lempel, 1977) (see Supplementary Materials). Information density is defined formally as
where L(x) is the total binary code length of the compressed sequence, L is the cultural product size (measured in symbols), and α is the alphabet of symbols used in cultural products. When imitation q and invention μ are constant, the information density of modeled symbol sequences decays exponentially with each accumulated symbol count towards the theoretical entropy-production rate (Fig. 3b). This limit is high in diverse urns (μ > q) and low in urns dominated by imitation (q > μ).
Estimating structural complexity
Algorithmic complexity provides a robust measure for cultural randomness, and although uncomputable, it can be estimated by means of the Coding Theorem (Zenil et al., 2015). The more frequent a string x is, the lower its algorithmic complexity:
where m(x) is the algorithmic probability that a random program generates the string. An exhaustive search can be used to estimate the complexity of small strings x. Instead of analyzing the complexity of sequences of symbols (computer instructions or text characters), we measure the complexity (Zenil et al., 2019) in the bipartite network B relating instructions/words and sentences. Block decomposition method (BDM) decomposes the adjacency matrix of the network Bi into smaller sub-strings σj (for which the Coding Theorem provides a complexity estimation). By putting together these local complexity values we obtain the structural complexity for the full network Bi:
where Nj is the number of occurrences of the sub-string σj. Structural complexity of cultural products was computed using the PyBDM package, normalizing the block decomposition method metric using the size of the bipartite adjacency matrix ∣Bi∣ = L and the size of the alphabet (∣α∣):
This metric seeks the most straightforward generating strategy for recreating the network of how symbols (components) interact to form sentences (products). Intuitively, sentences that share one or more symbols have less structural complexity and display more redundancy. At modest degrees of imitation versus expert invention, we detect a peak in structural complexity (see Fig. 3c). When the degree of imitation is high (q > μ), the resulting network is simple and contains a lot of redundancy owing to symbol repetition. When expertise is high (μ > > q), the large number of unique symbols results in a sparse network with low complexity due to alphabet normalization.
Results
Boom-and-bust dynamics
The target datasets exhibit boom-and-bust dynamics, which are defined by a rapid or exponential rise in cultural and technological products followed by a rapid collapse. Figure 4 depicts the growth in numbers of cultural products versus the boom-bust pattern in estimated numbers of imitators and experts. Starting with a system composed of expert inventors, the interplay between cultural reinforcement and individual strategies dilutes their influence. Following an initial period of rapid diversity expansion, frequency-dependent imitation saturates the market with duplicate technologies and impedes experts’ capacity to generate unique products, dramatically limiting the global pace of innovation. As estimated by our model, the abundance of imitators (dotted red line) is greatest for the Atari case (Fig. 4). Even if the population of experts (dashed green line) exceeds that of imitators (dotted red line) in the declining phase, the historical pattern of cultural-diversity loss cannot be reversed (see Fig. 4b).
For a Atari 2600 video games, b cryptocurrencies, and c Reddit posts, we show the temporal dynamics predicted by the population-based model. We show the real cultural productivity, N(t) = x(t) + y(t), during that period (open blue circles), the predicted cultural productivity (orange solid line) and the population of experts x(t) and imitators y(t) at any given time t (green and red dashed lines, respectively). As an inset for each case, we report the expected population growth (2p(t) − 1) due to product novelty p(t) in that period (see text).
Comparison between datasets and controls
Next, we analyze the time evolution of three multi-scale metrics presented above, namely lexical diversity through the Zipf’s law exponent, information density and structural complexity. These metrics, as previously mentioned, are directly connected to the dynamics of imitators and experts: imitation-driven systems have lower richness (and a greater Zipf’s exponent), lower information density, and lower structural complexity.
This analysis is shown in Fig. 5 for the Atari (blue line) and Commodore Vic-20 (orange line) datasets, with the latter serving as a control (using cumulative number of symbols on the x-axis for comparability). In the early stages of these systems, both datasets exhibit comparable Zipf’s law exponents (Fig. 5a). However, there is a considerable increase in exponent values at the start of the exponential-growth phase (gray dotted line 1982), indicating an increase in the ratio (q/μ) of imitators to experts. Figure 5b displays the estimated information per machine symbol. The general pattern is consistent in the expected zone of expertise dilution, with Atari and Commodore systems separating immediately after the start of the boom and bust cycle. The decline in average complexity (blue curve) of Atari 2600 video games during peak cultural diversity (red curve) is shown in Fig. 5c, which is consistent with predictions for increasing imitation in a Polya urn generative process. In contrast, the average complexity of Commodore Vic-20 video games shows no temporal trend (Fig. 5d).
a Zipf's law exponent evolution for a given accumulated number of machine instructions in Atari 2600 (blue) and Commodore Vic-20 (orange). Solid line represents the average exponent of 25 replicate sub-samplings and shaded region encompasses 1 standard deviation of this distribution. b Decay of information density for the accumulated number of symbols n(t) in Atari 2600 (blue) and Commodore Vic-20 (orange). Solid line represents the average information density of 25 replicates within-year orderings and the shaded region encompasses one standard deviation of the distribution. As a guide, vertical dashed lines mark the dates before (1982) and after (1984) the crash of Atari video games in panels a and b. The evolution of log-transformed size-normalized structural complexity (NBDM) in c Atari 2600 and d Commodore Vic-20 video games. Red line shows the cultural product diversity N(t) in each domain for c and d. Asterisk-marked regions indicate statistically significant drops in complexity (see Supplementary Materials).
In Fig. 6 we explore structural patterns of cryptocurrency publications (blue line) compared to a scientific publication control dataset (orange line). The evolution of the Zipf’s law exponent shows a departure from the control behavior starting at 2017 (Fig. 6a), when an explosion in redundant products took place. Information density paints a similar if attenuated trend, with scientific publications and cryptocurrency datasets displaying similar slopes in information density (Fig. 6b). By 2015, however, the addition of new symbols further reduces information density and increases redundancy. Later cultural products in the cryptocurrency dataset have increasingly more overlap with prior elements in the corpus. Finally, in the bottom-row panels we compare the normalized structural cultural product complexity for the two datasets. Whereas in optics publications the average complexity has not changed significantly in more than a decade (despite variations in the cultural productivity as shown by the red line), in cryptocurrency there is a significant decrease in complexity during the crash and in the year leading up to it.
a Zipf's law exponent evolution for a given accumulated word count in cryptocurrency white papers (blue) and scientific publications (orange). Solid line represents the average exponent of 25 replicate sub-samplings, and shaded region encompasses one standard deviation of this distribution. b Decay of information density for the accumulated number of symbols n(t) in cryptocurrency white papers (blue) and scientific publications (orange). The solid line is the average information density of 25 replicates within-year orderings, while the shaded region represents one standard deviation of the distribution. The evolution of log-transformed size-normalized structural complexity (NBDM) in c cryptocurrency white papers and d scientific publications. As a guide, the red line indicates the cultural product diversity N(t) in each domain for c and d. Asterisk-marked regions indicate statistically significant drops in complexity (see Supplementary Materials).
Finally, the same analysis is carried out in the Reddit posts of two different communities. Whereas target (blue) and control (orange) datasets start at similar Zipf’s exponent values (Fig. 7a), by day 120 (or 20,000 symbols) the cultural products in r/PunPatrol become significantly less rich in linguistic terms than their counterparts in r/Politics. In terms of normalized information density (Fig. 7b), r/Politics displays higher per symbol information than the r/PunPatrol dataset. Moreover, between days 130 and 150 there is a marked decrease in information density, signaling an enhanced redundancy of the posts produced during this period (which coincides with peak cultural productivity). We do not observe significant change in product complexity (Fig. 7c), which could be due to the short nature of the communications and thus the lack of a robust signal. In order to test this hypothesis, we analyzed the cultural complexity of the coarse-grained datasets, aggregating all posts in 10-day periods. The coarse-graining precludes us from performing statistical significance analyses but the aggregated product trend shows a marked decrease in structural complexity during the boom-and-bust period of r/PunPatrol, whereas r/Politics remains fairly constant (see Supplementary Material).
a Zipf's law exponent evolution for a given accumulated word count in the online communities r/PunPatrol (blue) and r/Politics (orange). Solid line represents the average exponent of 25 replicate sub-samplings, and shaded region encompasses one standard deviation of this distribution. b Decay of information density for varying number of accumulated symbols in the r/PunPatrol (blue) and r/Politics (orange). Solid line represents the average information density of 25 replicates within-year orderings, and the shaded region encompasses one standard deviation of the distribution. The evolution of log-transformed size-normalized structural complexity (NBDM) in c r/PunPatrol and d r/Politics. As a guide, the red line indicates the cultural product diversity N(t) in each domain for c and d.
Discussion
Theoretical and empirical studies of cultural evolution assume that the frequency of cultural traits reflect the dynamics of selection and adaptation to changing environments (Lewis and Laland, 2012; Miu et al., 2018; Deffner and Kandler, 2019). Adaptability to a changing environment needs a steady supply of variation (Whitehead and Richerson, 2009; O’Brien and Shennan, 2010), but coalescing into few dominant forms or behaviors—cultural conformity (Claidière and Whiten, 2012)— is the necessary consequence of selecting the best solution discovered in a stable environment (Miu et al., 2018). This adaptive perspective describes the evolution of cultural and technological systems via domain-specific fitness functions (Mesoudi, 2008; Mesoudi and O’Brien, 2008; Caldwell and Millen, 2008; Thompson and Griffiths, 2021). An open question is how to incorporate the structural characteristics of cultural variants into theoretical models (Deffner and Kandler, 2019). When the cultural products involve complex encoding (for example, documents), any model that abstracts them with a small number of traits (or traits without interrelationships) may be unable to capture the cultural dynamics resulting from these interactions (Buskell et al., 2019) because the “relevant” cultural traits are identified a priori.
Here, we present a more a general framework using: (1) a data-driven approach, (2) a null model of recombination-based innovation, and (3) the notion of open-ended evolution. Our framework avoids abstract (or simplified) representations of cultural products. Instead, we directly monitor multi-scale diversity in cultural products naturally encoded with symbols (code or words). Although networks have been employed in cultural-evolution research, such as when modeling the social dynamics of innovation (Cantor et al., 2021; Derex and Mesoudi, 2020), using networks to capture the complexity of cultural products is far less frequent (Valverde et al., 2002; Buskell et al., 2019). In order to avoid idiosyncratic results due to the choice of metrics or scale of analysis, we propose a more general approach that encompasses multiple measures of diversity: lexical diversity, information density and structural complexity. More accurate and reliable estimates of imitation and innovation rates should be possible if representation biases are reduced.
Previous work has shown the build-up of cumulative culture is more dependent on the combination of existing components than on the introduction of unique products (Kandler and Laland, 2009; Lewis and Laland, 2012; Boyd et al., 2013; Valverde and Sole, 2015), as well as the global impact of component diversity when developing technological products (Hidalgo and Hausmann, 2009). Similarly, our null model generates synthetic products by the recombination of existing components (imitation) with new ones (expert invention). We have shown that the generative approach makes testable predictions in real-world systems, most notably the emergence of multi-scale diversity with the imitation-to-invention ratio, which changes dynamically within the population (Fig. 2b).
Another key feature is a dynamical motif of cultural productivity: the exponential growth followed by an equally rapid collapse, commonly referred to as boom-and-bust (see Fig. 4). Prior work has usually explained this dynamical feature by including exogenous effects: environmental degradation (Butzer, 2012), changes in carrying capacities, mismanagement of expectations (Hirshleifer and Plotkin, 2021) or hype (Kriechbaum et al., 2021). Here, we connect the decline in cultural productivity with the dilution of expertise, which highlights how the supply of experts affects growth and innovation.
In prehistory, cultural evolution was slower in tempo, with technological stability across lengthy periods of time (O’Brien and Shennan, 2010). However, recent times have been dominated by the persistent search for novelty, keeping the diversity and complexity of technologies growing over large time-scales (Duran-Nebreda and Valverde, 2023). This is the defining trait of open-ended evolution (Taylor et al., 2016), the characterization of an evolutionary process as the endless new adaptations to a changing environment instead of stability. These evolutionary dynamics are reminiscent of the novelty-search algorithm (Lehman and Stanley, 2008), which suggests a new interpretation of cultural evolutionary processes not based on the selection of specific traits, but by the creation and maintenance of diversity. The successful application of novelty-search algorithms to complex engineering challenges exemplifies this idea (Lehman and Stanley, 2011), indicating how we can expand the theory of cumulative cultural evolution to comprehend the origins and consequences of cultural diversity and transmission biases. Our study highlights that the explicit search for novelty is an underappreciated component of the theory of cumulative cultural evolution (Gabora, 2019).
Finally, the framework described here serves as a starting point for system-specific analyses, including additional constraints regarding the effects of memory and more sophisticated population structure (Gleeson et al., 2014; Bentley et al., 2014; Kandler and Crema, 2019). Future research should build on our theoretical predictions to create a system of “early warning signals”, which can be used to actively monitor excessive imitation and, hopefully, lessen the economic impact of expertise dilution.
Data availability
Example scripts for the methods described above, as well as processed datasets, may be obtained from the open repository at the following link: https://figshare.com/projects/Dilution_of_expertise_in_the_rise_and_fall_of_collective_innovation/141851.
References
Axelrod R, Cohen MD (2008) Harnessing complexity, Basic books
Bass FM (1969) A new product growth model for consumer durables. Manag Sci 15:215–227
Bentley RA, Ormerod P (2009) Tradition and fashion in consumer choice: bagging the scottish munros. Scott J Polit Econ 56:371–381
Bentley RA, Caiado CC, Ormerod P (2014) Effects of memory on spatial heterogeneity in neutrally transmitted culture. Evol Hum Behav 35:257–263
Bentley RA, Garnett P, O’Brien MJ, Brock WA (2012) Word diffusion and climate science. PLoS ONE 7:e47966
Bentley RA, Carrignon S, Ruck DJ, Valverde S, O’Brien MJ (2021) Neutral models are a tool, not a syndrome. Nat Hum Behav 5:807–808
Bentley RA, O’Brien MJ (2017) The acceleration of cultural change: from ancestors to algorithms, MIT Press
Bird S, Klein E, Loper E (2009) Natural language processing with Python: analyzing text with the natural language toolkit, O’Reilly Media
Boyd R, Richerson PJ, Henrich J, Lupp J (2013) The cultural evolution of technology: facts and theories. In: Cultural evolution: society, technology, language, religion. MIT Press, p 119
Buskell A, Enquist M, Jansson F (2019) A systems approach to cultural evolution. Palgrave Commun 5:1–15
Butzer KW (2012) Collapse, environment, and society. Proc Natl Acad Sci 109:3632–3639
Caldwell CA, Millen AE (2008) Experimental models for testing hypotheses about cumulative cultural evolution. Evol Hum Behav 29:165–171
Cantor M (2021) Social network architecture and the tempo of cumulative cultural evolution. Proc Roy Soc B 288:20203107
Claidière N, Whiten A (2012) Integrating the study of conformity and culture in humans and nonhuman animals. Psychol Bull 138:126
Coscia M (2014) Average is boring: how similarity kills a meme’s success. Sci Rep 4:1–7
Coscia M (2017) Popularity spikes hurt future chances for viral propagation of protomemes. Comm ACM 61:70–77
Dawkins R (1997) Climbing mount improbable, WW Norton & Company
Deffner D, Kandler A (2019) Trait specialization, innovation, and the evolution of culture in fluctuating environments. Palgrave Commun 5:1–10
Derex M, Mesoudi A (2020) Cumulative cultural evolution within evolving population structures. Trends Cogn Sci 24:654–667
Doncieux S, Laflaquière A, Coninx A (2019) Novelty search: a theoretical perspective. In: GECCO ’19: Genetic and Evolutionary Computation Conference, Prague, July 2019, p. 99. https://doi.org/10.1145/3321707.3321752
Duran-Nebreda S, Valverde S (2023) The natural evolution of computing. In: Kendal J, Kendal R, Tehrani J (eds.) Oxford handbook of cultural evolution, Oxford University Press, Oxford
ElBahrawy A, Alessandretti L, Kandler A, Pastor-Satorras R, Baronchelli A (2017) Evolutionary dynamics of the cryptocurrency market. Roy Soc Open Sci 4:170623
Eriksson K, Jansson F, Sjöstrand J (2010) Bentley’s conjecture on popularity toplist turnover under random copying. Ramanujan J 23:371–396
Ferrer i Cancho R, Solé RV (2001) Two regimes in the frequency of words and the origins of complex lexicons: Zipf’s law revisited. J Quant Linguist 8:165–173
Gabora L (2019) Creativity: Linchpin in the quest for a viable theory of cultural evolution. Curr Opin Behav Sci 27:77–83
Gerlach M, Altmann EG (2013) Stochastic model for the vocabulary growth in natural languages. Phys Rev X 3:021006
Gladwell M (2006) The tipping point: how little things can make a big difference, Little, Brown
Gleeson JP, Cellai D, Onnela JP, Porter MA, Reed-Tsochas F (2014) A simple generative model of collective online behavior. Proc Natl Acad Sci 111:10411–10415
Henrich J (2001) Cultural transmission and the diffusion of innovations. Am Anthropol 103:992–1013
Hidalgo CA, Hausmann R (2009) The building blocks of economic complexity. Proc Natl Acad Sci 106:10570–10575
Hirshleifer D, Plotkin JB (2021) Moonshots, investment booms, and selection bias in the transmission of cultural traits. Proc Natl Acad Sci 118:e2015571118
Iacopini I, Milojevic’ S, Latora V (2018) Network dynamics of innovation processes. Phys Rev Lett 120:048301
Kandler A, Laland KN (2009) An investigation of the relationship between innovation and cultural diversity. Theor Popul Biol 76:59–67
Kandler A, Crema ER (2019) Analysing cultural frequency data: neutral theory and beyond. In: Handbook of evolutionary research in archaeology, Springer, p 83
Kriechbaum M, Posch A, Hauswiesner A (2021) Hype cycles during socio-technical transitions: the dynamics of collective expectations about renewable energy in germany. Res Pol 50:104262
Lambert B (2020) The pace of modern culture. Nat Hum Behav 4:352–360
Lehman J, Stanley KO (2011) Abandoning objectives: evolution through the search for novelty alone. Evol Comp 19:189–223
Lehman J, Stanley KO (2008) Exploiting open-endedness to solve problems through the search for novelty. In: Bullock S, Noble J, Watson R, Bedau M (eds) Proceedings of the Eleventh International Conference on Artificial Life (ALIFE XI), Winchester, Cambridge, Massachusetts, MIT Press, pp. 329–336
Van Lente H, Rip A (1998) The rise of membrane technology: from rhetorics to social reality. Soc Stud Sci 28:221–254
Leroi AM, Lambert B, Rosindell J, Zhang X, Kokkoris GD (2020) Neutral syndrome. Nat Hum Behav 4:780–790
Leventhal LA (1986) 6502 assembly language programming. McGraw-Hill
Lewis HM, Laland KN (2012) Transmission fidelity is the key to the build-up of cumulative culture. Phil Trans Roy Soc B: Biol Sci 367:2171–2180
MacKenzie DA (1993) Inventing accuracy: a historical sociology of nuclear missile guidance, MIT press
Mahmoud H (2008) Pólya urn models, CRC press
Mesoudi A (2008) An experimental simulation of the “copy-successful-individuals” cultural learning strategy: Adaptive landscapes, producer-scrounger dynamics, and informational access costs. Evol Hum Behav 29:350–363
Mesoudi A, O’Brien MJ (2008) The cultural transmission of great basin projectile-point technology I: an experimental simulation. Am Antiq 73:3–28
Miller GA (1995) Wordnet: a lexical database for English. Commun ACM 38:39–41
Milojevic’ S (2015) Quantifying the cognitive extent of science. J Informetrics 9:962–973
Miu E, Gulley N, Laland KN, Rendell L (2018) Innovation and cumulative culture through tweaks and leaps in online programming contests. Nat Commun 9:1–8
Miu E, Gulley N, Laland KN, Rendell L (2020) Flexible learning, rather than inveterate innovation or copying, drives cumulative knowledge gain. Sci Adv 6: eaaz0286
Montfort N, Bogost I (2009) Racing the beam: The Atari video computer system, MIT Press
Nichols T (2017) The death of expertise: the campaign against established knowledge and why it matters, Oxford University Press
O’Brien MJ, Shennan SJ (2010) Issues in anthropological studies of innovation. In: O’Brien MJ, Shennan SJ (eds.) Innovation in cultural systems: contributions from evolutionary anthropology, MIT Press, p. 3
Park G, Shin SR, Choy M (2020) Early mover (dis) advantages and knowledge spillover effects on blockchain startups’ funding and innovation performance. J Bus Res 109:64–75
Piantadosi ST (2014) Zipf’s word frequency law in natural language: a critical review and future directions. Psychon Bull Rev 21:1112–1130
Rogers E (2003) Diffusion of innovations. Simon & Schuster, New York
Ruiz-Casado M, Alfonseca E, Castells P (2005) Automatic assignment of wikipedia encyclopedic entries to wordnet synsets. In: International Atlantic Web Intelligence Conference, Springer, p. 380
Schumpeter JA et al. (1939) Business cycles, vol. 1, Mcgraw-hill, New York
Solé RV, Ferrer-Cancho R, Montoya JM, Valverde S (2002) Selection, tinkering, and emergence in complex networks. Complexity 8:20–33
Taylor T (2016) Open-ended evolution: perspectives from the OEE workshop in York. Artif Life 22:408–423
Thompson B, Griffiths TL (2021) Human biases limit cumulative innovation. Proc Roy Soc B 288:20202752
Tria F, Loreto V, Servedio VDP, Strogatz SH (2014) The dynamics of correlated novelties. Sci Rep 4:1–8
Vaesen K, Houkes W (2021) Is human culture cumulative? Curr Anthropol 62:218–238
Valverde S, Solé R (2015) Punctuated equilibrium in the large-scale evolution of programming languages. J Roy Soc Interface 12:20150249
Valverde S, Ferrer-Cancho R, Solé RV (2002) Scale-free networks from optimal design. Europhys lett 60:512
Whitehead H, Richerson PJ (2009) The evolution of conformist social learning can cause population collapse in realistically variable environments. Evol Hum Behav 30:261–273
Zenil H, Soler-Toscano F, Delahaye JP, Gauvrit N (2015) Two-dimensional kolmogorov complexity and an empirical validation of the coding theorem method by compressibility. PeerJ Comput Sci 1:e23
Zenil H, Kiani NA, Zea AA, Tegnér J (2019) Causal deconvolution by algorithmic generative models. Nat Mach Intell 1:58–66
Ziv J, Lempel A(1977) A universal algorithm for sequential data compression IEEE T Inf Theor 23:337–343
Acknowledgements
SDN is supported by Beatriu de Pinós grant 2019-BP-00206, program of the AGAUR Generalitat de Catalunya. SV is supported by the Spanish Ministry of Science and Innovation through the State Research Agency (AEI), grant PID2020-117822GB- I00/AEI/10.13039/501100011033. SDN would like to thank Matt Jackson for discussions on the cryptocurrency market. SV expresses gratitude to Cecília Valverde-Tres for critical observations about the nature of video games. We thank Niles Eldredge, Chris Buckley and James Waddington for useful discussions about the tempo and mode of cultural and technological evolution, and Blai Vidiella and Josep Sardanyés for a careful review of our manuscripts and helpful suggestions.
Author information
Authors and Affiliations
Contributions
SD-N and SV conceived the research, SD-N and SV conducted the experiments, SD-N, MJO, RAB, and SV analyzed the results. All authors wrote, reviewed, and accepted the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
This article does not present research with ethical considerations.
Informed consent
This article does not contain any studies with human participants performed by any of the authors.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Duran-Nebreda, S., O’Brien, M.J., Bentley, R.A. et al. Dilution of expertise in the rise and fall of collective innovation. Humanit Soc Sci Commun 9, 365 (2022). https://doi.org/10.1057/s41599-022-01380-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-022-01380-5