Abstract
Languages differ markedly in the number of colour terms in their lexicons. The Himba, for example, a remote culture in Namibia, were reported in 2005 to have only a 5-colour term language. We re-examined their colour naming using a novel computer-based method drawing colours from across the gamut rather than only from the saturated shell of colour space that is the norm in cross-cultural colour research. Measuring confidence in communication, the Himba now have seven terms, or more properly categories, that are independent of other colour terms. Thus, we report the first augmentation of major terms, namely green and brown, to a colour lexicon in any language. A critical examination of supervised and unsupervised machine-learning approaches across the two datasets collected at different periods shows that perceptual mechanisms can, at most, only to some extent explain colour category formation and that cultural factors, such as linguistic similarity are the critical driving force for augmenting colour terms and effective colour communication.
Similar content being viewed by others
Introduction
Languages differ markedly in the number of colour terms in their lexicons. The languages of some remote populations are reported to have no or as few as two colour terms whereas most European languages have many more; at least 11 according to most definitions of a colour term (Berlin and Kay, 1969/1991; Wierzbicka, 2015). We wish to consider the mechanisms whereby the number of colour terms increases in a language and to report data where this has occurred in a remote population. Furthermore, we wish to show that understanding of colour term acquisition may be enhanced by considering machine learning.
The assessment of colour terms in remote populations is not without its problems. Using paper swatches, as in all previous studies, obtaining colour name responses to a large number of samples can be time-consuming. Thus, studies vary greatly in the number of colour samples they have used, from as few as 23 (Lindsey et al., 2015) to the much more extensive World Color Survey (Kay et al., 2010), where responses were obtained for 320 samples. Even here, the colour terms were obtained from only highly saturated colour samples as is general in cross-cultural studies of colour naming (Berlin and Kay, 1969/1991, Bimler and Uusküla, 2017; Gibson et al., 2017; Kay et al., 2010; Lindsey et al., 2015; Roberson et al., 2005), despite worries about the outcomes being affected by the variation in that dimension (Paramei, 2005; Roberson et al., 2005; Witzel, 2016; Witzel, 2018; Witzel et al., 2015). To our knowledge, there have been few, if any, studies with remote populations that have used computerised colour presentations to overcome these problems, perhaps because of worries about uncontrolled colour reproduction and the unfamiliarity of computer screens to indigenous populations. The latter objection has been shown to be of no concern for the Himba (Biederman et al., 2009; Linnell et al., 2018) and the former is now easily overcome (Mylonas et al., 2019; Paggetti et al., 2016). In consequence, we revisited the Himba who, when tested in 2004 (Roberson et al., 2005), were found to use a 5-colour-term grue language, by which is meant that the same word is used for green and blue regions of colour space (Kay, 1975). We will not only examine the colours tested in 2004 but also those from the inner core of colour space. Here, we may find colour terms that could not have been found in ours and all other previous cross-cultural research.
We wish to consider the augmenting of colour terms to a colour lexicon by which we do not mean the addition of any colour term but only those that can be considered to be colour categories (Berlin and Kay, 1969/1991; Davidoff, 2015; Gibson et al., 2017; Levinson, 2000; Lindsey et al., 2015; Mylonas and MacDonald, 2016). For example, in English, the term crimson denotes a type of red—not a different category—so would be an addition rather than an augmentation of the colour lexicon. There have been many attempts to answer the augmentation question. The earliest extensive attempt was by Berlin and Kay (1969/1991), who used the term “basic” for the major colour terms and declared an order for the acquisition of colour categories. In their view, augmentation occurred by partitioning existing colour terms that were previously able to name all colour space. Though behavioural rules were given by which a term could be considered basic, their origin was thought to be in universal colour physiology (Kay and McDaniel, 1978). Their physiological account proposed six colour terms that align with the postulated opponent channels of Hering and all other colour terms arise from their mixture (Hering, 1878/1964; Kay and McDaniel, 1978). The idea that primary colours are associated with the opponent-process cells in early vision has been disputed (Abramov and Gordon, 1994; Valberg, 2001; Wuerger et al., 2005). Nevertheless, these primary perceptual categories contain examples that are held to be unique in that they are perceived to contain no other colour and have been considered by some important in the development of colour categories (Forder et al., 2017; Kuehni, 2005; Philipona and O’Regan, 2006, but see also Jameson, 2010).
A notable subsequent alternative explanation is that colour categories appear maximally spaced within the 3D sub-volume of perceptual colour space. Colour lexicons, it is argued, develop by optimising the division of an irregular perceptual colour space to maximise similarity within a category and minimise similarity across categories (Boynton and Olson, 1987; Jameson and D’Andrade, 1997; Regier et al., 2007; Regier et al., 2015; Zaslavsky et al., 2018). These accounts are based on discrimination data and, though this could be considered independently of the underlying physiology (Jameson and D’Andrade, 1997), they are presumed reliant on early perceptual mechanisms (Kay and McDaniel, 1978; Zaslavsky et al., 2019). An optimal division of the surface of the colour solid into six well-formed categories by Regier et al. (2007) corresponded to the English terms: white, black, red, yellow, green and blue-purple. However, a subsequent study showed that the optimal criterion produced inadequate results for colour lexicons with more than 6 terms (Jraissati and Douven, 2017) and it is unclear whether the optimal partition principle can hold across the colour space (Lindsey and Brown, 2014).
There is a somewhat similar proposal, though from a clearly cultural perspective, whereby a category is achieved through language (colour terms) rather than early level colour physiology (Roberson et al., 2000). In that approach, the greater similarity for within-category colours is known as Categorical Perception (CP) though, in practice, to determine CP a colour category needs to have a large extension in colour space and is unavailable, say, for assessing a category such as yellow (see Davidoff, 2015).
There are other culturally determined views on augmentation; for example, the emergence hypothesis (Levinson, 2000; Lyons, 1995) proposed that new colour categories emerge in regions of colour space that previously were not named or were named inconsistently (Everett, 2005; Gooyabadi et al., 2019; Kay and Maffi, 1999; Levinson, 2000; Lindsey and Brown, 2014; Lindsey et al., 2015). Yet, a further culturally based alternative for augmentation is that terms are simply borrowed from other cultures. Such loanwords are a more than “plausible” alternative for augmentation (Lindsey and Brown, 2009).
Turning to existing empirical data, there are at least two accounts of changes over time to a colour lexicon (Kuriki et al., 2017, Mylonas and MacDonald, 2016). Kuriki et al., found differences in current Japanese from those recorded by Uchikawa and Boynton (1987). Most of the changes are in the forms of additions or clustering of colour names but there was also the report of a new basic term for light blue as found in many European and other Asian languages (Androulaki et al., 2006; Paramei, 2005; Paramei & Bimler, 2021 for a review). Through a crowdsourcing colour naming experiment, Mylonas and MacDonald suggested the augmentation of the English inventory from the 11 basic colour terms reported by earlier studies (Boynton and Olson, 1987; Sturges and Whitfiled, 1995) to 13 terms including lilac and turquoise. The candidacy of turquoise as basic colour term is further supported by the recent category insertion hypothesis where an incipient basic colour category is added at the BLUE-GREEN category boundary (Paramei et al., 2018; Roberson et al., 2009; for a review see Paramei & Bimler, 2021).
For remote groups with smaller colour lexicons, all previous studies offer only a single snapshot of the development of colour lexicons on the surface of the colour solid (see Lindsey and Brown, 2006, Regier et al., 2015). It is, therefore, of great interest to return to a remote society and ask whether there have been augmentations to their colour lexicon. We note that the Himba, while still outwardly similar to the population of 15 years ago, now have more contact with other cultures. These contacts are not great, yet we have already documented that they affect local/global processing (Caparos et al., 2012, 2013), the perception of geometric illusions (Bremner et al., 2016) and lightness perception (Linnell et al., 2018). To consider whether there might also be changes to their colour categories, we clearly need and thus introduce a procedure to identify the minimal number of independent colour categories that can name all colours.
We wish to consider the long-standing debate on whether perceptual or linguistic similarity is the critical force driving the augmentation of colour lexicons from the field of machine learning. A debate that is also relevant for other modalities of perceptual learning, such as acoustic (Goudbeek et al., 2009), emotion (Azari et al., 2020) and object (Khaligh-Razavi and Kriegeskorte, 2014) category acquisition. In a computational framework, the question can be viewed as whether unsupervised learning or supervised learning is the most appropriate strategy to train an artificial intelligent system that can communicate about colour with speakers of different languages (Mylonas et al., 2010; Mylonas et al., 2013). In unsupervised learning, algorithms deduce some inherent structure to the data using only unlabelled samples and produce a set of universal categories based on perceptual similarity between colours (Kuriki et al., 2017; Lindsey and Brown, 2006; Regier et al., 2007; Yendrikhovskij, 2001; Zaslavsky et al., 2019). In supervised learning, algorithms learn colour categories from labelled data in different languages based on linguistic similarity between colours. There are many different supervised colour-naming models, using variants of Gaussian or Gaussian-Sigmoid distributions (Benavente et al., 2008; Lammens, 1994; Mylonas et al., 2010), multinomial conditional probability distributions (Chuang et al., 2008; Heer and Stone, 2012) and deep-neural networks (Cheng et al., 2017). Here, we use criteria expressed as an ensemble of random decision trees (Mylonas, 2020) that have been shown to be highly effective for many diverse supervised classification or regression problems (Breiman, 2001; Cutler et al., 2007; Gislason et al., 2006).
Effective algorithms for construction of ensembles of decision trees based on training examples ensure that models are strongly diversified by infusing randomisation into the learning algorithm and exploit at each run a different random subset of the training data. An advantage of them is that they do not assume commensurate feature dimensions, or normally distributed feature values. To generalise our observations to any colour and identify the indispensable colour terms in the Himba language, we will use a Rotated Split Trees (RST) approach in regression mode that predicts probabilities and provides state-of-the-art performance in computational colour naming models (Mylonas, 2020). Given our training set of colour points X = x1, ..., xn with their Himba naming responses Y = y1, ..., yT, and a free parameter B = 100 trees, RST ensembles B random split trees, fb = {T1,…,TB} by using for each tree T the full training dataset (Geurts et al., 2006). Prior to any splitting, a proper rotation matrix R is generated using Householder QR decomposition (Andrews et al., 2017; Blaser and Fryzlewicz, 2016; Householder, 1958). The rotated trees have different orientation and vastly dissimilar data partition and are capable of producing smoother, non-axis, parallel decision boundaries than un-rotated trees. The regular, un-rotated, trees, would make splits parallel to the axis in the feature space of the dataset by selecting at each node the split on the attribute that produces the maximum gain. In contrast, rotated trees, combine attribute values and produce a rotated hyperplane with a smaller number of splits that tend to outperform un-rotated trees by separating better instances of the dataset that pertain to distinguishable categories. For growing a tree, RST splits the training data at each node independently of the target variable fully at random, unlike the optimum criterion of Random Forests (Breiman, 2001). Top-down binary recursion continues until no further splits are possible, that is, until all samples have been partitioned into their own leaf node. The predictions of each tree are then aggregated to predict the distribution of colour names for each test colour sample \(\widetilde x\). In practice, the RST estimator favours colour names with high probability to maintain congruence between observed and predicted data. So, more frequent and consistent colour categories tend to subsume less common and inconsistent terms. In Table S1, we show a comparison of computational colour naming models on the Munsell array (n = 320 chips) against Sturges and Whitfield’s (1995) results in English (Mylonas, 2020). RST performed equally well (100% classification accuracy) with other state-of-the-art colour naming models (SFKM, TSMES and NICE, see also Parraga and Akbarinia, 2016) on Sturges and Whitfield’s results but RST also identified five additional terms on the Munsell array. Thus, RST better determines the number of colour categories from the data compared to previous models that constrained their lexicons only to the 11 basic colour terms. In addition, RST produces perfect performance on estimated distributions of the 11 basic terms.
In contrast, perception-based-learning methods process unlabelled colours to group them into clusters based on statistical regularities of the data. k-means is the most common clustering method where colour samples are assigned into a predefined number of k categories based on the Euclidean distance from each category’s centroid in CIELAB (Kuriki et al., 2017; Lindsey and Brown, 2006; Yendrikhovskij, 2001; Zaslavsky et al., 2019). The number of k clusters needs to be defined in advance based on the number of colour terms in the observed data or through statistical analysis. Then the k-means algorithm can be used to construct a set of imaginary colour naming systems without any colour naming observations.
To evaluate the performance of unsupervised and supervised machine-learning methods we will measure classification accuracy against observed data collected at different time periods and in different colour spaces, namely CIELAB and sRGB. The reasons for examining model performance in different colour coordinate systems are twofold. First, we would desire models to be neutral about the approximately perceptually uniform structure of CIELAB and the non-uniform perceptual structure of sRGB. We selected CIELAB over CIELUV for consistency against earlier studies and because the latter can only marginally improve the accuracy of machine-learning methods over CIELAB (Table 5.2 in Mylonas, 2020). Second, we wish to quantify, against observed data, the divergence of colour categories produced by unsupervised perceptual learning in different colour spaces reported earlier using computer simulations (Steels and Belpaeme, 2005) that we feel has not been given appropriate attention by recent studies (Chaabouni et al., 2021).
Comparing different machine-learning methods and selecting the most effective model for communicating with humans at different time periods provides a new framework to advance our understanding of colour categorisation and helps identify the crucial factors that determine category acquisition.
Methods
Participants
There are several groups of Bantu origin in north-west Namibia but the Himba are the most remote; they still have very few Western artifacts including clothes and the women cover themselves daily in ochre. Himba is part of the Niger-Congo language family (Zone B). Himba is a dialect of Herero and they can communicate with speakers of that language. They are no longer entirely pastoralists and grow some maize (Bollig, 2010, p. 206).
Fifty-five native Himba speakers (female: 23, male: 32, mean age = 27.4, age range = 16–60, mean years of schooling = 1.4; schooling range 0–10) from remote villages in north-west Namibia completed the experiment. Of these, 31 were below the mean age (i.e., young) and 38 never went to school. The educational attainment among Himba people remains low with 65% of the adults found to be non-literate in this region (Ndimwedi, 2016). Participants were compensated for their time with gifts of flour. The study received ethical approval from Goldsmiths University of London (N°1390, 4th of June 2018).
Stimuli and apparatus
Test stimuli were 2 degrees uniformly coloured discs with a black outline of 1 pixel. The stimuli consisted of 589 simulated samples approximately uniformly distributed in the Munsell Renotation Data and restricted in the sRGB gamut plus 11 achromatic samples (Mylonas and MacDonald, 2010; Newhall et al., 1943). To achieve an approximately uniform sampling within the Munsell colour solid, we followed the suggestions of Billmeyer in Sturges and Whitfield (1995). Specifically, a variable number of hues were sampled at different levels of Value and Chroma. At Chroma 2, 10 hues were sampled, whilst at each successive Chroma step the sampled hues were increased by 10. That means from Chroma 8 to the boundaries of the sRGB gamut, all 40 hues were sampled.
The overlap on the surface colours against the sampling of the World Color Survey is 91% due to the limits of the sRGB gamut but we have shown in earlier studies (Mylonas and MacDonald, 2010) and in Table S1 that we can estimate the distribution of basic colour terms in English with 100% accuracy on the surface of the Munsell solid. The 600 in total colour samples were presented one at a time and in a random order for each observer and against a neutral grey background with luminance of 40 cd/m2.
Two Asus Transformer Mini T102HA (10.1”) were calibrated using a ColorCal CRS colorimeter (Cambridge Research Systems, Rochester, UK) and a RadOMA spectroradiometer (Gamma Scientific, San Diego, California). The measured CIE 1931 chromaticity coordinates of the white point of the monitors were x = 0.3067, y = 0.3318, and x = 0.3055, y = 0.3296 with a correlated temperature of 6816 K and 6907 K, respectively. Repeating the spectro-radiometric measurements of the monitors a month later after the fieldwork showed only a minimal drift of their white point over time (<0.003). The stimulus presentation was controlled by PsychoPy-version 1.84.2 software (Peirce, 2007).
Procedure
Observers were seated inside a tent during daytime approximately 80 cm away from a monitor. The task of the observers was to name out loud the colour of the stimulus so that others would know to which colour they were referring. Observers were free to use as broad or narrow names as they liked. They were not instructed to answer “don’t know” if unsure but such answers were always accepted without question. Under direction, responses were both audio-recorded and typed by a research assistant who spoke the native language of the participants.
Results
The new Himba colour naming dataset included in total 33,000 raw naming responses for 600 colour samples from 55 observers (mean age = 27.38, SD Age = 9.79, age range = 16–60; Female = 41.82%, Male = 58.18%). For the data analysis, we considered colour names given by two or more observers. Unique responses (0.8%) from single observers were excluded because we could not be confident that other observers would understand the colour name and, therefore, these responses were considered idiosyncratic. Contrary to Lindsey et al. (2015) where the Hadza observers were explicitly instructed to use a specific don’t know response to cluster together difficult to name regions, Himba observers did not offer a name to a colour in 665 responses. These were sparsely distributed to 434 samples of colour space (maximum 4 don’t know responses to any sample) and were excluded from further analysis (see Fig. S1). This filtering resulted in a dataset of 32,087 responses. Before considering outcomes from machine learning, we first analyse our data in terms of frequency and modal naming as is usual in previous studies.
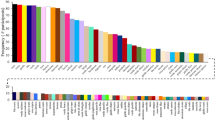
Frequency of colour terms
In line with the analysis in Roberson et al. (2005), we report the frequency of each colour term in our new Himba data and the number of observers producing each term. The meaning of frequency for our data needs clarification. It is, as usual, the number of times that each colour name is used to describe our colour stimuli but, as we sample from the whole of colour space, frequency of any colour term is likely to increase with the extent of a category in colour space. Figure 1 shows the centroids of the more frequent Himba colour names given by two observers or more scaled by their frequency of occurrence. Serandu (19.6%; reddish) was the most frequent colour name followed by burou (19.3%; bluish). Both terms were offered by all 55 Himba speakers. These were followed by grine (12.4% by 51 observers; greenish). Zoozu (6.9% by 39 observers; blackish) was the fourth most frequent term followed closely by dumbu (5.9% by 45 observers; yellowish), vapa (5.3% by 54 observers; whitish), pinge (5.1% by 32 observers; pinkish), zorondu (3.7% by 20 observers; a second blackish term), ranje (3.2% by 28 observers; orange-ish), ngara (3.2% by 33 observers; pale yellowish) and vinde (3.1% by 33 observers; brownish). Colour terms with relatively lower frequency of use (<3%) include worindja, peese, honi, pepera, vahe, baraona, kuze, dovazu, otji, siriva, hurune, gerei and mbambi. We found no purple terms in the Himba colour lexicon. The nearest terms to purple, peese (2.1% by 15 observers) and pepera (1.6% by 4 observers), both describe an overlapping magenta-ish region. The lack of a Himba purple term rather questions the claim that indigenous cultures share the same categories as infants (Skelton et al., 2017).
In total, the Himba offered 24 colour terms shown in Fig. S2 for naming the 600 approximately uniformly distributed Munsell samples of the computerised experiment, a large increase over the 9 colour terms (5 frequent and 4 infrequent) that were reported in our previous study for naming the 160 fully saturated samples of the physical Munsell Book of Color (Roberson et al., 2005) and the 10 colour terms elicited in a list task (Grandison et al., 2014). In agreement with earlier studies, Himba speakers did not make use of modifiers in their responses.
The high frequency of grine offered by 51 out of 55 observers (mean age = 27.38; SD = 9.84) requires further investigation because in our previous study, grine was an infrequent term (0.5%) that was offered by only 2 observers out of 31 (Roberson et al., 2005) though Grandison et al. (2014) in their list task found it was offered by 43 out of 62 observers. For stimuli (n = 98) where grine was now the most frequent term, the ratio of using grine over burou was higher, t(53) = 3.1, p < 0.003, for younger (n = 31; younger mean age = 21.06, SD = 4.09, age range = 16–27; Mratio = 0.83, SD = 0.28) than for older (n = 24; older mean age = 35.54, SD = 9.07, age range = 28–60; Mratio = 0.55, SD = 0.37) Himba. Those who had attended school (n = 17; educated mean age = 22, SD = 7, age range = 16–41; Mratio = 0.91, SD = 0.1) also used grine more than burou for these stimuli than did Himba who had not been to school (n = 38; non-educated mean age = 29.79, SD = 10.05, age range = 16–60; Mratio = 0.61, SD = 0.38), t(53) = 3.2, p = 0.002. However, education by itself was not the main determinant of colour term change as, considering only the young observers (n = 31), there was no difference between the educated (n = 14; younger educated mean age = 19.57, SD = 4.16, age range = 16–26; Mratio = 0.91, SD = 0.1) vs. non-educated (n = 17; younger non-educated mean age = 22.29, SD = 3.70, age range = 16–27; Mratio = 1.5, SD = 0.36) young Himba; t(29) = 1.5, p = 0.14. Furthermore, we found no significant differences t(53) = 0.12, p = 0.24 between male (Mratio = 0.66, SD = 0.36) and female (Mratio = 0.77, SD = 0.33) Himba in using grine over burou for greenish samples. We found very large colour differences between the centroids of the GRUE category in the earlier data and the new BLUE (burou) category ΔΕab = 45.1 and also against the centroid of the new GREEN category ΔΕab = 17.95 that provide support for the augmentation of the Himba colour lexicon. Yet, colour differences above 10 CIELAB ΔE units cannot be trusted (Xu et al., 2001) and alternative methods are required to demonstrate the augmentation of the new colour terms.
Consensus of modal terms
Continuing with analyses of our new data in line with the previous, we consider consensus that describes the agreement among observers in naming colour samples (Brown and Lenneberg, 1954; Boynton and Olson, 1987). The modal term with the highest consensus for each colour sample was determined as the peak of the conditional probability P(n | c) that each name n = 24 was reported for each colour c = 600 (Chuang et al., 2008; Heer and Stone, 2012). Figure 2 shows the 600 colour samples named by most Himba using 10 modal terms. 73% of all stimuli were named with 0.5 (max = 1) or above agreement involving the major modal terms for c colour samples: serandu, c = 219; burou, c = 131; grine, c = 98; zoozu, c = 69; dumbu, c = 42 and vapa, c = 35. The high consensus of the frequent grine term for a large number of samples confirms its status as an important new colour category in Himba. There were also a few areas with lower agreement (>0.2 and <0.5) that involved colour samples of the above terms plus of the less-frequent ngara c = 3; vinde, c = 1; pinge, c = 1 and peese, c = 1. These minor modal terms could not have been found without sampling the interior of the colour space but being the most frequent term for an inconsistently named colour sample was not a sufficient condition to show high consensus. Similarly, previous studies using thresholds for a colour sample being named with consensus gave undefined results for rarely named colours (Boynton and Olson, 1987; Conway et al., 2020; Davies and Corbett 1995; Lindsey et al., 2015). Our consensus analysis supports earlier conclusions that the modality of colour terms is not a simple dichotomous but a continuous gradual characteristic that can reveal potentially important colour terms in further investigations (Witzel, 2019). For example, while we used almost double or greater number of samples than earlier studies, the mean colour difference of the four nearest neighbours across our 600 stimuli was ΔΕab = 7.14 and it could be that the density of our sampling was still not sufficient to capture the regions of these minor modal terms with higher consensus. In later sections we will examine the indispensability of these terms using computational models but first we will compare naming differences from 2005 to the present and then consider the naming that occurs when using the full colour gamut.
Comparison of Himba naming in 2005 and 2019
To illustrate the change in naming behaviour between the earlier and new studies, in Fig. 3 we show the estimated categories on the traditional Mercator projection of the surface of the Munsell Book of Color (n = 320 samples) by RST using the Himba data of our earlier study (Roberson et al., 2005) and the Himba data of this study. The classification of the Munsell array into the five Himba colour terms (serandu, dumbu, zoozu, burou, and vapa) by RST when trained by the earlier Himba data was overall consistent with the distributions of the five modal terms reported in Fig. 1 of Roberson et al. (2005) with a classification accuracy of 88% for the n = 160 samples. We note that using our probabilistic approach for identifying modal terms (peak of P(n|c)) in the earlier data, we found an additional minor modal term (vinde) for a few inconsistently brownish and purplish samples but RST classified them to the major modal terms. RST with our new data show six colour terms on the Munsell array (the earlier five terms plus grine). There was a large area (19.4%) on the surface of the colour solid named consistently across observers as grine. RST found no minor terms on the surface on the Munsell system.
A Simulated Munsell array (n = 320 chips) of hue (horizontal axis) against value/lightness (vertical axis) with each disc having equal size (top). B Segmentation of Munsell array by RST into five Himba colour terms (burou 30.0%, serandu 26.9%, zoozu 17.5%, dumbu 16.3% and vapa 9.4%) based on data of Roberson et al. (2005) (middle) and C into 6 Himba terms (serandu 28.1%, burou 20.6%, grine 19.4%, vapa 13.4%, zoozu 11.3% and dumbu 7.2%) based on Himba data of the new study (bottom). Disc size corresponds to the confidence of classification by the RST algorithm for the old and new data. The colour of each disc corresponds to the centroid of each colour term. Black square outlines show the location of green and blue foci in English (Sturges and Whitfield, 1995).
We considered if the grine term could have been latent in our 2005 data but there is no evidence of separate green and blue foci within the GRUE category. In fact, the confidence for the boundary chips (7.5BG) between GREEN and BLUE in the new data (Mconf = 0.6, SD = 0.1) is significantly lower, t(14) = 3.5519, p = 0.003, than in the old data (Mconf = 0.8, SD = 0.1). In other words, the chips with the highest confidence of the GRUE category have become boundary colours between GREEN and BLUE categories. Similarly, the location of the colour chips with the highest confidence for grine (Pconf = 0.8, h = 7.5GY, V = 6) and for burou (Pconf = 0.9, h = 7.5PB, V = 5) in our new data were boundary colours in our earlier data. We also note that our highest confidence stimuli correspond roughly with the locations of the green and blue foci in English (Sturges and Whitfield, 1995).
Colour naming across the full colour gamut
To explore the confidence of Himba colour naming across the full colour gamut we classified a grid in CIELAB of 4-unit bins at 8 lightness levels constrained in the sRGB gamut (Heer and Stone, 2012) using RST and the recent Himba data. Figure 4 shows categories with high confidence (of various shapes due to the non-parametric nature of RST), separated by boundaries of lower confidence where there was higher naming confusion across the colour gamut.
The test samples (n = 5693) were classified to 7 colour categories: the six most common terms that we identified on the surface of the colour solid: serandu (assigned to 34.5% of samples), grine (23.2%), burou (22.9%), zoozu (8.1%), dumbu (7.7%), vapa (3.5%), and the additional but smaller brownish category vinde (0.2%) in the interior of the colour space. The colour samples of the other minor modal terms, ngara, pinge and peese, were replaced by major neighbour modal terms. Although vinde is assigned to fewer samples and with relatively lower confidence than the other major Himba terms, unlike the other minor modal terms, is an indispensable term retained at two different lightness levels (L* = 33–44) by our RST analysis in this dataset. Interestingly, there is no neutral category at mid lightness levels nor a category between red and blue as the Himba are missing both consistent grey and purple terms.
Comparing supervised and unsupervised learning
To gain some leverage on whether cultural (i.e., linguistic) or perceptual similarity is the critical driver for effective colour communication with the Himba, we evaluated the classification accuracy of supervised (RST) learning in a leave-one-out cross validation mode and unsupervised (k-means) learning on predicting the observed modal terms for each colour stimulus in both Himba datasets. First, we consider the 160 colour samples on the surface of the Munsell system in the approximately perceptually uniform colour space of CIELAB used by Roberson et al. (2005), second the 600 colour stimuli used in this study in CIELAB and finally we compare the performance of both methods, again for the new dataset, but in a different colour space, namely sRGB, a non-uniform but the most widely used colour space of the Internet.
To investigate unsupervised learning, we used a k-means algorithm. The output of the k-means algorithm is not labelled; hence to compare model performance and avoid local optima, we constructed a distance matrix between the centroids of the perceptual k categories, and the centroids of the observed categories obtained in the colour naming experiments and then we assigned optimally the first to the latter categories using the Munkres assignment algorithm (Kuhn, 1955). We repeated this process 100 times and retained the optimal imaginary k system of categories that produced the smallest mean Euclidean colour difference in CIELAB (Zaslavsky et al., 2019). We confirmed that a larger number of iterations did not significantly change the results.
Culture-based-learning approaches learn colour categories directly from labelled data but the output is not always correct due to noisy data labels as the naming process can be long, costly and prone to error. Indeed, evaluating supervised classifiers on data on which they were trained is generally misleading. To ensure that the predicted classes are generalisable to unknown samples we employed a leave-one-out cross validation strategy and trained our models on all other chips and predicted the name of the test sample that was not known in advance. For each Himba dataset that we assessed, we built j separate RST classifiers where j is equal to the number of colour examples in each dataset (c = 160 and c = 600). Each RST classifier was trained on c − 1 labelled colour samples, with a different colour sample left out. The communication accuracy for each colour sample was then computed by the classifier, which was trained with it left out. Then we aggregate the results of all these classifiers for all left out test colour samples.
For Roberson et al. (2005), on the surface of the Munsell solid, the classification accuracy of k-means with k = 5 (equal to the reported modal terms) was 64% while RST produced a better accuracy by classifying 89% of the samples correctly. RST identified five colour categories (serandu, dumbu, zoozu, burou, and vapa). The vinde term was not identified on the surface of the colour space in the leave-one-out mode by RST. A McNemar test (Dietterich, 1998) showed that the two proportions were significantly different χ2(1, N = 160) = 32, p < 0.01 with a Yates’ correction. Given that we found a 6th dispensable modal term in Roberson’s data, we also tested the k-means algorithm with k = 6 but its performance deteriorated further with a classification accuracy of 54%.
Considering the new Himba data that also cover the interior of the colour space, the k-means with k = 10 (equal to the number of the modal terms) classified 40% of the 600 samples correctly while the RST produced again superior performance with a classification accuracy of 93% including the major modal terms plus a smaller vinde category in the interior of the colour space. A McNemar test showed that the two proportions were significantly different χ2(1, N = 600) = 296, p < 0.01 with a Yates’ correction. It is possible to set k = 24 equal to the number of all Himba colour terms given by two observers or more by using an automatic process for determining the number of k clusters using the Elbow method (Thorndike, 1953). When carried out, performance of k-means dropped to a classification accuracy of just 16%. Considering earlier results that showed the unfitness of perceptual-learning methods (Jraissati and Douven, 2017; Regier et al., 2007) to capture more than 6 categories, we also tested the k-means approach with k = 6 equal to the number of major modal terms but again its classification accuracy of 60% was significantly lower than RST’s χ2(1, N = 600) = 170, p < 0.01 with a Yates’ correction.
In our third comparison of the two learning approaches in a different coordinate system, we set k = 7 equal to the number of indispensable terms identified by RST for a direct comparison and we tested both methods on the 600 stimuli specified in the sRGB colour space (Fig. 5). The k-means algorithm achieved 49% classification accuracy while the RST retained its performance with 93% accuracy. Again a McNemar test showed that the two proportions were significantly different χ2(1, N = 600) =243, p < 0.01 with a Yates’ correction. The k-means approach with k = 7 in both CIELAB (59%) and sRGB (49%) colour spaces produced significant diverging results χ2(1, N = 600) = 25, p < 0.01, confirming, with empirical data, an earlier report using simulations that explanations of colour categories being based on statistical regularities of the data are spurious (Steels and Belpaeme, 2005).
Comparison of supervised (RST) and unsupervised (k-means) machine-learning methods for the earlier Himba dataset on the surface of the Munsell system n = 160 (Roberson et al., 2005; left) and the current Himba data across the Munsell system, n = 600 in CIELAB (middle) and in sRGB colour spaces (right).
Overall, our results show that supervised learning significantly excelled unsupervised learning for effective colour communication with the Himba. It excelled for data collected at different time periods, various number of colour terms, surface and interior colours as well as different colour spaces.
Discussion
Theories of augmentation have been essentially conjectural as there is little actual augmentation data but we now provide, along with Kuriki et al. (2017) for Japanese and Mylonas and MacDonald (2016) for English, information concerning the language of a remote group where we have seen just such a development. In 2005, the Himba were reported to use a 5-colour-term grue language. Today, they have seven colour categories. If a regular pattern of colour term evolution exists as suggested by Kay et al., (1991), Himba has evolved from a Stage V to a Stage VI language with 7 colour terms using their classification scheme. One of these new categories (the brown term vinde) could have been present in 2005 since it is only with our present methodology that we can investigate the desaturated interior of colour space. In fact, the term was in inconsistent (non-categorical) use then for a variety of saturated brownish and purplish colours. The augmentation of the other term is because Himba is no longer a grue language with the possibility that the change has been gradual (Grandison et al., 2014). It might be thought that 15 years would provide insufficient time to observe the introduction of a GREEN category. However, there has been an increase in tourism with accompanying roads and infrastructure and therefore contact with other cultures and it might not require much contact to produce cognitive change (see Caparos et al., 2012). In any case, laboratory studies might have advised otherwise given that the acquisition of a new colour category can take a matter of days with sufficient practice (Özgen and Davies, 2002). It is easy to imagine that many of the languages in the World Color Survey would have reported more important colour names should they have also examined desaturated colours and revisited these preindustrial societies.
Before considering any claims about augmentation from our machine-learning data, we need to assure that the arrival of the new colour terms is not a result of the new methodologies. The computational procedures of the new method gave the same outcome of a 5-colour term language for our 2005 data so any differences cannot be due to the change to RST. Could it be that the new procedure produced, for the many other additional colours, somewhat different hues that were greener than their equivalent paper swatches? Our own studies (Mylonas and MacDonald, 2016; Paramei et al., 2018) show that this is not so but, in any case, the Himba can only name the stimuli as green if they have that colour term and clearly in 2004, they did not. It still could be that the colours were slightly different and the new boundary between their green and blue terms would be in a different place if naming had been measured from paper swatches. However, the boundary between GREEN and BLUE in our new data is where it would be either if the category had been imported from another culture or if it were perceptually driven. So, there is no reason to believe that the new computerised procedures by themselves would have produced any different outcomes than that obtained with paper swatches. We therefore turn to consideration of what are the driving forces for augmentation of colour terms.
One hypothesis for the Himba grue term having split in the last 15 years is that there might be optimal ways of dividing colour space and so predict how a 5-colour-term grue language might form 6 categories (Regier et al., 2007; see also Kay and Regier, 2007). It was argued that these proposed optimal partitions could be based on the uneven shape of perceptual colour space where several large “bumps” of saturation presumably produce areas with greater consensus among speakers across languages (Jameson and D’Andrade, 1997; Jameson, 2005). Indeed, the speed with which the augmentation has taken place might argue that the change “was waiting to happen”. However, the new bluish (burou) and greenish (grine) categories were not latent in the GRUE category of the old data (Roberson et al., 2005) as has been suggested (Kay and McDaniel, 1978; Lindsey et al., 2015; Regier and Kay, 2004). The colour chips with the highest confidence of the GRUE category in our earlier data have become boundary colours between the new grine and burou categories in our current data. Alike, the location of the chips with the highest confidence for grine and for burou in our new data were boundary colours in our earlier data. So, there is no evidence that latent categories were responsible for augmenting the colour lexicon in the adult Himba nor indeed that they drive colour naming in the development of colour naming in Himba children (Roberson et al., 2004).
Further insight into augmentation can be obtained from our machine-learning data but it is important to issue a caveat. All the machine-learning models are statistical techniques and by themselves do not predict the underlying mechanisms of change. Even the k-means models do not necessarily entail that there is a physiological underpinning of the perceptual structure that they discover (Davidoff, 2015; Jameson and D’Andrade, 1997). However, our evaluation of supervised (RST) and unsupervised (k-means) machine-learning approaches suggests that perceptual similarity alone cannot explain colour categorisation and that linguistic similarity is the driving force for facilitating effective colour communication with the Himba at different time periods, for any number of categories, on the surface and across the colour gamut and in different colour spaces. Even for a language with only five terms, the unsupervised (perceptual structure) is suboptimal compared to the consistent performance of supervised learning.
In contrast to supervised cultural learning, the communication accuracy of unsupervised perceptual learning falls short mainly because minimising the variance in the data tends to produce equal size clusters that fail to fit human colour categories of various sizes and also because exploiting statistical regularities found in data is sensitive to scaling and produces diverging results in different coordinate systems (Steels and Belpaeme, 2005). As a result, perceptual learning produces a suboptimal universal hypothetical scheme that ignores the variation on the number and distribution of human colour categories in different languages (Mylonas and MacDonald, 2012). Generally, the main advantage of unsupervised learning is that no human labelled data are required but in the case of colour naming this is not true as they still need human feedback to define the number of categories and optimise their performance (Lindsey and Brown, 2006; Zaslavsky et al., 2019). Contextual information found in sufficiently representative large sets of natural images could boost their performance (Yendrikhovskij, 2001) but again their performance will be sensitive to scaling of different colour spaces (Steels and Belpaeme, 2005).
It is not certain which of the supervised (cultural) explanations for the need of additional terms (Gibson et al., 2017) is most appropriate for the augmentation of the colour lexicon in the Himba. However, the emergence hypothesis (Levinson, 2000) that highlights regions of colour space with less consensus and without a name would seem an inadequate explanation for the augmentation of the Himba green term. Observers in our 2005 study were sure about their responses; they were consistent and with very few sparsely distributed unnamed stimuli. In any case, as the Himba did not have areas of blue/green colour space unnamed, the emergence hypothesis could not provide an explanation for the splitting of the grue term. Indeed, augmentation of colour terms in English is also indifferent to whether their region is on a boundary between two existing categories or is inserted within an existing category. Mylonas and MacDonald (2016) reported the augmentation of colour terms in British English from the 11 terms of Berlin and Kay (1969/1991) to 13 terms by the addition of turquoise and lilac. Neither the emergence nor the partitioning hypothesis alone could explain these results as turquoise emerged at the boundary region between blue and green while lilac partitioned the large colour category of purple in agreement with the results of Lindsey and Brown (2014) that showed both processes also in the development of modern American colour terms (teal and lavender). The category insertion hypothesis could only explain the addition of turquoise but not of lilac. Nevertheless, it would be possible to propose an emerging case for other terms in the Himba colour lexicon that are obviously related to objects (Conklin, 1973; Davidoff et al., 1999; Levinson, 2000) and where there were areas of inconsistent colour naming. The vinde (brown) Himba term that is present at the boundaries between GREEN (grine), BLACK (zuzou) and YELLOW (dumbu) categories in the interior of the colour space is from cattle appearance, and the pale yellowish term ngara is from a flower that may be borrowed from a neighbouring Bantu language (Nurse and Philippson, 2006). A similar desaturated LIGHT BROWN category (color de coyuche) borrowed from Spanish and denoting the colour of organic cotton was reported by MacLaury (2007) in Zapotec (see Jameson, 2018 for a digitised archive of MacLaury’s dataset).
The augmentation that we have shown for the Himba seems unlikely to be simply the result of schooling as suggested by Grandison et al. (2014) but very much as if the Himba, especially the younger ones (Griber et al., 2021), have imported a green term, probably from Herero who recently started using the term ngirine (Nguaiko, 2010) instead of the earlier tarazu (Kolbe, 1883); a process we refer to as cultural transfer or simply loanwords. The centroid of the newly acquired Himba word for GREEN was indeed located at much the same place in colour space as it is in English, but it is also in the same place in the neighbouring language of Herero where its words for green and blue come from European languages (Roberson et al., 2005). Inspection of the less-frequent Himba terms (e.g., ngara~light yellow, pinge~pink and ranje~orange) suggests that there are other loanwords on the way to becoming independent colour terms.
Of course, we cannot claim that loanwords have been the mechanism for augmentation in all languages. However, it is important to note (see Witzel and Gegenfurtner, 2018) that all colour names in all languages derive from the colours of objects. It is important because one might argue that there could be a different, perhaps physiological, origin for the colour term in the language from which the term was borrowed. Loanwords would seem to be important in their adoption to colour lexicons and much more the case than has been widely accepted. Even as apparently elementary a colour as red can be traced back to the Proto-Indo-European Breudh^ for red ochre and copper and is related to the Sanskrit word, rudhiraB for blood (Alexander and Kay, 2014; Jones, 2013). Other major colour terms have similar roots in naming; green has its roots in the Germanic word Bghro^ that refers to growing and flourishing (Jones, 2013; Welsch and Liebmann 2004, p. 64), which links green to plants. Orange originates in the Sanskrit word narangah for orange trees (Jones, 2013). So, it could be that new colour categories largely arrive in a lexicon simply by being imported from other languages and, it could even be that perceptual similarity had no role in the origin of the colour terms.
In conclusion, our findings showing the augmentation of a green term provide further evidence against the claim that primary colour categories are constrained by early perceptual mechanisms (Abramov and Gordon, 1994; Bosten and Boehm, 2014; Emery et al., 2017; Malkoc et al., 2005; Mylonas and Griffin, 2020; Valberg, 2001; Wool et al., 2015; Wuerger et al., 2005) and challenge explanations based on this claim (Berlin and Kay, 1969/1991; Kay and McDaniel, 1978; Kuehni, 2005; Philipona and O’Regan, 2006; Regier et al., 2007). Our findings from machine learning give priority to linguistic similarity as the mechanism for augmentation. While we recognise that there is some commonality in the organisation of colour categories across the world’s languages that could be due to perceptual similarity expressed as variation of saturation on the surface of the Munsell system (Lindsey and Brown, 2009; Olkkonen et al., 2010; Regier et al., 2007; Witzel, 2016; Witzel et al., 2015), one needs to look for complete explanations elsewhere (Davidoff, 2015; Gibson et al., 2017). To explain the augmentation of colour lexicons, we need to address how colour naming functions are learned by individuals in communities through interactions with other cultures, context and technological development.
Data availability
The dataset generated during the current study are available in the Dataverse repository: https://doi.org/10.7910/DVN/MGDCX6.
References
Abramov I, Gordon J (1994) Color appearance: on seeing red-or yellow, or green, or blue. Ann Rev Psychol 45(1):451–485. https://doi.org/10.1146/annurev.ps.45.020194.002315
Alexander M, Kay C (2014) The spread of red in the historical thesaurus of English. In: Anderson W, Biggam CP, Hough CA, Kay C (eds.) Colour studies: a broad spectrum. John Benjamins. pp. 126–139
Andrews JTA, Jaccard N, Rogers TW, Griffin LD (2017) Representation-learning for anomaly detection in complex X-ray cargo imagery. Anomaly detection and imaging with X-Rays (ADIX) II. vol. 10187. SPIE digital library
Androulaki A, Gomez-Pestana N, Mitsakis C, Jover J, Coventry K, Davies I (2006) Basic colour terms in modern Greek: Twelve terms including two blues. J Greek Linguist 7(1):3–47
Azari B, Westlin C, Satpute AB, Hutchinson JB, Kragel PA, Hoemann K, Khan Z, Wormwood JB, Quigley KS, Erdogmus D, Dy J, Brooks DH, Barrett LF (2020) Comparing supervised and unsupervised approaches to emotion categorization in the human brain, body, and subjective experience. Sci Rep 10(1):20284. https://doi.org/10.1038/s41598-020-77117-8
Benavente R, Vanrell M, Baldrich R (2008) Parametric fuzzy sets for automatic color naming. J Opt Soc America A 25(10):2582–2593. https://doi.org/10.1364/JOSAA.25.002582
Berlin B, Kay P (1969/1991) Basic color terms: their universality and evolution. University of California Press
Biederman I, Yue X, Davidoff J (2009) Representation of shape in individuals from a culture with minimal exposure to regular, simple artifacts: Sensitivity to nonaccidental versus metric properties. Psychol Sci 20(12):1437–1442. https://doi.org/10.1111/j.1467-9280.2009.02465.x
Bimler D, Uusküla M (2017) A similarity-based cross-language comparison of basicness and demarcation of “blue” terms. Color Res Appl 42(3):362–377. https://doi.org/10.1002/col.22076
Blaser R, Fryzlewicz P (2016) Random rotation ensembles. J Mach Learn Res 17(1):126–151
Bollig M (2010) Risk management in a hazardous environment: A comparative study of two pastoral societies. (206) Springer Science & Business Media
Bosten JM, Boehm AE (2014) Empirical evidence for unique hues? J Opt Soc Am A 31(4):A385–A393. https://doi.org/10.1364/JOSAA.31.00A385
Boynton RM, Olson CX (1987) Locating basic colors in the OSA space. Color Res Appl 12(2):94–105. https://doi.org/10.1002/col.5080120209
Breiman L (2001) Random forests. Mach Learn 45(1):5–32. https://doi.org/10.1023/A:1010933404324
Bremner AJ, Doherty MJ, Caparos S, Fockert J, de, Linnell KJ, Davidoff J (2016) Effects of culture and the urban environment on the development of the Ebbinghaus illusion. Child Dev 87(3):962–981. https://doi.org/10.1111/cdev.12511
Brown RW, Lenneberg EH (1954) A study in language and cognition. J Abnorm Soc Psychol 49(3):454–462. https://doi.org/10.1037/h0057814
Caparos S, Linnell KJ, Bremner AJ, de Fockert JW, Davidoff J (2013) Do local and global perceptual biases tell us anything about local and global selective attention? Psychol Sci 24(2):206–212. https://doi.org/10.1177/0956797612452569
Caparos S, Ahmed L, Bremner AJ, de Fockert JW, Linnell KJ, Davidoff J (2012) Exposure to an urban environment alters the local bias of a remote culture. Cognition 122(1):80–85. https://doi.org/10.1016/j.cognition.2011.08.013
Chaabouni R, Kharitonov E, Dupoux E, Baroni M (2021) Communicating artificial neural networks develop efficient color-naming systems. Proceedings of the National Academy of Sciences of the USA, 118(12). https://doi.org/10.1073/pnas.2016569118
Cheng Z, Li X, Loy CC (2017) Pedestrian color naming via convolutional neural network. In: Lai S-H, Lepetit V, Nishino K, & Sato Y (eds.) Computer Vision–ACCV 2016. Springer International Publishing. pp. 35–51
Chuang J, Hanrahan P, Stone M (2008) A probabilistic model of the categorical association between colors. Proceedings of the 16th Color Imaging Conference–CIC 2008. pp. 6–11, Portland, Oregon, USA
Conklin HC (1973) Color categorization. Am Anthropol 75(4):931–942. https://doi.org/10.1525/aa.1973.75.4.02a00010
Conway BR, Ratnasingam S, Jara-Ettinger J, Futrell R, Gibson E (2020) Communication efficiency of color naming across languages provides a new framework for the evolution of color terms. Cognition 195:104086. https://doi.org/10.1016/j.cognition.2019.104086
Cutler DR, Edwards TC, Beard KH, Cutler A, Hess KT, Gibson J, Lawler JJ (2007) Random forests for classification in ecology. Ecology 88(11):2783–2792. https://doi.org/10.1890/07-0539.1
Davidoff J, Davies I, Roberson D (1999) Colour categories in a stone-age tribe. Nature 398(6724):203–204. https://doi.org/10.1038/18335
Davidoff J (2015) Color categorization across cultures. In: Elliott AJ, Fairchild MD, Franklin A (eds.) Handbook of color psychology. Cambridge University Press. pp. 259–278
Davies IL, Corbett GG (1995) A practical field method for identifying probable basic colour terms. Lang World 9(1):25–36
Dietterich TG (1998) Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput 10(7):1895–1923. https://doi.org/10.1162/089976698300017197
Emery KJ, Volbrecht VJ, Peterzell DH, Webster MA (2017) Variations in normal color vision. VII. Relationships between color naming and hue scaling. Vis Res 141:66–75. https://doi.org/10.1016/j.visres.2016.12.007
Everett DL (2005) Cultural constraints on grammar and cognition in Pirahã ‘another look at the design features of human language’. Curr Anthropol 46(4):621–646. https://doi.org/10.1086/431525
Forder L, Bosten J, He X, Franklin A (2017) A neural signature of the unique hues. Sci Rep 7:42364. https://doi.org/10.1038/srep42364
Geurts P, Ernst D, Wehenkel L (2006) Extremely randomized trees. Mach Lear 63(1):3–42. https://doi.org/10.1007/s10994-006-6226-1
Gibson E, Futrell R, Jara-Ettinger J, Mahowald K, Bergen L, Ratnasingam S, Gibson M, Piantadosi ST, Conway BR (2017) Color naming across languages reflects color use. Proc Natl Acad Sci USA 114(40):10785–10790. https://doi.org/10.1073/pnas.1619666114
Gislason PO, Benediktsson JA, Sveinsson JR (2006) Random forests for land cover classification. Pattern Recogn Lett 27(4):294–300. https://doi.org/10.1016/j.patrec.2005.08.011
Gooyabadi M, Joe K, Narens L (2019) Further evolution of natural categorization systems: an approach to evolving color concepts. J Opt Soc Am A 36(2):159–172. https://doi.org/10.1364/JOSAA.36.000159
Goudbeek M, Swingley D, Smits R (2009) Supervised and unsupervised learning of multidimensional acoustic categories. J Exp Psychol Hum Percept Perform 35(6):1913–1933. https://doi.org/10.1037/a0015781
Grandison A, Davies IRL, Sowden P (2014) The evolution of GRUE. In: Anderson W, Biggam CP, Hough C, Kay C (eds.) Colour studies: a broad spectrum. John Benjamins. pp. 53–66
Griber YA, Mylonas D, Paramei GV (2021) Intergenerational differences in Russian color naming in the globalized era: linguistic analysis. Human Soc Sci Commun 8(1):1–19. https://doi.org/10.1057/s41599-021-00943-2
Heer J, Stone M (2012) Color naming models for color selection, image editing and palette design. Proceedings of the 2012 ACM Annual Conference on Human Factors in Computing Systems, 1007–1016. https://doi.org/10.1145/2207676.2208547
Hering E (1878/1964) Outlines of a theory of the light sense (Hurvich LM, Jameson D, Trans.). Harvard University Press
Householder AS (1958) Unitary triangularization of a nonsymmetric matrix. J Assoc Comput Mach (ACM) 5(4):339–342. https://doi.org/10.1145/320941.320947
Jameson KA (2005) Why GRUE? An interpoint-distance model analysis of composite color categories. Cross-Cult Res 39(2):159–204. https://doi.org/10.1177/1069397104273766
Jameson K (2010) Where in the World Color Survey is the support for color categorization based on the Hering primaries. In: Cohen JD, Matthen M (eds.), Color Ontology and Color Science. MIT Press. pp. 179–202
Jameson K, D’Andrade R (1997) It’s not really red, green, yellow, blue: an inquiry into perceptual color space. In: Hardin CL, Maffi L (eds.) Color categories in thought and language. Cambridge University Press. pp. 197–223
Jameson KA (2018) ColCat: A color categorization digital archive and research wiki. In: MacDonald LW, Biggam CP, Paramei GV (eds.) Progress in colour studies: cognition, language and beyond. John Benjamins Publishing Company
Jones WJ (2013) German colour terms: A study in their historical evolution from earliest times to the present. John Benjamins
Jraissati Y, Douven I (2017) Does optimal partitioning of color space account for universal color categorization? PLOS ONE 12(6):e0178083. https://doi.org/10.1371/journal.pone.0178083
Kay P (1975) Synchronic variability and diachronic change in basic color terms. Lang Soc 4(3):257–270
Kay P, McDaniel CK (1978) The linguistic significance of the meanings of basic color terms. Language 54(3):610–646. https://doi.org/10.2307/412789
Kay P, Maffi L (1999) Color appearance and the emergence and evolution of basic color lexicons. Am Anthropol 101(4):743–760. https://doi.org/10.1525/aa.1999.101.4.743
Kay P, Regier T (2007) Color naming universals: The case of Berinmo. Cognition 102(2):289–298. https://doi.org/10.1016/j.cognition.2005.12.008
Kay P, Berlin B, Maffi L, Merrifield W, Cook R (2010) The World Color Survey. CSLI Publications
Kay P, Berlin B, Merrifield W (1991) Biocultural implications of systems of color naming. J Linguist Anthropol 1(1):12–25
Khaligh-Razavi S-M, Kriegeskorte N (2014) Deep supervised, but not unsupervised, models may explain IT cortical representation. PLOS Comput Biol 10(11):e1003915. https://doi.org/10.1371/journal.pcbi.1003915
Kolbe FW (1883) An English-Herero dictionary: With an introduction to the study of Herero and Bantu in general. JC Juta
Kuehni RG (2005) Focal color variability and unique hue stimulus variability. J Cogn Cult 5(3):409–426. https://doi.org/10.1163/156853705774648554
Kuhn HW (1955) The Hungarian method for the assignment problem. Naval Res Logist Quart 2(1–2):83–97. https://doi.org/10.1002/nav.3800020109
Kuriki I, Lange R, Muto Y, Brown AM, Fukuda K, Tokunaga R, Lindsey DT, Uchikawa K, Shioiri S (2017) The modern Japanese color lexicon. J Vis 17(3):1–1. https://doi.org/10.1167/17.3.1
Lammens J (1994) A computational model of color perception and color naming. Doctoral dissertation, State University of New York at Buffalo
Levinson SC (2000) Yélî Dnye and the theory of basic color terms. J Linguist Anthropol 10(1):3–55. https://doi.org/10.1525/jlin.2000.10.1.3
Lindsey DT, Brown AM (2006) Universality of color names. Proc Natl Acad Sci USA 103(44):16608–16613. https://doi.org/10.1073/pnas.0607708103
Lindsey DT, Brown AM (2009) World Color Survey color naming reveals universal motifs and their within-language diversity. Proc Natl Acad Sci USA 106(47):19785–19790. https://doi.org/10.1073/pnas.0910981106
Lindsey DT, Brown AM (2014) The color lexicon of American English. J Vis 14(2):17. https://doi.org/10.1167/14.2.17
Lindsey DT, Brown AM, Brainard DH, Apicella CL (2015) Hunter-gatherer color naming provides new insight into the evolution of color terms. Curr Biol 25(18):2441–2446. https://doi.org/10.1016/j.cub.2015.08.006
Linnell KJ, Bremner AJ, Caparos S, Davidoff J, de Fockert JW (2018) Urban experience alters lightness perception. J Exp Psychol Hum Percept Perform 44(1):2–6. https://doi.org/10.1037/xhp0000498
Lyons J (1995) Colour in language. In: Lamb T, Bourriau J (eds.) Colour: art & science. Cambridge University Press. pp. 194–224
MacLaury RE (2007) Categories of desaturated-complex color: Sensorial, perceptual, and cognitive models. In: Maclaury RE, Paramei GV, Dedrick D (eds.) Anthropology of color: interdisciplinary multilevel modeling. John Benjamins. pp. 125–150
Malkoc G, Kay P, Webster MA (2005) Variations in normal color vision. IV. Binary hues and hue scaling. J Opt Soc Am A 22(10):2154–2168. https://doi.org/10.1364/JOSAA.22.002154
Mylonas D, MacDonald L (2016) Augmenting basic colour terms in English. Color Res Appl 41(1):32–42. https://doi.org/10.1002/col.21944
Mylonas D, Griffin LD (2020) Coherence of achromatic, primary and basic classes of colour categories. Vis Res 175:14–22. https://doi.org/10.1016/j.visres.2020.06.001
Mylonas D (2020) Colour communication within different languages. Doctoral dissertation, University College London, UK
Mylonas D, Griffin DL, Stockman A (2019) Mapping colour names in cone excitation space. 25th Symposium of the International Colour Vision Society–ICVS 2019, Riga, Latvia, 5–9 July 2019
Mylonas D, MacDonald L (2010) Online colour naming experiment using Munsell samples. Proceedings of the 5th European Conference on Colour in Graphics, Imaging, and Vision–CGIV 2010, 27–32, Joensuu, Finland
Mylonas D, MacDonald L (2012) Colour naming for colour communication. In: Best J (ed.) Colour design: theories and applications. Woodhead Publishing. pp. 254–270
Mylonas D, MacDonald L, Wuerger S (2010) Towards an online color naming model. Proceedings of the 18th Color and Imaging Conference–CIC 2010, 140–144, San Antonio, Texas, USA
Mylonas D, Stutters J, Doval V, MacDonald L (2013) Colournamer, a synthetic observer for colour communication. In: MacDonald L, Westland S, Wuerger S (eds.) AIC 2013, 12th Congress of the International Colour Association, 701–704, Newcastle, UK
Ndimwedi JN (2016) Educational barriers and employment advancement among the marginalized people in Namibia: The case of the OvaHimba and OvaZemba in the Kunene region. Master Thesis, University of the Western Cape
Newhall SM, Nickerson D, Judd DB (1943) Final Report of the O.S.A. subcommittee on the spacing of the Munsell colors. J Opt Soc Am 33(7):385–411. https://doi.org/10.1364/JOSA.33.000385
Nguaiko NE (2010) The new Otjiherero dictionary: English - Herero Otjiherero-Otjiingirisa. AuthorHouse
Nurse D, Philippson G (2006) The Bantu languages. Routledge
Olkkonen M, Witzel C, Hansen T, Gegenfurtner KR (2010) Categorical color constancy for real surfaces. J Vis, 10(9). https://doi.org/10.1167/10.9.16
Özgen E, Davies IRL (2002) Acquisition of categorical color perception: a perceptual learning approach to the linguistic relativity hypothesis. J Exp Psychol: Gen 131(4):477–493. https://doi.org/10.1037/0096-3445.131.4.477
Paggetti G, Menegaz G, Paramei GV (2016) Color naming in Italian language. Color Res Appl 41(4):402–415. https://doi.org/10.1002/col.21953
Paramei GV (2005) Singing the Russian Blues: an argument for culturally basic color terms. Cross-Cult Res 39(1):10–38. https://doi.org/10.1177/1069397104267888
Paramei GV, Griber YA, Mylonas D (2018) An online color naming experiment in Russian using Munsell color samples. Color Res Appl 43(3):358–374. https://doi.org/10.1002/col.22190
Paramei GV, Bimler DL (2021) Language and psychology. In: Steinvall A, Street S (eds.) A Cultural History of Color, Vol. 6, The Modern Age: From 1920 to present (Ch. 6, pp. 117–134). London: Bloomsbury
Parraga CA, Akbarinia A (2016) NICE: A computational solution to close the gap from colour perception to colour categorization. PLOS ONE, 11(3). https://doi.org/10.1371/journal.pone.0149538
Peirce JW (2007) PsychoPy—Psychophysics software in Python. J Neurosci Method 162(1–2):8–13. https://doi.org/10.1016/j.jneumeth.2006.11.017
Philipona DL, O’Regan JK (2006) Color naming, unique hues, and hue cancellation predicted from singularities in reflection properties. Vis Neurosci 23(3–4):331–339. https://doi.org/10.1017/S0952523806233182
Regier T, Kay P, Khetarpal N (2007) Color naming reflects optimal partitions of color space. Proc Natl Acad Sci USA 104(4):1436–1441. https://doi.org/10.1073/pnas.0610341104
Regier T, Kemp C, Kay P (2015) Word meanings across languages support efficient communication. In: MacWhinney B, O’Grady W (eds.) The Handbook of Language Emergence. John Wiley & Sons, Inc. pp. 237–263
Regier T, Kay P (2004) Color naming and sunlight. Psychol Sci 15:288–289
Roberson D, Davies I, Davidoff J (2000) Color categories are not universal: Replications and new evidence from a stone-age culture. J Exp Psychol. Gen 129(3):369–398. https://doi.org/10.1037/0096-3445.129.3.369
Roberson D, Hanley JR, Pak H (2009) Thresholds for color discrimination in English and Korean speakers. Cognition 112(3):482–487. https://doi.org/10.1016/j.cognition.2009.06.008
Roberson D, Davidoff J, Davies IRL, Shapiro LR (2004) The development of color categories in two languages: a longitudinal study. J Exp Psychol. Gen 133(4):554–571. https://doi.org/10.1037/0096-3445.133.4.554
Roberson D, Davidoff J, Davies IRL, Shapiro LR (2005) Color categories: Evidence for the cultural relativity hypothesis. Cogn Psychol 50(4):378–411. https://doi.org/10.1016/j.cogpsych.2004.10.001
Skelton AE, Catchpole G, Abbott JT, Bosten JM, Franklin A (2017) Biological origins of color categorization. Proc Natl Acad Sci USA 114(21):5545–5550. https://doi.org/10.1073/pnas.1612881114
Steels L, Belpaeme T (2005) Coordinating perceptually grounded categories through language: a case study for colour. Behav Brain Sci 28(4):469–489. https://doi.org/10.1017/S0140525X05000087
Sturges J, Whitfield A (1995) Locating basic colours in the Munsell space. Color Res Appl 20(6):364–376. https://doi.org/10.1002/col.5080200605
Thorndike RL (1953) Who belongs in the family? Psychometrika 18(4):267–276. https://doi.org/10.1007/BF02289263
Uchikawa K, Boynton RM (1987) Categorical color perception of Japanese observers: Comparison with that of Americans. Vis Res 27(10):1825–1833. https://doi.org/10.1016/0042-6989(87)90111-8
Valberg A (2001) Unique hues: An old problem for a new generation. Vis Res 41(13):1645–1657. https://doi.org/10.1016/S0042-6989(01)00041-4
Welsch N, Liebmann CC (2004) Farben: natur, technik, kunst. Akademischer Verlag, Spektrum, p. 64
Wierzbicka A (2015) The meaning of colour words in a cross-linguistic perspective. In: Elliott AJ, Fairchild MD, Franklin A (eds.) Handbook of Color Psychology. Cambridge University Press. pp. 295–316
Witzel C (2016) New insights into the evolution of color terms or an effect of saturation? i-Perception 7(5):2041669516662040. https://doi.org/10.1177/2041669516662040
Witzel C (2019) Misconceptions about colour categories. Rev Philos Psychol 10:499–540. https://doi.org/10.1007/s13164-018-0404-5
Witzel C, Gegenfurtner KR (2018) Color perception: Objects, constancy, and categories. Ann Rev Vis Sci 4(1):475–499. https://doi.org/10.1146/annurev-vision-091517-034231
Witzel C, Cinotti F, O’Regan JK (2015) What determines the relationship between color naming, unique hues, and sensory singularities: Illuminations, surfaces, or photoreceptors? J Vis 15(8):19. https://doi.org/10.1167/15.8.19
Witzel C (2018) The role of saturation in colour naming and colour appearance. In: MacDonald WL, Biggam CP, & Paramei G (eds.), Progress in colour studies: cognition, language and beyond. John Benjamins. pp. 41–58
Wool LE, Komban SJ, Kremkow J, Jansen M, Li X, Alonso J-M, Zaidi Q (2015) Salience of unique hues and implications for color theory. J Vis 15(2):10–10. https://doi.org/10.1167/15.2.10
Wuerger SM, Atkinson P, Cropper S (2005) The cone inputs to the unique-hue mechanisms. Vis Res 45(25–26):3210–3223. https://doi.org/10.1016/j.visres.2005.06.016
Xu H, Yaguchi H, Shioiri S (2001) Testing CIELAB-based color-difference formulae using large color differences. Opt Rev 8(6):487. https://doi.org/10.1007/BF02931740
Yendrikhovskij SN (2001) A computational model of colour categorization. Color Res Appl 26(S1):S235–S238. 10.1002/1520-6378(2001)26:1+<::AID-COL50>3.0.CO;2-O
Zaslavsky N, Kemp C, Regier T, Tishby N (2018) Efficient compression in color naming and its evolution. Proc Natl Acad Sci USA 115(31):7937–7942. https://doi.org/10.1073/pnas.1800521115
Zaslavsky N, Kemp C, Tishby N, Regier T (2019) Color naming reflects both perceptual structure and communicative need. Topic Cogn Sci 11(1):207–219. https://doi.org/10.1111/tops.12395
Acknowledgements
The authors thank Debi Roberson for making available the earlier Himba colour naming data, Andrew Stockman for the use of facilities at the Colour Vision Research Laboratory of University College London and Jerone Andrews for his support towards the computational model. This work was supported by the British Academy/Leverhulme Grant SG171176. DM was partly supported by the University College London (UCL) Computer Science—Engineering and Physical Sciences Research Council, UK, Doctoral Training Grant: EP/M506448/1–1573073 and by the FY22 TIER 1 Seed Grant from Northeastern University, USA.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethical approval
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. The study received ethical approval from Goldsmiths College, University of London (No.1390, 4th of June 2018).
Informed consent
Informed consent was obtained individually for every participant; these were provided in a culturally sensitive manner. Our Himba interpreter first approached the chief of the village for permission to be there. We never approached participants to ask them to take part. They approached us and the interpreter informed them of our study and that they can withdraw at any time. All participants could not read.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mylonas, D., Caparos, S. & Davidoff, J. Augmenting a colour lexicon. Humanit Soc Sci Commun 9, 29 (2022). https://doi.org/10.1057/s41599-022-01045-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-022-01045-3