Abstract
COVID-19 has spread rapidly around the globe. While there has been a slow down of the spread in some countries, e.g., in China, the African continent is still at the beginning of a potentially wide spread of the virus. Owing to its economic strength and imbalances, South Africa is of particular relevance with regard to the drastic measures to prevent the spread of this novel coronavirus. In March 2020, South Africa imposed one of the most severe lockdowns worldwide and subsequently faced the number of infections slowing down considerably. In May 2020, this lockdown was partially relaxed and further easing of restrictions was envisaged. In July and August 2020, daily new infections peaked and declined subsequently. Lockdown measures were further relaxed. This study aims to assess the recent and upcoming measures from an epidemiological perspective. Agent-based epidemic simulations are used to depict the effects of policy measures on the further course of this epidemic. The results indicate that measures that are either lifted too early or are too lenient have no sufficient mitigating effects on infection rates. Consequently, continuous exponential infection growth rates or a second significant peak of infected people occur. These outcomes are likely to cause higher mortality rates once healthcare capacities are occupied and no longer capable to treat all severely and critically infected COVID-19 patients. In contrast, strict measures appear to be a suitable way to contain the virus. The simulations imply that the initial lockdown of 27 March 2020 was probably sufficient to slow the growth in the number of infections, but relaxing countermeasures might allow for a second severe outbreak of COVID-19 in our investigated simulation region of Nelson Mandela Bay Municipality.
Similar content being viewed by others
Introduction
The continued absence of approved vaccinations and medical treatments in the current COVID-19 epidemic (Greenstone and Nigam, 2020) causes broad uncertainty on adequate non-medical countermeasures and policy responses. Since droplet infections are currently assumed to be the main transmission path of the virus (Gengler et al., 2020), social distancing measures and lockdowns established as the main tools to mitigate infection numbers. Owing to exponential growth rates of COVID-19 infections, both the timing and extent of such measures are considered essential (Scarselli et al., 2021). The impact of measures on the transmission dynamics is dependent on their respective characteristics (Chinazzi et al., 2020; Dignum et al., 2020; Martin-Calvo et al., 2020; Rocklov et al., 2020; Sugishita et al., 2020; Vrugt et al., 2020), thus policymakers’ decisions must pinpoint the specific situation in order to mitigate the utilisation of healthcare capacities efficiently and balance social, economic and epidemiological issues. The United States are one example of the impact of delayed countermeasures, with lockdowns and other measures having been implemented slowly. The total cases surged from 1678 to 307,318 between 16 March 2020 and 6 April 2020 and range above 5,800,000 at the time of writing (27 August 2020) (Johns Hopkins Coronavirus Resource Center, 2020; World Health Organisation, 2020a, c).
Trade-offs between effective countermeasures and economic activity are known (Dignum et al., 2020; Silva et al., 2020) and of particular interest in developing and transition countries as they come along with limited economic resilience, medical treatment abilities, testing capacities and options to practice social distancing. In comparison to most countries of the Global North, the infection dynamics in South Africa and other Sub-Saharan African countries are likely to be additionally driven by factors such as a comparably young population, the distinct prevalence of other infectious diseases such as tuberculosis or HIV and the (spatial) distribution of citizens and economic wealth (Ataguba, 2020; Bannon and Collier, 2003; Davids et al., 2020; Phua et al., 2020; World Health Organisation, 2019, 2020c). Thus, governments of the Global South are forced to react under even greater pressure and uncertainty than in countries with larger testing and healthcare capacities and are nevertheless confronted with the need to anticipate the impact of policy measures.
South Africa is a transition country with one of the highest case numbers is the world, but currently faces a sudden drop in new case numbers. From mid-July to mid-September, the number of reported active cases in South Africa declined from ~170,000 to 50,000, which led the South African President Cyril Ramaphosa to announce that his country has presumably passed the peak of infections. Several lockdown measures were eased or ended under consideration of economic and social concerns (Al Jazeera, 2020). A presentation of interim results of an unpublished seroprevalence study for several districts in Cape Town on 2 September 2020 cautiously supports optimistic assumptions about future case numbers in South Africa (Bloomberg, 2020, Hsiao, 2020). However, since reliable data, especially on unreported cases in South Africa, are scarce, the present analysis aims to contribute to the on-going debate on appropriate countermeasures and the current epidemiological status in South Africa. The impact of different lockdown characteristics and timing on further infection dynamics is simulated and discussed. A particular focus of the analysis is on the possible consequences of fading out measures too early. The South African Nelson Mandela Bay Municipality (NMBM) is selected as a research area, as it is an example of urban areas in the Global South (see Fig. 1). From a spatial perspective, South African cities are characterised by large socioeconomic disparities and segregation (Davids et al., 2020). About 35 Million people live below the upper poverty line and the unemployment rate is about 30%. The country is characterised by few agglomerations. Sustained and harsh lockdown measures, such as those initially implemented by the South African government in the beginning of the epidemic, can thus lead to many people having to fight for their economic survival (Department Statistics South Africa, 2019a, b). Comparatively limited capacities of the health system may result in a lack of intensive medical care throughout the country (Bossert et al., 2021; Davids et al., 2020; Schröder et al., 2021), particularly in the poor and densely populated townships or the remote rural areas. The impact of the high prevalence of potential comorbidities (e.g., HIV, tuberculosis) has not yet been conclusively assessed, but is suspected to be detrimental (Hogan et al., 2020).
The first cases of COVID-19 in South Africa were reported in early March 2020, with the total number of reported cases and deaths rising to 1353 and 27, respectively. By mid-June, cumulative infections exceeded 100,000, with about 2000 deaths. The previous peak of new daily cases was reached in mid-July, with about 14,000 new cases reported daily. Since then, the number of daily new cases has decreased significantly (Johns Hopkins Coronavirus Resource Center, 2020; World Health Organisation, 2020b). It remains uncertain whether current policy measures or other effects such as increased (but unobserved) immunity, weather changes or habituated behaviour of the population are responsible for the decline, to name but a few. In April 2020, the government has published a catalogue of measures (South African Department of Health, 2020) divided into five general lockdown levels, with level 5 corresponding to the disaster response measures as applied from 26 March to 30 April. A less stringent Level 4 lockdown was then imposed until the end of May, followed by several variations of level 3 measures, with an increasing number of activities being allowed. Since 17 August, the restrictions have been set to level 2 (Davids et al., 2020; Wikipedia, 2020).
As a novel approach, transportation simulations are applied to mimic human social interactions that are required for COVID-19 transmission (Bontempi et al., 2020; Squazzoni et al., 2020). Reliable data on social interactions at the micro-level are scarce (Bontempi et al., 2020). Agent-based models (ABMs) are thus currently becoming popular as they are able to bridge this gap based on sociological or behavioural economic theories and assumptions. Using demographic as well as network and location data, human behaviour and the resulting social contacts can be simulated to a certain extent and contact-driven infection events can be computed from known infection parameters such as infectivity (Davids et al., 2020; Dignum et al., 2020; Gomez et al., 2020; Hackl and Dubernet, 2019; Muller et al., 2020). Compared to purely mathematical epidemiological modelling, which became famous in the twentieth century and is still widely used (Hethcote, 2000; Kermack et al., 1927; Remuzzi and Remuzzi, 2020; Squazzoni et al., 2020), agent-based approaches are often better suited to account for spatial effects, inhomogeneous information and the stochastic character of biological systems such as human social interactions (Shi et al., 2014). Anthropocentric ABMs can track such human contact events within a realistic synthetic population in a simulated area throughout the day (Horni et al., 2016). To overcome habitual mono-disciplinarity in scientific attempts to understand current epidemics (Bontempi et al., 2020; Squazzoni et al., 2020), ABMs are generally able to integrate a variety of approaches.
The present analysis is based on transportation science, behavioural economics and epidemiological models to simulate an epidemic from spatial and demographic data and corresponding assumptions. As a novel approach, the multi-agent transport simulation framework MATSim (Horni et al., 2016) is used to simulate the movements of a synthetic population in a synthetic network of links and nodes on a common day. The network data is taken from OpenStreetMap (OpenStreetMap contributors, 2017) and consists of linked streets and locations of certain categories such as shops, workplaces or schools. A synthetic population, previously created from South African Census data (Joubert, 2018) is used to populate the network and perform different activities during the day, such as working, having leisure time or spending time at home. In the simulation, all activities are connected by means of transport, e.g., cars, minibus taxis or walking. The MATSim-related epidemic simulation framework Episim (VSP TU Berlin, 2020) is used to track the movements of these agents in the network. All encounters of infected and uninfected agents are identified as potential infection events and an infection then occurs based on a stochastic process. In a next step, the infected agents pass through an extended SIR model, that is parameterised based on the preliminary epidemiological findings on COVID-19. SIR models exist with various extensions and are among the most common models for analysing epidemics (Anderson and May, 2010; Keeling and Rohani, 2008; Kermack et al., 1927; Roche et al., 2011). In Episim, the agents’ state of health goes through different stages, in short, the agents are either susceptible, infected or recovered.
The present analysis shall contribute to the debate on appropriate policy interventions in South Africa. A particular focus is set on the duration of the measures and their impact on the spread of COVID-19. It has recently been suggested that the intensive care units in South Africa may not be sufficient to cope with the current situation (Bossert et al., 2021; Schroder et al., 2021). At the same time, the current status of the COVID-19 pandemic in South Africa has not yet been definitively determined. Accordingly, the timing of termination or reinforcement of interventions is of particular importance to successfully contain the spread of the virus. The results imply that if measures are terminated too early, the healthcare system may be overburdened again.
A second purpose of this case study is to further promote the potential of agent-based transportation simulation as a viable approach to bridging the gap between insufficient micro-data on social contact and the impact of policies on human behaviour.
Methods
The analysis consists of two main steps. First, MATSim-based transportation simulations are used to compose realistic movement and activity profiles of a synthetic population in a network of streets and locations. Second, Episim-based epidemic simulations identify potential infection events and compute the resulting disease progression based on the MATSim output. The corresponding code including underlying datasets can be downloaded from https://www.comses.net/codebases/d4e5bb89-973d-486b-ab46-26781306ffc9/releases/1.0.0/.
Transportation simulation
The underpinning transportation simulations are conducted with MATSim version 12.0-2019w48-SNAPSHOT (Horni et al., 2016) and are based on a 10% population sample for NMBM derived from the 2011 Census and 2004 travel survey data (Joubert, 2018). The main descriptive statistics of the synthetic population are presented in Table 1. The population comprises a total of 114,346 agents living in 32,597 households (3.51 agents per household). The age pyramid shown in Fig. 2 and the average age of the synthetic population of 30.27 years show a population structure with higher proportions among the young population groups. The agents move within a virtual network generated from OpenStreetMap data (OpenStreetMap contributors, 2017) (see Table 1 for network statistics). In the course of a simulation run, each agent performs one or more activities, with a run being virtual 108,000 seconds or 30 h long, starting at midnight and ending at 6 a.m. the following day. The activities are divided into the following groups: “home”, “work”, “educ_primary”, “educ_higher”, “shopping”, “leisure” and “other”. Table 2 shows the absolute numbers and Fig. 3 the spatial concentration of activities. It can be seen that relatively few activities related to work are carried out. This is due to the process of population synthesis, where all activities not clearly identified as primary labour activities fall under the category of “other”. The infectivity parameter for “other” is set to a comparably low value, in order not to overestimate the impact of this mixed indicator.
The simulation has a total of six travel modes that allow agents to travel between activities. The so-called teleportation modes such as pedestrian, bicycle and passenger allow the agents to travel at a predefined speed along a direct air line to their destination. Furthermore, the so-called network modes allow agents to travel with vehicles through the virtual network. These include cars, but also formal public transport in the form of public bus and train, and informal public transport as a minibus taxi. Currently, all formal bus operations in NMBM have been suspended (Algoa Bus Company, 2020). It can therefore be assumed that customers are substituting regular bus services with minibus taxis. The MATSim population file is modified accordingly.
Minibus taxis are the backbone of the region’s transport system, while motorised individual transport is of less importance. Public minibus taxis are expected to play an important role in the epidemic simulation, as both the probability and intensity of contact are assumed to be high. In addition, the relatively crowded vehicles mix people from different places of work and residence. In 2014, there were 2374 minibus taxis in NMBM with an average capacity of 15 passengers (Neumann et al., 2015). In order to represent minibus transport, a Demand Responsive Transport (DRT) framework is implemented into the model (Bischoff et al., 2017). The reduced population sample usually requires adjustments to network and vehicle capacities to match the real scenario load.
However, in the following scenario, this would result in minibus taxi capacities of 1.5 seats, which is problematic for the epidemic simulation. Furthermore, due to a lack of sufficient data on stops and timetables the DRT module cannot be set up as a stop-based service, which would be more similar to the operating schemes of minibus taxis. Instead, DRT vehicles operate as a door-to-door system and thus require adjustments in number of vehicles and passenger capacity to achieve similar trip distances and contact times. Finally, rounding errors can occur with this set-up, as 1 agent represents 10 real people. To address these concerns, after several calibration runs, a model with 2374 DRT vehicles with a capacity of 15 seats is chosen based on occupancy rate, travel distances and the rejection rate (see Table 1 for DRT statistics).
The different modules of the simulation such as agents, the road network, the locations of activities or the available transportation modes can be further specified and adapted to specific real-world cases. In this way, analyses of different disciplines can be conducted, e.g. for evaluating the efficiency of transport systems or changes in people’s behaviour as a result of interventions.
Epidemic simulation
The Episim framework (VSP TU Berlin, 2020) builds on the output of a preceding MATSim and is designed to detect possible infection events and corresponding infection chains. MATSim simulates the trajectories of agents as they perform their activities and travel within the network. The underpinning OSM-based network file contains information on the types and locations of the different activities. These static locations are complemented by the means of transport, i.e., the specific vehicles, derived from the MATSim-generated plans file. The same file contains information about the timetables of the individual agents. By merging these information, it is possible to identify potential infection events. Episim uses the activity and transportation locations as individual containers. Only agents, that sojourn in the same container at the same time, can infect each other with a certain probability. Moreover, only infectious agents can infect other agents and only susceptible agents can be infected.
Disease progression
Once the agents are infected, they go through different stages of an extended SIR model (Kermack et al., 1927) (see Fig. 4). An exposed state and the option to self-quarantine extend the model to an SEIQR model. Subsequent to an infection, an initially healthy and thus susceptible agent evolves from susceptible to exposed to infectious. Owing to the incubation period, it is assumed that agents are not infectious before day 4 after infection (Anderson et al., 2020; Lauer et al., 2020; Rocklov et al., 2020). From this stage on, a stochastic process determines whether the infected agents are asymptomatic and recover without complications or show mild symptoms or become seriously sick. The probability of an asymptomatic infection was set to 80%, which refers to the upper bound of the findings of current studies, in order not to overestimate the number of infections according to the conservative approach of the analysis (Birhanu et al., 2020). In the case of symptomatic infection, infected agents are assumed to self-quarantine, as the dangerousness and infectivity of COVID-19 are widely known. The self-quarantine lasts 14 days and is assumed to block all social contact, even within the household. Agents who went into self-quarantine remain technically mobile in the simulation. However, they are neither contagious nor susceptible and thus cannot participate in infection events. About 4.5% of all infected agents become seriously sick ten days after infection. Of these, a share of 25% becomes critical the following day. Infectious agents recover 16 days after infection and patients with severe disease after 23 days (Muller et al., 2020; Silal et al., 2020; Verity et al., 2020). The distinction between seriously sick and critical agents allows to check the utilisation of the healthcare system. Seriously sick agents require basic hospital care and may become critical, i.e., they require respiratory support and thus intensive care.
At this stage, the setup requires two assumptions: First, all infected agents finally recover. As recovered agents are assumed to be immune and no longer infectious, omitting death does not bias further infection events. Immunity is currently a matter of intensive research and discussion. Although there is indication that immunity might be neither absolute nor permanent, it is assumed both for simplicity and lack of evidence that recovered agents are immune (Edridge et al., 2020; Wu et al., 2020). Second, it is assumed that every infected person has sufficient space, economic wealth and social support to withdraw and live in full quarantine for two weeks. Finally, births and natural deaths are not included in the model because simulations cover a relatively short period of time.
Infection events
In Episim, infection events are based on a probabilistic model and occur solely in containers. These containers are created from OSM data and the agent activities are generated by MATSim. Each container is assigned to a certain category, such as Work, Minibus Taxis or Leisure, and is associated with a certain infectivity parameter. For example, a crowded and unventilated minibus taxi is more likely to be the site of an infection event than a sprawling public park. The contact intensities are depicted in Table 3 and are taken from the original Episim configuration. As the original framework was configured for Berlin, Germany, some values were adjusted to reflect regional conditions in the NMBN. The parameter for home-based activities was increased from 3 to 6 in consideration of larger household sizes and general living conditions. The value for minibus taxis providing public transport services was set to 20 (the original value for public transport was 10 and referred to public transport in Berlin).
Once a susceptible and a contagious agent are in the same container, an infection occurs with a certain probability described by
Here, Pn,t denotes the infection probability of susceptible agent n at day t in a contact with an infectious agent m. The infection probability is determined by three contact-specific parameters qm,t, inm,t and τnm,t. Moreover, the parameter θ is a calibration parameter and is used to adjust simulated to real infection numbers in a subsequent calibration process. q denotes the shedding rate, i.e., the general infectivity of the virus, which could vary by time and agent. i is an activity-specific parameter that is intended to take into account the different contact intensities at different locations. τ denotes the time that the agents m and n spent together in the same container. In the present analysis, θ is set to 1.5 × 10−7 (see Figs. 5 and 6) and q is assumed to be equal for all simulated contacts. The chosen parameters for i are depicted in Table 3. Since it is unlikely that a person in a container interacts with every other person, each agent can infect at most three other agents.
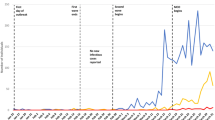
Fifty percent and 80% confidence intervals for the estimations are depicted in blue. Ten Agents are initially infected (black dot) on 01 May. The dotted vertical lines refer to different periods of lockdown levels starting at 27 March 2020 with level 5. Lockdown level 4 was initiated on 01 May and eased to level 3 on 01 June 2020. The level 3 measures were altered during the subsequent weeks with major changes on 12 July 2020, when new school closures were announced. At the same time, several other stricter restrictions were already in power.
Fifty and 80% confidence intervals for the estimations are depicted in blue. The dotted vertical lines refer to different periods of lockdown levels starting at 27 March 2020 with level 5. Lockdown level 4 was initiated on 01 May and eased to level 3 on 01 June 2020. The level 3 measures were altered during the subsequent weeks with major changes on 12 July 2020, when new school closures were announced. At the same time, several other stricter restrictions were already in power.
Policy interventions
The South African government has published a catalogue of countermeasures for five different levels of lockdowns (South African Department of Health, 2020), which are summarised in Table 4. The restrictions aim to mitigate social contacts by limiting economic, educational or social activities to a reasonable level. Table 4 clusters the proposed measures into groups related to the activity groups used in the simulations. The qualitative policy descriptions were translated into quantitative restriction parameters to approximate the impact of the different levels on economic and social life (see Table 3). This approach requires a number of assumptions, such as that the entire population is able and willing to follow the instructions. However, again following the idea of a conservative approach, these assumptions should result in an underestimation of future case numbers and still allow for several conclusions. The translation of qualitative statements into quantitative numbers is by nature prone to errors and the results must be interpreted with respect to this uncertainty. However, the catalogue provides valuable points of reference and makes it possible not only to put the various measures for the agents’ activities in an ordinary relationship, but to refer them to each other. Minor misinterpretations can be cured by adjusting the calibration parameter in a subsequent step of the model calibration.
The Episim framework enables the simulation of non-medical policy interventions of different types and severity. By reducing the prevalence of certain activities carried out by the MATSim agents during the day, the impact of different real-world measures can be reproduced or anticipated in the simulations.
The activities that an agent performs during the day are taken from the plans file of the MATSim output and correspond with locations from the OSM network file. In Episim, these locations are used to create containers of certain categories, such as Home, Work, Leisure or Shopping. By default, all activity parameters are equal to 1 and thus all agents perform activities in full accordance with their designated plans. If a government decided to fully restrict only leisure activities, the corresponding activity parameter for Leisure would be 0. Accordingly, the decision not to allow half of the workforce to work would result in an activity parameter of 0.5.
As a part of its COVID-19-strategy, the government of South Africa has published a catalogue of lockdown rules with different levels (South African Department of Health, 2020). Level 5 corresponds to very strict regulations, such as curfews from 8 p.m. to 5 a.m. and orders to stay at home except for absolutely necessary reasons. Public transport is severely restricted, as are non-essential occupations. On the contrary, level 1 advises the population to behave considerately and follow general personal measures such as wearing masks and keeping a distance of 2 m, but does not restrict personal movement or economic activity in general.
For an impact evaluation of lockdown levels on the infection dynamics the published regulations have been translated into activity parameters, which are used to incorporate the effect of reduced activities during the lockdown periods (see Table 3).
Epidemic calibration
The policy parameters are then included in a series of calibration simulations that are adjusted to real infection data by varying the parameter θ in the infection equation (1). Accordingly, changes in θ affect the probability of infection between two agents. Since real case numbers for the NMBM are not available, values were calculated on the basis of the number of cases in South Africa and as an approximation according to the percentage of the population (ECDC, 2020). θ enters the infection equation non-linearly and affects all infectivity parameters of the activities equally to maintain their order. The parameter θ was adjusted in an iterative process with the intention of obtaining a value that yields an infection count that approximates case numbers in real data, is robust to small changes, and does not systematically overestimate case numbers or the rate of spread.
For the analyses, θ was set to 1.5 × 10−7. The simulations start with ten randomly selected infected agents and the onset of infections is adjusted to the beginning of May. Here, the number of official cases exceeded the threshold of 100, which, given the 10% population sample, corresponds to 10 infected agents. The simulated infection chains are adjusted to the number of reported cases until 27 July 2020 (see Figs. 5 and 6). The current state of research is not yet conclusive by how much the real number of cases exceeds the reported cases. Thus, the simulations were calibrated to the reported cases in a conservative approach, intentionally under- but not overestimating the true infection dynamics. By that, the results must be interpreted with caution as they represent a hypothetical scenario without unreported cases. This approach allows specific conclusions to be drawn on correlations between non-medical countermeasures and infection dynamics.
The stochastic selection of initially infected agents introduces some between-run variance due to changes in their daily social contacts. The selection of ten instead of one infected agent already mitigates this bias and the analysis is also based on an ensemble of 100 simulations. Figures 5 and 6 depict 100 different random realisations and their averages for θ = 1.5 × 10−7 and variations of 5% and 10% in both directions to check the sensitivity of the models.
Table 5 presents the evaluation of the different scenarios by sum of squares of errors and slopes of regression degrees. The evaluation periods were set from the beginning of June and the beginning of July until 27 of July. The earlier periods are not used because they are probably too distorted by the modified initial conditions (ten randomly infected agents on 01 May). Although the quality measures do not allow for an unambiguous ranking of the results, 1.5 × 10−7 was chosen as calibration parameter. 1.5 × 10−7 has only the second or third best squared sum of errors (SSEs) values in the model comparisons, but the slope of the longer-term regression degrees is smaller but similar to the value of the reported cases. A slightly higher θ might result in a better fit, but runs the risk of overestimating rather than underestimating the real cases, which can be observed in particular in the regression coefficients for the daily new cases in July.
Results
The main results of the simulations are depicted in Figs. 7 to 10 and are presented in form of a simulated time series of active corona cases per day. The cumulative number of recoveries is additionally displayed as it allows to check for robustness and adds a cumulative perspective. Each figure is divided into six panels, representing one possible policy scenario each, with lockdown measures ranging from level 1 (no or lax measures) to level 5 (strict measures). The lockdown intensities are taken from an official scenario description by the South African government (South African Department of Health, 2020) (see Table 4) and differentiate several activity types such as work, leisure or education. All simulations started on 12 May 2020, when the number of active infections in the real-world equalled 100 and a level 4 lockdown was in place. Level 3 measures were introduced on 1 June and reinforced with new school closures on 27 July 2020. When conducting the simulations, it was assumed that this tightened lockdown would last for 30 days until 26 August 2020 to have a noticeable effect. From August 26, different durations of the proposed lockdown levels will be simulated to analyse the impact of early or delayed lifting of the different measures.
All lockdown measures end after 30 days on 25 September 2020. The six panels refer to the different policy scenarios ranging from level 5 (very strict lockdown) to level 1 (no lockdown measures). The grey lines represent the case numbers of 100 simulations with various seeds for each policy scenario. The coloured lines denote the mean total number of active infections (orange) and the mean cumulative number of recovered infections (green), respectively. The confidence intervals are computed at a 50% and an 80% level. The vertical lines denote the dates of earlier governmental lockdown measures (black, dotted) and the simulated measures of 30 days (red, dashed). On 1 June 2020, the lockdown measures were relaxed from level 4 to level 3. On 27 July 2020, lockdown level 3 remained active, but schools were closed again and several other restrictions were in placed such as alcohol selling bans (referred to as lockdown level 3 (strict)).
The general shape of the infection curves is similar for all results. Until 26 August 2020, a sustained exponential with few deviations can be observed. From 26 August 2020 on, the curves differ in terms of infection dynamics. As expected, strict and long lockdowns tend to decrease the active case numbers, while lax and short lockdown lead to a faster spread of the virus. Figure 7 depicts the result for additional 30 day lockdown periods from 26 August until 25 September 2020. The period prior to the anticipated measures was characterised by a strict level 3 lockdown. Thus, as expected, reducing the lockdown intensity to level 1 or 2 leads to increased virus activity and an approximate tenfold increase in active cases within 30 days. Maintaining the stricter level 3 measures leads in a downward sloping curve. Obviously, the mitigating impact of the measures requires some time before it becomes visible. Stricter measures are able to slightly reduce the number of active infections. In all six measure cases, the subsequent end of all measures on 25 September 2020 leads to an accelerated increase in active numbers. In all scenarios, the infection curves peak between October and November, which due to high numbers of both infected and recovered and thus a large number of immune persons. Notably, the peak of infected individuals in all scenarios occurs at about the same time at the intersection with the recovery curve, with both variables having scenario-dependent values between 200,000 and 300,000 representing between half and two-thirds of the NMBM population.
A change from from 30 to 60 days of simulated additional measures (Fig. 8) leads to strong effects on case numbers. The general trends apply, as described above, in terms of accelerated growth in numbers for lax lockdown levels and a decline in the stricter scenarios. Although this decline is not sufficient to mitigate the case numbers even after the measures end on 25 October 2020, the peak of infections is shifted several weeks into the future and occurs in early 2021.
All lockdown measures end after 60 days on 25 October 2020. Compared to the lockdown scenarios of 30 days (Fig. 7), the mitigating effect of the measures is much stronger and leads to a temporal trend reversal in the three strict policy scenarios. After the end of measures, the active case numbers return to steep exponential growth paths.
Figures 9 and 10 refer to 90 and unlimited days of lockdowns, respectively. Consistent with the previous comparison, the extended strict measures are able to reduce case numbers. In scenarios with unlimited measure duration, the virus dies out under a level 5 lockdown by the end of 2020 in most simulations. However, ending the lockdown even at low case numbers leads to a return to the exponential growth path in the surviving infection chains.
All lockdown measures end after 90 days on 24 November. Compared to the lockdown scenarios of 30 or 60 days (Figs. 7 and 8), the simulation of strict lockdown levels (from level 3 upwards) corresponds with an increased number of dying-out infections during the measures period. In the case of lockdown levels 4 and 5, the extended measure period reduced active infections to a level, that multiple infection chains end even in the days after ending the lockdown measures. Nevertheless, the remaining infection chains return to exponential growth rates.
Table 6 provides an overview on the infection locations by computing the share of infections per activity class for all lockdown levels and durations. In all configurations most agents are infected at home (~96% to 86%), followed by minibus taxis (17% to 0%) and educational activities (11% to 2%). Despite some minor variations, mainly due to the stochastic part of the simulations and the relative character of the values shown, a higher lockdown level and a longer lockdown duration results in a lower share of out-of-home activities. Since more agents are forced to stay home under a harsh lockdown, they are more often infected by returning infectious family members. This trend is amplified by the comparatively high average and maximum household size (see Table 1). The prevalence of infections per activity class generally correlates with the infectivity parameters (see Table 3) and the prevalence of activities (see Table 2). The infectivity parameters for minibus taxis and primary education activities were set to comparably high values and education activities are the second most frequent activity class after other activities. The shift of infection locations from out-of-home activities to the agents’ homes with stricter measures is much less evident or even imperceptible for the short lockdown durations of 30 and 60 days compared to the other groups. This is due to a comparably long period without any measures following the corresponding lockdown period, which then balances the values again.
Discussion
Most simulation configurations with lenient measures indicate a peak of active cases in autumn 2020. From then on, the dynamics of the epidemic slow down, as both currently infected and recovered (and thus non-susceptible) agents account for about half and up to two-thirds of the population, respectively. This proportion is in line with current epidemiological estimates of the required thresholds for herd immunity (Fontanet and Cauchemez, 2020; Kwok et al., 2020; Randolph and Barreiro, 2020).
The development of infection numbers over time is determined by the level and duration of the lockdown. In general, continuous and strict lockdowns can be confirmed as effective measures to flatten infection curves and postpone large numbers of cases into the future or even eventually eradicate the virus (Tian et al., 2020; Vasconcelos et al., 2020). This finding is consistent with the observed effectiveness of the stringent measures in Wuhan, China (Lau et al., 2020). With lax measures, the effect of subsequent exponential growth of infected individuals over time outweighs the effect of reduced social contacts (Anderson et al., 2020). The measures that are sufficient to produce decreasing case numbers in the simulations are between a strict and a lax level 3 variant. However, since θ and other parameters were chosen to underestimate case numbers, the actual level required for containment could also be at level 4 or 5. In any case, it can be assumed that level 2 measures will prove insufficient in a period of rapidly increasing case numbers.
In all scenarios, a complete termination of the lockdown ultimately leads to a renewed increase in infections. Except for a comparatively long and strict lockdown scenario, the measures are not sufficient to eradicate the virus. However, they can considerably reduce the number of new cases and therefore relieve the burden on the health system. The strict measures can thus prove to be a means of gaining time to expand the capacities of the health system and to research medical treatment and prevention measures. However, as the case numbers of any active epidemic return to an exponential growth path after the measures have ended, an on-and-off strategy of strict measures could prove risky and of little benefit.
The results presented above were generated based on an agent-based transport simulation framework. Agent-based transportation simulations typically aim to model realistic human behaviour at a micro-level in relation to their environment. As the artificial agents interact in the network, contact durations can be tracked as important infection parameters and used to simulate infection chains. Agent-based modelling can easily integrate available data, but the approach also allows bridging data gaps with theory-based assumptions. As an example, agents’ daily movements from home to work can be modelled either using detailed travel diaries or, if no such data are available, based on the assumptions, e.g., that humans act in a utility maximising way, i.e., choose the fastest route or the most appropriate transport mode.
The idea of MATSim is to link the different activities of agents throughout the day with appropriate means of transport. The population data used in this analysis contain information about the agents’ daily schedules and the class of each activity performed. Thus, such models can pass more detailed lockdown parameters to the simulation than other current approaches. However, choosing and calibrating these parameters is challenging because their exact values are usually unknown and can hardly be translated into quantitative numbers. Other contributions address the problem by using, e.g., mobility data or severity indices or simply not distinguishing between constraints for different activities (Davids et al., 2020; Silva et al., 2020).
The present simulation setup is associated with a number of limitations resulting from the assumptions made for calibration. The main role of the utilised policy parameters is to balance the infection locations by class and to model the impact of specific policies and network effects. Deriving the policy parameters from the government’s published policy catalogue thus puts the parameters in a sufficiently accurate context. However, unlike the simulated agents, many people are not able to follow the regulations accurately, so real-world out-of-home infections may be underestimated (with the exception of education activities, which are easier to monitor). In the epidemic simulation, 100 initially infected people or 10 randomly selected infected agents were assumed. The higher number of initially infected agents reduced the variance in the ensemble of realisations. However, this procedure creates artificial conditions at the beginning of the simulations and distorts the natural infection process in the first few days, thus reducing the validity of the results. The short-term distorting effect was accepted in favour of a sustainably lower variance in the simulations.
The Episim simulations are finally calibrated by adjusting the calibration parameter θ. The strategy of underestimating infection numbers leads to a systematic underestimation of daily case numbers in the simulations and to more (still) susceptible agents than in reality. Accordingly, the simulated scenarios are likely to have a delayed peak of infections and a prolonged epidemic course. The 27 July 2020 was chosen as the cut-off date for the calibration. By the date of writing, official case numbers in South Africa peaked at ~14,000 (daily new) or 350,000 to 450,000 (cumulative) at the end of July and have declined log-linearly since then. In September, during a period of comparatively lax measures, daily new cases consolidated between ~1000 and 2000, with a cumulative total of 650,000 cases. One possible interpretation of the simulated results in relation to these developments is that, as intended, the simulations underestimated the infection dynamics and that the peak in new cases observed by South Africa in July 2020 is related to the peaks in the simulations dating to autumn 2020 at the earliest. In this case, with a population of about 58 million and an estimated required proportion of insusceptible agents of at least 50% during the peak, about 98% of all infections in South Africa would have been unreported. This value is higher than previous estimates of up to 87% of unreported cases (Hao et al., 2020; Pei, 2020), but could be explained by the demographic and economic structure of South Africa.
The observed peak in July and August (see Fig. 11) could turn out to be an intermediate peak, followed by a temporary decline in case numbers. On the one hand, the consolidation of cases in September could give support to this hypothesis and might denote the beginning of a second period with higher infection numbers. On the other hand, comparatively lax level 2 measures were applied during this time and could slow down the decline. Other possible explanations relate to unobserved epidemic parameters that were not included in the simulation, such as environmental influences (Bontempi et al., 2020), changes in hygiene and social distance behaviour, weather changes or mutations of the virus.
Conclusion
The results stress that from a purely epidemiological point of view, a strict and long lockdown is a theoretically first-best countermeasure in all simulations. A strict lockdown leads to significantly fewer infections compared to all other scenarios and does thus reduce the impact on the limited healthcare system capacities. Under the assumptions discussed above, the simulations suggest that a certain combination of chosen intermediate measures might be sufficient to consolidate the number of active cases. The results cannot confirm beyond doubt President Cyril Ramaphosa’s statement that infections have peaked. However, assuming a high proportion of unreported cases and in view of the intended underestimation of infection dynamics, the simulations carefully indicate a soundness of this assumption.
Data availability
The simulation setup used for this study can be downloaded from the following link: https://www.comses.net/codebases/d4e5bb89-973d-486b-ab46-26781306ffc9/releases/1.0.0/. The original epidemic simulation framework used during the current study is available under https://github.com/matsim-org/matsim-episim/tree/d796bc4bfdff27d9112f6de5932b7615c9a0420a. The population data analysed during the current study are available under https://doi.org/10.17632/dh4gcm7ckb.1.
References
Al Jazeera (2020) COVID-19: what people with HIV should know. https://www.ajmc.com/newsroom/covid19-questions-hivpositive-individuals-want-answered. Accessed 07 Apr 2020
Algoa Bus Company Official Homepage. https://www.algoabus.co.za/. Accessed 05 Apr 2020
Anderson RM, May RM (2010) tious diseases of humans: dynamics and control. Reprinted. Oxford Univ. Press, Oxford
Anderson RM, Heesterbeek H, Klinkenberg D, Hollingsworth TD (2020) How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 395(10228):931–934
Ataguba JE (2020) COVID-19 Pandemic, a War to be Won: understanding its Economic Implications for Africa. Appl Health Econ Health Policy 18:325–328
Bannon I, Collier P (2003) Natural resources and violent conflict: options and actions. https://openknowledge.worldbank.org/handle/10986/15047. Accessed 07 Feb 2021
Birhanu A, Feyisa TO, Chala G (2020) The proportion of asymptomatic cases among SARS-CoV-2 infected patients: a systematic review. Eur J Clin Biomed Sci 6(5):84–89
Bischoff J, Maciejewski M, Nagel K (2017) City-wide shared taxis: a simulation study in Berlin. In: IEEE 20th International Conference on Intelligent Transportation Systems (ITSC). IEEE. pp. 275–280
Bloomberg (2020) Exposure to Covid-19 reaches 40% among some Cape Town residents. https://www.iol.co.za/news/south-africa/western-cape/exposure-to-covid-19-reaches-40-among-some-cape-town-residents-81591c85-c980-45eb-baea-62110cdec428. Accessed 21 Sept 2020
Bontempi E, Vergalli S, Squazzoni F (2020) Understanding COVID-19 diffusion requires an interdisciplinary, multi-dimensional approach. Environ Res 188:109814
Bossert A, Kersting M, Timme M, Schröder M, Feki A, Coetzee J, Schlüter J (2021) Limited containment options of COVID-19 outbreak revealed by regional agent-based simulations for South Africa. F1000Research 10:98
Chinazzi M, Davis JT, Ajelli M, Gioannini C, Litvinova M, Merler S, Pastore y Piontti A, Mu K, Rossi L, Sun K, Viboud C, Xiong X, Yu H, Halloran ME, Longini Jr IM, Vespignani A (2020) The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 368(6489):395–400. https://doi.org/10.1126/science.aba9757
Davids A, Du Rand G, Georg CP, Koziol T, Schasfoort JA (2020) Social Learning in a Network Model of Covid-19. medRxiv. https://doi.org/10.1101/2020.07.30.20164855
Department Statistics South Africa (2019b) Work & Labour Force. http://www.statssa.gov.za/?page_id=737&id=1. Accessed 07 Apr 2020
Department Statistics South Africa-Republic of South Africa (2019a) Five facts about poverty in South Africa. http://www.statssa.gov.za/?p=12075. Accessed 07 Apr 2020
Dignum F, Dignum V, Davidsson P, Ghorbani A, van der Hurk M, Jensen M, Kammler C, Lorig F, Ludescher LG, Melchior A, Mellema R, Pastrav C, Vanhee L, Verhagen H (2020) Analysing the combined health, social and economic impacts of the corovanvirus pandemic using agent-based social simulation. Mind Machine 1–18. https://doi.org/10.1007/s11023-020-09527-6
ECDC (2020) Download today’s data on the geographic distribution of COVID-19 cases worldwide. https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide. Accessed 20 Sept 2020
Edridge AWD, Kaczorowska JM, Hoste ACR, Bakker M, Klein M, Loens K, Jebbink MF, Matser A, Kinsella CM, Rueda P, Ieven M, Goossens H, Prins M, Sastre P, Deijs M, van der Hoek L (2020) Seasonal coronavirus protective immunity is short-lasting. Nat Med 26:1691–1693. https://doi.org/10.1038/s41591-020-1083-1
Fontanet A, Cauchemez S (2020) COVID-19 herd immunity: where are we? Nat Rev Immunol. https://doi.org/10.1038/s41577-020-00451-5
Gengler I, Wang JC, Speth MM, Sedaghat AR (2020) Sinonasal pathophysiology of SARS-CoV-2 and COVID-19: a systematic review of the current evidence. Laryngoscope Investigative Otolaryngology. https://doi.org/10.1002/lio2.384
Gomez J, Prieto J, Leon E, Rodriguez A (2020) INFEKTA: a general agent-based model for transmission of infectious diseases: studying the COVID-19 propagation in Bogota-Colombia. https://doi.org/10.1101/2020.04.06.20056119
Greenstone M, Nigam V (2020) Does social distancing matter? University of Chicago, Becker Friedman Institute for Economics Working Paper (2020-26). https://doi.org/10.2139/ssrn.3561244
Grimm V, Berger U, DeAngelis DL, Polhill JG, Giske J, Railsback SF (2010) The ODD protocol: a review and first update (2010). Ecol Model 221(23):2760–2768
Grimm V, Berger U, Bastiansen M, Eliassen F, Ginot S, Giske V, Goss-Custard J, Grand T, Heinz SK, Huse GHA, Jepsen JU, Jørgensen C, Mooij WM, Müller B, Pe’er G, Piou C, Railsback SF, Robbins AM, Robbins MM, Rossmanith E, Rüger N, Strand E, Souissi S, Stillman RA, Vabø R, Visser U, DeAngelis DL (2006) A standard protocol for describing individual-based and agent-based models. Ecol Model 198(1):115–126
Hackl J, Dubernet T (2019) Epidemic spreading in urban areas using agent-based transportation models. Future Internet 11:92
Hao X, Cheng S, Wu D, Wu T, Lin X, Wang C (2020) Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature 584(7821):420–424
Hethcote HW (2000) The mathematics of infectious diseases. SIAM Rev 42(4):599–653
Hogan AB, Jewell BL, Sherrard-Smith E, Vesga JF, Watson OJ, Whittaker C, Hamlet A, Smith JA, Winskill P, Verity R, Baguelin M, Lees JA, Whittles LK, Ainslie KEC, Bhatt S, Boonyasiri A, Brazeau NF, Cattarino L, Cooper LV, Coupland H, Cuomo-Dannenburg G, Dighe A, Djaafara BA, Donnelly CA, Eaton JW, van Elsland SL, FitzJohn RG, Fu H, Gaythorpe KAM, Green W, Haw DJ, Hayes S, Hinsley W, Imai N, Laydon DJ, Mangal TD, Mellan TA, Mishra S, Nedjati-Gilani G, Parag KV, Thompson HA, Unwin HJT, Vollmer MAC, Walters CE, Wang H, Wang Y, Xi X, Ferguson NM, Okell LC, Churcher TS, Arinaminpathy N, Ghani AC, Walker PGT, Hallett TB (2020) Potential impact of the COVID-19 pandemic on HIV, tuberculosis, and malaria in low-income and middle-income countries: a modelling study. Lancet Global Health 8(9):e1132–e1141
Horni A, Nagel K, Axhausen KW (2016) The multi-agent transport simulation MATSim. Ubiquity Press. https://doi.org/10.5334/baw
Hsiao M (2020) Sep 2020 COVID 19 ECHO clinic-YouTube. https://www.youtube.com/watch?v=ZH-nOWgSZBU. Accessed 21 Sep 2020
Johns Hopkins Coronavirus Resource Center (2020) COVID-19 Map-Johns Hopkins Coronavirus Resource Center. https://coronavirus.jhu.edu/map.html. Accessed 27 Aug 2020
Joubert JW (2018) Synthetic populations of South African urban areas. Data Brief 19:1012–1020
Joubert JW (2014) Population generation. https://matsim.atlassian.net/wiki/spaces/MATPUB/pages/15269933/Nelson+Mandela+Bay. Accessed 01 Mar 2021
Keeling MJ, Rohani P (2008) Modeling infectious diseases in humans and animals. https://doi.org/10.1093/bmb/ldp0410
Kermack WO, Mc Kendrick A, Walker GT (1927) A contribution to the mathematical theory of epidemics. Proc R Soc London Ser A 115(772):700–721
Kwok KO, Lai F, Wei WI, Wong SYS, Tang JWT (2020) Herd immunity-estimating the level required to halt the COVID-19 epidemics in affected countries. J Infect 80(6):e32–e33
Lau H, Khosrawipour V, Kocbach P, Mikolajczyk A, Schubert J, Bania J, Khosrawipour T (2020) The positive impact of lockdown in Wuhan on containing the COVID-19 outbreak in China. J Travel Med. https://doi.org/10.1093/jtm/taaa037
Lauer SA, Grantz KH, Bi Q, Jones FK, Zheng Q, Meredith HR, Azman AS, Reich NG, Lessler J (2020) The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann Int Med 172(9):577–582
Martín-Calvo D, Aleta A, Pentland A, Moreno Y, Moro E (2020) Effectiveness of social distancing strategies for protecting a community from a pandemic with a data driven contact network based on census and real-world mobility data. https://covid-19-sds.github.io. Accessed 01 Mar 2021
Müller SA, Balmer M, Neumann A, Nagel K (2020) Mobility traces and spreading of COVID-19. Technische Universität Berlin. https://doi.org/10.14279/depositonce-9835
Neumann A, Röder D, Joubert JW (2015) Towards a simulation of minibuses in South Africa. J Transport Land Use 8(Feb. 1):137–154
OpenStreetMap contributors (2017) OpenStreetMap. https://www.openstreetmap.org
Pei S (2020) SenPei-CU/COVID-19: COVID-19. https://doi.org/10.5281/ZENODO.3699624
Phua J, Weng L, Ling L, Egi M, Lim CM, Divatia JV, Shrestha BR, Arabi Y, Ng J, Gomersall C, Nishimura M, Koh Y, Du B (2020) Intensive care management of coronavirus disease 2019 (COVID-19): challenges and recommendations. Lancet Respir Med. https://doi.org/10.1016/S2213-2600(20)30161-2
Randolph HE, Barreiro LB (2020) Herd immunity: understanding COVID-19. Immunity 52(5):737–741
Remuzzi A, Remuzzi G (2020) COVID-19 and Italy: what next? Lancet 395(10231):1225–1228
Roche B, Drake JM, Rohani P (2011) An Agent-Based Model to study the epidemiological and evolutionary dynamics of Influenza viruses. BMC Bioinformatics 12(87). https://doi.org/10.1186/1471-2105-12-87
Rocklöv J, Sjödin H, Wilder-Smith A (2020) COVID-19 outbreak on the Diamond Princess cruise ship: estimating the epidemic potential and effectiveness of public health countermeasures. J Travel Med. https://doi.org/10.1093/jtm/taaa030
Scarselli D, Budanur NB, Timme M, Hof B (2021) Discontinuous epidemic transition due to limited testing. Nat Commun 12:2586. https://doi.org/10.1038/s41467-021-22725-9
Schröder M, Bossert A, Kersting M, Aeffner S, Coetzee J, Timme M, Schlüter J (2021) COVID-19 in Africa-outbreak despite interventions? Sci Rep 11:4956
Shi ZZ, Wu CH, Ben-Arieh D (2014) Agent-based model: a surging tool to simulate infectious diseases in the immune system. Open J Model Simul 02(01):12–22
Silal S, Pulliam J, Meyer-Rath G, Nichols B, Jamieson L, Kimmie Z, Moultrie H (2020) Estimating cases for COVID-19 in South Africa Update: 19 May 2020. https://www.gov.za/sites/default/files/gcis_documents/SACMC_19052020.pdf. Accessed 21 Sept 2020
Silva PCL, Batista PVC, Lima HS, Alves MA, Guimarães FG, Silva RCP (2020) COVID-ABS: an agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions. Chaos Solitons Fract 139:110088
South African Department of Health (2020) COVID-19 Risk Adjusted Strategy-SA Corona Virus Online Portal. https://sacoronavirus.co.za/covid-19-risk-adjusted-strategy. Accessed 08 Sept 2020
South African Government (2020) School calendar. https://www.gov.za/about-sa/school-calendar?gclid=CjwKCAjwtNf6BRAwEiwAkt6UQsw-NyWjoig6o4bQYlG0XtPIK4KsE6i4NKLutXEJzP-6pE3Iu0iavRoCWbcQAvD_BwE. Accessed 07 Sept 2020
Squazzoni F, Polhill JG, Edmonds B, Ahrweiler P, Antosz P, Scholz G, Chappin É, Borit M, Verhagen H, Giardini F, Gilbert N (2020) Computational Models that matter during a global pandemic outbreak: a call to action. J Artif Societ Soc Simul 23(2). https://doi.org/10.18564/jasss.4298
Sugishita Y, Kurita J, Sugawara T, Ohkusa Y (2020) Effects of voluntary event cancellation and school closure as countermeasures against COVID-19 outbreak in Japan. PLoS ONE 15(12):e0239455. https://doi.org/10.1371/journal.pone.0239455
te Vrugt M, Bickmann J, Wittkowski R (2020) Effects of social distancing and isolation on epidemic spreading modeled via dynamical density functional theory. Nat Commun 11:5576. https://doi.org/10.1038/s41467-020-19024-0
Tian H, Liu Y, Li Y, Wu CH, Chen B, Kraemer MUG, Li B, Cai J, Xu B, Yang Q, Wang B, Yang P, Cui Y, Song Y, Zheng P, Wang Q, Bjornstad ON, Yang R, Grenfell BT, Pybus OG, Dye C (2020) An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science. https://doi.org/10.1126/science.abb6105
Vasconcelos GL, Macêdo AMS, Ospina R, Almeida FAG, Duarte-Filho GC, Brum AA, Souza ICL (2020) Modelling fatality curves of COVID-19 and the effectiveness of intervention strategies. PeerJ 8:e9421. https://doi.org/10.7717/peerj.9421
Verity R, Okell LC, Dorigatti I, Winskill P, Whittaker C, Imai N, Cuomo-Dannenburg G, Thompson H, Walker PGT, Fu H, Dighe A, Griffin JT, Baguelin M, Bhatia S, Boonyasiri A, Cori A, Cucunubá Z, FitzJohn R, Gaythorpe K, Green W, Hamlet A, Hinsley W, Laydon D, Nedjati-Gilani G, Riley S, van Elsland S, Volz E, Wang H, Wang Y, Xi X, Donnelly CA, Ghani AC, Ferguson NM (2020) Estimates of the severity of coronavirus disease 2019: a model-based analysis. Lancet Infect Dis 20(6):669–677
VSP TU Berlin (2020) MATSim Episim development branch-snapshot commit: d796bc4bfdff27d9112f6de5932b7615c9a0420a 07.04.2020. https://github.com/matsim-org/matsim-episim/tree/d796bc4bfdff27d9112f6de5932b7615c9a0420a
Wikipedia (2020) COVID-19 pandemic in South Africa. https://en.wikipedia.org/w/index.php?title=COVID-19_pandemic_in_South_Africa&oldid=979348230. Accessed 20 Sept 2020
World Health Organisation (2019) Global tuberculosis report 2019. https://doi.org/10.14279/depositonce-9835
World Health Organisation (2020a) Coronavirus disease 2019 (COVID-19) Situation Report-56. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200316-sitrep-56-covid-19.pdf?sfvrsn=9fda7db2_6. Accessed 21 Sept 2020
World Health Organisation (2020b) Coronavirus disease 2019 (COVID-19) Situation Report-72. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200401-sitrep-72-covid-19.pdf?sfvrsn=3dd8971b_2. Accessed 19 Sept 2020
World Health Organisation (2020c) Coronavirus disease 2019 (COVID-19) Situation Report-77. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200406-sitrep-77-covid-19.pdf?sfvrsn=21d1e632_2. Accessed 19 Sept 2020
Wu J, Liang B, Chen C, Wang H, Fang Y, Shen S, Yang X, Wang B, Chen L, Chen Q, Wu Y, Liu J, Yang X, Li W, Zhu B, Zhou W, Wang H, Li S, Lu S, Liu D, Li H, Krawczyk A, Lu M, Yang D, Deng F, Dittmer U, Trilling M, Zheng X(2021) SARS-CoV-2 infection induces sustained humoral immune responses in convalescent patients following symptomatic COVID-19. Nat Commun 12:1813. https://doi.org/10.1038/s41467-021-22034-1
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kersting, M., Bossert, A., Sörensen, L. et al. Predicting effectiveness of countermeasures during the COVID-19 outbreak in South Africa using agent-based simulation. Humanit Soc Sci Commun 8, 174 (2021). https://doi.org/10.1057/s41599-021-00830-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-021-00830-w