Abstract
Research on international food prices or volatility transmission have concentrated on importing countries and have largely underestimated the importance of food insecurity or food poverty issues in food-exporting countries. This article identifies the causality between global and regional wheat pric in exporting countries and explores the determinants of price volatility pass-throughs using a Glosten, Jagannathan and Runkle generalised autoregressive conditional heteroskedasticity (GJR-GARCH) model with dynamic conditional correlation (DCC) specifications. Findings indicate that causal relationships between world and local prices are bi-directional and that self-sufficiency plays an important role in reducing international price volatility spillovers. Moreover, the consumption of substitute goods such as maize or rice functions as a shock absorber, alleviating volatility transmissions from the international market. Due to the COVID-19 crisis, food prices are more destabilised in many countries, along with various factors such as Russia’s and Kazakhstan’s export restrictions on grain commodites and international transport and supply chain disruptions. Based on the findings of our analysis, high self-sufficiency or autarky policies could help resilience to the shocks from these unexpected events against local retail markets in exporting countries such as the United States.
Similar content being viewed by others
Introduction
The 2008 food commodity boom triggered social unrest in low-income food-importing countries, driving 44 million people into poverty (World Bank, 2011) and making food insecurity issues an international priority in policy circles. This directed a considerable number of scientists to analyse the causes behind the price hikes and evaluate their impacts on socioeconomic or health outcomes in food-importing nations (e.g., Arndt et al., 2008; Ivanic and Martin, 2008; Tanaka et al., 2012). However, food poverty and food insecurity are also prevalent in food-exporting countries (Dowler and O’Connor, 2012). High Food Insecurity (HFI) increased in agricultural exporting nations during the economic recession, as delineated by extended reliance on food foundation charities in the UK, Australia and New Zealand (Lambie-Mumford and Dowler, 2014; Patterson et al., 2017; Santini and Cavicchi, 2014; Stuckler and Basu, 2013).
Canada, for instance, has one of the lowest poverty rates among seniors in the world greatly due to its income support programme for people aged 65 years old or older, yet has struggled with solving food insecurity problems for non-pensioners (Emery et al., 2013). According to the 2014 Canadian Community Health Survey, 12% of Canadian households were found to be food insecure. HFI significantly rose from 2008 to 2011 and continued to be persistently high (Tarasuk et al., 2016). For Canada as a whole, 8.9 and 6.9% of all adults either were concerned about food running out or had no food (and no money for more), respectively (Statistics Canada, 2014). Furthermore, 33.5% of households with a lone female parent were food insecure, of which 9.2% were categorised as ‘severe food insecurity’ households. Surprisingly, HFI affected one in six children in Canada, and food insecurity was more prevalent among households with children under the age of 18 years than households without children. These are just the numbers for Canada—food insecurity or food poverty prevails across nations with high production of agricultural commodities (e.g., Caraher and Coveney, 2016; Clendenning et al., 2016; Emery et al., 2013; Sonnino, 2016).
A country that is a net exporter of an agricultural commodity, that is, has self-sufficiency in the good, would be perceived as securing better food access by segregating local from global markets. The ability to segregate markets is one of the reasons why food-importing governments aim to enhance their self-sufficiency in food (Tanaka and Hosoe, 2011). However, the global wheat price seems to co-move with local prices to a certain extent for exporters. For instance, Fig. 1 exhibits Pearson correlations of 0.59, 0.57, 0.45 and 0.16 between international wheat prices and retail wheat flour prices in Canada, Kazakhstan, the UK, and the United States, respectively. As discussed above, the correlations between international price and local prices in exporting regions could have affected the food access of low-income households in the exporting regions.Footnote 1 Indeed, Götz et al. (2013) demonstrated price transmissions into exporting countries such as Russia, Ukraine, Germany and the United States during the 2008 food crisis.
The extant literature regarding price transmission of food commodities is vast, with around 500 recently published papers resulting from an AgEcon database search using the term ‘price transmission’ (Kouyaté and von Cramon-Taubadel, 2016). A considerable number of papers analysed price pass-throughs within developing countries (e.g., Abdulai, 2000; Baulch, 1997; Guo and Tanaka, 2019; Lutz et al., 2006; Myers, 2008; Rashid, 2004; Sayed and Auret, 2020; Van Campenhout, 2007). Fewer papers explore price correlations from global to local markets (e.g., Conforti, 2004; Minot, 2011; Mundlak and Larson, 1992; Quiroz and Soto, 1995; Robles et al., 2010), many of which apply error correction models to establish the international market connections. The only paper that investigated international price volatility transmissions in agricultural sectors was by Ceballos et al. (2017), in which a bivariate T-BEKK-GARCH model was used.
The majority of the past literature focuses on the price transmission between global markets and food-importing nations; hence, exporting countries have been ignored. These papers assume that domestic markets in exporting nations are resistant to external shocks. However, exporters, as stated above, also encountered food insecurity in recent years. Considering the facts of the international–local market connectivity and the food insecurity circumstances in exporting countries, it is crucial to estimate agricultural price linkages between the markets to discover potential determinants of the pass-throughs.
The effectiveness of food self-sufficiency has long been discussed as a counter policy measure (Bishwajit et al., 2013; Hamilton, 1918; Kako, 2009; Keynes, 1933). Following the 2008 food crisis, several national governing bodies in countries such as Senegal, India, the Philippines, Qatar, Bolivia and Russia indicated an interest in a self-sufficiency policy (Clapp, 2017). Despite the continuing popularity of these policies, few studies have quantified the effects of agricultural autarky policy other than Tanaka and Hosoe (2011), Tanaka (2018), and Guo and Tanaka (2019). These works analysed the impacts of variations in self-sufficiency in rice and wheat but used a computable general equilibrium model whose trustworthiness has sometimes been criticised due to the unreliability of point-estimated parameters. Therefore, papers that assess the effectiveness of self-sufficiency policy to international price transmissions are significantly deficient, particularly regarding a rigorous econometric framework.
This paper makes the following contributions to the literature. First, our paper is, to our knowledge, the first to tackle the international price transmission issue in an agricultural sector with a focus on the food security of exporting countries. Second, the method used in our analysis is a Glosten, Jagannathan and Runkle generalised autoregressive conditional heteroskedasticity model (GJR-GARCH) with dynamic conditional correlation (DCC) specifications. This model allows for the depiction of time-variant correlated relationships between markets; therefore, better capturing the linkage variations in prices between different markets than the conventional method (i.e., the GARCH-BEKK). Our method also permits factor identification with a focus on self-sufficiency policy of international wheat volatility transmissions with yearly outputs. The identification of underlying factors of international price transmissions has never been conducted in the previous research. Outcomes from empirical testing are extremely useful for policy-makers to prevent or alleviate price shocks from external markets. Finally, this work reveals the direction of causal relations and the transmission speed between world and local wheat prices in exporting countries. Uncovering the directions is particularly valuable because unidirectional effects seem to be discernible when poor harvests in countries with large agricultural production perturb global markets. However, the reverse causality from international to local markets in exporting countries would not be palpable.
We selected Canada, Kazakhstan, the UK, and the United States as the representatives of exporting countries, spanning from January 2006 to December 2017.Footnote 2 Our main findings can be summarised as follows. First, we identify two-way causality between international and exporting local markets of wheat using the conditional correlation function (CCF) approach. In particular, the one-month lagged price in the international wheat market is found to Granger-cause the current wheat price of the local market in exporting countries. Second, empirical results of the GARCH-DCC model reveal that close and time-varying relationships exist in connectivity pairs of price volatility between the global market and the individual wheat-exporting countries. Finally, the results of panel analysis indicate that the self-sufficiency rate in wheat significantly reduces the price volatility transmission between the global and local wheat markets in exporting countries. Specifically, we conclude that the higher the self-sufficiency rate, the lower the dynamic conditional correlations. Further, the consumption of maize or rice also can be considered as a potential factor that can diminish the impact of excess volatility from international markets to local markets.
The remainder of this paper is organised as follows. Section ‘Data and sample statistics’ offers a brief description of the data used in this paper. Section ‘Empirical method’ introduces the econometric methodology. Section ‘Empirical results and interpretation’ addresses the empirical findings and interprets the results. Section ‘Conclusion and policy implications’ makes the concluding remarks, discusses the policy implications and indicates future research topics.
Data and sample statistics
We use a two-step procedure to identify the factors behind volatility transmissions from international to local markets. For the first-step experiments, we estimate the dynamic conditional correlations between global and individual regional prices from January 2006 to December 2017. The IMF commodity prices, which provide monthly international prices for a variety of commodities, are used for the wheat price (U.S. No. 2 Hard Red Winter) in the world market. We selected Canada, Kazakhstan, the UK and the United States as the local market countries to achieve the goal of drawing policy implications concerning the effectiveness of the self-sufficiency strategy in exporting nations for data availability.Footnote 3 Retail wheat flour prices were used as the domestic price to probe into the degree of the international–local market linkages for consumers of wheat-related goods rather than wholesale wheat prices because consumers do not usually purchase and consume wheat itself. For local prices in Canada, Kazakhstan, the UK and the United States, we quoted price data of flour-based mixes from Statistics Canada, wheat (milling soft) from the UN FAO Global Information and Early Warning System (GIEWS), self-raising flour from the UK Office for National Statistics (ONS), and white flour from the U.S. Bureau of Labor Statistics. To remove the effects of differing local inflation, these data were converted into U.S. dollars using the Federal Reserve Economic Data (FRED) exchange rates. Considering the influence of seasonal fluctuations, it is reasonable to use seasonally adjusted price data. Thus, all our wheat price series were adjusted using the X-13-ARIMAFootnote 4 method. Moreover, for each data series, continuously compounded monthly returns are computed as ln(Xt/Xt−1) × 100, where Xt is the monthly value of wheat prices.
Figure 2 shows time-series plots of the price (international and domestic wheat prices in four exporting countries). As the figure shows, all the return series fluctuate between positive and negative regions and display different patterns across different countries. Regarding the international wheat price, Canada and the UK’s wheat prices showed a downward trend during the 2007–2008 global food crisis. In contrast, upward trends were apparent in Kazakhstan and the United States during the same period. Table 1 presents the descriptive statistics of all the price series. From Table 1, note that all mean values are positive (except for the UK), indicating the rise of wheat prices during our sample period on average. We can also observe that the standard deviation of the international wheat price has the highest value and that the UK’s standard deviations are relatively higher than those of the other countries. The results of a Jarque–Bera test indicate that the null hypothesis of normality is rejected at the 1% significance level for all price series, which indirectly supports the existence of an autoregressive conditional heteroskedasticity (ARCH) effect. The nonzero skewness and positive excess kurtosis of all price returns exhibit a leptokurtic distribution (i.e., fat tails). In addition, we checked the stationarity of each price index before estimating dynamic conditional correlations. The results of augmented Dickey–Fuller (ADF)Footnote 5 and Phillips and Perron (PP)Footnote 6 unit root tests suggest that none of the price series has unit roots in their first log-differenced forms. Lag length selection is based on Bayesian information criterion (BIC).Footnote 7 For robustness, we also employed the Kwiatkowski–Phillips–Schmidt–Shin (KPSS)Footnote 8 unit root test and find no unit roots in our samples. These results indicate that all the wheat price series are stationary and guarantee the suitability of the empirical model to investigate the price volatility transmissions.
In contrast, Van Dijk et al. (2005) suggest that causality in variance tests suffers from severe size distortions if structural breaks exist in the variances of time series data. Therefore, pre-testing for breaks in volatility provides an effective solution to overcome this problem. In this study, Bai and Perron’s (1998, 2003) structural break test, which allows for the simultaneous estimation of unknown multiple structural breaks, is used to examine the structural changes in mean and volatilityFootnote 9 of each wheat price series. The results of the structural break tests are shown in Table 2, which reveals that all sequential F statistics of 0 vs. 1 are found to be insignificant. This finding indicates that the null hypothesis of no structural change in the mean and variance for all variables cannot be rejected at the 1% level. Therefore, we conclude that a structural break does not exist in both mean and variance for each wheat price return during our sample periods.
For the second-step experiments, to tackle the data limitation problems, we consider the four selected countries as a whole by applying panel analysis to investigate the major factors underlying price volatility transmission in wheat-exporting countries. In our model, the dependent variable is the DCC between global and local wheat prices, which was estimated in the first step. Table 3 provides the definitions of the potential factor variables used, and Table 4 displays the summary statistics for the explanatory variables in the panel estimation. Regarding our assumption that the self-sufficiency rate (SSR) could be a significant factor in determining the DCC, we apply the yearly SSR of wheat in each exporting country. The SSR of wheat is defined as Production/(Production + Import − Export). Figure 3 shows the time-series SSR for each country. Interestingly, the SSR of exporting countries fluctuated dramatically during our sample period. Figure 3 and Table 4 reveal that the average value and standard deviation of Canada’s SSR are relatively higher than the other countries, while the UK’s SSR displays the lowest average value and standard deviation.
Moreover, considering the substitution effect between different food commodities, we also employ the consumption of maize (MAIZE) and consumption of rice (RICE) as independent variablesFootnote 10 for each country. Following Table 4, note that the consumption of maize and rice show different characteristics in wheat-exporting countries. For example, compared with other countries, the UK’s domestic consumption of maize and rice exhibit relatively high values. In comparison, the standard deviations of rice’s consumption in Kazakhstan are relatively higher than in other countries. This indicates that extreme change tends to occur more frequently for Kazakhstan. All yearly data of SSR and consumption are obtained from FAOSTATFootnote 11 from 2006 to 2017. Because the SSR data are available only at yearly frequencies, monthly DCC must be converted into yearly data by averaging monthly estimated series.Footnote 12
Empirical method
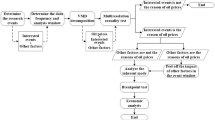
The procedure of econometric analysis in this paper contains three steps. First, a univariate GJR-GARCHFootnote 13 model was used to estimate the time-varying variances for each wheat price index. Second, using the standardised residuals from the first step, the CCF approach is applied to detect the lead–lag relationships between international and local wheat prices in four wheat-exporting countries. Then, Engle’s (2002) DCC model and Hafner and Franses’s (2009) generalised dynamic conditional correlation (G-DCC) are employed to estimate the volatility spillover between international and local prices. Finally, we use a panel model to examine how wheat self-sufficiency and other factors impact wheat price volatility transmission in wheat-exporting countries.
Let ri,t(i = 1, 2) be the wheat price index (i = 1: Global price, i = 2: Local price). An autoregression with one lag process for ri,t conditional on the information set ψt−1 can be expressed as follows:
where
In the mean equation (Eq. 1), εt is a random error term with conditional variance hi,t. In Eq. (2), ηi,t denotes independent and identically distributed (i.i.d.) standardised residuals. The variance equation (Eq. 3) specifies a GJR-GARCH process with an asymmetric term. In Eq. (3) the parameter κi is designed to capture a possible asymmetric return volatility relationship. Therefore, λi + κi implies the negative shocks, while λi represents the positive shocks. Using the estimated parameters obtained from the GJR-GARCH model, the standardised residuals \(\xi _{i,t}\left( {\xi _{i,t} = \varepsilon _{i,t}/\sqrt {h_{i,t}} } \right)\) can be computed. We take both the standardised residual series together and let the vector defined as \(\xi _t =\{ {\xi _{1,t},\,\xi _{2,t}}\}\). Then, following the Cheung and Ng (1996) procedure, the sample cross-correlation coefficient at lag m, that is, \(\widehat r_{\xi _1\xi _2}\left( m \right)\), can be calculated from the consistent estimates of the conditional mean for international and local wheat prices. This leaves us with
where \(\widehat c_{\xi _1\xi _2}\left( m \right)\) is the m-th lag sample cross-covariance given by:
where \(\widehat c_{\xi _1\xi _1}\left( 0 \right)\) and \(\widehat c_{\xi _2\xi _2}\left( 0 \right)\) are defined as sample variances of \(\widehat \xi _{1,t}\) and \(\widehat \xi _{2,t}\), respectively. T is the sample size. Causality in the mean of international and local wheat prices can be tested by examining \(\widehat r_{\xi _1\xi _2}\left( m \right)\), the univariate standardised residual CCF. Because \(\widehat \xi _{1,t}\) and \(\widehat \xi _{2,t}\) are independent, the existence of their first moments implies:
Where → shows convergence distribution. Equation (6) suggests that the univariate standardised residual CCF can be used to detect causal relations and identify patterns of causation in the first moment. This test statistic can be used to test the null hypothesis of no causality in the mean. To test a causal relationship at a specified lag m, we compare \(\sqrt T \widehat r_{\xi _1\xi _2}\left( m \right)\) with the standard normal distribution. If the test statistic is larger than the critical value of the normal distribution, the null hypothesis will be rejected. This test allows for more flexible specifications of the innovation and is suitable for analysing the lead–lag causal relationships between two variables. Based on the results of leads–lags estimated, we measured the volatility correlation pairs between global and local markets with the GJR-GARCH-DCC approach. Following Engle (2002), the time-varying conditional variance matrix is given by:
Ht is a 2 × 2 conditional variance–covariance matrix, and \(\Gamma _t = {\mathrm{diag}}\left[ {\sqrt {h_{1,t}} ,\,\sqrt {h_{2,t}} } \right]\) is the diagonal matrix containing the conditional standard deviations on the diagonal. Θt is the conditional correlation matrix, given by:
where \(P_t^ \ast = {\mathrm{diag}}\left[ {\sqrt {p_{11,t}} ,\,\sqrt {p_{22,t}} } \right]\) is a diagonal matrix with the square root of the diagonal element of Pt. Pt is a symmetric positive definite matrix given as follows:
where \(\overline P\) is the 2 × 2 unconditional matrix of the standardised residuals ξi,t. Equation (9) is the standard version of the DCC model, and the parameters α and β are nonnegative with a sum of less than unity. Furthermore, the trend of the generalised DCC (G-DCC) model can be specified as:
where A and B are 2 × 2 parameter matrices. Because the expectations of \(\overline P\) cannot be feasible, \(\overline P\) is replaced with a sample analogue, \(T^{ - 1}\mathop {\sum}\nolimits_{t = 1}^T {\xi _t\xi _t^\prime }\).
Further, Cappiello et al. (2006)Footnote 14 modified the correlation evolution by introducing the presence of asymmetries into the DCC model and constructed the asymmetric DCC (A-DCC) model, as in the following expression:
where \(\overline N\) represents the unconditional matrices of ψt = I[ξt < 0]⊗ξt(I[.] is an indicator function equal to 1 if ξt < 0 and 0 otherwise, while ‘⊗’ indicates the Hadamard product). In the estimation, \(\overline N\) is replaced with a sample analogue, \(T^{ - 1}\mathop {\sum}\nolimits_{t = 1}^T {\psi _t\psi _t^\prime }\). Then, the asymmetric generalised DCC (AG-DCC) model is the specification of the A-DCC model if the scalars are replaced by matrices that can be expressed by
Moreover, the correlation estimator q12 at time t can be defined as:
Finally, we estimate the parameters of the DCC, G-DCC, A-DCC and AG-DCC models by employing the Gaussian quasi-maximum likelihood estimation (QMLE)Footnote 15 with the BFGSFootnote 16 optimisation algorithm. The joint log-likelihood function L(ζ, ψ) can be written as the sum of a volatility part and a correlation part, expressed as:
where T refers to the number of observations and N denotes the number of equations. Moreover, the univariate GJR-GARCH parameters in Γt are denoted as ζ, where ζ = (π, ϕ, λ, γ, κ) and the dynamic correlation parameters in Θt are denoted as ψ, where ψ = (α, β). The time-varying conditional correlation coefficients are computed based on each GJR-GARCH-DCC model. To guarantee the robustness of our results, we estimated all models and selected the best model specification based on the BIC.
In the final step, we investigated the underlying factors that influence wheat price volatility transmission from international to local markets in wheat-exporting countries. Before performing the panel analysis, it was necessary to check for the existence of heteroskedasticity or serial correlation in the error term, as well as any cross-sectional dependence in the cross-country panel. In this paper, we use the modified Wald test (Wooldridge, 2010) to identify the heteroskedasticity. Moreover, Pesaran’s test (Pesaran, 2004) and Wooldridge’s test (Wooldridge, 2010) were employed to investigate contemporaneous correlation and autocorrelation, respectively. Based on the results of the pretest, we construct the following three panel regression models:
where DCC is the dynamic conditional correlations at a yearly frequency, μ is the constant term, SSR is the annualised self-sufficiency rates and vi,t is the heteroskedastic error term. MAIZE and RICE are the log-transformed values of maize and rice consumption, respectively. We used these three models to estimate the parameters δ1 to δ5, which measure the impact of the independent variables that influence price volatility transmission. In our paper, the feasible generalised least-squares (FGLS) regression is used as the benchmark model for our panel analysis. The advantage of the FGLS method is that it allows heteroskedasticity or autocorrelation in the error term. To guarantee the robustness, we verified our empirical results by using a Prais–Winsten regression with panel-corrected standard errors (PCSEs). Beck and Katz (1995) suggest that the PCSEs lead to a more accurate estimation than the FGLS model.
Empirical results and interpretation
Causality-in-mean and causality-in-variance tests
The analysis of price volatility transmission involves a two-step procedure. In the first step, based on the standardised residuals obtained from each GJR-GARCH model, we examined the causality and detected the lead–lag relationship between international and local prices. Lead–lag cross-correlation is the correlation between the past price returns of one market and the current price returns of the other market. Table 5 presents the significance of lags causality-in-mean for each country. Lags are measured in months, and the values of the CCF-based lags are reported from 1 to 12. Table 5 reveals a bi-directional causality-in-mean between the international price and the local price, indicating a close relationship between the global and local wheat markets. Furthermore, evidence that causality from international prices to local prices exists in lag 1 is identified in all countries, which implies that international price leads local price by approximately one month.
Therefore, we can conclude that in our sample period, the international price can be considered a leading indicator of local price in wheat-exporting countries. Based on these results, we lagged the local price of each wheat-exporting country by one period (one month) to capture the information from the global market to the local market with a one-month time lag. In addition, the results of causality-in-variance tests are reported in Table 6. The squared standardised residuals are used to test the null hypothesis that there is no causality-in-variance. The results are quite similar to Table 5, showing that significant bi-directional causality-in-variance exists between international and local wheat prices.
Estimation of the GJR-GARCH-DCC model
First, we used BIC to choose the most appropriate model for each country. Table 7 presents the results of the model selection. The standard DCC was selected to estimate the dynamic conditional correlations in Canada, Kazakhstan and the UK because the model has the lowest BIC values. In the case of the United States, although the DCC model demonstrated the lowest BIC value, the dynamic conditional correlation could not be calculated using DCC. Thus, the G-DCC model was selected as the best fit for the United States.
Second, Table 8 shows the parameter estimates for each GJR-GARCH-DCC model and their corresponding statistical significance values. It is evident that the ARCH term (λ), representing short-term persistence volatility, and the GARCH term (γ), representing long-term persistence volatility, are statistically significant for all countries except the United States. In addition, the relatively higher summation of ARCH and GARCH terms for Kazakhstan and the UK indicate a faster speed of the convergence of volatility to its long-run equilibrium in these two countries.
In contrast, it is also clear that the asymmetric term κ is statistically significant at the 1% level in the domestic wheat prices of Canada and the UK. These findings indicate that the asymmetric effect (negative shocks have a greater impact on future volatility levels than positive shocks of the same magnitude) can be identified in these two countries. Moreover, the coefficients of ARCH and GARCH terms for each country have positive values and satisfy the mean-reverting condition,Footnote 17 implying that our estimated models adequately fit the data. Similarly, the parameters of the DCC model and G-DCC model are estimated using QMLE. The estimation results of the two specifications of the DCC model for all countries are also given in Table 7. Specifically, in the standard DCC and G-DCC specifications, the necessary condition of α + β < 1 holds for every pair of global and local prices. These indicate that the dynamic conditional correlations are mean-reverting for global and local prices.
Finally, the conditional cross-correlation coefficient q12,t in Eq. (13) can be estimated by maximising the integrated log-likelihood functions in Eq. (14). Figure 4 plots the evolution of the estimated time-varying DCCs of each country. Interestingly, as Fig. 4 shows, some different types of correlation patterns emerge across different countries. Remarkably, the DCCs for the United States exhibit mainly high positive levels and a relatively large fluctuation when compared with the other countries. In our sample period, the DCCs of the United States showed two notable peak values in April 2012 and October 2013, then sharply declined at the end of 2013. In comparison, our findings provide concrete evidence that the DCCs fluctuate between both positive and negative values in Canada, Kazakhstan and the UK. Specifically, we can observe an increase in dynamic correlations in October 2008, with the peak value for Canada after the 2007–2008 food crisis. In contrast, the DCCs of Kazakhstan represent a downward trend during the food crisis, with the lowest levels of correlations in February 2009.
Table 9 provides descriptive statistics for the four countries’ correlations. It is evident that the means of the DCCs are positive in all exporting countries. This suggests that increases or declines in the volatility of international wheat prices can cause increases or declines in the volatility of domestic wheat prices in exporting countries. In particular, DCCs for the United States have the highest mean value (0.274) with a range of 0.046–0.996. Based on the FAOSTAT data, Canada, Kazakhstan, the UK and the United States are among the largest wheat exporters in the world. The phenomenon that the mean values of the DCCs for the large exporters are positive may arise because international price movements are relatively more immediately transmitted to local prices in those regions, or local prices in exporting countries may affect the international price. These results are consistent with the earlier evidence of bi-directional causality between international price and local price; meanwhile, the former lead the latter about one month in wheat-exporting countries. Finally, we note that the DCCs for the United States showed the strongest variability of all countries, with the highest standard deviation (0.154), whereas Kazakhstan’s DCCs are the most stable, with the lowest standard deviation (0.047).
Panel data analysis for the effect of self-sufficiency rate
To investigate further how wheat self-sufficiency and other factors impact the price volatility transmission, we proceed to estimate the panel model based on Eqs. (15–17). As mentioned in the third section of the method, in a first step, the existence of heteroskedasticity, serial correlation, and cross-sectional dependence need to be explored in the three models. The results of the pretests are shown in Table 10. First, the test statistics significantly reject the null hypothesis of no heteroskedasticity in all our models. This result suggests that the impact of heteroskedasticity must be included in our panel analysis.
Second, because the Wooldridge test cannot reject the null hypothesis of no autocorrelation in all three models, we perform the panel estimation without considering serial correlation in the error term. Third, Pesaran’s test suggests that the null hypothesis of cross-sectional independence can be rejected in model 1 and cannot be rejected in model 2 and model 3. Therefore, we can conclude that cross-sectional dependencies exist only in model 1.
Based on the results of the pretests, we applied the FGLS model as our base panel regression, and PCSEs were used to check the robustness of the results of estimation. Table 11 reports the results of model 1, which only includes the explanatory variable of SSR. First, it is interesting to find that the coefficients of SSR are negative and significant at the 1% level for two types of panel regressions. These results suggest that the SSR of wheat is a significant factor affecting the dynamic conditional correlations between global and local wheat prices in wheat-exporting countries. Moreover, the negative coefficient indicates that an increase in the SSR will decrease the DCCs. Hence, it is reasonable to expect that the higher the SSR, the lower the correlations. This suggests that increasing the SSR of wheat can be considered a key factor that helps to reduce volatility pass-throughs between global and local markets.
Table 12 represents the results of model 2, which chooses the SSR and MAIZE simultaneously as the explanatory variables. From Table 9, we can verify that both the coefficients of SSR and MAIZE are negative and significant for the two model specifications. Although the magnitude of MAIZE’s coefficient is much smaller than that of SSR, the consumption of maize also appears to play a role in the price volatility transmission of wheat between global and local markets. Also, the negative sign means that a higher level of maize consumption tends to decrease the level of volatility transmission. That is, wheat-exporting countries could ameliorate the degree of unpredictability in the global wheat market by increasing the consumption of maize.
Finally, Table 13 shows the results of model 3, including two explanatory variables of SSR and RICE. Similar to the finding for model 2, the coefficients of SSR and RICE proved to be significant and negative across two different estimation methods. These results show that there is a substitutive relationship between rice and wheat, implying an increase in the consumption of rice will reduce the level of price volatility transmission between the global and local wheat markets. The substitution effect between rice and wheat reveals almost equal magnitudes when comparing that between maize and wheat. Therefore, increasing rice’s consumption in wheat-exporting countries also could be considered a strategy to diminish the impact of excess volatility from global wheat markets.
Overall, our empirical results of panel analysis confirm that increasing the SSR of wheat can be a key factor that helps to reduce volatile pass-throughs between global and local markets in wheat-exporting countries. As the causality tests detect feedback effects between the international and local prices, a rise in SSR could be considered as an effective policy for reducing exposure to volatility from international to local prices in wheat-exporting countries, and vice versa. As mentioned, Tanaka (2018) proved the utility of Egypt’s autarky policy in measuring the stabilisation of the domestic wheat price. Tanaka applied a different method to an importing country, but his conclusions are consistent with our outcome, namely a higher SSR assists in mitigating price volatility transmissions. Furthermore, our results indicate that a substitution effect does exist between wheat and maize, or between wheat and rice in wheat-exporting countries. A potential explanation for this finding might be that substituting the consumption of a good that becomes more expensive with one that is relatively cheap could buffer price shocks transmitted from external markets, causing demand for the expensive product to fall. For instance, the high price of wheat induces substitution behaviour between cereal goods such as maize and rice, which may partly reduce volatility transmission.
Conclusion and policy implications
This paper explored the Granger causality between global and local wheat markets in exporting countries, uncovering the underlying factors behind price volatility pass-throughs using GJR-GARCH with DCC specifications and econometric panel models from January 2006 to December 2017. Our main findings are as follows. First, we found bi-directional relationships between international and domestic wheat markets in respective exporting countries. The one-month lagged global market price, in particular, is found to influence regional wheat prices at the current point in time. Second, we uncovered the close and time-variant connectivity pairs between international and wheat-exporting markets. Finally, higher self-sufficiency in wheat could weaken the price associations between international and local markets. Moreover, it is found that the consumption of a substitute good, such as rice or corn, can assuage volatility transmissions from the global market. These outcomes imply that policy-makers in cereal exporting regions should attend to shielding local markets from global food market turbulence for consumers who have risk-averse preferences.
Notably, although a higher SSR leads to a lower DCC (a weaker international connection), boosting agricultural production in exporting regions to alleviate price co-movements induces a decrease in production in importing regions under the assumption that the global demand for wheat is constant. Guo and Tanaka (2019) concluded that self-sufficiency contributes to market steadiness in importing regions. Therefore, the balance of production between exporting and importing regions needs to be considered to minimise or lessen unpredictable destabilisation at the global level. The coefficients for self-sufficiency in wheat estimated by Guo and Tanaka (2019) are generally higher than those in the present paper, suggesting that raising self-sufficiency in wheat production by 1% could stabilise domestic price movements more effectively in importing countries than exporting countries.
A policy recommendation derived from the main findings is that wheat-exporting governments could raise their own self-sufficiency in wheat to insulate domestic markets from tempestuous overseas markets and better protect indigenous low-income people who are in food insecurity. This implies that higher self-sufficiency enhances national food security for food availability and also for food access in emergent situations (e.g., the COVID-19 crisis) where the international transport system is paralysed. We also find that local markets in exporting countries affect global markets (bi-directionality), which suggests that steadier regional markets lead to steadier international markets, which is beneficial for importing regions.
The food supply shortage has become a serious issue due to the COVID-19 pandemic in the US, which is expected to reach 100,000 coronavirus deaths imminently (Stanglin et al., 2020). Although the meat supply chain disruption is of particular concern due to working conditions in meat processing facilities, another genuine issue in the food supply chain is wheat flour, since more people are baking at home during lockdowns (Wolf, 2020). To make matters worse, in response to the pandemic, Russia and Kazakhstan have imposed export bans or quotas on grain commodities (Reinhart and Subbaraman, 2020). Guo and Tanaka (2019) analysed the link between international wheat price transmissions and self-sufficiency in wheat importing countries. They found that high self-sufficiency in wheat stabilises domestic retail wheat flour prices, which is a similar conclusion to the one we drew in the present experiments. Based on the evidence presented from Guo and Tanaka (2019) and this study, high self-sufficiency or autarky is effective in calming retail wheat flour prices in both wheat exporting and importing countries. The autarky policy measure could function as a cushion against international price fluctuations provoked by Russia’s and Kazakhstan’s export restrictions, and may help the resilience of the disconnected food supply chain.
Though the focus of our analysis was on retail prices, one of the major determinants for domestic prices (e.g., retail, wholesale and farm-gate prices) would be agricultural crop harvests. Since the domestic markets are closely linked with each other (e.g., Haile et al., 2017), the stabilisation of agricultural production is likely to calm those markets as well. Governmental investments in the development of such scientific fields as meteorology, geography and space technology can improve weather or climatic forecasting information for farmers. These improvements will be useful to stabilise production and, therefore, various types of markets, including both domestic markets (retail, wholesale, and producer prices) and international markets (export and import prices).
Cost-effectiveness is a key criterion for policy implementation. Even though we verified the utility of the food autarky measure for reducing transmitted volatilities, the direct and indirect costs of improving self-sufficiency still need to be evaluated. Rises in import tariffs or subsidies to farmers are common approaches to the enhancement of a self-sufficiency rate. These methods, however, impose tremendous economic burdens on society, entailing subsidy payments and inefficient resource allocation in exchange for curtailing transmissions. One method of actualising the strategy would be the budget-neutral approach Tanaka (2018) proposed, in which additional import tariff revenue is used for a subsidy to farming operations. This method theoretically bears no additional financial burden to accomplish higher self-sufficiency because it equates tariff revenue with an expense on farming. Hence, governments, at least, do not harm their fiscal conditions.
In contrast to the considerable economic burden of subsidy or tariff, food consumption diversification may be much more efficient in implementation costs once people’s food consumption patterns are altered. Though it would not be straightforward to adjust nationwide food preferences or eating habits, Japan is a good example of a country that has succeeded in diversifying food consumption patterns after World War II, accepting both food and non-food culture from the West. Japanese citizens leaned heavily toward traditional Japanese meals based mainly on rice before the war but eat a wide variety of international foods today. If nationals unevenly consume grains or food commodities, there could be room to expedite volatility cushions between the boundaries.
We obtained the yearly DCCs between international and domestic wheat prices by averaging the monthly DCC. Some previous studies have suggested that the dynamic conditional correlation-mixed data sampling (DCC-MIDAS) model is useful for converting short-term DCC to long-term DCC. It would be interesting to compare our findings with the empirical results derived from different models. We leave this exercise for a future research project.
Data availability
The datasets generated and analysed in this study are available in the Global Information and Early Warning System repository: http://www.fao.org/giews/en/; and Bureau of Labor Statistics: https://data.bls.gov/pdq/SurveyOutputServlet; Statistics Canada: https://www.statista.com/statistics/443670/average-retail-price-for-flour-in-canada/; Office for National Statistics: https://www.ons.gov.uk/economy/inflationandpriceindices/datasets/consumerpriceindicescpiandretailpricesindexrpiitemindicesandpricequotes; FRED: https://fred.stlouisfed.org/. The data that support the findings of this study can be obtained from the corresponding author upon request.
Notes
The four countries are the regions used in the experiments of this article. See the Data section for the criteria for country selection.
The criteria for country selection are expressed in the Data section.
The four countries alone are available for monthly wheat flour price covering the time period. There are two reasons for including Kazakhstan despite GDP per capita for Kazakhstan being only one-fifth that of the other developed nations (i.e., the UK, the United States and Canada). First, wheat is a necessary good, meaning that wheat consumption does not rely on income level. Second, sample size is extremely limited without the region in our panel analysis.
X-13-ARIMA is the U.S. Census Bureau’s software package for seasonal adjustment.
Dickey and Fuller (1979).
Phillips and Perron (1988). The null hypothesis of the ADF and PP tests is that the series contains a unit root.
BIC is calculated as BIC = −2LL + Nln(T), where LL is the maximum log-likelihood and N is the number of parameters in the specification.
Kwiatkowski et al. (1992). The null hypothesis of the KPSS test is that the data series is stationary.
Following Tamakoshi and Hamori (2014), we first apply the AR (1) model to examine the structural breaks in the mean. Then, the residuals can be obtained from this estimation process. Second, we identify the structural breaks in the variance through the following equation: \(\sqrt {\pi /2} \left| {\widehat \varepsilon _t} \right| = c + \mu _t\), where the transformed residual on the left-hand side indicates the unbiased estimator of the standard deviation of εt from the AR (1) model.
MAIZE and RICE are the log-transformed values of maize and rice’s consumption, respectively.
David and Amir (2017) use the same method to obtain yearly DCC by taking the average of the monthly DCC.
See Glosten et al. (1993) for details of the GJR-GARCH model. The multivariate GARCH model has been found to be useful in examining volatility spillover effects in time series data.
See Bollerslev and Wooldridge (1992).
BFGS (Broyden, Fletcher, Goldfarb and Shanno) is a quasi-Newton optimisation method that uses information about the gradient of the function at the current point to calculate the best direction to look to find a better point. All estimation is done using RATS Pro 10.0.
The coefficients of ARCH, GARCH and asymmetric terms should satisfy \(\gamma + \lambda + \frac{1}{2}\kappa\, < \,1\).
References
Abdulai A (2000) Spatial price transmission and asymmetry in the Ghanaian maize market. J Dev Econ 63(2):327–349
Arndt C, Benfica R, Maximiano N, Nucifora AMD, Thurlow T (2008) Higher fuel and food prices: Impacts and responses for Mozambique. Agr Econ 39:497–511
Bai J, Perron P (1998) Estimating and testing linear models with multiple structural changes. Econometrica 66:47–78
Bai J, Perron P (2003) Computation and analysis of multiple structural change models. J Appl Econom 18:1–22
Baulch B (1997) Transfer costs, spatial arbitrage and testing for food market integration. Am J Agr Econ 79:477–487
Beck N, Katz JN (1995) What to do (and not to do) with time series cross-section data. Am Polit Sci Rev 89(3):634–647
Bishwajit G, Sarker S, Kpoghomou M, Gao H, Jun L, Yin D (2013) Self-sufficiency in rice and food security: a South Asian perspective. Agr Food Secur 2(10):10
Bollerslev T, Wooldridge JM (1992) Quasi-maximum likelihood estimation and inference in dynamic models with time-varying covariances. Economet Rev 11(2):143–172
Cappiello L, Engle RF, Sheppard K (2006) Asymmetric dynamics in the correlations of global equity and bond returns. J Financ Economet 4(4):537–572
Caraher M, Coveney J (2016) Food poverty and insecurity: The poor in a world of global austerity. In: Caraher M, Coveney J (eds) Food poverty and insecurity: International food inequalities. Springer, Cham, pp 1–9
Ceballos F, Hernandez MA, Minot N, Robles M (2017) Grain price and volatility transmission from international to domestic markets in developing countries. World Dev 94:305–320
Cheung Y-W, Ng LK (1996) A causality-in-variance test and its application to financial market prices. J Econometr 72:33–48
Clapp J (2017) Food self-sufficiency: making sense of it, and when it makes sense. Food Policy 66:88–96
Clendenning J, Dressler WH, Richards C (2016) Food justice or food sovereignty? Understanding the rise of urban food movements in the USA. Agr Hum Values 33:165–177
Conforti P (2004) Price transmission in selected agricultural markets. Commodity and Trade Policy Research Working Paper No 7. Food and Agriculture Organization, Rome
David LB, Amir R (2017) Stocks and bonds during the gold standard. Econ Lett 159:119–122
Dickey DA, Fuller WA (1979) Distribution of the estimators for autoregressive time series with a unit root. J Am Stat Assoc 74(36):427–431
Dowler EA, O’Connor D (2012) Rights-based approaches to addressing food poverty and food insecurity in Ireland and UK. Soc Sci Med 74:44–51
Emery JCH, Fleisch VC, McIntyre L (2013) How a guaranteed annual income could put food banks out of business. SSP Research Papers 6(37), University of Calgary
Engle FR (2002) Dynamic conditional correlation: a simple class of multivariate GARCH models. J Bus Econ Stat 20(3):339–350
Glosten LR, Jagannathan R, Runkle DE (1993) On the relation between the expected value and the volatility of the nominal excess return on stocks. J Finance 48:1779–1801. https://doi.org/10.1111/j.1540-6261.1993.tb05128.x
Götz L, Glauben T, Brümmer B (2013) Wheat export restrictions and domestic market effects in Russia and Ukraine during the food crisis. Food Policy 38:214–226
Guo J, Tanaka T (2019) Determinants of international price volatility transmissions: the role of wheat self-sufficiency in developing countries. Pal Commun 5(124):1–13. https://doi.org/10.1057/s41599-019-0338-2
Hafner C, Franses P (2009) A generalised dynamic conditional correlation model: simulation and application to many assets. Economet Rev 28(6):612–631
Haile MG, Kalkuhl M, Algieri B, Gebreselassie S (2017) Price shock transmission: evidence from the wheat-bread market value chain in Ethiopia. Agr Econ 48:769–780
Hamilton WH (1918) The requisites of a national food policy. J Polit Econ 26(6):612–637. https://doi.org/10.1086/253112
Hou Y, Li S (2016) Information transmission between US and China index futures markets: an asymmetric DCC GARCH approach. Econ Model 52:884–897
Ivanic M, Martin W (2008) Implications of higher global food prices for poverty in low-income countries. Agr Econ 39:405–416
Kako T (2009) Sharp decline in the food self–sufficiency ratio in Japan and its future prospects. Paper presented at the International Association of Agricultural Economists Conference, Beijing, China, pp 16–22
Keynes JM (1933) National self-sufficiency. Yale Rev 22(4):755–769
Kouyaté C, von Cramon-Taubadel S (2016) Distance and border effects on price transmission: a meta-analysis. J Agr Econ 67(2):255–271
Kwiatkowski D, Phillips PC, Schmidt P, Shin Y (1992) Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J Econometr 54(1):159–178
Lambie-Mumford H, Dowler E (2014) Rising use of ‘food aid’ in the United Kingdom. Brit Food J 116:1418–1425
Lutz C, Kuiper WE, van Tilburg A (2006) Maize market liberalisation in Benin: a case of hysteresis. J Afr Econ 16(1):102–133
Minot N (2011) Transmission of world food price changes to markets in Sub-Saharan Africa, IFPRI Disc Paper 1059, Washington, DC
Mundlak Y, Larson D (1992) On the transmission of world agricultural prices. World Bank Econ Rev 6(3):399–422
Myers R (2008) Evaluating the efficiency of inter-regional trade and storage in Malawi maize markets. Report for the World Bank, Michigan State University, East Lansing, Michigan
Newey WK, West KD (1994) Automatic lag selection in covariance matrix estimation. Rev Econ Stud 61:631–653
Patterson PB, McIntyre L, Anderson LC, Mah CL (2017) Political rhetoric from Canada can inform healthy public policy argumentation. Health Promot Int 32:871–880
Pesaran MH (2004) General diagnostic tests for cross section dependence in panels. https://doi.org/10.17863/CAM.5113
Phillips PC, Perron P (1988) Testing for a unit root in time series regression. Biometrika 75(2):335–346
Quiroz J, Soto R (1995) International price signals in agricultural prices: do governments care? Documento de Investigacion 88, ILADES Postgraduate Economics Program, Universidad Alberto Hurtado/Georgetown University, Santiago, Chile
Rashid S (2004) Spatial integration of maize markets in post-liberalised Uganda. J Afr Econ 13(1):102–133
Reinhart CM, Subbaraman R (2020) How can we prevent a COVID-19 food crisis? World Economic Forum. https://www.weforum.org/agenda/2020/05/preventing-a-covid-19-food-crisis/. Accessed 22 May 2020
Robles L, Torero M, Cuesta J (2010) Understanding the impact of high food prices in Latin America. Economia 10(2):117–164
Santini C, Cavicchi A (2014) The adaptive change of the Italian Food Bank foundation: a case study. Brit Food J 116:1446–1459
Sayed A, Auret C (2020) Volatility transmission in the South African white maize futures market. Eurasian Econ Rev 10:71–88
Sonnino R (2016) The new geography of food security: exploring the potential of urban food strategies. Geogr J 182(2):190–200
Stanglin D, Hauck G, Tucker H (2020) Coronavirus live updates: New York opens further for Memorial Day travel; sick hairstylist may have exposed 91; US nears 100,000 deaths. USA TODAY 23rd May. https://www.usatoday.com/story/news/health/2020/05/23/coronavirus-news-hertz-files-bankruptcy-us-nears-100000-deaths/5243655002/. Accessed 26 May 2020
Statistics Canada (2014) Canadian Community Health Survey. https://www.canada.ca/en/health-canada/services/food-nutrition/food-nutrition-surveillance/health-nutrition-surveys/canadian-community-health-survey-cchs.html. Accessed 20 Jan 2019
Stuckler D, Basu S (2013) The body economic: why austerity kills. HarperCollins Publishers, New York
Tamakoshi G, Hamori S (2013) An asymmetric dynamic conditional correlation analysis of linkages of European financial institutions during the Greek sovereign debt crisis. Eur J Financ 19(10):939–950
Tamakoshi G, Hamori S (2014) Causality-in-variance and causality-in-mean between the Greek sovereign bond yields and Southern European banking sector equity returns. J Econ Finan 38(4):627–642
Tanaka T (2018) Agricultural self–sufficiency and market stability: a revenue-neutral approach to wheat sector in Egypt. J Food Sec 6(1):31–41
Tanaka T, Hosoe N (2011) Does agricultural trade liberalization increase risks of supply-side uncertainty? Effects of productivity shocks and export restrictions on welfare and food supply in Japan. Food Policy 36(3):368–377
Tanaka T, Hosoe N, Qiu H (2012) Risk assessment of food supply: a computable general equilibrium approach. Cambridge Scholars Publications
Tarasuk V, Mitchell A, Dachner N (2016) Household food insecurity in Canada, 2014. Research to identify policy options to reduce food insecurity (PROOF) Toronto. http://nccdh.ca/resources/entry/proof-research-to-identify-policy-options-to-reduce-food-insecurity. Accessed 31 Jan 2019
Van Campenhout B (2007) Modelling trends in food market integration: method and an application to Tanzanian maize markets. Food Policy 32:112–127
Van Dijk D, Osborn DR, Sensier M (2005) Testing for causality in variance in the presence of breaks. Econ Lett 89(2):193–199
Wooldridge JM (2010) Econometric analysis of cross section and panel data. MIT Press, Cambridge
World Bank (2011) Food price hike drives 44 million people into poverty. No: 2011/333/PREM
Wolf ZB (2020) Forget pork. Here’s why you can’t buy flour. CNN. https://edition.cnn.com/2020/05/02/politics/what-matters-may-1/index.html. Accessed 22 May 2020
Acknowledgements
The research is in part supported by a Grant-in-Aid from the Japan Society for the Promotion of Science (Grant Number (A)18K14533).
Author information
Authors and Affiliations
Contributions
TT and JG designed the research. TT conceived the study with inspiration from his previous studies. TT also performed the background of the paper and discussed the policy implications of the empirical results. JG constructed the econometric model and edited the programme code for analysing. JG also analysed and interpreted the data regarding the common determinants of wheat price volatility transmission from international to local markets in wheat-importing countries. The authors equally contributed to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tanaka, T., Guo, J. How does the self-sufficiency rate affect international price volatility transmissions in the wheat sector? Evidence from wheat-exporting countries. Humanit Soc Sci Commun 7, 26 (2020). https://doi.org/10.1057/s41599-020-0510-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-020-0510-8