Abstract
Fractal patterns that repeat at varying size scales comprise natural environments and are also present in artistic works deemed to be highly aesthetic. Observers’ aesthetic preferences vary in relation to fractal complexity. Previous work demonstrated that fractal preference consistently peaks at low-to-moderate complexity for patterns that repeat in a statistical manner across scale, whereas preference for exact repetition fractals peaks at a higher complexity due to the presence of order introduced by symmetry and exact recursion of features. However, these highly consistent preference trends have been demonstrated only in adult populations, and the extent to which exposure, development, or individual differences in perceptual strategies may impact preference has not yet been established. Here, we show differences in preference between fractal-type, but no differences between child and adult preferences, and no relationship between systemizing tendencies (demonstrated by the Systemizing Quotient and Ponzo task) and complexity preferences, further supporting the universality of fractal preference. Consistent preferences across development point toward shared general aesthetic experience of these complexities arising from a fluency of fractal processing established relatively early in development. This in part determines how humans experience natural patterns and interact with natural and built environments.
Similar content being viewed by others
Introduction
Fractal aesthetics of nature and art
The aesthetics of nature are influenced by fractal complexity (Mandelbrot, 1982; Taylor et al., 1999). Recursion (the number of pattern repetitions across scales) and fractal dimension D (the rate of pattern shrinkage between repetitions) set the relative contributions of coarse-to-fine structure for the overall fractal pattern, thus determining its visual complexity (Boselie and Leeuwenburg, 1985; Eysenck, 1942). The character of the pattern repetition (“statistical” versus “exact”) further influences perceived complexity, as does the degree of the pattern’s spatial symmetry (the presence of invariant geometric transformations such as reflections and rotations). The dependence of aesthetic preference on complexity has been established for both statistical (Fig. 1A, B) (Hagerhall et al., 2015; Taylor et al., 2011 as a review) and exact (Bies et al., 2016a) (Fig. 1C, D) repetitions of fractal patterns.
Statistical fractals are prevalent in natural scenery (e.g. trees, mountains, clouds, rivers) (Mandelbrot, 1982) and preference for them has been shown to peak at low–moderate complexity (approximately D = 1.3–1.4 on a scale between D = 1.1 and 1.9) and steadily decrease with additional complexity (Taylor et al., 2011; Taylor and Sprott, 2008). The paintings of Jackson Pollock reflect these findings in that the artist’s layering of paint establishes a fractal structure (Taylor et al., 1999, 2007), and preference for cropped black and white versions of these works peaks at mid-complexity (Spehar et al., 2003). Moreover, traditional and contemporary art from diverse cultures contain fractal properties (Graham and Field, 2008; Graham and Redies, 2010), suggesting a universal preference for patterns of low-moderate perceived complexity with subgroups of preference for different D-values (Bies et al., 2016a; Spehar et al., 2016; Street et al., 2016; Pyankova et al., 2019). Notably, an analysis of famous artworks indicates preference for lower D-values with age-related conditions including Alzheimer’s and Parkinson’s diseases (Forsythe et al., 2017). Contrasting the overall preference for low–mid-complexity statistical fractals, increased tolerance of fractal complexity elicited by the symmetries and precise repetition of exact fractals generates preference for higher D-values (Bies et al., 2016a).
Previous research indicates that heightened preference and psychophysical performance are associated with common low–moderate natural patterns (Spehar et al., 2003; Sprott, 1993; Taylor et al., 2005) reminiscent of savanna scenes (Falk and Balling, 2010). Fractal Fluency theory suggests the visual system is tuned, either through repeated exposure or evolutionary mechanisms, to better process complexities most encountered in the surrounding natural environment (Falk and Balling, 2010; Taylor et al., 2018, Hagerhall et al., 2008) and it is this efficiency that leads to fractal preference. In contrast, unnatural Euclidean patterns and environments have been linked to increased strain on the visual system producing headaches (Penacchio and Wilkins, 2015) and lower aesthetic preference (Taylor, 1998). Additional studies recommend installations of naturalistic low–moderate D fractals to reduce occupants’ stress levels in built environments (Hagerhall et al., 2015; Taylor et al., 2005). Combined, the above studies highlight the importance of understanding fractal fluency for optimizing our visual environments across all age groups.
Impact of individual differences and age
Perceptual integration of contextual information varies across development and can impact susceptibility to visual illusions (Hadad, 2018). Differences in general perceptual strategies or age-related handling of contextual information may alter the perception of patterns, either by influencing the degree to which local compared to global features of patterns are processed (Billington et al., 2008), or the degree of contextual experience and familiarity an individual has with different pattern complexities (Roder et al., 2000). A local bias reflecting a predilection for small-scale, detailed structure might guide preference for more complex patterns, whereas a global bias may produce a preference for larger scale structure which is more discernable in patterns with low–mid range complexity. Likewise, the so-called Goldilocks effect may account for changes in preference (Kidd et al., 2012). Beginning in infancy, an individual incrementally acquires knowledge of more complicated and novel aspects of the surrounding environment, thus gradually learning how to comprehend more complex patterns and concepts. After decades of exposure to natural patterns, this theory suggests that understanding of visual patterns will have deepened compared to that of early childhood, shifting preference towards the most complex patterns an individual can process (Roder et al., 2000; Kidd et al., 2012). To define the impact of these factors on fractal aesthetics, it is vital to consider a wider sample of participant ages (children as well as adults) and account for the impact of individual perceptual biases (determined by assessing Systemizing Quotient (SQ) scores (Baron-Cohen et al., 2001) and susceptibility to global context effects in the Ponzo Task (Hadad, 2018), see Fig. 2 (Walter et al., 2008)). Overall, if robust trends found in adults are present in children (especially since few tasks result in steady performance across a wide age gap (Stevenson, 1972)), it would support the conclusion that these preferences are likely resulting from a common visual tuning established earlier in life. This would be of notable interest in part because early life is often largely spent in Euclidian shelters, which are inherently less complex than nature’s fractal environments (Clements, 2004).
Methods
Participants
To examine the extent to which preference for complexity in fractal patterns may change across development, 178 participants comprised of students from the University of Oregon and guests of the Eugene Science Center were recruited for the current study. Eighty-two of the participants were adults recruited through the University of Oregon’s SONA participant pool system (75 females, age ranging between 18 and 40 years, mean age 20 years old), and the other 96 participants were children between the ages of 3 and 10 years old (43 females, mean age 6.5 years old) who visited the Eugene Science Center. We sampled roughly equal numbers of male and female children from each age range (3–4, 5–6, 7–8, and 9–10 years old), and at least 20 children were recruited for each age group. Adult participants received class credit for their participation in the current study, whereas child participants received either stamps or stickers for their time. Informed consent was acquired following protocol approved by the Institutional Review Board at the University of Oregon. Consent for child participants was obtained through a consent form signed by the child’s parent or legal guardian in addition to verbal consent from the child, whereas adult participants completed a single consent form.
Visual displays
Stimuli were displayed on a Microsoft Surface-Pro touch screen electronic tablet which was placed on a table in front of participants and propped up at an angle within reaching distance ~25 cm from the participants. Questionnaires given to adult participants were presented on an additional hand-held touch screen electronic tablet (iPad) while child participants completed perceptual tasks.
Stimuli and tasks
Fractal stimuli and preference task
Fractals are complex because they possess structural similarity across scales. Exact fractals are built by precisely repeating a pattern at different magnifications. In contrast, statistical fractals are built by introducing randomness into their construction which disrupts the precise repetition such that only the pattern’s statistical qualities repeat across scales. Two sets of statistical (Fig. 1A, B) and exact (Fig. 1C, D) fractals were used. Exact midpoint displacement fractals (Fig. 1C) were generated according to an algorithm described by Fournier (Fournier et al., 1982; Bies et al., 2016a, b). Exact H-tree fractals (Fig. 1D) repeat an H-pattern at increasingly fine size scales. The statistical fractals were created using a variant of the midpoint displacement method (Fournier et al., 1982; Bies et al., 2016b). Two different sets of statistical fractals of varying complexity were generated from two different seeds. The complexity of a fractal pattern is determined by the rate at which the exact or statistical pattern deceases in size with each iteration of the repetition process (Mandelbrot, 1982; Taylor et al., 2011). The rate is set by the pattern’s fractal dimension or “D”, which ranges from 1.1 to 1.9 (1.1, 1.3, 1.5, 1.7, and 1.9) in our stimulus sets (see Fig. 1 for an example stimulus set).
Participants viewed either exact or statistical fractal patterns presented in two randomized blocks, with each block consisting of only one fractal pattern stimulus set (exact midpoint displacement or H-tree; statistical midpoint displacement seed #1 or #2). Each stimulus set consisted of five unique patterns of different complexity or D-value (e.g., Fig. 1A). A two-alternative forced choice task was used, resulting in 10 trials (10 fractal pairs) per block. All fractal pattern complexities were paired once within a block, resulting in each complexity being presented four times within a block. Stimulus pairing and presentation order were random with the constraints that (1) all fractal pattern complexities were paired only once, (2) half of the 10 trials consisted of patterns with higher complexity on the right side and half on the left side, and (3) each pattern of a given complexity appeared on both left and right sides. Between trials, a smiley face icon served as a fixation point that had to be touched to produce the next pair of images.
Ponzo stimuli and task
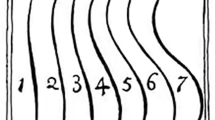
Following the fractal preference task, participants completed 10 trials of a Ponzo task. In this task participants were presented with vertical lines angled towards the centre of the screen and two horizontal lines placed between the slanted vertical lines in the upper and lower halves of the screen (see Fig. 2 for an example stimulus). The length of each horizontal line was randomly generated such that it did or did not intersect the vertical lines, and each horizontal line was larger or smaller than the other. Participants adjusted the lower line to match the length of the upper line. Accuracy and directional bias of adjustments were measured as a difference in pixels between the upper and lower-line segments and whether these adjustments overestimated or underestimated the target length.
Questionnaire
After the fractal preference and Ponzo tasks, all adult participants completed the SQ questionnaire. The quotient was determined based upon participants’ ratings of the degree to which the statements were like or unlike themselves, which provided a score of overall systemizing and emotional tendencies (Baron-Cohen et al., 2001). A children’s SQ (Auyeung et al., 2009) was completed by parents or guardians on a separate electronic tablet while child participants completed the fractal preference and Ponzo tasks.
Procedure and design
Participants were presented with either exact or statistical fractals and completed three practice trials prior to two blocks of two alternative forced choice decisions. The practice stimuli were different than the experimental stimuli. Participants were instructed to touch the fixation image to initiate the presentation of pairs of fractal patterns. Image pairs remained on the screen until participants made a selection by physically touching the image they preferred (“liked best”). Upon completion of the fractal preference task, participants were presented with a Ponzo illusion task. In this task participants were instructed to drag their finger along a line segment to adjust its length until it matched the length of a parallel line segment positioned above it. Adult participants completed an online questionnaire that contained demographic questions as well as the SQ. Parents or guardians of child participants completed a children’s version of this questionnaire while the child completed the other tasks. Throughout the experiment, researchers sat next to child participants and encouraged children to maintain focus on the tasks. At the conclusion of the experiment all participants were compensated and debriefed according to the protocols approved by the Institutional Board at the University of Oregon.
Results
Data from 82 adult participants (between 18 and 33 years old) and 96 child participants (between 3 and 10 years old) were retained from the 83 adults and 118 children who participated in the experiment. Data were excluded due to failure to (a) complete the study, (b) comprehend instructions, or (c) maintain focus during the experiment.
Fractal preference task
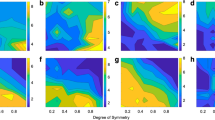
A three-way mixed 5 × 2 × 2 ANOVA (D-value (1.1, 1.3, 1.5, 1.7, 1.9) × age (3–10-year-old children, and 18 years and older adults) × Fractal-Type (statistical, exact)) was performed using IBM SPSS Statistics for Macintosh, Version 25.0) on preference data for the fractal patterns (recorded as proportion of trials a given pattern was chosen in a two-alternative forced choice pairing), with D-value as a within-subjects variable and Fractal-Type and Age as between-subjects variables (see Table 1). Mauchly’s test indicated a violation of the assumption of sphericity for D-value (χ2(9) = 292.18, p < 0.001**). Therefore, degrees of freedom were corrected using Greenhouse–Geisser estimates of sphericity (ε = 0.521). As indicated by a single asterisk for statistical significance of p < 0.05 and double asterisk for significance of p < 0.001, only a significant main effect of D-value emerged in the analysis (F(2.08, 362.67) = 3.79, p = 0.02*, 95% CI [0, 0.06], ηp2 = 0.02), [Age (F(1, 174) = 0.001, p = 0.97, 95% CI [0, 0.001], ηp2 < 0.001) and fractal-type (F(1, 174) = 2.13, p = 0.15, 95% CI [0, 0.06], ηp2 = 0.01)]. Furthermore, no significant interactions appeared between D-value and age (F(2.08, 362.67) = 2.37, p = 0.09, 95% CI [0, 0.04], ηp2 = 0.01), fractal-type and age (F(1, 174) = 0.001, p = 0.97, 95% CI [0, 0.001], ηp2 < 0.001), or among D-value, fractal-type and age (F(2.08, 362.67) = 0.36, p = 0.71, 95% CI [0, 0.02], ηp2 = 0.002). The sole significant interaction was between D-value and fractal-type (F(2.08, 362.67) = 2.94, p = 0.05*, 95% CI [0, 0.05], ηp2 = 0.02) (see Fig. 3). A follow-up three-way mixed 5 × 4 × 2 ANOVA (D-value (1.1, 1.3, 1.5, 1.7, 1.9) × age (3–4, 5–6, 7–8, and 9–10-year-old children) × fractal-type (statistical, exact)) was performed on child participant data (see Table 2). Once again, Mauchly’s test indicated a violation of the assumption of sphericity for D-value (χ2(9) = 88.30, p < 0.001**), thus degrees of freedom were corrected using Greenhouse–Geisser estimates of sphericity (ε = 0.634). No significant main effects were uncovered [D-value (F(2.54, 223.28) = 2.35, p = 0.08, 95% CI [0, 0.07], ηp2 = 0.03), age (F(3, 88) = 1.05, p = 0.38, 95% CI [0, 0.11], ηp2 = 0.03) and Fractal-Type (F(1, 88) = 0.97, p = 0.33, 95% CI [0, 0.09], ηp2 = 0.01)]. The only significant interaction was between D-value and fractal-type (F(2.54, 223.28) = 3.49, p = 0.02*, 95% CI [0, 0.09], ηp2 = 0.04) (see Fig. 3, middle panel).
Adult (left panel), child (middle panel), and all (right panel) participant data demonstrating an interaction between D-value and fractal-type. Fractal preference for both children and adults rose steadily for exact fractal patterns and peaked at higher complexity. Preference for statistical fractals peaked at low–moderate complexity (D = 1.3) and decreased with additional complexity. All sets of data were fit with second-order polynomial functions (dashed lines).
A series of planned comparisons on the full data set explored the locus of the significant interaction between D-value and fractal-type. Average preference for statistical fractals ranged from a low of 0.18 (SD = 0.14) for D = 1.9 to a high of 0.23 (SD = 0.09) for D = 1.3. Paired samples t-tests revealed that mean preference differed significantly between D = 1.1 (M = 0.18, SD = 0.12) and 1.3 (M = 0.23, SD = 0.09) [t(85) = −4.55, p < 0.001**, 95% CI [−0.17, −0.07], d = 0.45], D = 1.3 and 1.9 (M = 0.18, SD = 0.14) [t(85) = 2.03, p = 0.046*, 95% CI [−0.002, 0.24], d = 0.41], as well as D = 1.7 (M = 0.21, SD = 0.09) and 1.9 [t(85) = 2.26, p = 0.027*, 95% CI [0.01, 0.14], d = 0.24]. Seen in Fig. 3—right panel, across the five fractal complexities, preference for statistical patterns peaked with low–moderate D and decreased with more extreme D-values. Regarding exact fractals, average preference increased with additional complexity from a low of 0.17 (SD = 0.11) for D = 1.1–0.22 (SD = 0.11) for D = 1.9. Preference for exact patterns differed significantly between D = 1.1 (M = 0.17, SD = 0.11) and 1.5 (M = 0.21, SD = 0.07) [t(91) = −2.83, p = 0.006*, 95% CI [−0.18, −0.03], d = 0.44], D = 1.1 and 1.7 (M = 0.22, SD = 0.09) [t(91) = −2.73, p = 0.008*, 95% CI [−0.22, −0.03], d = 0.49], D = 1.1 and 1.9 (M = 0.22, SD = 0.11) [t(91) = −2.59, p = 0.011*, 95% CI [−0.23, −0.03], d = 0.48], D = 1.3 (M = 0.18, SD = 0.08) and 1.5 [t(91) = −2.15, p = 0.034*, 95% CI [−0.12, −0.005], d = 0.32], as well as D = 1.3 and 1.7 [t(91) = −2.11, p = 0.038*, 95% CI [−0.16, −0.005], d = 0.38] (see Table 3). Paired independent samples t-tests between preference for exact and statistical patterns across the five D-values demonstrated that preference for only two D-values were significantly impacted by fractal-type, D = 1.3 (t(176) = −3.30, p < 0.001**, 95% CI [0.22, 0.8], d = 0.52) and D = 1.9 (t(159.28) = 2.18, p = 0.030*, 95% CI [−0.62, −0.03], d = 0.32). For D = 1.3, exact fractal patterns elicited a significantly lower preference score (M = 0.18, SD = 0.08) than statistical patterns (M = 0.23, SD = 0.09). Conversely, for D = 1.9, exact fractal patterns engendered a significantly higher preference score (M = 0.22, SD = 0.11) than that of statistical patterns (M = 0.18, SD = 0.14).
To summarize, in a direct comparison of preference for exact and statistical fractals of differing complexity, our findings confirmed the established trends of a preference for low–moderate complexity D-values for statistical fractals (Taylor et al., 2011) and higher D-values for exact fractals (Bies et al., 2016a). Importantly, the lack of a significant effect of age on preference for D-values (no age × D-value interaction) suggests that preferences for fractal patterns are stable by early childhood. While the effect sizes for the F-tests are generally small, they are in alignment with results from previous research (Street et al., 2016) which demonstrate a wide range of effect sizes for preference tasks.
Individual differences tasks
The Ponzo task was completed by 82 adult and 29 child participants. Task accuracy was recorded as average difference in pixels (error) between the adjusted and target line lengths. Overall participant error was 33.24 pixels (SD = 37.11). Average adult error was 24.82 pixels (SD = 24.38), while average child error was 41.66 pixels (SD = 45.09). SQ scores were recorded as point totals for agreement with a series of statements regarding systemizing tendencies. SQ scores for adults can range from 0 to 150, whereas the children’s version of the questionnaire is roughly half the length with scores ranging from 0 to 56. Adults averaged an SQ score of 63.7 (SD = 20.68) points, while children averaged 25 (SD = 8.15) points.
We completed independent samples t-tests comparing adults’ and children’s Ponzo and SQ scores and a correlational analysis between SQ scores and Ponzo errors, since previous work links susceptibility to visual illusions that rely on context (including the Ponzo illusion) to lower SQ scores (Billington et al., 2008; Walter et al., 2008). Child and adult SQ scores were first standardized since they were recorded on different scales. A t-test comparing standardized SQ scores for adults versus children revealed no significant age-related differences in systemizing tendencies [t(109) = 0, p = 1.0, 95% CI [−0.42, 0.42], d = 0.00]. After log transforming Ponzo scores to address their non-normal distribution, a t-test comparing Ponzo scores for these groups showed significant age-related differences in Ponzo task accuracy [t(162) = −4.91, p < 0.001**, 95% CI [−1.08, −0.45], d = −0.77] (see Table 4). Distributions of the child data may have been particularly affected by attrition (due to inadequate comprehension of Ponzo task instructions by some child participants and lack of SQ completion by parents). No significant correlation was detected between SQ and Ponzo scores (r = −0.12, p = 0.22) likely explained by prior research regarding age-related differences in illusion susceptibility (Hadad, 2018). A one-tailed correlational analysis on SQ scores and Ponzo error in adult participants alone (n = 82) detected a significant correlation (r = −0.21, p = 0.028*) (with higher SQ scores relating to reduction in Ponzo errors), and was performed since the link between visual illusion susceptibility and SQ scores was previously established only in adult participants (Walter et al., 2008) and attrition of child participants (n = 23) reduced the data available.
To determine if individual differences in perceptual strategies (measured by either the SQ or Ponzo test) could significantly explain variance in fractal preference, we performed a 2-step multiple linear regression analysis to predict fractal preference from fractal-type, D-value, SQ score, and Ponzo error (see Table 5). The first step of the model, including fractal-type, D-value, and the interaction of the two variables, significantly explained variance in preference (F(3, 886) = 5.98, p < 0.001**, R2 = 0.02, 95% CI [0.0, 0.04]). The second step, adding SQ scores and Ponzo error to the model, was unable to significantly account for additional variance in fractal preference (F(5, 519) = 0.66, p = 0.66, R2 = 0.01, 95% CI [0.0, 0.02]). To rule out the impact of possible differences in data due to child participant attrition and SQ test dissimilarities, an additional regression was completed to predict adult preference alone, with a model containing SQ score and Ponzo error F(2, 407) = 0.00, p = 0.99, R2 < 0.001, 95% CI [0.0, 0.0]) (see Table 6). This model also failed to significantly explain variance in fractal preference. Thus, despite the robust measurement of processing bias in our sample, no significant linear relationship emerged between these factors and fractal preference.
Discussion
Fractal patterns that recur in a statistical manner are prevalent in natural environments (Spehar et al., 2003; Taylor et al., 2018; Hagerhall et al., 2008) and both statistical and exact fractals are found in the art of many cultures (Graham and Redies, 2010). Preference is shown to peak at low–moderate fractal complexity (D) for statistical fractals and at higher D-values for exact patterns (Bies et al., 2016a) (since simplicity is introduced into these patterns though symmetry and exact repetitions), supporting a Fractal Fluency model in which common natural patterns are most fluently processed. In the first direct comparison of preference for statistical and exact fractals, the current study bolsters previous findings by confirming these robust preference trends and establishes that these preferences are apparent by early childhood, suggesting that this common fractal aesthetic is formed earlier in development.
We investigated the degree to which individual differences in processing style (assessed using the SQ and Ponzo task) might account for trends in fractal preference. The presence of a local or global processing bias could alter preference for pattern complexity by shifting preference toward higher complexity patterns containing more fine-scale/local detail for a local bias, or, for a global bias, toward lower complexity patterns in which larger scale forms are more apparent. Despite a wide range in SQ scores and Ponzo task performance and replication of a systematic relationship between these two assessments for adult participants (higher SQ scores correlate with lower Ponzo task error), no relationship was found between processing bias and preference for fractal complexity. The non-significant relationship between processing style and trends in fractal preference might be indicative of a developmentally early-emerging and broadly universal aesthetic that reflects the environmental complexity of early-humans as opposed to the more Euclidian environment experienced by most modern day children. However, these findings may have been impacted by underpowered sample sizes (in which the child sample suffered from attrition on these two assessments), prompting replication in larger samples to further substantiate this result.
Prior to this study, exposure to and facility in processing fractal patterns might have been expected to vary across the lifespan due to environmental and developmental factors. If fractal aesthetics reflected the most commonly encountered complexities across repeated exposure, differences would be expected to arise between individuals who differ in decades of experience (particularly since typical early life is primarily spent within Euclidian structures of low visual complexity) (Clements, 2004). Additionally, change in preference across childhood from simpler to more complex fractal patterns would have been expected if pattern comprehension changed incrementally with age. Instead, our finding of consistent preference trends across childhood and through adulthood suggests a stable fractal aesthetic is established early in life. This leaves open the possibility that an early biological or evolutionary mechanism optimizes the visual system for processing fractals—the most common spatial structure (of low–moderate complexity) found in nature (Falk and Balling, 2010), supporting a universal Fractal Fluency theory. In addition to defining possible sub-group behaviours in preferences across the lifespan (Bies et al., 2016a; Street et al., 2016), future studies must examine earlier stages of development (from infancy to 3 years of age) to further define the impact of experience with fractal patterns on visual tuning and the development of what may be a universal aesthetic preference. Addressing the developmental impact on fluency of fractal processing is vital to understanding and regulating aesthetic experiences in both natural and built environments.
Data availability
The datasets analysed during the current study are available in the Dataverse repository: https://doi.org/10.7910/DVN/E8YPFG.
Code availability
Programme codes for both the fractal preference task and Ponzo task were written using PsychoPy software (Peirce et al., 2019), are available upon request.
References
Auyeung B, Sally W, Carrie A, Matthew A, Nelum S, Simon B-C (2009) The children’s empathy quotient and systemizing quotient: sex differences in typical development and in autism spectrum conditions. J Autism Dev Disord 39(11):1509. https://doi.org/10.1007/s10803-009-0772-x
Baron-Cohen S, Wheelwright S, Skinner R, Martin J, Clubley E (2001) The autism-spectrum quotient (AQ): evidence from Asperger syndrome/high-functioning autism, males and females, scientists and mathematicians. J Autism Dev Disord 31:5–17. https://doi.org/10.1023/A:1005653411471
Bies A, Blanc-Goldhammer DR, Boydston CR, Taylor RP, Sereno ME (2016a) The aesthetic response to exact fractals driven by physical complexity. Front Hum Neurosci 10:201
Bies AJ, Boydston CR, Taylor RP, Sereno ME (2016b) Relationship between fractal dimension and spectral decay rate in computer-generated fractals. Symmetry 8:66
Billington J, Baron-Cohen S, Bor D (2008) Systemizing influences attentional processes during the Navon task: an fMRI study. Neuropsychologia 46(2008):511–520
Boselie F, Leeuwenburg E (1985) Birkhoff revisited: beauty as a function of effect and means. Am J Psychol 98:1–39. https://doi.org/10.2307/1422765
Clements R (2004) An investigation of the status of outdoor play. Contemp Issues Early Child 5(1):68–80. https://doi.org/10.2304/ciec.2004.5.1.10
Eysenck HJ (1942) The experimental study of the ‘good Gestalt’—a new approach. Psychol Rev 49:344–364. https://doi.org/10.1037/h0057013
Falk JH, Balling JD (2010) Evolutionary influence on human landscape preference. Environ Behav 42(4):479–493. https://doi.org/10.1177/0013916509341244
Forsythe A, Williams T, Reilly RG (2017) What paint can tell us: a fractal analysis of neurological changes in seven artists. Neuropsychology 31(1):1–10. https://doi.org/10.1037/neu0000303
Fournier A, Fussell D, Carpenter L (1982) Computer rendering of stochastic models. Commun ACM 25:371–384
Graham DJ, Field DJ (2008) Variations in intensity for representative and abstract art, and for art from eastern and western hemispheres. Perception 37:1341–1352
Graham DJ, Redies C (2010) Statistical regularities in art: relations with visual coding and perception Vis Res 50:1503–1509. https://doi.org/10.1016/j.visres.2010.05.002
Hadad BS (2018) Developmental trends in susceptibility to perceptual illusions: not all illusions are created equal. Atten Percept Psychophys 80(6):1619–1628. https://doi.org/10.3758/s13414-018-1529-4
Hagerhall CM, Laike T, Taylor RP, Küller M, Küller R, Martin TP (2008) Investigations of human EEG response to viewing fractal patterns. Perception 37(10):1488–1494. https://doi.org/10.1068/p5918
Hagerhall CM, Laike T, Küller M, Marcheschi E, Boydston C, Taylor RP (2015) Human physiological benefits of viewing nature: EEG response to exact and statistical fractal patterns. J Nonlinear Dyn Psychol Life Sci 19:1–12
Kidd C, Piantadosi ST, Aslin RN (2012) The Goldilocks effect: human infants allocate attention to visual sequences that are neither too simple nor too complex. PLoS ONE 7(5):e36399. https://doi.org/10.1371/journal.pone.0036399
Mandelbrot BB (1982) The fractal geometry of nature. WH Freedman, New York
Peirce JW, Gray JR, Simpson S, MacAskill MR, Höchenberger R, Sogo H, Kastman E, Lindeløv J (2019). PsychoPy2: experiments in behavior made easy. Behav Res Methods. https://doi.org/10.3758/s13428-018-01193-y
Penacchio O, Wilkins AJ (2015) Visual discomfort and the spatial distribution of Fourier energy. Vis Res 108:1–7. https://doi.org/10.1016/j.visres.2014.12.013
Pyankova SD, Chertkova YD, Scobeyeva VA, Chertkova ER (2019). Influence of genetic factors on perception of self-similar objects. 530–537. https://doi.org/10.15405/epsbs.2019.07.69
Roder BJ, Bushnell EW, Sasseville AM (2000) Infants’ preferences for familiarity and novelty during the course of visual processing. Infancy 1:491–507
Spehar B, Clifford C, Newell B, Taylor RP (2003) Universal aesthetic of fractals. Chaos Graph 37:813–820
Spehar B, Walker N, Taylor RP (2016) Taxonomy of individual variations in aesthetic response to fractal patterns. Front Hum Neurosci 10:1–18
Sprott JC (1993) Automatic generation of strange attractors. Comput Graph 17:325–332. https://doi.org/10.1016/0097-8493(93)90082-K
Stevenson HW (1972) Children’s learning. Appleton-Century-Crofts, New York
Street N, Forsythe A, Reilly RG, Taylor RP, Boydston C, Helmy MS (2016) A complex story: universal preference vs. individual differences shaping aesthetic response to fractals patterns? Front Hum Neurosci 10:213
Taylor RP (1998) Splashdown. New Sci 159:30–31
Taylor RP, Guzman R, Martin TP, Hall GDR, Micolich AP, Jonas D et al. (2007) Authenticating Pollock paintings using fractal geometry. Pattern Recogn Lett 28:695–702. https://doi.org/10.1016/j.patrec.2006.08.012
Taylor RP, Juliani AW, Bies AJ, Spehar B, Sereno ME (2018) The implications of fractal fluency for bioinspired architecture. J. Biourban 6:23–40
Taylor RP, Micolich AP, Jonas D (1999) Fractal analysis of Pollock’s drip paintings. Nature 399:422
Taylor RP, Spehar B, Van Donkelaar P, Hagerhall CM (2011) Perceptual and physiological responses to Jackson Pollock’s fractals. Front Hum Neurosci 5:1–13. https://doi.org/10.3389/fnhum.2011.00060
Taylor R, Spehar B, Wise J, Clifford C, Newell B, Hägerhäll C, Purcell T, Martin T (2005) Perceptual and physiological responses to the visual complexity of fractal patterns. Nonlinear Dyn Psychol Life Sci 9:89–114. https://doi.org/10.1007/978-3-322-83487-4_4.
Taylor RP, Sprott JC (2008) Biophilic fractals and the visual journey of organic screen-savers. J Non-linear Dyn Psychol Life Sci 12:117–129
Walter E, Dassonville P, Bochsler TM (2008). A specific autistic trait that modulates visuospatial illusion susceptibility. J Autism Dev Disorder https://doi.org/10.1007/s10803-008-0630-2
Acknowledgements
We thank R. Florentine, A. Sherman, S. Wallner, and M. Walker for data collection.
Author information
Authors and Affiliations
Contributions
KER, RPT, DB, and MES contributed to the study design. MES and KER contributed to stimulus generation; KER to programming the experiments; KER, and NAL to testing and data collection; and MES and KER to the data analysis and interpretation. KER and MES drafted the manuscript. All authors contributed to the manuscript editing and approved the final version of the manuscript for submission.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Robles, K.E., Liaw, N.A., Taylor, R.P. et al. A shared fractal aesthetic across development. Humanit Soc Sci Commun 7, 158 (2020). https://doi.org/10.1057/s41599-020-00648-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-020-00648-y
This article is cited by
-
Fractal shifts and esthetic rifts: climate change and emotional well-being
Climatic Change (2022)