Abstract
Can green growth policies help protect the environment while keeping the industry growing and infrastructure expanding? The City of Kitakyushu, Japan has actively implemented eco-friendly policies since 1967 and recently inspired the pursuit of sustainable development around the world, especially in the Global South region. However, empirical studies on the effects of green growth policies are still lacking. This study explores the relationship between road infrastructure development and average industrial firm size with air pollution in the city through the Environmental Kuznets Curve (EKC) hypothesis. Auto-Regressive Distributed Lag (ARDL) and Non-linear Auto-Regressive Distributed Lag (NARDL) methods were applied on nearly 50-years’ time series data, from 1967 to 2015. The results show that the shape of the EKC of industrial growth, measured by average firm size, depends on the type of air pollution: inverted N-shaped relationships with NO2 and CO, and the U-shaped relationships with falling dust particle and Ox. Regarding infrastructure development, on the one hand, our analysis shows a positive effect of road construction on alleviating the amount of falling dust and CO concentration. On the other hand, the emissions of NO2 and Ox are shown to rise when plotted against road construction. The decline of CO emission, when plotted against both industrial growth and road development, indicates that the ruthlessness of the local government in pursuing green growth policies has been effective in this case. However, the story is not straightforward when it comes to other air pollutants, which hints at the limits of the current policies. The case of Kitakyushu illustrates the complex dynamics of the interaction among policy, industry, infrastructure, and air pollution. It can serve as an important reference point for other cities in the Global South when policies are formed, and progress is measured in the pursuit of a green economy. Finally, as an OECD SDGs pilot city and the leading Asian green-growth city, policymakers in Kitakyushu city are recommended to revise the data policy to enhance the findability and interoperability of data, as well as to invest in the application of big data.
Similar content being viewed by others
Introduction
Until now, Earth is the only known planet that shelters life, and, this life is under threat (Wallace-Wells, 2019). Nonetheless, many who are in power are not willing to act to protect it. In a recent discovery, the Trump Administration tried to block a State Department senior intelligence analyst to give testimony on climate change (Friedman, 2019). On the other side of the globe, the City of Kitakyushu, Japan, with governmental support, has been pursuing environment-friendly industrial policies since 1967 (Low, 2013), and in 2011, it was selected by OECD to be among four green growth cities in the world besides Paris, Stockholm, and Chicago (City of Kitakyushu, 2018). Kitakyushu city is also the inspiration of other cities in the Global South, such as Hai Phong—Vietnam and Surabaya—Indonesia, in pursuing sustainable development (Japan for Sustainability, 2013). This article presents striking results that could help evaluate the long-term impacts of Kitakyushu’s green growth policies on the relationship between industrial growth and infrastructure development with ambient air emissions.
The Environmental Kuznets Curve (EKC) hypothesis, grounded on the commonly assumed idea of “growth first, clean later” (Kijima et al., 2010; Özokcu and Özdemir, 2017), is relatively well-known among the theories that seek to explain the interaction between economic development and environmental degradation. This study explores the EKC of industrial growth (measured by average industrial firm size) and air pollution, as well as road infrastructure development (measured by total area of paved road) and air pollution. The five ambient air pollutants being studied are falling dust, SOx, NO2, Ox, and CO. The primary anthropogenic sources of these air pollutants include fossil fuel and biofuel combustion resulting from energy generation, transport, and industry (Anenberg et al., 2018; Lamsal et al., 2013; Lelieveld et al., 2015; Zhong et al., 2017). Air pollution is not only responsible for the death of more than four million people globally (WHO, 2019), but is also linked with climate change, which has disrupted almost every aspect of human existence (Barnes et al., 2019; Mora et al., 2018). Besides the direct effects of the greenhouse gases (GHGs), CO can indirectly intensify climate change through prolonging the lifetime of GHGs, oxidizing into CO2, and reacting with NOx and volatile organic compounds to form tropospheric ozone (Daniel and Solomon, 1998; Strode et al., 2015).
Since the first empirical results of the EKC (Grossman and Krueger, 1991; Panaĭotou, 1993; Shafik and Bandyopadhyay, 1992), the debate around the hypothesis has become more controversial with evidence on both sides (Crespo Cuaresma et al., 2017; Ota, 2017; Özokcu and Özdemir, 2017). In the literature of EKC, real GDP and GDP per capita are the most frequently used economic indicators to explore the EKC in all types of data, from panel data (Ge et al., 2018; Narayan and Narayan, 2010; Ozcan, 2013; Sharma, 2011; Sinha and Bhattacharya, 2016), to time-series (Ahmad et al., 2017; Ali et al., 2017; Bölük and Mert, 2015; Rafindadi, 2016) and cross-sectional data (Hill and Magnani, 2002). However, there appears a scarcity of studies done on the EKC of industrial growth, despite the fact that industrial growth contributes substantially to the economic growth and exert major effects on environmental degradation. Some recent studies include those of Abokyi et al. (2019), which examines the EKC of industrial growth in Ghana by using Industry value added; and Wang and Wang (2019), which validate the EKC of industrial agglomeration in China. Thus, the current study presents a new perspective on the EKC hypothesis—the average size of industrial firm, which is a completely new area of exploration to the best of our knowledge. The findings from this study are also expected to fill in the shortage of insights from microeconomic behavior in the literature of EKC (Kijima et al., 2010).
Another factor that might significantly affects the level of air pollution is the development of infrastructure. Infrastructure is the backbone of any countries, with a well-planned design, infrastructure expansion can contribute to sustainable development, otherwise, it will result in negative consequences on society and environment (Thacker et al., 2019). On the one hand, the expansion of high-quality roads may result in an increase in traveling demand (Cervero, 2003). On the other hand, building more high-quality roads will help enhance manufacturing productivity through increasing accessibility (Duran-Fernandez and Santos, 2014; Gibbons et al., 2019). Moreover, expanding road infrastructure was believed to reduce air pollution by cutting down the time of vehicles on the road, as well as frequent acceleration and deceleration due to traffic congestion (Zhang and Batterman, 2013). Therefore, we believe the expansion of high-quality road might have significant effects on air pollution emissions, especially in the case of a recycling-industrial city such as Kitakyushu city, Japan.
Unlike previous studies testing the EKC without noticing when the first environmental regulation took place, our study only concentrates on the time period from 1967, when Kitakyushu city first signed a pollution prevention agreement with the private sectors (Holroyd, 2018), to 2015 (City of Kitakyushu, n.d.). In this way, we can evaluate the effectiveness of green growth policies and environmental legislations in Kitakyushu city. Moreover, the current study also tests the EKC by a new approach: examining the relationship of air pollution emissions (measured by the emissions per capita of falling dust particle, SOx, NO2, CO, and Ox) with the average industrial firm size and total area of paved road by employing ARDL and NARDL analyses.
Methods and materials
Study site
This study selects Kitakyushu city as the study site for several reasons. First, Kitakyushu is a green-growth oriented city through recycling activities and its experiences can be generalized in other areas. Besides being featured as one of four green growth cities in the world besides Paris, Chicago, and Stockholm, Kitakyushu was also selected as a pilot city for OECD’s Territorial Approach to the Sustainable Development Goals project (City of Kitakyushu, 2018). Moreover, the city has received major national designations such as Eco-Town in 1997, Eco-Model-City in 2008, Smart Community Project in 2010, Future City Initiative in 2011, “Green Asia” Comprehensive Special Zone in 2011 (OECD, 2013), as well as other international recognitions (City of Kitakyushu, 2018). Thus, the results from this study could be viewed as a reference for other cities and regions within and outside of Japan, especially in the Global South, where many countries have close connections and collaborations with Japan, to achieve the Sustainable Development Goals.
Second, Kitakyushu is an outstanding example for the impact of stringent environmental regulation and control on improving environmental quality. “The seven-colored smoke”, which was created by dust and sulfur dioxide, was previously considered as a symbol of prosperity, especially after Kitakyushu was selected as one of four key-driven areas including Tokyo, Nagoya, Osaka, and Kitakyushu, to form a “Pacific Belt Zone” in order to reconstruct Japanese economy after the wartime (Yoshioka and Kawasaki, 2016). However, because of public pressure and political competition from Communist party with its environmental-friendly agenda, the local authority and private sector had to reach a general compromise by the first pollution control agreement in 1967 (Fujikura, 2007). Thanks to the “comprehensive, systematic, and steady” environmental control system in Kitakyushu after the agreement, the city was introduced in the 1985 OECD’s White paper on the environment as an outstanding transformation from a “city of gray” to a “city of green” (The World Bank, 1996).
Data and variables
Our analysis examines the non-linear relationship between the average industrial firm size and air pollution, and the linear relationship between the total area of paved road and air pollution in Kitakyushu city employing the dataset between 1967 and 2015. However, the data of some air pollutants had a shorter time span, for example, the concentration of NO2 per capita only ranged from 1970 to 2015. The dataset consists of seven types of data, namely: the emitting amount of falling dust particle, the concentration of SOx, NO2, Ox, and CO per capita, the average size of an industrial firm, and the total area of paved road.
Dependent variables
The data of air pollution were retrieved from the Section: Hygiene, Environment, and Pollution in the Longitudinal Statistics database of the City of Kitakyushu (City of Kitakyushu, n.d.). The dataset included the amount of falling dust particles, the concentration of SOx, NO2, Ox, and CO. We later divided the air pollutants’ emission by the population in Kitakyushu to achieve the air pollutants’ emission per capita (see Fig. 1.1–5). The population statistics were retrieved from the Section: Population (City of Kitakyushu, n.d.). The time period, measuring unit and other details of each air pollutants’ emission per capita is displayed in Table 1. All dependent variables were later logarithm transformed to ensure the normality of the dependent variable, represented by adding “ln” in front of the variable. For example, “lnDustper” illustrates the logarithm of the amount of falling dust per capita.
Air pollution, average industrial firm size, and total paved road area. 1. The amount of falling dust per capita plotting from 1967 to 2015. 2. The concentration of SOx per capita plotting from 1967 to 1999. 3. The concentration of NO2 per capita plotting from 1970 to 2015. 4. The concentration of Ox per capita plotting from 1971 to 2015. 5. The concentration of CO per capita plotting from 1975 to 2015. 6. The average industrial firm size (blue column) and total area of paved road (red line) plotting from 1967 to 2015.
Independent variables
There are four independent variables in the current study. The first three independent variables are the logarithm of the average industrial firm size, its quadratic and cubic forms. Those three independent variables are illustrated by “lnFirmsize”, “lnFirmsize2” and “lnFirmsize3”, respectively. The average industrial firm size is calculated by dividing the total shipment value of manufactured goods of industrial firms by the number of industrial firms in Kitakyushu city. The data were taken from the Section: Industry in the Longitudinal Statistics database (City of Kitakyushu, n.d.). The initial measuring unit of total shipment value was million JPY, but was exchanged to million US dollar using the constant rate in May 2019 (1 US dollar = approximate 110 JPY).
Another independent variable is “Road”, which represents the total area of paved road being built within the city area. The variable was later logarithm transformed and presented as “lnRoad”. The data were available from 1967 to 2015 in the Section: Construction and Housing (City of Kitakyushu, n.d.). The measuring unit of the total area of paved road is km2. The data of the average industrial firm size and total paved road area are presented by the blue column and red line, respectively in Fig. 1.6.
Models
In this study, the reduced-form function was chosen to test the shape of the relationship between air pollution and the average firm’s size along with the impact of road density because of several reasons. First, the reduced-form function is more suitable to apply than other non-linear functional forms or non-parametric and semi-parametric models. Second, some drawbacks of the parametric method cannot be solved by applying another type of methods, such as the use of spline or semiparametric methods (Özokcu and Özdemir, 2017). Third, the reduced-form has been widely used to test the EKC in various relationships between income and environmental degradation (Kijima et al., 2010).
We formulated our reduced-form function as linear, quadratic, and cubic equations according to previous works (Shafik and Bandyopadhyay, 1992; Grossman and Krueger, 1995; Panayotou, 1997; De Bruyn, 1997; Dinda, 2004; Galeotti and Lanza, 2005; Akbostancı et al., 2009; Özokcu and Özdemir, 2017) as follows, respectively:
It is worth noting that ln AirPollutiont represents all air pollutants emission per capita which were log-transformed.
The statistical model utilized in our analysis was Auto-regressive Distributed Lag (ARDLs) created by Pesaran, Shin, and Smith (Pesaran et al., 2001) to examine the cointegration between a dependent variable and a set of independent variables for several reasons. First, the ARDL model has been widely used across disciplines for almost two decades to model relationships based on time-series analysis (Kripfganz and Schneider, 2016). Second, the ARDL encompasses other cointegration models (Engle and Granger, 1987; Johansen, 1988; Phillips and Hansen, 1990) in terms of feasibility: (1) ARDL is employable if the variables are stationary at the level form, the first difference, or the mixture of both. Second, the ARDL model can provide unbiased results for a small sample size, which has been verified by Monte Carlo Simulation (Ahmad et al., 2017; Pesaran and Shin, 1999). Third, the ARDL model can fit well with endogenous variables, because it can solve the problem of endogeneity by selecting correct lag length for the variable and increasing the model dynamic (Pesaran and Shin, 1999). Lastly, the ARDL model provides not only an explanation for the long-run relationship but also look at the short-run dynamics through a simple linear function based on the Error Correction Mechanism (ECM).
Before conducting the ARDL analysis, Vector Auto-Regression (VAR) and Augmented Dickey-Fuller (ADF) tests are utilized. Through the VAR test, the optimal lag length was selected based on the three most widely employed criteria, namely Akaike Information Criterion (AIC), Schwarz Bayesian Information Criterion (BIC), and the Hannan-Quinn Information Criterion (HQIC) (Vrieze, 2012). The lowest lag number will be prioritized regardless of the criteria. The ADF test was used in this study to determine whether all variables are stationary at below second difference. Specifically, the level form and the first difference of each dependent and independent variables were tested under two conditions, respectively: unrestricted intercept—no trend and unrestricted intercept—trend.
Equations (2.1) to (2.3) show the ARDL models of long-run and short-run relationships between air pollutants and independent variables, where α0 is the constant, p is the length of lag and \(\varepsilon _t\) is the error term. In the first half of each model, the dynamics of the short-run is explained by variables with the summation signs. The second half of the model represents the long-run relationship.
We tested the cointegration of dependent and independent variables by the bound test. For example, in Eq. (3.3), when the null hypothesis of the bound test is accepted, β1 = β2 = β3 = β4 = β5 = 0, and there is no cointegration. On the other hand, if the null hypothesis is rejected, β1 ≠ β2 ≠ β3 ≠ β4 ≠ β5 ≠ 0, the cointegration exists. In order to determine whether to accept or reject the null hypothesis, the joint F-stat needs to be compared with the lower bound and the upper bound of the model. The lower bound considers all variables as I(0), while the upper bound considers all variables as I(1). The null hypothesis is accepted if the F-stat is lower than the lower bound critical value of I(0), whereas if the F stat is higher than the upper bound critical value of I(1), the null hypothesis can be rejected. In case that the F stat is between the lower bound critical value of I(0) and the upper critical value of I(1), the result becomes inconclusive. In this situation, to decide whether the model is cointegrated or not, the significance of error correction term (ECT) in the short-term linear function needs to be taken into account. Banerjee et al. (1998) implied that if the coefficient of lagged dependent variable, or so-called ECT, is negative and statistically significant, the cointegration of the model is confirmed. Moreover, it is also notable that if the coefficient of ECT is not negative or statistically significant, there will be no cointegration, despite a significant bound test. Equations (3.1) to (3.3) represent the long-run ARDL equations of the relationship:
Here, p, q, r, s, and u are lag values of each independent variable, respectively. Next, Eqs. (4.1) to (4.3) show the short-run dynamics of the relationship between air pollutants and independent variables:
Here, δ0 is the constant; δ1, δ2, δ3, δ4, δ5 are coefficients; ECTt−i is the error correction term of the EC models; γ is the coefficient of ECT; and τ is the error term. The error correction term (ECT) in these equations is the speed of the adjustment parameter, which reflects the speed adjusting to the long-run equilibrium of the model.
Taking the asymmetric impact of paved road construction into consideration and being inspired by Mahmood et al. (2019), the Nonlinear Autoregressive Distributed Lag (NARDL) is applied and compared with ARDL results. NARDL was developed from linear ARDL by Shin et al. (2014) to check the effect of positive and negative changes of an independent variable on the dependent variable separately. In this study, we test the asymmetrical effect of lnRoad on air pollution, by replacing “lnRoad” with “lnRoad_p” and “lnRoad_n” in the ARDL models. “lnRoad_p” and “lnRoad_n” are computed by partial sums of positive and negative changes in “lnRoad”, respectively, as follows:
The following Eqs. (6.1), (6.2), and (6.3) are NARDL models, or ARDL models after being converted by replacing lnRoad with Eqs. (5.1) and (5.2):
The long-run and short-run of the NARDL models are examined by similar means to the ARDL model. In addition, we also employ Wald test to examine the null hypotheses of the symmetrical effects of “lnRoad_p” and “lnRoad_n” in the long-run and short-run estimations.
Procedure
The current analysis was carried out through three stages. First, pre-estimation tests, namely: lag-selection test, Augmented Dickey and Fuller unit-root test, and bound test for the cointegration of the model, were conducted. Second, the ARDL model was employed to examine the short-run and long-run relationships between air pollutants and the set of independent variables. Durbin-Watson test, Breusch Godfrey Serial Correlation Lagrange Multiplier (LM) test, Breusch-Pagan/Cook-Weisberg test for Heteroskedasticity, ARCH test, Ramsey Reset test, CUSUM and CUSUMSQR tests were employed at the end to confirm the autocorrelation, serial correlation, heteroscedasticity, appropriateness of model specification, and variables’ stability. If any model does not pass the post-analysis tests, they would be rejected. Eventually, the finest models were selected for NARDL analysis to confirm the significance of the models. The NARDL analysis process was replicated from the ARDL analysis above.
The raw data from separate sources were initially downloaded, combined, and curated in one Excel file. The Excel file was later stored as CSV format before importing to EViews software (version 10) for in-depth analysis. In terms of the level of significance, 10% was chosen as the significance level for short-run and long-run analysis, while 5% was chosen as the significance level of the pre-estimation and post-estimation tests.
Results
Pre-estimation tests
The VAR test based on Akaike Information Criterion (AIC), Schwarz Bayesian Information Criterion (SBIC), and the Hannan-Quinn Information Criterion (HQIC) suggested 1 is the optimal lag length for most of the equations (see Table S1, Supplementary Information). The Augmented Dickey-Fuller unit root test was also employed to examine if all variables were stationary at level series or first-order difference series (see Table S2, Supplementary Information). The results concluded that all variables in the current study were stationary at I(0) and I(1).
EKC between industrial firm size and air pollution emissions
Based on the analysis statistics and post-estimation tests of both the ARDL and NARDL models, the two most appropriate shapes of the relationship between air pollution and average industrial firm size are the U-curve (“lnDustper” and “lnOxper” as dependent variables) and inverted N-curve (“lnNO2” and “lnCOper” as dependent variables). In cases of “lnNO2” and “lnCOper”, the EKC hypothesis is validated as air pollution emissions eventually decline when plotted against the industrial growth, despite an increasing period. However, as “lnDustper” and “lnOxper” rise after a certain level of industrial growth, the EKC hypothesis is rejected.
ARDL analysis results
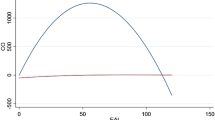
Among the three equations of “lnDustper” and “lnOxper”, Eq. (3.2) is the most appropriate representation for the relationship of “lnDustper” and “lnOxper” with the average industrial firm size and the total area of paved road, because the equation satisfies all the post-estimation tests. The models of “lnDustper” and “lnOxper” explain 92% and 68% of the variance, respectively. In the long-run, the coefficients of “lnFirmsize” (βlnFirmsize = −0.246, p-value < 0.01) and “lnFirmsize2” (βlnFirmsize2 = 0.530, p-value < 0.01) are negative and positive, respectively, which presents a U-shaped relationship between industrial firm size and the amount of falling dust per capita. The turning point is calculated to be at $10.21 million per firm after exponential transformation (see Fig. 2.1). Meanwhile, the relationship between the concentration of Ox per capita and the average firm size also exhibits a similar shape, with the turning point at $10.05 million per firm (βlnFirmsize = −2.686, p-value < 0.01 and βlnFirmsize2 = 0.582, p-value < 0.01, see Fig. 2.2 and Table 2).
Illustrations of the relationship between the average industrial firm size and air pollutions. 1. The U-shaped relationship between average industrial firm size and the amount of falling dust. 2. The U-shaped relationship between average industrial firm size and the concentration of Ox. 3. The inverted N-shaped relationship between average industrial firm size and the concentration of NO2. 4. The inverted N-shaped relationship between average industrial firm size and the concentration of CO.
The U-shaped relationships between industrial firm size and the amount of falling dust per capita, as well as the concentration of Ox per capita imply that air pollutions are initially alleviated, but they start to increase again when industrial firms grow to a certain size. In other words, the EKC of industrial growth is not valid in cases of falling dust and Ox. This result contradicts the study of Diao et al. (2009) which validates the EKC between economic growth and industrial dust discharged from 1995 through 2005.
The results in the short-run estimation also demonstrate a similar effect of industrial firm size on the amount of falling dust and concentration of Ox per capita like the long-run estimation (see Table 3). The coefficients of the error correction terms are negative and statistically significant, which again confirmed the cointegration of both models. The amount of falling dust and concentration of Ox per capita adjust by 65.2 and 70.4% each year, respectively, when they are far away from the equilibrium.
The current study also displays long-run inverted N-shaped relationships of the average industrial firm size with the concentration of NO2 (βlnFirmsize = −14.742, p-value < 0.05, βlnFirmsize2 = 6.629, p-value < 0.05, and βlnFirmsize3 = −1.005, p-value < 0.01) and CO per capita (βlnFirmsize = −67.831, p-value < 0.01, βlnFirmsize2 = 29.688, p-value < 0.01, and βFirmsize3 = −4.287, p-value < 0.01). We choose the results estimated for Eq. (3.3), because it does not only satisfy all the post-estimation tests, but also explain the most variance (R2 = 0.86 and 0.70 with “lnNO2per” and “lnCOper” as dependent variables, respectively). Even though the finding shows an inverted N-shaped curve between NO2 emission per capita and firm size, there is only one turning point at $9 million per firm, which is the third fundamental cubic equation’s reflection point (see Fig. 2.3). Meanwhile, the relationship between CO emission per capita and firm size obtains two turning points which are at $7.96 million and $12.71 million, respectively (see Fig. 2.4). The two curves indicate a similar pattern that air emission first declines as firms grow, then starts to slow down or even rises when firms grow to a certain level, but finally declines again.
The inverted N-shaped curves between firm size and the concentrations of NO2 and CO per capita in our study provide insights from the perspective of the microeconomic industrial growth on the validity of EKC in Japan (Rafindadi, 2016). They also contribute evidence for the EKC of industrial growth, in terms of average industrial firm size and NO2 and CO emissions, besides the U-shaped relationship between environmental efficiency and industrial agglomeration in China (Wang and Wang, 2019) and the inverted U-shaped relationship between industrial added value and CO2 emission in Ghana (Abokyi et al., 2019).
The short-run estimations also confirm the N-shaped relationship of the average industrial firm size with the concentration of NO2 and CO per capita in the long-run estimations (see Table 3). The adjustment speed to equilibrium of NO2 per capita (\(\beta _{ECT\left( {t - 1} \right)}\) = −0.416, p-value < 0.01) is slower than that of CO per capita (\(\beta _{ECT\left( {t - 1} \right)}\) = −0.703, p-value < 0.01).
NARDL analysis results
The most appropriate ARDL models of each type of air pollution is selected for the NARDL analysis, while the model with “lnSOxper” is rejected due to statistical insignificance. CUSUM and CUSMSQ tests are not reported due to collinearity while computing. Among the four selected models, two are in quadratic form (“lnDustper” and “lnOxper” as dependent variables), and the other two are in cubic form (“lnNO2per” and “lnCOper” as dependent variables) (see Table 4).
At first glance, the inverted N-shaped relationships of “lnNO2” and “lnCOper” with the average size of industrial firm in Kitakyushu city are confirmed by the NARDL models, but the turning points are slightly different from those provided by ARDL models (see Fig. 2). The turning point of NARDL model of “lnNO2per” is at $8.6 (βlnFirmsize = −20.064, p-value < 0.05, βlnFirmsize2 = 9.301, p-value < 0.05, and βlnFirmsize3 = −1.441, p-value < 0.05), while that of “lnCOper” are at $7.97 million and $12.62 million (βlnFirmsize = −74.358, p-value < 0.05, βlnFirmsize2 = 32.566, p-value < 0.05, and βFirmsize3 = −4.707, p-value < 0.05) (Fig. 3).
Illustrations of the relationship between the total area of paved road and air pollutions. 1. The relationship between total area of paved road and the amount of falling dust. 2. The relationship between total area of paved road and the concentration of CO. 3. The relationship between total area of paved road and the concentration of Ox. 4. The relationship between total area of paved road and the concentration of NO2.
In case of “lnDustper” and “lnOxper”, the NARDL models presented U-shaped relationships between air pollution emissions and industrial firm size, but the model of “lnDustper” had an autoregressive conditional heteroskedasticity. The turning points calculated from the NARDL models of “lnDustper” and “lnOxper” are $10.91 million and $9.32 million. The U-shaped relationship might be the result of insufficient pollution monitoring policies due to the changing industrial structure in Kitakyushu city might be an explanation for the increasing dust emission as firms grow larger. To elaborate, it is reported that there is a rising number of large firms in iron steel, chemical, and automobile sectors, etc. who have outsourced their activities to smaller firms receiving many incentives and less stringent regulation and inspection from the government (OECD, 2013).
In terms of Ox emission, even though it is closely related to the concentration of NO2 in the atmosphere, it is still very difficult to control as Ox emission is created through a complex photochemical reaction of NO2 with other substances in the air (Guderian, 1985).
Relationships between road infrastructure development and air pollution emissions
Our ARDL analysis finds that building more high-quality roads, in particular—paved road, corresponds to the decline of dust emission (βlnRoad = −0.361, p-value < 0.05), CO emission (βlnRoad = −0.357, p-value < 0.1), and the increase of the NO2 (βlnRoad = 0.341, p-value < 0.05), Ox emissions (βlnRoad = 0.347, p-value < 0.01) (see Table 2). The results of NARDL analysis also confirm the relationships between road infrastructure development and air pollution emissions (see Fig. 3). However, in all NARDL models, while the effect of increasing total area of paved road is significant, that of decreasing one is not. The null hypothesis of the symmetrical effect of road infrastructure development is tested and not rejected, which implies a symmetrical effect of road infrastructure development. The contradictory result between the Wald test and the coefficients of “lnRoad_p” and “lnRoad_n” can be because the total area of paved road only declined in one year which was in 2014, which in turns, created distortion in the results. Even though the distortion does not lead to any major difference between the results of ARDL and NARDL analyses, we would like to use the results of ARDL, instead of NARDL analysis, for discussion.
Given that Eq. (3.2) is the most suitable equation among the ARDL models, 10% increase in total area of paved road is corresponded with 3.38 and 3.35% decreases in the amount of falling dust per capita and the concentration of CO per capita, respectively. The short-run estimations also confirmed the negative associations in the long-run. The negative correlation of paved road infrastructure development with dust and CO emissions suggest a substantial role of high-quality road expansion in elevating the productivity through accessibility improvement (Duran-Fernandez and Santos, 2014; Gibbons et al., 2019). Especially in Kitakyushu city, recycling industries are extensively and intensively invested and promoted (City of Kitakyushu, 2018). As a result, local recycling industries might take advantage of the road infrastructure system to raise recycling productivity and indirectly alleviate the CO and dust emissions.
However, building more high-quality road infrastructure also leads to some side-effects. Contrary to the negative correlations of the total area of paved road with dust and CO emissions per capita, NO2 (βlnRoad = 0.341, p-value < 0.05) and Ox (βlnRoad = 0.348, p-value < 0.01) emissions per capita are positively associated with the expansion of paved road. The short-run estimations also presented similar patterns with the long-run. The concentration of NO2 and Ox per capita might increase by 3.3 and 3.37%, respectively, if there was 10% of the additional road being built. Although the road infrastructure development in Kitakyushu city might help reduce dust and CO emissions through rising industrial productivity, the construction of new road might possibly lead to urban sprawl and the increasing car dependency due to the rising traveling demand (Cervero, 2003; OECD, 2013). Therefore, policy-makers should concern both the favorable and adverse effects of new road construction for implementing better green growth policies and planning.
Discussion and conclusion
The trilemma of sustainable development
Through an analysis of almost 50 years of historical data, using both the ADRL and non-linear ADRL methods, this study has presented a trilemma among industrial growth, infrastructure development, and the emission reduction of air pollution and greenhouse gas.
The EKC of industrial growth
The current study is among the first to explain the EKC between industrial development and air pollution using the aggregate microeconomic data—the average industrial firm size calculated by the division of the total shipment value by the total number of firms in the city. From the aggregate microeconomic approach, this study validates the EKC hypothesis in terms of NO2 and CO emissions per capita but rejects the EKC hypothesis in terms of falling dust particle and Ox emissions per capita.
The initial decrease of air pollution in relation to the industrial growth after 1967 provides evidence for the effectiveness of the pollution prevention agreement between Kitakyushu government and the private sector in alleviating air pollution. This viewpoint is also supported by the fact that, from 1963, the municipal government had faced tremendous pressure from the local community due to poor environmental quality because of industrial development (Fujikura, 2007).
In this study, the existing inverted N-shaped relationships of NO2 and CO emissions with the industrial firm size hint at the vital contribution of large industrial enterprises to pollution reduction, as NO2 and CO are primarily the waste products of combustion of fuel for power generation and manufacturing. This result can be explained by previous studies, which have found large industrial firms to be more capable of replacing old, polluted, and energy-inefficient machines with better ones than small and mid-size firms (Andreoni and Levinson, 2001; Merlevede et al., 2006; Nielsen, 2018). Gaining the advantage of economies of scale over smaller firms, large firms are also able to consume fewer units of energy to produce a unit of output (Machado et al., 2016; Oh and Lee, 2016; Park et al., 2016). In addition, the energy sources in Kitakyushu city has been gradually shifted from coal and oil to natural gas and renewable energy since 1967, which leads to lower emissions of greenhouse gases and NO2 (De Gouw et al., 2014; Higazy et al., 2019; OECD, 2013). With 66% of energy in Kitakyushu city is consumed by industrial activities and energy conversion is more affordable to larger industrial firms, the emissions of NO2 and CO might be reduced as industrial firms grow. It has been reported that despite accounting for the largest proportion of energy consumption in Kitakyushu city, the industrial sector keeps growing while air emissions from energy generation are still under control (OECD, 2013). As such, the evidence points toward the EKC of NO2 and CO emissions are the results of (1) stringent pollution monitoring, controls and financial support of local government, (2) replacement of energy-efficient technologies, (3) economies of scale effects, and (4) the energy source conversion from coal and oil to natural gas and renewable sources.
However, our analysis also shows that the amount of falling dust particle and Ox, after the initial decline, starts to rise when the industrial sector expands to a level of $9.32 million to $10.91 million of shipment value per firm depends on the model of analysis. In 2013, the OECD report warned that where a rising number of large firms in iron steel, chemical, and automobile sectors, etc. are reported to outsource their activities to smaller firms to whom enforcement and inspection are more difficult to apply. This could essentially explain the analysis result. Hence, policy-makers in Kitakyushu city are suggested to revise inspection regulations with regards to small and medium firms in order to stay abreast of the changing dynamics of the industry.
The problems with infrastructure development
Besides the significant relationship between firm-level industrial growth and air pollution, we also found both negative and positive correlations of road infrastructure development with air pollution. On one hand, our analysis shows a positive effect of road construction on alleviating the amount of falling dust and CO concentration. These findings can be explained by the fact that as higher quality road is built, the manufacturing and recycling productivity and efficiency are elevated (Duran-Fernandez and Santos, 2014; Gibbons et al., 2019), which, in turns, leads to air emission reduction.
On the other hand, the emissions of NO2 and Ox are found to increase according to road infrastructure development. This finding points out the adverse effect of the policies facilitating recycling industrial growth in Kitakyushu city. Initially, the eco-industrial park in Kitakyushu city was planned to achieve industrial symbiosis, a closed system where the waste of an industry or a firm is fully consumed by others within the system. However, due to the demand for the revitalization of local economy, the eco-industrial park in Kitakyushu city has been turned into a hot spot of recycling industry, which was hoped to generate more economic profit, as well as to reduce environmental degradation (Ogihara, 2007). To attract investment to the recycling industry, the Kitakyushu government offers cheap and vast land located away from the residential area (Hammer et al., 2011), while more roads have been built to ensure the connectivity of industrial recycling firms with other industries and residential areas. In addition, to keep the growth rate of recycling industries, the road infrastructure needs expanding to make recycling materials and outputs flow among regions within and outside of Kitakyushu city. During the period from 2005 to 2010, the total amount of waste inputs from outside Kitakyushu city tripled, while the total amount of recycling outputs transported to locations within the eco-town, Kitakyushu city, and Fukuoka prefecture increased substantially (Tsuruta et al., 2016). Air pollution from transportation might rise dramatically due to recycling industrial activities, not to mention the increase in the number of personal vehicles because of increasing traveling demand (Cervero, 2003) and urban sprawl (OECD, 2013) when more roads are built.
Even in a stringent green growth regulation context, like Kitakyushu city, some air pollution emissions still eventually increase according to industrial growth and infrastructure expansion. This, as a result, creates a trilemma among industrial growth, infrastructure development, and air and greenhouse gas emission reduction. Indeed, dealing with climate change and air pollution while fostering industrial growth and road infrastructure development is a complicated business, which requires the involvement of multi-stakeholders, not only the government, the private sector, academia, but also the local community. We recommend policy-makers in Kitakyushu city promoting the usage of public transport instead of personal vehicles within the local community by raising awareness of air pollution and climate change.
Kitakyushu as a reference point of green growth for the global south?
It is clear that Japan has put significant efforts in finding a balance between the “industrial” and “green” parts of growth. Since the end of the 1990s, the Japanese government has considered the improvement of energy efficiency and energy innovations as the heart of a mission to achieve growth which was later upgraded into green growth (Government of Japan, 2007, 2010, 2014; Ministry of Economy, Trade and Industry, 1999). Many policies and strategies have been planned and implemented until currently, such as the Top Runner Program, Japan’s Strategy for a Sustainable Society, New Growth Strategy, Strategic Energy Plan, all of which consistently concentrate on fostering economic growth sustainably by creative innovations and the development of energy-related technologies (Government of Japan, 2007, 2010, 2014; Ministry of Economy, Trade and Industry, 1999). In the case of Kitakyushu city, the combination of political orientation, technological development, and economic incentives have resulted in two diverging patterns: the success with the general decline of NO2 and CO emissions when plotted against industrial growth, the worrying increase of dust particles and Ox after an early decline. It is clear there are limitations to the pioneering efforts of the local and national government in pursuing green growth.
Thus, the Kitakyushu city case can act as an important reference point for the pursuit of green growth in Japan, as well as the Global South. As a matter of fact, green growth orientation development has become more visible recently in many Global South countries, such as India and China (Death, 2015). One can argue if developing countries in the Global South manage to successfully implement green growth policies, the world can enjoy a much more sustainable future. To date, however, the effectiveness of the existing green growth practices in these developing countries has not been properly assessed (Li and Qiu, 2015). Hence, the lessons offered by Kitakyushu can be taken into account when policies are formed and progress is measured in the course of pursuing a green economy. The next parts will offer some of the suggestions from our results and the review of the literature.
In terms of CO emission, which is closely correlated with CO2 emission, this study found notable results that CO emission eventually declines when plotting against industrial development and road infrastructure expansion. This success partly thanks to the implementation of eco-town project—recycling industries, which have been shown in previous studies to significantly reduce the CO and CO2 emissions from the manufacturing process (Gielen and Moriguchi, 2002; Johnson et al., 2008; Zheng and Suh, 2019). As a result, three aspects of Kitakyushu’s eco-town project can be recommended. First, to achieve green growth development, collaboration across and within levels of government is required (Hammer et al., 2011). It is important for national and local governments to play a complementary role to each other. For Kitakyushu city’s eco-town project, while the national government provides legislative and financial support to the local government, the local government is responsible for collaborating with the private sector, providing any necessary support, and enforcing environmental regulations.
Second, technology innovations and green technology applications are the leverages of green growth in Kitakyushu. To enhance technology innovations and effectively apply green technology in the industrial sector, not only investment into green R&D and financial subsidy, but the cooperation among three stakeholders—government, private sector, and academia, need to be promoted (City of Kitakyushu, 2018). Through mutual corporation, the research outcome can be applied in practical context, and economic subsidies are given to multiply the effect of new technologies.
Third, the transparency of the green growth agenda in regional policies can also be one of the main contributors to the success in the alleviation of CO2 emissions in Kitakyushu city. Usually, the national green growth agenda is driven by sectoral ministries rather than people in charge of regional and spatial planning (Hammer et al., 2011). Nonetheless, Kitakyushu city has not only integrated the green growth agenda of Japan focusing on GHG emission reduction while maintaining the economic development (Government of Japan, 2010; Ministry of the Environment, 2016), but even set its own agenda reducing at least 50% of greenhouse gas emissions by 2050, while increase economic growth up to 40% by 2050 (OECD, 2013).
Last but not least, other cities in the Global South can indeed learn from the trilemma of Kitakyushu in pursuing industrial growth, infrastructure development and emission reduction of air pollution and greenhouse gas. It appears that this problem can be traced back to the strategic turn toward a focus on recycling activities rather than industrial symbiosis, as well as the trend of outsourcing to small and medium firm whom regulation is more difficult to enforce. Clearly, future studies that focus on the causes of this complex relationship and how to solve it will bring further insights. Nevertheless, the current lessons from the pioneering efforts of Kitakyushu will be helpful in the policy-planning for green growth in other cities.
Data policy and society 5.0 for the green growth future
This section will discuss the current data policy in Kitakyushu city, which is currently an OECD SDGs pilot city and the leading Asian green-growth city that might be the role model for other cities in the Global South. Apart from the openness of data, there are still several deficiencies in data management and stewardship in Kitakyushu city. First, judging by FAIR principles of data stewardship proposed by Wilkinson et al. (2016), the language barrier is one of the main problems hindering the findability and the interoperability of data. Currently, the data deposit on Kitakyushu’s website is only available in Japanese. To advance more and better science, as well as to play a role model for other cities in green growth development, Kitakyushu city is recommended to have its data related to green growth development available in other common languages in the Global South. Open and well-structured database not only enable scientific exploration but also enable the involvement of the general public in this process, thus, increasing the public trust (Vuong et al., 2018).
The data collection needs to be more detailed and specific to deal with the complex connections among emissions, concentrations, climate change, and impacts (National Research Council, 2011). For instance, with a more detailed and specific data on types of industrial firms, the results from this study could have explained more clearly the main sources of air pollution and greenhouse gas emissions. To acquire such detailed information from multiple sectors and sources, we suggest the local government to invest in the application of big data, which will offer new insights and address specific problems for innovating scientific research, as well as facilitating evidence-based policymaking (McNeely and Hahm, 2014; Michael and Miller, 2013; Vuong, 2018; Vuong, 2019).
Society 5.0, proposed in the 5th Science and Technology Basic Plan, aims to incorporate new technologies, such as IoT, big data, artificial intelligence (AI), for achieving economic development and solutions to social-environmental problems concurrently (Cabinet Office, 2019). As the Japanese government is nurturing the ambition of Society 5.0, Kitakyushu city can take this opportunity to revise its data policy employing big data for better green growth development. The complex interaction among industrial growth, road construction, and air pollution highlighted in this study might be a befitting case for the application of big data and artificial intelligence to solve urban problems (Duarte and Álvarez, 2019).
Methodology for future research
When employing the linear and non-linear ARDL analyses in this study, we found one shortfall of the non-linear ARDL model. The non-linear ARDL model seems to not work well with cumulative data, for instance, the total area of paved road. In fact, the total area of paved road in Kitakyushu accumulated over time and only declined in 2014, which creates outlier in the variable “lnRoad_n”, and eventually leads to inaccurate estimation of the asymmetric effect and the relationship between “lnRoad_n” and “lnAirPollution”. Thus, later studies should be aware of the properties of a variable before using non-linear ARDL analysis.
Future studies examining the EKC should employ not only the augmented model by squared and cubic variables, but also the new approach of Narayan and Narayan (2010), comparing the long-run and short-run coefficients of economic indicators, for comparison. Comparing the results from the two methods will help verify the robustness of the current findings, as well as cover some shortcomings of both methods; for example, the econometric weakness of the augmented approach and incapability to find a turning point of Narayan and Narayan’s approach.
Data availability
The datasets analyzed in this study are available in the Dataverse repository: https://doi.org/10.7910/DVN/4BEQ0X. These datasets were derived from the following public domains:
https://www.city.kitakyushu.lg.jp/soumu/file_0348.html;
https://www.city.kitakyushu.lg.jp/soumu/file_0351.html;
References
Abokyi E, Appiah-Konadu P, Abokyi F et al. (2019) Industrial growth and emissions of CO2 in Ghana: the role of financial development and fossil fuel consumption. Energy Rep 5:1339–1353. https://doi.org/10.1016/j.egyr.2019.09.002
Ahmad N, Du L, Lu J et al. (2017) Modelling the CO2 emissions and economic growth in Croatia: is there any environmental Kuznets curve? Energy 123:164–172. https://doi.org/10.1016/j.rser.2016.12.106
Akbostancı E, Türüt-Aşık S, Tunç Gİ (2009) The relationship between income and environment in Turkey: is there an environmental Kuznets curve? Energ Policy 37(3):861–867. https://doi.org/10.1016/j.enpol.2008.09.088
Ali W, Abdullah A, Azam M (2017) Re-visiting the environmental Kuznets curve hypothesis for Malaysia: fresh evidence from ARDL bounds testing approach. Renew Sust Energ Rev 77:990–1000. https://doi.org/10.1016/j.rser.2016.11.236
Andreoni J, Levinson A (2001) The simple analytics of the environmental Kuznets curve. J Public Econ 80(2):269–286. https://doi.org/10.1016/S0047-2727(00)00110-9
Anenberg SC, Henze DK, Tinney V et al. (2018) Estimates of the global burden of ambient PM2.5, Ozone, and NO2 on asthma incidence and emergency room visits. Environ Health Persp 126(10):107004. https://doi.org/10.1289/EHP3766
Banerjee A, Dolado J, Mestre R (1998) Error-correction mechanism tests for cointegration in a single-equation framework. J Time Ser Anal 19(3):267–283. https://doi.org/10.1111/1467-9892.00091
Barnes PW, Williamson CE, Lucas RM et al. (2019) Ozone depletion, ultraviolet radiation, climate change and prospects for a sustainable future. Nat Sustain 2:569–579. https://doi.org/10.1038/s41893-019-0314-2
Bölük G, Mert M (2015) The renewable energy, growth and environmental Kuznets curve in Turkey: an ARDL approach. Renew Sust Energ Rev 52:587–595. https://doi.org/10.1016/j.rser.2015.07.138
Cabinet Office (2019) Society 5.0. https://www8.cao.go.jp/cstp/english/society5_0/index.html. Accessed 23 Oct 2019
Cervero R (2003) Road expansion, urban growth, and induced travel: a path analysis. JAPA 69(2):145–163. https://doi.org/10.1080/01944360308976303
City of Kitakyushu (2018) Kitakyushu city the sustainable development goals report 2018. Institute for global environmental strategies, Kanagawa
City of Kitakyushu (n.d.) 2. 人口 [2. Population]. https://www.city.kitakyushu.lg.jp/soumu/file_0348.html. Accessed 13 June 2019
City of Kitakyushu (n.d.) 5. 工業 [5. Industry]. https://www.city.kitakyushu.lg.jp/soumu/file_0351.html. Accessed 13 June 2019
City of Kitakyushu (n.d.) 14. 建設、住宅 [14. Construction and Housing]. https://www.city.kitakyushu.lg.jp/soumu/file_0306.html. Accessed 13 June 2019
City of Kitakyushu (n.d.) 16. 衛生、環境、公害 [16. Hygiene, Environment, Pollution]. https://www.city.kitakyushu.lg.jp/soumu/file_0308.html. Accessed 13 June 2019
Crespo Cuaresma J, Danylo O, Fritz S et al. (2017) Economic development and forest cover: evidence from satellite data. Sci Rep 7(1):40678. https://doi.org/10.1038/srep40678
Daniel JS, Solomon S (1998) On the climate forcing of carbon monoxide. J Geophys Res-Atmos 103(D11):13249–13260. https://doi.org/10.1029/98JD00822
De Bruyn SM (1997) Explaining the environmental Kuznets curve: structural change and international agreements in reducing sulphur emissions. Environ Dev Econ 2(4):485–503. https://doi.org/10.1017/S1355770X97000260
De Gouw JA, Parrish DD, Frost GJ et al. (2014) Reduced emissions of CO2, NOx, and SO2 from U.S. power plants owing to switch from coal to natural gas with combined cycle technology. Earths Future 2(2):75–82. https://doi.org/10.1002/2013EF000196
Death C (2015) Four discourses of the green economy in the global South. Third World Q 36(12):2207–2224. https://doi.org/10.1080/01436597.2015.1068110
Diao XD, Zeng SX, Tam CM et al. (2009) EKC analysis for studying economic growth and environmental quality: a case study in China. J Clean Prod 17(5):541–548. https://doi.org/10.1016/j.jclepro.2008.09.007
Dinda S (2004) Environmental Kuznets Curve hypothesis: a survey. Ecol Econ 49(4):431–455. https://doi.org/10.1016/j.ecolecon.2004.02.011
Duarte F, Álvarez R (2019) The data politics of the urban age. Pal Commun 5(1):54. https://doi.org/10.1057/s41599-019-0264-3
Duran-Fernandez R, Santos G (2014) Regional convergence, road infrastructure, and industrial diversity in Mexico. Res Transp Econ 46:103–110. https://doi.org/10.1016/j.retrec.2014.09.007
Engle RF, Granger CWJ (1987) Co-Integration and error correction: representation, estimation, and testing. Econometrica 55(2):251. https://doi.org/10.2307/1913236
Friedman L (2019) White house tried to stop climate science testimony, documents show. https://www.nytimes.com/2019/06/08/climate/rod-schoonover-testimony.html. Accessed 14 June 2019
Fujikura R (2007) Administrative guidance of Japanese local government for air pollution control. In: Terao T, Otsuka K (eds) Development of Environmental Policy in Japan and Asian Countries. Palgrave Macmillan, London, p 90–116
Galeotti M, Lanza A (2005) Desperately seeking environmental Kuznets. Environ Mode Softw 20(11):1379–1388. https://doi.org/10.1016/j.envsoft.2004.09.018
Ge X, Zhou Z, Zhou Y et al. (2018) A spatial panel data analysis of economic growth, urbanization, and NOx emissions in China. Int J Environ Res Public Health 15(4):725. https://doi.org/10.3390/ijerph15040725
Gibbons S, Lyytikäinen T, Overman HG et al. (2019) New road infrastructure: the effects on firms. J Urban Econ 110:35–50. https://doi.org/10.1016/j.jue.2019.01.002
Gielen D, Moriguchi Y (2002) CO2 in the iron and steel industry: an analysis of Japanese emission reduction potentials. Energ Policy 30(10):849–863. https://doi.org/10.1016/S0301-4215(01)00143-4
Government of Japan (2007) Becoming a leading environmental nation in the 21st century: Japan’s strategy for a sustainable society. https://www.env.go.jp/en/focus/attach/070606-b.pdf
Government of Japan (2010) On the new growth strategy. https://www.cas.go.jp/jp/seisaku/npu/policy04/pdf/20100706/20100706_newgrowstrategy.pdf
Government of Japan (2014) Strategic energy plan. https://www.enecho.meti.go.jp/en/category/others/basic_plan/pdf/4th_strategic_energy_plan.pdf
Grossman G, Krueger A (1991) Environmental impacts of a North American Free Trade Agreement. National Bureau of Economic Research, Cambridge. https://doi.org/10.3386/w3914
Grossman GM, Krueger AB (1995) Economic growth and the environment. Q J Econ 110(2):353–377. https://doi.org/10.2307/2118443
Guderian R (1985) Air pollution by photochemical oxidants: formation, transport, control, and effects on plants. Springer Berlin Heidelberg, Berlin. http://public.eblib.com/choice/publicfullrecord.aspx?p=3091349
Hammer S, Kamal-Chaoui L, Robert A et al. (2011) Cities and green growth: a conceptual framework. OECD Regional Development Working Papers. https://doi.org/10.1787/5kg0tflmzx34-en
Higazy M, Essa KSM, Mubarak F et al. (2019) Analytical study of fuel switching from heavy fuel oil to natural gas in clay brick factories at Arab Abu Saed, Greater Cairo. Sci Rep 9(1):10081. https://doi.org/10.1038/s41598-019-46587-w
Hill RJ, Magnani E (2002) An exploration of the conceptual and empirical basis of the Environmental Kuznets Curve. Australian EP 41(2):239–254. https://doi.org/10.1111/1467-8454.00162
Holroyd C (2018) Green Japan: environmental technologies, innovation policy, and the pursuit of green. Growth. University of Toronto Press, Toronto
Japan for Sustainability (2013) ‘Kitakyushu Model’ for Green City Development Published in Three Languages. https://www.japanfs.org/en/news/archives/news_id034461.html?fbclid=IwAR2zr4lxkY8aNrh00iHbVH_5_kx5b__4RItTm2cMmDDPmgjDokpJioAl9eU. Accessed 11 Nov 2019
Johansen S (1988) Statistical analysis of cointegration vectors. J Econ Dyn Control 12(2–3):231–254. https://doi.org/10.1016/0165-1889(88)90041-3
Johnson J, Reck BK, Wang T et al. (2008) The energy benefit of stainless steel recycling. Energ Policy 36(1):181–192. https://doi.org/10.1016/j.enpol.2007.08.028
Kijima M, Nishide K, Ohyama A (2010) Economic models for the environmental Kuznets curve: a survey. J Econ Dyn Control 34(7):1187–1201. https://doi.org/10.1016/j.jedc.2010.03.010
Kripfganz S, Schneider DC (2016) ARDL: Stata module to estimate autoregressive distributed lag models. Chicago. https://www.stata.com/meeting/chicago16/slides/chicago16_kripfganz.pdf. Accessed 8 Apr 2019
Lamsal LN, Martin RV, Parrish DD et al. (2013) Scaling relationship for NO2 pollution and urban population size: a satellite perspective. Environ Sci Technol 47(14):7855–7861. https://doi.org/10.1021/es400744g
Lelieveld J, Evans JS, Fnais M et al. (2015) The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 525(7569):367–371. https://doi.org/10.1038/nature15371
Li Y, Qiu L (2015) A comparative study on the quality of China’s eco-city: Suzhou vs Kitakyushu. Habitat Int 50:57–64. https://doi.org/10.1016/j.habitatint.2015.08.005
Low M (2013) Eco-cities in Japan: past and future. J Urban Technol 20(1):7–22. https://doi.org/10.1080/10630732.2012.735107
Machado MM, de Sousa MCS, Hewings G (2016) Economies of scale and technological progress in electric power production: The case of Brazilian utilities. Energy Econ 59:290–299. https://doi.org/10.1016/j.eneco.2016.06.017
Mahmood H, Maalel N, Zarrad O (2019) Trade openness and CO2 emissions: evidence from Tunisia. Sustainability 11(12):3295. https://doi.org/10.3390/su11123295
McNeely CL, Hahm J (2014) The big (Data) bang: policy, prospects, and challenges: big (Data) bang. Rev Policy Res 31(4):304–310. https://doi.org/10.1111/ropr.12082
Merlevede B, Verbeke T, De Clercq M (2006) The EKC for SO2: foes firm size matter? Ecol Econ 59(4):451–461. https://doi.org/10.1016/j.ecolecon.2005.11.010
Michael K, Miller KW (2013) Big data: new opportunities and new challenges [Guest editors’ introduction]. Computer 46(6):22–24. https://doi.org/10.1109/MC.2013.196
Ministry of Economy, Trade and Industry (1999) Top runner program. Ministry of economy, trade and industry. https://www.iea.org/policiesandmeasures/pams/japan/name-21573-en.php. Accessed 20 Oct 2019
Ministry of the Environment (2016) Overview of the plan for global warming countermeasures. https://www.env.go.jp/press/files/en/676.pdf. Accessed 20 Oct 2019
Mora C, Spirandelli D, Franklin EC et al. (2018) Broad threat to humanity from cumulative climate hazards intensified by greenhouse gas emissions. Nat Clim Change 8(12):1062–1071. https://doi.org/10.1038/s41558-018-0315-6
Narayan PK, Narayan S (2010) Carbon dioxide emissions and economic growth: panel data evidence from developing countries. Energ Policy 38(1):661–666. https://doi.org/10.1016/j.enpol.2009.09.005
National Research Council (2011) America’s climate choices. National Academies Press, Washington. https://doi.org/10.17226/12781
Nielsen H (2018) Technology and scale changes: the steel industry of a planned economy in a comparative perspective. Econ His Dev Reg 33(2):90–122. https://doi.org/10.1080/20780389.2018.1432353
OECD (2013) Green Growth in Kitakyushu, Japan. OECD Green Growth Studies. https://doi.org/10.1787/9789264195134-en
Ogihara A (2007) Eco-industrial park policies in Japan and PRC. Paper presented at 3R Workshop on Effective Waste Management and Resource Use Efficiency in East and Southeast Asia, Manila, Philippines, 2007. https://iges.or.jp/en/pub/eco-industrial-park-policies-japan-and-prc
Oh D, Lee Y-G (2016) Productivity decomposition and economies of scale of Korean fossil-fuel power generation companies: 2001–2012. Energy 100:1–9. https://doi.org/10.1016/j.energy.2016.01.004
Ota T (2017) Economic growth, income inequality and environment: assessing the applicability of the Kuznets hypotheses to Asia. Pal Commun 3(1):17069. https://doi.org/10.1057/palcomms.2017.69
Ozcan B (2013) The nexus between carbon emissions, energy consumption and economic growth in Middle East countries: a panel data analysis. Energ Policy 62:1138–1147. https://doi.org/10.1016/j.enpol.2013.07.016
Özokcu S, Özdemir Ö (2017) Economic growth, energy, and environmental Kuznets curve. Renew Sust Energ Rev 72:639–647. https://doi.org/10.1016/j.rser.2017.01.059
Panaĭotou T (1993) Empirical tests and policy analysis of environmental degradation at different stages of economic development. International Labour Organization, Geneva
Panayotou T (1997) Demystifying the environmental Kuznets curve: turning a black box into a policy tool. Environ Dev Econ 2(4):465–484. https://doi.org/10.1017/S1355770X97000259
Park S-Y, Lee K-S, Yoo S-H (2016) Economies of scale in the Korean district heating system: a variable cost function approach. Energ Policy 88:197–203. https://doi.org/10.1016/j.enpol.2015.10.026
Pesaran MH, Shin Y (1999) An Autoregressive Distributed-Lag modelling approach to cointegration analysis. In: Strom S (ed) Econometrics and economic theory in the 20th Century. Cambridge University Press, Cambridge, p 371–413. https://doi.org/10.1017/CCOL521633230.011
Pesaran MH, Shin Y, Smith RJ (2001) Bounds testing approaches to the analysis of level relationships. J Appl Econom 16(3):289–326. https://doi.org/10.1002/jae.616
Phillips PCB, Hansen BE (1990) Statistical inference in instrumental variables regression with I(1) processes. Rev Econ Stud 57(1):99. https://doi.org/10.2307/2297545
Rafindadi AA (2016) Revisiting the concept of environmental Kuznets curve in period of energy disaster and deteriorating income: Empirical evidence from Japan. Energ Policy 94:274–284. https://doi.org/10.1016/j.enpol.2016.03.040
Shafik N, Bandyopadhyay S (1992) Economic growth and environmental quality: time-series and cross-country evidence. World Bank, Washington
Sharma SS (2011) Determinants of carbon dioxide emissions: empirical evidence from 69 countries. Appl Energy 88(1):376–382. https://doi.org/10.1016/j.apenergy.2010.07.022
Shin Y, Yu B, Greenwood-Nimmo M (2014) Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework. In: Sickles R, Horrace WC (eds) Festschrift in Honor of Peter Schmidt. Springer-Verlag, New York, p 281–314
Sinha A, Bhattacharya J (2016) Environmental Kuznets curve estimation for NO2 emission: a case of Indian cities. Ecol Indic 67:1–11. https://doi.org/10.1016/j.ecolind.2016.02.025
Strode SA, Duncan BN, Yegorova EA et al. (2015) Implications of carbon monoxide bias for methane lifetime and atmospheric composition in chemistry climate models. Atmos Chem Phys 15(20):11789–11805. https://doi.org/10.5194/acp-15-11789-2015
Thacker S, Adshead D, Fay M et al. (2019) Infrastructure for sustainable development. Nat Sust 2(4):324–331. https://doi.org/10.1038/s41893-019-0256-8
The World Bank (1996) Japan’s experience in urban environmental management: Kitakyushu, a case study. World Bank Environment and Natural Resources Division, Washington
Tsuruta T, Honda Y, Fujiyama A et al. (2016) Structural changes in the Kitakyushu eco-town initiative based on a multi-year survey of materials flow. Int J of Environ Sci Dev 7(12):908–912. https://doi.org/10.18178/ijesd.2016.7.12.903
Vrieze SI (2012) Model selection and psychological theory: a discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol Methods 17(2):228–243. https://doi.org/10.1037/a0027127
Vuong QH (2018) The (ir)rational consideration of the cost of science in transition economies. Nat Hum Behav 2(1):5–5. https://doi.org/10.1038/s41562-017-0281-4
Vuong QH, La VP, Vuong TT et al. (2018) An open database of productivity in Vietnam’s social sciences and humanities for public use. Sci Data 5:180188. https://doi.org/10.1038/sdata.2018.188
Vuong QH (2019) Breaking barriers in publishing demands a proactive attitude. Nat Hum Behav 3(10):1034. https://doi.org/10.1038/s41562-019-0667-6
Wallace-Wells D (2019) The uninhabitable earth: life after warming, First edition. Tim Duggan Books, New York
Wang Y, Wang J (2019) Does industrial agglomeration facilitate environmental performance: new evidence from urban China? J Environ Manage 248:109244. https://doi.org/10.1016/j.jenvman.2019.07.015
WHO (2019) Air Pollution. https://www.who.int/airpollution/en/. Accessed 8 May 2019
Wilkinson MD, Dumontier M, Aalbersberg IjJ et al. (2016) The FAIR guiding principles for scientific data management and stewardship. Sci Data 3(1):160018. https://doi.org/10.1038/sdata.2016.18
Yoshioka S, Kawasaki H (2016) Japan’s high-growth postwar period: the role of economic plans. Econ Soc Res Institute. The Government of Japan
Zhang K, Batterman S (2013) Air pollution and health risks due to vehicle traffic. Sci Total Environ 450–451:307–316. https://doi.org/10.1016/j.scitotenv.2013.01.074
Zheng J, Suh S (2019) Strategies to reduce the global carbon footprint of plastics. Nat Clim Change 9(5):374–378. https://doi.org/10.1038/s41558-019-0459-z
Zhong Q, Huang Y, Shen H et al. (2017) Global estimates of carbon monoxide emissions from 1960 to 2013. Environ Sci Pollut Res 24(1):864–873. https://doi.org/10.1007/s11356-016-7896-2
Acknowledgements
We thank Prof. Sudo Tomonori and Prof. Li Yan (Ritsumeikan Asia Pacific University) for their helpful advice and comments during the course of this research. We would also like to express our gratitude to the International Environmental Strategies Division of Kitakyushu city for providing necessary information.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vuong, QH., Ho, MT., Nguyen, HK.T. et al. The trilemma of sustainable industrial growth: evidence from a piloting OECD’s Green city. Palgrave Commun 5, 156 (2019). https://doi.org/10.1057/s41599-019-0369-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-019-0369-8