Introduction

Insights from the behavioural sciences are increasingly applied to policy settings (Slatev et al. 2017). Two popular tools in both research and practice are nudges, interventions aimed at influencing behaviour without limiting or forcing options (Sunstein 2014), and boosts, interventions aimed at fostering competencies that improve capacity for choice (Grüne-Yanoff and Hertwig 2016; Hertwig 2017). Although commonly discussed in the same scientific and policy context, few studies have directly compared nudges and boosetts (Hertwig and Grüne-Yanoff 2017).

Direct comparisons of these tools would offer critical insight into the contexts and populations in which one intervention may offer superior features, or where each may serve as useful complements to the other. As has been argued for explicitly in recent literature (Hertwig and Grüne-Yanoff 2017), this is of particular importance in policy contexts that are increasingly characterised by substantial economic and social inequalities, which can result in greater risk taking (Payne et al. 2017) and greater costs to vulnerable populations.

In this study, we compare the effects of two nudges (a disclosure and a descriptive social norm), a boost (explicit training to better understand choices), and a control condition. Each intervention is considered potentially useful for encouraging advantageous financial decisions under risk (Pedroni et al. 2017), a domain with well-studied patterns for suboptimal choice (Cox et al. 2015). Specifically, we explored a decision context in which participants choose between one of two options (one risky and one certain), with one being more advantageous than the other. To date, no research has produced insights in these methods with directly comparing the nudges and boosts.

Recent research suggests that individuals quickly learn to choose advantageously in environments that promote certain behaviours with better payoffs (Erev and Roth 2014). We consider decisions as advantageous if they have a higher expected value (EV; the total value multiplied by the probability of occurrence) than the alternatives (Kagel and Roth 2016). Decisions were considered suboptimal if individuals choose the prospect with a lower EV.Footnote 1 A prospect is an option comprising specific monetary value and probability of occurrence (Von Neumann et al. 2007).

Disclosures are nudges that present decision-relevant information in an explicit way, ensuring an individual is aware of critical, salient details prior to a choice. ‘Information’ in this context refers to the calculated EVs of prospects (Sunstein 2014), which are rooted in two empirically driven theoretical assumptions:

  1. (1)

    Reducing uncertainty with decision-relevant information increases advantageous choice (Bell 1982, 1985, Lempert 2002);

  2. (2)

    Disclosure nudges can create an emphasis framing, making relevant information more salient (Chong and Druckman 2007).

The second nudge, a descriptive social norm, informed participants of the most popular choice, which was the prospect with the highest EV. This application of descriptive social norms is rooted in two assumptions:

  1. (1)

    Individual decisions will seek to align with normative group behaviours (Cialdini and Goldstein 2004; Sherman et al. 2014)

  2. (2)

    A social norm will have greater influence if the norm is made more salient (Cialdini et al. 1991).

Boosts aim to promote individual understanding of statistical information to enhance decision-making capabilities (Berkowits et al. 2015; Hogarth and Soyer 2015; Lusardi et al. 2017; Dhami et al. 2018). Boosting is rooted in the assumption that some heuristics are used unconsciously, while others are explicitly learned and deliberately applied (Gigerenzer and Selten 2002; Johnson et al. 2013). If this is accurate, individuals should be able to exert effortful thinking to recognise and override heuristic judgements, to the extent to which they are aware that a choice resulting from heuristics is incorrect. Kahneman concludes that people are mostly unaware of cognitive errors and are therefore unable to override them (Kahneman 2003). On that assumption, using boosts is a riskier approach to increase advantageous choice because, regardless of individual judgement ability, flawed heuristics may still result in suboptimal decisions.

In the studies we present here, the boost taught participants a specific skill and a decision rule. Specifically, participants were taught how to calculate the EV of a prospect and were then told to choose the prospect with the highest EV. In doing so, applying the rule should be most likely to increase overall payoff. This boost derived from studies that use ‘rule-of-thumb’ training to promote advantageous choice, finding that such training showed larger effects on financial choice than formal accounting training (Drexler et al. 2014).

Prospect Theory postulates that for losses, a certain (guaranteed) loss has a lower subjective magnitude than an uncertain (unguaranteed) loss, which explains increased frequency of risky choices (Tversky and Kahneman 1992). For gains, a certain outcome has a higher subjective magnitude than an uncertain one; thus, increasing the frequency of certain choices. Individuals are therefore more likely to be risk-averse for gains and risk-seeking for losses (Tversky and Kahneman 1986, 1991). This is evident in the framing effect: the idea that the presentation of a prospect will influence how it is judged. This forms the fundamentals of prevailing theory that individuals may be inconsistent in choosing two logically equivalent prospects if framed differently (Kahneman and Tversky 1984).

The Reflection Effect posits that a single, common parameter governs risk-seeking such that individuals who are more risk-averse for gains are also less risk-averse for losses (Kahneman and Tversky 1979). A recent paper challenges this, concluding that there is no significant correlation between risk preferences (i.e., the tendency to take or to avoid risk) for gains and losses on an individual level (Kurnianingsih and Mullette-Gillman 2015). Specifically, although the Reflection Effect holds on the population level, it is not strictly consistent within individuals. Thus, the effectiveness of an intervention may vary substantially depending on the option they seek to promote and on the prospect’s frame.

This approach is further meaningful as individual differences in risk preference are also critical to consider, particularly if there is a population-level application involved (Ruggeri et al. 2017). Such applications are commonly the case in behavioural interventions within policy settings. Sunstein argued that strong behavioural preferences moderate the effectiveness of interventions (Sunstein 2017). Indeed, even if an intervention is theoretically sound, targets a relevant construct, and is implemented correctly, individual, contextual and population-specific mediators can make them ineffective, or even irrelevant (Chaiyachati et al. 2018).

Certain risk preferences correlate with specific sociodemographic backgrounds. Findings indicate that risk aversion increases with age (Hallahan et al. 2004) and falls with greater education attainment (Grable 2000) and higher income (Hartog et al. 2002). Other studies have found that women are more likely to be risk-averse than men (Eckel and Grossman 2002), married people more risk-averse than singles (Hallahan et al. 2004), and people who have never moved to another country more risk-averse than immigrants (Halek and Eisenhauer 2001). Finally, unemployed individuals (Halek and Eisenhauer 2001) and self-employed workers (Masclet et al. 2009) are less likely to be risk-averse than salaried workers, and public-sector employees are more likely to be risk-averse than private-sector employees (Hartog et al. 2002).

Using an online assessment of participants making a series of binary decisions, we were able to:

  1. (1)

    Infer the effects (on choice) of disclosure nudges, boosts, and descriptive social norms to identify intervention effectiveness in promoting advantageous choice;

  2. (2)

    explore how prospect framing influenced intervention effectiveness;

  3. (3)

    investigate whether sociodemographic factors moderate intervention effectiveness;

  4. (4)

    determine if findings are consistent between a US and a Serbian sample;

  5. (5)

    compare patterns between hypothetical choices and consequential items using real money.

Method

Design

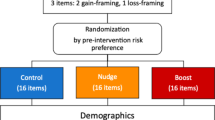
To control for potential confounding effects of individual differences on choice, we used matched controls to allocate participants to four different groups—control, disclosure, descriptive social norm, and the boost group. Before being exposed to an intervention, participants made a binary decision involving a risky and certain prospect with equal EVs. The item asked, ‘Which of the following would you prefer: A 50% chance to win $2000 or a 50% chance to win nothing, or A 100% chance to win $1000’; 0.5 × 2000 = 1000 is equal to 1000, so no option was more advantageous. This allowed for an equal allocation of participants that choose the risky option to all groups. Participants also made two additional binary decisions where one prospect was more advantageous than the other. The three decisions established participant ‘baseline decisions’, which were later compared with their postintervention decisions.

Participants in the control groups were not subject to an intervention. Participants in the disclosure group received information on prospect EVs, which served as an explicit indication of the most advantageous prospect. In the social norm group, participants were exposed to a descriptive social norm which told them which prospect was selected most by other participants. Participants in this condition were informed that the prospect with the highest EV was the most popular choice. The design of nudges should steer decisions towards advantageous prospects (Thaler and Sunstein 2008). Participants in the boost group learned the concept of EV, how EVs are calculated, and why choosing prospects with higher EVs overall leads to more advantageous decisions. The intervention ended with a test where participants had to calculate the EVs of three prospects. Participants in this group were encouraged to use calculators. Boost design ensures that participants can calculate EVs to make advantageous choices as they were not allowed to continue the survey until they answered the three practice items correctly.

Once allocated, participants made decisions on eight discrete, binary items. Each item consisted of one certain prospect (100% chance of occurring) and one risky prospect (uncertain chance of occurring). Each prospect differed in monetary value, framing, and risk. This designed allowed us to explore when risky choices are more likely to occur, and how interventions affect this. A pilot study was conducted for experimental item selection (see Supplementary Information (SI)).

Four items had certain prospects worth $200 and were considered low magnitude. The other four had certain prospects worth $1000 and were considered high magnitude. In each magnitude bracket, the difference in EV between the two prospects remained constant, regardless of whether they were framed as losses or gains. Thus, risky prospects of the same magnitude always yield the same EV. See the SI for a table showing the prospects of all the experimental items.

Items presented risky prospects as either high-risk (25% chance of occurring) or low-risk (75% chance of occurring). Depending on whether the risky prospect had a lower or higher EV than its respective certain prospect, items were either low-advantage or high-advantage, respectively. Choosing risky prospects was suboptimal for low-advantage items and advantageous for high-advantage items. To illustrate: one of the items asked, ‘Which one of the following do you prefer: A 25% chance to win $910 or a 75% chance to win nothing or A 100% chance to win $200’; 0.25 × 910 = 227.50 is greater than 200, so the risky option is the advantageous option.

Prospects in low-advantage items were framed as losses, while prospects in high-advantage items were framed as gains. This controlled for the effects of framing on decisions (Tversky and Kahneman 1992). Specifically, risky prospects in low-advantage items are less likely to be chosen because they are less advantageous. In gain frames, they are even less likely to be chosen because risky choice occurs less in this context (Tversky and Kahneman 1991). The use of loss frames for low-advantage items avoided the counter-effects of gain frames steering participants away from risk. Such a design is not necessary for high-advantage items, because participants are more likely to choose the risky prospect as it is more advantageous than the certain prospects. Altogether, this paradigm allowed for the exploration of choice, when certain choices either did or did not increase EV, in contexts with different monetary values, expressed either as gains or losses.

To test changes in advantageous choice, we summed the number of advantageous choices each participant made for the four items with a gain frame, and four items with a loss frame. We will refer to these sums as Advantageous Choice Scores (ACS), ranging from 0 to 4. If these two scores were positively correlated we would have combined them into a single score ranging from 0 to 8, where 8 would mean consistently choosing the advantageous option. However, as they did not correlate strongly, we analysed risky decisions for losses and gains independently.

Decision items were randomised to avoid order effects. To avoid any stereotype threats, the nine sociodemographic items were asked last (Nardi 2018). All variables are associated with specific risk preferences and likely to influence choice for some participants. Our aim was to assess general patterns of choice under risk along with certain interventions, and then to see of these patterns replicate in a different country and language. As we do not focus on cross-national comparisons, we present replication findings after the original trial, rather than contemporaneously. Details on replication methods are in SI, as they are generally identical to the main study methods.

Experimental procedures

The study was administered through Qualtrics. US participants were told that their decisions would not result in real monetary outcomes. Responding to all items was mandatory, although participants had the right to leave the study at any point. Informed consent was obtained from all participants.

Participants first responded to three decision items. They were then split into one of the four groups. Unless they were in the control group, they were exposed to an intervention. They then responded to eight decision-making items. Finally, participants were asked about calculator use, and answered nine sociodemographic questions. The survey used this order because the sociodemographic questions could prime answers to the decision items, an effect known as social priming (Molden 2014).

Study data will be publicly available on GitHub.

Participants

A power analysis was run to determine the smallest sample size suitable to detect the effects of an ANOVA. The alpha level set to 0.05 and a power set to 0.8. The estimation indicated that the minimum number of participants had to be 123, with a final sample of 1009 achieved. The larger than necessary sample size was recruited to run more complex analyses for which power analysis was harder to conduct.

For the initial study, participants had to be from the US and above the age of 18. The study expressed monetary values in US dollars. The 1124 participants were recruited via Amazon Mechanical Turk.

Measures

Decision-making items

The eight items are described in the previous section.

Baseline risk-taking

Three items were used to measure participant preintervention baseline decisions on risk. They are described earlier and are available in the SI.

Sociodemographic variables

We measured: age, gender, country of residence, highest level of completed education, relationship status, parental status, employment status, work sector (public or private), immigration status, and annual household income.

Other

Participants were asked whether they used a calculator.

Replication

For the replication study, the items were translated from English to Serbian by one of the members of our research team, who is a Serbian–English bilingual. The translation was proofread, edited, and back-translated by four individuals that speak both English and Serbian. Decision-making items used euros rather than dollars, as people in Serbia are more familiar with this currency and often use it in private transactions. Income bands were modified to fit recently published deciles in Serbia for the demographic items. The replication survey used two additional consequential items expressed in Serbian dinars that resulted in real-life financial outcomes for the participants. One item was framed as a loss while the other framed as a gain. Consequential item values in dinars were identical in number to euros, though the real value is ~1 euro to 100 dinars. Participants were recruited through Ipsos, a market survey company with an office in Serbia.

Statistical modelling

All Bayesian models reported for the US sample were conducted using the brms package (v. 1.9; Bürkner 2017) which is an R-wrapper (v. 3.4.3) for STAN (v. 2.16). All models used improper flat priors across all parameters. Each model used 589 as a seed and sampled four chains with 4000 iterations in each, discarding the first 1000 samples for burn in, resulting in 12,000 posterior samples for each model. All model parameters converged with Rhat values of 1, down to 3° of precision.

All Bayesian models reported for the Serbian sample were conducted using the brms package (v. 2.7) (56) which is an R-wrapper (v. 3.5.2) for STAN (v. 2.18.1). All models used improper flat priors across all parameters. Each model used 671 as a seed and sampled four chains with 4000 iterations in each, discarding the first 1000 samples for burn in, resulting in 12,000 posterior samples for each model. All model parameters converged with Rhat values of 1, down to 3° of precision.

The lasso regressions were fit using glmnet (v. 2.0–13) (Friedman et al. 2010). The data were split into five folds using the groupKFold function in the caret package (v. 6.0–87), using 589 as a seed. The AUROC to compute the GINI coefficients for the logistic model comparisons were computed using pROC (v. 1.10; Robin et al. 2011).

Bootstrapped confidence intervals for Spearman correlations were computed by drawing 100,000 new samples with replacement, computing the correlation coefficients for each of these simulated samples and checking the 2.5th and 97.5th percentile of the resulting distribution of correlation coefficients. The resampling and correlations were conducted in pandas (v. 0.24.1).

Results

US sample

In total, 1124 participants completed the survey. To increase the probability that data for analyses included only participants that paid attention during the survey, participants whose total survey duration was faster than 110 s (meaning that they had taken <5 s per question, on average) were excluded (105 participants). We also excluded participants who had total survey durations >3 standard deviations of the mean in log(seconds) (1279 s; ten participants). The final sample was 1009 participants. After exclusions, all groups were approximately balanced, with 257 people in the control condition, 254 in the social norm condition, 263 in the disclosure condition, and 235 in the boost condition. The final sample was gender balanced between females (n = 494; 49%) and males. Participant ages ranged from 19 to 89 (m = 38.1, sd = 12.6), 60% had a college degree or higher, 17% had junior college, and 23% had high school or less).

Decision patterns and relationship between decisions for gains and losses

We first tested whether advantageous decisions for gains and losses correlated. We found that ACS in the gain frame only had a weak relationship with ACS in the loss frame (Spearman’s ρ = −0.12, bootstrapped 95% CI = −0.05 to −0.18, p = 0.0002; see Fig. 1), in line with recent research on risk preferences (Kurnianingsih and Mullette-Gillman 2015; Tymula et al. 2013). Consequently, we separated the ACS for gains and losses, giving two separate outcome measures ranging from 0 to 4; ACSgains and ACSlosses.

Fig. 1
figure 1

Advantageous choices do not correlate strongly between the gain and loss frame, and participants were generally risk-averse. Advantageous decision-making in the gain frame was not strongly associated with advantageous decision-making in the loss frame within participants, as ACS scores were only weakly correlated between the gain frame and the loss frame (a). Observations have been made semi-transparent and jittered to enhance readability. Participants typically favoured suboptimal choices for gains (b), and advantageous choices for losses (c), meaning that most participants were typically risk-averse (d)

Full size image

For the gain frame, the risky option consistently had a higher EV than the certain option. Consequently, ACSgains both capture how many times the advantageous option was chosen, and how many times the risky option was chosen. Conversely, for the loss frame the certain option always had the highest EV, so ACSlosses capture both the number of advantageous choices and the number of certain choices. Therefore, ACSgains can also be interpreted as a measure of risk-seeking, and ACSlosses can be interpreted as a measure of risk aversion. We find that ACSgains and ACSlosses are distinct computational quantities when we compare the experimental scores with the baseline questions.

To further test the effect of frame on choices we ran two Bayesian linear regressions predicting ACSgains from baseline performance. The first model only used the congruent baseline item to predict ACS, the second model used the sum of all three items. We used approximate leave-one-out cross-validation (loo CV) to compute the Expected Log pointwise Predictive Density (ELPD) for a new dataset to compare the fit of the two models. ELPD is a measure of predictive error similar to AIC, BIC, or DIC. However, ELPD is robust in several contexts where the other measures perform poorly, such as when the number of parameters is high relative to the number of observations, or when the parameters are hierarchically structured (Vehtari et al. 2017). When comparing two models using ELPD, one computes the difference between the two models, and the standard error of the comparison, estimating uncertainty. In the results presented later, we show the difference between the more complex model and the simpler model such that positive numbers signify an advantage for the complex model, with the standard error of the comparison shown in parentheses. The model with only the congruent baseline item explained ACSgains slightly better than the model containing all three items (ELPD = −25.2 (21.7)). We ran a similar test for ACSlosses with the same result (ELPD = −14.1 (21.6)). Note that both of these differences are within or near the standard error of the estimate, so we cannot conclude that the congruent item does better than the combined baseline measure. What we can conclude is that the two models are nearly equivalent, implying no information is added by the non-congruent items. Our sample could be described as generally risk-averse: of the total 11,099 financial choices participants made, 71% favoured the certain prospect.

Choice at baseline and postintervention decision-making

To investigate how baseline choices and the interventions influenced choice in the gain and loss frames, we ran a set of Bayesian linear models. We ran four nested models each for the gain and loss frame, predicting the ACS:

  1. 1.

    Intercept-only: null model,

  2. 2.

    Model adding a predictor for baseline advantageous choice: baseline model:

  3. 3.

    Model adding a predictor for the interventions: intervention model

  4. 4.

    Model adding an interaction term between the baseline advantageous choice and the interventions: interaction model.

The final model allowed us to test whether baseline choice moderated the strength of the interventions. For example, it would test whether the boost had a greater effect for participants who made suboptimal choices at baseline.

Accounting for baseline choices improved model fit compared with the null model for gains (ELPD = 155.1(29.4)) and for losses (ELPD = 196.4(26.9)). In addition, accounting for the interventions improved predictive power even when baseline choices were accounted for (ELPDgains = 40.4(15.2), ELPDlosses = 16.4(9.2), and adding the interaction term further improved model performance (ELPDgains = 12.7(10.9), ELPDlosses = 7.8(7.3)), suggesting that the interventions had different effects based on baseline performance. Though the most complex models were the best at fitting the data, it is important to note that the improvement of the interaction models relative to the main effect models is within 95% CI based on the standard errors. To get a sense of which interventions lead to the most advantageous financial choices in the gain and loss frames, and how they interacted with baseline performance, we analysed the posterior probabilities of the coefficients in the most complex models (See Fig. 2).

Fig. 2
figure 2

Baseline choices strongly moderates the effectiveness of the interventions. The overall strongest intervention in the gain frame was the boost (a) and the strongest intervention in the loss frame was the disclosure nudge (b). Disaggregating the participants by baseline performance suggests that participants who made more advantageous decisions at baseline also made more advantageous decisions post interventions across all groups. This was true for both the gain frame and for the loss frame. Participants who made suboptimal choices at baseline benefitted most from the interventions (c–f). a–d show model-free analyses in that they show the disaggregated means and the error bars show bootstrapped 95% confidence intervals. e, f show the posterior estimates of the means for the various groups computed from the most complex Bayesian regression model

Full size image

By comparing the posterior samples of the coefficients for various groups, we could directly compare how different interventions influenced the experimental choices as a function of the baseline choices (See Fig. 3). We found that choices at baseline positively predicted experimental choices, such that participants who picked the item with the highest EV at baseline had higher ACS, on average, across conditions. In addition, participants who picked the option with lower EV at baseline tended to benefit most from the interventions.

Fig. 3
figure 3

Direct comparison of interventions with and between gains and losses. The interventions were more effective for participants who chose the suboptimal option at baseline. Different interventions performed best for the gain frame items and the loss frame items. The graphs show the probability that the column intervention is associated with a higher ACS than the row intervention, for the gain frame (a, c) and the loss frame (b, d) and separating those who were choosing advantageously at baseline (a, b) and those who were not (c, d). For example, the ‘0.17’ in the upper left corner of the a means that there is a 17% probability that the social norm is associated higher ACS than the control group in the gain frame, for participants who picked more advantageous options at baseline. Note that ‘1’ should not be interpreted as indicating certainty that one group is greater than the other. It indicates that for our 12,000 posterior samples, the column posterior was consistently greater than the row posterior, so given the model assumptions, it is very probable that the column intervention is associated with higher ACS than the row intervention

Full size image

For the gain frame, among those who picked the high EV option at baseline, the only reliable difference between the groups was that the boost group had lower ACS than the control group. However, for those who were making suboptimal choices at baseline, the disclosure nudge was reliably associated with higher ACS compared with the social nudge and the control group. Meanwhile, the boost was associated with a reliable increase in advantageous choices compared with all other groups.

For the loss frame, for the participants who picked the more advantageous option at baseline, the boost was reliably associated with lower ACS than the two nudges. For the participants who chose the suboptimal option at baseline, the social nudge and the boost were reliably associated with higher ACS than the control group, while the disclosure nudge was associated with reliably higher ACS than all other groups. There were no other differences between the groups. Because the Bayesian model framework does not make assumptions about long-running frequencies, we did not correct for multiple comparisons, as would be proper in a frequentist analysis (Berry and Hochberg 1999).

Altogether, the intervention effects were greater for those who chose the suboptimal option at baseline and there were few reliable between-group differences for those participants who picked more advantageous options at baseline. The boosts were associated with the most advantageous choices for the gain frame, while the disclosure nudge was associated with the most advantageous choices for the loss frame.

Relationship between sociodemographic variables and risk preferences

Next, we attempted to replicate the relationship between sociodemographic variables and risk preferences through a machine learning approach. We evaluated 13 demographic variables, see Table 1.

Table 1 Sociodemographic variables included in the lasso regressions
Full size table

Because of the large number of predictors, we used lasso regressions to isolate the variables with the strongest relationship with the outcome of interest. Lasso regression has a cost function that combines traditional maximum-likelihood methods with a shrinkage function that pushes small coefficients toward zero. The extent of shrinkage is determined by the tuning parameter λ. Here, λ was calibrated by loo CV and the out-of-sample performance of the best fitting model was determined by fivefold cross-validation.

To test the association between sociodemographic variables and risk preferences, we used logistic regression models to predict baseline choices for the full sample. We evaluated the out-of-sample model performance with GINI coefficients. GINI coefficients are a signal-theoretic measure that captures how well a model can discriminate between two options, where chance performance gives a coefficient of 0 and perfect discrimination gives a coefficient of 1, it is directly linked to AUROC so that GINI = 2 × AUROC − 1 (Fawcett 2006). For the loss frame, GINI coefficients ranged between −0.07 and 0.06 (M = −0.01), in line with chance performance. In other words, none of the sociodemographic variables reliably predicted baseline risk-taking in the loss frame. For the gain frame, GINI coefficients ranged between 0.05 and 0.2 (M = 0.12), which is small, but consistently better than chance. However, none of the variables had coefficients that were consistently different from 0 for all five folds, so none of the sociodemographic variables reliably predicted risk preference in the gain frame across the entire sample. See SI for the lasso regression coefficient plots.

The analyses suggested that none of the sociodemographic variables was reliably associated with risk preferences at baseline. It is possible that our analyses were underpowered through using binary outcomes to capture risk preferences. To account for this, we tested whether the sociodemographic variables predicted risk preferences as measured in the experimental trials for the control group; unlike the other groups, control group choices can be considered a pure measure of risk preference as we did not actively manipulate their choices. Again, we calibrated λ by loo CV, and we estimated out-of-sample performance by fivefold cross-validation, comparing the mean residuals of the calibrated lasso models with an intercept-only model. The calibrated lasso models did not outperform the null model for the gain frame, nor for the loss frame (see Fig. 4), suggesting that none of the sociodemographic variables reliably predicted risk preferences for the control group.

Fig. 4
figure 4

Sociodemographic variables did not predict risk preferences or moderate experimental interventions. We used fivefold cross-validation to evaluate the out-of-sample performance of predicting ACS scores for lasso regressions containing all the sociodemographic variables. None of the lasso models consistently outperform the null model, suggesting that there are not any strong sociodemographic predictors of baseline risk-taking, nor any strong sociodemographic moderators of the intervention effects. Error bars show 95% bootstrapped confidence intervals

Full size image

Effects of sociodemographic variables on intervention effectiveness

We also wanted to test whether the sociodemographic variables moderated the interventions’ effectiveness. We repeated the procedure used on the control group for each of the intervention groups. None of the lasso regressions reliably outperformed the null models concerning out-of-sample residual deviance, suggesting that the sociodemographic variables were not associated with baseline risk-taking, nor did they moderate any of the experimental effects.

For completeness, we explored the coefficient plots to see whether any of the coefficients in the lasso regressions were consistently different from 0. For the control group, we found no such variables, reinforcing that none of the sociodemographic variables is associated with risk-taking. However, for the social nudge, we found that single participants made more advantageous choices than participants who were in a relationship in the gain frame. To explore the strength of this effect, we ran a linear regression where we predicted ACS in the gain frame as a function of relationship status exclusively for the participants in the social norm group. The effect of relationship was significant (β = −0.14 (0.05), t(252) = −2.6, p = 0.01), but the model explained <3% of the variance in ACS so the effect is very small in the context of moderation. Similarly, for the disclosure nudge, students had slightly higher ACS than non-students in the loss frame (β = 0.61(0.29), t(261) = 2.1, p = 0.03) but this model explained <2% of the variance in the outcome. For the boost, students showed higher ACS than non-students (β = 0.63(0.25), t(232) = 2.50, p = 0.01) and men had higher ACS than women (β = −0.37(0.18), t(232) = 2.08, p = 0.04) in the loss frame. However, the model including both effects accounted for <5% of the variance of the outcome.

In sum, we found no evidence that any sociodemographic variable predicted baseline risk preference. In addition, though we found some potential moderators of intervention effectiveness in the loss frame, the lasso regressions containing these moderators failed to consistently outperform the null models in terms of out-of-sample prediction error. This suggests that these are likely too weak to be practically meaningful and should be tested again in future iterations, as there is a high possibility they would fail to replicate.

In addition, the lack of strong sociodemographic moderators indicates the general choice patterns observed may be reliably stable across groups. This would be particularly helpful in the context of applications to policy, which often require considerable nuance for broad effectiveness across groups or precision targeting. As this also applied to variability in outcomes between control, disclosure, descriptive social norms, and boosts, it strengthens their value as insights in the context of choice under uncertainty.

Replication with a Serbian sample

To provide further evidence for our main results, we conducted preregistered replicationFootnote 2 in a Serbian sample (N = 414). Details on the replication sample characteristics and the preregistration can be found in the SI; the methodology was identical to the prior study. We again found a weak negative correlation for ACS between gains and losses (Spearman’s ρ = −0.16, bootstrapped 95% CI = −0.06 to −0.26, p = 0.0009), in line with our original results (Spearman’s ρ = −0.12). Because the unsigned value of the correlation was lower than the criterion we had set up for combining the scores in the preregistration (0.30), we again treated the loss-frame items and gain-frame items as separate outcome measures. The Serbian sample was generally risk-averse, to a similar extent as the American sample: of a total 5382 financial choice observations, participants chose the certain prospect 69% of the time.

Our selection criteria for baseline items are in the SI. Using the same approach as in the American sample, a model predicting ACSgains performed as well as a model predicting ACSgains from all the baseline items (ELPD = −17.5 (13.1)). As such, it appears that only the congruent baseline item predicts ACSgains, in line with our original results. Similarly, for ACSlosses, there was no reliable difference between a model including the congruent item, and a model containing the sum of all three baseline items (ELPD = 2.2 (13.7)).

We predicted ACS based on baseline performance and the interventions by running the same four nested Bayesian linear models as we did for the US sample, again comparing model fit with ELPD. Based on the US sample, we anticipated the baseline model would perform better than the null model, the intervention model would perform better than baseline, and the interaction model would perform better than intervention. This would have meant identical replication. For gains, we found that the baseline model outperformed the null model, and the intervention model outperformed the baseline model, but the interaction model did not outperform the intervention model, see Table 2. In other words, the ACSgains was predicted by congruent baseline choices and the assigned condition, but there was no interaction between baseline performance and the effect of condition in the Serbian sample.

Table 2 Model comparisons for the gain frame
Full size table

We repeated the same modelling steps for ACSlosses. Here, the baseline model outperformed the null model, but no other model outperformed the baseline model, see Table 3. For the Intervention model, the credible intervals of all interventions crossed 0, but the disclosure intervention had the strongest effect, in line with our prior study. All interventions had the majority of their probability mass in the expected direction (improving ACS), though the credible intervals were too wide to rule out a null effect, or even a small negative effect.

Table 3 Model comparisons for the loss frame
Full size table

Consequential items

To further elucidate the validity of our approach, we added two additional and consequential items in the replication sample. Participants were told that their choices were legitimate, and they would enter a genuine payoff based on their preference. As the main study items use values not feasible for such conditions, euros were simply switched to Serbian dinars (i.e., €230 to RSD230), which is roughly 1% of the original value. For gains, 31% chose the advantageous item (control 28%, social norm 25%, disclosure 24%, and boost 46%). For losses, 77% chose the advantageous item (control 76%, social norm 73%, disclosure 81%, and boost 77%).

In line with our preregistered analysis plan, we computed the precision and sensitivity of the hypothetical items to predict the consequential items for the same structure. For the gain item, sensitivity was 0.65, and precision was 0.63. For the loss item, sensitivity was 0.71, and precision was 0.60. Because these values were below our prespecified threshold of 0.80 to treat the hypothetical and consequential items as interchangeable, we repeated the same modelling steps outlined in the previous sections, with the distinction that this time we presented the single consequential gain frame item in a logistic model. As for ACSgains, the baseline model outperformed the null model, and the intervention model outperformed the baseline model. In this case, uncertainty in the models obscures whether the advantage of intervention is robust (see Table 4). However, the intervention models for ACSgains and for the consequential gain item are qualitatively similar, see Fig. 5.

Table 4 Model comparisons for the consequential gain frame item
Full size table
Fig. 5
figure 5

The boost intervention improves performance for hypothetical and consequential choices in the gain frame. a, b Means of ACSgains and proportion of advantageous choices, respectively, based on condition and baseline performance. Error bars show 95% bootstrapped CI. c, d Posterior probabilities for ACSgains and P(Advantageous Choice) based on the intervention models (Model 3) for ACSgains and consequential choices for gains, respectively

Full size image

The symmetry in results between the consequential and hypothetical items is further emphasised by examining the pattern of overlap between the coefficients in the intervention models (see Fig. 6).

Fig. 6
figure 6

The boost intervention is robustly superior to all other conditions for hypothetical and consequential choices in the gain frame. Figure 6 shows the probability that the column intervention is associated with a higher ACS than the row intervention (a), or with a higher probability of making an advantageous choice for the consequential item (b). For example, the ‘0.19’ in the upper left corner of a means that there is a 19% probability that the social norm is associated with higher ACS than the control group in the gain frame. Note that ‘1’ should not be interpreted as indicating certainty that one intervention is superior. It indicates that for our 12,000 posterior samples, the column posterior was consistently greater than the row posterior, so given the model assumptions, it is very probable that the column intervention is associated with more advantageous choices than the row intervention

Full size image

We repeated the same modelling steps for the consequential loss frame item. No model reliably beat the null model, see Table 5. This null finding may reflect a lack of power, as we only evaluated a single item and most people in this sample was risk-averse, so they selected the best option independent of the intervention.

Table 5 Model comparisons for the consequential loss frame item
Full size table

For completeness, we include the model-free figures for the loss frame items (Fig. 7).

Fig. 7
figure 7

None of the interventions reliably improves performance for hypothetical and consequential choices in the loss frame. a, b Means of ACSgains and proportion of advantageous choices, respectively, based on condition and baseline performance. Error bars show 95% bootstrapped CI

Full size image

Discussion

The utility of behavioural science in policy is increasingly recognised and this trend shows little sign of slowing. As behavioural applications continue to develop, a nuanced understanding of the most effective methods in the most appropriate contexts for the most relevant groups is critical (Slatev et al. 2017). This is not a matter of determining whether one method—such as nudges or boosts—is better than the other, but instead, when, where, how, and for whom is one more likely to be effective than another, or even, when they might be optimal applied together. We identify such insights in assessing decision-making patterns between three intervention conditions and a control.

For participants that made relatively suboptimal choices at baseline, the boost condition showed the largest effects, most notably in the gain frame. This finding provides impetus to explore the potential value of boosts specifically as a tool for reducing inequalities. Such disparities are often exacerbated in the context of uncertainty (Payne et al. 2017), particularly for individuals who make an unsuccessful, high-risk choice early, which is typically associated with choosing subsequent high-risk options (Vermeer et al. 2014). This may position boosts as a complementary tool in policies to mitigate high-risk behaviours in disadvantaged populations, which are known to increase inequalities (Payne et al. 2017).

In line with Thaler and Sunstein’s libertarian paternalism, such an approach could be seen as libertarian educationalism: the same high-risk options may be on offer, but individuals could be reasonably informed about them in advance (Thaler and Sunstein 2008). We note that our findings do not imply that such high-risk choices should be removed entirely, or even regress to a level in line with those who made more advantageous choices at baseline. However, even small effects at reducing inequalities are beneficial to disadvantaged individuals as well as the communities to which they belong (Payne et al. 2017).

There was an inverse pattern for ACS in the group that was advantageous at baseline, with scores decreasing from control through all conditions in the gain items. This pattern, based on baseline advantageous choice, is more indicative than any sociodemographic variable in our studies. This may indicate that additional information may serve as a distraction for those who otherwise might have made an advantageous choice (Jensen et al. 2017). It is worth noting that scores were lowest and variability largest in the boost condition, which has implications for further exploration in future research.

One argument for the effectiveness of disclosure nudges and boosts comes from Sunstein (2016), who suggests that these interventions educate, therefore promoting deliberative, slow thinking. Kahneman argues that such thinking is less likely to be influenced by heuristics and is, thus, less error-prone (and results in more advantageous choice) (Kahneman 2011). The boosts in our study promoted deliberative capacities in having to calculate the EVs of three prospects. Disclosure nudges prompted participants to think deliberatively by making the trade-off of each prospect clearer. To give an example: information that a risky prospect has a higher EV than a certain prospect allows participants to evaluate whether they would prefer to take such a risk. This libertarian educationalist approach educates and informs, thus allowing individuals to make their own decisions, rather than guiding them towards specific decisions.

Decision-making for gains and losses can be observed as two different behavioural domains within which an intervention may be more or less effective; in this context, boosts were more effective for gains, while disclosure nudges were more effective for losses. There was no evident reflection effect, which suggests that some of the mechanisms underlying choices for gains and losses may be independent (Kurnianingsih and Mullette-Gillman 2015; Tymula et al. 2013). Future research should continue to compare intervention effectiveness for these two behavioural domains. Such research could be of great practical use, given that it is currently not clear why the boost was more effective for gains than for losses; the same holds for disclosure nudges.

It is possible that the descriptive social norm in this study uses social information for a group that is not meaningful (Sherman et al. 2014). Participants received information on the average decisions of participants doing an online survey, who are the people that they do not know, cannot identify and cannot be identified by; thus, such a description may not exert substantial social influence. An alternative explanation could posit that the intervention was ineffective because the social norm was not salient compared with the presented financial information (Cialdini et al. 1991). In line with prevailing theories on influence, the financial information was more decision relevant and thus more influential (Sunstein 2016; Cialdini 2007). An effective use of descriptive social norms should present norms that are meaningful, both in the specific context and to the population to which they are applied and are at least as salient as the other information presented to the decision makers (Jachimowicz et al. 2018).

None of the sociodemographic variables reliably predicted risk preferences in our sample (including gender, age, income, and education status, see Table 1 for the full list), which stands contrary to existing arguments (Hallahan et al. 2004; Grable 2000; Masclet 2009). One possible explanation for the disparity between prior findings and ours is that prior methods used self-report measures of risk preferences (e.g., Eckel and Grossman 2002), whereas our study used direct behavioural measures of risk preference. This suggests that there may be a difference between how much risk people take and how much risk they think they will take. Recent findings support this counterargument by highlighting a lack of cross-methods consistency for measuring risk preferences (Pedroni et al. 2017). This lack of awareness suggests that certain individuals with extreme risk preferences (i.e., always avoid or take risks) might not be aware of their potentially damaging financial decisions, as both taking and avoiding risk can be beneficial (and vice-versa: both can also be harmful). Identifying such individuals through direct behavioural observations should be a policy imperative, seemingly at the same level or even as more critical than broad sociodemographic indicators.

By replicating in Serbia, we confirm our hypothesis that patterns of risk hold generally consistent across populations, as do the intervention effects. While some effects are milder or less differentiated between intervention and baseline groups, these appear to be explained primarily by a smaller sample than US. Furthermore, as the boost appears to be significant across conditions, it signals that intervention effectiveness may vary between populations and warrant further trials in additional settings.

Most exciting in the Serbian sample is the general replication of patterns for consequential choices. Naturally, it was not feasible to use the same values in both the hypothetical and consequential question sets. There was therefore some concern values might either be too small to elicit any need for risk aversion or too large to reasonably reflect prior scenarios for comparison. In the end, converting from euros to Serbian dinars, effectively adjusting to 1% of the original net values, did not appear to have any major influence on general choice preferences. This indicates that classic patterns of risk aversion hold consistent between hypothetical and consequential behaviours, and that lowering the real values has no broad impact, at least in a controlled setting.

Conclusions

Decision-making under uncertainty is of critical importance to behavioural and policy research, particularly as the integration between psychological and economic sciences continues (Camerer 1999). While nudges and boosts are just two sets of tools in the toolkit, they offer important insights for research and policy practice (Cohen et al. 2016). To capitalise on that potential, it is critical to consider the most appropriate contexts, populations, and methods for implementing interventions, rather than presuming one is universally superior to the other (Slatev et al. 2017). This is particularly true in everyday financial choices, where the framing of options may have a major influence over the decision. It is also critical in contexts where decisions could reduce or exacerbate harmful economic inequalities due to unnecessary risk taking (Payne et al. 2017).

The current research advances our understanding of nudges and boosts in decisions under uncertainty along two points. First, we find that boosts were typically more effective for those who initially made suboptimal choices. Policymakers should therefore consider likely risk-taking behaviours of populations being considered, as effects may be less meaningful for certain contexts and choices. Second, the effect of nudges and boosts differ depending on loss and gain framing, such that behaviours where a payoff is being considered are likely to yield different outcomes than when expenses are to be incurred. Choosing appropriate behavioural interventions should therefore be preceded by ensuring appropriate fit for context and population. A final general insight is that social determinants were not strong indicators of choice in this context, implying that knowing a single behaviour or preference may be more powerful than a number of demographic measures.

Collectively, these insights provide clarity to highly nuanced, complex patterns across population behaviours in the context of financial choice under uncertainty. Most importantly, they highlight relevant implications for the design of policy interventions that impact behaviours with direct consequences for the well-being of individuals and populations.