Abstract
From a gene-culture evolutionary perspective, the recent rise in obesity rates around the Developed world is unprecedented; perhaps the most rapid population-scale shift in human phenotype ever to occur. Focusing on the recent rise of obesity and diabetes in the United States, we consider the predictions of human behavioral ecology (HBE) versus the predictions of social learning (SL) of obesity through cultural traditions and/or peer–to–peer influence. To isolate differences that might discriminate these different models, we first explore temporal and geographic trends in the inverse correlation between household income and obesity and diabetes rates in the U.S. Whereas by 2015 these inverse correlations were strong, these correlations were non-existent as recently as 1990. The inverse correlations have evolved steadily over recent decades, and we present equations for their time evolution since 1990. We then explore evidence for a “social multiplier” effect at county scale over a ten-year period, as well as a social diffusion pattern at state scale over a 26–year period. We conclude that these patterns support HBE and SL as factors driving obesity, with HBE explaining ultimate causation. As a specific “ecological” driver for this human behavior, we speculate that refined sugar in processed foods may be a prime driver of increasing obesity and diabetes.
Similar content being viewed by others
Introduction
In the United States, where adult obesity prevalence rates have been rising since the 1970s (Kranjac and Wagmiller, 2016), about two-thirds of adults are now overweight and over 100,000 U.S. deaths per year are attributed to obesity (Ogden et al., 2014). With obesity rates having tripled in many U.S. states over the past 25 years, this rise in obesity prevalence has accelerated. In 1990, about 11% of a typical U.S. state population was obese and no state had more than 15% obesity in its adult population. By 2015, U.S. obesity rates had more than doubled, with several states above 35% adult obesity and no state below 20% obesity in the population (Centers for Disease Control and Prevention, 2017a). In one generation, the change has been so dramatic that the obesity rate in any U.S. state in 2015 would have been an extreme outlier in the U.S. in 1990.
From a gene-culture evolutionary perspective, the recent rise in obesity rates, occurring across the Developed world (Goryakin et al., 2017), is unprecedented. In the past, human niche construction evolved over a time scale of centuries or millennia (Creanza and Feldman, 2016; Milot et al., 2011). For example, the evolution of lactase persistence among Neolithic populations of central Europe was rapid in evolutionary terms but nevertheless took place over thousands of years, in coevolution with the intensification of dairying economies (Brock et al., 2015; Gerbault et al., 2013). In contrast, industrially–processed foods have transformed Western human diets in less than a century. Not only has this made calories and junk food abundant and inexpensive in high-income countries, but there appear to be other effects such as reduction of gut microbiome diversity (Smits et al., 2017; Muscogiuri et al., 2018).
In the simplest view, obesity in Developed economies is a result of over-abundance of inexpensive food calories combined with decreases in daily physical activity in the industrialized world and its built environment (Mattson et al., 2014; Mullan et al., 2017). Negative energy balance is not the only factor, however, and with heterogeneity across socioeconomic groups, the specific causes for the rapid and recent increase in U.S. obesity remain unclear (Cook et al., 2017; Dwyer–Lindgren et al., 2013; Flegal et al., 2016).
One thing that is clear in high-income countries is that, despite decades of economic growth, obesity disproportionately affects the poor—the “poverty–obesity paradox” (Hruschka and Han, 2017). The proportion of obese individuals in industrialized nations now correlates inversely with median household income. This phenomenon is called the “reverse gradient” because it is the reverse of the pattern in developing countries, where higher income correlates with higher body mass. In the United States and other developed countries, lower income households tend to have higher rates of obesity (Hruschka, 2012; Subramanian et al., 2011). In 2015, over 35% of the population was obese in U.S. states where median household incomes were below $45,000 per year, whereas obesity was less than 25% of state populations where median incomes were above $65,000 (Centers for Disease Control and Prevention, 2017c). Similarly in Europe today, poor individuals are 10% to 20% more likely to be obese (Salmasi and Celidon, 2017). This pattern is unique to Developed economies; within China, for example, an inverse correlation between income and obesity/diabetes is observed only in the most economically developed regions (Tafreschi, 2015).
Cultural evolution potentially offers a less proximate, more ultimate explanation for the recent rise in obesity. Evolutionary approaches to behavioral change include human behavioral ecology and cultural evolutionary theory; the former tends to prioritize optimality of adaptive behavior while the latter tends to prioritize social learning. Generally speaking, human behavioral ecology (HBE) emphasizes the plasticity of human physiology and behavior, by which individuals minimize risk to survival and optimize their long-term reproductive payoffs (Higginson et al., 2017). As wealth mitigates survival risk, HBE predicts a positive correlation between BMI and wealth, as humans have evolved to store calories as insurance against future famine or food shortage (Shrewsbury and Wardle, 2012; Higginson et al., 2017; Tapper, 2017). In the poorest 80% of the world’s societies, body mass index (BMI) generally increases with household wealth (Subramanian et al., 2011)—except below about 400 USD per capita, when poverty is such that BMI is uniformly low (Hruschka et al., 2014). In high-income countries, HBE predicts greater obesity among the poor, partly because humans have evolved behavioral “rules” that lead to overeating in rich environments and partly because poorer people have more immediate risks and concerns than outweigh long-term mortality risk of being obese (Dittmann and Maner, 2017; Dohle and Hafmann, 2017; Higginson et al., 2017; Mani et al., 2013; Smith, 2017).
The HBE hypothesis predicts that obesity has recently evolved in strong correlation with both the food environment and with income/wealth. The “Insurance Hypothesis” (Nettle et al., 2017) uses HBE to explain why the reverse is true in Developed countries where extreme BMI (obesity) is more frequent among the poor. Under the Insurance Hypothesis (IH), “individuals should store more fat when they receive cues that access to food is uncertain” (Nettle et al., 2017). Poor people in high-income countries receive such cues, as they experience more stress and greater existential risk for multiple reasons. Prominent among these risks is malnutrition, yet empty calories are still inexpensively available as processed foods and sugar-sweetened beverages (Bray et al., 2004; Johnson et al., 2007; Jürgens et al., 2005; Bocarsly et al., 2010). The IH is consistent with observations of women in high-income countries, who are more likely to be obese when confronted by food insecurity (Nettle et al., 2017). An alternative explanation, however, occurs at the societal level in high-income countries, where heavier women tend to marry into poorer households due to through “anti-fat discrimination” in marriage (Hruschka, 2012; Hruschka and Han, 2017).
In contrast, social learning (SL) explanations emphasize learned behavior in groups: behaviors are inherited from parents and learned socially from contemporaries through the generations of family traditions or community cultures (Bentley et al., 2016; Colleran and Mace, 2015; Colleran, 2016). Dietary habits are often determined as much by cultural traditions as they are by nutritional needs and family economics (Anderson and Whitaker, 2010; Anderson, 2012; Hughes et al., 2010; Lhila, 2011; Mata et al., 2017; Redsell et al., 2010; Vizireanu and Hruschka, 2018). Cultural factors may therefore underlie local differences in obesity and diabetes rates, which exhibit effects of local neighborhood and its built environment (Alvarado, 2016; Carroll et al., 2016; Mullan et al., 2017; Kowaleski-Jones et al., 2017), family size (Datar, 2017), ethnic group and age group (Cook et al., 2017).
Under SL, obesity may also increase through social influence. A widely-discussed argument, first presented by Christakis and Fowler (2007), is that obesity “spreads” through social influence in networks of family and friends (Christakis and Fowler, 2013). Relatedly, recent modeling and experimental studies show how a minority group can initiate rapid change in social conventions, provided the minority reaches a ‘critical mass’ (Centola et al., 2018; Couzin et al., 2011). Under SL, therefore, a new behavior can become a new social norm relatively quickly, if obesity were indeed a new social norm.
The alternative to the social-learning explanation is homophily, if obesity clusters in social networks merely because those clusters are similar people in the same environments (Shalizi and Thomas, 2011). Homophily could be viewed either as similar behavior derived from shared cultural ancestry or else as similar behavior that reflects adaptations to similar environments. Outside of carefully monitored conditions (Centola et al., 2018; Hobaiter et al., 2014), however, it is difficult if not impossible to distinguish social influence from homophily, even if obesity is observed to cluster in social networks, without a fine–grained temporal dimension to the data (Christakis and Fowler, 2013; Shalizi and Thomas, 2011; Thomas, 2013).
Unlike the small-scale social network study of obesity versus specific friends and kin members (Christakis and Fowler, 2007), this study examines annual, population-scale obesity rates aggregated by U.S. county. If the aggregated data are time–stratified, however, we can still attempt to test the SL hypothesis. We will use multiple measures (obesity, leisure, income) and ten years of county-scale data to assess any “social multiplier” effects. The social multiplier effect is identified when the rate of behavior among a group is greater than what would be predicted based on individual–scale variables alone. Identification of groups is a problem in the empirical literature on social interactions (Blume et al., 2011), but useful proxies have based on Zip codes (Corcoran et al., 1992) and census tracts (Weinberg et al., 2004).
A study of crime rates (Glaeser et al., 2003), for example, used statistics of individuals to predict crime rates and regressed those on crime rates in groups. This is how the social multiplier was defined at the county level, specifically by comparing the coefficient b in the regression,
with the coefficient b' in its group counterpart
where ωig denotes the choice of individual i in county g and xi is a vector of observable individual-specific characteristics; the social multiplier is defined as the coefficient ratio, b'/b (Blume et al., 2011).
In this approach, estimating the social multiplier requires an estimate of individual-level rates, which do not exist in aggregated data. Faced with this problem, Glaeser et al., (2003) used nationwide arrest rates by age that, when combined with demographic data, provided a predicted level of crime in each neighborhood. These predicted rates were then regressed actual crime rates at the county level, yielding a coefficient of 1.7 at the county level, which was their estimate of the social multiplier at that scale of aggregation (Glaeser et al., 2003).
The data we use here are aggregated by U.S. county annually: over three thousand county-level time series of obesity, leisure and income rates over ten-year period (2004 to 2013). This amounts to ten sets of annual data, on several variables, for 3110 U.S. counties. If, controlling for the effects of household income, we find that lack of physical activity, or leisure rate, has a disproportionate effect on obesity rate in 2013 compared with 2004, then there may be support for the social multiplier effect. We have only aggregated statistics but we have the advantage of a time series. In principle there exists an individual-level, effectively physiological, connection between lack of exercise (leisure) and obesity rates, which we assume remains constant through time. The correlation between obesity and leisure rates should reflect this individual relationship as a baseline, plus any social multiplier effects over time.
In other words, change in the leisure–obesity correlation between 2004 and 2013 ought to reflect the social multiplier effect. As there are also unobservable connections between leisure and obesity, however, we follow the cautious approach of Glaeser et al., (2003), who “take these results warily, as they may well overstate the true social multiplier.”
To investigate whether obesity increased in the classic S–shaped pattern consistent with social learning, we carried out regression analysis on the annual data for each state over the 1990–2016 period. A simple linear increase in obesity rate since 1990 serves as our null hypothesis, with the alternative hypothesis being a non-linear time trend. If the null hypothesis of non-linearity could not be rejected, by implication an S–curve would not be present in the data.
We applied two separate but complementary approaches. First, we tested the null of linearity against a general non–linear alternative, using the methodology of local linear regression (Cleveland and Devlin, 1988). We used the “loess” command in R. Local linear regression fits simple linear models to localized subsets of the data to describe the deterministic part of the variation in the data, point by point, without specifying a global functional form. An input parameter in the loess command (“span”) allows the “equivalent number of parameters” (ENP) to be varied. ENP serves as a measure of the non–linearity of the series. The approach enables ANOVA tests to be carried out of the null of linearity against a range of non-linear alternatives. Local linear regression is a powerful approach, but does not yield a specific functional form.
For the second approach, we tested the null of linearity against a specific non–linear functional form, namely that of a classic adoption curve (Bass, 1969; Bentley and Ormerod, 2010; Henrich, 2001). We have:
where Ft,i is the obesity rate in year t of U.S. state i, μi is the chance in state i that a person becomes obese (i.e., BMI of 30 or above) through individual behavior and qi is the probability within state i, where Ft,i are already obese, that a person becomes obese through social influence. This ODE can be solved for Ft,i,
where M is the magnitude of change and F0,i is set as the obesity rate of U.S. state i in year 1990. This equation can be fitted to the obesity data, with the goodness of fit reported as the adjusted R2 statistic, defined as:
where v is the total number of explanatory variables in the model (not including the constant term), and n is the sample size. The linear model has v = 2 parameters (slope and intercept), whereas the Bass model has v = 3 parameters (p, q, and M).
Here we focus on an under–studied, but revealing question: in the U.S., how has the correlation between household income and obesity changed in the past 25 years? In the U.S., obesity and diabetes rates currently have a strong negative correlation with household income (Hruschka, 2012). These correlations have been demonstrated cross-sectionally but not longitudinally, however, and therefore it is not possible to establish their causality (Boden and McLeod, 2017). In industrialized economies, the increase in obesity prevalence has been fastest among low income levels, as fast as tripling within a generation among certain subpopulations.
Data
Annual, age-adjusted data on obesity rates at the county level, for years 2004 to 2015, were obtained from the publicly accessible archive maintained by the Center for Disease Control and Prevention (www.cdc.gov/diabetes/data). For these county-level data, we also make use of the CDC age-adjusted estimates, (Klein and Schoenborn, 2001), in which rates are age adjusted to the 2000 U.S. standard population using age groups, 20–44, 45–64, and 65 or older (Centers for Disease Control and Prevention, 2017b). Older obesity data at the state level since 1990 were obtained from the annual reports of the Trust for America’s Health and the Robert Wood Johnson Foundation (stateofobesity.org). For analyzing the time-series of state-level obesity rates, we cautiously added data from the years 1991 and 1998 from a different source (Mokdad et al., 1999) to examine more closely any potential non-linear change in the 1990s.
Due to missing data at the county level, we excluded Alaska from all analyses at county level, while including Alaska for state-level analysis. We also used five years of CDC data on age-adjusted annual CDC diabetes rates, 2009–2013, in U.S. counties (Centers for Disease Control and Prevention, 2017d). The estimates of diabetes rates are derived through telephone surveys, normalizes the data using population data from the US Census, and smooths the estimates such that three years of data are averaged in each annual estimate (Centers for Disease Control and Prevention, 2017c).
Importantly, we use age–adjusted rates for both obesity and diabetes in our analysis, and so we do not include the age profile of an area as an explanatory factor. This adjustment has already been carried out by the CDC in the data which we use. By using age–adjusted data, we minimize the effect of demographics in our results. To anticipate, we also note for reference that our results were essentially the same when we used data that were not age–adjusted.
Estimates of leisure–time physical inactivity come from the CDC Behavioral Risk Factor Surveillance System, a system of health-related telephone surveys, which began in 1984 with 15 U.S. states, and now collects data in all 50 states through over 400,000 adult interviews each year (Centers for Disease Control and Prevention, 2017c). The “leisure” statistic indicates the fraction of population who are designated as physically inactive, meaning they answered “no” to the question, “During the past month, other than your regular job, did you participate in any physical activities or exercises such as running, calisthenics, golf, gardening, or walking for exercise?”
Food desert data were recently made available through the Food Access Research Atlas (FARA) project (Rhone et al., 2017). The estimates are derived from the 2010 US Census and the 2010–2014 American Community Survey, in which census tracts are categorized by median income, vehicle availability, and Supplemental Nutrition Assistance Program (SNAP) participation (Rhone et al., 2017). To this geographic dataset are added two 2015 lists of supermarkets, supercenters, and large grocery stores to represent sources of affordable and nutritious food (Rhone et al., 2017). The FARA records for each U.S. Census tract the number and share of people more than a certain distance to a supermarket: in urban areas, that specified distance is half a mile or 1 mile, whereas in rural areas the distances are 10 miles or 20 miles (Rhone et al., 2017). Also recorded is whether the population in the census tract has overall low access to vehicles. Census tracts are also designated as rural, urbanized (over 50,000 people) or urban cluster (2500 to 50,000 people); for the purposes of estimating the urban/rural ratio of a county, we counted both urbanized and urban cluster tracts as being urban. Because food deserts are defined quite differently for urban (0.5 mile) versus rural (10 miles) counties in the FARA, we consider just those counties whose populations we calculated as at least seven–eighths (87.5%) urban, totaling n = 250 counties across the U.S.
Results
We find the reverse gradient has only existed for less than thirty years. In the U.S. in 1990, when population–scale obesity rates were about a third of what they are today, there was no correlation between income and obesity or diabetes. The inverse correlations between income and diabetes/obesity rates have developed only within the past thirty years. By 2015, the correlation was stronger than ever: in states where median household incomes were below $45,000 per year, like Alabama, Mississippi and West Virginia, over 35% of the population was obese, whereas obesity was less than 25% of state populations where median incomes were above $65,000, such as in Colorado, Massachusetts or California.
In the U.S., there is considerable geographic heterogeneity in obesity prevalence. Figure 1 shows maps of obesity rates and diabetes rates by county in 2013 (Table 1). By 2013, the reverse gradient in the U.S. was pronounced; the simple correlation between obesity and ln (income) across n = 3110 U.S. counties was r = −0.486 and between ln (income) and diabetes was r = −0.531. All reverse gradients are better determined against the logged income data than against median income itself. Plots of ln (income) against both diabetes and obesity (Fig. 2), aggregated at county level, reveal mild degrees of non–linearity in each of the relationships.
Reverse gradients across U.S. counties in 2013 (in all states except Alaska) between the natural logarithm of household income and rates of a obesity (regression slope = −9.66) and b diabetes (slope = −4.93). Also shown are correlations between prevalence of physical inactivity (“leisure”) versus c obesity (slope = 0.643) and d diabetes (slope = 0.288). Correlation values within each state are listed in Table 1
State-level data on annual obesity and diabetes rates, available for years 1990 through present, together with age–adjusted and inflation–adjusted income data from the U.S. Census, show how the reverse gradient in the U.S. changed over twenty–five years (Fig. 3). For the year 1990 (data from n = 43 states for this first year of data), the Pearson correlation between state-level obesity and the natural log of median household income was r = −0.240 [−0.502, 0.061], which is not significant (p = 0.116).
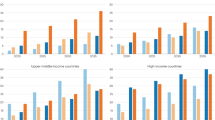
Negative gradient between household income and obesity and diabetes rates. Scatterplots showing a Obesity vs. ln (income) by state, 1990 and 2015; b Diabetes vs. ln (income) by state, 1990 and 2015. For 1990 (blue), the slopes are −2.39 for obesity and −0.75 for diabetes; for 2015, the slopes −16.26 for obesity and −8.18 for diabetes. Panels c, d show the change in these correlations over time, between ln (income) and c Obesity and d Diabetes, at both state (solid) and county (dashed) levels
Twenty–five years later, a strong inverse correlation had developed between median household income and rates of obesity and diabetes (Figs. 3a, b). In 2015, the correlation between ln (income) and obesity rate across all 50 states was r = −0.697 [−0.816, −0.522], which is highly significant (p < 0.00001); even limited to the 43 states also recorded in 1990, the correlation in 2015 still yields r = −0.699 [−0.824, −0.508] (p < 0.00001).
A similar change is evident for the reverse gradient involving diabetes and ln (income); insignificant for 1990 (r = −0.090 [−0.380, 0.216], p = 0.566) and highly significant by 2015 with r = −0.706 [−0.823, −0.532] (p < 0.00001). Again, if we restrict the 2015 data to the 42 states available in 1990 (one state fewer than in the obesity data), the correlation between ln (income) and diabetes rate yields r = −0.684 [−0.816, −0.483] (p < 0.00001).
Figures 3a, b show the actual and fitted values of the regressions of obesity and diabetes, respectively, on the log of income in both 1990 and 2015. In 1990, neither slope was significantly different than zero at the state level. In the regressions using 2015 state data, the slope coefficients for obesity are −0.163 ± 0.024 (R2 = 0.476) and for diabetes −0.080 ± 0.011 (R2 = 0.491). Figure 4 shows how the slope coefficient in these regressions has evolved, using data in 1990, 1995, 2000, 2003, and then annually from 2005 onwards.
Figure 5 shows how, at 5–year intervals from 1990 to 2015, the rate of growth in obesity or diabetes per year was inversely related to median household income. The temporal evolution of these reverse gradients, for the rates of obesity and diabetes, respectively, can be described by the following equations:
where Xt is the natural logarithm of median household income in year t. The colored lines in Fig. 5 show how well Eqs 6a and 6b represent the actual reverse gradients of ln (income) versus obesity and diabetes rates, respectively, across 25 years of evolution of these negative gradients. The evolving slope coefficients imply that above an annual income level of $250,000 for obesity and $150,000 for diabetes, any further increases in income have negligible effects in term of further reducing obesity and diabetes (Fig. 5c).
Available data at the U.S. county level are available only from year 2004, so do not capture the start of this phenomenon, but these data include not only diabetes and obesity rates but also a “leisure” statistic derived from self–reported activity levels. Across all 3110 counties in any given year, the leisure statistic correlates best with both obesity but also with income, reflecting the feedback between income, health habits and obesity (Table 2). For the leisure statistic in 2013, for example, the relationship with both obesity and diabetes is strongly positive and linear (Figs. 2c, d) with r = 0.719 [0.701, 0.735] for leisure versus obesity, and r = 0.686 [0.667, 0.704] for leisure versus diabetes.
We find that each year 2004 to 2013 the leisure and income statistics were a good predictor of (r2 > 0.5) obesity rates at the county level (Table 2). Notably, the respective regression coefficient on leisure grew from about 0.40 to 0.63 (Table 2, Fig. 6). This means that if we applied the 2004 regression coefficient, the actual obesity rate would be 1.56 times our prediction based on 2013 leisure rate. Hence following Glaeser et al., (2003), we estimate the social multiplier as at least 1.56, since by 2004 there had already been a decade of sharp increase in obesity rates.
Change in multiple regressions, U.S. counties, 2004–2013. For regressions predicting obesity rates, the open circles (with blue curve) show the coefficient on the leisure statistic; black filled circles show coefficient on ln (income). The dashed line shows the trend through the black filled circles (R2 = 0.36). Data are shown in Table 2
This steady increase change in coefficient (Table 2) is not due to change in the leisure rate, which rose and fell: the average county rate increased from 25.3% in 2004 to a peak of 26.9% in 2009 and then fell to 24.7% by 2013. We are not aware of an individual–level reason why the relationship between lack of exercise and obesity will have changed in ten years. We therefore posit 1.56 as a measure of social multiplier effect at county level.
For the time series of state–level obesity rates from 1990 to 2016, regression analyses serve to rule out any strong social–shaped pattern in obesity rise for any of the U.S. states. Figure 7 shows typical examples. Using the local linear regression approach (see Methods), the null hypothesis of linearity could not be rejected for seven of the 46 states examined (the few we excluded lacked data points for the early 1990s): Connecticut; Delaware; Iowa; Louisiana; Maine; Vermont; Wisconsin; Wyoming. For a further seven states, linearity could be rejected at the standard 5 per cent level, but only when the alternative exhibits a mild degree of non-linearity, with the Equivalent Number of Parameters being just 2.33: Idaho, Illinois; Kentucky; North Dakota; Oregon; Virginia; West Virginia. In the adoption-curve analysis, this favors “r–curves” of individual learning (Fig. 7). Adjusted r-squared values (Table 3) are strong where the individual parameter p is the same magnitude as the social parameter q, and fit almost as well with the “social” parameter, q, set to zero (Table 3) to represent pure individual learning.
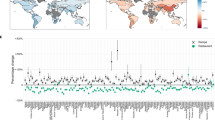
Lastly, the effect of food deserts is also evident, among a subset of U.S. counties (Fig. 8, Table 4). As described in our Methods, from the FARA data we consider just those counties whose populations we calculated as at least seven eights (87.5%) urban, totaling n = 250 counties across the U.S. In these urban counties, the regression of obesity rates versus the share of population without access to supermarkets within half a mile yields Pearson’s r = 0.292 [0.175, 0.401], which is significant (p < 0.00001). For diabetes, however, the correlation with this food desert variable in 2013 is not significantly different from zero (p = 0.223). For these same urban counties, food deserts among low income census tracts has stronger correlation with obesity (Fig. 8b), with r = 0.563 [0.472, 0.642], and now a significant correlation with diabetes rate r = 0.462 [0.359, 0.544]; both correlations are highly significant (p < 0.000001).
Food desert index versus obesity rate for 250 urban counties in the U.S. in 2013. In a the food desert index is the share of the urban population living a half mile or more from a supermarket. The blue line shows the regression (Pearson’s r = 0.292 ± 0.11). In b the food desert index is the share of low-income population living a half mile from supermarket. Blue line shows the regression (Pearson’s r = 0.563 ± 0.08)
Food deserts are, of course, closely related to income. We confirm the validity of the individual correlations between obesity and diabetes and income and leisure in Table 2 by running simple multiple regressions of obesity and diabetes on income and leisure. The results are set in Table 5. Although each overall fit could be slightly improved with mild non–linearities, the simple regressions show that both ln (income) and leisure have significant effects on obesity and diabetes.
Our analyses here use data aggregated from both sexes, as the same correlations for each sex were quite similar to the results for both sexes aggregated together. In 2013 for example, among the 43 states with sufficient data points for men and women (excluding AK, CT, DE, HI, NH, and RI), the reverse gradient between income and diabetes is significant for both sexes at p < 0.01 in 30 states. In some states, however, there are small differences. In eight states the reverse gradient in 2013 is significant at p < 0.01 for one sex and p < 0.05 for the other. In Arizona, New Mexico, New Jersey and Utah, the reverse gradient is significant for men but not for women, whereas in Massachusetts, it is significant for women but not for men.
Discussion
Here we have explored the origins and development of the inverse correlation between household income and obesity/diabetes rates in the U.S. We used data on mean household incomes and rates of obesity and diabetes at the level of U.S. state, which date back to 1990, as well as county level statistics that offer larger sample sizes and higher spatial resolution but only extend back the early 2000s.
Using age–adjusted U.S. data on mean household incomes and rates of obesity and diabetes—at state level since 1990 and county level since the mid 2000s—we found that the reverse gradient originated and evolved over a period of about 25 years. Here, we report that this reverse gradient did not exist in the U.S. in 1990 but has increased markedly since then.
Specifically, across the U.S. states by 2015 there were highly significant correlations between ln (income) and state–level rates of obesity (r = −0.697, p < 0.00001) and diabetes (r = −0.706, p < 0.00001), whereas in 1990 neither correlation was yet evident. By 2013, the age-adjusted prevalence of obesity in the U.S. was 35% among men and 40% among women (Flegal et al., 2016)—across all age adult groups, obesity rates among U.S. women have been 4% to 5% higher than among men (Arroyo–Johnson and Mincey, 2016). Since 1990, this change was continual, such that we determine equations for the linear development of these reverse gradients since 1990.
In the U.S., an inverse correlation between obesity and median household income (logarithm) developed from nonexistent in 1990 into a steep inverse correlation, known as the “reverse gradient”, 25 years later. The reverse gradient involving diabetes prevalence also developed in the U.S. over the same period; this lagged the reverse gradient with obesity in 1990 but had fully caught up with it after 2010 (Fig. 3). Both facets of the reverse gradient developed remarkably quickly in the U.S., in about one generation.
Any hypotheses for the recent rise in obesity must account for the obesity epidemic having emerged only in the last few decades in the U.S. We observed that over ten years, the regression coefficient on leisure in predicting obesity increased from 0.40 to 0.63. We interpret this to be a social multiplier effect, as a physiological effect ought to have had that same coefficient through time. Our social multiplier estimate of 1.56 is close to that of crime and U.S. wages, both about 1.7, estimated by Glaeser et al., (2003) at similar scales of aggregation. While this is some evidence for social influence, these estimates might overstate the true social multiplier, due to correlation between demographics and unobservable elements (Glaeser et al., 2003).
Our simple S-curve approach was more illuminating than we had expected (see Kandler and Powell, 2018), because they were unexpectedly linear or perhaps slightly r-shaped (sensu Henrich 2001), i.e., the adoption patterns do not show much evidence for social (S-shaped) diffusion. A plausible explanation for the steady, 25-year increase in state–level obesity rates is a higher-obesity younger generation progressively entering the adult cohort.
The recent origin of the reverse gradient appears to favor the Insurance Hypothesis of HBE. The time series reveal only weak evidence of social learning in most states, insufficient to falsify the HBE hypothesis that obesity increased due to individual responses to a changing nutritional/economic environment. Additionally, there is a lack of evidence for a deep cultural history to obesity. While economic development may be a prerequisite for the reverse gradient (Tafreschi, 2015), the U.S. and Europe possessed developed economies for a century before the reverse gradient materialized. In Western Europe, there was still no reverse gradient as of 2008 (García Villar and Quintana-Domeque, 2009). The second is the fact that the reverse gradient developed smoothly over time, as described by Eq 6, which indicates the close relationship between income levels and propensity toward obesity. These observations are consistent with the Insurance Hypothesis, which is predicated on an evolved tendency for lower-income people to perceive risks in their local environment and over–compensate through excessive calorie intake.
There are alternatives to the Insurance Hypothesis, as an explanation based upon the behavioral responses of individuals. At the scale of economic geography, a significant factor is food deserts, where “easy geographic access to fast-food outlets and convenience stores encourages individuals to consume foods that are high in energy and saturated fats” (Mullan et al., 2017). Over 50 million people, almost 18% of the U.S. population, live in low–income areas without convenient access to a supermarket (Rhone et al., 2017). In high–income, highly urbanized countries, diabetes correlates positively with the percentage living in urban areas (Goryakin et al., 2017).
Some research has focused on the effect of highly processed foods, which typically contain much more added sugar than unprocessed foods (Lhila, 2011; Bocarsly et al., 2010; Jürgens et al., 2005; Martínez Steele et al., 2016; Stanhope et al., 2009). Excessive sugar intake, which may be addictive (Avena et al., 2008) is a causal factor in diabetes (Hu and Malik, 2010; Shang et al., 2012; Cornelsen et al., 2016) and may also be a causal factor in high obesity rates (Basu et al., 2013; Hu and Malik, 2010; Shang et al., 2012).
Americans have consumed refined sugar since the nineteenth century, however, so the question remains why the obesity increase, and the reverse gradient happened only in the past three decades. One possible explanation is the recent introduction of high fructose corn syrup (HFCS) into the food economy. Fructose, which decreases insulin sensitivity in obese people (Stanhope et al., 2009), has been used in commercial sugar–sweetened beverages since about 1970. That said, the trend might be due to unobserved individual–level effects, such as the more leisure, the more HFCS drinks consumed. The timing is suggestive; Fig. 9 shows a timeline of the increase in contribution of refined sugar and HFCS to U.S. diet, together with the increase in U.S. obesity rate. While overall sugar consumption rose gradually in the 20th century, from 12% of U.S. food energy in 1909 to 19% by the year 2000, the use of high fructose corn syrup in the U.S. increased from virtually zero per capita in 1970 to over 60 pounds per capita annually in the U.S. in 2000 (Gerrior et al., 2004), about half of total sugar consumption. HFCS became the main sweetener in soft drinks. By 2016 in the U.S., sweetened beverages constituted over 7% of household food expenditures and over 9% of expenditures for low-income households in the SNAP program (Garasky et al., 2016).
A timeline of the increase in contribution of refined sugar and high fructose corn syrup (HFCS) to U.S. diet, together with the increase in U.S. obesity rate. The data for sugar, dairy and HFCS consumption per capita are from USDA Economic Research Service (Johnson et al., 2009) except for sugar consumption before 1967, which are historical estimates (Guyenet et al., 2017). Obesity data (% of U.S. adult population) are from the Robert Wood Johnson Foundation’s Trust for America’s Health (stateofobesity.org). Total U.S. television advertising data are from the World Advertising Research Center (www.warc.com). The y–axis on the left covers all data series except advertising expenditures, which uses the y–axis on the right
The metabolic effects of HFCS include complications of glucose metabolism, lipid profile and insulin resistance (Pereira et al., 2017; Johnson et al., 2016; Bocarsly et al., 2010; Bray et al., 2004; Jürgens et al., 2005). HFCS as the driver of obesity and diabetes epidemics would be consistent with HBE in the general sense of human physiology having evolved around a diet containing little sugar and no refined carbohydrates. Hunter–gatherers generally do not exhibit obesity, diabetes, or cardiovascular disease (Kaplan et al., 2017). The HFCS explanation is also consistent with the Insurance Hypothesis, in that poor families are most subject to food scarcity (Hernandez, 2015) and HFCS-sweetened beverages predominate the food economy of poor regions of the U.S.
Conclusions
In conclusion, we find a steady increase, since 1990, in the “reverse gradient” or negative correlation between median household income and both obesity and diabetes rates. In 1990, there was no correlation across the US between either obesity and income or diabetes and income, yet by 2015 strong negative correlations existed across and within U.S. States. We have determined equations for the continual development of these reverse gradients over the past 25 years.
To explain this change, we find evidence in support for both HBE and “social multiplier” effect, a balance similar to empirical studies of other human behavior (Aral et al., 2009). We ascribe more weight to the HBE explanation, in that evolved mechanisms that increase fat storage in response to resource scarcity should promote obesity in high-income countries, where the poor have greater exposure to junk food and other cheap calories including processed sugars (Hill et al., 2017; Wells, 2017).
We speculate that the rapid increase in consumption of high fructose corn syrup (HFCS) may have been a key driver. The obesity and diabetes epidemics could be driven by the commercial oversupply and widespread marketing of inexpensive high-sugar foods, especially HFCS–sweetened beverages (Johnson et al., 2007; Song et al., 2012; Basu et al., 2013).
A fuller explanation of the timing and geography of the obesity epidemic will require the specific history of societal–level factors. Besides the suggestive temporal concurrence between obesity, food deserts and HFCS–sweetened beverages, additional clues lie in the considerable variation in the strength and evolution of the reverse gradient within different states of the U.S. This marked geographic variation in the slope of the reverse gradient indicates that government health policies can mitigate the effect of socioeconomic disparities. To explore the scale of these drivers, future work would review and compare state level health policies versus how the negative gradient evolved in those states.
Data availability
All data we used for this study are publicly–accessible, aggregated data. The datasets analyzed during the current study are available in the Dataverse repository: https://doi.org/10.7910/DVN/SMTX3X. These datasets were derived from the following public domain resources: Age–adjusted data on obesity rates at the county and state level for years 2004 to 2015 (Centers for Disease Control and Prevention, 2017d), as well as diabetes rates for 2009-2013 (Centers for Disease Control and Prevention, 2017d), are available from CDC. Available at: www.cdc.gov/diabetes/data/countydata/countydataindic State-level obesity rates since 1990 were obtained from the annual reports of the Trust for America’s Health (Robert Wood Johnson Foundation). Available at: stateofobesity.org/adult-obesity. Estimates of “leisure” (physical inactivity) are available from the CDC Behavioral Risk Factor Surveillance System (Centers for Disease Control and Prevention, 2017a). These CDC data come from health-related telephone surveys, which began in 1984 with 15 U.S. states, and now collects data in all 50 states through over 400,000 adult interviews each year. Available at: www.cdc.gov/diabetes/data/countydata/countydataindic. Food desert designations for the U.S. were recently made available through the Food Access Research Atlas (FARA) project (Rhone et al., 2017). The estimates are derived from the 2010 US Census and the 2010-2014 American Community Survey, in which census tracts are categorized by median income, vehicle availability, and SNAP participation. Available at: www.ers.usda.gov/webdocs/publications/82101/eib-165.pdf?v=42752.
References
Alvarado SE (2016) Neighborhood disadvantage and obesity across childhood and adolescence: Evidence from the NLSY children and young adults cohort (1986-2010). Soc Sci Res 57:80–98
Anderson PM (2012) Parental employment, family routines and childhood obesity. Econ Hum Biol 10:340–351
Anderson SE, Whitaker RC (2010) Household routines and obesity in us preschool-aged children. Pediatrics 125:420–428
Aral S, Muchnik L, Sundararajan A (2009) Distinguishing influence-based contagion from homophily-driven diffusion in dynamic networks. Proc Natl Acad Sci USA 106(51):21544–21549
Arroyo–Johnson C, Mincey KD (2016) Obesity epidemiology trends by race/ethnicity, gender, and education: National Health Interview Survey, 1997–2012. Gastroenterol Clin North Am 45(4):571–579
Avena NM, Rada P, Hoebel BG (2008) Evidence for sugar addiction: behavioral and neurochemical effects of intermittent, excessive sugar intake. Neurosci Biobehav Rev 32:20–39
Bass FM (1969) A new product growth model for consumer durables. Manag Sci 15:215–227
Basu S, Yoffe P, Hills N, Lustig RH (2013) The relationship of sugar to population-level diabetes prevalence: An econometric analysis of repeated cross-sectional data. PLoS One 8(2):e57873
Bentley RA, Ormerod P (2010) A rapid method for assessing social versus independent interest in health issues. Soc Sci Med 71:482–485
Bentley RA, Brock WA, O’Brien MJ (2016) Evaluating reproductive decisions as discrete choices under social influence. Philos Trans R Soc B 371:20150154
Blume LE, Brock WA, Durlauf SN, Ioannides YM (2011) Identification of social interactions. Handb Social Econ 1B:853–963
Bocarsly ME, Powell ES, Avena NM, Hoebel BG (2010) High-fructose corn syrup causes characteristics of obesity in rats: Increased body weight, body fat and triglyceride levels. Pharmacol Biochem Behav 97(1):101–106
Boden J, McLeod G (2017) Epidemiological foundations for the insurance hypothesis: Methodological considerations. Behav Brain Sci 40:e109
Bray GA, Nielsen SJ, Popkin BM (2004) Consumption of high–fructose corn syrup in beverages may play a role in the epidemic of obesity. Am J Clin Nutr 79(4):537–543
Brock WA, O’Brien MJ, Bentley RA (2015) Validating niche–construction theory through path analysis. Archaeol Anthropol Sci 8:819–837
Carroll SJ, Paquet C, Howard NJ, Coffee NT, Taylor AW, Niyonsenga T, Daniel M (2016) Local descriptive norms for overweight/obesity and physical inactivity, features of the built environment, and 10–year change in glycosylated haemoglobin in an Australian population-based biomedical cohort. Soc Sci Med 166:233–243
Centers for Disease Control and Prevention (2017a) Behavioral risk factor surveillance system. http://www.cdc.gov/brfss. Accessed on 20 Oct 2016
Centers for Disease Control and Prevention (2017b) Behavioral risk factor surveillance system: methods and references for county–level estimates and ranks and state–level modeled estimates. http://www.cdc.gov/brfss. Accessed on 20 Oct 2016
Centers for Disease Control and Prevention (2017c) Data and statistics, diabetes. http://www.cdc.gov/diabetes/data. Accessed on 20 Oct 2016
Centers for Disease Control and Prevention (2017d) Data and statistics, overweight and obesity. http://www.cdc.gov/obesity. Accessed on 20 Oct 2016
Centola D, Becker J, Brackbill D, Baronchelli A (2018) Experimental evidence for tipping points in social convention. Science 360:1116–1119
Christakis NA, Fowler JH (2007) The spread of obesity in a large social network over 32 years. N Engl J Med 357:370–379
Cleveland WS, Devlin SJ (1988) Locally weighted regression: an approach to regression analysis by local fitting. J Am Stat Assoc 83:596–610
Christakis NA, Fowler JH (2013) Social contagion theory: examining dynamic social networks and human behavior. Stat Med 32:556–577
Colleran H (2016) The cultural evolution of fertility decline. Philos Trans R Soc B 371:20150152
Colleran H, Mace R (2015) Social network-and community-level influences on contraceptive use: evidence from rural Poland. Proc R Soc B 282:20150398
Cook WK, Tseng W, Tam TC, John I, Lui C (2017) Ethnic-group socioeconomic status as an indicator of community–level disadvantage: A study of overweight/obesity in Asian American adolescents. Soc Sci Med 184:15–22
Corcoran M, Gordon R, Laren D, Solon G (1992) The association between men’s economic status and their family and community origins. J Hum Resour 27:575–601
Cornelsen L, Adams J, Gasparrini A, Iskander D, Knai C, Mytton O, Petticrew M, Scott C, Smith R, Thompson C, White M, Cummins S (2016) Impact of a levy on sales of sugar–sweetened beverages within a national chain of restaurants: Interrupted time-series analysis. Lancet 388:S15
Couzin ID, Ioannou CC, Demirel G, Gross T, Torney CJ, Hartnett A, Conradt L, Levin SA, Leonard NE (2011) Uninformed individuals promote democratic consensus in animal groups. Science 334(6062):1578–1580
Creanza N, Feldman MW (2016) Current opinion in genetics and development. Lancet 41:85–92
Datar A (2017) The more the heavier? Family size and childhood obesity in the U.S. Soc Sci Med 180:143–151
Dittmann AG, Maner JK (2017) A life–history theory perspective on obesity. Behav Brain Sci 40:e115
Dohle S, Hafmann W (2017) Toward a mechanistic understanding of the impact of food insecurity on obesity. Behav Brain Sci 40:e116
Dwyer–Lindgren L, Freedman G, Engell RE, Fleming TD, Lim SS, Murray CJL, Mokdad AH (2013) Prevalence of physical activity and obesity in U.S. counties, 2001–2011: A road map for action. Popul Health Metr 11:7
Flegal KM, Kruszon–Moran MS, Caroll MD, Fryar CL, Ogden CL (2016) Trends in obesity among adults in the United States, 2005 to 2014. JAMA 315(21):2284–2291
Garasky S, Mbwana K, Romualdo A, Tenaglio A, Roy M (2016) Foods typically purchased by snap households. United States Department of Agriculture, Food and Nutrition Service. http://www.fns.usda.gov/research-and-analysis. Accessed on 17 Feb 2017
García Villar J, Quintana-Domeque C (2009) Income and body mass index in Europe. Econ Hum Biol 7:73–83
Gerbault P, Roffet–Salque M, Evershed R, Thomas M (2013) How long have adult humans been drinking milk? Int Union Biochem Mol Biol 65:983–990
Gerrior S, Bente L, Hiza H (2004) Nutrient Content of the U.S. Food Supply, 1909–2000. United States Department of Agriculture
Glaeser EL, Sacerdote BI, Scheinkman JA (2003) The social multiplier. J Eur Econ Assoc 1(2-3):345–353
Goryakin Y, Rocco L, Suhrcke M (2017) The contribution of urbanization to non–communicable diseases: evidence from 173 countries from 1980 to 2008. Econ Hum Biol 26:151–163
Guyenet S, Landen J, Houser RF, Baghdady G (2017) Sugar consumption in the U.S. diet between 1822 and 2005. OnlineStatBook Project, case study 27, http://www.onlinestatbook.com. Accessed on 28 Apr 2017
Henrich J (2001) Cultural transmission and the diffusion of innovations. Am Anthropol 103(4):992–1013
Hernandez DC (2015) The impact of cumulative family risks on various levels of food insecurity. Soc Sci Res 50:292–302
Higginson AD, McNamara JM, Dall SRX (2017) Towards a behavioural ecology of obesity. Behav Brain Sci 40:e118
Hill S, Proffitt Leyva R, DelPriore D (2017) Predicting human adiposity—sometimes—with food insecurity: Broaden the model for better accuracy. Behav Brain Sci 40:e119
Hobaiter C, Poisot T, Zuberbühler K, Hoppitt W, Gruber T (2014) Social network analysis shows direct evidence for social transmission of tool use in wild chimpanzees. PLoS Biol 12(9):e1001960
Hruschka DJ (2012) Do economic constraints on food choice make people fat? A critical review of two hypotheses for the poverty–obesity paradox. Am J Hum Biol 24(3):277–285
Hruschka DJ, Hadley C, Brewis A (2014) Disentangling basal and accumulated body mass for cross–population comparisons. Am J Phys Anthropol 153:542–550
Hruschka DJ, Han SY (2017) Anti-fat discrimination in marriage more clearly explains the poverty–obesity paradox. Behav Brain Sci 40:e120
Hu FB, Malik VS (2010) Sugar–sweetened beverages and risk of obesity and type 2 diabetes: epidemiologic evidence. Physiol Behav 100(1):47–54
Hughes CC, Sherman SN, Whitaker RC (2010) How low–income mothers with overweight preschool children make sense of obesity. Qual Health Res 20:465–478
Johnson ML, Distelmaier K, Lanza IR, Irving BA, Robinson MM, Konopka AR, Shulman GI, Nair KS (2016) Mechanism by which caloric restriction improves insulin sensitivity in sedentary obese adults. Diabetes 65:74–84
Johnson RJ, Segal MS, Sautin Y, Nakagawa T, Feig DI, Kang DH, Gersch MS, Benner S, Sánchez–Lozada L (2007) Potential role of sugar (fructose) in the epidemic of hypertension, obesity and the metabolic syndrome, diabetes, kidney disease, and cardiovascular disease. Am J Clin Nutr 86:899–906
Johnson RK, Appel LJ, Brands M, Howard BV, Lefevre M, Lustig RH, Sacks F, Steffen LM, Wylie–Rosett J (2009) Dietary sugars intake and cardiovascular health: a scientific statement from the American Heart Association. Circulation 120:1011–1020
Jürgens H, Haass W, Castañeda TR, Schürmann A, Koebnick C, Dombrowski F, Otto B, Nawrocki AR, Scherer PE, Spranger J, Ristow M, Joost HG, Havel PJ, Tschöp MH (2005) Consuming fructose–sweetened beverages increases body adiposity in mice. Obes Res 13:1146–1156
Kandler A, Powell A (2018) Generative inference for cultural evolution. Philos Trans R Soc B 373(1743):20170056
Kaplan H, Thompson RC, Trumble BC, Wann LS, Allam AH, Beheim B, Frohlich B, Sutherland ML, Sutherland JD, Stieglitz J, Rodriguez DE, Michalik DE, Rowan CJ, Lombardi GP, Bedi R, Garcia AR, Min JK, Narula J, Finch CE, Gurven M, Thomas GS (2017) Coronary atherosclerosis in indigenous south American Tsimane: a cross–sectional cohort study. Lancet 389:1730–1739
Klein RJ, Schoenborn CA (2001) Age adjustment using the 2000 projected U.S. population. Healthy People Stat Notes 20:1–10
Kowaleski-Jones L, Brown BB, Fan JX, Hanson HA, Smith KR, Zick CD (2017) The joint effects of family risk of obesity and neighborhood environment on obesity among women. Soc Sci Med 195:17–24
Kranjac AW, Wagmiller RL (2016) Decomposing trends in adult body mass index, obesity, and morbid obesity, 1971–2012. Soc Sci Med 167:37–44
Lhila A (2011) Does access to fast food lead to super-sized pregnant women and whopper babies? Econ Hum Biol 9:364–380
Mani A, Mullainathan S, Shafir E, Zhao J (2013) Poverty impedes cognitive function. Science 341:976–980
Martínez Steele E, Baraldi LG, Louzada ML, Moubarac JC, Mozaffarian D, Monteiro CA (2016) Ultra–processed foods and added sugars in the U.S. diet: Evidence from a nationally representative cross–sectional study. BMJ Open 6:e009892
Mata J, Dallacker M, Hertwig R (2017) Social nature of eating could explain missing link between food insecurity and childhood obesity. Behav Brain Sci 40:e122
Mattson MP, Allison DB, Fontana L, Harvie M, Longo VD, Malaisse WJ, Mosley M, Notterpek L, Ravussin E, Scheer FA, Seyfried TN, Varady KA, Panda S (2014) Meal frequency and timing in health and disease. Proc Natl Acad Sci USA 111:16647–16653
Milot E, Mayer FM, Nussey DH, Boisvert M, Pelletier F, Réale D (2011) Evidence for evolution in response to natural selection in a contemporary human population. Proc Natl Acad Sci USA 108:17040–17045
Mokdad AH, Serdula MK, Dietz WH, Bowman BA, Marks JS, Koplan JP (1999) The spread of the obesity epidemic in the United States, 1991-1998. JAMA 282(16):1519–1522
Mullan B, Ntoumanis N, Thøgersen-Ntoumani C, Lipp OV (2017) It’s a bit more complicated than that: A broader perspective on determinants of obesity. Behav Brain Sci 40:e124
Muscogiuri G, Balercia G, Barrea L, Cignarelli A, Giorgino F, Holst JJ, Laudisio D, Orio F, Tirabassi G, Colao A (2018) Gut: A key player in the pathogenesis of type 2 diabetes? Crit Rev Food Sci Nutr 58(8):1294–1309
Nettle D, Andrews C, Bateson M (2017) Food insecurity as a driver of obesity in humans: the insurance hypothesis. Behav Brain Sci 40:e105
Ogden CL, Carroll MD, Kit BK, Flegal KM (2014) Prevalence of childhood and adult obesity in the United States, 2011–2012. JAMA 311:806–814
Pereira RM, Botezelli JD, da Cruz Rodrigues KC, Mekary RA, Cintra DE, Pauli JR, da Silva ASR, Ropelle ER, de Moura LP (2017) Fructose consumption in the development of obesity and the effects of different protocols of physical exercise on the hepatic metabolism. Nutrients 9:article 405
Redsell SA, Atkinson P, Nathan D, Siriwardena AN, Swift J, Glazebrook C (2010) Parents’ beliefs about appropriate infant size, growth and feeding behaviour: Implications for the prevention of childhood obesity. BMC Public Health 10:7–11
Rhone A, Ver Ploeg M, Dicken C, Williams R, Breneman V (2017) Low–income and low–supermarket–access census tracts, 2010–2015. United States Department of Agriculture, Economic Information Bulletin, EIB–165. http://ageconsearch.umn.edu/record/262134
Salmasi L, Celidon M (2017) Investigating the poverty–obesity paradox in Europe. Econ Hum Biol 26:70–85
Shalizi CR, Thomas AC (2011) Homophily and contagion are genetically confounded in observational social network studies. Sociol Methods Res 40:211–239
Shang XW, Liu AL, Zhang Q, Hu XQ, Du SM, Ma J, Xu GF, Li Y, Guy HW, Du L, Li TY, Ma GS (2012) Report on childhood obesity in China (9): Sugar–sweetened beverages consumption and obesity. Biomed Environ Sci 25(2):125–132
Shrewsbury V, Wardle J (2012) Socioeconomic status and adiposity in childhood: a systematic review of cross–sectional studies 1990–2005. Obesity 16:275–284
Smith TG (2017) Household–level financial uncertainty could be the primary driver of the global obesity epidemic. Behav Brain Sci 40:e128
Smits SA, Leach J, Sonnenburg ED, Gonzalez CG, Lichtman JS, Reid G, Knight R, Manjurano A, Changalucha J, Elias JE, Dominguez–Bello MG, Sonnenburg JL (2017) Seasonal cycling in the gut microbiome of the Hadza hunter-gatherers of Tanzania. Science 357:802–806
Song WO, Wang Y, Chung CE, Song B, Lee W, Chun OK (2012) Is obesity development associated with dietary sugar intake in the U.S.? Nutrition 28:1137–1141
Stanhope KL, Schwarz JM, Keim NL, Griffen SC, Bremer AA, Graham JL, Hatcher B, Cox CL, Dyachenko A, Zhang W, McGahan JP, Seibert A, Krauss RM, Chiu S, Schaefer EJ, Ai M, Otokozawa S, Nakajima K, Nakano T, Beysen C, Hellerstein MK, Berglund L, Havel PJ (2009) Consuming fructose–sweetened, not glucose–sweetened, beverages increases visceral adiposity and lipids and decreases insulin sensitivity in overweight/obese humans. J Clin Invest 119(5):1322–1334
Subramanian SV, Perkins JM, Özaltin E, Davey Smith G (2011) Weight of nations: a socioeconomic analysis of women in low– to middle–income countries. Am J Clin Nutr 93:413–421
Tafreschi D (2015) The income body weight gradients in the developing economy of China. Econ Hum Biol 16:115–134
Tapper K (2017) Children respond to food restriction by increasing food consumption. Behav Brain Sci 40:e129
Thomas AC (2013) The social contagion hypothesis: comment on ‘Social contagion theory: examining dynamic social networks and human behavior’. Stat Med 32:581–590
Vizireanu M, Hruschka DJ (2018) Lay perceptions of healthy eating styles and their health impacts. J Nutr Educ Behav 50:365–371.e1
Weinberg B, Reagan P, Yankow J (2004) Do neighborhoods affect hours worked? Evidence from longitudinal data. J Labor Econ 22:891–924
Wells JCK (2017) Obesity is not just elevated adiposity, it is also a state of metabolic perturbation. Behav Brain Sci 40:e130
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bentley, R.A., Ormerod, P. & Ruck, D.J. Recent origin and evolution of obesity-income correlation across the United States. Palgrave Commun 4, 146 (2018). https://doi.org/10.1057/s41599-018-0201-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-018-0201-x