Abstract
Normal aging often results in an increase in physiological tremors and slowing of the movement of the hands, which can impair daily activities and quality of life. This study, using lightweight wearable non-invasive sensors, aimed to detect and identify age-related changes in wrist kinematics and response latency. Eighteen young (ages 18–20) and nine older (ages 49–57) adults performed two standard tasks with wearable inertial measurement units on their wrists. Frequency analysis revealed 5 kinematic variables distinguishing older from younger adults in a postural task, with best discrimination occurring in the 9–13 Hz range, agreeing with previously identified frequency range of age-related tremors, and achieving excellent classifier performance (0.86 AUROC score and 89% accuracy). In a second pronation–supination task, analysis of angular velocity in the roll axis identified a 71 ms delay in initiating arm movement in the older adults. This study demonstrates that an analysis of simple kinematic variables sampled at 100 Hz frequency with commercially available sensors is reliable, sensitive, and accurate at detecting age-related increases in physiological tremor and motor slowing. It remains to be seen if such sensitive methods may be accurate in distinguishing physiological tremors from tremors that occur in neurological diseases, such as Parkinson’s Disease.
Similar content being viewed by others
Introduction
Aging is accompanied by the progressive deterioration of physiological and psychological functions due to a combination of structural changes such as the decline in strength in muscle, joints, bones, etc.1 and/or neurological conditions such as brain atrophy2. These deteriorations can affect the performance of daily activities involving arm motion3 and result in increased tremors4,5,6,7 and slowing of voluntary movement8,9.
Tremor is defined as a rhythmic, involuntary movement of a body part10. Depending on its etiology tremor may present in the form of rest (limb fully supported, such as on the arms of a chair, against gravity), kinetic (during movement), and/or postural tremor (while holding a limb in a particular position against gravity)11. All humans have tremors of small magnitude and high frequency called physiological tremor (PT)12, which increase in severity with age13,14,15. However, tremors may also occur as a result of a number of other conditions, including drugs16 or neurological disorders such as essential tremor (ET) or Parkinson’s Disease (PD)3. PT presents in the form of postural and/or kinetic tremor12; however, in our study, we have focused on postural PT, which may be helpful not only in identifying changes in aging but also in distinguishing hard to differentiate tremor symptoms in movement disorders such as PD versus ET or PD versus advanced physiologic tremor (e.g., reviews by Lenka et al.3 and Deuschl17).
Tremors generally have relatively constant frequency and variable amplitude (as reviewed by Wyne18), hence frequency domain analysis might lead to a more reliable detection and characterization of tremor than a time domain analysis. Previous research has found differences in ranges of tremor frequencies across conditions, for example with PT frequency in the 8–12 Hz range, PD tremor frequency in the 3–8 Hz band, and ET frequency spanning the 4–12 Hz range5.
Currently, the most reliable diagnostic tests for tremors are based on clinical scoring systems19. These scoring systems contain a substantial amount of error20 due to their inherent subjectivity21. In the past several years, a push towards more objective measures of tremors has been made. Numerous studies have analyzed the frequency domain of sensor signals for reliable and accurate measures of tremor22,23,24,25,26,27. For example, using accelerometer and electromyograph recordings of short 3-s windows in ET and PD patients, Luft and colleagues observed excellent classifier (\(\sim\) 91% accuracy) in categorizing short 3-s time windows as either tremor or non-tremor28. Using only acceleration data from inertial measurement unit (IMU) sensors, Ali and colleagues29, have been successful in distinguishing between ET participants and healthy control. This study also found that the sensors located on the forearm had the best classification results. To the best of our knowledge, we are the first to use accelerometer and gyroscope data from non-invasive, wrist-worn IMU sensors to investigate subtle healthy age-related changes in PT.
Many studies, such as by Ali and colleagues29, have successfully used machine learning techniques (ML) techniques to help identify characteristics of tremor in different human diseases (see review by De et al.19). Although there are numerous applicable ML techniques, Support Vector Machine (SVM) is one of the most efficient machine learning algorithms30. While ML techniques like SVM can handle large numbers of variables, feature selection is crucial in ML because it improves model performance by reducing overfitting, enhancing model interpretability, and contributing to computational efficiency. The Minimal Redundancy Maximal Relevance (MRMR) algorithm first introduced by Peng et al.31 is a powerful algorithm that identifies a subset of input features (independent variables) by simultaneously maximizing relevance to the target variable and minimizing redundancy among selected features. Other feature selection methods in ML studies have used standalone methods such as analysis of variance32,33,34,35,36,37 or a two-step process combining the MRMR algorithm with secondary techniques such as with Fischer scores38, kernel canonical correlation analysis39 and kernel principal component analysis40. However, we are not aware of any studies that have used the MRMR algorithm followed by a variance threshold as a feature selection technique for an SVM to distinguish PT in young and older adults.
Age-related slowness of movement has also been examined in various studies to track age-related decline. In one such study, recording, and analyzing surface electromyographic waveforms from biceps brachii (agonist) and pronator teres (antagonist) muscles, Lewis and Brown8 found an age-related increase in motor response time (RT) to an auditory cue in the elderly. In a longitudinal study of aging, Fozard et al.41 found a slowing of simple RT to a single cue and a relatively greater slowing of RT to multiple randomized cues (disjunctive RT) across decades. Their study indicated consistent slowing and increased variability of reaction time to auditory cues with age. Other sensor-based studies have found increased response time with aging to various types of cues42,43,44,45,46. We investigated if commercially available lightweight sensors could be used not only to detect age-related increases in tremor but also slowing of voluntary arm movement in older participants, in order to capture a more complete picture of age-related changes in arm motion.
In summary, the overall goal of our study was to determine whether affordable, non-invasive IMU sensors could not only detect and identify changes in age-related arm motion changes in tremor and voluntary movement initiation but also achieve excellent classifier performance. The classifier performance serves to validate the efficacy of the set of selected motion signals in distinguishing age-related changes in tremors.
Given previous findings that sensors located on the forearm had the best signals for tremor classification29, we mounted our IMUs on the wrists. Using a power spectral density analysis, we transformed the 12 kinematic variables from the time domain to obtain the distributions of power in the frequency spectrum. Additionally, to optimize the identification of distinguishing tremor characteristics, we used a two-step process for feature selection (MRMR and analysis of variance) and then used the selected features in an SVM ML technique. Our goals were: (1) to identify which kinematic features show the most discriminating power between the two subject populations for changes in tremor; (2) to measure how well the ML classifier performed to classify the tremor of younger and older subjects; and (3) to test if the non-invasive wrist sensors could also reliably detect RT slowing in an older adult population.
Results
Analysis of tremor (Postural task)
Feature selection
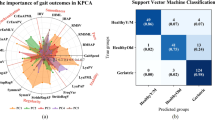
The MRMR algorithm, followed by the selection of features that accounted for at least 90% of the variance47,48,49, resulted in a final set of 5 features: (1) linear acceleration, Y-axis and (2) linear velocity, Y-axis, (3) angular velocity, Yaw-axis (4) angular velocity, Roll-axis, and (5) angular acceleration, Yaw-axis (See Table 1 and Fig 1). Physiologically these features indicate tremors in elbow flexion/extension (linear acceleration and linear velocity in Y-axis), elbow pronation/supination (angular velocity in Roll-axis) and wrist adduction/abduction (angular velocity and acceleration in Yaw-axis). The variance explained by each variable was 29.1%, 22.3%, 16.1%, 15.4%, and 9.1% respectively.
Features Selected for Classification. From features selected after the MRMR algorithm, use features that explain \(\sim\) 90% of variance. Five features selected were Total Power of (1) linear acceleration in Y-axis (\(P_{a_y}\)), (2) linear velocity in Y-axis (\(P_{v_y}\)), (3) angular velocity in Yaw-axis (\(P_{\omega _{Yaw}}\)), (4) angular velocity in Roll-axis (\(P_{\omega _{Roll}}\)) and (5) angular acceleration in Yaw-axis (\(P_{\alpha _{Yaw}}\)). The variance explained by each variable was 27%, 23%, 16%, 15% and 10% respectively.
Classification
Using the 5 selected features as predictors in an SVM classifier, we tested which frequency ranges of these features provide the best classification performance (see Table 2). The best AUROC performance (0.86) and accuracy performance (89%) was seen in the 9–13 Hz range, a range that is very close to the range of PT identified in past literature (8–12 Hz5). The worst performance was seen in the lower frequency ranges, 2–6 Hz range for AUROC (0.65) and 4.5–8.5 for accuracy (55%), see Fig 2 and Table 2.
Performance of SVM Classifier. AUROC curves for the entire frequency range i.e. 2–15 Hz (grey), frequency range with best performance (dark blue), and frequency range with worst performance (light blue). Best performance was seen at 9–13 Hz (AUROC = 0.86) and worst performance was seen at 2-6Hz (AUROC = 0.65).
Model validation
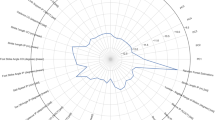
As seen in Fig. 3, our model was able to predict group membership best, in the 9–13 Hz frequency range, as indicated by the highest mean AUROC score (0.86) when compared to the performance of any individual feature (highest mean AUROC score = 0.51) as well as to the average performance of all other 791 randomly selected 5 features (.77).
Spider plot of mean AUROC scores of 1000 epochs. The scores for each kinematic feature, the Model, and the average score for the 791 other possible random combinations of 5 features (RFC) in the 9–13 Hz frequency range are shown. The Model in the figure is the SVM classifier with 5 features selected based on the algorithm described in section “Feature selection”. The Model has the highest mean AUROC score.
Analysis of Response Time (Pronation–Supination task)
Figure 4 shows that older adults had a significant slowing of RT (147 ms) compared to younger adults (76 ms) (71 ms difference, Wilcoxon ranked-sign test; W = \(-3.765\), \(p= 0.016\), \(\eta ^{2}= 0.5124\)).
Discussion
Using lightweight, commercially available sensors, we demonstrate here a method that achieves excellent classification performance of tremors in younger versus older adults as well as a method to quantify motor slowing in the initiation of arm movements. For tremors, our research identified five wrist kinematic variables in a postural task that optimally distinguish tremors in older adults from their younger counterparts. These selected features exhibit peak classifier performance in the 9–13 Hz range, matching closely with previously identified5 wrist PT frequency ranges. By using a combination of these selected features our model classifier predicting group membership achieves excellent performance and outperforms models using only any one individual feature (mean AUROC = 0.86 vs. mean AUROC = 0.51, respectively). Additionally, these same sensors were also sensitive enough to detect a \(\sim\) 71 ms slowing in voluntary arm movement initiation in older adults, agreeing with previous studies showing age-related slowing50. The methods reported herein may be useful in guiding future research aimed at distinguishing between different neurological disorders.
Importance of feature selection
Several studies have explored the kinematic composition of tremors27,51,52,53,54. However, to the best of our knowledge, we are the first to employ a data-driven feature selection process to do so. Our method demonstrates the efficacy of employing feature selection techniques to discern the primary components of PT from a pool of 12 kinematic variables, shedding light on the crucial factors that distinctly contribute to the age-related changes in tremors.
Given that postural PT is a universal characteristic of adult humans12 but escalates in severity with age13,14,15, our results suggest that the distinct shift in postural PT composition severity with age is primarily observed in the Y-, Yaw-, and Roll-axes.
It is interesting to note that the Y-axis shows the most significance in the results of our feature selection. It suggests that, although we measured at the wrist, the tremor may originate in more proximal arm joints (such as the elbow or shoulder). In their analysis of postural tremors within their neurotypical older subject population Chan and colleagues27 found that tremors at the elbow were significantly more severe than at the wrist.
We also observed significant tremor components in the Roll-axis. Rahimi and colleagues documented motion measurements in ET and PD patients in three degrees of freedom52, a setup mapping to our Y-axis, Yaw-axis, and Roll-axis, and found tremor in the Roll-axis to be indicative of ET. As part of our protocol inclusion/exclusion criteria, our participants did not have a history of diagnosed ET. However, we know from the literature that ET frequency is in the 4–12 Hz range5 which has overlap with the range of PT frequency (i.e. 8–12 Hz5), and also tends to increase with age55. Chan and colleagues27 found that elbow pronation–supination (mapping to Roll-axis in our study) showed the biggest difference in severity in their comparison of tremor composition between PD patients with subclinical tremor and age-matched controls. These findings suggest a potential overlap in the tremor composition of of ET, PT and subclinical PD in the Roll-axis with differences in frequency range and severity. Our use of the MRMR algorithm for feature selection was a critical step to help identify the features with maximum relevance for distinguishing tremor differences between groups.
Our feature selection approach is generalizable and could be used to distinguish the changes in tremor composition that occur in healthy aging from pathological aging populations. Identifying the crucial component features distinguishing tremors arising from different pathophysiologies may aid in differential diagnosis, help track progression, and/or lead to more targeted medical interventions and assistive devices.
Importance of frequency range
Using a data-driven approach, we identified that the 9–13 Hz frequency range best-differentiated tremors between our older and younger participant groups. Interestingly, this frequency range largely overlaps with wrist tremor frequencies labeled PT (8–12 Hz)5. However, some studies have also reported observing PT in the lower (1–4 Hz)56 and higher (15–30 Hz) ranges57. As PT frequency is affected by limb weight58, these alternative frequency ranges may be explained by the different placements of the sensors used in these studies. Further, IMU sensors suffer from low-frequency noise (< 4 Hz59) and, according to Chang and colleagues, there is a physiological limit to hand motion frequency somewhere within the 15–20 Hz range60. These effects suggest caution on the interpretation of differences found in either very low or high frequency56,57 results and necessitate further analysis. For this reason, many recent studies investigating arm movements, including our own study, bandpass their IMU signals, eliminating frequencies below 2 Hz61 and above 15 Hz60,62 to filter out noise from the sources mentioned above.
As briefly reviewed earlier, tremors may also occur as a result of other conditions, including ET and PD. However, previous research has suggested differences in the affected frequency ranges for these different tremor conditions. For example, changes in the 3–8 Hz range are associated with PD while changes in a broader range, 4–12 Hz, have been associated with tremors in ET patients5. It remains to be understood what the underlying physiological changes are that produce these frequency-specific changes (review by Hallett63). However, identifying such behavioral biomarkers is the first step in identifying, quantifying, and tracking changes. This baseline is also necessary to evaluate the effectiveness of interventions in reducing the severity of specific tremors, especially in patients who may have a combination of conditions that lead to tremors.
Age-related motor slowing
Aging is associated with reductions in peripheral muscle strength and motor control (e.g., see reviews by64,65). However, high-resolution structural magnetic resonance imaging (MRI) shows that there is already cortical thinning by middle age with prominent atrophy in the primary motor cortex (e.g.,66; review by Clark and Taylor67), suggesting additional central functional (brain) deterioration with age. Further, some evidence suggests that as motor control declines in older adults, they become more reliant on cognitive control mechanisms68. Unfortunately, prefrontal structures that support cognitive control show the largest age-related decline68, potentially leading to further slowing and deficits in motor control. We found significant differences in RT (71 ms) between younger and older participants in a pronation–supination task using both a fixed and a relative threshold value for initiation of movement. Hence, such a simple behavioral biomarker may serve as a measure of cognitive control of voluntary movements and provide a simple yet sensitive tool to track these functional and difficult-to-measure age-related changes.
Studies in healthy younger adults have shown that the mean RT to temporally varied auditory stimuli is approximately 284 ms50 however our results show a much faster mean RT than this value (mean RT for younger adults = 76 ms and mean RT for older adults = 147 ms). These results are likely due to a combination of practice before task recording69 as well as motor anticipation, given the experimenter counted down from 3 prior to saying “Start”.
The younger participants also had significantly more “early starts” (i.e., initiation of movement before the experimenter said “Start”). We know from literature that there is primer muscle onset latency, i.e. slowness of activation of muscles in advance of reaction time movements, associated with aging70. Also, anticipatory movements require cognitive control71 which, as established before, has been shown to decline with age44,72. Thus, reduced motor readiness and impaired anticipatory movements likely led to the slow RT in the older population.
Movement artifacts
It is possible that we achieved such an effective classifier differentiating between the younger and older participants (AUROC score = 0.86, Accuracy = 89%) because we sampled during a postural (no movement) task, in contrast to past studies such as the one conducted by Luft and colleagues28. Although PT is also observed in kinetic tremor63 in an overlapping frequency range (8–12 Hz)73, a postural task may mitigate motion artifacts. Chan and colleagues, in their analysis of tremor between PD patients and age-matched controls, also found that the postural task showed the best results in tremor differences27. It is possible that motion artifacts may lead to added complexity in the measured feature signals, subsequently affecting both classifier performance and interpretation of results. Future studies are needed to investigate whether the tremor classification performance between older and younger adults differs in tasks with and without movement.
Limitations
One possible limitation is medication differences. That is, it is possible that the increase in tremors in the older population may have occurred as a result of increased medication in the elderly16. Previous reports suggest that antihistamines and antidepressants can potentially exacerbate tremors74,75. Two subjects in our older population were on antidepressant medication, with one of these subjects simultaneously taking antihistamines. Similarly, there were three subjects in our young adult group who were taking anti-depressant medication. To test if medication differences affected our findings, we re-analyzed our data after removing these 5 participants. We found similar findings. Namely, we found the same five wrist kinematic variables, which resulted in peak classifier performance in the 9–13 Hz range, with performance (AUROC of 0.88) closely matching the full data set (AUROC of 0.86). In addition, we found a similar slowing in voluntary arm movement initiation (72 ms vs. 71 ms for the full data set). Hence, medication differences did not alter our main findings.
Another possible limitation of our study is the unequal sample sizes. Unequal sample sizes in classification models can be a cause of bias and insufficient power. However, some have argued that a larger control (as opposed to experimental) group, such as we have, may lead to more power76. More importantly, some studies have shown that the AUROC77 and/or F1 score78 are acceptable metrics to evaluate the performance of imbalanced groups in classification. However, there is some debate regarding which one is the more robust metric for this scenario. Our results show a very high mean AUROC score. We also calculated a mean F1 score (average score over a 1000 epochs) for the classification model in the 9–13 Hz and also obtained a high performance metric (F1 score = 0.88). These metrics suggest our findings were reliable with both metrics, suggesting no bias.
In this study, we split all the observations between training and testing sets. However, given there were two observations (two wrists) per subject, there exists the possibility that different observations from the same participant were included in both training and testing sets. Having an observation from the same subject in both training and testing sets could have possibly biased the model (making model performance metrics more optimistic), due to possibly higher inter-subject variance and lower intra-subject variance. However, in a small, unbalanced sample size such as ours, it is also possible that restricting the model to fewer subjects in training (as would be needed to avoid the above issue) increases overfitting of the model to the training data by learning participant-specific patterns rather than a generalizable pattern (biasing model performance metrics to underperform). A future study with a larger, more balanced sample size is needed to better explore how performance of the algorithm changes by splitting the data so that all observations from a participant are either in training or testing sets but not both, similar to the study by Gholamiangonabadi and colleagues79.
Finally, it is possible that the RT analysis could have been biased by the experimenter purposely pressing the button for the “Start” event marker too early or fast for the Older participants, thus resulting in the appearance of a slower RT in this group. We used the countdown (i.e. “3.2.1.Start”) to decrease experimenter button press variability (as well as participant RT) based on findings in the literature that auditory rhythms decrease movement variability (e.g. Varlet et al.80). Further, if the experimenter was biased to go slower for older participants (delaying button press), this would decrease RT in Older participants, the opposite of what we found. Nonetheless, our design made it more difficult for any experimenter bias. Ideally, the stimulus (i.e. “Start”) and event marking would have been automated to occur synchronously. Unfortunately, the Consensys Pro software, which was used for data acquisition and event marking, did not have the capability of generating or recording an external sound or external event marker. A future study interested in more accurately capturing auditory-initiated response differences will have to use a different sensor system that allows for event marking of an auditory cue.
Future directions
These findings suggest many possible exciting future directions, such as identifying features that distinguish healthy aging from other tremor disorders (with onsets in the aging population) or identifying universal features that can differentiate multiple disorders and healthy aging at the same time. Indeed, examination of kinematic biomarkers either across broader more evenly distributed ages or across repeated sampling (i.e., repeated sampling over short temporal intervals to detect changes) may also potentially provide key features to help identify and disentangle age-related from disease-related tremors. A larger number of trials per participant may also enable the study of the individuality of tremors in participants using an analysis similar to that by Kopnarski and colleagues81.
Since tremors are affected by limb weight58, it may be that the classifier would perform even better with similar kinematic features from a lighter appendage, like the fingers, or worse from a heavier appendage like the legs. However, past studies investigating physiological and sub-clinical PD tremor27 have interestingly found that inertial sensors measuring at the proximal joints of the arm show significantly more tremor than at the distal joints. Future studies using our method to analyze PT at different joints in the arm could shed more light on this debate.
The portability of IMUs could facilitate remote monitoring of tremor-related diseases, reducing the need for patients to travel to the hospital/clinic as frequently. Such portable IMUs may also make it possible to identify tremor episodes over extended periods. Wearable devices, such as Fitbit smartwatches, have already been adopted by many people. These devices carry similar inertial sensors82. Together these methods have great potential to enhance telehealth approaches to diagnosis and tracking interventions and inform the design of assistive devices for older adults. However, many challenges remain, such as capturing data offsite in an unsupervised setting.
Methods
Participants
Twenty-three younger (ages 18–20, 12 female) and nine older (ages 49–57, 7 female) adults participated in this study. Only two younger and one older adults were left-handed. Data from 5 younger subjects was not included due either to technical issues with data collection (3 subjects; sensor disconnect or software crash during data upload) or due to the subject not following instructions (2 subjects; moving repeatedly during the recording when instructed not to move). Hence, data from eighteen younger (7 female, age 18–20, mean = 19, SD = ± 1) and nine older (7 female, age 49–70, mean = 56, SD = ± 8) participants was used for analysis. Prior to providing informed consent, all of the older participants completed the University of California, San Diego Brief Assessment of Capacity to Consent (UBACC)83, to ensure there was no age-related cognitive decline diminishing their capacity to consent. All older participants were above the threshold (UBACC ≥ 15/20) and were considered to have adequate capacity to provide informed consent. All participants provided written informed consent approved by Purdue University’s Institutional Review Board (IRB-2021-179 for younger participants, and IRB-2022-1299 for older participants) and in accordance with the Declaration of Helsinki. Younger participants were recruited from, and received course credit (via SONA Systems), while older participants were recruited via flyers and were compensated $15 for their participation. Finally, older participants completed the Montreal Cognitive Assessment (MOCA) to screen for any mild cognitive impairment. All older participants were above the threshold (MOCA Score ≥ 23) indicating no mild cognitive impairment84,85.
Behavioral tasks. (a) Postural task: Each participant was asked to stretch their arms out in front of the body with palms down. A 30-s recording was taken with the participant not moving while maintaining this position (b) pronation–supination task: Each participant was asked to extend their arms out in front of their body with the palms down and then after a warning signal (“3, 2, 1, Start”) to turn their palms up and down 20 times as fast and as fully as possible. The model in the figure is not a study participant and consent was obtained prior to the use of media.
Measurement system
Two lightweight Shimmer3 IMU Units86 were attached to the wrists via elastic bands and recorded tri-axial linear acceleration (along X, Y, and Z axes in m/s\(^{2}\)) and tri-axial angular velocity data (about the Roll, Pitch, and Yaw axes in deg/s). Sampling frequency was set to 100 Hz, consistent with previous tremor studies5, and sensors were paired with the ConsensysPRO87 software (on a laptop) via Bluetooth transmission to acquire movement signals and event markers (in ms) data.
Sensor Setup. (a) Shimmer sensor secured to the participant’s wrist with elastic wristbands. (b) Shimmer Sensor Axes. Data was collected in the X, Y, Z, Roll, Pitch, and Yaw axes which were defined as shown. Physiologically these axes translate to elbow medial/lateral rotation, elbow flexion/extension, shoulder flexion/extension, elbow pronation/supination, wrist flexion-extension, and wrist adduction/abduction.
Tasks
Each participant performed two tasks: A Postural task (see Fig. 5a) for analysis of tremor and a Pronation–Supination task (see Fig. 5b) for analysis of RT. In each task, we recorded one trial from each wrist, for a total of 2 observations per participant per task. Both these tasks are part of the clinical motor symptom assessment test for Parkinson’s Disease (MDS-UPDRS) and the official instructions were adapted88.
Starting position
For both tasks, the participant was first instructed to assume the starting position, with both arms stretched out in front of the body, keeping elbows at a 180°angle, forearms and wrists straight and parallel to the floor, with palms down and their back against the backrest and feet comfortable touching the floor (Fig. 5a).
Postural task
In this task, after assuming the starting position, the participant was then instructed to hold this position for 30-s without moving, until the experimenter said “Stop” (Fig. 5a).
Pronation–supination task
In this task, after assuming the starting position, the participant was asked to turn the palm up and down alternately (referred to here as one repetition) 20 times as fast and as fully as possible while keeping the elbows at a 180°angle, forearms and wrists straight and parallel to the armrest, until the experimenter said “Stop” (Fig. 5b).
Experiment procedure
After the assessment of capacity to consent (older subjects only), informed consent (all participants), and MOCA (older subjects only), a SHIMMER3 IMU was secured on the right and left wrist of the participant (as shown in Fig. 6a).
Sensor check
A sensor check test was first performed to ensure proper operation of the sensors for each arm and for each of the 6 axes (X, Y, Z, Roll, Pitch, and Yaw, defined as shown in Fig 6b).
Task order, instruction, and practice
After checking the sensors, all subjects performed the Postural task first and then the Pronation–Supination task. For each task, the participant was first given the instructions and procedures for the task. In the pronation–supination task, participants were told that after assuming the starting position, the participant should start only when they heard the experimenter say the words “Three. Two. One. Start” and stop each task when they heard the experimenter say “Stop”. Participants were then asked to assume the starting position and show the experimenter in order to demonstrate that they understood the instructions.
Recording, zeroing, start and stop
For each task, after practice, each participant was asked to assume the starting position and to stay as still as possible. Then, the experimenter started the recording, zeroed the sensors (Zero Signals), and announced to the participant the warning (“3, 2, 1”) followed by the start (“Start”) signal. After completion of each task, the experimenter announced ”Stop” and ended the recording. When the experimenter announced the words “Start” and “Stop,” they simultaneously pressed a button, which created an event marker in the data file. The ConsensysPro software has a built-in event marker and timer, which were used to mark the start and end of data collection and the task start and end cues (simultaneously with the words “Start” and “Stop” as shown in Figs. 7a,b), as well as used to measure the 30-second task time.
Task Timeline. (a) Postural Task (b) pronation–supination task. All signals were first set to zero (Zeroing). Shading indicates time period analyzed (a) and range of calculated RT onsets across participants (b). As shown in the figure the experimenter started the data collection after zeroing the signals (and before announcing “Start”) and ended data collection after announcing “Stop”.
Pre-processing data
All the data processing was conducted using MATLAB R2022a.
Filter data
A 2–15 Hz band-pass filter was applied to the linear acceleration and angular velocity signals in both Postural Task and pronation–supination task data to remove low-frequency sensor drift and high-frequency noise.
Pre-processing, postural task data only
After filtering, the following steps were applied to the Postural Task data:
Calculate linear velocity
For each participant, the linear acceleration data (from “Zero signals” to “End” in Fig. 7a) was integrated to calculate linear velocity using the trapezoidal method,
where v(t) and a(t) are the linear velocity and acceleration, respectively, for the time range \(t_{i}\). The initial velocity at the start of recording was assumed to be zero (i.e., \(v(0) = 0\)).
Numerically integrating accelerometer signals introduces a drift in the processed velocity signal89 and many methods have been proposed to eliminate this drift90,91,92,93,94,95,96. We used a widely accepted method suggested in Slack and Ma97, wherein we detrend the signal (using the MATLAB function “detrend”) by removing the best straight-fit line from the data. Supplementary Fig. S1a illustrates two example participants’ data in the Y-axis (older participant in green, younger in black) showing the numerical integration of the linear acceleration signal to calculate the linear velocity signal.
Calculate angular acceleration
The filtered angular velocity (\(\omega\)) signals from the “Start” to the “Stop” events were differentiated to obtain the corresponding angular accelerations (\(\alpha\)) along the roll, pitch, and yaw axes:
where \(\alpha (t)\) is the angular acceleration (\(\alpha\)) and \(\omega (t)\) is the angular velocity as a function of time t.
Supplementary Fig. S1b illustrates two example participants’ data in the Yaw-axis (older participant in green, younger in black) showing differentiation of the angular velocity signal to calculate the angular acceleration signal.
Calculate total power in power spectrum density
In order to identify differences in tremor, we converted the 12 kinematic variables (linear and angular velocities and accelerations) from the time domain to the frequency domain, as many previous studies have done29,98,99,100; then conducted a Power Spectral Density (PSD) analysis to obtain the distribution of power in the frequency spectrum. To avoid any initiation (“Start”) and termination (“Stop”) motion artifacts, we only analysed the middle 20-s period of the 30-s Postural task. For each of the 12 kinematic variables, we normalized the power spectra by dividing all values by the maximum power value observed. Supplementary Fig. S1c shows an example of PSD analysis of one of the kinematic variables (angular acceleration in Yaw-axis) across Older (in green) and Younger (in black) groups and nicely illustrates that group differences are much more apparent in the frequency spectrum. For each participant, the Total Power was calculated using Eq. 3 as follows:
where P(f) is the power at a particular frequency (f) in the periodogram. The frequency window over which Total Power (\(P_{total}\)) is calculated is i to j. We used the entire frequency range (2–15 Hz) for feature selection but also evaluated narrower frequency ranges (in frequency windows of 4 Hz with an increment of 0.5 Hz as shown by the beige bar in Supplementary Fig. S1c for classification as further discussed below.
To test for differences in Total Power values between the signals from the left and right wrist in each group, we conducted a pairwise Wilcoxon rank-sign test and found that their medians were not significantly different (all p > 0.05; see Supplementary Tables S1, S2). This finding is in agreement with past literature that found bilateral symmetry in PT101. Hence we used both left and right wrist data as separate observations for analysis of tremor (section “Analysis of tremor (postural task)”) and RT (section “Data analysis response time (pronation–supination task)”).
Analysis of tremor (Postural task)
Left and right wrists of each participant were considered as separate observations, so that our dataset consisted of n = 54 observations (36 observations for Younger and 18 for Older participant group). Each observation contained a label (0 = Younger participant; 1 = Older participant) and k = 12 kinematic variables (normalized total power values for each of the 12 kinematic variables across the entire frequency range). To evaluate which kinematic features (i.e., tremor signals) best distinguish between the Younger and Older populations we used binary classification. We used a three-step algorithm of (1) Data Splitting (2) Feature Selection and (3) SVM Classification. The algorithm was run for 1000 epochs.
Data splitting
We selected 80% of the observations in the dataset and assigned them to a training set and the remaining 20% to a testing set. Each epoch (1000 total) utilized a different randomly selected training data and testing data sample.
Feature selection
We used the Minimum Redundancy Maximum Relevance (MRMR) method (fscmrmr function in MATLAB) on the training set to reduce the number of features (from k, to k\('\), where k′ ≤ k) and identify the optimal set of kinematic features (normalized total power scores of the entire frequency range) to classify Younger and Older participants. This method indicates how well a specific feature (percent variance accounted for) predicts the outcome variable (i.e., whether a participant is a member of the Younger or Older group) while minimizing redundancy (i.e., minimizing the correlation of the kinematic variables)31. The average variance explained for each feature across all epochs is shown in Table 1. For each epoch, we selected a subset of features, k\('\), that exceeded 90% of the total variance in the outcome (i.e., we added variables until their sum exceeded 90%). In addition, for each epoch, we created reduced training and testing sets, including only the selected features, k\('\), for each observation. These reduced training and testing data sets were used in the SVM classification.
SVM classification
In each epoch, the reduced training dataset was used to train an SVM classifier model. The goal of the classifier was to discriminate between Younger and Older participants. SVM has been shown to be superior at binary classification30,102,103 compared to various other ML techniques used to identify tremor characteristics (see review by De et al.19) and has been extensively used in previous studies for similar applications (e.g., Ali and colleagues29). For each SVM model, we used a linear kernel, with auto hyperparameter optimization and standardized features (using the fitcsvm function in MATLAB) to train the model on the reduced training set. The reduced testing set was used to test the performance of the model on classifying unseen data.
We analyzed the performance of the classifier using the total frequency range (2–15 Hz) for these features as well as using 4 Hz frequency windows, in increments of 0.5 Hz, to determine if particular frequency ranges provided better classification. The 4 Hz interval was chosen because previous research examining physiological tremor (PT) as well as tremors in many movement disorders has found differences in tremor frequencies in smaller frequency ranges, such as 4 Hz. As we discuss in the introduction, prior literature has reported PT frequencies occur in the 8–12 Hz range and PD resting tremor in the 3.5–7.5 Hz range5, ranges that would be captured by shifting, in 0.5 Hz increments, a 4 Hz interval.
Evaluation metrics
True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN) were used to calculate the Area Under the Receiver Operating Characteristic curve score (AUROC score) and accuracy, as metrics to evaluate the performance of the classifier. The AUROC score was obtained using the MATLAB function perfcurve and the accuracy (classification accuracy) was calculated using Eq. (4).
Mean testing accuracy of 1000 epochs was used as the accuracy of the classification.
Model validation
We used a bootstrapped method to evaluate the model performance as described in the sections above to reduce the bias of a single model by averaging the predictions of multiple models trained on different samples (resampled 80% training and 20% testing in each epoch). Traditional cross-validation methods such as Leave-One-Out, K-Cross, and Holdout (See review by Yates and colleagues104) have indeed been used extensively in the literature and may have perhaps been computationally more efficient than our bootstrapped method. However, these methods are generally used to compare different models to find the one with the least error. In our study, we seek to evaluate the feature set not the particular classification model. Given our small sample size, we believe this method allows for more number of possible training and testing sets than Leave-One-Out, K-Cross, and Holdout methods leading to a more robust testing of the feature set as predictors.
To test if the performance (mean AUROC score over 1000 epochs) of our feature set, obtained from the method described in section “Feature selection”, is able to predict group membership (Older or Younger participant) better than that of any individual feature on its own or indeed any other 791 possible combinations of 5 features from the set of 12 features (\(\left( {\begin{array}{c}12\\ 5\end{array}}\right)\) = 792 features) in the 9–13 Hz frequency range, a model validation procedure was performed with the SVM classifier, similar to the analysis conducted by Sotirakis et al.105. We compared the performance of our model to the performance of any individual feature as well as to the average performance of all possible combinations of 5 features in predicting group membership.
Data analysis Response Time (Pronation–Supination task)
Angular velocity in the Roll axis was used to calculate movement latency in the pronation–supination task since the motion was significantly localized to that axis. \(t_s\) was the time at which the task start event marker was pressed (“Start”). The initiation of motion was defined as the timepoint, \(t_m\), at which instantaneous angular acceleration in the Roll axis exceeded 5% of peak value of \(\frac{\Delta \omega _{Roll}}{\Delta t}\) motivated by the method used in Kita et al.106. Hence, response time (RT) was equal to \(t_m - t_s\). As a result, any participants who started before the “Start” event marker had a negative RT value. We expected participants to anticipate the task cue signal and thus have a distribution of RTs near or shortly after the start event time.
Conclusion
We have presented preliminary evidence of a method to detect age-related changes in wrist tremor and voluntary movement initiation latency. Our findings demonstrate that analyzing simple kinematic variables available in affordable, commercial sensors can detect and track these age-related arm motion changes. Our method was sufficiently sensitive to detect increased small physiological tremor-like wrist motions and slowed movement initiation times in healthy older individuals as compared to young adults. It remains to be seen if it can help improve the detection and evaluation of tremors in the clinic with various etiologies and whether further advances are needed for telehealth.
Code availability
The underlying code for this study and training/validation datasets are not publicly available since it is still being further analyzed but some parts may be made available to qualified researchers on reasonable request to the corresponding author.
References
Carmeli, E., Patish, H. & Coleman, R. The aging hand. J. Gerontol. A Biol. Sci. Med. Sci. 58, M146–M152 (2003).
Markov, N. T. et al. Age-related brain atrophy is not a homogenous process: Different functional brain networks associate differentially with aging and blood factors. Proc. Natl. Acad. Sci. 119, e2207181119 (2022).
Lenka, A. & Jankovic, J. Tremor syndromes: An updated review. Front. Neurol. 12, 684835 (2021).
Tse, W. et al. Prevalence of movement disorders in an elderly nursing home population. Arch. Gerontol. Geriatr. 46, 359–366 (2008).
Hess, C. W. & Pullman, S. L. Tremor: Clinical phenomenology and assessment techniques. Tremor Other Hyperkinetic Mov. 2, 02 (2012).
Zesiewicz, T. Overview of essential tremor. Neuropsychiatr. Disease Treat. 6, 401 (2010).
Veluvolu, K. C. & Ang, W. T. Estimation and filtering of physiological tremor for real-time compensation in surgical robotics applications. Int. J. Med. Robot. Comput. Assist. Surg. 6, 334–342 (2010).
Lewis, R. D. & Brown, J. M. Influence of muscle activation dynamics on reaction time in the elderly. Eur. J. Appl. Physiol. 69, 344–349 (1994).
Inglin, B. & Woollacott, M. Age-related changes in anticipatory postural adjustments associated with arm movements. J. Gerontol. 43, M105–M113 (1988).
Veluvolu, K. C. & Ang, W. T. Estimation of physiological tremor from accelerometers for real-time applications. Sensors 11, 3020–3036 (2011).
Anouti, A. & Koller, W. C. Tremor disorders. Diagnosis and management. Western J. Med. 162, 510 (1995).
Elias, W. J. & Shah, B. B. Tremor. JAMA 311, 948–954. https://doi.org/10.1001/jama.2014.1397 (2014).
Marshall, J. The effect of ageing upon physiological tremor. J. Neurol. Neurosurg. Psychiatry 24, 14–17 (1961).
Sturman, M. M., Vaillancourt, D. E. & Corcos, D. M. Effects of aging on the regularity of physiological tremor. J. Neurophysiol. 93, 3064–3074 (2005).
Morrison, S., Newell, K. M. & Kavanagh, J. J. Differences in postural tremor dynamics with age and neurological disease. Exp. Brain Res. 235, 1719–1729 (2017).
Baizabal-Carvallo, J. F. & Morgan, J. C. Drug-induced tremor, clinical features, diagnostic approach and management. J. Neurol. Sci. 435, 120192 (2022).
Deuschl, G. et al. The clinical and electrophysiological investigation of tremor. Clin. Neurophysiol. 136, 93–129 (2022).
Wyne, K. T. A comprehensive review of tremor. J. Am. Acad. Phys. Assist. 18, 43–50 (2005).
De, A., Bhatia, K. P., Volkmann, J., Peach, R. & Schreglmann, S. R. Machine learning in tremor analysis: Critique and directions. Mov. Disord. 38, 717–731. https://doi.org/10.1002/mds.29376 (2023).
Evers, L. J., Krijthe, J. H., Meinders, M. J., Bloem, B. R. & Heskes, T. M. Measuring parkinson’s disease over time: The real-world within-subject reliability of the mds-updrs. Mov. Disord. 34, 1480–1487 (2019).
Winder, J. Y., Roos, R. A., Burgunder, J.-M., Marinus, J. & Reilmann, R. Interrater reliability of the unified Huntington’s disease rating scale-total motor score certification. Mov. Disord. Clin. Pract. 5, 290–295 (2018).
Randall, J. E. & Stiles, R. N. Power spectral analysis of finger acceleration tremor. J. Appl. Physiol. 19, 357–360 (1964).
Mamorita, N., Iizuka, T., Takeuchi, A., Shirataka, M. & Ikeda, N. Development of a system for measurement and analysis of tremor using a three-axis accelerometer. Methods Inf. Med. 48, 589–594 (2009).
Niazmand, K., Kalaras, A., Dai, H. & Lueth, T. C. Comparison of methods for tremor frequency analysis for patients with parkinson’s disease, in 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), vol. 2, 693–697 (2011).
Li, J. et al. A wearable multi-segment upper limb tremor assessment system for differential diagnosis of Parkinson’s disease versus essential tremor. IEEE Trans. Neural Syst. Rehabil. Eng. 31, 3397–3406 (2023).
Gajewski, J., Mazur-Rózycka, J., Górski, M. & Busko, K. Reference values of the forearm tremor power spectra for youth athletes. J. Hum. Kinet. 86, 133–143 (2023).
Chan, P. Y. et al. Motion characteristics of subclinical tremors in Parkinson’s disease and normal subjects. Sci. Rep. 12, 4021 (2022).
Luft, F. et al. A power spectral density-based method to detect tremor and tremor intermittency in movement disorders. Sensors 19, 4301 (2019).
Ali, S. M. et al. Wearable sensors during drawing tasks to measure the severity of essential tremor. Sci. Rep. 12, 5242 (2022).
Karamizadeh, S., Abdullah, S. M., Halimi, M., Shayan, J. & Rajabi, M. J. Advantage and drawback of support vector machine functionality, in 2014 International Conference on Computer, Communications, and Control Technology (I4CT) (2014).
Peng, H., Long, F. & Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 27, 1226–1238 (2005).
Bharathi, A. & Natarajan, A. M. Cancer classification using support vector machines and relevance vector machine based on analysis of variance features. J. Comput. Sci. 7, 1393–1399 (2011).
Zhao, Z., Zhang, R., Cox, J., Duling, D. & Sarle, W. Massively parallel feature selection: An approach based on variance preservation. Mach. Learn. 92, 195–220 (2013).
Al Fatih Abil Fida, M., Ahmad, T. & Ntahobari, M. Variance threshold as early screening to boruta feature selection for intrusion detection system, in 2021 13th International Conference on Information & Communication Technology and System (ICTS), 46–50 (2021).
Siti Ambarwati, Y. & Uyun, S. Feature selection on magelang duck egg candling image using variance threshold method, in 2020 3rd International Seminar on Research of Information Technology and Intelligent Systems (ISRITI), 694–699 (2020).
Wu, Q. Q., Wang, Y. D., Wang, Z. Y. & Liu, K. H. Unsupervised feature selection algorithm based on spectral clustering and analysis of variance, in Future Information Engineering and Manufacturing Science, 175–178 (2015).
Cheng, W., Wang, T., Wen, W., Li, J. & Gao, R. X. Mathematical methods and modeling in machine fault diagnosis. Math. Probl. Eng. 2014, 1–8 (2014).
Lv, C. et al. A classification feature optimization method for remote sensing imagery based on fisher score and MRMR. Appl. Sci. 12, 8845 (2022).
Sakar, C. O., Kursun, O. & Gurgen, F. A feature selection method based on kernel canonical correlation analysis and the minimum redundancy-maximum relevance filter method. Exp. Syst. Appl. 39, 3432–3437 (2012).
Hua, Z. et al. A feature dimensionality reduction strategy coupled with an electronic nose to identify the quality of egg. J. Food Process. Eng. 44, e13873 (2021).
Fozard, J. L., Vercruyssen, M., Reynolds, S. L., Hancock, P. A. & Quilter, R. E. Age differences and changes in reaction time: The baltimore longitudinal study of aging. J. Gerontol. 49, P179–P189 (1994).
Nelson, R. J., McCandlish, C. A. & Douglas, V. D. Reaction times for hand movements made in response to visual versus vibratory cues. Somatos. Motor Res. 7, 337–352 (1990).
Robinovitch, S. N., Normandin, S. C., Stotz, P. & Maurer, J. D. Time requirement for young and elderly women to move into a position for breaking a fall with outstretched hands. J. Gerontol. A Biol. Sci. Med. Sci. 60, 1553–1557 (2005).
Kanekar, N. & Aruin, A. S. The effect of aging on anticipatory postural control. Exp. Brain Res. 232, 1127–1136 (2014).
Bao, T. et al. Vibrotactile display design: Quantifying the importance of age and various factors on reaction times. PLOS ONE 14, e0219737 (2019).
Barela, J. A., Rocha, A. A., Novak, A. R., Fransen, J. & Figueiredo, G. A. Age differences in the use of implicit visual cues in a response time task. Braz. J. Motor Behav. 13, 86–93 (2019).
Ivosev, G., Burton, L. & Bonner, R. Dimensionality reduction and visualization in principal component analysis. Anal. Chem. 80, 4933–4944 (2008).
Thompson, C. G., Kim, R. S., Aloe, A. M. & Becker, B. J. Extracting the variance inflation factor and other multicollinearity diagnostics from typical regression results. Basic Appl. Soc. Psychol. 39, 81–90 (2017).
Nizamis, K. et al. Characterization of forearm muscle activation in Duchenne muscular dystrophy via high-density electromyography: A case study on the implications for myoelectric control. Front. Neurol. 11, 231 (2020).
Shelton, J. & Kumar, G. P. Comparison between auditory and visual simple reaction times. Neurosci. Med. 01, 30–32 (2010).
Rahimi, F., Bee, C., South, A., Debicki, D. & Jog, M. Variability of hand tremor in rest and in posture-a pilot study, in 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 470–473 (IEEE, 2011).
Rahimi, F. et al. Dynamic decomposition of motion in essential and parkinsonian tremor. Can. J. Neurol. Sci. 42, 116–124 (2015).
Wang, J., Gupta, S. K. & Barry, O. Towards data-driven modeling of pathological tremors, in International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, vol. 83914, V002T02A030 (American Society of Mechanical Engineers, 2020).
Fajardo, J. Jr. & Melo, L. F. D. Towards a modular pathological tremor simulation system based on the Stewart platform. Sensors 23, 9020 (2023).
Louis, E. D. The roles of age and aging in essential tremor: An epidemiological perspective. Neuroepidemiology 52, 111–118 (2019).
Carignan, B., Daneault, J.-F. & Duval, C. Quantifying the importance of high frequency components on the amplitude of physiological tremor. Exp. Brain Res. 202, 299–306 (2010).
Raethjen, J., Pawlas, F., Lindemann, M., Wenzelburger, R. & Deuschl, G. Determinants of physiologic tremor in a large normal population. Clin. Neurophysiol. 111, 1825–1837 (2000).
Hömberg, V., Hefter, H., Reiners, K. & Freund, H. Differential effects of changes in mechanical limb properties on physiological and pathological tremor. J. Neurol. Neurosurg. Psychiatry 50, 568 (1987).
Seo, W., Cho, B., Lee, J. & Baek, K. R. Implementation of imu using wavelet transform and variable iir filter, in The Sixteenth International Symposium on Artificial Life and Robotics (2011).
Chang, W. et al. A hierarchical hand motions recognition method based on imu and semg sensors, in 2015 IEEE International Conference on Robotics and Biomimetics (ROBIO), 1024–1029 (IEEE, 2015).
Yi, A., Zahedi, A., Wang, Y., Tan, U. -X. & Zhang, D. A novel exoskeleton system based on magnetorheological fluid for tremor suppression of wrist joints, in 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), 1115–1120 (IEEE, 2019).
Van Meulen, F. B., van Beijnum, B. -J. F., Buurke, J. H. & Veltink, P. H. Assessment of lower arm movements using one inertial sensor, in 2017 International Conference on Rehabilitation Robotics (ICORR), 1407–1412 (IEEE, 2017).
Hallett, M. Overview of human tremor physiology. Mov. Disord. 13, 43–48 (1998).
Enoka, R. M. et al. Mechanisms that contribute to differences in motor performance between young and old adults. J. Electromyogr. Kinesiol. 13, 1–12 (2003).
Clark, B. C. & Manini, T. M. Sarcopenia \(\ne\) dynapenia. J. Gerontol. A Biol. Sci. Med. Sci. 63, 829–834 (2008).
Salat, D. H. et al. Thinning of the cerebral cortex in aging. Cereb. Cortex 14, 721–730 (2004).
Clark, B. C. & Taylor, J. L. Age-related changes in motor cortical properties and voluntary activation of skeletal muscle. Curr. Aging Sci. 4, 192–199 (2011).
Seidler, R. D. et al. Motor control and aging: links to age-related brain structural, functional, and biochemical effects. Neurosci. Biobehav. Rev. 34, 721–733 (2010).
Bernardi, N. F., De Buglio, M., Trimarchi, P. D., Chielli, A. & Bricolo, E. Mental practice promotes motor anticipation: Evidence from skilled music performance. Front. Hum. Neurosci. 7, 451 (2013).
Inglin, B. & Woollacott, M. Age-related changes in anticipatory postural adjustments associated with arm movements. J. Gerontol. 43, M105–M113 (1988).
Pezzulo, G., Hoffmann, J. & Falcone, R. Anticipation and anticipatory behavior. Cogn. Process. 8, 67–70 (2007).
Stöckel, T., Wunsch, K. & Hughes, C. M. Age-related decline in anticipatory motor planning and its relation to cognitive and motor skill proficiency. Front. Aging Neurosci. 9, 283 (2017).
Almeida, M. F. S., Cavalheiro, G. L., Furtado, D. A., Pereira, A. A. & Andrade, A. O. Quantification of physiological kinetic tremor and its correlation with aging, in 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2631–2634 (IEEE, 2012).
Naicker, P., Anoopkumar-Dukie, S., Grant, G. D. & Kavanagh, J. J. The effects of antihistamines with varying anticholinergic properties on voluntary and involuntary movement. Clin. Neurophysiol. 124, 1840–1845 (2013).
Fenelon, G. Antidepressants and Movement Disorders. Medication-Induced Movement Disorders (Ed J Friedman) 141–9 (Cambridge University Press, 2015).
Oldfield, M. Unequal sample sizes and the use of larger control groups pertaining to power of a study. Dstl 1 (2016).
Wardhani, N. W. S., Rochayani, M. Y., Iriany, A., Sulistyono, A. D. & Lestantyo, P. Cross-validation metrics for evaluating classification performance on imbalanced data, in 2019 International Conference on Computer, Control, Informatics and Its Applications (IC3INA), 14–18 (IEEE, 2019).
Bischke, B., Helber, P., Borth, D. & Dengel, A. Segmentation of imbalanced classes in satellite imagery using adaptive uncertainty weighted class loss, in IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, 6191–6194 (IEEE, 2018).
Gholamiangonabadi, D., Kiselov, N. & Grolinger, K. Deep neural networks for human activity recognition with wearable sensors: Leave-one-subject-out cross-validation for model selection. IEEE Access 8, 133982–133994 (2020).
Varlet, M., Williams, R. & Keller, P. E. Effects of pitch and tempo of auditory rhythms on spontaneous movement entrainment and stabilisation. Psychol. Res. 84, 568–584 (2020).
Kopnarski, L., Lippert, L., Rudisch, J. & Voelcker-Rehage, C. Predicting object properties based on movement kinematics. Brain Inform. 10, 29 (2023).
Accelerometer sensor guide (accessed 14 Feb 2024). http://web.archive.org/web/20080207010024/http://www.808multimedia.com/winnt/kernel.htm
Jeste, D. V. et al. A new brief instrument for assessing decisional capacity for clinical research. Arch. Gen. Psychiatry 64, 966 (2007).
Islam, N. et al. Accuracy of the montreal cognitive assessment tool for detecting mild cognitive impairment: A systematic review and meta-analysis. Alzheimer’s Dementia 19, 3235–3243 (2023).
Carson, N., Leach, L. & Murphy, K. J. A re-examination of montreal cognitive assessment (moca) cutoff scores. Int. J. Geriatr. Psychiatry 33, 379–388 (2017).
Shimmer. Shimmer3 imu unit. Shimmer Wearable Sensor Technology (2022). https://shimmersensing.com/product/shimmer3-imu-unit/
Shimmer. ConsensysPRO software. Shimmer Wearable Sensor Technology (2022). https://shimmersensing.com/product/consensyspro-software/
Goetz, C. G. et al. Mds-updrs. MDS-Unified Parkinson’s Disease Rating Scale (MDS-UPDRS) (2008). www.movementdisorders.org/MDS/MDS-Rating-Scales/MDS-Unified-Parkinsons-Disease-Rating-Scale-MDS-UPDRS.htm
Djuric-Jovicic, M. D., Jovicic, N. S., Popovic, D. B. & Djordjevic, A. R. Nonlinear optimization for drift removal in estimation of gait kinematics based on accelerometers. J. Biomech. 45, 2849–2854 (2012).
Mayagoitia, R. E., Nene, A. V. & Veltink, P. H. Accelerometer and rate gyroscope measurement of kinematics: An inexpensive alternative to optical motion analysis systems. J. Biomech. 35, 537–542 (2002).
Aminian, K., Najafi, B., Büla, C., Leyvraz, P.-F. & Robert, P. Spatio-temporal parameters of gait measured by an ambulatory system using miniature gyroscopes. J. Biomech. 35, 689–699 (2002).
Luinge, H. J. & Veltink, P. H. Inclination measurement of human movement using a 3-d accelerometer with autocalibration. IEEE Trans. Neural Syst. Rehabil. Eng. 12, 112–121 (2004).
Dejnabadi, H., Jolles, B. M., Casanova, E., Fua, P. & Aminian, K. Estimation and visualization of sagittal kinematics of lower limbs orientation using body-fixed sensors. IEEE Trans. Biomed. Eng. 53, 1385–1393 (2006).
O’Donovan, K. J., Kamnik, R., O’Keeffe, D. T. & Lyons, G. M. An inertial and magnetic sensor based technique for joint angle measurement. J. Biomech. 40, 2604–2611 (2007).
Favre, J., Jolles, B., Aissaoui, R. & Aminian, K. Ambulatory measurement of 3d knee joint angle. J. Biomech. 41, 1029–1035 (2008).
Cooper, G. et al. Inertial sensor-based knee flexion/extension angle estimation. J. Biomech. 42, 2678–2685 (2009).
Slack, P. S. & Ma, X. Tremor amplitude determination for use in clinical applications. Meas. Sci. Technol. 18, 3471–3478 (2007).
Samadi, E., Ahmadi, H., Nowshiravan Rahatabad, F., Frequency domain approach. Analysis of hand tremor in Parkinson’s disease. Front. Biomed. Technol. 7, 105–111 (2020).
Heida, T., Wentink, E. & Marani, E. Power spectral density analysis of physiological, rest and action tremor in Parkinson’s disease patients treated with deep brain stimulation. J. Neuroeng. Rehabil. 10, 70 (2013).
Locatelli, P., Alimonti, D., Traversi, G. & Re, V. Classification of essential tremor and Parkinson’s tremor based on a low-power wearable device. Electronics 9, 1695 (2020).
Morrison, S. & Newell, K. M. Bilateral organization of physiological tremor in the upper limb. Eur. J. Appl. Physiol. 80, 564–574 (1999).
Khan, M. S. & Coulibaly, P. Application of support vector machine in lake water level prediction. J. Hydrol. Eng. 11, 199–205 (2006).
Dibike, Y. B., Velickov, S., Solomatine, D. & Abbott, M. B. Model induction with support vector machines: Introduction and applications. J. Comput. Civ. Eng. 15, 208–216 (2001).
Yates, L. A., Aandahl, Z., Richards, S. A. & Brook, B. W. Cross validation for model selection: A review with examples from ecology. Ecol. Monogr. 93, e1557 (2023).
Sotirakis, C. et al. Identification of motor progression in Parkinson’s disease using wearable sensors and machine learning. npj Parkinson’s Disease 9, 142 (2023).
Kita, K., Du, Y. & Haith, A. M. Evidence for a common mechanism supporting invigoration of action selection and action execution. J. Neurophysiol. 130, 238–246 (2023).
Acknowledgements
We thank all the individuals who participated in this study and the Purdue University Department of Psychological Sciences’ SONA Systems for helping us recruit participants for the younger population group. We also thank Jett Stad for his help with data collection and the anonymous reviewers for their suggestions and comments. This work was supported by funds from Purdue University to Dr. Anne B Sereno, Lynn Fellowship and Bottorff Fellowship awarded to Aditya Shanghavi, and the National Defense Science and Engineering Graduate Fellowship awarded to Elizabeth M. Frazier.
Author information
Authors and Affiliations
Contributions
Experiment Design—A.S., A.B.S.; Data Collection—R.P., A.S.; Algorithm Development—A.S. A.B.S., S.A., D.L.; Data Analysis—A.S., A.B.S; Interpretation of Results—A.S., A.B.S., D.L., S.A., E.M.F.; Writing Manuscript—A.S., A.B.S., D.L., E.M.F., S.A. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shanghavi, A., Larranaga, D., Patil, R. et al. A machine-learning method isolating changes in wrist kinematics that identify age-related changes in arm movement. Sci Rep 14, 9765 (2024). https://doi.org/10.1038/s41598-024-60286-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-60286-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.