Abstract
MxNi1-xFe2O4 spinel ferrite (M = Mn, Zn, and x = 0, 0.05) has been successfully synthesized by co-precipitation technique with hydrazine hydrate reduction agent (instead of NaOH) and Ethylene glycol surfactant. The XRD spectra of the samples illustrated high crystallinity. The structural characterization of pure and doped fcc NiFe2O4 were calculated by Scherrer, Modified Scherrer, Williamson–Hall, and SSP methods. In comparison of several methods, the Scherrer method is unreasonable method and W–H method has an acceptable range and can calculate both < L > and strain without restriction. The specific surface area in Zn-doped increased, demonstrate increment of adsorption properties in Ni ferrite structure. TEM images revealed the shape of grains is spherical, cubic, and irregular, with a grain size in the range of 35–65 nm. Hysteresis loops illustrated the magnetic behavior of samples. From the reflectance data, the band gap energies were estimated at 1.984, 1.954, and 1.973 eV for un-doped, Mn, and Zn-doped NiFe2O4 respectively (red shift). The almost low value of Urbach energy for pure, Mn, and Zn -doped NiFe2O4 indicates low structural disorder, which can approve the high crystallinity of samples. Direct band gap energy (Eg), refractive index, and extinction coefficient were estimated by the Kramers–Kronig method with linear optical evaluations. The Eg by K-K method is in good agreement with the Eg by Kubelka–Munk function.
Similar content being viewed by others
Introduction
Spinel ferrites in the general formula of AFe2O4, in which A is a divalent metal (Mg, Co, Ni, Zn, Fe, Mn, etc.), are the most widely magnetic nanoparticles (MNPs) due to their outstanding properties such as high permeability and high electrical resistivity1,2, and thus, have many applications3,4. Ferrite structure, including both M and Fe ions, can inform richer redox reactions in comparison to the single-metal oxides2,5. Among spinel ferrites, NiFe2O4 has specific properties such as high electrochemical stability, high permeability at high frequency, and catalytic behavior5,6,7. These features have enabled nickel ferrite semiconductors8 to be used in various applications such as sodium-ion batteries, gas sensors, electromagnetic wave absorption, photocatalysis, water oxidation processes, and biomedical applications9,10. The unit cell of spinel ferrites has eight fcc cells. It consists of 32 closely packed oxygen atoms in fcc sites and 24 metal cations distributed between 64 divalent tetrahedral (A) and 32 trivalent octahedral (B) sites. In these sites, metal cations are inscribed by four oxygen ions in tetrahedral sites and six oxygen ions in octahedral sites. NiFe2O4 spinel ferrite has an inverse spinel structure with 8 Ni2+ ions occupying preferentially B sites, whereas 16 Fe3+ ions have been equally distributed between A and B sites in the form of [Fe3+]A[Ni2+Fe3+]BO411.
The cation distribution is a crucial parameter in the alteration of structural, magnetic, and optical properties of NiFe2O4 spinel ferrite. It dependent on the composition and microstructure of spinel ferrite which strongly affected by the synthesis method, synthesis conditions, and metals substitution12. Nickel ferrite NPs can be fabricated by using a range of wet chemical routes such as sol–gel auto-combustion13, hydrothermal14, and co-precipitation1. The co-precipitation method, due to its simplicity, low cost, low synthesis temperature, and size homogeneity in nano order, is widely used in the synthesis of spinel ferrites1,15. On the other hand, doping ferrite nanocrystals with various cations of transition metals such as Ni, Mg, Cr, Mn, Zn, Co, Cu, etc., can also alter the cation distribution in ferrites leading to a modification in their structural and optical properties16,17.
Mn and Zn-doped nickel ferrite can attain appealing optical features by alternating in cation distribution in A and B sites. Mn-doped NiFe2O4 has large permeability, resistivity, and small fatality compared with other dielectrics18. Zn-doped NiFe2O4 are specified by high surface area, high electrical resistivity, and large permeability at a high-frequency region of electronics devices (GHz)19,20. Aakash et al. reported electrical and dielectric reactions of transition metal ions (Zn2+, Cd2+, Mn2+, and Cr3+) and showed that the hopping length decreased by an increment in Zn, Cd, and Cr content while observed a little increment in Mn-doped nickel ferrite. They depicts all the dopant elements of NiFe2O4 have a good dielectric behavior21. Seema Kumari et al. synthesized Mn and Zn-doped MxNi1-xFe2O4 spinel ferrites using the co-precipitation method by NaOH as reduction agent and demonstrated the crystallite size of Mn and Zn doped nickel ferrite decreased to a range of 50–60 nm with an increase in the band gap energy in all dopant elements22. Aafiya and his coworkers prepared Zn-doped NiFe2O4 using the sol–gel auto-combustion process. They showed considerable absorbance in the visible light region and an increased direct band gap energy by Zn-doped23. According literature, there are almost no studies that have investigated about the structural and optical properties of Mn and Zn-doped NiFe2O4 synthesized with co-precipitation method by Hydrazine hydrate reduction agent and Ethylene glycol surfactant. Furthermore, there are no comprehensive literature in the optical properties of un-doped and Mn and Zn-doped NiFe2O4 such as Urbach energy and refractive index by DRS analysis and numerical relationships. In this study, in addition to the DRS analysis for optical characteristics, Kramers–Kronig (K-K) relations were utilized as the numerical method that is relevant to the complex part of the system to research the linear optical properties of the system and compare them to experimental results 24. Band gap energy, refractive index (real part), extinction (imaginary part), and absorption coefficient are the important optical parameters that can be estimated through the K-K method through the use of the DRS data.
Experimental
Reagents and synthesis
In this work, Iron (III) chloride hexahydrate (FeCl3·6H2O, 98%, Merck), Nickel chloride hexahydrate (NiCl2.6H2O, 98% Merck), Manganese (II) chloride dihydrate (MnCl2·2H2O, 98%, Merck), Zinc (II) chloride (ZnCl2, 98%, Merck), Ethylene glycol (Merck) and Hydrazine hydrate (NH2.NH2.H2O) (Merck 100%), were used without any further purification.
NiFe2O4 and M0.05Ni0.95Fe2O4 (M = Mn, Zn) nanoparticles were synthesized by the chemical co-precipitation technique. 0.1 M of nickel chloride and 0.2 M of iron chloride solutions with stoichiometric ratios Ni:Fe = 1:2, were solved separately in deionized water. The as-prepared solutions were mixed and stirred intensely for 20 min to obtain a homogenous mixture. Ethylene glycol was added into the solution as a surfactant with stoichiometric ratios surfactant: metals = 0.5:1, and mixed at 60 °C. Surfactant disturb the fixity of the mixed solution and makes the electrostatic repulsion force that can prevent the clumping of particles in the synthesis process and help control crystallite size25. Subsequently, a suitable amount of hydrazine hydrate as a reduction agent was added dropwise into the solutions under vigorous stirring, and black color precipitates formed in the pH = 10 and the nucleation of nanoparticles initializes. Hydrazine hydrate can control the PH of the reaction and so decreases the clumping of particles to control the particle size without any impurities in the reaction mixture26. The prepared slurry was kept under vigorous magnetic stirring for 1:45 min at 80 °C and then was cooled to RT. The precipitate was separated through the strong magnet, rinsed several times by water and ethanol to get the neutral PH, and dried in a hot air oven for 24h at 60 °C. Finally, the grinding powder was annealed at 800 °C for 2 h in a muffle furnace. The annealing temperature and time are essential factors in synthesized nanoparticles because, the initialization of phase transition processes and, consequently, the formation of a spinel structure of the NiFe2O4 begin at this temperature. Also, in high annealing temperatures, the structural defects that are due to synthesis at lower annealing temperatures, are improved26. The above procedure was repeated to prepare of Mn and Zn-doped NiFe2O4 NPs by adding manganese chloride and zinc chloride in stoichiometric ratios M:Ni:Fe = 0.05:0.95:2, in the solution.
Characterization and measurements
Structure determination of the specimens characterized via X-ray diffraction (XRD) patterns by using Philips PW 1730 diffractometer with Cu-Kα radiation (λ = 1.54056Å) in the 2θ = 10–80 degrees and patters were plotted by the X’Pert high score plus software. The microstructural characterizations of NPs were recorded by the transmission electron microscopy (TEM) analysis set (Philips EM 208S Netherland). The magnetic characteristics of the samples was measured using a vibrating sample magnetometer (VSM-MDKB) in the 1.4 T field at room temperature. The optical properties were measured through the diffuse reflectance spectroscopy (DRS) measurement (Sinco S4100 Korea). The linear optical calculations were done by MATLAB coding.
Result and discussion
Structural analysis
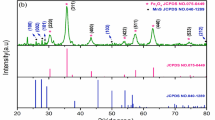
XRD patterns of NiFe2O4, Mn, and Zn-doped NiFe2O4 nanopowders which were annealed at 800 °C and named NFO, MNFO, and ZNFO, respectively, are depicted in Fig. 1a. It can be observed that all the appearance diffraction peaks for NFO, MNFO, and ZNFO spinel ferrites can have perfect condition indexed to reflection at (111), (220), (311), (222), (400), (422), (511), (440), (620), (533) and (622) crystal planes of NiFe2O4 inverse spinel structure with the cubic spinel structure (fcc) and Fd3m space group that have an accommodation with the standard spectrum JCPDS Card (No. 96-591-0065). The sharp peaks in the patterns of specimens can denote that the structure of samples has a high crystallinity phase in the inverse spinel structure of NiFe2O4. It can be associated with heat treatment, in high annealing temperature, the impurities eliminate, and the stress of the unit cell diminishes, hence atoms appoint more appropriately at the suitable lattice sites so the crystallinity increases and single crystal form instead of polycrystal structure, so more substantial Bragg’s diffraction apparent27. Also use of hydrazine hydrate can diminish the molesting phase. From Fig. 1a, the XRD pattern in NFO demonstrates a weak impurity peak in 2θ = 67.95°, which can be due to holder contamination of the XRD device in the laboratory. XRD pattern of MNFO in Fig. 1a shows no impurity phase or extra diffraction peaks related to Mn oxides or Mn impurity or clusters. Also, the pattern depicts that the diffraction peak intensities increased and peaks wide decreased in the Mn-doped compared to un-doped nickel ferrite, that this can imply the highest crystallinity and increment in crystallite size of MNFO. A bit shift in the position of the diffraction peaks of MNFO and ZNFO patterns in Fig. 1a can be attributed to the distinction in dopant ionic radii22,27 that is shown in Fig. 1b for the (311) plan. ZNFO spectra in Fig. 1a indicate no new crystalline phases corresponding to secondary phases, ZnO, Zn, or impurity phases in the structure of ZNFO spinel ferrite. The broadening and low-intensity peaks of ZNFO can imply a decrement in crystallinity and crystallite size despite the MNFO. According to the above mentioned, it can result that Mn and Zn doped ions are entirely incorporated in ions sites of NiFe2O4 structure and have a different effect in structural properties. Also, from the Fig. 1a, it is evident that all XRD patterns of synthesized samples demonstrated the diffraction peak intensity of the (311) crystal plane was the highest that indicating the preferential orientation growing of NiFe2O4 crystal structure is along the (311) crystal plane23,27. The peak positions (2θ) of the synthesized samples were estimated by using X’Pert High Score Plus software and tabulated in Table 1.
Lattice parameter, x-ray density, and hopping length
The lattice parameter (a) and cell volume (V) can be computed from the XRD patterns by the following equations by X’Pert High Score Plus software:
dhkl is the inter-planer distance in h, k, l miller indices, as can be seen from Table 2, the lattice parameter in MNFO and ZNFO increased in comparison to NFO, which can be associated with the cation distribution. When spinel ferrite is doped, the dopant ion is generally replaced in the sites that are proportional to ionic radii28. In Mn-doped NiFe2O4, with regarding MnFe2O4 as partial inverse spinel ferrite with 80% Mn2+ at tetrahedral and 20% Mn2+ at octahedral sites, because of larger ionic radius of Mn2+ (0.66 Å) to Fe2+ (0.49 Å) ions at A sites and larger ionic radius of Mn2+ (0.83 Å) to Ni2+ (0.69 Å) ions at B sites of inverse spinel NiFe2O4, the lattice parameter increased, and the unit cell can be expanded. Also, in the Zn-doped NiFe2O4, the Zn2+ ions have a preference to present in the tetrahedral sites with larger ionic radius (0.65 Å) to Fe2+ (0.49 Å) ions in A sublattice hence the lattice constant in ZNFO can be larger than NFO29,30. The amount of x-ray density (ρx) is estimated by the following relation:
where M is the molecular weight, Z = 8 is the number of molecules per unit cell, and N = 6.022 × 1023 (atoms/mol) is the Avogadro number. From Table 2, it can be seen that the \({\rho }_{x}\) decreased in Mn and Zn-doped NFO. This can be due to the decreasing surface tension that was created by the lattice constant, the size effect, and the expansion of the unit cell by replacing Zn+2 or Mn+2 ions instead of Ni+2 ions1.
The hopping length is the parameter that gives information about the distance between magnetic ions and the strength of the spin interaction of ions that is defined as the following equations31:
where LA is the hopping length at the A site (the shortest interval between the A site and the oxygen atom), and LB is the hopping length at the B site (the shortest interval between the B site and the oxygen atom)32. As can be seen in Table 2, LA and LB increased in MNFO and ZNFO compared to NFO. This increase can be due to the alteration in ionic radii in the A and B sites by the insertion of Mn2+ and Zn2+ dopant ions as explained in the lattice constant alteration section, so this induces increment in lattice constant, and unit cell and the hopping length between magnetic ions in Mn and Zn doped NiFe2O4 increased.
Crystallite size
The crystallite size is the parameter that has a crucial role in all properties of MNPs, so in this research, to the precise calculation of the crystallite size and strain of the nanopowders, four essential methods have been used: Debye–Scherrer, Modified Debye–Scherrer, Williamson-Hall, and the Size Strain plot methods. The full width at half maximum (FWHM) of all peaks position has been estimated by X’Pert high score plus software and fitted with this software. The peaks broadening of diffraction patterns can be due to crystallite size and local lattice strain that both are physical broadenings, and also by instrumental broadening31. To calculate the precise crystallite size value of nanopowder, the instrumental broadening must be deleted from observed broadening, so according to Marzieh Rabiei et al.33 and M. A. Islam et al.31 the following equation represents the refined broadening:
In this relation, βi is the instrumental broadening, βo is the observed broadening, and βd is the reformed broadening that was used to calculate crystallite size. In many articles, broadening of crystalline silicon is used as instrumental broadening (βinstrumental = βstandard = 0.196 degrees) for calibration and removal from the observed peak width33.
Debye–Scherrer method
The Scherrer method was generally used to calculate crystal size for the most intense peak, which is depicted as follows32:
Here, L is the crystallite size, K is the structure factor that usually takes as 0.9, λ is the wavelength of the X-rays source (λ = 0.15405 nm), θ is the braggˊs angle of the peak, and β is the full width at half maximum (FWHM) of the most intense diffraction peak. To compute the average crystallite size, the most substantial (311) peak was used in the Sherrer equation, and the estimated value was tabulated in Table 3.
Modified Debye–Scherrer (Monshi–Scherrer) method
In the Scherrer method, nanocrystalline size L was calculated for the most intense peak and supposed that crystallite size must be a constant value for different peaks of sample. In contrast, by increasing of 2θ value, the amount of cos θ is not retained constant, so caused an error in the L value33. Monshi et al. in 201234 used the Modified Scherrer method to decreasing the errors or \(\sum (\pm {\Delta ln\beta )}^{2}\) to calculate a more precise value of nanocrystalline size and was estimated by making logarithm on both sides of the Scherrer equation33:
The average value of crystallite size is calculated by plotting Ln β (radians) versus Ln(1/Cosθ) for all the selected peaks as y = ax + b equation as shown in Fig. 2 and Ln (Kλ/L), or y-intercept is approximated by the linear fitting of the plot through the origin software31. The fixed L value is determined by the following equation:
In addition, in the Monshi–Scherrer method, the slope of the plot must be one, therefore, some of the peak points must be deleted from the plot to achieve the slop of almost one, as can be seen in Fig. 2. but for the other next two methods, the points of plots weren’t deleted to the appropriate comparison between methods. The calculated data are presented in Table 3.
Williamson-Hall method
In the Scherrer and Modified Sherrer method, the XRD peaks broadening only arises from the crystallite size and cannot be considered the microstructures of the lattice and intrinsic strain effect, therefore, Scherrer and Modified Scherrer methods can only determine the crystallite size, but Williamson–Hall method considers the strain in addition of the crystallite size in peak broadening of all crystallographic orientations and estimate both L and strain ε value of the crystal structure. A total physical broadening (btot) has been estimated by the following equations35:
Figure 3 shows the bhkl cosθ plot drawn against 4 sinθ by XRD data for all samples. The linear fitting in this graph was done by origin software, and the slope and y-intercept of the graph were specified, and the ε and L values tabulated in Tables 3 and 4.
Size–Strain Plot method (SSP)
In this method, lower-angle reflections are more important than higher-angle reflections. Because at higher angles of diffraction peaks, the data of the XRD pattern has less modality, and diffraction peaks have an overlap. Functions used in the SSP method are the Gaussian and Lorentzian functions, which describe the strain and size profile of crystalline materials, respectively. The total broadening of the SSP method is defined as follows33:
where βL and βG are the peaks broadening, which have been derived from Lorentz and Gaussian functions, the SSP method is expressed through the following equation33:
where dhkl is the lattice distance for different (hkl) planes. To calculate the size and strain of nanoparticles, the plot was drawn with \({({d}_{hkl}{\beta }_{hkl}cos\theta )}^{2}\) as a y-axis and \({{d}_{hkl}}^{2}{b}_{hkl}cos\theta\) as x-axis and y = ax + b as linear fit to experimental data by using the origin software as exhibited in Fig. 4. The values of L and ε were tabulated in Table 3 and Table 4. However, in the case of strain value, because of the negative intercept value for NFO and ZNFO, the strain value cannot be calculated. Figure 5a illustrates the compares of average crystallite size by all used methods for all specimens.
In comparison methods of the calculating crystallite size, Scherrer method is unreasonable method but other methods have acceptable range according literature and among them, Williamson-Hall method can be estimated both size and strain values in acceptable range without some restrictions that exist in M-Scherrer and SSP methods as explained. From the calculating crystallite size for synthesized MNPs, according to Table 3 and Fig. 5a, the crystallite size of MNFO increased compared to NFO MNPs. It can be explained that Mn2+ dopant cations have stronger Mn2+-o2– bonds in comparison to Ni2+-o2– bonds, so this can cause the crystallite size increased. Another reason can be attributed to the electronic configuration of Mn2+ (3d5) in comparison to Ni2+(3d8). Mn2+ ions have more electrons than Ni2+ ions, hence Mn2+ ions attitude to more covalent interaction with its ligand and oxygen anions compared to Ni2+ ions so that, these factors can result in increasing the crystallite size of MNFO spinel ferrite2.
According to Table 3 and Fig. 5a, the decrement in crystallite size of ZNFO, at first, can be attributed to the cation distribution of the ZNFO structure. Bulk NiFe2O4 has an inverse spinel structure, however, in the nano-sized NiFe2O4, the spinel structure can have a mixed spinel structure for the size smaller than a few nm or by doping11 that in this structure, divalent cations distributed in both A and B sites [Fe x3+M1-x2+]A[Mx2+Fe 2-x3+]BO4. In the ZNFO structure, Zn2+ ions strongly prefer to be in the tetrahedral site of NiFe2O4 structure and caused mixed spinel structure, so this can cause disorder in the favorable Fe3+ ions site in tetrahedral sublattice and this excluded the growth of grains16,30. Second, it can be related to the complete electronic configuration of the Zn2+ ion (3d10) and lake of interaction electrons that resulted in fewer interactions with its ligands and oxygen ions, so crystallite size decreased. The third reason can be related to the lower bond energy of Zn2+-O2– (159 kJ/mol) compared to Ni2+-O2- bond energy (451 kJ/mol) which causes a decrement in crystallite size20.
Specific surface area
In the materialˈs structure, the specific surface area (SSA) can be specified physical and chemical processes of materials and is the overcoming variable for adsorption applications of nanoparticles, which is expressed by the following equation36:
where S is the specific surface area, which has an inverse relation with crystallite size and X-ray density. Table 3 depicts the SSA values via crystallite size estimated by the four mentioned methods for all samples. As can be seen, the specific surface area was reduced by Mn-doped NiFe2O4 because of an increment in crystallite size, whereas by Zn-doped NiFe2O4, the specific surface area increased due to decreasing crystallite size. The high specific surface area of synthesized nanopowders would assist the adsorption properties by incrementing of the active sites of NiFe2O4 nanoparticles for catalyst applications22,37. Figure 5b demonstrates variations of the specific surface area calculated by four methods.
Lattice strain and micro-strain
In the NiFe2O4 structure, oxygen atomsˊ positions in tetrahedral and octahedral sites mean: FeO6, NiO6, and FeO4 can be changed by Mn2+ and Zn2+ doped ions, and this highly disturbs the lattice and affect physical and chemical properties, especially structural parameters such as strain, dislocation density, stacking fault coefficient and packing factor6.
In the crystalline structure, interstitial atoms and lattice dislocations can induce pressure on the atoms and slightly stray them from their usual positions. This pressure is defined as lattice strain (εls), which can deform the unit length in the crystal structure. This parameter is calculated by the following equation38:
The deformation of atoms in the crystal structure, which can be due to displacement, domain boundary defects, and point defects, occurs in one per million parts of the materials and is called the micro-strain (εms) that is defined by the following equation38:
Table 4 depicts the strain values for all samples. As can be seen, the strain values of MNFO decreased, and the strain of ZNFO increased in comparison to NFO, which can be a result of the crystallinity of XRD patterns in Fig. 1a. Furthermore, the structural parameters such as dislocation density and stacking fault coefficient are impressive in the strain value of synthesized nanopowders. It should be noted that the negative value of the micro-strain in the Williamson-Hall method implies a compressive strain in the samples. It can be due to the different ions with different ionic radii, including Ni2+, Fe3+, Mn2+, and Zn2+, in the structures of samples1,39. Variations of micro-strain and lattice strain are shown in Fig. 6a.
Dislocation density and stacking fault coefficient
Dislocation density is the parameter that demonstrates irregularity within a crystal structure and specifies the number of dislocation lines length per unit volume of the crystal structure and defined with the following equations40:
The negative value of dislocation density by the Williamson-Hall method can be due to the discretion of chosen dislocation basis, which is represented in Table 541.
In the fcc structure of spinel ferrite, the stacking sequence is the form of ABCABCABC layers. When any kind of perturbation happens in this sequence, the stacking fault appears and can shift the peaks position of nanoparticles compared to order reference spectra peaks32. This coefficient (SF) is determined by the following equation:
where θ is the Bragg’s angle, which here, the Bragg’s angle of the strongest peak (311) regarded to calculating SF coefficient, and \(\Delta 2\theta\) is the difference in reference and observed 2θ values40. As present in Table 5, the stacking faults are shallow values in order of 0.0001, that this depicts that the positions of observed peaks are very close to the expected values, and the bit-shifted values can be related to created disorder by Mn2+ and Zn2+ dopant agents. The SF value of MNFO and ZNFO respectively decreased and increased in compare NFO. The decrement SF parameter in MNFO conforms to the reduction of disorder and increasing crystallinity that evident from the decreasing of peak wide and increasing intensity at (311) peak in XRD section. In contrast, increasing SF value in ZNFO depicts decreasing crystallinity and increment in the defect that can be estimated from larger peak wide and lower peak intensity. Alterations of dislocation density and stacking fault coefficient are illustrated in Fig. 6b.
Packing factor
The packing factor is determined from the following relation:
L is the particle size, and d is inter-planer spacing29. The values of the packing factor for all samples are represented in Table 5 and illustrated in Fig. 6c.
Microstructural analysis
Figure 7 shows the TEM images of three samples of NiFe2O4 ferrites. As can be seen, the synthesized MNPs are high crystallized because of heat treatment, at high annealing temperature (800 °C), the lattice strain broadening decreased by declining or eliminating contamination species through the diffusion of tiny grains (impurity) into the bigger ones (Ostwald ripening procedure) and microstructures of spinel ferrites were refined29. Also, Fig. 7 demonstrates that the shape of MNPs in NFO, MNFO, and ZNFO is almost both spherical and cubic type with a bigger and smaller size, and also irregular shapes for the other grains, which are separated by a grain boundary. Irregular shapes can arise from the first, agglomeration of the particles42, which can be because of first, heat treatment (Ostwald ripening process), and the second, magnetic interaction between particles that arise from the magnetic nature of some components such as Fe, Ni, and Mn in the structure of spinel ferrites42.
Wide particles sizes distribution was estimated by histogram distribution as shown in Fig. 7. The grains size of NFO range from 21 to 138 nm for 98 MNPs, the MNFO sample range from 17.06 to 246.06 nm for 72 MNPs, and the ZNFO sample range from 14 to 85 nm for 140 MNPs. Average grains sizes were obtained at 53.32 nm, 64.96, and 35.33 nm for NFO, MNFO, and ZNFO, respectively. As can be seen, the average grains size estimated for all tree samples by TEM images are more significant than their respective average crystallites sizes that were determined by XRD analysis, which illustrates in Fig. 5a. This difference can arise from the high ratio of surface area to volume which cause to gathering of several crystallite size to form bigger grain size also other reason can be related to agglomeration in high calcination temperature to earn a minimum of Gibbs energy43. However, in comparing the average grains size of NFO, MNFO, and ZNFO to each other, there is a good agreement whit XRD results. The difference in the average particles size between doped and un-doped nanopowders can be attributed to metal oxides’ formation reaction in various kinetics in ferrite structure or arise from the diverse ionic radius of metal ions that induced strain in the lattice structure27.
Magnetic properties
Hysteresis loops of the NiFe2O4 MNPs were obtaid by the vibrating sample magnetometer (VSM) at 300 K, as depicted in Fig. 8. Ms values of NFO, MNFO, and ZNFO nanoparticles were represented 30.49 emu/g, 31.84 emu/g, and 36.25 emu/g respectively. Furthermore, the Coercivity fields of hysteresis loops for NFO, MNFO, and ZNFO illustrated the values 126.15 Oe, 113.55 Oe, and 124.67 Oe, respectively.
Optical properties
Reflectance
Electronic interactions and optical characterization of the nanoparticles were investigated by diffused reflectance spectroscopy (DRS) in the UV–visible region. In this region, the hardship of getting absorption due to enhanced scattering is deleted. Figure 9 demonstrates the reflectance spectra of the synthesized specimens in the range of λ = 300–900 nm at room temperature. As it can be seen, in λ < 350 nm, there is a sharp decrement in reflectance spectra and a broad dip in the range of λ = 350–600 nm, which are in the UV and visible light region that achieve minimum value in about λ = 476 nm for NFO, MNFO, and ZNFO spinel ferrites. The reflectance peak around λ = 714 nm in the visible region has a bit shift to a higher wavelength in Mn-doped spectra. Accordance Fig. 9, the NFO spinel ferrite depicted a greater reflectance at the range of about 600–800 nm in the visible region compared to the MNFO and ZNFO spinel ferrites, which can be implied a reduction of reflectance in Mn and Zn-doped nickel ferrite in the visible region. From Fig. 9, in the reflectance spectra of MNFO, the minimum reflectance around 750 nm in the visible region slightly shifted to a higher wavelength, that this can be due to various optically active sub-levels that conformed intranet the band gap of MNFO. In the near-IR ranges (λ > 800 nm), the reflectance increased in compared to the visible region.
Kubelka–Munk function
The optical band gap (Eg) is the main parameter in optoelectronic applications. To calculate Eg, the Kubelka–Munk function (F(R)) is utilized by absorption spectra from DRS data that is defined as the following relation44,45:
where \({\text{F}}\left({R}_{\infty }\right)\) is the Kubelka − Munk function, \({R}_{\infty }\) is the diffuse reflectance ratio between the reference sample and measured one, \({R}_{\infty }={R}_{sample/{R}_{refrence}}\), S and K are respectively the scattering and the absorption Kubelka–Munk coefficients44. Absorbance spectra in spinel ferrites structure is related to the excitation of electrons from the valence band to the conduction band by photon radiation (O-2p ligand to Fe-3d metal level) or the 3d5-3d4 4s1 transition in Fe3+ ions19. The band gap energy can be assessed by Tauc’s equation29:
In which A is the proportionality constant that describes the degree of disorder in the sample, \(\mathrm{h\nu }\) is the incident photon energy, and Eg is the band gap energy of the semiconductor. The value of n is related to the nature of electronic transition and can be the values of n = 1/2, 2, 3/2, or 3 that n = 1/2 is for direct allowed transition, and n = 2 is for indirect allowed transition29. The Eg can be estimated with the plotting of (F(R)\(\mathrm{h\nu }\))2 in terms of the photon energy (\(\mathrm{h\nu }\)) and extrapolating the liner part of the plot for zero absorption spectra, (α \(\mathrm{h\nu }\)) = 0 as shown in Fig. 10a and represented in Table 6. As can be seen in Table 6, the Eg value of NFO was estimated at 1.984 which are comparable with those presented in the literature1. The Eg values of MNFO, and ZNFO MNPs were estimated at 1.956, and 1.973 eV, respectively. As shown, the bandgap energy of MNFO and ZNFO nanoparticles decreased comparing to NFO nanoparticles (redshift). K. Sasikumar and his coworkers estimated Eg of Mn-doped NiFe2O4 thin films to be around 3.3 eV in different Mn values (Ni1-xMnxFe2O4, x = 0, 3, 6, 9, and 12 wt%)46. In a study by C. Barathiraja, Mn doped Ni ferrite prepared by a facile microwave combustion method and found that Eg value was 2.11 eV for 10% Mn doped, which enhanced in compare to un-doped NiFe2O4 (2.02 eV)47. P.Annie Vinoshaa et al. synthesized Ni1-xZnxFe2O4 (x = 0.01, 0.03, 0.05, and 0.10) by co-precipitation route with NaOH reduction agent. They found Eg value has an enhanced trend in comparison to pure Ni ferrite and has Eg = 2.17 eV amount for 5% Zn doped NiFe2O437. Compared to previous literature, in this study Eg values of Mn and Zn doping Ni ferrite decreased which may can be advantageous in photocatalytic activity48. In photocatalyst application, the bandgap energy must be in the range of 3.0 > Eg > 1.23 for visible light activity, so the narrow Eg values of NiFe2O4 and 5% doped Ni spinel ferrites can be helpful candidate for photocatalytic applications49,50. Furthermore, reduction of Eg value for doped samples can be suggest that Mn2+ and Zn2+ ions interred in the structure of NiFe2O4 spinel ferrite.
The amount of the direct band gap appertained to many factors such as crystallite size, degree of structural disorder in the lattice, and presence of impurities6. According to XRD data in Mn-doped nickel ferrite, the crystallite size increased, so this can decrease the Eg value of MNPs because of the quantum confinement effect in semiconductor ferrites48, which is in accordance with estimated results as depicted in Fig. 10b. Also when the grain size is enhanced at a high annealing temperature (800 °C), as mentioned in TEM results, the grain boundaries are reduced, therefore, this decreases the scattering of carriers at grain boundaries, so that the Eg value can be diminished51. In Zn-doped NiFe2O4 despite the decrement in crystallite size of ZNFO from XRD data because of increment in the degree of the structural disorder means greater dislocation density, lattice strain, and micro-strain according to XRD results in Tables 4 and 5, the sub-bands formed and merged between the band gap which formed a continuous band that reduced the band gap energy of ZNFO spinel ferrite52 as shown in Fig. 10b. Also, the ionic radius can be the other reason for the band gap decrement of MNFO and ZNFO spinel ferrites. Ionic radiuses of Mn and Zn dopant cations are greater than Fe3+ and Ni2+ cations in tetrahedral and octahedral sites according to XRD results, hence the lattice constant increased, and in this condition, electrons constraint to the nucleus be more lose which expresses the electrons need less energy to leave the nucleus, therefore the band gap decrease and be narrow53.
Furthermore, the decrement of direct band gap energy can be ascribed to the sp-d exchange interactions between delocalized conduction band electrons and localized electrons in the d-shell of Mn2+ or Zn2+ ions that are substituted instead of Ni2+ ions. The exchange interactions of the Mn and Zn ions increased valence band potential and decreased conduction band potential, which decreased the band gap energy and a redshift happened52. So, it can be concluded that by Mn and Zn doping NiFe2O4, the band gap energy is reduced, which can be helpful in the improvement of optoelectronic applications49.
The absorption band tail (Urbach energy)
For further investigation on the pre-absorption edge and expounding the effects of defects and Mn and Zn doping on the crystal lattice of NiFe2O4, the Urbach energy (EU) is defined. The EU is a crucial parameter for the estimation of the defects in material. These defects create absorption tails (localized states) between the conduction band and valence band in band states that named Urbach tails, and relative energy is called Urbach energy, as demonstrated in Fig. 1154. The Urbach energy can be calculated by using the following relations54,55:
where, α is the absorption coefficient (F(R) ≈ α), α0 is a constant, E = hυ is the incident photon energy, and \(\upbeta =2{\mathrm{\alpha }}_{0}/S\) is a constant. The Urbach energy is determined by linear fitting of plotting ln(α) vs. (hν) and the reverse slope of the line as shown in the following equation:
Amounts of the Urbach tail energy of prepared samples are shown in Fig. 12 and tabulated in Table 6. The EU values of all MNPs are almost low values that can imply a low degree of disorder and defects in the synthesized samples, which agree well with XRD results. The reason can be attributed to the high annealing temperature. Heat treatment causes the structure of the material to be organized, therefore, structural disorders of the material decrease29. Also, synthesized methods and conditions can be important in this characterization56. This condition often implies excellent electronic properties, such as high carrier mobility and low density of localized states51,57.
From Table 6, the EU value increased (blue shift) with Mn and Zn substitution that proves, Mn2+ and Zn2+ dopant cations can systematically enhance the structural and electronic disorder in semiconductor Ni ferrites by a change in the bond angles and bond lengths in the lattice space of spinel ferrite. So, these factors can create localized states that increase the Urbach energy in the band gap region57,58. Also, when the impurity atom is introduced in the host lattice, the presence of the Mn2+ and Zn2+ dopant ions instead of some Fe3+ and Ni2+ sites in the tetrahedral and octahedral sublattice as explained in the XRD part, altered the Columbic potential of Ni2+ and Fe3+ sites because of difference in the ionic radii and atomic number (Z) therefor this effects in systematic scaling of the Urbach energy and organized the disordered states near to the valance and conduction bands57. From Table 6, the band gap energy decreased in contrast Urbach energy for doped samples which is accordance to the inverse relation between Eg and EU.
Linear optical study (Kramers–Kronig method)
In semiconductor materials, the refractive index complex is the key parameter in deciding the quality and nature of optoelectronic devices to plan hetero-structure lasers and in solar cell applications19. So, the accurate value of the refractive index and the calculation method to obtain it would be significant. Among numerical methods59, the Kramers–Kronig method is the more accurate and simple method that is utilized in the present study to determine the accurate real and imaginary parts of refractive index complex by DRS data to investigate linear optical properties, and are expressed by following relations60,61:
where n(ω) is the refractive index and k(ω) is the extinction coefficient. These coefficients were determined by the reflectance of a material as a function of polarization and the angle of incidence photon radiation, as given by the following equations60,62:
Here, ω is the angular frequency, \(\mathrm{\varphi }\left(\omega \right)\) is the phase division of the reflected (\({\text{R}}\left(\omega \right))\) and incident radiations, which is calculated by the Fourier transform and is expressed as follows60:
It is worth to note that all the calculation of this section (n, k) were done by MATLAB coding.
Refractive index The refractive index is the critical parameter that indicates the relative velocity and the spread of refraction of light through the material63. Plots of refractive index n(ω) for synthesized MNPs as a function of hυ in the range of λ = 350–650 nm by Kramers–Kronig method were illustrated in Fig. 13a. As can be seen, at the beginning for NFO spinel ferrite, the amount of refractive index enhanced in the range of hυ = 1.9–2.3 eV (λ = 619–516 nm) and attain a refractive peak at the point of 1.75 eV (λ = 548.166 nm) in the UV–visible region that it can be due to normal dispersion law. The refractive index in the visible region is decisive for solar cells, photocatalytic, and optoelectronic devices38,63. By increasing incident photon energy and decreasing wavelength (λ = 516–350 nm) in the plot, the n index sharply decreases. As can be seen, the refractive index of the MNFO MNPs has a slight decrease in n value at the peak region compared to NFO. It can be assigned to the absorption of the basic band gap. The refractive curve of ZNFO MNPs demonstrates a slight increment in the peak region compared to NFO spinel ferrite, which probably can imply a decrement of porosity in Zn-doped nickel ferrite that causes an increase in the refractive index.
Extinction coefficient Figure 13b depicts the alterations of extinction coefficient (k) for synthesized nanopowders by Kramers–Kronig method. It is evident that there is one primary broad k value around 2 eV value and wavelength of 621 nm in the UV–visible region for NFO spinel ferrite. In other definitions, at this wavelength (621 nm) the fraction of light lost induced by photons absorption and scattering is maximum64. By the Mn and Zn doping nickel ferrite, the k value slightly decreased in the peak region. Also, in the k spectra, the wavelength point of doped nickel ferrite in minimum absorbance value (E = 2.3 eV, λ = 538 nm) slightly shifted to lower photon energy and higher wavelength. The maximum amounts of n and k are represented in Table 7.
Direct band gap (Kramers–Kronig method) To the assessment of the band gap energy of the MNPs by the Kramers–Kronig (K-K) method, the absorption coefficient is utilized as follows:
where k is the extinction coefficient calculated by K–K method (Sect. “Linear optical study (Kramers–Kronig method)”) and λ is the wavelength. Figure 14 depicts the absorption coefficient curve, and Table 7 represents the maximum value of α. The Eg of prepared specimens by K-K method was estimated using the absorption coefficient α instead of the F(R) in Eq. (23). The curve of band gap determination of un-doped and doped synthesized MNPs versus energy by K-K method is depicted in Fig. 15, and the estimated Eg values are tabulated in Table 6. From Fig. 15 and Table 6, it is evident that the Eg values calculated from the K-K method are in comparable accordance with the band gap values calculated by Kubelka–Munk function as depicted in Fig. 10b.
Conclusions
In brief, we demonstrate that the co-precipitation technique with different material means hydrazine hydrate as reduction agent and ethylene glycol surfactant and heat treatment can provide an efficient way for the synthesis of MxNi1-xFe2O4 (M = Mn, Zn, and x = 0,0.05) spinel ferrites. The XRD spectra for the fcc structure of NFO, MNFO, and ZNFO, demonstrates that the samples have a high crystallinity without any molesting peak that can be due to the different material in synthesis process and heat treatment. The < L > , strain and other structural parameters were calculated by several methods and in comparison of methods, Williamson-Hall method is reasonable method without any restrictions. Band gap energies showed redshift by Mn2+ and Zn2+ ions substitution and the reduction trend of Eg in Mn and Zn-doped NiFe2O4 may can be useful in photocatalytic activity. The Urbach energy increased with a decrease in band gap energy and has an almost low value for NFO, MNFO, and ZNFO that indicates low structural disorder in accordance with XRD results. Estimated band gap energies by the Kramers–Kronig method are in good accordance with the Kubelka–Munk function method and can be a reasonable numerical method for band gap energy computing. By the K-K method, the refractive index illustrates that all samples have a maximum refractive index in the visible region.
Data availability
Data sets generated during the current study are available from the corresponding author on reasonable request.
References
Joshi, S. et al. Structural, magnetic, dielectric and optical properties of nickel ferrite nanoparticles synthesized by co-precipitation method. J. Mol. Struct. 1076, 55–62 (2014).
Sharifi, S., Yazdani, A. & Rahimi, K. Incremental substitution of Ni with Mn in NiFe2O4 to largely enhance its supercapacitance properties. Sci. Rep. 10, 1–15 (2020).
Šutka, A. & Gross, K. A. Spinel ferrite oxide semiconductor gas sensors. J. Sens. Actuators B Chem. 222, 95–105 (2016).
Kefeni, K. K., Msagati, T. A. M. & Mamba, B. B. Ferrite nanoparticles: Synthesis, characterisation and applications in electronic device. Mater. Sci. Eng. B Solid State Mater. Adv. Technol. 215, 37–55 (2017).
Narang, S. B. & Pubby, K. Nickel spinel ferrites: A review. J. Magn. Magn. Mater. 519, 167163 (2021).
Pottker, W. E. et al. Influence of order-disorder effects on the magnetic and optical properties of NiFe2O4 nanoparticles. Ceram. Int. 44, 17290–17297 (2018).
Amulya, M. A. S. et al. Sonochemical synthesis of NiFe2O4 nanoparticles: Characterization and their photocatalytic and electrochemical applications. Appl. Surf. Sci. Adv. 1, 100023 (2020).
Attia, S., Helaïli, N., Bessekhouad, Y., Azoudj, Y. & Trari, M. Effect of Ni toward the optical and transport properties of the spinel solid solution NixCu1-xFe2O4 nanoparticles. J. Environ. Chem. Eng. 10, 108601 (2022).
Wu, F., Wang, X., Li, M. & Xu, H. A high capacity NiFe2O4/RGO nanocomposites as superior anode materials for sodium-ion batteries. Ceram. Int. 42, 16666–16670 (2016).
Alijani, H. Q. et al. Biosynthesis of spinel nickel ferrite nanowhiskers and their biomedical applications. Sci. Rep. 11, 17431 (2021).
Iranmanesh, P., Tabatabai Yazdi, S., Mehran, M. & Saeednia, S. Superior magnetic properties of Ni ferrite nanoparticles synthesized by capping agent-free one-step coprecipitation route at different pH values. J. Magn. Magn. Mater. 449, 172–179 (2018).
Abraime, B. et al. Influence of synthesis methods with low annealing temperature on the structural and magnetic properties of CoFe2O4 nanopowders for permanent magnet application. J. Magn. Magn. Mater. 500, 166416 (2020).
Zhang, W. et al. Structural and magnetic properties of Ni–Cu–Co ferrites prepared from sol-gel auto combustion method with different complexing agents. J. Alloys Compd. 816, 152501 (2020).
Majid, F. et al. Synthesis and characterization of NiFe2O4 ferrite: Sol–gel and hydrothermal synthesis routes effect on magnetic, structural and dielectric characteristics. J. Mater. Chem. Phys. 258, 123888 (2021).
Ghosh, M. P. et al. Tuning the microstructural, optical and superexchange interactions with rare earth Eu doping in nickel ferrite nanoparticles. J. Mater. Chem. Phys. 241, 122383 (2020).
Yoon, D.-H. & Muksin, R. K. Controlling the Magnetic Properties of Nickel Ferrites by Doping with Different Divalent Transition Metal (Co, Cu, and Zn) Cations. J. Supercond. Novel Magn. 29(2), 439–45 (2016).
Ghosh, M. P. et al. Copper doped nickel ferrite nanoparticles: Jahn-Teller distortion and its effect on microstructural, magnetic and electronic properties. Mater. Sci. Eng. B Solid State Mater. Adv. Technol. 263, 114864 (2021).
Köseoǧlu, Y. Structural, magnetic, electrical and dielectric properties of Mn xNi1-xFe2O4 spinel nanoferrites prepared by PEG assisted hydrothermal method. Ceram. Int. 39, 4221–4230 (2013).
Massoudi, J. et al. Magnetic and spectroscopic properties of Ni-Zn-Al ferrite spinel: From the nanoscale to microscale. RSC Adv. 10, 34556–34580 (2020).
Istikhomah, N. et al. Effect of Zn concentration on crystal structure and magnetic properties of ZnxNi1-xFe2O4 nanoparticles fabricated by co-precipitation method. 2017 IEEE 12th Nanotechnol. Mater. Devices Conf. NMDC 2017(2018), 151–152 (2017).
Aakash, G. M. P. & Mukherjee, S. Dielectric and electrical characterizations of transition metal ions-doped nanocrystalline nickel ferrites. Appl. Phys. A 125(12), 853 (2019).
Kumari, S., Sharma, R., Thakur, N. & Kumari, A. Removal of organic and inorganic effluents from wastewater by using degradation and adsorption properties of transition metal-doped nickel ferrite. J. Environ. Sci. Pollut. Res. https://doi.org/10.1007/s11356-023-26567-4 (2023).
Aafiya, A. M. et al. Synthesis and role of structural disorder on the optical, magnetic and dielectric properties of Zn doped NiFe2O4 nanoferrites. J. Mol. Struct. 1253, 132205 (2022).
Elhosiny Ali, H. et al. Kramers-Kronig analysis of the optical linearity and nonlinearity of nanostructured Ga-doped ZnO thin films. J. Opt. Laser Technol. 135, 106691 (2021).
El Foulani, A. H. et al. Effect of surfactants on the optical and magnetic properties of cobalt-zinc ferrite Co0.5Zn0.5Fe2O4. J. Alloys Compd. 774, 1250–9 (2019).
Egizbek, K. et al. Stability and cytotoxicity study of NiFe2O4 nanocomposites synthesized by co-precipitation and subsequent thermal annealing. J. Ceram. Int. 46, 16548–16555 (2020).
Dippong, T., Cadar, O. & Levei, E. A. Effect of transition metal doping on the structural, morphological, and magnetic properties of NiFe2O4. Materials 15(9), 2996 (2022).
Nadumane, A. et al. Sunlight photocatalytic performance of Mg-doped nickel ferrite synthesized by a green sol-gel route. J. Sci. Adv. Mater. Devices 4, 89–100 (2019).
Zulqarnain, M. et al. Structural tuning interlinking various optical, dielectric and magnetic trends in annealed Mn0.5Zn0.5Fe2O4 spinel ferrites nanostructures. J. Magn. Magn. Mater. 565, 170252 (2023).
Zhou, X., Wang, J., Zhou, L. & Yao, D. The improved saturation magnetization and initial permeability in Mn–NiZn ferrites after cooling in vacuum. J. Appl. Phys. A Mater. Sci. Process. 128, 306 (2022).
Islam, M. A. et al. Structural characteristics, cation distribution, and elastic properties of Cr3+ substituted stoichiometric and non-stoichiometric cobalt ferrites. RSC Adv. 12, 8502–8519 (2022).
Mukhtar, F. et al. Structural and magnetization crossover in electrodeposited FeAl2O4-effect of: In situ oxidation. RSC Adv. 9, 38183–38194 (2019).
Rabiei, M. et al. Comparing methods for calculating nano crystal size of natural hydroxyapatite using X-ray diffraction. Nanomaterials 10(9), 1627 (2020).
Monshi, A., Foroughi, M. R. & Monshi, M. R. Modified Scherrer equation to estimate more accurately nano-crystallite size using XRD. World J. Nano Sci. Eng. 02, 154–160 (2012).
Nath, D., Singh, F. & Das, R. X-ray diffraction analysis by Williamson-Hall, Halder-Wagner and size-strain plot methods of CdSe nanoparticles- a comparative study. J. Mater. Chem. Phys. 239, 122021 (2020).
Mubasher, M. M. et al. Comparative study of frequency-dependent dielectric properties of ferrites MFe2O4 (M = Co, Mg, Cr and Mn) nanoparticles. J. Appl. Phys. A Mater. Sci. Process. 126(5), 334 (2020).
Vinosha, P. A., Xavier, B., Krishnan, S. & Das, S. J. Investigation on zinc substituted highly porous improved catalytic activity of NiFe2O4 nanocrystal by co-precipitation method. J. Mater. Res. Bull. 101, 190–198 (2018).
Hasan, N. et al. Magnetic, optoelectronic, and rietveld refined structural properties of Al3+ substituted nanocrystalline Ni-Cu spinel ferrites: An experimental and DFT based study. J. Magn. Magn. Mater. 573, 170675 (2023).
Mirzaee, S., Azizian-Kalandaragh, Y. & Rahimzadeh, P. Modified co-precipitation process effects on the structural and magnetic properties of Mn- doped nickel ferrite nanoparticles. J. Solid State Sci. 99, 106052 (2020).
Kulkarni, A. B. & Mathad, S. N. Variation in structural and mechanical properties of Cd-doped Co-Zn ferrites. Mater. Sci. Energy Technol. 2, 455–462 (2019).
Arsenlis, A. & Parks, D. J. Crystallographic aspects of geometrically-necessary and statistically-stored dislocation density. J. Acta Mater. 47(5), 1597–611 (1999).
Bashir, A. K. H. et al. Investigation of electrochemical performance, optical and magnetic properties of NiFe 2 O 4 nanoparticles prepared by a green chemistry method. J. Phys. E (Amsterdam, Neth.) 119, 114002 (2020).
Basak, M., Rahman, M. L., Ahmed, M. F., Biswas, B. & Sharmin, N. Calcination effect on structural, morphological and magnetic properties of nano-sized CoFe2O4 developed by a simple co-precipitation technique. J. Mater. Chem. Phys. 264, 124442 (2021).
Rambadey, O. V., Kumar, A., Sati, A. & Sagdeo, P. R. Exploring the Interrelation between Urbach energy and dielectric constant in Hf-substituted BaTiO3. ACS Omega 6(47), 32231–32238 (2021).
Alahmari, F., Almessiere, M. A., Ünal, B., Slimani, Y. & Baykal, A. Electrical and optical properties of Ni0·5Co0.5-xCdxNd0.02Fe1·78O4 (x ≤ 0.25) spinel ferrite nanofibers. J. Ceram. Int. 46(15), 24605–14 (2020).
Sasikumar, K. et al. Structural, optical, and magnetic properties of Mn-doped nickel ferrite (Ni1-xMnxFe2O4) thin films deposited by jet nebulizer spray pyrolysis technique. J. Supercond. Novel Magn. 34(8), 2189–2198 (2021).
Barathiraja, C., Manikandan, A., Uduman Mohideen, A. M., Jayasree, S. & Antony, S. A. Magnetically recyclable spinel MnxNi1−xFe2O4 (x= 0.0–0.5) nano-photocatalysts: Structural, morphological and opto-magnetic properties. J. Supercond. Novel Magn. 29(2), 477–86 (2016).
Massoudi, J., Smari, M., Nouri, K. & Dhahri, E. Magnetic and spectroscopic properties of Ni – Zn – Al ferrite spinel: From the nanoscale to microscale †. J. RSC Adv. 2020, 34556–80 (2020).
Ismael, M. Ferrites as solar photocatalytic materials and their activities in solar energy conversion and environmental protection: A review. Sol. Energy Mater. Sol. Cells 219, 110786 (2021).
Arumugham, N. et al. Nickel ferrite-based composites and its photocatalytic application–A review. J. Hazard Mater. Adv. 8, 100156 (2022).
Harrabi, D. et al. Study of structural and optical properties of Cu–Cr substituted Mg–Co spinel ferrites for optoelectronic applications. J. Inorg. Organomet. Polym. Mater. 33(1), 47–60 (2023).
Lu, Q., Wei, Z., Wu, X., Huang, S. & Ding, M. Electronic structure and optical properties of spinel structure Zn 1–x Ni x Al2O4 nanopowders synthesized by sol – gel method. J. Chem. Phys. Lett. 772, 138582 (2021).
Sinha, A. & Dutta, A. Structural, optical, and electrical transport properties of some rare-earth-doped nickel ferrites: A study on effect of ionic radii of dopants. J. Phys. Chem. Solids 145, 109534 (2020).
Lemziouka, H. et al. Synthesis, structural, optical and dispersion parameters of La-doped spinel. Vacuum 182, 109780 (2020).
Norouzzadeh, P., Mabhouti, K., Golzan, M. M. & Naderali, R. Investigation of structural, morphological and optical characteristics of Mn substituted Al-doped ZnO NPs: A Urbach energy and Kramers-Kronig study. Optik 204, 164227 (2020).
Xu, J., He, X., Xu, K., Liao, H. & Zhang, C. Synthesis and optimization strategies of nanostructured metal oxides for chemiresistive methanol sensors. J. Ceram. Int. 49(13), 21113–21132 (2023).
Kumar, A., Rambadey, O. V. & Sagdeo, P. R. Unorthodox approach to realize the correlation between the dielectric constant and electronic disorder in Cr-doped PrFeO3. J. Phys. Chem. C 125(13), 7378–7383 (2021).
Kumar, A., Warshi, M. K., Sagdeo, A. & Sagdeo, P. R. Investigations on the electronic structure of the strongly correlated electron system Cr-doped PrFeO3. J. Phys. Chem. C 125(25), 14048–14055 (2021).
Manthrammel, M. A. et al. Optical analysis of nanostructured rose bengal thin fi lms using Kramers – Kronig approach: New trend in laser power attenuation. J. Opt. Laser Technol. 112, 207–214 (2019).
Ganesh, V. et al. The detailed calculations of optical properties of indium-doped CdO nanostructured films using Kramers-Kronig relations. J. Non-Cryst. Solids 552, 120454 (2021).
Mabhouti, K., Norouzzadeh, P. & Taleb-Abbasi, M. Effects of Fe Co, or Ni substitution for Mn on La0.7Sr0.3MnO3 perovskite: Structural, morphological, and optical analyses. J. Non-Cryst. Solids 610, 122283 (2023).
Ferreyra, R. A., Zhu, C., Teke, A. & Morkoç, H. Group III nitrides. In Springer Handbook of Electronic and Photonic Materials (eds Kasap, S. & Capper, P.) 1 (Springer International Publishing, 2017).
Munawar, H. B. et al. Structural, electronic, magnetic, and optical properties of MFe2O4 (M= Ni, Fe, Co) spinel ferrites: A density functional theory study. J. Quantum Chem. 123, e27124 (2023).
Soliman, T. S. & Abouhaswa, A. S. Synthesis and structural of Cd0.5Zn0.5F2O4 nanoparticles and its influence on the structure and optical properties of polyvinyl alcohol films. J. Mater. Sci. Mater. Electron. 31(12), 9666–74 (2020).
Author information
Authors and Affiliations
Contributions
N. Nazari: Investigation, Formal analysis, Conceptualization, Writing original draft, Data curation. MM. Golzan: Supervision, Conceptualization, Editing original draft. Kh. Mabhouti: Supervision, Conceptualization, Data curation, Software.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nazari, N., Golzan, M.M. & Mabhouti, K. Study of Urbach energy and Kramers–Kronig on Mn and Zn doped NiFe2O4 ferrite nanopowder for the determination of structural and optical characteristics. Sci Rep 14, 6407 (2024). https://doi.org/10.1038/s41598-024-57045-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-57045-7
Keywords
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.