Introduction

In recent years, chaos theory has risen its importance, and numerous investigations on chaotic systems have been observed. Different chaotic systems1,2 have been studied, particularly hidden3 and multi-stability attractors4. Chaos-based applications is a hot topic in science and engineering. Oscillators5, steganography6, synchronization7, control8, and parameter estimation have all employed chaotic systems. Some chaotic systems have a unique feature. They can have two or more coexisting attractors9. Every attractor can be achieved because of the same range of parameters, depending on the initial condition chosen. Multistable chaotic systems10 are such systems, and they have gotten a lot of attention in the recent decade because of their potential applications11. Several parameters of a multistable dynamical system are particularly sensitive to noise, initial conditions, and system parameters12. Although multi-stability makes some engineering fields more challenging, such as bridge vibration and wing design, chaotic systems with multi-stability are extremely beneficial in secure communication13. The appearance of hidden attractors has been associated with multi-stability14. Stable equilibrium systems and systems with hidden attractors are examples of multistable systems15. In multistable systems, self-excited attractors can be found using the typical computational process, but hidden attractors cannot be predicted through the typical computational approach16.

In recent decades, fractional calculus has been a significant mathematical technique used to represent critical challenges in various areas, including science, technology, and engineering such as, optimal power flow problems17, nonlinear output-error systems18, recommender systems with chaotic ratings behavior19, parameter estimation of nonlinear control autoregressive systems20, power management involving wind-load chaos and uncertainties21, Schrodinger equations22,23 and shallow water waves24. The power-law function is involved in the Liouville–Caputo fractional derivative. As a result, it's common that the physical meaning of the fractional derivative is elusive or non-existent. On the other hand, many researchers identified the physical significance of fractional derivatives25,26,27,28,29,30,31,32,33. The nonlocality property of fractional derivatives is useful in predicting certain materials' memory and heredity properties in certain circumstances. As a result, the fractional derivative34,35,36,37 can be defined physically as a memory search. Scholars from virtually all fields of science, technology, and engineering have been studying non-local operators of differentiation over the past few decades since they have the capability to incorporate more complex phenomena. Fractional order chaotic systems have also been a highly prominent and attractive topic in recent years. They've been studied by many researchers38. Chaotic systems, particularly fractional order-based chaotic systems39, have influenced attention as circuit design capability has improved with the introduction of integrated circuits40.

The more complex the physical problems, the more complex the mathematical differentiation operators that were developed. In order to perform a single differentiation, the fractal-fractional operator combines fractional differentiation with fractal derivative. These physical processes, for example, exhibit traits of a fractal nature. There is a sort of fractal derivative that may be found in practical mathematics, and it is one in which the variable is scaled in accordance with ta. We thought that by coming up with this nonstandard derivative, we would be able to replicate aspects of the physical world that was no longer governed by the conventional physical rules26. Two parameters representing power-law, exponential decay, or Mittag–Leffler memory processes were presented by Atangana41, and the order parameter order stands for fractal derivative, which can be used to define the fractal dimension. This new set of derivatives also included an order parameter that stands for fractal derivative. Some of the previous work that has been presented in this new field has been applied either to a system of fractional ordinary differential equations or, in a few exceptional cases, to a straightforward equation for heat or diffusion42,43,44,45,46,47.

Motivated from the above literature, it have been found that fractional and fractal-fractional differential operator is a best tool to include the memory effect, crossover behavior and fractal characteristics all at once. Thus, there is a need to modify the existing chaotic systems through fractional or fractal-fractional differential operators of various singular and non-singular kernels. Therefore, in this research we have considered a chaotic system which is based on a circuit design with the following considerations:

  • The considered chaotic problem is modelled in terms of nonlinear system of ODEs.

  • The integer ODEs system is generalized through the fractal-fractional differential operator of power law kernel.

  • The system dissipation and equilibria have been calculated.

  • The existence and uniqueness of the solutions have been proved.

  • The Ulam stability have been proved.

  • Numerical algorithm for the non-linear fractal-fractional system have been stated.

  • The obtained graphical results have been portraited through 2D and 3D phase portraits.

Mathematical preliminaries

This section provides an overview of some essential ideas and prepositions that will be used in subsequent parts of the investigation41,48,49.

Definition 2.1

If \(g\left( \tau \right)\) is differentiable on \(\left( {a,b} \right)\) with fractional order α and fractal order \(\beta\) and \(g\left( \tau \right)\) is differentiable on the opened interval \(\left( {a,b} \right)\), then the Fractal-Fractional derivative of \(g\left( \tau \right)\) with fractional order \(\alpha\) and fractal order β in Riemann–Liouville sense with power law can be written as:

$$_{a}^{FFRL} \wp_{\tau }^{\alpha ,\beta } g\left( \tau \right) = \frac{1}{{\Gamma \left( {m - \alpha } \right)}}\frac{d}{{d\tau^{\beta } }}\int\limits_{a}^{\tau } {g\left( x \right)\left( {\tau - x} \right)^{m - \alpha - 1} dx,}$$
(1)

where \(m - 1 < \alpha \le m,\,\,\,0 < m - 1 < \beta \le m.\)

$$\frac{dg\left( x \right)}{{dx^{\beta } }} = \mathop {\lim }\limits_{\tau \to x} \,\frac{f\left( \tau \right) - f\left( x \right)}{{\tau^{\beta } - x^{\beta } }}.$$
(2)

Definition 2.2

If \(g\left( \tau \right)\) is fractal differentiable on \(\left( {a,b} \right)\) with fractal order \(\beta\) and \(g\left( \tau \right)\) is differentiable on the opened interval \(\left( {a,b} \right)\), then the Fractal-Fractional derivative of \(g\left( \tau \right)\) with fractional order \(\alpha\) and fractal order β in Caputo sense with power law is:

$$_{a}^{FFP} \wp_{\tau }^{\alpha ,\beta } g\left( \tau \right) = \frac{1}{{\Gamma \left( {m - \alpha } \right)}}\int\limits_{a}^{\tau } {\frac{dg\left( x \right)}{{dx^{\beta } }}\left( {\tau - x} \right)^{m - \alpha - 1} dx,}$$
(3)

where \(m - 1 < \alpha \le m,\,\,\,0 < m - 1 < \beta \le m.\)

$$\frac{dg\left( x \right)}{{dx^{\beta } }} = \mathop {\lim }\limits_{\tau \to x} \,\frac{f\left( \tau \right) - f\left( x \right)}{{\tau^{\beta } - x^{\beta } }}.$$
(4)

Definition 2.3

The fractal-fractional integral of Power law kernel can be expressed as follows:

$${}_{0}^{FFP} I_{\tau }^{\alpha } f(\tau ) = \frac{\beta }{N(\alpha )}\int\limits_{0}^{\tau } {x^{\alpha - 1} } u\left( x \right)\left( {\tau - x} \right)^{\alpha - 1} dx.$$
(5)

Definition 2.4

Numerical solution to the Caputo ODE of fractional order is defined as follows50:

Consider nonlinear fractional ODE:

$${}_{0}^{C} \wp_{t}^{\alpha } z(\tau ) = f\left( {\tau ,z(\tau )} \right)\;\;{\text{with}}\;{\text{z}}(0) = z_{0} ,$$
(6)

The numerical algorithm for Eq. (6) is as follows:

$$z_{n + 1} = z_{0} + \frac{1}{\Gamma (\alpha )}\sum\limits_{j = 0}^{n} {\left[ \begin{gathered} \frac{{h^{\alpha } f\left( {\tau_{j} ,z\left( {\tau_{j} } \right)} \right)}}{{\alpha \left( {\alpha + 1} \right)}}\left\{ {\left( {n + 1 - j} \right)^{\alpha } \left( {n + 2 - r + \alpha } \right) - \left( {n - j} \right)^{\alpha } \left( {n + 2 - r + 2\alpha } \right)} \right\} \hfill \\ - \frac{{h^{\alpha } f\left( {\tau_{j - 1} ,z\left( {\tau_{j - 1} } \right)} \right)}}{{\alpha \left( {\alpha + 1} \right)}}\left\{ {\left( {n + 1 - j} \right)^{\alpha + 1} - \left( {n - j} \right)^{\alpha } \left( {n + 2 - r + \alpha } \right)} \right\} \hfill \\ \end{gathered} \right]} .$$
(7)

Mathematical formulation

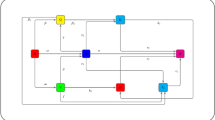
In this study, we investigate a new type of chaotic system that was presented in51:

$$\left. \begin{aligned} & \frac{{dx_{1} }}{d\tau } = z_{1} , \hfill \\ & \frac{{dy_{1} }}{d\tau } = - x_{1} - z_{1} , \hfill \\ & \frac{{dz_{1} }}{d\tau } = ax_{1} + by_{1} - z_{1} + x_{1} y_{1} - cx_{1} z_{1} + 1, \hfill \\ \end{aligned} \right\}.$$
(8)

with initial conditions:

$$x_{1} \left( 0 \right) = x_{1}^{*} ,\,\,y_{1} \left( 0 \right) = y_{1}^{*} \;\;{\text{and}}\;\;z_{1} \left( 0 \right) = z_{1}^{*} .$$
(9)

Here \(a,b\) and \(c\) are the three non-negative parameters.

The integer order system given in Eq. (8) can be transformed to the fractal-fractional order chaotic system by applying the definition given in Eq. (3). Thus, by applying the procedure given in41, Eq. (8) will take the following form:

$$\left. \begin{aligned} & {}_{0}^{FFP} \wp_{\tau }^{\alpha ,\beta } = z_{1} , \hfill \\ & {}_{0}^{FFP} \wp_{\tau }^{\alpha ,\beta } = - x_{1} - z_{1} , \hfill \\ & {}_{0}^{FFP} \wp_{\tau }^{\alpha ,\beta } = ax_{1} + by_{1} - z_{1} + x_{1} y_{1} - cx_{1} z_{1} + 1, \hfill \\ \end{aligned} \right\}.$$
(10)

The fractional order and fractal dimension are represented by \(\alpha\) and \(\beta\), respectively, with \(0 < \alpha ,\beta \le 1\).

Dissipation and equilibria

The model in the system (8) is dissipative because:

$$\nabla V = \frac{\partial }{{\partial x_{1} }}\left( {\frac{{dx_{1} }}{d\tau }} \right) + \frac{\partial }{{\partial y_{1} }}\left( {\frac{{dy_{1} }}{d\tau }} \right) + \frac{\partial }{{\partial z_{1} }}\left( {\frac{{dz_{1} }}{d\tau }} \right) = - \left( {1 + cx_{1} } \right) < 0.$$
(11)

For the fixed points of the chaotic system (8), we consider \(\frac{{dx_{1} }}{d\tau } = \frac{{dy_{1} }}{d\tau } = \frac{{dz_{1} }}{d\tau } = 0\). Hence system (8) can be written as:

$$\left. \begin{aligned} & 0 = z_{1} , \hfill \\ & 0 = - x_{1} - z_{1} , \hfill \\ &0 = ax_{1} + by_{1} - z_{1} + x_{1} y_{1} - cx_{1} z_{1} + 1, \hfill \\ \end{aligned} \right\}.$$
(12)

Here we have only one equilibrium point, i.e., \(\left( {x_{1} ,y_{1} ,z_{1} } \right) = \left( {0, - \frac{1}{b},0} \right)\).

Existence and uniqueness of the fractal-fractional model

The presence of a unique solution to the fractal-fractional model, provided in Eq. (10), is established in this portion of the study. We could reformulate the Eq. (10) in the following manner because the integral is differentiable:

$$\left. \begin{gathered} {}_{0}^{RL} \wp_{\tau }^{\beta } \left( {x_{1} \left( \tau \right)} \right) = \beta \tau^{\beta - 1} \left( {\Psi_{1} \left( {\tau ,x_{1} } \right)} \right), \hfill \\ {}_{0}^{RL} \wp_{\tau }^{\beta } \left( {y_{1} \left( \tau \right)} \right) = \beta \tau^{\beta - 1} \left( {\Psi_{1} \left( {\tau ,y_{1} } \right)} \right), \hfill \\ {}_{0}^{RL} \wp_{\tau }^{\beta } \left( {z_{1} \left( \tau \right)} \right) = \beta \tau^{\beta - 1} \left( {\Psi_{1} \left( {\tau ,z_{1} } \right)} \right). \hfill \\ \end{gathered} \right\}.$$
(13)

where \(0 < \alpha ,\beta \le 1\) and,

$$\left. \begin{aligned} & \Psi_{1} \left( {\tau ,x_{1} } \right) = z_{1} , \hfill \\ & \Psi_{1} \left( {\tau ,y_{1} } \right) = - x_{1} - z_{1} , \hfill \\ & \Psi_{1} \left( {\tau ,z_{1} } \right) = ax_{1} + by_{1} - z_{1} + x_{1} y_{1} - cx_{1} z_{1} + 1, \hfill \\ \end{aligned} \right\}.$$
(14)

We can rewrite system (13) as:

$$\left. \begin{aligned} & {}_{0}^{RL} \wp_{\tau }^{\omega } {\rm H}\left( \tau \right) = \beta \tau^{\beta - 1} \Phi \left( {\tau ,{\rm H}\left( \tau \right)} \right), \hfill \\ & {\rm H}\left( 0 \right) = {\rm H}^{*} \hfill \\ \end{aligned} \right\}.$$
(15)

where

$${\rm H}\left( \tau \right) = \left\{ \begin{gathered} x_{1} \left( \tau \right) \hfill \\ y_{1} \left( \tau \right) \hfill \\ z_{1} \left( \tau \right) \hfill \\ \end{gathered} \right.,\,\,\,\,{\rm H}\left( 0 \right) = \left\{ \begin{gathered} x_{1} \left( 0 \right) \hfill \\ y_{1} \left( 0 \right) \hfill \\ z_{1} \left( 0 \right) \hfill \\ \end{gathered} \right.,\,\,\,\,\,\Phi \left( {\tau ,{\rm H}\left( 0 \right)} \right) = \left\{ \begin{gathered} \Psi_{1} \left( {\tau ,x_{1} } \right) \hfill \\ \Psi_{1} \left( {\tau ,y_{1} } \right) \hfill \\ \Psi_{1} \left( {\tau ,z_{1} } \right) \hfill \\ \end{gathered} \right..\,\,$$
(16)

Now, by replacing \({}_{0}^{RL} \wp_{\tau }^{\alpha }\) with \({}_{0}^{C} \wp_{\tau }^{\alpha }\) and applying the fractional integral, we get:

$${\rm H}\left( \tau \right) = {\rm H}\left( 0 \right) + \frac{\beta }{\Gamma \left( \alpha \right)}\int\limits_{a}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \Phi \left( {\kappa ,{\rm H}\left( \kappa \right)} \right)} d\kappa .$$
(17)

Let \({\rm P}\left( \psi \right)\) be a Banach space of the real-valued continuous functions with supremum norm defined on the interval \(\psi = \left[ {0,\Upsilon } \right]\) and \(\chi = {\rm P}\left( \psi \right) \times {\rm P}\left( \psi \right) \times {\rm P}\left( \psi \right)\) with the norm \(\left\| \Gamma \right\| = \sup \left\{ {\left| {\Gamma \left( \tau \right)} \right|:\,\tau \in \psi } \right\}\).

Now, transform the problem (10) into a fixed-point problem. Define an operator \(\coprod :\chi \to \chi\) as:

$$\coprod \left( {{\rm H}\left( \tau \right)} \right) = {\rm H}\left( 0 \right) + \frac{\beta }{\Gamma \left( \alpha \right)}\int\limits_{a}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \Phi \left( {\kappa ,{\rm H}\left( \kappa \right)} \right)} d\kappa .$$
(18)

For the existence theory, we use the following theorem52,53.

Theorem 5.1

Assume that the operator \(\coprod :\chi \to \chi\) is completely continuous and the set defined by:

\(\mho \left( \coprod \right) = \left\{ {\Phi \in \chi :\,{\rm H} = \delta \coprod \left( {\rm H} \right);\,\delta \in \left[ {0,1} \right]} \right\}\) be bounded. Then \(\coprod\) has a fixed point \(\chi\).

Theorem 5.2

Let \(\Phi :\psi \times \chi \to {\mathbb{R}}\) is a continuous function. Then the operator \(\coprod\) is compact.

Proof

Let \({\rm M}\) us a bounded set in \(\chi\). Then there is \(\vartheta_{\Phi } > 0\) with \(\left| {\Phi \left( {\tau ,{\rm H}\left( \tau \right)} \right)} \right| \le \vartheta_{\Phi } ,\,\,\forall {\rm H} \in {\rm M}.\) So for any \({\rm H} \in {\rm M}\) one can get:

$$\begin{aligned} \left\| {\coprod \left( {\text{H}} \right)} \right\| & \le \frac{{\beta \vartheta_{\Phi } }}{\Gamma \left( \alpha \right)}\mathop {\max }\limits_{\tau \to \psi } \int\limits_{0}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} d\kappa ,} \hfill \\ & \le \frac{{\beta \vartheta_{\Phi } }}{\Gamma \left( \alpha \right)}\mathop {\max }\limits_{\tau \to \psi } \int\limits_{0}^{1} {\varphi^{\beta - 1} \left( {1 - \varphi } \right)^{\alpha - 1} \tau^{\beta + \alpha - 1} d\varphi ,} \hfill \\ & \le \frac{{\beta \vartheta_{\Phi } {\rm T}^{\beta + \alpha - 1} }}{\Gamma \left( \alpha \right)}B\left( {\alpha ,\beta } \right), \hfill \\ \end{aligned}$$
(19)

where \(B\left( {\alpha ,\beta } \right)\) is the beta function. Thus, \({\rm M}\left( \coprod \right)\) it is uniformly bounded.

Next, for the equicontinuity of the operator \(\coprod\), for any \(\tau_{1} ,\tau_{2} \in \psi\) and \({\rm H} \in {\rm M},\) we have:

$$\begin{aligned} \left\| {\coprod \left( {{\text{H}}\left( {\tau_{1} } \right)} \right) - \coprod \left( {{\text{H}}\left( {\tau_{2} } \right)} \right)} \right\| & \le \frac{{\beta \vartheta_{\Phi } }}{\Gamma \left( \alpha \right)}\mathop {\max }\limits_{\tau \to \psi } \left| {\int\limits_{0}^{{\tau_{1} }} {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} d\kappa - \int\limits_{0}^{{\tau_{2} }} {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} d\kappa } } } \right|, \hfill \\ & \le \frac{{\beta \vartheta_{\Phi } }}{\Gamma \left( \alpha \right)}\mathop {\max }\limits_{\tau \to \psi } \left( {\tau_{1}^{\alpha + \beta - 1} - \tau_{2}^{\alpha + \beta - 1} } \right) \to 0\,\,{\text{as}}\,\,\tau_{1} \to \tau_{2} . \hfill \\ \end{aligned}$$
(20)

Therefore, \(\coprod\) it is equicontinuous. Since \(\coprod\) it is a bounded and continuous operator. So, by Arzela-Ascoli theorem is completely continuous.

Theorem 5.3

Let for all \(\tau \in \psi\) and \({\rm H} \in {\mathbb{R}}\), there is a real number \(\vartheta_{\Phi } > 0\) with \(\left| {\Phi \left( {\tau ,\coprod \left( \tau \right)} \right)} \right| \le \vartheta_{\Phi }\) . Then the considered model (10) has at least one solution in the given space \(\chi .\)

Proof

Consider a set \(\mho \left( \coprod \right) = \left\{ {\Phi \in \chi :\,{\rm H} = \delta \coprod \left( {\rm H} \right);\,\delta \in \left[ {0,1} \right]} \right\}\) and show that \(\mho\) it is bounded. Suppose \({\rm H} \in \mho\), then \({\rm H} = \delta \coprod \left( {\rm H} \right)\). For \(\tau \in \psi\), one can easily obtain:

$$\left\| {\rm H} \right\| \le \frac{{\beta \vartheta_{\Phi } {\rm T}^{\alpha + \beta - 1} }}{\Gamma \left( \alpha \right)}B\left( {\alpha ,\beta } \right).$$
(21)

Hence \(\mho\) is bounded. So, Theorems 5.1 and 5.2\(\coprod\) has at least one fixed point. Thus, the considered system (10) has at least one solution.

For further analysis, suppose the following hypothesis:

Hypothesis 5.1

There is a constant \(\hbar_{\Phi } > 0\) such that for every \({\rm H},\overline{\rm H} \in \chi\), we have:

$$\left| {\Phi \left( {\tau ,{\rm H}} \right) - \Phi \left( {\tau ,\overline{\rm H}} \right)} \right| \le \vartheta_{\Phi } \left| {{\rm H} - \overline{\rm H}} \right|.$$
(22)

For uniqueness, we use Banach's Contraction Theorem52,53:

Theorem 5.4

Under Hypothesis 5.1and if \(\Xi < 1\). Then the solution of the considered system (10) is unique, where

$$\Xi = \frac{{\beta \hbar_{\Phi } {\rm T}^{\alpha + \beta - 1} }}{\Gamma \left( \alpha \right)}B\left( {\alpha ,\beta } \right).$$
(23)

Proof

Let we define \(\mathop {\max }\limits_{\tau \to \psi } \left| {\Phi \left( {\tau ,0} \right)} \right| = \omega_{\Phi } < \infty\) such that \(\varpi \ge \frac{{\beta {\rm T}^{\alpha + \beta - 1} B\left( {\alpha ,\beta } \right)\omega_{\Phi } }}{{\Gamma \left( \alpha \right) - \beta {\rm T}^{\alpha + \beta - 1} B\left( {\alpha ,\beta } \right)\hbar_{\Phi } }}\).

We show that \(\coprod \left( {\Re_{\omega } } \right) \subset \Re_{\omega }\) where \(\Re_{\omega } = \left\{ {{\rm H} \in \chi :\left\| {\rm H} \right\| \le \omega } \right\}\). For \({\rm H} \in \Re_{\omega }\), we have:

$$\begin{aligned} \left\| {\coprod \left( {\rm H} \right)} \right\| & \le \frac{\beta }{\Gamma \left( \alpha \right)}\mathop {\max }\limits_{\tau \in \psi } \int\limits_{0}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \left( {\left| {\Phi \left( {\tau ,{\rm H}\left( \tau \right)} \right) - \Phi \left( {\tau ,0} \right)} \right| + \left| {\Phi \left( {\tau ,0} \right)} \right|} \right)d\kappa ,} \hfill \\ & \le \frac{{\beta {\rm T}^{\alpha + \beta - 1} B\left( {\alpha ,\beta } \right)\left( {\hbar_{\Phi } \left\| {\rm H} \right\| + \omega_{\Phi } } \right)}}{\Gamma \left( \alpha \right)} \hfill \\ & \le \frac{{\beta {\rm T}^{\alpha + \beta - 1} B\left( {\alpha ,\beta } \right)\left( {\hbar_{\Phi } \varpi + \omega_{\Phi } } \right)}}{\Gamma \left( \alpha \right)} \hfill \\ & \le \Xi . \hfill \\ \end{aligned}$$
(24)

Let the operator \(\coprod :\chi \to \chi\) define it by (18). Then in view of Hypothesis 5.1, for every \(\tau \in \psi\) and for every \({\rm H},\overline{\rm H} \in \chi\), we have:

$$\begin{aligned} \left\| {\coprod \left( {\rm H} \right) - \coprod \left( {\overline{\rm H}} \right)} \right\| & \le \frac{\beta }{\Gamma \left( \alpha \right)}\mathop {\max }\limits_{\tau \in \psi } \left| \begin{gathered} \int\limits_{0}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \Phi \left( {\kappa ,{\rm H}\left( \kappa \right)} \right)d\kappa } \hfill \\ - \int\limits_{0}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \Phi \left( {\kappa ,\overline{\rm H}\left( \kappa \right)} \right)d\kappa } \hfill \\ \end{gathered} \right| \hfill \\ & \le \omega \left\| {{\rm H} - \overline{\rm H}} \right\|. \hfill \\ \end{aligned}$$
(25)

Hence \(\coprod\) is, a contraction from (25). Thus, the integral Eq. (17) has a unique solution, and so does the system (10) has a unique solution.

Ulam stability

In this section, we develop and present some results on the stability of the model (10). We will consider a small perturbation \(\Upsilon \in P\left( \psi \right)\) that depends only on the solution and \(\Upsilon \left( 0 \right) = 0\). Further:

$$\left| {\Upsilon \left( \tau \right)} \right| \le \varepsilon ,\,\,\,{\text{for}}\,\,\varepsilon > 0,$$
(26)
$${}^{FFP}\wp_{\tau }^{\alpha ,\beta } \left( {{\rm H}\left( \tau \right)} \right) = \Phi \left( {\tau ,{\rm H}\left( \tau \right)} \right) + \Upsilon \left( \tau \right).$$
(27)

Lemma 6.1

The modified problem's solution is as follows:

$$\left\{ \begin{aligned} & {}^{FFP}\wp_{\tau }^{\alpha ,\beta } \left( {{\rm H}\left( \tau \right)} \right) = \Phi \left( {\tau ,{\rm H}\left( \tau \right)} \right) + \Upsilon \left( \tau \right), \hfill \\ & {\rm H}\left( 0 \right) = {\rm H}^{*} , \hfill \\ \end{aligned} \right.$$
(28)

Satisfies the following relation:

$$\left| {{\rm H}\left( \tau \right) - \left( {{\rm H}\left( 0 \right) + \frac{\beta }{\Gamma \left( \alpha \right)}\int\limits_{a}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \Phi \left( {\kappa ,{\rm H}\left( \kappa \right)} \right)} d\kappa } \right)} \right| \le \left( {\frac{{\beta {\rm T}^{\alpha + \beta - 1} }}{\Gamma \left( \alpha \right)}B\left( {\alpha ,\beta } \right)} \right)\varepsilon = {\mathbb{C}}_{\alpha ,\beta } \varepsilon .$$
(29)

Theorem 6.1

Under Hypothesis 5.1 and Lemma 6.1, the integral Eq. (17) solution is Ulam-Hyers stable. Consequently, the considered system is Ulam-Hyers stable if \(\Xi < 1\), where \(\Xi\) is given by (23).

Proof

Suppose \({\rm K} \in \chi\) be a unique solution and \({\rm H} \in \chi\) be any solution of (10), then:

$$\begin{aligned} \left| {{\rm H}\left( \tau \right) - {\rm K}\left( \tau \right)} \right| & = \left| {{\rm H}\left( \tau \right) - \left( {{\rm K}\left( 0 \right) + \frac{\beta }{\Gamma \left( \alpha \right)}\int\limits_{a}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \Phi \left( {\kappa ,{\rm K}\left( \kappa \right)} \right)} d\kappa } \right)} \right| \hfill \\ & \le \left| {{\rm H}\left( \tau \right) - \left( {{\rm H}\left( 0 \right) + \frac{\beta }{\Gamma \left( \alpha \right)}\int\limits_{a}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \Phi \left( {\kappa ,{\rm H}\left( \kappa \right)} \right)} d\kappa } \right)} \right| \hfill \\ & \quad + \left| \begin{gathered} {\rm H}\left( {{\rm H}\left( 0 \right) + \frac{\beta }{\Gamma \left( \alpha \right)}\int\limits_{a}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \Phi \left( {\kappa ,{\rm H}\left( \kappa \right)} \right)} d\kappa } \right) \hfill \\ - \left( {{\rm K}\left( 0 \right) + \frac{\beta }{\Gamma \left( \alpha \right)}\int\limits_{a}^{\tau } {\kappa^{\beta - 1} \left( {\tau - \kappa } \right)^{\alpha - 1} \Phi \left( {\kappa ,{\rm K}\left( \kappa \right)} \right)} d\kappa } \right) \hfill \\ \end{gathered} \right| \hfill \\ & \le {\mathbb{C}}_{\alpha ,\beta } \varepsilon + \frac{{\beta \hbar_{\Phi } {\rm T}^{\alpha + \beta - 1} }}{\Gamma \left( \alpha \right)}B\left( {\alpha ,\beta } \right)\left\| {{\rm H} - {\rm K}} \right\|. \hfill \\ \end{aligned}$$
(30)

We can write the above inequality as:

$$\left| {{\rm H}\left( \tau \right) - {\rm K}\left( \tau \right)} \right| \le {\mathbb{C}}_{\alpha ,\beta } \varepsilon + \Xi \left\| {{\rm H} - {\rm K}} \right\|.$$
(31)

From (31), we can write:

$$\left| {{\rm H}\left( \tau \right) - {\rm K}\left( \tau \right)} \right| \le \left( {\frac{{{\mathbb{C}}_{\alpha ,\beta } }}{1 - \Xi }} \right)\varepsilon .$$
(32)

Therefore, the result (32) concludes that the solution of (10) is Ulam-Hyers stable, and therefore this supposed problem is Ulam-Hyers stable as well.

Numerical scheme for the fractal-fractional model

Consider the system (10)

$$\left. \begin{gathered} {}_{0}^{RL} \wp_{\tau }^{\alpha } \left( {x_{1} \left( \tau \right)} \right) = \beta \tau^{\beta - 1} \left( {\Phi_{1} \left( {\tau ,y_{1} } \right)} \right), \hfill \\ {}_{0}^{RL} \wp_{\tau }^{\alpha } \left( {y_{1} \left( \tau \right)} \right) = \beta \tau^{\beta - 1} \left( {\Phi_{2} \left( {\tau ,y_{2} } \right)} \right), \hfill \\ {}_{0}^{RL} \wp_{\tau }^{\alpha } \left( {z_{1} \left( \tau \right)} \right) = \beta \tau^{\beta - 1} \left( {\Phi_{3} \left( {\tau ,y_{3} } \right)} \right). \hfill \\ \end{gathered} \right\}$$
(33)

We can also write:

$$\left. \begin{gathered} {}_{0}^{C} \wp_{t}^{\alpha } \left( {x_{1} \left( \tau \right)} \right) = \Theta_{1} \left( {\tau ,x_{1} } \right), \hfill \\ {}_{0}^{C} \wp_{t}^{\alpha } \left( {y_{1} \left( \tau \right)} \right) = \Theta_{2} \left( {\tau ,y_{1} } \right), \hfill \\ {}_{0}^{C} \wp_{t}^{\alpha } \left( {z_{1} \left( \tau \right)} \right) = \Theta_{3} \left( {\tau ,z_{1} } \right). \hfill \\ \end{gathered} \right\},$$
(34)

Now by replacing \({}_{0}^{RL} \wp_{\tau }^{\alpha }\) with \({}_{0}^{C} \wp_{\tau }^{\alpha }\) and applying the procedure given in Eq. (7), we obtain the numerical algorithm in the following form:

$$x_{1} \left( {\tau_{n + 1} } \right) = x_{1} \left( {\tau_{0} } \right) + \frac{1}{\Gamma (\alpha )}\sum\limits_{j = 0}^{n} {\left[ \begin{gathered} \frac{{h^{\alpha } \Theta_{1} \left( {\tau_{j} ,x_{1} \left( {\tau_{j} } \right)} \right)}}{{\alpha \left( {\alpha + 1} \right)}}\left\{ {\left( {n + 1 - j} \right)^{\alpha } \left( {n + 2 - r + \alpha } \right) - \left( {n - j} \right)^{\alpha } \left( {n + 2 - r + 2\alpha } \right)} \right\} \hfill \\ - \frac{{h^{\alpha } \Theta_{1} \left( {\tau_{j - 1} ,x_{1} \left( {\tau_{j - 1} } \right)} \right)}}{{\alpha \left( {\alpha + 1} \right)}}\left\{ {\left( {n + 1 - j} \right)^{\alpha + 1} - \left( {n - j} \right)^{\alpha } \left( {n + 2 - r + \alpha } \right)} \right\} \hfill \\ \end{gathered} \right]} ,$$
(35)
$$y_{1} \left( {\tau_{n + 1} } \right) = y_{1} \left( {\tau_{0} } \right) + \frac{1}{\Gamma (\alpha )}\sum\limits_{j = 0}^{n} {\left[ \begin{gathered} \frac{{h^{\alpha } \Theta_{2} \left( {\tau_{j} ,y_{1} \left( {\tau_{j} } \right)} \right)}}{{\alpha \left( {\alpha + 1} \right)}}\left\{ {\left( {n + 1 - j} \right)^{\alpha } \left( {n + 2 - r + \alpha } \right) - \left( {n - j} \right)^{\alpha } \left( {n + 2 - r + 2\alpha } \right)} \right\} \hfill \\ - \frac{{h^{\alpha } \Theta_{2} \left( {\tau_{j - 1} ,y_{1} \left( {\tau_{j - 1} } \right)} \right)}}{{\alpha \left( {\alpha + 1} \right)}}\left\{ {\left( {n + 1 - j} \right)^{\alpha + 1} - \left( {n - j} \right)^{\alpha } \left( {n + 2 - r + \alpha } \right)} \right\} \hfill \\ \end{gathered} \right]} ,$$
(36)
$$z_{1} \left( {\tau_{n + 1} } \right) = z_{1} \left( {\tau_{0} } \right) + \frac{1}{\Gamma (\alpha )}\sum\limits_{j = 0}^{n} {\left[ \begin{gathered} \frac{{h^{\alpha } \Theta_{3} \left( {\tau_{j} ,z_{1} \left( {\tau_{j} } \right)} \right)}}{{\alpha \left( {\alpha + 1} \right)}}\left\{ {\left( {n + 1 - j} \right)^{\alpha } \left( {n + 2 - r + \alpha } \right) - \left( {n - j} \right)^{\alpha } \left( {n + 2 - r + 2\alpha } \right)} \right\} \hfill \\ - \frac{{h^{\alpha } \Theta_{3} \left( {\tau_{j - 1} ,z_{1} \left( {\tau_{j - 1} } \right)} \right)}}{{\alpha \left( {\alpha + 1} \right)}}\left\{ {\left( {n + 1 - j} \right)^{\alpha + 1} - \left( {n - j} \right)^{\alpha } \left( {n + 2 - r + \alpha } \right)} \right\} \hfill \\ \end{gathered} \right]} .$$
(37)

Discussion and results

This section of the article contains graphical representations of the results obtained from the recent study. This study offers the dynamics of a newly designed circuit under the consideration of fractal-fractional derivative of power law kernel. The problem has been analized for both fractional order parameter \(\alpha\) and fractal dimension \(\beta\). Simulations are performed and results are computed using MATLAB software. For the initial values, we have considered \(x_{1} \left( 0 \right) = 5.4,\,\,y_{1} \left( 0 \right) = - 1.8\) and \(z_{1} \left( 0 \right) = 3.3\) while \(a = 0.1,\,b = 5\,\) and \(c = 0.3\).

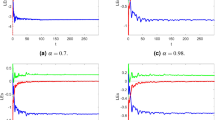
Using \(\alpha = \beta = 1\) and keeping the other variables constant, Figs. 1 and 2 illustrate the classical behavior of a chaotic attractor. The influence that the fractional parameter \(\alpha\) has on the chaotic attractor behavior is seen in Figs. 3, 4, 5, 6, 7, 8. As seen in Figs. 3 and 4, the dynamics converges to its static equilibrium when fractional parameter \(\alpha\) is reduced while in the classical/integer order, it always evolve around its equilibrium. Further, it can be noticed that the time period and amplitude of the oscillations reduces by reducing \(\alpha\). The impact \(\alpha\) on the dynamic of chaotic attractors conforms to the same configuration as that which is shown in Figs. 5, 6, 7, 8. From the figures depicting the effects of effect \(\alpha\) on chaotic attractors, perhaps the current fractal-fractional theory provides us with several solutions, rather than one as in classical/integer order. It provides us an alternative, and if we make the necessary adjustments, we may be able to get the best outcome possible by combining the results of our experiments with the theoretical data. Figures 9, 10, 11, 12, 13, 14 illustrates the effect that the fractal dimension \(\beta\) has on the dynamics of chaotic attractors. We made the observation that decreasing the value of the fractal dimension parameter \(\beta\) causes the chaotic attractor dynamics to persist for a longer period of time while the amplitude approximately remains the same. There are various 2D and 3D phase graphs produced in order to better understand the dynamical behavior of the considered chaotic system. For the purpose of making the differences between them more evident, we compare each figure to the classical order. We can observe the dynamics of the problem-limited cycles and periodic orbits that have been described based on the graphs that have been displayed so far.

Figure 1
figure 1

The classical case's chaotic attractor dynamics i.e., α = β = 1.

Full size image
Figure 2
figure 2

Classical systems' 2D and 3D phase portraits of the chaotic attractor dynamics case i.e., α = β = 1.

Full size image
Figure 3
figure 3

An analysis of the chaotic attractors for this case when α = 1 (line) and α = 0.95 (dash).

Full size image
Figure 4
figure 4

The case's chaotic attractor dynamics, shown in 2D and 3D phase portraits when α = 1 (line) and α = 0.95 (dash).

Full size image
Figure 5
figure 5

An analysis of the chaotic attractors for this case when α = 1 (line) and α = 0.90 (dash).

Full size image
Figure 6
figure 6

The case's chaotic attractor dynamics, shown in 2D and 3D phase portraits when α = 1 (line) and α = 0.90 (dash).

Full size image
Figure 7
figure 7

An analysis of the chaotic attractors for this case when α = 1 (line) and α = 0.85 (dash).

Full size image
Figure 8
figure 8

The case's chaotic attractor dynamics, shown in 2D and 3D phase portraits when α = 1 (line) and α = 0.85 (dash).

Full size image
Figure 9
figure 9

An analysis of the chaotic attractors for this case when β = 1 (line) and β = 0.95 (dash).

Full size image
Figure 10
figure 10

The case's chaotic attractor dynamics, shown in 2D and 3D phase portraits when β = 1 (line) and β = 0.95 (dash).

Full size image
Figure 11
figure 11

An analysis of the chaotic attractors for this case when β = 1 (line) and β = 0.90 (dash).

Full size image
Figure 12
figure 12

The case's chaotic attractor dynamics, shown in 2D and 3D phase portraits when β = 1 (line) and β = 0.90 (dash).

Full size image
Figure 13
figure 13

An analysis of the chaotic attractors for this case when β = 1 (line) and β = 0.85 (dash).

Full size image
Figure 14
figure 14

The case's chaotic attractor dynamics, shown in 2D and 3D phase portraits when β = 1 (line) and β = 0.85 (dash).

Full size image

Concluding remarks

This study has been carried out for the chaotic system based on circuit design presented by a three-dimensional chaotic system. The problem is modelled in the form of nonlinear integer order ODEs along with the initial conditions. In addition, theoretical analyses of the problem such as equilibria and dissipation have been calculated while the existence and uniqueness of the solutions have been proved. In order to generalize the classical model, we used a fractal-fractional differential operator of power law. To get the graphical solution, a numerical approach is also stated, after which it is implemented using the MATLAB software for simulations. Several graphs are used to illustrate the strange attractors that the chaotic system produces.

According to our observations, the chaotic system exhibits certain unusual behaviors as it fluctuates. Because of this, the outcomes of the current model can be significantly changed, and since fractional-order parameters and fractal dimensions are involved in the current study to make it more general. In addition, it is obvious from the figures shown above that a reduction in fractional parameter \(\alpha\) will result in decrease in amplitude as well as time period of oscillations while a decrease in fractal parameter \(\beta\) would result in increase in the periods of the trajectories. Modifying these parameters is most likely to produce results that are comparable to those obtained numerically with the experimental results. It is noteworthy to notice that, when \(\alpha = \beta = 1\), we may recover the integer order results from the modified fractal-fractional one.