Abstract
During foraging honeybees are always endothermic to stay ready for immediate flight and to promote fast exploitation of resources. This means high energetic costs. Since energy turnover of foragers may vary in a broad range, energetic estimations under field conditions have remained uncertain. We developed an advanced model, combining the benefits of mechanistic and correlative models, which enables estimation of the energy turnover of stationary foragers from measurements of body surface temperature, ambient air temperature and global radiation. A comprehensive dataset of simultaneously measured energy turnover (ranging from 4 to 85 mW) and body surface temperature (thorax surface temperature ranging from 33.3 to 45 °C) allowed the direct verification of model accuracy. The model variants enable estimation of the energy turnover of stationary honeybee foragers with high accuracy both in shade and in sunshine, with SD of residuals = 5.7 mW and R2 = 0.89. Its prediction accuracy is similar throughout the main range of environmental conditions foragers usually experience, covering any combination of ambient air temperature of 14–38 °C and global radiation of 3–1000 W m−2.
Similar content being viewed by others
Introduction
Honeybees are able to exploit nectar and pollen sources fast and efficiently by means of persistent endothermy throughout the foraging cycle (Fig. 1a;1,2,3,4,5,6,7,8). Keeping the body temperature high allows for immediate flight on their trips between flowers and increases suction speed 7,9.
Body temperature and heat exchange of foraging honeybees. (a) Infrared thermogram of honeybees (Apis mellifera carnica) foraging sucrose solution. Note heated thoraxes resulting from intense endothermy with activated flight muscles. Part of the heat has warmed the head and the abdomen. Ambient air temperature (Ta) = 13 °C. (b) Main paths of heat flow, inside the body and in and out of it. Circles symbolize spiracles (6 on thorax, and 12 on abdomen;56,57). M = metabolism, mainly of flight muscles plus standard metabolism of other tissues.
However, in the endothermic state heterothermic insects of the small size of honeybees have to cope with an enormous heat loss because of their unfavourable relation of surface to mass1,10. The challenge is high because environmental conditions like ambient air temperature and solar radiation may vary in a broad range during foraging (Fig. 2)7,8. In addition, variation of the quality and availability of food influence thermoregulation of foragers strongly both outside the colony3,4,11,12 and inside it13,14. Therefore, measurements of metabolic rate (and thus energy turnover) show a large variation in stationary foragers at artificial food sources15,16,17,18, in (free) flight19,20,21,22, and in bees flying from flower to flower23,24. Because of this strong dependence on environmental and experimental conditions (Figs. 2, 3a; Ref.22) the applicability of laboratory measurements for estimations of energy costs under field conditions seems quite uncertain. Inside the honeybee colony estimation of the heat production of endothermic bees is even more problematic. The contribution of individuals to heat production is not accessible by direct respiratory or heat production measurements, because the energy turnover may change by a factor of 5–100 due to changes in endothermy upon transfer of a bee to a respiration measurement chamber25.
Mean thorax surface temperature per stay at an artificial flower (Tthorax) in relation to ambient air temperature (Ta) and global radiation. Shade ≤ 100 W m-2, sunshine > 100 W m−2. Bees fed 1.5 M sucrose solution in unlimited flow (data from17), or 0.5 M sucrose in unlimited flow and limited flow of 15 µl min−1 (data from18). For simultaneously measured energy turnover see Fig. 3a and supplementary Fig. S2.
Energetics of honeybees foraging in shade (≤ 100 W m−2) or in sunshine (> 100 W m−2), from simultaneous measurements of CO2 production and body surface temperature (Tbody = mean of head, thorax and abdomen). (a) Energy turnover of sucrose gathering honeybees in dependence on body temperature excess (elevation of mean body temperature per stay above ambient air temperature: Tbody–Ta). For measured thorax temperatures see Fig. 2. (b) Heat conductance estimate from these data in dependence on ambient air temperature (Ta). Bees fed 1.5 M sucrose in unlimited flow (data from17), and 0.5 M sucrose solution in unlimited flow or limited flow of 15 µl min−1 (data from18).
Therefore, it would be a great advance to have the possibility to estimate the energy turnover of bees from measurements of body temperature and easily accessible environmental parameters like ambient air temperature (Ta) and solar radiation. Models of heat exchange allowing this may be of a mechanistic or a correlative nature. Mechanistic models of insect heat exchange (e.g.21,26,27,28) rely on detailed knowledge of physical and physiological parameters of heat exchange. Correlative models (e.g.29,30,31) use known relationships without detailed knowledge of all underlying mechanisms32.
In previous investigations we had gathered a comprehensive dataset of simultaneous measurements of body surface temperature and respiratory metabolism of stationary foragers under widely varying environmental conditions17,18, covering the greater part of the range of natural variation in ambient air temperature and global radiation honeybees usually experience outside their colony. These datasets provided a unique possibility to develop a model of heat exchange between honeybees and their environment and to prove its accuracy. However, in honeybees several parameters of the heat exchange process cannot be determined well enough experimentally. Total convection acting on a foraging bee, for example, is not accessible well enough under true field conditions. While it might be possible to measure wind and free thermal convection directly, the exact heat loss via respiratory convection seems not easily accessible. The absorption of solar radiation and the heat exchange via long-wave infrared radiation is usually modelled by describing the insect body by standard geometrical shapes (e.g.21,28; supplementary Fig. S1a). In honeybees, body hairs, wings and variation of absorptivity at visual wavelengths due to changes in body posture influence radiative and convective heat exchange considerably and make estimation uncertain (compare supplementary Fig. S3).
Therefore, we here present a mixed approach of honeybee heat exchange with the environment, combining the benefits of mechanistic and correlative models. Our model variants use detailed physical input wherever available but correlative weighting of parameters by coefficients determined iteratively. The simultaneous measurement of body surface temperature, metabolism and environmental parameters in our dataset allows exact verification of model accuracy.
Materials and methods
The basic model
In thermal steady state, total energy gain of an animal equals energy loss (e.g.33,34:
(for abbreviations used see Table 1, iteratively calculated coefficients are written in italics there and below). Energy ‘gain’ of a live animal consists of metabolic heat production (M) and radiation heat gain (Rgain). Energy loss makes up of convective (Ecv), evaporative (Eev), conductive (Ecd) and radiation heat loss (Rloss), Eq. (1) taking the form of
If metabolic heat production is to be determined from body temperature and environmental data, Eq. (2) can be rewritten as
Ecv can be estimated from the temperature difference between insect body (surface) temperature (mean of head, thorax and abdomen) and ambient air temperature (Tb–Ta; in °C), body surface area (Ab; in m2), and a convection coefficient (hb; in W m−2 °C−1):
Equation (3) then becomes
Conductive heat transfer (Ecd), taking place only from the distal leg tips in honeybees, was assumed to be very small in comparison to other parameters of heat exchange and therefore was neglected in further considerations.
To compensate for any uncertainties of radiative and evaporative heat transfer determination, coefficients rl, rg and elev were introduced:
Body surface areas of head, thorax and abdomen were calculated assuming spherical dimensions for the thorax (Ath), and an oblate or prolate rotational ellipsoid for the head (Ahd) and the abdomen (Aab), respectively35 (supplementary Fig. S1a).
Evaporative heat loss Eev was estimated as ~ 4 mW from measurements in flying bees at Ta below 35 °C21,22. We did not consider the changes of Eev with Ta these authors measured due to cooling efforts at high Ta, because our bees’ mouthparts had been wet from drinking at all environmental conditions.
Radiative heat loss at normal environmental temperatures (0–50 °C) takes place in the medium to long infrared range (maximum radiation at 10.61–8.97 µm wavelength, respectively). It can be calculated according to the Stefan/Boltzmann law as
where Tb is the body temperature in Kelvin, εb is the infrared emissivity of the honeybee cuticle (0.9712; compare also Ref.36,37,38), and σ is the Stefan/Boltzmann constant (5.669 × 10−8 W m−2 K−4; Table 1). Reabsorption of the bees’ own radiative heat emission reflected from the ground was neglected due to the high IR absorptivity of the black paint that had covered the measurement chamber (αpaint = 0.95; see Fig. 2 in Stabentheiner et al.39).
Radiative heat gain consists of infrared heat gain (RgIR) according to the Stefan/Boltzmann law, and of solar heat gain (RgSOL), mainly taking place in the visible and near infrared range (compare28,39):
In the experiments providing the dataset used for model development17,18 RgSOL had been measured directly with custom-manufactured miniature thermoelectric global radiation sensors (Ahlborn FLA613GS/Mini spezial39).
Infrared (RgIR) and solar (RgSOL) radiation components absorbed by the honeybee body were assumed to act on half of the body surface area only (Ab/2), according to
where subscript initials ‘d’, ‘r’ and ‘ge’ denominate ‘direct’, ‘reflected’ and ‘ground emitted’ infrared and solar radiation, respectively. Cuticular infrared absorptivity was calculated from emissivity according to αbIR = εb = 0.9712. Solar absorptivity in the visual and near infrared range (αbSOL) was estimated as ~ 0.825, from the value of 0.91 reported by Willmer & Unwin40 and 0.903 reported by Stupski & Schilder28, corrected forreduced absorptivity towards the edges of the curved body surfaces according to a cosine law (see suppl. Figs. S1a and S3).
Experiments on respiratory frequency (fresp) and metabolism
Convective heat loss of living animals is made up of external free convection (in stationary bees) or forced convection (e.g. by headwind and wing movement in flight or by wind), and internal convection due to respiratory gas exchange (Fig. 1b). In stationary, non-flying bees respiratory heat loss has to be assumed to make up the greater part, being a function of respiratory frequency. However, we had not been able to determine the respiratory frequency (fresp) from our thermographic recordings in the dataset used for model development17,18. An initial hypothesis was that fresp and thus respiratory heat loss might be a function of the bees’ energy turnover because energetically more active bees will need more oxygen.
To determine the correlation between respiratory frequency and energy turnover, therefore, we trained honeybees to forage sucrose solution (0.5 M or 1.5 M) from an artificial flower on an inverted white plastic laboratory cup closer with a ring of holes drilled in its base, which allowed the air pumps to suck fresh air from underneath the flower (see supplementary Fig. S1b)39. This way the air stream of 500 ml/min (regulated with Side Trak 840-L mass flow controllers, Sierra Instruments) washed away the air around the bee sucking at a 1 cm higher position. A differential setup with two identical flowers was used, one for measurement of the bees and another one for a reference air stream (parallel measurement mode39). Measurement chambers consisted of a glass laboratory funnel attached to a small plastic cylinder, the base of which was attached to an iron spacer ring to fit the chamber to the underlying artificial flower during measurements via pieces of hard disc magnets (suppl. Fig. S1b). The measurement chamber was operated from a distance (∼ 1.5 m) via a rod to prevent the operators from influencing the measurements with their exhaled air. O2 consumption was measured with an Oxzilla II oxygen measurement device (Sable Systems, Las Vegas, USA) recalibrated regularly against the outside air. Loss of O2 depleted air upon chamber opening was compensated for by calibrations described in Stabentheiner et al.39. Data storage and evaluation was done with ExpeData software (Sable Systems). Respiratory frequency was determined from simultaneously recorded video sequences (30 Hz; Canon Power Shot SX200 IS), evaluated with the VLC Media Player.
Visualisation of the honeybee tracheal system
The honeybee tracheal system, important for respiratory heat exchange via internal convection and evaporation (Fig. 1b), was visualised by means of a micro computer tomograph (µCT) (microCT 40, SCANCO Medical, Bruettisellen, Switzerland). A fresh honeybee was scanned with a resolution of 7 µm, showing abdominal and thoracic air sacs and tracheae.
Data evaluation and statistics
Our comprehensive dataset allowed for direct comparison of measured values of energy turnover with the values calculated from the measured body surface temperature, ambient air temperature and global radiation, for each visit of the bees to our feeding station. Experimental data evaluation and model calculation was done in Excel (Microsoft) and Origin (OriginLab) software. Accuracy of fit of model variants was compared by calculation of the standard deviation of residuals (SDres) and R2 adjusted for degrees of freedom (df).
The fit was optimized by iterative variation of coefficients according to the nonlinear least square Levenberg–Marquardt (L–M) algorithm, an “iterative procedure which combines the Gauss–Newton method and the steepest descent method”41. Optimum fit, as estimated by Chi2 minimization (residual sum of square divided by df), was assumed when a reduced Chi2 tolerance value of 1 × 10–9 was reached41.
Results
Body surface
Body surface area (without wings and legs), as calculated by equations of suppl. Fig. S1a35, amounted to Ab = 163.7 mm2, with Ahd = 30.80 mm2, Ath = 47.78 mm2, and Aab = 85.91 mm2 (for measured body dimensions see legend of suppl. Fig. S1a). Our calculation resembles the value of 169.1 mm2 reported by Roberts and Harrison21, which they calculated with different geometrical approximations for head and abdomen than in the present study.
Simple mixed model
Using Eq. (7) to calculate the energy turnover of stationary foragers did not provide acceptable results (hb = 12.14393 W m−2 °C−1, rl = 0.68114, rg = 0.30352, and elev = 1.82501). The SD of residuals (SDres) was only reduced to 15.3 mW (adjusted R2 = 0.24078, ANOVA), from a SD of 17.59 mW of the original data (Fig. 3a).
Advanced mixed model
Calculating (or using) a fixed convection coefficient hb during the fit procedure, despite the vast variation of environmental conditions (Ta = 14.8–37.5 °C, global radiation = 3.4–921 W m−2; means per stay at an artificial flower), was identified as a main factor hindering accurate prediction of metabolism from body temperature. hb is made up of external (free or forced) and internal (respiratory) convection, the latter being of much greater importance in endothermic honeybee foragers than in ectothermic insects. However, during the experiments providing the dataset for model development17,18 we had not been able to measure the exact amount of external convection acting on the bees in the measurement chamber, and we do not know of a method to determine internal convective heat transport via tracheal respiration accurately in freely ranging bees. Calculation of a heat conductance estimate in shade (energy turnover/Tb–Ta, in mW °C−1) from the dataset revealed considerable changes not only with Ta but also with experimental conditions (e.g. unlimited or limited sucrose flow) (Fig. 3b; see also Ref.17). Foraging in the sun changed relations additionally (Fig. 3b). It has to be expected that internal convection via the honeybee tracheal system with its large air sacs (Fig. 4) makes up a considerable amount of convective heat loss because respiratory frequency had been found to amount to several Hz in foragers (Fig. 5; Ref.7) in comparison to only about 10–50 mHz in resting individuals42. Internal convection due to respiratory ventilation has to be expected to be quite small in the head but high in the thorax and the abdomen (Fig. 1b). Therefore, to improve accuracy, the convective heat exchange term (Ecv = hb × Ab(Tb–Ta)) had to be calculated independently for the three body parts, according to
Micro computer tomogram (µCT) of a honeybee, showing abdominal and thoracic air sacs and tracheae of the tracheal system for respiratory heat exchange via internal convection and evaporation (microCT 40, SCANCO Medical, Bruettisellen, Switzerland). Please note that abdominal length is usually up to ~ 60% longer in living animals. See supplementary Video S1 for a slice-wise journey through the whole bee.
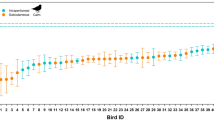
Since most of the heat produced by honeybee foragers originates from the thorax (Fig. 1a,b), introduction of respiratory heat loss into the model might be improved by introducing hb as a function of respiratory frequency (fresp), similar as was done by Henwood34 for changes of external convection due to the effect of wind. Our initial suggestion that fresp might be a direct function of metabolism, because one would expect more heating activity to require a better oxygen supply of the thoracic flight muscles, was not supported by our measurements (Fig. 5a). There was no sign of a correlation between these variables but fresp changed clearly with ambient air temperature (Fig. 5b)! From this finding that fresp = f(Ta) we concluded that hb = f(Ta). A possibility to introduce the dependence of convective heat loss on Ta into Eq. (12) is to introduce the convection coefficients of head, thorax and abdomen (hca, hth, hab) as a function of Ta, making the convective heat exchange term take the form of
the coefficients ahxx and bhxx being determined by numerical (iterative) calculation. Calculated coefficients can be found in Table 2a. This way, the accuracy of the model could be significantly improved, with SDres = 5.78 mW (Fig. 6b) and the residual standard error of the mean (SEMres) being as small as 0.196 mW. This model variant explains ~ 89% of total variability (adjusted R2 = 0.89085; N = 872, df = 863; ANOVA).
Energetics and model results of sucrose gathering honeybees foraging in shade (≤ 100 W m−2) or in sunshine (> 100 W m−2), in dependence on ambient air temperature (Ta). (a) Energy turnover; original data of bees fed 1.5 M sucrose solution in unlimited flow (from17), and 0.5 M sucrose in unlimited flow or limited flow of 15 µl min−1 (from18); N = 872 visits to artificial flowers; SD = 17.59 mW. (b) Residuals of model calculation according to the use of Eq. (13) in Eq. (6), see Table 2a for model coefficients; green bar = ± 1 SDres, light yellow bar = ± 2 SDres, R2 = adjusted for degrees of freedom; residual standard error of mean (SEMres) = 0.196 mW.
However, a subsequent analysis about the effect of individual predictors on the dependent variable (evaluating their relative “importance”), via the estimated standard errors of the regression coefficients and the associated t-test probabilities43,44, revealed the coefficient bhab to contribute quite insignificantly to the regression (P >|t|= 0.8341; Table 2; compare41). This may be due to the fact that hab calculated according to hab = (ahab + bhab × Ta) from Eq. (13) changed only marginally with Ta (see suppl. Fig. S4). Simplifying Eq. (13) to
led to a quite similar prediction accuracy (SDres = 5.78 mW; adj. R2 = 0.89097). For coefficients see Table 2b. All attempts to eliminate further coefficients or predictor variables from the model led to a decreased accuracy.
Advanced three-compartment model
Convection, however, does not only occur between the bee body and the adjacent air. Forced convection by haemolymph circulation between body parts also transfers considerable amounts of heat, not only from the thorax (the main heat source) to head and abdomen but also back from the cooler body parts to the thorax (Fig. 1b). A “three-compartment model” approach45, replacing the temperature excess of the body parts head and abdomen to ambient air temperature (Thd–Ta and Tab–Ta) by the difference between the thorax and these body parts (Tth–Thd and Tth–Tab), respectively, with
led to the same accuracy, with SDres = 5.78 mW and adj. R2 = 0.89085. For coefficients see Table 3a.
Again, simplifying Eq. (15) to
resulted in a similar accuracy, with SDres = 5.78 mW and adj. R2 = 0.89097. For coefficients see Table 3b.
Discussion
In ecology, animal energetic modelling may be mechanistic, building solely on physical and physiological input, or correlative, using known relationships without detailed knowledge of all underlying mechanisms and the exact magnitude of factors32. The mechanistic approach requires more investment of time and resources to determine the underlying causal processes in detail28,32. The alternative correlative approach usually saves resources and time and often may provide faster and more accurate results32. Mechanistic models are thought to be better transferable to different environmental conditions than correlative ones. The accuracy of such models, however, depends strongly on the exact knowledge of heat exchange parameters, which may change with foraging condition in honeybees (Fig. 3b; compare17,18,22). We therefore take a stand for mixed models, based on sufficient experimental datasets and proper consideration of physics and physiology but correlative weighting of parameters where necessary.
Heat exchange, for example, does not only occur between the insect body and the environment but also between body parts by two mechanisms: forced convection via haemolymph circulation and respiration (Fig. 1). Abdominal volume, and thus surface for radiative and convective heat exchange, usually changes during foraging because a bee can load nectar of nearly the own weight during a foraging trip46, and body postures relative to the sun may change (compare suppl. Fig. S3). Physiological needs and effects of environmental variation on body function have to be considered and verified by experiments 8, because physiological regulatory mechanisms are complex and hardly predictable from physical assumptions. The interrelation between physical mechanisms and physiological regulation is often not clearly accessible. The surprising finding that respiratory frequency (fresp), as a correlative of (internal) respiratory convection, correlated with ambient air temperature (Ta) but not with oxygen consumption (Fig. 5) underpins the need of an experimental foundation for theoretical considerations. We suggest this change with Ta to originate from the change of the function of the abdominal muscles for tracheal ventilation with Ta (compare47,48), because abdominal temperature follows Ta more closely than the temperature of other body parts (e.g.7,18).
A main factor influencing heat loss of endothermic animals is the difference of body temperature to ambience (Tb–Ta; e.g.24,26,27,34,45,49). In honeybees heating their thorax up in flight preparation, a rather straight correlation between oxygen turnover and Tthorax–Ta has been reported50. In thermoregulating bees in thermal steady state, however, this relationship is not a simple one (compare Fig. 6a). The relation changes strongly with ambient temperature, radiation and foraging condition, and shows a huge variability (Fig. 3a, suppl. Fig. S2; compare17,18). Figure 3b shows that in stationary endothermic honeybees the simple calculation of a heat conductance estimate (mW °C−1) delivers considerably differing results for bees drinking sucrose solution in unlimited and limited flow. Foraging in sunshine provides even more variation because foragers can use solar heat gain to save energy or to speed up foraging17,18. Therefore, since honeybees must not be treated as simple physical objects but have many possibilities of physiological and behavioural reaction to environmental variation (Fig. 1;6,8,9,17,18,21,22), the accuracy of purely mechanistic models of heat exchange will remain limited. The solution are mixed models as presented here, integrating correlative and mechanistic approaches32. Our model variants use physical input of relevant heat exchange parameters but a correlative weighting of this input via the calculated coefficients. The correlative (iterative) determination of multiple coefficients, however, implies that they are not determined completely independent from each other when the underlying algorithm is searching for the optimal fit (Tables 2, 3)44. Therefore, always the full coefficient set is necessary for best predictions. Since honeybees own a variety of physiological and behavioural mechanisms to regulate heat flow inside the body and heat exchange with the environment (Fig. 1b), heat exchange coefficients calculated correlatively may differ from mere static physical calculations, and even may take ‘unexpected’ values. The negative values calculated for head (hhd) and abdomen (hab) as drawn in supplementary Fig. S4 (calculated according to Table 2a) may be interpreted in a way that these body parts on average receive more heat than they emit to the environment, from the thorax via haemolymph circulation and tracheal ventilation, and from the sun (compare Fig. 1). A different coefficient set will have to be determined for bees in free flight, because the relation between external convection by headwind and wing movement, and internal convection by respiration and possibly blood flow, will change.
We tried to build our model variants as detailed as necessary for high prediction accuracy but keep them as simple as possible to achieve a high practical usability. The great advantage of our mixed approach is its high and proven accuracy, which is quite similar throughout most of the natural variation of the environmental factors ambient air temperature and global radiation (Fig. 6b). The model variants allow estimation of energetic costs from measurements of body (surface) temperature of bees foraging for example on water sources and honeydew droplets, and on many types of flowers where bees remain stationary for some time. This kind of flowers includes composite plants like dandelion (Taraxacum sp.), sunflower (Helianthus sp.), thistle (Cirsium sp.), and some stonecrops (Sedum sp.), etc. For bees foraging in shade with more frequent and longer flights between flowers, for example on plants like apricot (Prunus sp.) or raspberry (Rubus sp.), the laboratory measurements of bees hovering or flying in a measurement chamber21,22 may provide a preliminary approximation of energy turnover. However, to provide best results, these measurements have to be repeated under outdoor conditions (see22) which include measurement of ambient air temperature and global (solar) radiation in addition to respiration and body temperature. Tracking of honeybee flights in flower patches (e.g.51,52,53,54,55) will help to better quantize the relative amounts of stationary thermoregulation and flight. For longer lasting free flights out to a flower patch and back, outdoor measurements (e.g.22) will allow a preliminary estimation of energy costs in shade if flight time is known. Again, for best results simultaneous measurement of respiration and body temperature in combination with relevant environmental parameters is necessary to deliver best results for energetic modelling of honeybee foraging.
Conclusion
With a mixed model approach of honeybee heat exchange, integrating the benefits of mechanistic and correlative models, we were able to predict the energy turnover of stationary honeybee foragers from measurements of body (surface) temperature and basic environmental parameters. The model provides high and proven accuracy throughout the main ranges of environmental variation bees usually experience during foraging, of ambient air temperature ~ 14–38 °C, and of global radiation ~ 3–1000 W m−2.
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Esch, H. Über die Körpertemperaturen und den Wärmehaushalt von Apis mellifica. Z. Vergl. Physiol. 43, 305–335 (1960).
Heinrich, B. Thermoregulation of African and European honeybees during foraging, attack, and hive exits and returns. J. Exp. Biol. 80, 217–229 (1979).
Schmaranzer, S. & Stabentheiner, A. Variability of the thermal behaviour of honeybees on a feeding place. J. Comp. Physiol. B 158, 135–141 (1988).
Waddington, K. D. Foraging profits and thoracic temperature of honey bees (Apis mellifera). J. Comp. Physiol. B 160, 325–329 (1990).
Schmaranzer, S. Thermoregulation of water collecting honey bees (Apis mellifera). J. Insect Physiol. 46, 1187–1194 (2000).
Kovac, H. & Schmaranzer, S. Thermoregulation of honeybees (Apis mellifera) foraging in spring and summer at different plants. J. Insect Physiol. 42, 1071–1076 (1996).
Kovac, H., Stabentheiner, A. & Schmaranzer, S. Thermoregulation of water foraging honeybees—balancing of endothermic activity with radiative heat gain and functional requirements. J. Insect Physiol. 56, 1834–1845 (2010).
Kovac, H. & Stabentheiner, A. Thermoregulation of foraging honeybees on flowering plants. Ecol. Entomol. 36, 686–699 (2011).
Kovac, H., Käfer, H. & Stabentheiner, A. The energetics and thermoregulation of water collecting honeybees. J. Comp. Physiol. A 204, 783–879 (2018).
Heinrich, B. The Hot-Blooded Insects: Strategies and Mechanisms of Thermoregulation (Springer, 1993).
Dyer, F. C. & Seeley, T. D. Interspecific comparisons of endothermy in honeybees (Apis): deviations from the expected size-related patterns. J. Exp. Biol. 127, 1–26 (1987).
Stabentheiner, A. & Schmaranzer, S. Thermographic determination of body temperatures in honey bees and hornets: calibration and applications. Thermology 2, 563–572 (1987).
Stabentheiner, A., Kovac, H. & Hagmüller, K. Thermal behavior of round and wagtail dancing honeybees. J. Comp. Physiol. B 165, 433–444 (1995).
Stabentheiner, A. Thermoregulation of dancing bees: thoracic temperature of pollen and nectar foragers in relation to profitability of foraging and colony need. J. Insect Physiol. 47, 385–392 (2001).
Balderrama, N. M., Almeida, L. O. & Núñez, J. A. Metabolic rate during foraging in the honey bee. J. Comp. Physiol. B 162, 440–447 (1992).
Moffatt, L. & Núñez, J. A. Oxygen consumption in the foraging honeybee depends on the reward rate at the food source. J. Comp. Physiol. B 167, 36–42 (1997).
Stabentheiner, A. & Kovac, H. Energetic optimisation of foraging honeybees: flexible change of strategies in response to environmental challenges. PLoS ONE 9, e105432 (2014).
Stabentheiner, A. & Kovac, H. Honeybee economics: optimisation of foraging in a variable world. Sci. Rep. 6, 28339 (2016).
Wolf, Th. J., Schmid-Hempel, P., Ellington, C. P. & Stevenson, R. D. Physiological correlates of foraging efforts in honey-bees: Oxygen consumption and nectar load. Funct. Ecol. 3, 417–424 (1989).
Harrison, J. F., Fewell, J. H., Roberts, S. P. & Hall, H. G. Achievement of thermal stability by varying metabolic heat production in flying honeybees. Science 274, 88–90 (1996).
Roberts, S. P. & Harrison, J. F. Mechanisms of thermal stability during flight in the honeybee, Apis mellifera. J. Exp. Biol. 202, 1523–1533 (1999).
Woods, W. A. Jr., Heinrich, B. & Stevenson, R. D. Honeybee flight metabolic rate: does it depend upon air temperature?. J. Exp. Biol. 208, 1161–1173 (2005).
Moffatt, L. Changes in the metabolic rate of the foraging honeybee: effect of the carried weight or of the reward rate?. J. Comp. Physiol. A 186, 299–306 (2000).
Moffatt, L. Metabolic rate and thermal stability during honeybee foraging at different reward rates. J. Exp. Biol. 204, 759–766 (2001).
Stabentheiner, A., Vollmann, J., Kovac, H. & Crailsheim, K. Oxygen consumption and body temperature of active and resting honeybees. J. Insect Physiol. 49, 881–889 (2003).
Casey, T. M. Biophysical ecology and heat exchange in insects. Am. Zool. 32, 225–237 (1992).
Lactin, D. J. & Johnson, D. L. Convective heat loss and change in body temperature of grasshopper and locust nymphs: relative importance of wind speed, insect size and insect orientation. J. Therm. Biol. 23, 5–13 (1998).
Stupski, S. D. & Schilder, R. J. Operative temperature analysis of the honey bee Apis mellifera. J. Exp. Biol. 224, jeb231134 (2021).
Varjú, D. & Núñez, J. A. Energy balance versus information exchange in foraging honeybees. J. Comp. Physiol. A 172, 257–261 (1993).
Stabentheiner, A. et al. Effect of climate on strategies of nest and body temperature regulation in paper wasps, Polistes biglumis and Polistes gallicus. Sci. Rep. 12, 3372 (2022).
Kovac, H., Käfer, H., Petrocelli, I., Amstrup, A. B. & Stabentheiner, A. Energetics of paper wasps (Polistes sp.) from differing climates during the breeding season. Insects 13, 800 (2022).
Kearney, M. & Porter, W. Mechanistic niche modelling: combining physiological and spatial data to predict species’ ranges. Ecol. Lett. 12, 334–350 (2009).
Porter, W. P. & Gates, D. M. Thermodynamic equilibria of animals with environment. Ecol. Monogr. 39, 227–244 (1969).
Henwood, K. A field-tested thermoregulation model for two diurnal Namib desert tenebrionid beetles. Ecology 56, 1329–1342 (1975).
Samietz, J., Salser, M. A. & Dingle, H. Altitudinal variation in behavioural thermoregulation: local adaptation vs. plasticity in California grasshoppers. J. Evol. Biol. 18, 1087–1096 (2005).
Kovac, H. & Stabentheiner, A. Effect of food quality on the body temperature of wasps (Paravespula vulgaris). J. Insect Physiol. 45, 183–190 (1999).
Gallego, B., Verdú, J. R., Carrascal, L. M. & Lobo, J. M. A protocol for analysing thermal stress in insects using infrared thermography. J. Therm. Biol. 56, 113–121 (2016).
Verdú, J. R., Cortez, V., Oliva, D. & Giménez-Gómez, V. Thermoregulatory syndromes of two sympatric dung beetles with low energy costs. J. Insect Physiol. 118, 103945 (2019).
Stabentheiner, A., Kovac, H., Hetz, S. K., Käfer, H. & Stabentheiner, G. Assessing honeybee and wasp thermoregulation and energetics—New insights by combination of flow through respirometry with infrared thermography. Thermochim. Acta 534, 77–86 (2012).
Willmer, P. G. & Unwin, D. M. Field analyses of insect heat budgets: reflectance, size and heating rates. Oecologia 50, 250–255 (1981).
Origin Help 2022—15.3.3 Theory of Nonlinear Curve Fitting. https://www.originlab.com/doc/en/Origin-Help/NLFit-Theory. Accessed 29 Sept 2022, 11:00
Kovac, H., Stabentheiner, A., Hetz, S. K., Petz, M. & Crailsheim, K. Respiration of resting honeybees. J. Insect Physiol. 53, 1250–1261 (2007).
Mason, C. D. & Perreault, W. D. Jr. Collinearity, power, and interpretation of multiple regression analysis. J. Marketing Res. 28, 268–280 (1991).
Graham, M. H. Confronting multicollinearity in ecological multiple regression. Ecology 84, 2809–2815 (2003).
Stavenga, D. G., Schwering, P. B. W. & Tinbergen, J. A three-compartment model describing temperature changes in tethered flying blowflies. J. Exp. Biol. 185, 325–333 (1993).
von Frisch, K. Tanzsprache und Orientierung der Bienen (Springer, 1965).
Coelho, J. R. The effect of thorax temperature on force production during tethered flight in the honeybee (Apis mellifera) drones, workers and queens. Physiol. Zool. 64, 823–835 (1991).
Glass, J. R. & Harrison, J. F. The thermal performance curve for aerobic metabolism of a flying endotherm. Proc. R. Soc. B 289, 20220298 (2022).
Tsuji, J. S., Kingsolver, J. G. & Watt, W. B. Thermal physiological ecology of Colias butterflies in flight. Oecologia 69, 161–170 (1986).
Goller, F. & Esch, H. Oxygen consumption and flight muscle activity during heating in workers and drones of Apis mellifera. J. Comp. Physiol. B 161, 61–67 (1991).
Waddington, K. D. & Holden, L. D. Optimal foraging: on flower selection by bees. Am. Nat. 114, 179–196 (1979).
Schmid-Hempel, P. & Schmid-Hempel, R. Efficient nectar-collecting by honeybees I. Economic models. J. Anim. Ecol. 56, 209–218 (1987).
Schmid-Hempel, P. & Schmid-Hempel, R. Efficient nectar-collecting by honeybees II. Response to factors determining nectar availability. J. Anim. Ecol. 56, 219–227 (1987).
Ratnayake, M. N., Dyer, A. G. & Dorin, A. Tracking individual honeybees among wildflower clusters with computer vision-facilitated pollinator monitoring. PLoS ONE 16, e0239504 (2021).
Cassano, J. & Naug, D. Metabolic rate shapes differences in foraging efficiency among honeybee foragers. Behav. Ecol. 33, 1188–1195 (2022).
Bailey, L. The respiratory currents in the tracheal system of the honey-bee. J. Exp. Biol. 31, 589–593 (1954).
Snodgrass, R. E. Anatomy of the honeybee (Comstock, 1956).
Acknowledgements
The research was funded by the Austrian Science Fund (FWF): P16584-B06, P20802-B16, P25042-B16 and P35461-B.
Author information
Authors and Affiliations
Contributions
A.S. and H.K. conceived, designed and performed the experiments and the model design and contributed reagents/materials/analysis tools, A.S. analysed the data, A.S. and H.K. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Supplementary Video 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stabentheiner, A., Kovac, H. A mixed model of heat exchange in stationary honeybee foragers. Sci Rep 13, 4655 (2023). https://doi.org/10.1038/s41598-023-31320-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-023-31320-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.