Abstract
We examine the effect of isovalent substitutions and co-doping on the ionic dielectric constant of paraelectric titanates (perovskite, Ruddlesden-Popper phases, and rutile) using density functional perturbation theory. Substitutions increase the ionic dielectric constant of the prototype structures, and new dynamically stable structures with εion ~ 102–104 are reported and analyzed. The boosting of ionic permittivity is attributed to local defect-induced strain, and maximum Ti–O bond length is proposed as a descriptor. The Ti–O phonon mode that is responsible for the large dielectric constant can be tuned by a local strain and symmetry lowering from substitutions. Our findings help explain the recently observed colossal permittivity in co-doped rutile, attributing its intrinsic permittivity boosting solely to the lattice polarization mechanism, without the need to invoke other mechanisms. Finally, we identify new perovskite- and rutile-based systems that can potentially display colossal permittivity.
Similar content being viewed by others
Introduction
Achieving materials with a very large (colossal) dielectric permittivity (CP) is crucial for various technological applications, including miniaturization of on-chip capacitive elements in transistors, high density memory, sensors, as well as high power density energy storage1. Due to their temperature and electric field stability, paraelectric materials are preferred for CP over ferroelectrics whose dielectric constant is high but also unstable near the phase transition temperature. With recent experimental reports on colossal permittivity in paraelectric TiO2 rutile via co-doping2,3, microscopic mechanisms for permittivity boosting need to be well understood. The apparent CP due to polarization of charge depletion layers at contacts, grain boundaries, interfaces, and other spatial heterogeneities4,5 (the so-called Maxwell–Wagner effect), is classified as “extrinsic”. Other extrinsic mechanisms include thermally activated conductivity by carrier hopping. A notable example is CaCu3Ti4O12, having a colossal permittivity close to 105 by the Maxwell–Wagner effect4,6,7,8. On the other hand, possible bulk mechanisms including ionic polarization, metal–insulator transition, and charge density wave formation8 can be classified into “intrinsic”, i.e. bulk mechanisms that are active at all temperatures. Of these the ionic polarization is of greatest practical interest, as other mechanisms incur high dielectric losses, limiting applications. Since the early reports of large, temperature-dependent permittivity in insulating tetragonal YBa2Cu3O6+x9,10, the overlap of intrinsic and extrinsic processes has complicated pinpointing the microscopic origins of the apparent CP. In co-doped rutile, a thermally activated process, most likely the transport of hopping carriers, was found to be responsible for the largest part of the apparent colossal permittivity3. At the same time, a nonactivated, intrinsic mechanism of permittivity boosting coexists in Nb + In co-doped rutile. The mechanism does not switch off at low temperatures; in fact, the enhanced permittivity increases with decreasing temperature3,11. The temperature trend follows that of pure rutile, suggesting a common microscopic origin. While theory accounts well for the observed dielectric constant of pure rutile, and attributes it largely to the ionic mechanism, no theoretical explanation exists for permittivity boosting in co-doped rutile. Originally, the “electron-pinned defect-dipoles” mechanism has been proposed in In + Nb co-doped TiO2 rutile2, suggesting the electronic nature of the large response. Further studies of In + Ta and Al, Ga, In + Nb co-doped TiO212,13 also attributed the observed colossal permittivity to the electronic mechanism. On the other hand, the studies of Nb + In co-doped TiO2 single crystals at sufficiently low temperature where thermally excited carriers are frozen suggested that the enhancement of the permittivity should stem from intrinsic effects3,11.
Here we show that the ionic mechanism can indeed account for boosting the permittivity in co-doped rutile and other substituted metal oxides. To this end, we perform a computational study of the ionic part of the dielectric permittivity of co-doped and substituted rutile and other Ti-containing dielectric oxides. We focus on substitutions in stable paraelectric prototypes, such as rutile TiO2, perovskite CaTiO3, and Ruddlesden–Popper Sr2TiO4 and and Sr3Ti2O7, modified via co-doping or isovalent replacement. From the analysis of the results, the permittivity increase in these materials is attributed to impurity-induced local strain, which enhances the dielectric response by softening the Ti–O phonon mode. We find that the frequency of the mode dominating the dielectric response can be changed over a wide range by substitutions, offering a possibility to precisely engineer the ionic dielectric constant.
Results and discussion
We examine the effects of isovalent substitutions and co-doping for titanates on phonons, Born effective charges, and ionic part of the dielectric constant. The electronic part of the dielectric constant is typically ~ 1–10 across most insulators and was not considered here in detail. The prototypes for substitution include mineral perovskite CaTiO3 with Pnma structure, rutile TiO2, as well as Ruddlesden-Popper phases Sr2TiO4 and Sr3Ti2O7. Ca, Sr → Ba, Pb, Sr, Ca substitutions in perovskites, as well as III–V (Al, Ga, In, Sc, Y, La–V, Nb, Ta) and II-VI (Mg, Ca, Sr, Ba–Cr, Mo, W) co-doping in rutile are performed. A more detailed description of the parent compounds and substitutions is given in the Supplementary Information. A total of 150 rutile and 1178 perovskite and Ruddlesden-Popper structures were calculated. The goal is to analyze the structures where substitutions increase εion and identify relevant phonon modes. Among dynamically stable titanates (ν2 > 0), we found the maximum Ti–O bond length, max(dTi-O), reflecting maximum local strain, to be a good descriptor of the highest achievable ionic dielectric constant. The correlation between εion and max(dTi-O) is rationalized in terms of the softening of the phonon mode that corresponds to the Ti–O bond stretching. The descriptor was considered by analogy with Goldschmidt factor14, which is used as a descriptor for structural stability of perovskites. As high ionic dielectric constant is dominated by the Ti–O mode, lowering its frequency significantly increases the dielectric response.
The ionic part of the dielectric tensor εion αβ is calculated as a sum over the gamma point phonon modes s according to15,16
Here, e is an elementary charge, M0 is a convenient mass reference, typically taken to be 1 amu16, V a unit cell volume, \({\bar{Z}^*}_{s \alpha }={\sum }_{\kappa \beta }{Z^*}_{\kappa ,\alpha \beta }{\left({M}_{0}/{M}_{\kappa }\right)}^{1/2}{\xi }_{s ,\kappa \beta }\) is the αth Cartesian component of the unnormalized effective charge vector for phonon mode s, and νs is mode frequency. ξs,κβ are the eigenvectors of the dynamical matrix, normalized according to Σκβξs,κβ ξs’,κβ = δss’, and Z*κ,αβ are the atomic Born effective charges, describing the proportionality15,17 between forces on atoms the and macroscopic electric field as \({eZ^*}_{\kappa ,\alpha \beta }=\partial {F}_{\kappa ,\beta }/\partial {\mathcal{E}}_{\alpha }\). Here, Fκ,β is the βth component of the force acting on the κth atom, and \({\mathcal{E}}_{\alpha }\) is the αth component of the macroscopic electric field. As the mixed second derivatives of the total energy, Born effective charges can also be expressed as the derivatives of the components of the polarization vector \({\mathcal{P}}_{\alpha }\) with respect to the atomic displacements τκ,β as: \({eZ^*}_{\kappa ,\alpha \beta }=V\partial {\mathcal{P}}_{\alpha }/\partial {\tau }_{\kappa ,\beta }\). By analyzing the contributions to the ionic dielectric constant from the sum-over-modes Eq. (1), one can gain insights into the mechanisms of the dielectric constant boosting. Note that only modes with nonzero effective charges contribute to the static tensor Eq. (1). In order for the component of the mode effective charge \(\bar{Z}^*\) to be large in any given direction, both the atomic Born effective charges Z* and dynamical matrix eigenvector ξ need to have large components in that direction for the same atom.
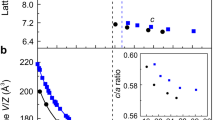
Figure 1a shows the dielectric constants in substituted/co-doped oxides as a function of max(dTi-O), with a visible peak around max(dTi-O) ≃ 2.02 Å. The average ionic dielectric constants of co-doped rutile TiO2 as a function of max(dTi-O) is also shown in Fig. S1. Other geometric descriptors, such as the cationic radius of co-dopants, do not provide a good correlation with <εion>, as seen from Figs. S5 and S6. The value of max(dTi–O) near the peak of εion is higher than the typical bond lengths in titanates with moderate dielectric constants (e.g., in rutile, with the calculated <εion> = 140, max(dTi–O) = 1.98 Å), raising the possibility of mode softening by local strain from substitutions. The soft ferroelectric Ti–O mode has been studied extensively in titanates18,19, and its sensitivity to external perturbations such as volume changes or degree of Ti 3d–O 2p hybridization has been well recognized. In rutile, volume increase drives the Ti–O A2u mode softening20, with frequency becoming imaginary and structure developing instability and possibly becoming ferroelectric at a certain extensive strain. The instability is manifested across different titanates21, and stabilized by anharmonic effects22. In Fig. 1b, we show the increase of <εion> with max(dTi–O) in Ti rutile under uniform strain.The dielectric constant has a pole where the A2u mode becomes unstable with its frequency becoming zero. The shaded area near the pole corresponds to the range of the maximum dielectric constants in Fig. 1a. It is seen that the maximum εion in substituted/co-doped oxides is reached in the same range of max(dTi–O) where the softening of Ti–O mode occurs in rutile. By examining the microscopic origin of the large response, it is indeed confirmed that the same soft Ti–O mode is responsible for the large dielectric constant in these oxides. Note that we do not find similar mode softening in Si- or Sn-based rutile structures, as seen from Figs. S2 and S3, where the dependencies of the dielectric constant on strain in TiO2, SiO2, and SnO2 rutile structures are compared.
(a) Ionic part of the dielectric constant, εion, as a function of max(dTi–O), the maximum length of the Ti–O bond in substituted/co-doped titanates. Different colors correspond to different prototype structures; (b) <εion> vs. max(dTi–O) in rutile under uniform strain, showing a pole at the ferroelectric transition when the frequency of the A2u mode becomes imaginary. The shaded area corresponds to the range of the maximum dielectric constants in (a); the vertical dashed line shows max(dTi–O) at equilibrium lattice constant.
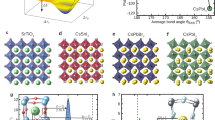
As an illustration, consider Ba2Sr2Ti4O12, obtained from the orthorhombic CaTiO3 by Ca → Ba, Sr substitutions, Fig. 2a and b. The structure has alternating planes of Ba and Sr normal to the z axis and is dynamically stable. It has an anisotropic ionic dielectric tensor with <εion> = 3373, εion zz = 9015, dominated by the lowest optical mode at ν4 = 0.521 THz, contributing 99.9% of εion zz. This is unlike CaTiO3, where many modes contribute to εion, as seen from the summary given in Table S1. In Ba2Sr2Ti4O12, max(dTi–O) = 2.01 Å, similar to that of the dynamically unstable cubic BaTiO3, but unlike that structure, shorter Ti–O bonds are also present. Apparently, the ferroelectric Ti–O mode of BaTiO3 is stabilized by insertion of Sr planes, preventing the formation of unstable Ti–O chains. This effect can also be viewed as the softening of the infrared-active modes of CaTiO3 by Ca → Ba and Ca → Sr substitutions. Just like the rutile, the infrared-active modes of CaTiO3 are softened by tension23. Projecting this low energy mode onto the modes of cubic BaTiO3 shows that it is mostly made up of the ferroelectric Ti–O mode of BaTiO3, with a small contribution from the displacement of Ba against the Ti–O cage. Similarly, a large εion zz = 1228 is achieved in a Ba2Ca2Ti4O12(α) structure with alternating Ba and Ca planes, Fig. 2c. Note that the frequencies of the dominant modes are similar in the Ba2Sr2Ti4O12 and Ba2Ca2Ti4O12(α) structures, and the larger εion zz in Ba2Sr2Ti4O12 is due to its larger \({{\bar{Z}^*}_{4z}}\)= 3.72, compared to \({{\bar{Z}^*}_{4z}}\)= 1.33 in Ba2Ca2Ti4O12(α) in Fig. 2c. The dominant mode frequency is higher in another, Ba2Ca2Ti4O12(β), structure shown in Fig. 2d, ν5 = 2.02 THz, with \({{\bar{Z}^*}_{5z}}\)= 3.52, giving εion zz = 568 for that structure, as compared to ν4 = 0.53 THz, \({{\bar{Z}^*}_{4z}}\)= 1.33 for the Ba2Ca2Ti4O12(α) in Fig. 2c. Thus, the frequency and effective charge of the dominant mode is sensitive not only to composition, but also to the atomic arrangement on the lattice at a fixed composition. By comparing the eigen displacements of the dominant modes ν4 and ν5 for the structures in Fig. 2c and d, respectively, the former has a significant motion of Ca and Ba planes against each other in the z direction, which is prevented in the latter by staggering Ca and Ba as in Fig. 2d. This staggered arrangement leads to dominant mode hardening from 0.53 to 2.02 THz.
Phonon mode frequencies and their contributions to the sum over modes expression Eq. (1) for the ionic dielectric constant in substituted and co-doped titanates with a high εion zz as well as the reference perovskite and rutile structures. Positions of Ca, Sr, Ba atoms and Ti, In, Nb in the unit cell are shown for perovskites and rutile, respectively, and O atoms are omitted. Dark blue—Ca, orange—Sr, green—Ba, blue—Ti, dark green—Nb, purple—In.
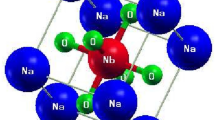
We find this mechanism of permittivity enhancement through softening/mixing Ti–O modes to act in other substituted titanates. We obtain εion zz = 252 in BaCa3Ti4O12 (not shown), a modest enhancement over the prototype CaTiO3 with εion zz = 108. The dominant mode 5 in BaCa3Ti4O12 at 2.51 THz contributes ~ 184 to its εion zz. Projection onto the modes of Pnma BaTiO3 shows it to be a linear combination of the modes at 4.17i THz, 3.26 THz, and 5.26 THz of BaTiO3. The former is the ferroelectric Ti–O mode, whereas the latter two are Ba-only modes. Here, the stable A-site modes are mixed into the Ti–O mode, leading to its stabilization. Thus, lowering the symmetry of the structure via substitution is important for the stabilization of the Ti–O mode. This is to be expected, as the Ti–O chain structure instability is nonlocal, i.e., Ti and O atoms are coherently displaced along an infinite Ti–O chain, and there exists a minimum correlation length for the mode to become unstable24. The instability has been extensively analyzed18,24, with Ti 3d–O 2p hybridization and a partially covalent nature of the Ti–O bond being determined essential to the ferroelectricity18,19. The 1D chain-like nature of the instability was noted from the mode’s nearly flat zero-frequency isosurfaces in the Brillouin zone25. Real-space analysis has shown24 that the minimum length of the Ti–O chain for the instability to appear is ~ 10 atoms or 5 unit cells; thus any stabilizing perturbation must act on a shorter scale. In the Nb-In co-doped rutile, a soft mode with a large dielectric constant contribution appears at ν = 0.594 THz, as seen in Fig. 2e. In pure rutile, Fig. 2f, the active A2u mode has a frequency of 5.28 THz.
The visualizations of phonon modes responsible for the large dielectric response are shown in Fig. 3. In Ba2Sr2Ti4O12 and Ba2Ca2Ti4O12(α), shown in Fig. 3a and b, the atomic displacements are very similar to those of the ferroelectric BaTiO3 mode, which is also confirmed by mode projections. In contrast, in the Nb-In co-doped rutile, the mode is localized on a single Ti atom in the xy plane, and delocalized along the z direction, as seen in Fig. 3c, giving it a chain-like character, possibly due to symmetry breaking by co-doping.
Eigen displacements ξν,κα/Mκ1/2 of phonon modes relevant to the dielectric constant in substituted titanates (a) mode 4 in Ba2Sr2Ti4O12; (b) mode 5 in Ba2Ca2Ti4O12(β); (c) mode 4 in Nb-In co-doped TiO2 rutile. Blue—Ti, red—O, orange—Sr, dark blue—Ca, green—Ba, dark green—Nb, purple—In. For clarity, atoms outside of Ti–O cages are not shown in (a) and (b).
We also note that the value εion zz = 9015 obtained for one of Ba2Sr2Ti4O12 structures may be close to a practically achievable maximum value for the ionic dielectric constant. From Eq. (1), one has εion ≃205 × (Z*/ν)2, assuming a cubic unit cell with a side of 6 Å, and mode frequency ν in THz. Thus, in order to have εion ~ 104, one needs Z*≃7 for ν = 1 THz. As larger Z* values to achieve even higher εion seem unrealistic, further increasing εion then requires decreasing the mode frequency below 1 THz, which may eventually result in instability and switching to a ferroelectric state.
In order to assess the feasibility of synthesis of doped titanates, we calculate their formation energies by computing the energies of the reactions
for III–V and II–VI substitutions in co-doped rutile, respectively, and
for the perovskites and Ruddlesden–Popper phases, respectively. The formation energy is defined as the energy difference per atom between the compounds on the left and right sides of the reaction. The obtained formation energies of titanates are shown in Fig. 4a, along with their band gaps. As can be seen from the figure, most of the substituted titanates have negative formation energies, favoring mixing, and moreover, have large band gaps. On the other hand, achieving co-doping in rutile could be more difficult, and some of the resulting compounds could be metallic. At the same time, there are a number of thermodynamically stable rutile compounds with moderate band gaps. Configurational energies, defined as the maximum formation energy difference among the structures of the same stoichiometry, are shown in Fig. S7. These can be rather small, e.g., ~ 3 meV/atom for Ba2Sr2Ti4O12, compared with its formation energy of ~ − 145 meV/atom. The closeness in energy among different configurations indicates that their mixing should occur at finite temperatures, and thermodynamic averaging, together with consideration of anharmonic effects, should be performed in order to estimate the dielectric constant at nonzero temperature.
CP materials must possess sufficiently large band gaps in order to prevent dielectric breakdown, which is believed to be electronic in nature26. Our calculated average ionic dielectric constants as a function of the band gap are shown in Fig. 4b, and the electronic contribution to the dielectric constant is shown in Fig. S4. Note that the electronic contribution does not exceed 10 for materials with band gaps > 0.6 eV. It is seen that generally insulators with larger dielectric constants tend to have smaller band gaps. This undesirable trend is consistent with the empirically known inverse relation between the dielectric constant and dielectric breakdown strength27. Discovering CP materials with both high dielectric constant and wide band gap remains a challenge that must be addressed in the future work.
Based on the results of first-principles calculations, we show that co-doping and substitutions offer a versatile and efficient pathway to increase the ionic dielectric constant in titanate paraelectrics. Most of the obtained compounds are found to be both dynamically and thermodynamically stable, offering a good prospect of experimental synthesis. Large ionic dielectric constants εion ~ 104 can be achieved in some compounds, establishing them as new candidates for colossal permittivity materials. The microscopic origin of the permittivity increase, namely the softening of the optically active phonon mode by a local defect-induced strain, may point to a new direction to search for colossal permittivity in other materials.
Methods
The ionic dielectric response was calculated using density functional perturbation theory (DFPT) approach, as implemented in the VASP package. PBEsol functional28 with Hubbard U correction was used. U = 3 eV was applied to d electrons in transition metals, except for Ti and Sc, where U = 0 was used. The full list of the U values is given in the Supplementary Information. The k point grid density of 3000 k points·atom (approximately corresponding to a distance of ~ 0.2 Å−1 between the k points) was used for the integration over the Brillouin zone. Full cell shape and atomic position relaxations were carried out prior to DFPT calculations.
Data availability
The datasets generated during the current study will be available at https://doi.org/10.17632/n9j8h4h9g3.1 following a 6 month embargo from the date of publication to allow for patenting of research findings.
References
Yang, Z., Du, H., Jin, L. & Poelman, D. High-performance lead-free bulk ceramics for electrical energy storage applications: Design strategies and challenges. J. Mater. Chem. A 9(34), 18026–18085. https://doi.org/10.1039/D1TA04504K (2021).
Hu, W. et al. Electron-pinned defect-dipoles for high-performance colossal permittivity materials. Nat. Mater. 12(9), 821–826. https://doi.org/10.1038/nmat3691 (2013).
Kawarasaki, M., Tanabe, K., Terasaki, I., Fujii, Y. & Taniguchi, H. Intrinsic enhancement of dielectric permittivity in (Nb + In) Co-doped TiO2 single crystals. Sci. Rep. 7(1), 5351. https://doi.org/10.1038/s41598-017-05651-z (2017).
Lunkenheimer, P. et al. Origin of apparent colossal dielectric constants. Phys. Rev. B 66(5), 052105. https://doi.org/10.1103/PhysRevB.66.052105 (2002).
Cohen, M. H., Neaton, J. B., He, L. & Vanderbilt, D. Extrinsic models for the dielectric response of CaCu3Ti4O12. J. Appl. Phys. 94(5), 3299–3306. https://doi.org/10.1063/1.1595708 (2003).
Subramanian, M. A., Li, D., Duan, N., Reisner, B. A. & Sleight, A. W. High dielectric constant in ACu3Ti4O12 and ACu3Ti3FeO12 Phases. J. Solid State Chem. 151(2), 323–325. https://doi.org/10.1006/jssc.2000.8703 (2000).
Homes, C. C., Vogt, T., Shapiro, S. M., Wakimoto, S. & Ramirez, A. P. Optical response of high-dielectric-constant perovskite-related oxide. Science 293(5530), 673–676. https://doi.org/10.1126/science.1061655 (2001).
Lunkenheimer, P. et al. Colossal dielectric constants in transition-metal oxides. Eur. Phys. J. Spec. Top. 180(1), 61–89. https://doi.org/10.1140/epjst/e2010-01212-5 (2009).
Samara, G. A., Hammetter, W. F. & Venturini, E. L. Temperature and frequency dependences of the dielectric properties of YBa2Cu3O6+x (X≊0). Phys. Rev. B 41(13), 8974–8980. https://doi.org/10.1103/PhysRevB.41.8974 (1990).
Rey, C. M., Mathias, H., Testardi, L. R. & Skirius, S. High dielectric constant and nonlinear electric response in nonmetallic YBa2Cu3O6+δ. Phys. Rev. B 45(18), 10639–10646. https://doi.org/10.1103/PhysRevB.45.10639 (1992).
Taniguchi, H., Sato, D., Nakano, A. & Terasaki, I. Permittivity boosting in “yellow” (Nb + In) Co-doped TiO2. J. Mater. Chem. C 8(39), 13627–13631. https://doi.org/10.1039/D0TC03539D (2020).
Dong, W. et al. Colossal permittivity with ultralow dielectric loss in In + Ta Co-doped rutile TiO2. J. Mater. Chem. A 5(11), 5436–5441. https://doi.org/10.1039/C6TA08337D (2017).
Tuichai, W., Danwittayakul, S., Srepusharawoot, P., Thongbai, P. & Maensiri, S. Giant dielectric permittivity and electronic structure in (A3+, Nb5+) Co-doped TiO2 (A = Al, Ga and In). In 10th Asian Meet. Electroceramics AMEC-10 2017, 43, S265–S269. https://doi.org/10.1016/j.ceramint.2017.05.255.
Goldschmidt, V. M. Die gesetze der krystallochemie. Naturwissenschaften 14(21), 477–485. https://doi.org/10.1007/BF01507527 (1926).
Gonze, X. & Lee, C. Dynamical matrices, born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B 55(16), 10355–10368. https://doi.org/10.1103/PhysRevB.55.10355 (1997).
Zhao, X. & Vanderbilt, D. First-principles study of structural, vibrational, and lattice dielectric properties of hafnium oxide. Phys. Rev. B 65(23), 233106. https://doi.org/10.1103/PhysRevB.65.233106 (2002).
Souza, I., Íñiguez, J. & Vanderbilt, D. First-principles approach to insulators in finite electric fields. Phys. Rev. Lett. 89(11), 117602. https://doi.org/10.1103/PhysRevLett.89.117602 (2002).
Cohen, R. E. & Krakauer, H. Lattice dynamics and origin of ferroelectricity in BaTiO3: Linearized-augmented-plane-wave total-energy calculations. Phys. Rev. B 42(10), 6416–6423. https://doi.org/10.1103/PhysRevB.42.6416 (1990).
Cohen, R. E. Origin of ferroelectricity in perovskite oxides. Nature 358(6382), 136–138. https://doi.org/10.1038/358136a0 (1992).
Montanari, B. & Harrison, N. M. Pressure-induced instabilities in bulk TiO2 rutile. J. Phys. Condens. Matter 16(3), 273–292. https://doi.org/10.1088/0953-8984/16/3/008 (2004).
Sophia, G., Baranek, P., Sarrazin, C., Rérat, M. & Dovesi, R. First-principles study of the mechanisms of the pressure-induced dielectric anomalies in ferroelectric perovskites. Phase Transit. 86(11), 1069–1084. https://doi.org/10.1080/01411594.2012.754442 (2013).
Choi, W. I., An, J. S., Jang, I. & Kim, D. S. Strain and temperature-dependent dielectric permittivity of cubic SrTiO3: Self-consistent phonon theory calculations. Curr. Appl. Phys. 29, 78–82. https://doi.org/10.1016/j.cap.2021.06.004 (2021).
Cockayne, E. & Burton, B. P. Phonons and static dielectric constant in CaTiO3 from first principles. Phys. Rev. B 62(6), 3735–3743. https://doi.org/10.1103/PhysRevB.62.3735 (2000).
Ghosez, P. S. H., Gonze, X. & Michenaud, J. P. Ab initio phonon dispersion curves and interatomic force constants of barium titanate. Ferroelectrics 206(1), 205–217. https://doi.org/10.1080/00150199808009159 (1998).
Yu, R. & Krakauer, H. First-principles determination of chain-structure instability in KNbO3. Phys. Rev. Lett. 74(20), 4067–4070. https://doi.org/10.1103/PhysRevLett.74.4067 (1995).
Ridley, B. K. Quantum Processes in Semiconductors (Oxford University Press, 2013). https://doi.org/10.1093/acprof:oso/9780199677214.001.0001.
McPherson, J. W., Kim, J., Shanware, A., Mogul, H. & Rodriguez, J. Trends in the ultimate breakdown strength of high dielectric-constant materials. IEEE Trans. Electron Devices 50(8), 1771–1778. https://doi.org/10.1109/TED.2003.815141 (2003).
Perdew, J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100(13), 136406. https://doi.org/10.1103/PhysRevLett.100.136406 (2008).
Acknowledgements
We thank Drs. Pradeep R. Varadwaj, Hiroki Taniguchi, Van An Dinh, Yoshitada Morikawa, and Koichi Hayashi for their fruitful discussions. The work was also supported by the JSPS Grant-in-Aid for Transformative Research Areas (A) (21H05560).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kutana, A., Shimano, Y. & Asahi, R. Permittivity boosting by induced strain from local doping in titanates from first principles. Sci Rep 13, 3761 (2023). https://doi.org/10.1038/s41598-023-30965-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-023-30965-6
This article is cited by
-
Machine learning and atomistic origin of high dielectric permittivity in oxides
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.