Abstract
We investigate the electronic response of single-walled carbon nanotubes (SWCNTs) and a carbon nanobelt (CNB) to N-linked and O-linked SARS-CoV-2 spike glycoproteins, using ab initio quantum mechanical approach. The CNTs are selected from three zigzag, armchair, and chiral groups. We examine the effect of carbon nanotube (CNT) chirality on the interaction between CNTs and glycoproteins. Results indicate that the chiral semiconductor CNTs clearly response to the presence of the glycoproteins by changing the electronic band gaps and electron density of states (DOS). Since the changes in the CNTs band gaps in the presence of N-linked are about two times larger than the changes in the presence of the O-linked glycoprotein, chiral CNT may distinguish different types of the glycoproteins. The same results are obtained from CNBs. Thereby, we predict CNBs and chiral CNTs have suitable potential in sequential analysis of N- and O-linked glycosylation of the spike protein.
Introduction
The outbreak of the SARS-CoV-2 pandemic (COVID-19) reveals the urgent need for high-accurate, sensitive, selective, and inexpensive long-term biomaterial detection techniques1. One of the great challenges in the detection of SARS-CoV-2 is that it damages the target RNA when opening its viral capsid. Therefore, small pieces of RNA are release into the bloodstream, which makes it hard to detect by traditional sensors1. Biosensors are exceptional alternatives to traditional detecting tools2. Nanotechnology opens new windows in developing and designing biosensors in combination with nanomaterials3. Among nanomaterials, carbon nanotubes (CNTs) are hollow, one-dimensional (1D) carbon fibers. CNTs are longer than a micrometer and have a diameter ranging between 1 and 20 nm4. CNTs show a unique combination of electrical, optical, mechanical, and chemical properties5,6. Consequently, CNTs offer great promises for a variety of applications, including biosensing7. When combined with specific polymers, CNTs can be used as optical sensors for a wide range of analytes, including reactive oxygen species, insulin, dopamine, and nitric oxide8. The emission wavelengths of single-walled CNTs (SWCNTs) are close to the infrared range9, in which water and blood have limited interference10. CNT-based sensors react to the specific analyte, and this reaction manifests in the intensity of the fluorescence and causes red or blue shifts in wavelengths11. Due to a very large specific surface area12, CNTs can combine with many glycoprotein molecules7,13. This property makes CNTs a suitable candidate to detect SARS-CoV2 virus7,13,14.
SARS-CoV-2 spike is characterized by a large number of N-linked and O-linked glycosylation proteins15,16. Glycosylation of spike virus protein plays a vital role in virus stability and its ability in suppressing immunological surveillance17. Hence, it is important to characterize the glycosylation sequence. There are two main strategies in employing a biosensor18: (i) detection of viral nucleic acid sequence, (ii) detection of viral biomolecules, such as surface proteins. Determining the sequence of N-linked or O-linked glycan proteins can lead to detection of both spike mutation sequence and surface protein.
The present study aimed to investigate and analyze the ability of CNTs and carbon nanobelts (CNBs) in detection and quantification of N-linked and O-linked sequences. Our study is based on the changes in the electronic properties of CNTs and CNBs in the presence of N-linked or O-linked glycan molecules, using density functional theory (DFT). CNBs are observed in SWCNTs laser vaporization process19,20. Over the last few years, there has been significant progress in the synthesis of carbon nanorings and CNBs21. CNTs with a selective and predictable chirality are synthesized using a bottom-up approach from a CNB template that corresponds to the target CNT structure22. Armchair CNBs (6,6), (8,8), (12,12) and more recently zigzag CNB(18,0), which have been considered the most difficult type to synthesize, among those have been successfully fabricated21,23,24.
In practice, depending on the manufacturing approach, CNTs can be implemented in the sensor platform in different ways. Owing to their electrical and electrochemical properties, CNTs are very promising materials for integration into electrochemical biosensors7. Recently, a biosensor for SARS-CoV-2 spike antigen detection, based on a CNT-field effect transistor has been developed which shows very sensitive, selective performance25,26 . CNTs are used as signal transducers in field-effect biosensors. Our results show that in addition to a signal transducer, CNT is capable of selective recognition of glycoproteins for virus detection.
Since electronic properties of CNTs highly depend on the chirality and structural geometry (i.e., whether they are semiconductors or metals)27,28 , we have built three groups of zigzag (m = 0), armchair (n = m), and general chiral (n > m > 0) CNTs, in size that allows computational capabilities. Here n, m are chiral indexes, as shown in Fig. 1a. We analyzed the variation in the electronic band structure and electron density of state (DOS) upon glycan adsorption. These properties characterize the electronic response of sensors29. Our results show that chiral semiconductor CNTs have the potential to be developed as viral sensing materials due to their high electrical response to virus glycoproteins. To investigate the capability of CNBs as biosensors, we have calculated the electronic gap, binding energy, chemical potential, ionization potential, electron affinity, chemical hardness, and electron felicity in the presence of a glycoprotein molecule. We also used time-dependent density functional theory (TD-DFT) to calculate the absorption spectra of a CNB sample and monitored the change in its spectrum after being introduced to the N-linked and O-linked glycan. Our results show that the presence of the N-linked or O-linked glycan molecules, can change the electronic band gap of the chiral semiconductor CNTs and CNBs, and therefore, they can be used for monitoring Corona-like virus spikes. Outcomes enable us to predict those structures that may show more sensitive optical and electronic responses in sensing devices, while our results can be detected experimentally through signals given by the built-in electronic device in biosensors.
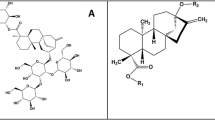
(a) The structure of SWCNT can be shown by a graphene sheet wrapped along a chiral vector Ch. a1 and a2 show the graphene primitive vectors. Three types of CNT (zigzag, armchair, and chiral) are illustrated. (b) Cross-section and lateral surface of CNB(8,8) with Lengths L1 = 5.57 Å and L2 = 6.82 Å. (c) The simplest N- and O-linked of glycan molecular structures found in SARS-Cov-2.
Results
Symmetry-dependent electronic properties of CNT
The chirality (n,m) indicates how a graphene sheet has been folded to form a CNT. We can show the structure of an SWCNT by taking two hexagons of a graphene sheet and rolling up the sheet to overlap these two hexagons30. A vector that connects the center of two hexagons is named a chiral vector, as seen in Fig. 1a. Chiral vector Ch is written in terms of the primitive vectors a1 and a2 of the graphene lattice in the form of Ch = na1 + ma2, with n and m being integer numbers. If n = m = j, with j being zero or any positive integer number, the resulting nanotube is called an armchair (n,n) CNT. A zigzag CNT(n,0) is formed when n = j and m = 0. Other combinations of n and m are called chiral CNT31. An SWCNT has metallic properties with a zero electronic gap, if n − m = 3j32, otherwise, the SWCNT behaves as a semiconductor with an electronic gap that depends on the chirality (n,m) and inversely proportions with CNT diameter31. Therefore, the geometry of a CNT plays an important role in its electronic properties. In the reciprocal space, the allowed states are called cutting lines. The chirality of the CNT determines the orientation of the cutting lines33. Depending on whether the cutting line crosses the degenerate K and K’ points of the Brillouin zone (BZ), an SWCNT behaves as either metallic (M) with n − m = 3j, or a semiconductor (S) with n − m ≠ 3j34. In a metallic CNT, the cutting lines crosse the K points. Depending on at what ratio the K points divide the cutting lines, the metallic CNTs can be classified into M1 or M2 types. Following Ref.34, we name the greatest common divisor of the (2n + m,2 m + n) by dR and of the two integers (n,m) by d. In the M1-type CNT dR = d, while in the M2-type CNT dR = 3d34. On the other hand, CNT cutting lines do not crosse the K point in a semiconductor CNT. There are two types of semiconductor CNTs. If n − m = 3j + 1, the CNT is S1-type semiconductor and if n − m = 3j − 1, it is called S2-type CNT. In an S1-type CNT the distance of the K point from the nearest cutting line passing inside the BZ is two-thirds of the distance between two adjacent cutting lines, while for an S1-type, this is a one-third34. An armchair CNT (n,n) is always M2-type metallic. For a zigzag CNT three types are possible: M1-type (3j, 0), S1-type (3j + 1,0) or S2-type (3j + 2,0). For a chiral CNT each of the four types M1, M2, S1 (n − m = 3j + 1), and S2 (n − m = 3j + 2) is possible34.
Pristine CNTs
From the armchair group, we investigate the electronic band structure and electron DOS of the three (2,2), (3,3) and (4,4) CNTs. Here n − m = 0, and therefore, these CNTs should be metals, as confirmed also by the computational outcomes given in Table 1, Figs. 2 and S1 in supplementary data. The bands are extended from point Γ at the center of BZ to the boundary point at Z = π/c, where “c” shows the periodicity length along the tube axis. The corresponding cutting lines of these three CNTs cross both K and K’ points, which means they are M2-metallic. In the same way, the corresponding DFT-band structures indicate metallic features, with valence bands crossing the Fermi level.
Top: cutting lines in zone folding illustration of armchair and zigzag CNTs. Bottom: the corresponding DFT electronic band structures. Valence and conduction bands are represented in red and blue colours, respectively. Fermi energy EF is set to zero.
We study four zigzag CNTs with chirality (3, 0), (4, 0), (5, 0) and (8, 0). The related data are given in Table 1. According to the n − m = 3j rule, CNT(3, 0) should be a metal, as it is truly predicted, and shown in Fig. 2, by cutting lines crossing the K or K’ points. Therefore, CNT(3,0) is an M1-metal type. Likewise, both the zone folding picture and the DFT band structure, shown in Fig. 2, predict CNT(8, 0) is a semiconductor. There is an exception for CNTs(4,0) and (5,0). Cutting line analysis of the zone folding approach in Fig. 2 predicts that these CNTs are semiconductor types S1 and S2, respectively. However, the corresponding DFT band structures in this figure and DOS presented in Figure S1 predict metallic features, despite n − m not being a multiple of 3. The same DFT predictions are previously reported35,36. In fact, the high curvatures of the wall structures in these two small tubes induce σ-π surface hybridization. Consequently, the relaxed structures show a significant deviation from the ideal rolled-up graphene sheet configuration, which leads to failure of the zone folding approach prediction. Previously, it was shown that zone folding approach prediction is reliable only for CNTs with diameters larger than 1 nm37,38.
Band structures and cutting lines in BZ of pristine chiral CNTs (3,1), (3,2), (4,1), (4,2), (6,5), and (7,6) are shown in Fig. 3 and the related data are given in Table 1. Among them, CNT(4,1) is a metal and the other chiral CNTs are semiconductors. Electronic states of CNT(4,1) cross K and K’ points separately, and therefore this nanotube is an M1-metallic. In the remaining chiral CNTs no electronic state crosses point K, or K’, and depending on the values of the n − m, they are S1- or S2-type semiconductors.
Top: cutting lines in zone folding illustration of chiral CNTs. Bottom: the corresponding DFT electronic band structures. Valence and conduction bands are represented in red and blue colours, respectively. Fermi energy EF is set to zero.
Pristine CNBs
Among synthesized CNB series, we investigate the electronic properties of CNB(8,8). To investigate the effect of the CNB length on the electronic properties, we added an additional layer to the initial L1 size CNB(8,8), see Fig. 1. By this, the length of the CNB increases from L1 = 5.57 Å to the L2 = 6.82 Å, and the optimized structures have the diameters of 1.15 Å and 1.16 Å, respectively. Figure 1c shows the optimized structures of these two CNBs. We have used DFT to predict several electrochemical indicators, including electronic gap (Egap), chemical potential (μ), chemical hardness (η), electron affinity (EA), ionization potential (IP), binding energy (ΔΕΒ) and electron felicity (ω) to distinguish chemical features of the corresponding CNB + glycan compounds. These properties are defined as44,45,46:
Discussion
CNT (CNB) and glycan molecules form a weak bound state through a van der Waals (vdW) interaction characterized by the charge density rearrangement at the compound interface. The corresponding calculated binding energies are about 0.3 eV with equilibrium distances larger than 3 Å. Charge density difference (Δρ) illustrates the change in the charge distribution in a compound relative to its isolated components. Here, Δρ is defined by ρ(CNT + glycan compound)-[ρ(isolated CNT) + ρ(isolated glycan)]. Δρ for CNT(3,1) and CNT(4,2) in the presence of glycan molecule are shown in Fig. 4. Figure confirms that after interaction no electric charge is shared between two species, but the charge density of both CNT and glycan molecule is perturbed in the interface. Formation of interfacial electric dipole and quadrupole moments is the consequent of charge accumulation (Δρ > 0 in yellow colour) and charge depletion (Δρ < 0 in blue colour) on interfacial surface.
Δρ for (a): CNT(4,2) in the presence of an O-linked glycan molecule, (b): CNT(3,1) in the presence of an O-linked glycan molecule. Charge accumulation in yellow colour and charge depletion area in blue colour are shown.
According to our outcomes, the metallic CNTs almost show no response to the presence of glycoproteins. However, the band structures and gaps of semiconductor CNTs are influenced by the glycoprotein molecules. Variation in the band gaps in the presence of the glycans respect to the pristine CNTs (∆Egap = Egap(CNT)-Egap(CNT + glycan)) are reported in Table 2. Data in Table 2 indicate that the electronic response of a semiconductor CNT to the presence of N-linked glycan is about two times larger than to O-linked glycan. Comparing the band structures of pristine CNTs with those of the CNT + N-linked complexes shows that both valence and conduction bands of CNT + N-linked complexes move toward the Fermi level, see Figs. 5 and S2.
Band structure of semiconductor CNTs in the presence of glycan molecules. Valence and conduction bands are represented in red and blue colours, respectively. Fermi energy EF is set to zero.
However, in interaction with O-linked glycan, this is the conduction band that mostly influenced by the interaction and moves toward Fermi level. As the valence band approaches the Fermi level, it is possible that the semiconductor tube becomes a metal, as seen for CNT(7,6) + N-linked complex, in which the valence band nearly coincides the Fermi level at the BZ boundary point, however it is still a semiconductor.
Now we discuss how CNB electrochemical features are influenced by the interaction with the glycan molecules. CNT(8,8) is an armchair 1D tube, which according to m − n = 3j law should be a metal with a zero band gap. In contrast, due to quantum confinement effect, zero-dimensional (0D) L1 size CNB(8,8) has relatively a wide electronic gap of 2.39 eV. With increasing the length of the CNB from L1 to L2, the 0D structure becomes closer to 1D CNT(8,8) and the gap reduces to 0.72 eV. Likewise, the electronic response of the CNB to the presence of the glycans decreases with increasing the length of the CNB, as one concludes from comparing the ∆Egap given in Table 3. According to the information given in Table 3, the CNB with length L1 is a better option for detecting glycans than CNB with longer length L2, owing to a better sensitivity, showing larger band gap variation, and more stability (higher chemical hardness). In addition, the binding energy for L1 size CNB + glycan complexes is larger than for L2 complexes.
In Fig. 6, we pictorially show the changes in the energy of HOMO and LUMO levels of CNBs in the presence of glycoprotein molecules. According to Fig. 6, at length L1, the presence of the glycan molecules pulls up the HOMO level and pushes down the LUMO level. Thus, the energy gap undergoes a serious change. However, at size L2, the glycan molecules reduce the energy of both HOMO and LUMO levels, and no significant change is achieved in the band gap.
HOMO and LUMO energy levels of glycan molecules and pristine CNB(8,8) with lengths L1 and L2. Renormalized energy levels of CNBs in the presence of glycan molecules are shown.
Hydrogen bond strength could be classified into three groups depending on the amount of binding energy. Strong bond energies are greater than 0.65 eV, moderate bond energies happen at between 0.2 and 0.65 eV, and weak bonds energies are less than 0.2 eV47. The calculated binding energies given in Table 3, show that the hydrogen bonds strength for the CNB in the presence of the N-linked glycoprotein are moderate for both CNBs. While the corresponding values are weak for both sizes CNB in the presence of O-linked glycan. Also, binding energies given in Table 3 reveal that the vdW interactions between CNBs and glycan molecules are greater for smaller lengths.
The HOMO and LUMO orbitals representation of the individual glycans, L1 size CNB(8,8), and CNB(8,8) + glycan composite systems are shown in Fig. 7. Additional information is given in supplementary data. The introduction of high electronegativity anions by glycan molecules causes intense changes in the electronic properties of the CNB. The HOMO orbital isosurface shows a charge localization on the amine or ketone functional group of the glycan molecules, so that N-linked and O-linked groups suppress the electronic dynamics of the combined structure through nonbonding electron pairs in the functional groups. That means, the nonbonding pair of electrons in the nitrogen and oxygen atoms dominate the HOMO state and impose a new level inside the HOMO–LUMO gap of pristine CNB, as seen in Fig. 7. This finding is confirmed by the DOS diagrams given in Fig. 7. Also, the presence of the nitrogen and oxygen atoms increases the chemical potential of the L1 size CNB, and the electron can more easily be excited, or the structure can be ionized with less energy than before. As a result, changes in the electron DOS and the HOMO–LUMO orbital representation suggest the possibility of serious changes in the optical response of the CNB, due to interaction with the glycans. We will discuss this issue further.
DOS, HOMO, and LUMO isosurface of (a): N-linked, (b): O-linked glycan molecules, (c): pristine CNB(8, 8), (d): CNB(8, 8) + N-linked, (e): CNB(8, 8) + O-linked glycan complexes.
The optical properties of sensor materials are of the important practical features of interest. Thereby, we show how the absorption spectrum of CNB is changed by the presence of the intended glycan. B3LYP functional takes advantage of the cancellation of localization and delocalization errors, which makes it a more reliable functional to predict absorption spectrum of materials48,49. Consequently, we use B3LYP in addition to the PBE functional in this section. TD-B3LYP predicted spectra of L1 size CNB in the presence of glycoprotein molecules are shown in Fig. 8. The corresponding TD-PBE spectra are given in Figure S3. B3LYP predicts that the glycan molecules have almost no absorption in the visible region. Similarly, the absorption spectrum of pristine CNB is almost in the ultraviolet area, and the absorption tails approach the visible region. By absorption of N-linked, O-linked, or simultaneously O- and N-linked glycans, the spectra of the CNB + glycan complexes show redshifts toward the visible region due to involvement in vdW interactions. Owing to stronger interaction, the absorption of N-linked glycan gives larger red shift than absorption of the O-linked glycan.
TD-B3LYP predicted absorption spectrum of pristine CNB, glycan molecules, and CNB + glycon complex. As the glycoprotein approaches the CNB, the absorption spectra shift toward the visible region.
In conclusion, we investigated the change in the electronic properties of several CNTs and a selected CNB in the presence of N-linked and O-linked glycoprotein molecules. Our results show that, depending on the size and chirality, the semiconductor chiral CNTs can be good options to use as biosensor materials. Depending on the electronic gap and length of the nanobelt, CNB show appropriate electronic and optical sensitives that are required for biosensor materials. The present study gives important findings in diagnosis materials for viral diseases based on CNTs.
Methods
Virus spikes are often decorated by a large number of N-linked and O-linked glycoproteins. The structures of the N-linked and O-linked glycans are taken from Ref.50 and shown in Fig. 1c. For smaller CNTs, calculations were performed within the framework of the plane-wave pseudopotential approach and Perdew-Burke-Ernzerhof (PBE) functional, using Quantum- Espresso computational package51,52.The Grimme’s vdW correction (PBE-D2) is added to our calculations to introduce the long-range effect of vdW interactions53. The simulation was performed at room temperature (300 K). The cutoff energy on the plane-wave kinetic energy was set to 45 Ha. A Monkhorst k-point mesh was used to sample the Brillouin zone54. The volume of the supercell and the atomic positions of the structures were optimized under conditions where the forces acting on atoms are less than 5 meV/Å. Periodic boundary conditions along the growth direction have been applied to all structures. Cutting lines are plotted using Wolfram Demonstrations project33,55,56.
Band structure of larger tubes CNTs(6,5) and (7,6), which have smaller wall curvatures, are calculated within self-consistent Slater Koster tight binding semi-empirical methods, as implemented in the DFTB + package, using fine BZ k-point mesh57. Previously, it was shown that semi-empirical tight binding method provides CNT band gap prediction in an accuracy comparable to DFT schemes58. For smaller CNT (3,1), we obtained a difference of about 0.1 eV in the band gap from PBE-DFT and DFTB. However, since our goal is to find the variation in band gap of CNT in the presence of glycan molecules, our results benefited from band gap cancelation errors. We applied PBE and hybrid B3LYP functionals and imported atomic orbitals using the LANL2DZ basis set to find the geometrical orientation and electronic properties of the N-linked and O-linked glycoprotein molecules near CNBs59. The UV–Vis spectra were calculated in the TD-DFT framework. All CNB calculations were performed using the Gaussian 98 package60.
Data availability
Data generated or analysed during this study are included in this published article and its supplementary information file.
References
Bhalla, N., Pan, Y., Yang, Z. & Payam, A. F. Opportunities and challenges for biosensors and nanoscale analytical tools for pandemics: Covid-19. ACS Nano 14, 7783–7807 (2020).
Pinheiro, T. et al. based biosensors for covid-19: a review of innovative tools for controlling the pandemic. ACS Omega 6, 29268–29290 (2021).
Zhang, Y. & Chen, X. Nanotechnology and nanomaterial-based no-wash electrochemical biosensors: from design to application. Nanoscale 11, 19105–19118 (2019).
Ebbesen, T. W. Carbon nanotubes. Annu. Rev. Mater. Sci. 24, 235–264 (1994).
Kuchibhatla, S. V., Karakoti, A., Bera, D. & Seal, S. One dimensional nanostructured materials. Prog. Mater. Sci. 52, 699–913 (2007).
Mamalis, A., Vogtländer, L. & Markopoulos, A. Nanotechnology and nanostructured materials: trends in carbon nanotubes. Precis. Eng. 28, 16–30 (2004).
Tîlmaciu, C.-M. & Morris, M. C. Carbon nanotube biosensors. Front. Chem. 3, 59 (2015).
Giraldo, J. P. et al. A ratiometric sensor using single chirality near-infrared fluorescent carbon nanotubes: application to in vivo monitoring. Small 11, 3973–3984 (2015).
Tange, M., Okazaki, T. & Iijima, S. Selective extraction of semiconducting single-wall carbon nanotubes by poly (9, 9-dioctylfluorene-alt-pyridine) for 1.5 μm emission. ACS Appl. Mater. Interfaces 4, 6458–6462 (2012).
Antaris, A. L. et al. A high quantum yield molecule-protein complex fluorophore for near-infrared ii imaging. Nat. Commun. 8, 1–11 (2017).
Schroeder, V., Savagatrup, S., He, M., Lin, S. & Swager, T. M. Carbon nanotube chemical sensors. Chem. Rev. 119, 599–663 (2018).
Peigney, A., Laurent, C., Flahaut, E., Bacsa, R. & Rousset, A. Specific surface area of carbon nanotubes and bundles of carbon nanotubes. Carbon 39, 507–514 (2001).
He, P. et al. Rational design and fabrication of surface molecularly imprinted polymers based on multi-boronic acid sites for selective capture glycoproteins. Chem. Eng. J. 367, 55–63 (2019).
Thakor, A. S. & Gambhir, S. S. Nanooncology: the future of cancer diagnosis and therapy. CA A Cancer J Clinicians 63, 395–418 (2013).
Shajahan, A., Pepi, L. E., Rouhani, D. S., Heiss, C. & Azadi, P. Glycosylation of sars-cov-2: structural and functional insights. Anal. Bioanal. Chem. 413, 7179–7193 (2021).
Gong, Y., Qin, S., Dai, L. & Tian, Z. The glycosylation in sars-cov-2 and its receptor ace2. Signal Transduct. Target. Ther. 6, 1–24 (2021).
Huang, H.-C. et al. Hyperglycosylated spike of sars-cov-2 gamma variant induces breast cancer metastasis. Am. J. Cancer Res. 11, 4994 (2021).
Krejcova, L. et al. Nanoscale virus biosensors: state of the art. Nanobiosens. Dis. Diagn. 4, 47–66 (2015).
Kiang, C.-H. & Goddard, W. A. III. Polyyne ring nucleus growth model for single-layer carbon nanotubes. Phys. Rev. Lett. 76, 2515 (1996).
Liew, K. M., Jianwei, Y. & Zhang, L. W. Mechanical Behaviors of Carbon Nanotubes: Theoretical and Numerical Approaches (William Andrew, 2016).
Li, Y. et al. Chemical synthesis of carbon nanorings and nanobelts. Accounts Mater. Res. 2, 681–691 (2021).
Omachi, H., Nakayama, T., Takahashi, E., Segawa, Y. & Itami, K. Initiation of carbon nanotube growth by well-defined carbon nanorings. Nat. Chem. 5, 572–576 (2013).
Povie, G., Segawa, Y., Nishihara, T., Miyauchi, Y. & Itami, K. Synthesis and size-dependent properties of [12], [16], and [24] carbon nanobelts. J. Am. Chem. Soc. 140, 10054–10059 (2018).
Omachi, H., Segawa, Y. & Itami, K. Synthesis of cycloparaphenylenes and related carbon nanorings: a step toward the controlled synthesis of carbon nanotubes. Accounts Chem. Res. 45, 1378–1389 (2012).
Zamzami, M. A. et al. Carbon nanotube field-effect transistor (cnt-fet)-based biosensor for rapid detection of sars-cov-2 (covid-19) surface spike protein s1. Bioelectrochemistry 143, 107982 (2022).
Thanihaichelvan, M. et al. Selective and electronic detection of covid-19 (coronavirus) using carbon nanotube field effect transistor-based biosensor: a proof-of-concept study. Mater. Today Proc. 49, 2546–2549 (2022).
Marana, N. L., Albuquerque, A. R., La Porta, F. A., Longo, E. & Sambrano, J. R. Periodic density functional theory study of structural and electronic properties of single-walled zinc oxide and carbon nanotubes. J. Solid State Chem. 237, 36–47 (2016).
Goldt, A. E. et al. Highly efficient bilateral doping of single-walled carbon nanotubes. J. Mater. Chem. C 9, 4514–4521 (2021).
Srimathi, U., Nagarajan, V. & Chandiramouli, R. Germanane nanosheet as a novel biosensor for liver cirrhosis based on adsorption of biomarker volatiles–a DFT study. Appl. Surf. Sci. 475, 990–998 (2019).
Wilder, J. W., Venema, L. C., Rinzler, A. G., Smalley, R. E. & Dekker, C. Electronic structure of atomically resolved carbon nanotubes. Nature 391, 59–62 (1998).
Dass, D. & Vaid, R. Chirality dependence of electronic band structure and density of states in single-walled carbon nanotubes. Afr. Rev. Phys. 12 (2018).
Radosavljevic, M. et al. Electronic structure of atomically resolved c-nts. Appl. Phys. Lett 82, 4131 (2003).
Dresselhaus, G., Dresselhaus, M. S. & Saito, R. Physical Properties of Carbon Nanotubes (World Scientific, 1998).
Samsonidze, G. G. et al. The concept of cutting lines in carbon nanotube science. J. Nanosci. Nanotechnol. 3, 431–458 (2003).
Kamal, C. & Chakrabarti, A. Comparison of electronic and geometric structures of nanotubes with subnanometer diameters: a density functional theory study. Phys. Rev. B 76, 075113 (2007).
Matsuda, Y., Tahir-Kheli, J. & Goddard, W. A. III. Definitive band gaps for single-wall carbon nanotubes. J. Phys. Chem. Lett. 1, 2946–2950 (2010).
Machón, M., Reich, S., Thomsen, C., Sánchez-Portal, D. & Ordejón, P. Ab initio calculations of the optical properties of 4-å-diameter single-walled nanotubes. Phys. Rev. B 66, 155410 (2002).
Charlier, J.-C., Blase, X. & Roche, S. Electronic and transport properties of nanotubes. Rev. Modern Phys. 79, 677 (2007).
Barone, V. & Scuseria, G. E. Theoretical study of the electronic properties of narrow single-walled carbon nanotubes: beyond the local density approximation. J. Chem. Phys. 121, 10376–10379 (2004).
Kayang, K. et al. A comparative study of the interaction of nickel, titanium, palladium, and gold metals with single-walled carbon nanotubes: a DFT approach. Results Phys. 12, 2100–2106 (2019).
Lanzillo, N. A., Kharche, N. & Nayak, S. K. Substrate-induced band gap renormalization in semiconducting carbon nanotubes. Sci. Rep. 4, 1–5 (2014).
Li, Y., Hodak, M., Lu, W. & Bernholc, J. Selective sensing of ethylene and glucose using carbon-nanotube-based sensors: an ab initio investigation. Nanoscale 9, 1687–1698 (2017).
Bachilo, S. M. et al. Structure-assigned optical spectra of single-walled carbon nanotubes. Science 298, 2361–2366 (2002).
Putz, M. V. Koopmans’ analysis of chemical hardness with spectral-like resolution. Sci. World J. 2013 (2013).
Parr, R. G., Szentpály, L. V. & Liu, S. Electrophilicity index. J. Am. Chem. Soc. 121, 1922–1924 (1999).
Zhan, C.-G., Nichols, J. A. & Dixon, D. A. Ionization potential, electron affinity, electronegativity, hardness, and electron excitation energy: molecular properties from density functional theory orbital energies. J. Phys. Chem. A 107, 4184–4195 (2003).
Desiraju, G. R. & Steiner, T. The Weak Hydrogen Bond: in Structural Chemistry and Biology Vol. 9 (International Union of Crystal, 2001).
Marsusi, F., Sabbaghzadeh, J. & Drummond, N. Comparison of quantum Monte Carlo with time-dependent and static density-functional theory calculations of diamondoid excitation energies and stokes shifts. Phys. Rev. B 84, 245315 (2011).
Cohen, A. J., Mori-Sánchez, P. & Yang, W. Insights into current limitations of density functional theory. Science 321, 792–794 (2008).
Hassan, S.-U., Donia, A., Sial, U., Zhang, X. & Bokhari, H. Glycoprotein-and lectin-based approaches for detection of pathogens. Pathogens 9, 694 (2020).
Giannozzi, P. et al. Advanced capabilities for materials modelling with quantum espresso. J. Phys. Condens. Matter 29, 465901 (2017).
Giannozzi, P. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006).
Monkhorst, H. J. & Pack, J. D. Special points for brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Carducci, O. M. The wolfram demonstrations project. MAA Focus 28, 8–9 (2009).
Fakültesi, F. E. & Bölümü, F. Calculation of cutting lines of single-walled carbon nanotubes. (2012).
Hourahine, B. et al. Dftb+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 152, 124101 (2020).
Niranjan, M. K. Theoretical investigation of electronic bandgaps of semiconducting single-walled carbon nanotubes using semi-empirical self-consistent tight binding and ab-inito density functional methods. J. Phys. Commun. 4, 015004 (2020).
Chiodo, S., Russo, N. & Sicilia, E. Lanl2dz basis sets recontracted in the framework of density functional theory. J. Chem. Phys. 125, 104107 (2006).
Petersson, G. A. et al. Calibration and comparison of the gaussian-2, complete basis set, and density functional methods for computational thermochemistry. J. Chem. Phys. 109, 10570–10579 (1998).
Acknowledgements
The authors thanks to the Research Council of Semnan University for providing computational facilities.
Author information
Authors and Affiliations
Contributions
1- S.M. is PHD student wrote the first draft of the manuscript and did the calculations. 2- F.M. and N.M. are PHD supervisors and conducted the project. 3- M.Q. is an advisor.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Monavari, S.M., Marsusi, F., Memarian, N. et al. Carbon nanotubes and nanobelts as potential materials for biosensor. Sci Rep 13, 3118 (2023). https://doi.org/10.1038/s41598-023-29862-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-023-29862-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
