Introduction

Room temperature injection and detection of spin-polarized carriers from ferromagnetic semiconductors (FMSs), which possess both the properties of ferromagnets and semiconductors, are crucial for realizing future semiconductor-based spintronics devices1,2. Indeed, one of the 125 big questions raised about two decades ago was, “Is it possible to create magnetic semiconductors that work at room temperature?”3 So far, all room-temperature spin injection and detection experiments use ferromagnetic metals because of their high Curie temperature (TC). However, ferromagnetic metals suffer from the “conductivity mismatch” problem when used in heterojunctions with semiconductors, resulting in very low spin injection/detection efficiencies in semiconductor spintronics devices4,5. Thus, it is crucial to develop ferromagnetic semiconductors with high TC and room-temperature spin injection capability. Meanwhile, successful spin injection has been reported only in prototypical Mn-doped III-V FMS (Ga,Mn)As at very low temperature < 120 K6,7,8. This is because these Mn-doped FMSs show ferromagnetic order only at low temperature (the maximum Curie temperature TC is 200 K in (Ga,Mn)As)9. Recently, Fe-doped III-V FMSs, such as (In,Fe)As, (Ga,Fe)Sb, and (In,Fe)Sb, are shown to be promising because of their high TC (> 300 K)10,11,12,13,14,15,16,17. The origin of ferromagnetism as well as the electronic structures and magnetic properties of Fe-doped FMSs have also been studied by first-principles calculations18,19, which suggest that the ferromagnetic interaction between Fe atoms occurs at the second nearest-neighbor and third nearest-neighbor in the semiconductor hosts. It is also shown that high TC in Fe-doped FMSs may come from high impurity concentration and is not due to the carrier-induced mechanism because Fe3+ does not introduce carriers20. Furthermore, TC over 1000 K for Fe-doped FMSs is predicted, based on n- or p-type Fermi level shift21. Thus, Fe-doped FMSs are very promising for future applications because high Curie temperature (TC > 500 K) is necessary for practical applications22. Very recently, a giant magnetoresistance over 500% was observed in n-type (In,Fe)As/p-type (Ga,Fe)Sb spin diodes at low temperatures23. Despite all of these intensive efforts, room-temperature spin injection from Fe-doped FMSs has not yet been demonstrated.

Recently, we show macroscopic ferromagnetism in (Ga,Fe)Sb by observing clear ferromagnetic resonance (FMR) at room temperature12,13. So far, spin pumping24,25, electrical spin injection26,27, spin Seebeck effect28, and other optical methods29 have been used to study the spin injection from a ferromagnetic (FM) layer into a non-magnetic (NM) layer. Among those methods, spin pumping, which employs FMR, is one of the most efficient methods, because a pure spin current can be transported through a FM/NM interface even under a conductivity mismatch condition30. The injected spin current is detected by the inverse spin Hall effect (ISHE) in the NM layer, which converts the spin current to a charge current via spin–orbit interaction (SOI)31. The efficiency of this spin-to-charge conversion is characterized by the inverse spin Hall angle (ISHA). However, because the ISHE output voltage is proportional to the magnetization of the FM layer, which is only 45 emu/cc for (Ga,Fe)Sb at room temperature, one needs to use a spin Hall material with a large spin Hall effect as the spin detector. From this viewpoint, topological insulators can be utilized to detect spin injection from the (Ga,Fe)Sb32,33. Recently, it was found that Bi1-xSbx (0.07 ≤ x ≤ 0.22) is a three-dimensional topological insulator (TI) with strong SOI and large spin Hall angle (SHA) > 134. This large SHA was also observed in non-epitaxial BiSb layers deposited by magnetron sputtering35,36,37,38,39, which means that poly-crystalline BiSb can also be used for spin detection by using its large SHA. Non-trivial topologically protected surface states of BiSb have been confirmed by angle-resolved photoemission spectroscopy (ARPES)40,41,42, quantum oscillations43,44, resistivity-temperature characteristics45,46, and very recently, scanning tunneling microscopy (STM) measurements47.

In this work, we prepare a BiSb/(Ga,Fe)Sb heterostructure, where we use (Ga,Fe)Sb (TC > 300 K) as a FMS layer and BiSb as the NM layer, and demonstrate spin injection by spin pumping and spin detection by ISHE at room temperature. Furthermore, by carefully analyzing the voltage signals at various magnetic field directions, temperatures, and microwave powers, we distinguish the intrinsic ISHE signals from parasitic galvanomagnetic contributions, such as anomalous Hall effect (AHE) and planar Hall effect (PHE)8,48,49. Our study provides an important step towards realization of room-temperature semiconductor spintronics devices, such as spin diodes and spin transistors.

Results

Sample growth and experimental procedure

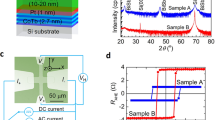
Figure 1a (top panel) shows the schematic structure of our sample. In the BiSb/(Ga0.75,Fe0.25)Sb heterostructure, (Ga,Fe)Sb layer was first grown by molecular beam epitaxy (MBE) followed by BiSb growth using sputtering (see “Methods”). The growth process was monitored in situ by reflection high-energy electron diffraction (RHEED). Figure 1b–d (top panel) show RHEED patterns observed along the \([\overline{1}{\text{1}}{{0}}]\) axis of the sample. During the MBE growth, the (Ga,Fe)Sb thin film showed bright and streaky RHEED [Fig. 1b (top panel)], thereby indicating good two-dimensional growth of a zinc-blende crystal structure. After etching the GaSb cap layer, we observed spotty RHEED, indicating that the (Ga,Fe)Sb surface is exposed [Fig. 1c (top panel)]. Finally, we observed a ring RHEED pattern after depositing BiSb [Fig. 1d (top panel)], indicating poly-crystalline BiSb in our sample. In this way, we deposited a poly-crystalline BiSb film on top of the epitaxial (Ga,Fe)Sb thin film. We characterized the magnetic properties of the BiSb (7 nm)/(Ga,Fe)Sb (50 nm) heterostructure (sample A) and a reference (Ga,Fe)Sb (50 nm) thin film (sample B) using magnetic circular dichroism (MCD) spectroscopy and superconducting quantum interference device (SQUID) magnetometry (see Sections 1 and 2 in the Supplementary Information (S.I.) for detailed characterizations). From the MCD and SQUID characterizations, we confirmed the intrinsic ferromagnetism of (Ga,Fe)Sb in both samples A and B, and that (Ga,Fe)Sb is not affected by the etching of the GaSb cap layer and the BiSb overgrowth. Also, we note that 50 nm-thick (Ga0.75,Fe0.25)Sb has in-plane magnetic anisotropy at room temperature but changes to perpendicular magnetic anisotropy at low temperatures50. These results are further supported by magnetic-field angle dependence of the FMR spectra of (Ga,Fe)Sb in samples A and B, which indicates that there is almost no difference in magnetic anisotropy and the FMR occurs at the same resonance fields in both samples (see Section 3 in S.I. for more details).

Figure 1
figure 1

(a) Schematic illustration of the (001)-oriented sample structure composed of BiSb (7 nm)/(Ga,Fe)Sb (50 nm)/AlSb (100 nm)/AlAs (10 nm)/GaAs (50 nm) grown on a semi-insulating (SI) GaAs (001) substrate. (b–d) In-situ reflection high energy electron diffraction (RHEED) patterns observed along the \([\overline{1}{\text{1}}{{0}}]\) axis with a streaky RHEED pattern during the MBE growth of (Ga,Fe)Sb (b), a spotty RHEED pattern of the interface after anti-sputtering (c), and a ring RHEED pattern of BiSb during sputtering (d). The black dotted line in (c) corresponds to the interface between BiSb and (Ga,Fe)Sb layer. (e) Sample alignment and coordinate system used in the spin pumping measurement. A microwave magnetic field μ0h was applied along the [110] axis of the sample. θH is the angle of the magnetic field H with respect to the [001] axis, respectively, where H is in the (110) plane. (f) Ferromagnetic resonance (FMR) spectra and (g) corresponding electromotive force (EMF) voltage peaks of the BiSb/(Ga,Fe)Sb heterostructure (sample A) measured at various magnetic field H directions (θH = −90° to 90°) at 300 K.

Full size image

For spin pumping measurements, we used an electron spin resonance spectrometer whose cavity resonates in the transverse electric TE011 mode at a microwave frequency of 9.14 GHz. Figure 1e (top panel) shows the BiSb/(Ga,Fe)Sb bilayer structure and coordinate axes used in our spin pumping experiment. For electrical measurements, we have connected the two gold wires at both edges of the sample with a distance of l = 2 mm apart as shown in Fig. 1e (top panel). For the measurements, a static magnetic field μ0H is applied along the \([{1}\overline{\text{1}}{{0}}]\) direction in the film plane (i.e. θH = 90°), which corresponds to the easy magnetization axis of (Ga,Fe)Sb. Here, θH is the out-of-plane angle between H and the [001] axis. A microwave magnetic field μ0h was applied along the [110] axis. The detailed measurement procedure is described in S.I.

Room-temperature spin pumping and spin-to-charge conversion

Figure 1f (bottom panel) shows the FMR spectra at various θH measured at a microwave power of 200 mW. The resonance field μ0HR of the FMR spectra changes from 290 to 336 mT when θH is changed from ± 90° (H // \([{1}\overline{\text{1}}{{0}}]\) and [\(\overline{\text{1}}{{10}}\)]) to 0° (H // [001]). This indicates that the 50 nm-thick (Ga0.75,Fe0.25)Sb film in this work has the in-plane magnetic anisotropy with an easy magnetization axis along the \([{1}\overline{\text{1}}{{0}}]\) axis at 300 K. Figure 1g (bottom panel) shows the electromotive force (EMF) signal V (offset voltage Voffset is subtracted) at various θH. As shown in Fig. 1g (bottom panel), the V–μ0H curves exhibit voltage extrema corresponding to the resonance fields (μ0HR) in the FMR spectra, which indicates that the observed voltage signals were generated by FMR. Also, the θH-dependence of EMF is consistent with the formula EMF ∝ jS × σ, where jS and σ are the spin current and spin polarization vector of the spin current, respectively51,52. When θH is changed from 90° to –90°, the voltage signal changes its sign from positive to negative, but its magnitude is the same, which cannot be explained by the Seebeck effect. The maximum EMF signal is obtained at θH = 90° and –90°, where jS is perpendicular to the σ. On the other hand, the EMF signal disappears at θH = 0°, when jS is parallel to σ. This indicates that the observed EMF signal is consistent with the well-established model of spin injection by spin pumping and spin-to-charge conversion by ISHE.

Next, we investigated EMF vs. magnetic field (μ0H) at various microwave power magnitudes to further confirm the ISHE in our sample. Figure 2a,b show the microwave power dependence of EMF for sample A at 300 K for θH = 90° (H // [\({1}\overline{\text{1}}{{0}}\)]) and –90° (H // [\(\overline{\text{1}}{{10}}\)]), respectively. We note that in both directions, the EMF is proportional to the applied microwave power, which further discards the contribution of the Seebeck effect53. Next, for qualitative analysis, we decomposed the obtained EMF–μ0H curves into a symmetric (Lorentzian) voltage component \({{V}}_{\text{sym}}^{ *}\) and an asymmetric (dispersive) voltage component \({{V}}_{\text{asym}}^{ *}\), using the following fitting expression:

$$\begin{aligned} \text{EMF (}{V } - \, {{V}}_{\text{offset}}) & = {{V}}_{\text{sym}}^{ *} +{{V}}_{\text{asym}}^{ *} , \\ & = {{V}}_{\text{sym}}\frac{{\left({\mu}_{0}{\Delta}{{H}}\right)}^{2}}{{\left({\mu}_{0}{{H}} \, - \, {{\mu}_{0}{{H}}}_{\text{R}}\right)}^{2}+ {\left({\mu}_{0} {\Delta}{{H}}\right)}^{2}} + {{V}}_{\text{asym}}\frac{-{2}{{\mu}}_{0} {\Delta}{{H}}{(}{\mu}_{0}{{H}} \, - \, {{\mu}_{0}{{H}}}_{\text{R}}{)}}{{\left({\mu}_{0}{{H}} \, - {{ \, {\mu}}_{0}{{H}}}_{\text{R}}\right)}^{2} +{ \left({\mu}_{0}{\Delta}{{H}}\right)}^{2}}, \end{aligned}$$
(1)

where μ0ΔH is the half-width at half maximum of the FMR linewidth and μ0HR is the resonance field. Here, Vsym is the magnitude of symmetric (Lorentzian) voltage component and Vasym is the magnitude of an asymmetric (dispersive) voltage component. According to a previous work on spin pumping using (Ga,Mn)As, Vsym includes contributions from the ISHE and PHE, while Vasym originates from the AHE8. As shown in Fig. 2a,b, the experimental data (solid curves) is well reproduced by the fitting function (black dotted curves) of Eq. (1). From Fig. 2c, the estimated Vsym and Vasym components are directly proportional to the applied microwave power, which is an important identity of ISHE. This is also evidenced by the θH dependence of the EMF [Fig. 1g (bottom panel)], where we observed nearly similar voltage extrema ~ 6 μV when θH = 90° (H // [1\(\overline{\text{1}}\)0]) and −90°(H // [\(\overline{\text{1}}\)10]).

Figure 2
figure 2

(a) and (b) Magnetic field μ0H dependences of the voltage signal V (offset voltage Voffset is subtracted) in the BiSb/(Ga,Fe)Sb heterostructure (sample A) measured at 300 K at various microwave powers, ranging from 10 to 200 mW, for θH = 90° and –90°, respectively. The black dotted curves represent fitting which includes a summation of the symmetric and antisymmetric voltage components. (c) Microwave power dependence of the symmetric voltage component magnitude Vsym and antisymmetric voltage component magnitude Vasym at θH = 90° and –90°. The errors bars in (c) are standard deviations obtained from the fitting of the EMF peaks.

Full size image

Next, in order to distinguish the contribution of spin-pumping to Vsym from the parasitic contribution of the PHE in sample A [BiSb/(Ga,Fe)Sb], we performed the FMR measurements on the reference sample B [(Ga,Fe)Sb without BiSb]. In Fig. 3a–c, we compare the EMF signals of sample A and sample B at various θH. While we notice both the strong symmetric and asymmetric components in sample A, the symmetric component is absent in sample B. This result suggests that the contribution of the PHE to Vsym in (Ga,Fe)Sb is negligible. This also negates the contribution of anomalous Nernst effect (ANE) in (Ga,Fe)Sb which also has the symmetric component Vsym. We then use Eq. (1) to fit to the voltage signals and estimate the magnitude of the voltage components Vsym and Vasym for sample A and \({{V}}_{\text{sym}}^{\text{ref}}\) and \({{V}}_{{\text{a}}{\text{sym}}}^{\text{ref}}\) for reference sample B. Figure 3d shows the estimated voltage components as a function of θH. We see that \({{V}}_{\text{sym}}^{\text{ref}}\)<< \({{V}}_{{\text{a}}{\text{sym}}}^{\text{ref}}\) (~ 100 times different) for sample B, which means that the voltage contribution from PHE of (Ga,Fe)Sb is negligible at 300 K. Meanwhile, the parasitic contribution from AHE of (Ga,Fe)Sb at 300 K to the asymmetric voltage component exists in both samples. However, in the case of sample A, Vsym > Vasym, which means that ISHE is stronger and dominant over AHE.

Figure 3
figure 3

(a)–(c) Voltage signals V–Voffset for the BiSb/(Ga,Fe)Sb heterostructure (sample A, red big circles) and reference (Ga,Fe)Sb sample (sample B, green small circles) observed for various magnetic field H directions (θH) at 300 K, where H is in the (110) plane. The microwave power is 200 mW. Blanked circles are experimental data, and a black color dotted line is a fitting curve. Symmetric and antisymmetric component curves, obtained from the fitting, are also shown by small solid circles and squares, respectively. (d) The derived symmetric voltage component magnitude (Vsym) and antisymmetric voltage component magnitude (Vasym) of sample A (red solid symbols) and sample B (green blank symbols) at 300 K. The circles and squares represent Vsym and Vasym, respectively. The errors bars in (d) are standard deviations obtained from the fitting of the EMF peaks.

Full size image

Temperature dependence of the spin injection by spin-pumping

Next, we investigated the temperature dependence of the spin injection by spin pumping from (Ga,Fe)Sb to BiSb. Figure 4a shows the temperature dependence of the resistivity of samples A and B. We note that sample A (with the BiSb layer, red circles) shows larger conductivity than sample B (without BiSb, black circles) at all temperatures, which reflects the much higher electrical conductivity of the BiSb layer37. The estimated electrical conductivities (σGaFeSb, σBiSb) of (Ga,Fe)Sb and BiSb at 300 K are shown in Table 1. Because σBiSb (1.8 × 105 Ω−1 m−1) >  > σGaFeSb (1.4 × 103 Ω−1 m−1), the charge current mostly flows in the BiSb layer. In previous studies on BiSb thin films35,45,46, contribution of the topological surface states (SSs) to the total conductivity of the BiSb layer was estimated by using the parallel conduction model of the surface states and the bulk states. There, it was reported that a 10-nm-thick BiSb layer has a large bandgap of ~ 200 meV due to the quantum size effect, and that the SSs account for ~ 95% of the total current in BiSb even at room temperature. We used a similar parallel conduction model for our 7 nm-thick BiSb thin film and found that ~ 97% of the current flows in the SSs of BiSb at room temperature (see Sections 5–7 in S.I. for more details). This is also consistent with the recent observation using STM in 5.5 nm-thick BiSb thin films, where the band gap of BiSb is found to be further increased to 490 meV due to the strong quantum confinement, and that the Fermi level is in the band gap, so that most of the current flows in the SSs of BiSb47. We will use this information later for the estimation of the ISHA of BiSb.

Figure 4
figure 4

(a) Temperature dependence of the resistivity of the BiSb (7 nm)/(Ga,Fe)Sb (50 nm) heterostructure (sample A, red open circles) and the 50 nm-thick (Ga,Fe)Sb reference (sample B, black open circles). (b) Perpendicular magnetic field μ0H dependence of the anomalous Hall resistance (RAHE) of sample B measured at various temperatures. (c) Saturation values (\({\it\text{R}}_{{{\text{AHE}}}}^{{\text{0}}}\)) of RAHE as a function of temperature in sample B. (d) In-plane magnetic field direction (φH) dependence of the planar Hall resistance (RPHE) of sample B with the applied magnetic field of 50 mT, 80 mT, and 100 mT measured at 300 K. φH is the angle of the in-plane magnetic field with respect to the [\({1}\overline{\text{1}}{{0}}\)] axis. (e) μ0H dependences of the voltage signal V (offset voltage Voffset is subtracted) of sample A measured with 200 mW at various temperatures, ranging from 300 to 10 K, for θH = 90°. The black dotted curves represent fittings which were used to derive the magnitude of the symmetric voltage (Vsym) and antisymmetric voltage (Vasym) components. (f) Vsym and Vasym of sample A as a function of temperature. Red solid circles and black solid squares represent Vsym and Vasym, respectively. The errors bars are standard deviations obtained from the fitting of the EMF peaks.

Full size image
Table 1 Parameters used for the ISHA estimation.
Full size table

We then evaluated the temperature dependence of AHE in reference sample B [(Ga,Fe)Sb without BiSb]. For this purpose, we prepared a Hall bar of 200 μm (length) × 50 μm (width) and measured the temperature dependence of AHE with H // [001]. Figure 4b shows the anomalous Hall resistance (RAHE) as a function of temperature, which increases with decreasing temperature. We know that the saturation values of RAHE, \({{R}}_{\text{AHE}}^{0}\), reflects the AHE from the (Ga,Fe)Sb film; however, due to the presence of the ordinary Hall effect (OHE) along with the AHE, it is difficult to saturate RAHE, especially at high temperatures. Thus, we use RAHE values at 1 T as \({{R}}_{\text{AHE}}^{0}\) which is closer to the saturation values of RAHE. Figure 4c shows \({{R}}_{\text{AHE}}^{0}\) as a function of temperature in sample B, where we see a clear increase in \({{R}}_{\text{AHE}}^{0}\) with decreasing temperature. We also measured the planar Hall resistance (RPHE) as a function of in-plane H angle φH (where φH is the angle between H and the [1\(\overline{\text{1}}\)0] axis), at a constant μ0H of 50 mT, 80 mT, and 100 mT at 300 K [Fig. 4d]. We note that in comparison with \({{R}}_{\text{AHE}}^{0}\) (= ~ 9 Ω), RPHE (= ~ 0.6 Ω) is much smaller at 300 K. Furthermore, although RPHE would follow cos(2φH) dependence, RPHE is actually dominated by the cos(φH) component (see Fig. 4d). This cos(φH) component is due to a small misalignment of the magnetic field from the xy plane, leading to the AHE contribution, while the PHE contribution of \({{R}}_{{\text{P}}{\text{HE}}}^{0}\) cos(2φH) is negligible in Fig. 4d, where \({{R}}_{{\text{P}}{\text{HE}}}^{0}\) is the magnitude of RPHE. Therefore, we conclude \({{R}}_{{\text{P}}{\text{HE}}}^{0}\) << \({{R}}_{\text{AHE}}^{0}\) at room temperature. This result is consistent with the absence of the Vsym component in sample B observed in Fig. 3d.

Next, we measured the temperature dependence of the EMF at θH = 90° in sample A, as shown in Fig. 4e. We found that the EMF peak position i.e. resonance field (μ0HR) changes from 290 to 270 mT when temperature decreases from 300 to 10 K. This change is likely because μ0HR depends on the magnetic anisotropy and the magnetization, both of which have temperature dependency. However, the magnitude and shape of the EMF signals depend on temperature. For example, the EMF peak at 10 K is significantly broader than that at 300 K. To understand this behavior, we fit Eq. (1) to the experimental data to estimate Vsym and Vasym at each temperature. Figure 4f shows the temperature dependence of Vsym and Vasym. At low temperatures, we see clear enhancement of parasitic component Vasym by a factor of 3 at 10 K as compared with that at 300 K, which is consistent with the temperature dependence of RAHE shown in the Fig. 4c. Meanwhile, Vsym shows close values (4.1 ± 0.2–5.1 ± 0.2 µV) at all temperatures, suggesting that the spin injection by spin pumping has small temperature dependence.

Estimation of spin-to-charge conversion efficiency

In this section, we estimate the spin-to-charge conversion efficiency of BiSb, and discuss why BiSb is important to detect spin injection by spin pumping from (Ga,Fe)Sb. We first estimated the spin current density \({{j}}_{\text{S}}^{\text{BiSb/GaFeSb}}\) in sample A [BiSb/(Ga,Fe)Sb] by using the following equation25:

$${{j}}_{\text{S}}^{\text{BiSb/GaFeSb}} = \frac{{{g}}_{\text{r}}^{\uparrow \downarrow}{{\gamma}}^{2}{\left({\mu}_{0}{\it\text{h}}\right)}^{2}{\hbar}\left({4}{\pi}{\mu}_{0}{{{M}}}_{\text{S}}{\gamma} +\sqrt{{\left({4}{\pi}{\mu}_{0}{{{M}}}_{\text{S}}{\gamma}\right)}^{2} + { 4} {\omega}^{2}}\right)}{{8}{\pi}{\alpha}^{2}\left[{\left({{4}{\pi}{\mu}_{0}{{M}}}_{\text{S}}{\gamma}\right)}^{2} \, + 4 {\omega}^{2}\right]},$$
(2)

Here, γ = gμB/\(\hbar\) is the gyromagnetic ratio, where g, μB, and \(\hbar\) are the g factor, Bohr magneton, and Dirac’s constant, respectively, and α = \(\sqrt{3}{\it\gamma}{\Delta H}_{\text{BiSb/GaFeSb}}/{2}{\it\omega}\) is the damping constant, and μ0ΔHBiSb/GaFeSb (= 35 ± 0.5 mT) is the FMR spectral linewidth of sample A when H // [\({1}\overline{\text{1}}{{0}}\)]. Also, μ0h, μ0MS, and \({{g}}_{\text{r}}^{\uparrow \downarrow}\) are the microwave magnetic field, saturation magnetization, and real part of the spin mixing conductance, respectively. The real part of the spin mixing conductance is obtained by

$${{g}}_{\text{r}}^{\uparrow \downarrow} = \frac{{2}\sqrt{3}{\pi}{\mu}_{0}{{{M}}}_{\text{S}}{\gamma}{{d}}_{\text{GaFeSb}}}{{{g}}{\mu}_{\text{B}}{\omega}}\left({\Delta}{{H}}_{\text{BiSb/GaFeSb}}{-\Delta}{{H}}_{\text{GaFeSb}}\right),$$
(3)

where μ0ΔHGaFeSb (= 32 ± 0.5 mT) is the FMR spectral linewidth of sample B when H // [\({1}\overline{\text{1}}{{0}}\)] and dGaFeSb is the thickness of the (Ga,Fe)Sb film. Using Eqs. (2), (3), and the parameters shown in Table 2, we estimated the value of \({{g}}_{\text{r}}^{\uparrow \downarrow}\) and spin current density \({{j}}_{\text{S}}^{\text{BiSb/GaFeSb}}\) at the BiSb/(Ga,Fe)Sb interface at 300 K. The values of \({{g}}_{\text{r}}^{\uparrow \downarrow}\) and \({{j}}_{\text{S}}^{\text{BiSb/GaFeSb}}\) are estimated to be 1.20 × 1019 m−2 and (5.35 ± 0.21) × 10–12 J m−2, respectively.

Table 2 Parameters obtained by fitting our model to the experimental FMR spectra.
Full size table

Finally, we estimated ISHA by using the well-known expression25:

$${{V}}_{{\text{ISHE}} \, } =\frac{{{l}}{\theta}_{\text{ISHE}}{\lambda}_{\text{BiSb}}{\text{tanh}}\left({{d}}_{\text{BiSb}}/{2}{{\lambda}}_{\text{BiSb}}\right)}{{\sigma}_{\text{GaFeSb}}{{{d}}}_{\text{GaFeSb}} + {\sigma}_{\text{BiSb}}{{{d}}}_{\text{BiSb}}}\left(\frac{{2}{\text{e}}}{\hbar}\right){{j}}_{\text{S}}^{\text{BiSb/GaFeSb}},$$
(4)

where, σGaFeSb, σBiSb, dGaFeSb, dBiSb are the electrical conductivities and thicknesses of the (Ga,Fe)Sb and BiSb layers, respectively; l is the length between the electrodes, e is the electron charge, \(\hbar\) is the Dirac constant, and θISHE is the inverse spin Hall angle. The estimated values of these parameters are shown in Table 1. As we discussed above, conduction of the charge current in BiSb occurs only in the SSs of the BiSb. Thereby, we modify Eq. (4) by replacing dBiSb with dS and λBiSb with λS in the numerator part, where dS and λS are the thickness and spin diffusion length of the surface states in the BiSb layer. It is reported that the surface state thickness and spin diffusion length of Bi is dS = 2.0 ± 0.2 nm and λS = 2.4 ± 0.3 nm54. Because BiSb in this work is a topological insulator with a band gap significantly larger than that of Bi, the surface state thickness is expected to be thinner than that of Bi. Therefore, we assume that dS ~ λS = 1.0–1.2 nm in Bi0.85Sb0.1541. The modified expression for ISHA estimation based on the dominant surface conduction is given by

$${{V}}_{\text{ ISHE}} = \frac{{{l}}{\theta}_{\text{ISHE}}{{{d}}}_{\text{S}}{\text{tanh}}\left({1}/{2}\right)}{{\sigma}_{\text{BiSb}}{{{d}}}_{\text{BiSb}}}\left(\frac{{2}{\text{e}}}{\hbar}\right){{j}}_{\text{S}}^{\text{BiSb/GaFeSb}},$$
(5)

Using the parameters in Table 1 and Eq. (5), we estimated ISHA \({\theta}_{\text{ISHE}}\) ~ 2.1–2.6. This \({\theta}_{\text{ISHE}}\) is close to the SHA value θSHE ~ 3.2 reported for non-epitaxial BiSb grown by MBE35 and 2.0–2.4 for sputtered BiSb36,37. As shown in Table 3, the spin-to-charge conversion efficiency at 300 K of BiSb is much larger than those reported in literature. Nevertheless, in the present study, we deposited poly-crystalline BiSb by sputtering on the etched surface of MBE-grown (Ga,Fe)Sb, which may have led to lower ISHA. Thus, an even higher ISHA value may be obtained by growing both BiSb and (Ga,Fe)Sb epitaxially. This large spin-to-charge conversion efficiency of BiSb is the key to detect spin injection by spin-pumping from (Ga,Fe)Sb with the tiny MS ~ 45 emu/cc at room temperature, which is 40 times smaller than that of Fe (1800 emu/cc).

Table 3 Comparison of the spin-to-charge conversion efficiency between our sample with other heterostructures.
Full size table

Conclusion

We have demonstrated spin injection by spin pumping and detection by ISHE in a BiSb/(Ga,Fe)Sb heterostructure at room temperature. This work is the first spin injection experiment using high-TC FMS. From the temperature, microwave power, and magnetic field direction dependences of the ISHE voltage as well as the spin pumping experiment on the reference (Ga,Fe)Sb sample, we conclude that the symmetric voltage component obtained in the BiSb/(Ga,Fe)Sb sample has a negligible galvanomagnetic effect. The result presented in this study opens new opportunities for semiconductor-spintronics device applications operating at room temperature.

Methods

Sample growth

The growth of the sample structure is divided into two parts. We first grew a heterostructure composed of (Ga0.75,Fe0.25)Sb (50 nm)/AlSb (100 nm)/AlAs (10 nm)/GaAs (100 nm) on a semi-insulating (SI) GaAs (001) substrate with a growth rate of 0.5 μm/h by molecular beam epitaxy (MBE), followed by growth of a 2 nm-thick GaSb cap layer to avoid surface oxidation. The substrate temperature (TS) was 550 °C for the GaAs and AlAs layers, 470 °C for the AlSb layer, 250 °C for the (Ga,Fe)Sb and GaSb layer. After that, we preserved a half part of the sample as a reference sample and transferred the other half part of the sample to the sputtering system for the BiSb deposition. There, we first etched the GaSb cap layer using Ar-plasma at room temperature. Then, we deposited a 7 nm-thick Bi0.85Sb0.15 layer with a rate of 5.8 nm/min on top of the 50 nm-thick (Ga,Fe)Sb layer by co-sputtering Bi and Sb targets with Ar-plasma at room temperature. During the MBE growth, the crystallinity and surface morphology of the samples were monitored in situ by reflection high-energy electron diffraction (RHEED) along the [\(\overline{\text{1}}{{10}}\)] azimuth with respect to the GaAs (001) substrate.

Characterizations

The MCD measurements were performed using a J700 system (built by JASCO Corporation) equipped with an electromagnet and a cryostat. AHE measurements were performed on samples etched into 50 × 200 μm Hall bars using photolithography and ion milling.

Spin pumping measurement

In spin pumping experiments, we used a JEOL electron spin resonance (ESR) spectrometer whose cavity resonates in the transverse electric (TE011) mode with a microwave frequency f of 9.14 GHz (X-band). We cut the samples into a 3 × 1 mm2 piece with edges along the \({[110]}\) (3 mm) and \({[1}\overline{\text{1}}{0]} \,\) (1 mm) axes. For electrical measurements, we have connected the two gold wires to the indium contacts at both edges of the sample with a distance of l = 2 mm. The sample was placed on the center of a quartz rod and inserted in the center of the microwave cavity. For the measurements, a static magnetic field μ0H is applied along the [1\(\overline{\text{1}}\)0] axis in the film plane (except for the measurements with varying θH), which corresponds to the easy magnetization axis of (Ga,Fe)Sb. A microwave magnetic field μ0h is applied along the [110] axis. Also, an ac modulation field μ0Hac (1 mT, 100 kHz) parallel to H is superimposed to obtain the FMR spectrum in its derivative form. The voltage between the indium contacts is detected by a nano-voltmeter (see S.I. Section 4).