Abstract
Wolbachia intracellular bacteria successfully reduce the transmissibility of arthropod-borne viruses (arboviruses) when introduced into virus-carrying vectors such as mosquitoes. Despite the progress made by introducing Wolbachia bacteria into the Aedes aegypti wild-type population to control arboviral infections, reports suggest that heat-induced loss-of-Wolbachia-infection as a result of climate change may reverse these gains. Novel, supplemental Wolbachia strains that are more resilient to increased temperatures may circumvent these concerns, and could potentially act synergistically with existing variants. In this article, we model the ecological dynamics among three distinct mosquito (sub)populations: a wild-type population free of any Wolbachia infection; an invading population infected with a particular Wolbachia strain; and a second invading population infected with a distinct Wolbachia strain from that of the first invader. We explore how the range of possible characteristics of each Wolbachia strain impacts mosquito prevalence. Further, we analyse the differential system governing the mosquito populations and the Wolbachia infection dynamics by computing the full set of basic and invasive reproduction numbers and use these to establish stability of identified equilibria. Our results show that releasing mosquitoes with two different strains of Wolbachia did not increase their prevalence, compared with a single-strain Wolbachia-infected mosquito introduction and only delayed Wolbachia dominance.
Similar content being viewed by others
Introduction
Wolbachia infection in arthropods, in particular, Aedes aeqypti mosquitoes is capable of inhibiting the transmission of arboviruses such as Zika (ZIKV), Chikungunya (CHIKV) and dengue viruses (DENV)1,2,3,4. These arboviruses have been estimated to infect over 390 million people annually causing significant global health problems1,5,6,7.
Aedes aegypti mosquitoes do not naturally host the intracellular biosymbiotic Wolbachia bacteria, but can be infected through microinfection3. The Wolbachia-based technique of arboviral vector control is predominantly aimed at two mechanisms: distrupting arboviral transmission between vectors and hosts; and suppressing the vector population8. Some Wolbachia features regulating the success of these mechanisms include immune system preactivation in the vectors, induction of cytoplasmic incompatibility (CI) rendering offspring unviable, imperfect maternal transmission of Wolbachia, loss of Wolbachia infection (LWI) due to high temperature, and superinfection by a second Wolbachia strain9,10,11,12. Based on these features, there are some tradeoffs exhibited by different Wolbachia strains, i.e., some strains induce CI (which is good) but also have LWI due to high temperature (which is bad) and vice versa13,14.
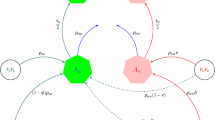
Presently, the wMel-Wolbachia strain is commonly used in the field, with releases in Australia15, Indonesia16, Brazil17, Colombia18, the United States of America and China19. The wAlbB Wolbachia strain was later introduced in Malaysia20, Thailand21, Taiwan22, India14 and wMelPop in Vietnam23, while other strains are yet to be field-tested. Single-strain Wolbachia experimental studies have shown that most crosses between Wolbachia-infected arthropods and wild-type mosquitoes induce unidirectional CI, that is, loss of fertility of a wild-type female mating with a Wolbachia-infected male mosquito, but not the reverse2,24,25,26. In addition, most Wolbachia-infected mosquitoes greatly lose their infection under high temperatures12,27 except those infected with the CI-inducing wAlbB and wAu-Wolbachia strains, which does not induce CI3,10,14. For double-strain Wolbachia experimental studies, CI is typically bidirectional, that is, any mismatch in Wolbachia strain among mating vectors results in infertility; however, CI does not affect crosses involving wAu-Wolbachia-infected males with other Wolbachia-infected females3,6,28,29, opening up a tantalising possibility of two different strains of Wolbachia-infected mosquitoes co-existing (Fig. 1).
Most existing Wolbachia modelling studies have only analysed single-strain Wolbachia dynamics in arthropod vectors11,30,31,32,33,34,35,36,37,38. Meanwhile, those studies that have modelled, discussed or compared the existence of multiple Wolbachia subpopulations1,4,6,28,39, only consider Wolbachia strains with the same CI induction and heat-susceptibility characteristics (e.g. wMel and wMelPop strains). Some recent studies compared two different and separate Wolbachia strains: wAu and wMel40, wAlbB and wMel1, and wAlbB/wMelCS and wMel6. The authors in40 investigated the use of vaccination and two Wolbachia strains (wAu and wMel) to reduce dengue incidence and showed that although both strains can be used to mitigate dengue, wAu performed better than wMel. Flores et al.6, showed that the transmission potential of Wolbachia-infected mosquitoes was greatly reduced for wMelCS and wAlbB compared to wMel. In addition, Xue et al.1, showed that wMel, wAlbB and wMelPop Wolbachia strains can effectively reduce arboviral transmission. However, of the three, wMelPop has the highest fitness cost to the mosquito and would require a sufficiently large number of wMelPop-infecfed mosquitoes to be introduced in order to establish themselves in the Wolbachia-free mosquito population1.
Keeling et al developed continuous-time models that captured the dynamics of mosquitoes with both one and two co-circulating Wolbachia strains28. They showed that in a single-strain model, a Wolbachia-infected population cannot invade a wild-type mosquito population unless the proportion of infected mosquitoes is high enough to break through the critical infection threshold—an example of the Allee effect41. For two strains, they showed that the models exhibit the founder control effect28: either of the strains could invade from low density levels if the other strain is present. Further, in a mixed mosquito population with two Wolbachia strains, the authors showed the coexistent equilibrium is unstable as one strain will knock out the other depending on the parameters and densities defining the strains. That is, a Wolbachia dominant strain defined by Wolbachia-favourable parameters will outperform the other28. However, moving from a homogeneous to a spatially heterogeneous system, the two Wolbachia strains may coexist locally. This could be established only by the inflow of two different Wolbachia strains in the areas defined between bounded regions of different patches of Wolbachia-infected mosquito habitats28. Similar studies investigated the introduction of Wolbachia-infected mosquitoes with different mortality and fertility rates and showed that Wolbachia-infected mosquitoes will not dominate the wild-mosquito population if the efficacy of the vertical (maternal) transmission is less than 75%42. In addition, Wolbachia infection was predicted to easily spread among the wild-type population for higher transmission rates43. Two recent modelling studies44,45 considered the spread of Wolbachia infection in mosquitoes via delay differential equations. They showed that Wolbachia infection will established itself and dominate the wild-type mosquito population if the Wolbachia release level surpasses the basic reproductive number of the Wolbachia-infected mosquitoes44,45. Another recent modelling study39 showed that the introduction of multiple Wolbachia strains could be more efficient than a single-strain introduction depending on the number, frequency and fitness cost of Wolbachia introductions. For low fitness cost imposed by Wolbachia, the single-strain introduction is efficient in achieving Wolbachia dominance with more frequent introductions of the same strain. In this work, we want to assess whether two-Wolbachia-strain introduction is better than one with respect to the Wolbachia loss and CI attributes of each strain.
As mentioned above, the wAu and wAlbB strains are heat-resistant however, wAu does not induce CI. On the other hand, the wMel strain does induce CI but is more heat sensitive. The wMel strain is effective at reducing transmission potential (quantified by the presence or absence of dengue virus in saliva-inoculated mosquitoes) but not as effective as wAlbB and wMelCS3,6. Therefore, the two-strain model involving different CI and heat loss features of Wolbachia strains such as wAu and wMel, wAu and wAlbB or wAlbB and wMel has the potential to demonstrate synergies of these strains. Such two-strain models have to the authors knowledge not previously been developed.
In this study, we develop a general two-strain Wolbachia model that could account for any two particular Wolbachia strains. We then adjust the model to capture two particular Wolbachia strains with contrasting high temperature and CI induction behaviours (Fig. 1). The general Wolbachia model is an extension of the single-strain Wolbachia transmission model considered in13, which explored the dynamics between crosses of wAu and wild-type, and wMel and wild-type mosquitoes. The results in13 showed that despite a lack of CI-induction, the single wAu strain could be more effective than wMel in sustaining Wolbachia infection as its Wolbachia infection retention feature could outweigh that of CI-inducing strains such as wMel, which is susceptible to high temperature. In our adjusted two-strain Wolbachia model, we consider both uni-and bi-directional CI together with temperature-induced Wolbachia loss where necessary. We also consider the effect of imperfect maternal transmission in the model. We analyse the resulting differential system by computing the basic and invasive reproductive numbers and explore the two-strain Wolbachia model’s practicality for Wolbachia dominance.
Methods
Model formation
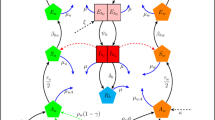
In this study, we formulate a general two-strain Wolbachia model which accommodates the combined interaction of two Wolbachia strains with arbitrary characteristics. The total mosquito population is categorised into three subpopulations namely the wild-type, uninfected mosquitoes (u), mosquitoes infected with the first Wolbachia strain (\(w_1\)) (e.g., wAu), and mosquitoes infected with the second Wolbachia strain (\(w_2\)) (e.g., wMel/wAlbB) (see Supplementary figure S2). The Supplementary figure S2 shows the population progression from matings of male and female adult mosquitoes (from nine possible mating pairs) to offspring, regulated by CI effects, imperfect maternal transmission (IMT) and Wolbachia infection loss for a general two-strain Wolbachia model. As a particular example, that includes the effects of both uni and bidirectional CI and IMT, Fig. 1 depicts the population progression following the feasible matings between wAu-like and wMel-like adult mosquitoes. Other schematics showing the two-strain Wolbachia combinations of wAu and wAlbB, and wMel and wAlbB are shown in the Appendices section (Supplementary Figures S3 and S4).
Model schematic of Mosquito-Wolbachia dynamics between uninfected mosquitoes u and Wolbachia-infected mosquitoes with strains \(\mathbf {w_1}\) (wAu-like) and \(\mathbf {w_2}\) (wMel-like). The green, red, and blue represent the uninfected, wAu-Wolbachia-infected and wMel-Wolbachia infected mosquito populations respectively. The lines (solid and dashed) represent the population progression where the dashed lines indicate the imperfect maternal transmission (IMT). The black arrows represent deaths. The cytoplasmic incompatibility (CI) induction which inhibits the production of offspring has been adjusted where required. \(A\longrightarrow\) Aquatic (eggs, larvae and pupae) mosquitoes and \(F\longrightarrow\) Adult mosquitoes.
Let F, M and A be the total number of female, male and aquatic mosquitoes respectively:
where subscripts denote the infection status of each subpopulation. Equation (1) describes the total sum of uninfected, \(w_1\)-Wolbachia-infected and \(w_2\)-Wolbachia-infected mosquitoes for adult female, male and aquatic individuals. In what follows, we assume \(M=F\) so as to simplify the system following observational studies that recorded no significant difference in male to female (Aedes aegypti and Aedes albopictus) mosquito ratio48,49. The mathematical equations describing the two-strain Wolbachia transmission dynamics together with the mosquitoes’ reproductive rates for the general case are written as:
where, \(i\epsilon \{w_1, w_2\}\) represents the infection status/type, the carrying capacity (K) is a derived parameter quantifying the availability of the mosquito ovipositional breeding sites in a given location where aquatic stage mosquitoes would mature into adulthood. For our purposes, K provides an upper bound on the size of the aquatic stage mosquito population in a particular location. The differential equations in (2) represent the dynamics of the compartments for the \(A_u, F_u, A_i, F_i\) which yield the number of uninfected aquatic stage, uninfected adult, i-infected aquatic stage and i-infected adult mosquitoes respectively. Therefore,
where \(\rho _{j}F_j \sum _{k\epsilon \{u,w_1,w_2\}}\left( [1-\eta _{jk}] [1-\phi _{jk}]F_k\right)\) is the proportion of mosquito offspring that are generated from the mating combination of a female mosquito with infection status i and any other (infected or uninfected) male mosquito and accounting for CI as necessary. The \(\xi _u\) and \(\xi _i\) in equation (3) represent the total reproductive rates (measured as eggs per day) across all breeding combinations for uninfected and i-infected aquatic mosquitoes respectively.
Each of the model parameters appearing in equations (2) and (3) are described in Table 1. To rescale the above differential system with respect to the total population size using K, we have that \(\sum _{k}A_k\), the sum of the aquatic stage mosquitoes with infection \(k\epsilon \{u, w_1, w_2\}\) is less than or equal to the carrying capacity, which yields
This implies that
From system (2), we also have the constraints \(F_i \le \dfrac{\tau _i K}{2(\sigma _i + \mu _i)}\), and \(F_u \le \dfrac{K}{2\mu _u}\left( \tau _u + \sum _{j}\dfrac{\sigma _j \tau _j}{\sigma _j + \mu _j}\right) .\) Combining the above results yields
where \(\alpha = 1+\dfrac{1}{2}\left( \dfrac{\tau _u}{\mu _u} + \sum _{j} \dfrac{\tau _{j}}{(\mu _{j} +\sigma _j)}\left( 1+\dfrac{\sigma _j}{\mu _u}\right) \right)\).
Given the above, it is straightforward to show that the closed set
is the feasible region for the system dynamics and is positively invariant30.
Rescaling each of the state variables in terms of the quantity \(\alpha K\) gives
Therefore, the general Wolbachia model in equation (2) in terms of population proportion becomes equation (4). Hence, in the scaled system (4), the sum of the state variables has an upper bound of 1. That is,
Results
Model equilibria
The main three features of our general, two-strain Wolbachia model (4) are: (i) loss of infection at high temperatures; (ii) cytoplasmic incompatability; and (iii) imperfect maternal transmission. With these Wolbachia characteristics, we want to calculate the system equilibria and determine the conditions for their stability. Theoretically, we investigate six possible equilibrium points: a mosquito-free equilibrium; a wild-type (infection-free) mosquito-only equilibrium; a single-strain Wolbachia-only equilibrium; a coexistent wild-type and single-strain Wolbachia-infected equilibrium; a coexistent two different Wolbachia strains equilibrium; and finally, a multi-strain equilibrium where all three mosquito subpopulations coexist. We find that the first four of these are possible, but the last two are not.
To facilitate our equilibrium analysis, we first calculate a set of basic and invasive reproductive numbers for each mosquito subpopulation, both in the presence and absence of other mosquitoes. The set of invasive reproductive numbers represent the number of new mosquitoes of a particular type (specified by the first index, prior to the | separator) that would be generated by a single mosquito of that type when introduced into various mosquito population backgrounds (specified by the second index, following the | separator). For example, the quantity \(R_{0i|u}\) is the average number of new mosquitoes with infection i that would be produced by a single i-infected mosquito throughout its lifespan, when it is introduced into a background of uninfected mosquitoes. Whereas, \(R_{0u|i}\) is the average number of new uninfected mosquitoes generated by the introduction of an uninfected mosquito into an endemic mosquito population with infection status i, throughout its lifetime. An exception to this convention are the quantities \(R_{0u}\) and \(R_{0i}\) which respectively give the number of the new uninfected and infected mosquitoes generated (per index) when no (or few) background mosquitoes are present. Following this definition we see that each of the \(R_0\) terms represent ratios and are therefore dimensionless. Hence, \(R_{0u}\) and \(R_{0i}\) are derived as:
where we have substituted in the values \(\phi _{uu} = \phi _{ii} = 0\). This is because CI does not affect the matings between mosquitoes with the same infection status. In the event of perfect maternal transmission (i.e., \(\eta _{ii} = 1\)) and infection retention (\(\sigma _i = 0\)), the basic reproductive numbers of the Wolbachia strains (\(R_{0i}\)) become analogous to the simpler expression given for the wild-type subpopulation (\(R_{0u}\)).
For the mosquito-free equilibrium, we find that it is ecologically unrealistic, however, we numerically showed that if \(\max {[R_{0u},R_{0i}]}<1\) the mosquito populations will go extinct, otherwise, they will persist (see Supplementary file and Figure S1).
Next, we will establish the single (Wolbachia-free and Wolbachia-infected) mosquito population equilibrium points and determine the conditions under which they are stable.
Wolbachia-free mosquitoes only
For the two-strain model (4), we first consider the existence and stability conditions for the persistence of Wolbachia-free mosquitoes only. We find that the infection-free equilibrium point is
where the overbar and superscript denote that these state variables are equilibrium values. The equilibrium point \(e_u\) exists if and only if \(R_{0u}>1\).
Using the next generation matrix method, we obtain the invasive reproductive numbers \(R_{0i|u}\) which are the average number of offspring that will be \(i\epsilon \{w_1, w_2\}\) Wolbachia-infected after introducing a single infected adult into a completely susceptible (wild-type) mosquito population. We find that for any two competing strains \(\phi _{iu}=\phi _{ii}=0\) (no CI induction between \(F_iM_u\) and \(F_iM_i\)), such that \(\xi _{u}\rightarrow \rho _u(1-\phi _{uu})F_u = \rho _u F_u\) and \(\xi _{i}\rightarrow 0\). In this case, we find
where \(R_{0i|u}\) in equation (5) is the invasive reproductive number with respect to infected mosquitoes with infection i. To establish the stability of \(e_u\), we evaluate the Jacobian at this equilibrium point, \((J^{e_u})\), and then calculate the characteristic equation \(|J^{e_u}-\lambda I|=0\), which gives:
where
Therefore, \(e_u\) is locally asymptotically stable if and only if \(R_{0u}>1\), \(R_{0w_1|u}<1\) and \(R_{0w_2|u}<1\) (see Fig. 2).
Wolbachia-free mosquito equilibrium point \(e_u\): The stability conditions for the numerical simulations using \(\rho _u = 10\), \(\rho _{w_1} = 13\), and \(\rho _{w_2} = 11\), leading to \(R_{0u}=98>1\), \(R_{0w_1|u}=0.66<1\) and \(R_{0w_2|u}=0.51<1\). Other parameters used are consistent with Table 1.
i-Wolbachia-infected mosquito population only
Here, we consider the stability conditions for the persistence of a single strain of i-Wolbachia-infected mosquitoes, and the extinction of all other subpopulations (j-Wolbachia-infected mosquitoes where \(j\ne i\)). For the equilibrium point \(e_i\), \(i\epsilon \{w_1,w_2\}\) to exist, there must be no loss of Wolbachia infection (\(\sigma _i=0\)) and the maternal transmission of Wolbachia infection to offspring must be perfect (\(\eta _{ii}=1\)). From the two-strain Wolbachia model (4), the equilibrium point \(e_i\), \(i\epsilon \{w_1,w_2\}\) is obtained as
which requires \(R_{0i}>1\). Once again we can use the Jacobian method to calculate the invasive reproductive number for the wild-type mosquito population against a background of type i-infected mosquitoes; this yields:
where \(R_{0u|i}\) in equation (6) is the invasive reproductive number due to uninfected mosquitoes and \(\phi _{ui}\) represents the effect of unidirectional CI between an i-infected male and an uninfected female.
We can also derive the invasive reproduction number of the other Wolbachia strain \(j \ne i\) in equation (7) as
where \(\phi _{ji}\) represents the bidirectional CI effect between a j-infected female and an i-infected male. \(\eta _{ji}\) and \(\eta _{jj}\) denote the proportion of mosquito offspring with j infection produced from a j-infected female mosquito mating with either an i-infected or j-infected male mosquito respectively.
Each of the Wolbachia strains \(i\epsilon \{w_1\text {or}w_2\}\) can establish itself when introduced separately (single Wolbachia-infected mosquito introduction) as their equilibrium points are stable13, for the parameter values listed in Table 1.
To establish the stability of the i-Wolbachia-infected population equilibrium point \(e_{i}\), we evaluate the Jacobian J of the system at \(e_{i}\) and compute the characteristic equation in equation (8) as follows:
where,
Therefore, the conditions for stability of \(e_{i}\) are: \(R_{0i}>1\), \(R_{0u|i}<1\), \(R_{0j|i}<1\) (\(i\ne j\)).
To demonstrate the \(e_i\) stability conditions for two specific Wolbachia strains, let \(w_1=w\text {Au}\) and \(w_2=w\text {Mel}\) describe the properties of wAu and wMel Wolbachia strains respectively. These two Wolbachia strains differ in their Wolbachia infection retention and CI effect. Therefore, accounting for these differences, the conditions for stability of the wAu Wolbachia-infected population equilibrium point (\(e_{w_1}\)) are given as \(R_{0w_1}>1\), \(R_{0u|w_1}<1\), \(R_{0w_2|w_1}<1\) (see Fig. 3a).
\(\mathbf {w_1}\)(wAu)-infected mosquito equilibrium point \(\mathbf {e_{w_1}}\): The graphs show the local stability conditions for \(e_{w_1}\). Using \(\rho _u = 10\), \(\rho _{w_1} = 40\), and \(\rho _{w_2} = 11\), (a) we set \(\eta _{w_1w_1}=1\), \(\sigma _{w_1}=0\) and the stability conditions \(R_{0w_1}>1\), \(R_{0u|w_1}<1\) and \(R_{0w_2|w_1}<1\) are satisfied. (b) On setting \(\eta _{w_1w_1}=0.97\), the \(e_{w_1}\) equilibrium point becomes unstable and shifts to \(e_{uw_1}\). Other parameters used are consistent with Table 1.
Figure 3a showed the stability of the wAu-Wolbachia-infected population provided that perfect maternal transmission (\(\eta _{w_1w_1}=1\)) and no Wolbachia infection loss (\(\sigma _{w_1} = 0\)) was observed. But as the maternal transmission becomes imperfect (\(\eta _{w_1w_1}<1\)), the equilibrium point becomes unstable due to leakage of uninfected mosquitoes as seen in Fig. 3b. Similarly, the same corresponding effect as observed in Fig. 3b is seen if there is an increase in the Wolbachia infection loss (\(\sigma _{w_1} > 0\)).
For the uninfected mosquito population to coexist with Wolbachia-infected mosquitoes, one of these two conditions must be satisfied: there must either be a continuous loss of Wolbachia infection (\(\sigma _{i}>0\)), or maternal transmission is imperfect (\(\eta _{ii}<1\)). Table 2 below provides the CI parameters used in this section.
By these adjustments, we have the coexistence equilibria described below.
Uninfected and single-infected mosquito populations
Here, we consider the general case of model (4), and in the subsections that follow, special cases are investigated. The general equilibrium point \(e_{ui}\) for coexisting uninfected and one of \(i\epsilon \{w_1,w_2\}\) infected mosquito populations is
where
and
as
where,
Therefore, for \(e_{ui}\) to exist for any i-Wolbachia strain, \(\eta _{ii}<1\) or \(\sigma _{i}>0\) given the conditions \(\beta \mu _{u} > \sigma _i\) and for \(H\ge 1\), \(\eta _{iu}\le \eta _{ii}\le 1\). To establish stability, \(R_{0i}>H\ge 1\), \(R_{0i|u} > 1\), \(\left( \frac{R_{0u}}{R_{0i}}\frac{\sigma _i}{\mu _u}R_{0i|u}+R_{0u|i}\right) >1\) and \(\eta _{ii}<1\) must be satisfied. According to the Routh-Hurwitz criterion for polynomials50, \(e_{ui}\) with equation 10 is stable if and only if \(\{\frac{b_1}{a_1},\frac{c_1}{a_1}\} >0\). Although \(e_{ui}\) could exist if \(R_{0i|u} < 1\), \(\left( \frac{R_{0u}}{R_{0i}}\frac{\sigma _i}{\mu _u}R_{0i|u}+R_{0u|i}\right) <1\), it is unstable as \(\frac{c_1}{a_1}<0\). Interestingly, \(e_{ui}\) will exist if the Wolbachia-infected mosquitoes do not go extinct when introduced into a completely susceptible wild-type mosquito population provided that there is either no perfect maternal transmission of Wolbachia infection \(\eta _{ii}<1\) or loss of Wolbachia infection at high temperature \(\sigma _{i}>0\) occured.
The demonstration of the uninfected and specific Wolbachia-infected mosquitoes’ existence has been done by13, where the authors considered the coexistence of uninfected and wAu-Wolbachia-infected mosquitoes. The existence conditions in13 are consistent with the existent conditions described in this section.
\(w_1\) and \(w_2\) infected mosquito populations
The equilibrium point for coexisting \(w_1\) and \(w_2\) infected mosquito populations in the absence of wild-type does not exist. This is because there is no dynamical link connecting the population progression of both strains. Although our model described that \(w_1\) strain does not induce CI, \(w_2\) does. Therefore, these two strains could not coexist in the absence of wild-type mosquitoes as a result of direct offspring competitive exclusion.
We proceed to investigate the three populations existence equilibrium point.
Uninfected, \(w_1\) and \(w_2\) infected mosquito populations
The equilibrium point for the uninfected, \(w_1\) and \(w_2\) populations will only exist if \(R_{0w_1|u}>1\), \(R_{0u|w_1}<1\), \(R_{0w1|u}>R_{0w2|u}\), \(R_{0w_2|w_1}>1\) (see Supplementary file). The last two conditions are incompatible if the maximum proportion of offspring generated via maternal transmission is perfect, i.e., \(\textrm{max}\{\eta _{ij}=1\}\). This shows that there is no biologically stable equilibrium, only a temporary coexistence can be demonstrated numerically and this has potential advantages.
The numerical simulations showing pseudo existence of \(\mathbf {e_{uw_1w_2}}\). For \(R_{0u},R_{0w_1},R_{0w_2}>1\), using \(\rho _u = 10\), \(\rho _{w_1}=41.5\) and \(\rho _{w_2}=30\), (a) Showed that mosquitoes with strains wAu (with maternal transmission of \(\eta _{w_1w_1}=0.97\)), wMel (\(\eta _{w_2w_2}=0.97\)) and wild-type exist for a time and then one of the Wolbachia infected mosquitoes-wMel is eliminated by the other dominating wAu-infected mosquito population showing instability. (b) Showed that an infinitesimal decrease in the reproductive rate of wAu-infected mosquitoes, i.e. (\(\rho _{w_1}=41.4\)), eliminates wAu-infected mosquito population and allows for the coexistence of uninfected and wMel-infected mosquitoes. Other parameters are consistent with Table 1.
For the three (uninfected, wAu-infected, wMel-infected) mosquito populations to temporarily exist, we require \(R_{0u}, R_{0w_1}, R_{0w_2}>1\) (see Fig. 4). It is observed that, the populations can only exist at most for some time (1-2 years) in this case, however, the dominating Wolbachia strain will eventually knock out the other depending on parameters contributing to its invading force or characteristics such as maternal transmission of Wolbachia infection, reproductive and loss of Wolbachia infection rates (Fig. 4). This is called the founder control as established in28. Interestingly, some mathematical and biological implications could be derived between the pseudo-stable times prior to the founder control effect. These implications are elaborated in the next section (Section 5) outlining the tradeoffs between using one and two strains of Wolbachia infected mosquitoes to control arboviral infections.
The trade off between one and two Wolbachia strains
The competitions between the Wolbachia uninfected and infected mosquitoes vary. However, these competitiveness is based on the contributions of CI, per capita reproductive rate and loss of Wolbachia to their reproduction rates. First, in the absence of loss of Wolbachia infection, two different Wolbachia infected mosquitoes that each possess CI (i.e. four out of nine possible mating combinations will induce CI) could be advantageous compared to other paired combinations. In addition, this advantage could also outweigh that of a CI-inducing single Wolbachia strain (one out of four possible mating combinations only induce CI). However, this is not the case as the temperature effect will take its course on the Wolbachia-infected mosquitoes due to seasonally-varying weather conditions.
Therefore, considering the effect of temperature, we model the \(\sigma _i\) (the loss of Wolbachia infection rates for the \(i\epsilon \{w_1,w_2\}\) Wolbachia infection) as a function of seasonal variations (with time) for Wolbachia loss in equation (14)
where \(\sigma _{m_i}\) describes the maximum value of the seasonal fluctuation in the Wolbachia loss for the corresponding strains \(i\epsilon \{w_1,w_2\}\). \(\varOmega\) represents the phase shift of the transcedental function that positions the model with the seasonal variation. Figure 5a shows the Wolbachia frequency levels for a single-strain (wAu, wMel and wAlbB) and a combination of double-strain (wAu with wMel, wAu with wAlbB and wMel with wAlbB) Wolbachia-infected mosquitoes in the presence/absence of CI and Wolbachia infection loss properties. Figure 5a is disintegrated into Figures (b),(c),(d),(e),(f) and (g). Figure 5b describes the single-strain wAu-Wolbachia-infected mosquito dominance after 7-8 months in the absence of Wolbachia heat loss and CI induction. On the other hand, Fig. 5c visualises the effect of LWI on single-strain wMel-Wolbachia-infected mosquitoes seasonally over the years despite lack of CI. Figure 5d shows similar dynamics as in Fig. 5b but had a decreased number of wild type mosquitoes and as a result, increased number of wAlbB mosquitoes due to lack of CI. For the double-strain (wAu with wMel), Wolbachia-infected mosquitoes, Fig. 5e shows that the two strains could be maintained before exhibiting the founder control and as such, a gradual dominating strain (wAu in this case) knocks out the other (wMel) after 1.4 years. This occured as wMel-mosquitoes with CI continually lose their Wolbachia infection due to heat while the non CI-inducing wAu-mosquitoes do not, therefore strengthening the fact that the gains from not losing Wolbachia infection outweigh those of CI13. Further, Fig. 5f shows that the combination of the two (wAu and wMel) Wolbachia strains would lead to a longer time for dominance to occur as seen in Fig. 5a.
For the other two-strain combinations i.e wAu and wAlbB, and wMel and wAlbB (Fig. 5f,g), there is an increase in the frequency levels of Wolbachia compared to wAu- and wMel-only strain (as seen in Fig. 5a). However, it was observed that wAlbB-only Wolbachia strain was able to dominate faster and performed best in all comparisons in terms of having higher affinity to retain Wolbachia infections in mosquitoes at high weather temperatures in the absence of CI (Fig. 5a).
Therefore, starting a Wolbachia rollout with two strains simultaneously may not be advantageous as the time to dominate the population could be reached faster using a single strain with high Wolbachia retention at high temperature in the absense of CI (see Fig. 5).
Wolbachia frequency levels for both single and double-strain Wolbachia-infected mosquitoes in the presence/absence of CI and Wolbachia infection loss. (a) Showed the Wolbachia frequency levels of both one-strain—wAu; wMel; wAlbB, and two-strain—wAu & wAlbB; wAu & wMel; and wMel & wAlbB Wolbachia-infected mosquitoes, accounting for the effects of uni- and bidirectional CIs and the LWI (parameters used can be found in Table 3). (b) Showed the adult mosquitoes for wAu-Wolbachia only competition with the wild type mosquitoes as in wAu only Wolbachia frequency in (a). (c) Showed the adult mosquitoes for wMel-Wolbachia competition only with uninfected mosquitoes as in wMel only in (a). (d) Showed the adult mosquitoes for wAlbB-Wolbachia competition only with uninfected mosquitoes as shown in (a). (e) Showed the adult mosquito population of the two strain competition of wAu and wMel together with wild-type mosquitoes for the Wolbachia frequency of wAu and wMel in (a). (f) Showed the adult populations for uninfected, wAu- and wAlbB-infected mosquitoes for the Wolbachia frequency in (a). (g) Showed the adult populations for wAlbB- and wMel-infected mosquitoes for the Wolbachia frequency in (a).
Discussion
In this paper we set out to explore the impact of introducing two Wolbachia strains simultaneously. Using information on the ecological dynamics of multiple Wolbachia strains with various characteristics1,6,28,29,39, we were interested in exploring stable co-existence and synergistic effects. We found neither of these. Specifically, we found that the fitter Wolbachia-infected mosquito strain would dominate and eliminate the other strain meaning that co-existence would always be temporary. Furthermore, the temporary co-existence did not increase prevalence of Wolbachia strains, and either had no impact or reduced prevalence.
Our motivation for examining co-existence was based on the recognition that some studies have shown that a Wolbachia strain: wAu, does not exhibit either unidirectional or bidirectional cytoplasmic incompatibility (CI)3,10. That is, when a wAu-infected Wolbachia male mosquito is crossed with another strain Wolbachia-infected female, they produce offspring with the other Wolbachia strain. For this reason, we believed that combining wAu with other strains may not interfere with the dynamics of the other strain and could potentially be synergistic. This is particularly so because wAu has the positive feature of high heat tolerance, which plausibly may outweigh the lack of CI13,30. Therefore, we developed a two-strain general model (4) and tuned the parameters to reflect properties of wAu, wMel and wAlbB in turn.
Our two-strain general model described the transmission dynamics of uninfected and Wolbachia-infected mosquitoes with two different strains (Supplementary Figure S2). We derived the general mosquito-free reproduction numbers and further established the Wolbachia invasive reproduction numbers singly for the two strains using the Wolbachia-infection free equilibrium point. These invasive reproduction numbers were used to establish the local stability conditions of the equilibrium points and were in line with results from single strain models reported previously13. In the general model, we specifically examined wAu: with absent CI and good Wolbachia retention in heat and we combined this (in our in silico model) with wMel & wAlbB: CI present in both and loses/retains Wolbachia infection in heat, respectively. Considering the transmission dynamics involving these single strains, we established that there was local stability for each of wAu-infected and wAlbB-infected mosquitoes and that they would dominate uninfected mosquitoes provided there was no loss of Wolbachia infections due to high temperature and a complete maternal transmission is exhibited from male and female mosquito crosses with similar strains. However, a single population of only wMel-infected mosquitoes does not exist indefinitely, as uninfected mosquitoes emerge because of loss of infection in this strain at high temperatures.
For each of the strains wAlbB and wAu-infected mosquitoes, we assume perfect maternal transmission and no heat loss. Under these circumstances there is no stable equilibrium with uninfected mosquitoes. The system dynamically converges to a single-population equilibrium i.e either uninfected or wAu/wAlbB-only-infected population. This is because, the perfect maternal transmission blocks any leakage of uninfected offspring making the steady state of zero uninfected mosquitoes and 100% wAu-infected mosquitoes stable provided its invasive reproduction number is greater than one. In contrast, the coexistence of the uninfected and the CI-inducing wMel-infected mosquitoes exists as the wMel-infected mosquitoes are continuously losing their infections due to high temperature. Under these circumstances, the coexistence with uninfected mosquitoes will continue to exist provided there is Wolbachia infection loss. For all three strains, there is a potential uninfected-mosquito only equilibrium if the Wolbachia-infected mosquitoes are unable to invade an existing uninfected population (when the invasive reproduction number for Wolbachia infected mosquitoes is less than one).
While co-existence of a single strain of wMel and uninfected mosquitoes is stable (via loss of Wolbachia infection in mosquitoes), we found no such stability point for two different strains of Wolbachia-infected mosquitoes. Nevertheless, we showed through numerical simulation that under plausible parameter ranges, Wolbachia strains may coexist for a year or two. However, this co-existence is always temporary and cannot attain stability as one strain will dominate the other to exclusion. Once a population of mosquitoes is present in the population, it becomes harder for species to invade, and the founder strain will exclude any competing strain28. We showed numerically that before hitting founder control, the two different Wolbachia-infected mosquito populations coexisted for some time, providing some hope of establishing a synergistic effect. However, our study showed that introducing two strains of Wolbachia simultaneously could neither fast track the time to Wolbachia dominance in the wild-population nor increase the Wolbachia prevalence compared to a single Wolbachia strain release of the fitter strain (in our context wAlbB). This was also true for the combination of wAu and wMel, with wAu as a single strain out-performing the introduction of both strains simultaneously.
Our work therefore leads to the recommendation of rolling out one-strain of Wolbachia-infected mosquitoes with optimal characteristics (high Wolbachia infection retention at high temperature, high maternal transmission and complete CI) rather than attempting mixed strain rollouts.
Data availability
All data generated or analyzed during this study are included in this published article [and its supplementary information files].
References
Xue, L., Fang, X. & Hyman, J. M. Comparing the effectiveness of different strains of Wolbachia for controlling chikungunya, dengue fever, and zika. PLoS Negl. Trop. Dis. 12, e0006666. https://doi.org/10.1371/journal.pntd.0006666 (2018).
Walker, T. et al. The wMel Wolbachia strain blocks dengue and invades caged Aedes aegypti populations. Nature 476, 450–3. https://doi.org/10.1038/nature10355 (2011).
Ant, T. H., Herd, C. S., Geoghegan, V., Hoffmann, A. A. & Sinkins, S. P. The Wolbachia strain wAu provides highly efficient virus transmission blocking in Aedes aegypti. PLoS Pathog. 14, e1006815. https://doi.org/10.1371/journal.ppat.1006815 (2018).
Hoffmann, A. A., Ross, P. A. & Rasic, G. Wolbachia strains for disease control: Ecological and evolutionary considerations. Evol. Appl. 8, 751–68. https://doi.org/10.1111/eva.12286 (2015).
Bhatt, S. et al. The global distribution and burden of dengue. Nature 496, 504–7. https://doi.org/10.1038/nature12060 (2013).
Flores, H. A. et al. Multiple Wolbachia strains provide comparative levels of protection against dengue virus infection in Aedes aegypti. PLoS Pathog. 16, e1008433. https://doi.org/10.1371/journal.ppat.1008433 (2020).
Utarini, A. et al. Efficacy of Wolbachia-infected mosquito deployments for the control of dengue. N. Engl. J. Med. 384, 2177–2186. https://doi.org/10.1056/NEJMoa2030243 (2021).
Ogunlade, S. T. et al. A review: Aedes-borne arboviral infections, controls and Wolbachia-based strategies. Vaccines 9, 32. https://doi.org/10.3390/vaccines9010032 (2021).
Sim, S., Jupatanakul, N. & Dimopoulos, G. Mosquito immunity against arboviruses. Viruses 6, 4479–4504. https://doi.org/10.3390/v6114479 (2014).
Mancini, M. V., Herd, C. S., Ant, T. H., Murdochy, S. M. & Sinkins, S. P. Wolbachia strain wAu efficiently blocks arbovirus transmission in Aedes albopictus. PLoS Negl. Trop. Dis. 14, e0007926. https://doi.org/10.1371/journal.pntd.0007926 (2020).
Dorigatti, I., McCormack, C., Nedjati-Gilani, G. & Ferguson, N. M. Using Wolbachia for dengue control: Insights from modelling. Trends Parasitol. 34, 102–113. https://doi.org/10.1016/j.pt.2017.11.002 (2018).
Ross, P. A. et al. Heatwaves cause fluctuations in wMel Wolbachia densities and frequencies in Aedes aegypti. PLoS Negl. Trop. Dis. 14, e0007958. https://doi.org/10.1371/journal.pntd.0007958 (2020).
Ogunlade, S. T., Adekunle, A. I., Meehan, M. T., Rojas, D. P. & McBryde, E. S. Modeling the potential of w Au- Wolbachia strain invasion in mosquitoes to control Aedes -borne arboviral infections. Sci. Rep. 10, 1–16. https://doi.org/10.1038/s41598-020-73819-1 (2020).
Gunasekaran, K. et al. Sensitivity of wMel and wAlbB Wolbachia infections in Aedes aegypti Puducherry (Indian) strains to heat stress during larval development. Parasites Vectors 15, 221. https://doi.org/10.1186/s13071-022-05345-0 (2022).
O’Neill, S. L. et al. Scaled deployment of Wolbachia to protect the community from Aedes transmitted arboviruses. Gates Open Res. 2, 36. https://doi.org/10.12688/gatesopenres.12844.1 (2018).
O’Reilly, K. M. et al. Estimating the burden of dengue and the impact of release of wMel Wolbachia-infected mosquitoes in Indonesia: A modelling study. BMC Med. 17, 172. https://doi.org/10.1186/s12916-019-1396-4 (2019).
Pinto, S. B. et al. Effectiveness of Wolbachia-infected mosquito deployments in reducing the incidence of dengue and other Aedes-borne diseases in Niterói, Brazil: A quasi-experimental study. PLOS Neglect. Trop. Diseases15, e0009556, https://doi.org/10.1371/journal.pntd.0009556 (2021)
Velez, I. D. et al. The impact of city-wide deployment of Wolbachia-carrying mosquitoes on arboviral disease incidence in Medellín and Bello, Colombia: Study protocol for an interrupted time-series analysis and a test-negative design study. F1000Research8, 1327, https://doi.org/10.12688/f1000research.19858.1 (2019).
Ong, S. Wolbachia. & goes to work in the war on mosquitoes. Nature 598, S32–S34, https://doi.org/10.1038/d41586-021-02914-8. Bandiera_abtest: a Cg_type: Nature Index Number: 7882 Publisher: Nature Publishing Group Subject_term: Malaria (Public health, Health care, Infection, 2021).
Nazni, W. A. et al. Establishment of Wolbachia Strain wAlbB in Malaysian Populations of Aedes aegypti for Dengue Control. Curr. Biol.29, 4241–4248 e5, https://doi.org/10.1016/j.cub.2019.11.007 (2019).
Kittayapong, P. et al. Combined sterile insect technique and incompatible insect technique: The first proof-of-concept to suppress Aedes aegypti vector populations in semi-rural settings in Thailand. PLoS Negl. Trop. Dis.13, e0007771, https://doi.org/10.1371/journal.pntd.0007771 (2019)
Liu, W.-L. et al. Lab-scale characterization and semi-field trials of Wolbachia Strain wAlbB in a Taiwan Wolbachia introgressed Ae. aegypti strain. PLOS Neglected Tropical Diseases16, e0010084, https://doi.org/10.1371/journal.pntd.0010084 (2022). Publisher: Public Library of Science.
Nguyen, T. H. et al. Field evaluation of the establishment potential of wMelPop Wolbachia in Australia and Vietnam for dengue control. Parasit Vectors 8, 563. https://doi.org/10.1186/s13071-015-1174-x (2015).
Hoffmann, A. A., Hercus, M. & Dagher, H. Population dynamics of the Wolbachia infection causing cytoplasmic incompatibility in Drosophila melanogaster. Genetics 148, 221–31 (1998).
Flor, M., Hammerstein, P. & Telschow, A. Wolbachia-induced unidirectional cytoplasmic incompatibility and the stability of infection polymorphism in parapatric host populations. J. Evol. Biol. 20, 696–706. https://doi.org/10.1111/j.1420-9101.2006.01252.x (2007).
Hoffmann, A. A. et al. Successful establishment of Wolbachia in Aedes populations to suppress dengue transmission. Nature 476, 454–7. https://doi.org/10.1038/nature10356 (2011).
Ross, P. A., Ritchie, S. A., Axford, J. K. & Hoffmann, A. A. Loss of cytoplasmic incompatibility in Wolbachia-infected Aedes aegypti under field conditions. PLoS Negl. Trop. Dis. 13, e0007357. https://doi.org/10.1371/journal.pntd.0007357 (2019).
Keeling, M. J., Jiggins, F. M. & Read, J. M. The invasion and coexistence of competing Wolbachia strains. Heredity 91, 382–388. https://doi.org/10.1038/sj.hdy.6800343 (2003).
Telschow, A., Yamamura, N. & Werren, J. H. Bidirectional cytoplasmic incompatibility and the stable coexistence of two Wolbachia strains in parapatric host populations. J. Theor. Biol. 235, 265–74. https://doi.org/10.1016/j.jtbi.2005.01.008 (2005).
Adekunle, A. I., Meehan, M. T. & McBryde, E. S. Mathematical analysis of a Wolbachia invasive model with imperfect maternal transmission and loss of Wolbachia infection. Infect Dis Model 4, 265–285. https://doi.org/10.1016/j.idm.2019.10.001 (2019).
Xue, L., Manore, C. A., Thongsripong, P. & Hyman, J. M. Two-sex mosquito model for the persistence of Wolbachia. J. Biol. Dyn. 11, 216–237. https://doi.org/10.1080/17513758.2016.1229051 (2017).
Hughes, H. & Britton, N. F. Modelling the use of Wolbachia to control dengue fever transmission. Bull. Math. Biol. 75, 796–818 (2013).
Ndii, M. Z., Allingham, D., Hickson, R. I. & Glass, K. The effect of Wolbachia on dengue dynamics in the presence of two serotypes of dengue: symmetric and asymmetric epidemiological characteristics. Epidemiol. Infect. 144, 2874–82. https://doi.org/10.1017/S0950268816000753 (2016).
Ndii, M. Z., Hickson, R. I., Allingham, D. & Mercer, G. N. Modelling the transmission dynamics of dengue in the presence of Wolbachia. Math. Biosci. 262, 157–66. https://doi.org/10.1016/j.mbs.2014.12.011 (2015).
Campo-Duarte, D. E., Vasilieva, O., Cardona-Salgado, D. & Svinin, M. Optimal control approach for establishing wMelPop Wolbachia infection among wild Aedes aegypti populations. J. Math. Biol. 76, 1907–1950. https://doi.org/10.1007/s00285-018-1213-2 (2018).
Turelli, M. & Barton, N. H. Why did the Wolbachia transinfection cross the road? Drift, deterministic dynamics, and disease control. Evol. Lett. 6, 92–105. https://doi.org/10.1002/evl3.270 (2022).
Yu, J. & Zheng, B. Modeling Wolbachia infection in mosquito population via discrete dynamical models. J. Differ. Equ. Appl. 25, 1549–1567. https://doi.org/10.1080/10236198.2019.1669578 (2019).
Shi, Y. & Zheng, B. Discrete dynamical models on Wolbachia infection frequency in mosquito populations with biased release ratios. J. Biol. Dyn. 16, 320–339. https://doi.org/10.1080/17513758.2021.1977400 (2022).
Hancock, P. A., Sinkins, S. P. & Godfray, H. C. J. Population dynamic models of the spread of Wolbachia. The American Naturalisthttps://doi.org/10.1086/658121 (2015)
Ndii, M. Z., Beay, L. K., Anggriani, N., Nukul, K. N. & Djahi, B. S. Estimating the time reproduction number in Kupang City Indonesia, 2016–2020, and assessing the effects of vaccination and different Wolbachia strains on dengue transmission dynamics. Mathematics 10, 2075. https://doi.org/10.3390/math10122075 (2022).
Kramer, A. M., Berec, L. & Drake, J. M. Editorial: Allee effects in ecology and evolution. J. Anim. Ecol. 87, 7–10. https://doi.org/10.1111/1365-2656.12777 (2018).
Farkas, J. Z. & Hinow, P. Structured and Unstructured Continuous Models for Wolbachia Infections. Bull. Math. Biol. 72, 2067–2088. https://doi.org/10.1007/s11538-010-9528-1 (2010).
Li, Y. & Liu, X. Modeling and control of mosquito-borne diseases with Wolbachia and insecticides. Theor. Popul. Biol. 132, 82–91. https://doi.org/10.1016/j.tpb.2019.12.007 (2020).
Zheng, B., Tang, M. & Yu, J. Modeling Wolbachia spread in mosquitoes through delay differential equations. SIAM J. Appl. Math. 74, 743–770. https://doi.org/10.1137/13093354X (2014).
Huang, M., Tang, M., Yu, J. & Zheng, B. A stage structured model of delay differential equations for Aedes mosquito population suppression. Discrete Contin. Dyn. Syst. 40, 3467–3484. https://doi.org/10.3934/dcds.2020042 (2020).
Hoffmann, A. A. et al. Stability of the wMel Wolbachia Infection following invasion into Aedes aegypti populations. PLoS Negl. Trop. Dis. 8, e3115. https://doi.org/10.1371/journal.pntd.0003115 (2014).
Brady, O. J. et al. Modelling adult Aedes aegypti and Aedes albopictus survival at different temperatures in laboratory and field settings. Parasites Vectors 6, 351. https://doi.org/10.1186/1756-3305-6-351 (2013).
Mohammed, A. & Chadee, D. D. Effects of different temperature regimens on the development of Aedes aegypti (L.) (Diptera: Culicidae) mosquitoes. Acta Tropica 119, 38–43. https://doi.org/10.1016/j.actatropica.2011.04.004 (2011).
Lounibos, L. P. & Escher, R. L. Sex ratios of mosquitoes from long-term censuses of Florida tree holes. J. Am. Mosquito Control Assoc. 24, 11–15. https://doi.org/10.2987/5656.1 (2008).
Martcheva, M. An Introduction to Mathematical Epidemiology, vol. 61 (Springer, 2015).
Acknowledgements
The first author was funded by the College of Medicine and Dentistry at James Cook University, Australia PhD programme.
Author information
Authors and Affiliations
Contributions
S.T.O. initiated the project concept and developed the model, S.T.O., A.I.A. and M.T.M. analysed the model results. S.T.O., A.I.A., E.S.M. and M.T.M. contributed in drafting the manuscript and S.T.O. wrote the simulation codes. All authors have read, reviewed and finally approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ogunlade, S.T., Adekunle, A.I., McBryde, E.S. et al. Modelling the ecological dynamics of mosquito populations with multiple co-circulating Wolbachia strains. Sci Rep 12, 20826 (2022). https://doi.org/10.1038/s41598-022-25242-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-25242-x
This article is cited by
-
Quantifying the impact of Wolbachia releases on dengue infection in Townsville, Australia
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.