Abstract
Modern atomic clocks based on the interrogation of an atomic transitions in the optical regions require multiple lasers at different wavelength for producing atomic ions, trapping and laser cooling of neutral atoms or atomic ions. In order to achieve highest efficiency for laser cooling or any other atomic transition, frequencies of each of the lasers involved need to be stabilized by mitigating its drifts or fluctuations arise due to ambient temperature variation or other kind of perturbations. The present article describes simultaneous frequency stabilization of multiple number of lasers, required for production and laser cooling of ytterbium (171Yb) ions, to a reference transition frequency of rubidium (Rb) atoms. In this technique, a diode laser operating at ~ 780 nm is frequency stabilized to one of the Doppler broadening-free absorption peak of rubidium atoms (85Rb) and then used as a reference frequency for calibrating a wavelength meter and subsequent simultaneous frequency stabilization of four lasers operating at different wavelengths.
Similar content being viewed by others
Introduction
Frequency stabilization of lasers is a prerequisite for all kind of experiments related to laser cooling of atoms or atomic ions. Laser frequency stabilization or frequency locking is also an essential requirement for precision experiments1,2,3,4, e.g., optical frequency standards or optical clock based on the interrogation of ultra-narrow atomic transitions, which requires multiple number of stable laser frequencies. Optical atomic clock, realized through interrogation of a quadrupole transition {4f14 6 s 2S1/2|F = 0, mF = 0 > →4f145D 2D3/2|F = 2, mF = 0 >} of a single trapped ytterbium ion (171Yb+) ion at 435 nm, requires as many as four narrow linewidth(~ 23 MHz)5 and stable lasers at wavelengths around 399 nm, 369.5 nm, 935 nm and 760 nm respectively for probing transitions related to photoionization, laser cooling6,7 of ytterbium (171Yb+) ions and repumping of the metastable states of the ions5,8,9. Such a state-of-the art experiment demands accurate and precise regulation of all of its components, hence, all the required lasers need to be frequency stabilized so that desired transitions are probed accurately and effectively. Several techniques are being used for laser frequency locking or frequency stabilization, e.g., locking of laser’s output frequency to a highly stable Fabry-Parrot cavity using Pound–Drever–Hall technique10,11, another commonly used technique is locking of laser to a reference atomic transition frequency on its Doppler broadening free transition peak12,13,14 and now a days wavelength meters15,16,17 are also being used in different precision experiments. The choice of a locking technique depends on experimental demand for the level of accuracy. For example, precision spectroscopy or high accuracy metrology-related experiments demand relative frequency instabilities18 better than 10−15 whereas other experiments such as atomic spectroscopy or atom cooling can be performed with laser frequencies having short-term instabilities ≤ 10−10.
Laser cooled ytterbium ion (171Yb+) offers two ultra-narrow clock transitions in the optical domain, i.e., a quadrupole transition at 435 nm and an octapole transition at 467 nm with natural line width of 3 Hz and 3 nHz respectively18,19. Stabilizing of clock laser’s frequency, for probing such ultra-narrow transitions, requires tremendous effort for generating ultra-stable and ultra-narrow linewidth frequency using ultra low expansion (ULE) cavity1,20,21,22 and fast servo controller. Atomic transitions used for the production of ytterbium ions through photoionization, laser cooling of ions and repumping of the metastable states of the ions, have typical natural linewidth of tens of MHz and therefore the frequencies of those lasers need to be stabilized within same range, i.e., few tens of MHz for the above purposes5.
The present article reports about simultaneous and long terms frequency stabilization of four different lasers, used for production and laser cooling of ytterbium ions, through a wavelength meter. In order to measure the absolute frequencies of the laser, the wavelength meter is calibrated with respect to a Doppler broadening free absorption peak of Rb atoms23. Doppler broadening free absorption spectra of Rb atoms are recorded through saturated absorption spectroscopy (SAS) through a Rb vapour cell kept at room temperature. One of the key advantage of wavelength meter based laser frequency stabilization technique is that it allows simultaneous locking of multiple number of lasers with wide wavelength region.
Experimental setup
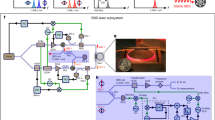
A wavelength meter (WS-7, Highfiness) along with a multichannel switch have been used in the experiment for measuring as well as stabilizing laser frequencies. This wavelength meter consists of a fiber-coupled optical unit based on Fizeau interferometer that create interference patterns and capable of covering a wide range of wavelength i.e., 350–1120 nm. Interference patterns generated within the wavelength meter are then detected by two charge-coupled device (CCD) arrays and laser frequencies are estimated, with an absolute measurement accuracy of 60 MHz, in comparison with a stored internal reference pattern. Initially, a built-in neon lamp in the wavelengthmeter is used to calibrate the wavelength meter and a multichannel fiber-switch is used for simultaneous measurement of multiple laser output frequencies. A proportional-integral-derivative (PID) regulator’s analog output is used for simultaneous frequency locking for all these lasers. Neon lamp cannot be used continuously as a reference for frequency calibration because it has limited shelf life and the wavelength meter is recalibrated in a regular interval of time. But during this calibration period the wavelength meter stops measuring wavelengths for certain time. In order to achieve highest possible accuracy and long term stability in the frequency measurement, the wavelength meter needs to be recalibrated in regular intervals of time and eventually introduces error in absolute frequency measurement during recalibration period. To overcome this shortcoming the wavelength meter has been calibrated and stabilized by a continuous and stable reference, so that it can be used uninterruptedly for a longer period of time avoiding multiple times recalibration. In our experiment we have calibrated the wavelength meter to a transition frequency of atomic Rubidium using Doppler-free SAS23,24,25,26,27 technique. In the present experiments, an atomic transition of 85Rb with absolute wavelength 780.24392 nm has been used as the reference for calibrating the wavelength meter and the schematic diagram of the experimental setup has been presented in Fig. 1. A tuneable extended cavity diode laser (ECDL), operating at ~ 780 nm, is used for recording absorption spectra of Rb atoms. Light from the laser is coupled to the wavelength meter through a single mode optical fibre and then collimated by a mirror, before entering the solid-state Fizeau-interferometers. As shown in Fig. 1, laser output is first split into two parts using a 90:10 beam splitter and the weaker part of the laser beam is carried to the wavelength meter through the multichannel switch. The stronger part of the laser is used for the experiment i.e., for recording Doppler broadening free absorption spectra of Rb atoms. The laser beam passes through a quarter wave ( λ/4) plate followed by a polarizing beam splitter (PBS) and further splits the beam into two parts i.e., the pump and probe beams. The optical axis of the quarter wave plates is rotated in such a way that one of the beam becomes a high intense pump beam (~ 1 mW) and passes through the Rb vapour cell. The weaker part of the beam (~ 0.1 mW) is used as probe beam and passes through the Rb vapour cell from the other end i.e., in counter-propagating direction to the pump beam. The SAS spectra is recorded by detecting the probe beam on a photodiode (APD430A/M, Thorlabs) and then the signal is connected to a PID controller (DigiLock 110, Toptica) and the laser is locked to on one of the atomic transitions of Rb and this locked laser signal is used as the reference signal for the wavelength meter.
Schematic representation of the experimental setup for laser locking using saturated absorption spectroscopy (SAS). Here, BS—90:10 beam splitter, W1, and W2—quarter-wave plates, PBS1 and PBS2—polarizing beam splitters, VC—Rb vapour cell, M1, M2, M3 and M4—mirrors, M5—cylindrical mirror, PD—photodiode, MS—multichannel switch, C—fibre coupler, F—Fizeau interferometer, CCD—charged coupled devices.
Results and discussion
Laser locking is a useful technique for stabilizing laser’s output frequency with respect to a reference transition frequency28 and very commonly used in the precision experiments. Locking a laser to a particular reference peak requires a feedback control in terms of an error signal, which is proportional to the offset or detuning of the frequency from its desired value, i.e., the reference frequency. The error signal is fed back to the laser controller for tuning its output frequency.
When a laser beam passes through an atomic vapour cell and its frequency is scanned around resonance absorption frequencies, specific absorption pattern is observed due to laser-atom interaction. But due to thermal motions of the atoms within the vapour cell, Doppler broadening occurs and results into frequency broadened absorption spectra, much broader than the natural linewidth. Let’s consider a group of atoms having linear velocity component vx along the propagation direction of the counter propagating laser beams, i.e., pump and probe beams. When the pump and probe beams interact with those group of atoms, resonant absorption frequency will be shifted due to Doppler Effect and the Doppler shift depends on the relative velocity of those atoms with respect to the laser beams, can be expressed as
where ν0 is the resonance frequency for the atoms are in rest, i.e., atoms have no velocity component along the propagation direction of the laser beams, c is the velocity of light, and ν is the Doppler-shifted resonance frequency. In order to minimize the Doppler broadening of absorption spectra, saturated absorption spectroscopy (SAS) technique is used where counter-propagating high intense laser beam, named as pump beam and low intense probe beam passes through the vapour cell in counter propagating configuration. The linewidth of these saturated absorption spectra is much narrower than the Doppler broaden absorption spectra. Width of the Doppler broadening free absorption spectra, i.e., saturated absorption spectra, depends on the natural linewidth of that atomic transition. Width of the SAS spectra also depends on the power of the incident laser beam and broadened linearly with the increase of laser power. Hence, the linewidth of the SAS spectra can also be optimized by reducing the power of the laser beam. Usually Doppler broaden absorption spectra have linewidth of hundreds of MHz but for SAS spectra linewidths are achieved within tens of MHz. Thus, output of any laser can be stabilized or locked to the peak of a reference SAS signal. In the present study Rb vapour cell has been chosen for generating SAS signal as Rb exists in vapour state at room temperature and no additional heating is required. In addition, atomic Rb provides many closely spaced transition frequency in the optical domain and eventually provide multiple number of Doppler broadening free SAS23,29,30,31 transitions frequencies over a wide wavelength range. Natural Rb atoms have two isotopes with relative abundance of 72% for 85Rb and 28% for 87Rb. In the present experimental setup, the D2 hyperfine transitions (5S1/2–5P3/2) of Rb atoms at ~ 780 nm have been probed for obtaining Doppler broadening free SAS peaks. Figure 2a depicts the absorption spectra with the SAS peaks for 87Rb (Fg = 1, 2) and 85Rb (Fg = 2, 3). In our experiment we are using 85Rb which have hyperfine transitions Fg = 3 to Fe = 4, Fg = 3 to Fe = CO34 (Crossover peak of Fe = 3 and Fe = 4) and Fg = 3 to Fe = CO24 (Crossover peak of Fe = 2 and Fe = 4) with corresponding linewidths of 13.73 MHz, 20.75 MHz and 21.83 MHz respectively. Our measured linewidths as mentioned in Table 1 are in good agreement with earlier measured and reported values29,32. One of the modulated SAS peak of 85Rb, corresponding to the transition Fg = 3 to Fe = CO34 at 780.24392 nm (shown in Fig. 2b) has been utilized for locking the laser frequency through a feedback controller.
(a) Doppler broadening free saturated absorption spectra (SAS) for D2 transition of 87Rb and 85Rb atoms (y-axis-signal strength (a.u.). (b) Doppler broadening free SAS peaks (red line) for hyperfine transitions Fg = 3 to Fe = 4, Fg = 3 to Fe = CO34 (Crossover peak of Fe = 3 and Fe = 4) and Fg = 3 to Fe = CO24 (Crossover peak of Fe = 2 and Fe = 4) of 85Rb and their first order derivative as error signal (blue), the peak corresponding Fg = 3 to Fe = CO34 transition (υ = 384.229149 THz) has been used as the reference signal for calibrating and locking the wavelength meter. (c) Wavelength variation of a frequency stabilized laser, while the wavelength meter uses inbuilt Neon lamp as the reference of calibration. (d) Wavelength variation of a frequency stabilized laser, while the wavelength meter is calibrated to the SAS peak of 85Rb.
Figure 2b depicts the SAS peaks and their first-order differential signal generated by the PID controller and this differential signal is used as the corresponding error signal for locking the laser to a specific SAS peak. The differential signal corresponding to a SAS peak represents the zero point in the error signal and both side of the zero points have opposite sign in the error signal. In this error signal (with modulation frequency of 3.97 kHz and amplitude 0.119 VPP), the negative and the positive slopes define the lowest and highest point of the locking frequencies and the zero point of the error signal has been used as the reference for calibration of the wavelength meter. In order to demonstrate the advantages or benefits of calibrating the wavelength meter to a reference SAS peak in comparison to inbuilt neon lamp, frequency stabilized laser frequency have been recorded over a very long period by calibrating the wavelength meter with the neon lamp and SAS peak of atomic Rb respectively.
Figure 2c demonstrate the frequency stability of the measured output of the laser operating at ~ 760 nm and locked to the wavelength meter, while the wavelength meter is calibrated with the inbuilt neon lamp. As it is evident from Fig. 2c that the wavelength meter needs recalibration in short time to ensure that the lasers remain locked at the desired value, as the neon lamp is not in on state continuously. During the recalibration period the measurement of wavelengthmeter stop and the laser starts drifting from its operating frequency. The output frequency shows huge fluctuation during the period of its calibration and it happens in regular interval, which is quite disturbing and not acceptable for many of the precision experiments like trapping of atoms through magneto optic traps (MOT) or laser cooling of atoms and atomic ions.
The above discussed issue regarding recalibrating the wavelength meter with the neon lamp at regular interval can be solved by using a SAS peak of Rb atoms as the reference of calibration instead of the neon lamp. As the reference SAS peaks of Rb atoms are highly stable and insensitive to atmospheric perturbation, it is capable of locking the laser outputs very efficiently over a very long time. The SAS peak is used as a continuous source for calibration and doesn’t require multiple times recalibration of the wavelength meter. Figure 2c,d depict the wavelength drift and its fluctuations of a frequency stabilized laser’s output, while the wavelength meter is calibrated with the inbuilt neon lamp and the SAS peak of the Rb atoms respectively. It has been observed that calibrating the wavelength meter with the SAS peak of the Rb atoms is quite advantageous as it give very good long term stability.
In order to estimate the short-term stability of the locked laser’s output frequency, the Fast Fourier Transformation (FFT) have been performed for the error signals corresponding to different SAS peaks of Rb atoms. The voltage spectral density of noise floors of the spectrum analyser along with the SAS peaks has been presented in Fig. 3. The respective noise density of the SAS peaks which have hyperfine transitions Fg = 3 to Fe = CO24 (Crossover peak of Fe = 2 and Fe = 4), Fg = 3 to Fe = CO34 (Crossover peak of Fe = 3 and Fe = 4) and Fg = 3 to Fe = 4 are estimated to be 0.23 μv/Hz1/2, 0.21 μv/Hz1/2and 0.14 μv/Hz1/2@2 kHz respectively, as presented in Fig. 3.
After calibrating and stabilizing the wavelength meter with the SAS peak of the Rb atoms, four lasers operating at different wavelengths have been locked using the PID controller of the wavelength meter. Operational wavelengths of those four laser are ~ 399 nm 369 nm (generated from second harmonic generated signal of 739 nm laser), 935 nm and 760 nm and are used in an experiment for the production and laser cooling of 171Yb+ ions. Through the calibrated wavelength meter all four lasers were locked simultaneously to their respective wavelength over a period of 15 h. Figure 4 shows drift of wavelengths and their fluctuations for all those four frequencies stabilized lasers, the corresponding histograms in the right hand side shows the distribution of deviations of the laser’s output frequency from their central frequencies with FWHM 15.02 MHz for 399 nm, 1.46 MHz for 739 nm laser, 2.42 MHz for 760 nm laser and 0.87 MHz for 935 nm laser. Above results show that the stability as well as the linewidth of the four different laser stay well within the required limit for using them efficiently in the experiment of production and laser cooling of 171Yb+ ion within a radio frequency ion trap.
Conclusion
A simple and effective method for frequency stabilization of multiple lasers using a wavelength meter has been presented. The wavelength meter is calibrated to a Doppler-broadening free D2 atomic transition of 85Rb through saturated absorption spectroscopy, instead of calibrating it to the in-build neon lamp. SAS peak of the atomic rubidium as the external reference enables the wavelength meter for uninterrupted measurement over very long period of time and consequently long term frequency stability achieved for the laser outputs. Four lasers of different wavelengths have been frequency stabilized through the wavelength meter for more than ten hours and all of them provide excellent frequency stability with a drift of 0.013(8) kHz/h estimated by measuring the shift of the mean frequency of the laser over a long period of time and line widths of 15.02 MHz for 399 nm, 1.46 MHz for 739 nm laser, 2.42 MHz for 760 nm laser and 0.87 MHz for 935 nm laser.
Data availability
The datasets generated and analysed during the current study are available at https://data.mendeley.com/datasets/9d3zxwyztm.
References
Jiang, Y. Y. et al. Making optical atomic clocks more stable with 10−16-level laser stabilization. Nat. Photonics 2011(5), 158–161 (2011).
Streed, E. W., Weinhold, T. J. & Kielpinski, D. Frequency stabilization of an ultraviolet laser to ions in a discharge. Appl. Phys. Lett. 93, 071103 (2008).
Rovera, G. D., Santarelli, G. & Clairon, A. A laser diode system stabilized on the Caesium D2 line. Rev. Sci. Instrum. 65, 1502 (1994).
Udem, T., Holzwarth, R. & Hänsch, T. W. Optical frequency metrology. Nature 416, 233–237 (2002).
Chepurov, S. V. et al. Optical frequency standard with ytterbium single ion. J. Phys. Conf. Ser. 793, 66 (2017).
Zalivako, I. et al. Improved wavelength measurement of 2s1/2 → 2p1/2 and 2d3/2 → 3[3/2]1/2 transitions in yb +. J. Russ. Laser Res. 40, 66 (2019).
Phillips, W. D. Laser cooling and trapping of neutral atoms. Rev. Mod. Phys. 70, 721 (1998).
Sharma, L. et al. Optical atomic clocks for redefining SI units of time and frequency. Mapan J. Metrol. Soc. India 35, 531–545 (2020).
Rapol, U. D., Krishna, A., Wasan, A. & Natarajan, V. THE European Physical Journal D Laser cooling and trapping of Yb from a thermal source. Eur. Phys. J. D 29, 409–414 (2004).
Lee, S. K., Han, B. W. & Cho, D. Automatic system to relock a laser frequency to a Fabry–Perot cavity. Rev. Sci. Instrum. 76, 026101 (2005).
Black, E. D. An introduction to Pound–Drever–Hall laser frequency stabilization. Am. J. Phys. 69, 79–87 (2001).
Preston, D. W. Doppler-free saturated absorption: Laser spectroscopy. Am. J. Phys. 64, 1432 (1998).
Debs, J. E., Robins, N. P., Lance, A., Kruger, M. B. & Close, J. D. Piezo-locking a diode laser with saturated absorption spectroscopy. Appl. Opt. 47(28), 5163–5166 (2008).
Sarkisyan, D. et al. Saturated-absorption spectroscopy revisited: Atomic transitions in strong magnetic fields (> 20 mT) with a micrometer-thin cell. Opt. Lett. 39(8), 2270–2273 (2014).
Saleh, K., Millo, J., Didier, A., Kersalé, Y. & Lacroûte, C. Frequency stability of a wavelength meter and applications to laser frequency stabilization. Appl. Opt. 54, 9446 (2015).
Kobtsev, S., Kandrushin, S. & Potekhin, A. Long-term frequency stabilization of a continuous-wave tunable laser with the help of a precision wavelengthmeter. Appl. Opt. 46(23), 5840–5843 (2007).
Metzger, N. K. et al. Harnessing speckle for a sub-femtometre resolved broadband wavemeter and laser stabilization. Nat. Commun. https://doi.org/10.1038/ncomms15610 (2017).
Jin, L. et al. Laser frequency instability of 2 × 10–16 by stabilizing to 30-cm-long Fabry–Pérot cavities at 578 nm. Opt. Express 26, 18699 (2018).
Tamm, C., Schnier, D. & Bauch, A. Radio-frequency laser double-resonance spectroscopy of trapped171Yb ions and determination of line shifts of the ground-state hyperfine resonance. Appl. Phys. B 601(60), 19–29 (1995).
Huntemann, N. et al. High-accuracy optical clock based on the octupole transition in Yb+171. Phys. Rev. Lett. 108, 090801 (2012).
Kryuchkov, D. S. et al. Compact high-finesse ULE cavities for laser frequency stabilization. Bull. Lebedev Phys. Inst. 48, 3–11 (2021).
Zhadnov, N. O. et al. Long ULE cavities with relative fractional frequency drift rate below 5 × 10–16/s for laser frequency stabilization. Bull. Lebedev Phys. Inst. 47, 257–261 (2020).
Theriault, S. Toward the realization of a wavelength standard at 780 nm based on a laser diode frequency locked to rubidium vapor. IEEE Trans. Instrum. Meas. 40, 66 (1991).
Corwin, K. L., Lu, Z.-T., Hand, C. F., Epstein, R. J. & Wieman, C. E. Frequency-stabilized diode laser with the Zeeman shift in an atomic vapor. Appl. Opt. 37, 3295 (1998).
Millett-Sikking, A., Hughes, I. G., Tierney, P. & Cornish, S. L. DAVLL lineshapes in atomic rubidium. J. Phys. B At. Mol. Opt. Phys. 40, 187 (2006).
Mccarron, D. J., Hughes, I. G. & Tierney, P. A heated vapor cell unit for dichroic atomic vapor laser lock in atomic rubidium. Rev. Sci. Instrum 78, 93106 (2007).
Harris, M. L., Cornish, S. L., Tripathi, A. & Hughes, I. G. Optimization of sub-Doppler DAVLL on the rubidium D2 line. J. Phys. B At. Mol. Opt. Phys. 41, 85–401 (2008).
Roy, A., Sharma, L., Panja, S. & De, S. ‘Loop Stabilized’ improved transfer cavity-based laser frequency stabilization. IEEE J. Quantum Electron. 58, 66 (2022).
Żaba, A. et al. Pump-probe spectra modeled with inclusion of a dipole-coupled but not dipole-probed F′ state, for the case of 85Rb 5S1/2(F)–5P3/2(F′) transitions. SPIE 8770, 87700Q (2013).
Failache, H., Valente, P., Ban, G., Lorent, V. & Lezama, A. Inhibition of electromagnetically induced absorption due to excited-state decoherence in Rb vapor. Phys. Rev. A At. Mol. Opt. Phys. 67, 7 (2003).
Siddons, P., Adams, C. S., Ge, C. & Hughes, I. G. Absolute absorption on rubidium D lines: Comparison between theory and experiment. J. Phys. B At. Mol. Opt. Phys. 41, 66 (2008).
Jacques, V., Hingant, B., Allafort, A., Pigeard, M. & Roch, J. F. Nonlinear spectroscopy of rubidium: An undergraduate experiment. Eur. J. Phys. 30, 921–934 (2009).
Acknowledgements
Authors are thankful to CSIR-NPL, New Delhi for the research grant. Shubham Utreja is thankful to Council of Scientific and Industrial Research (CSIR) and Harish is also thankful to University Grants Commission (UGC) for providing their research fellowship.
Author information
Authors and Affiliations
Contributions
1. Setting up the experimental setup and data analysis:- S.U and H.R 2. Participated in the experiment for data acquisition:- M.D 3. Planning of experiment and participated in analysis:- S.P.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Utreja, S., Rathore, H., Das, M. et al. Frequency stabilization of multiple lasers to a reference atomic transition of Rb. Sci Rep 12, 20624 (2022). https://doi.org/10.1038/s41598-022-24952-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-24952-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.