Abstract
Multiprobe measurements, such as NMR and hydrogen exchange studies, can provide the equilibrium constant, K, and rate constants for forward and backward processes, k and k′, of the two-state structural changes of a polypeptide on a per-residue basis. We previously found a linear relationship between log K and log k and between log K and log k′ for the topological exchange of a 27-residue bioactive peptide. To test the general applicability of the residue-based linear free energy relationship (rbLEFR), we performed a literature search to collect residue-specific K, k, and k′ values in various exchange processes, including folding-unfolding equilibrium, coupled folding and binding of intrinsically disordered peptides, and structural fluctuations of folded proteins. The good linearity in a substantial number of the log–log plots proved that the rbLFER holds for the structural changes in a wide variety of protein-related phenomena. Among the successful cases, the hydrogen exchange study of apomyoglobin folding intermediates is particularly interesting. We found that the residues that deviated from the linear relationship corresponded to the α-helix, for which transient translocation had been identified by other experiments. Thus, the rbLFER is useful for studying the structures and energetics of the dynamic states of protein molecules.
Similar content being viewed by others
Introduction
The double logarithmic plot of equilibrium constants, K, and rate constants, k, is generally called REFER (rate-equilibrium free energy relationship), and the linear relationship in the REFER plot is referred to as LFER (linear free energy relationship). LFER is widely observed in two-state chemical and enzymatic reactions and is utilized to estimate the reaction rates under arbitrary conditions1,2,3. In general, the perturbations of K and k result from modifications in the structures of target compounds. For example, the data points (log K, log k) of the Hammett plot are obtained from a series of derivatives of a reactant with different substituents, and those of the Brønsted plot are obtained from a series of acids. The LFER is also seen in protein folding processes. The ϕ-value analysis is based on the perturbation to K and k by mutations of an amino acid residue in a protein molecule and provides information on the localized structure formation around the mutated position in the transition state of the protein folding4,5,6,7,8.
NMR provides local information around nuclei at an atomic resolution. We used NMR to determine the residue-specific equilibrium constants, K, and residue-specific forward and backward rate constants, k and k′, of a 27-residue peptide, nukacin ISK-1, in a two-state slow exchange9,10. For accurate determination of the thermodynamic and kinetic parameters, the measurement bias arising from state-specific differences in the R1 and R2 relaxation rates of 1H and 15N nuclei must be removed. We found that the combination of the Π analysis method (developed by Palmer’s group11,12) and the HSQC0 experimental method (developed by Markley’s group13,14) offered an effective solution15. The determined thermodynamic and kinetic constants differed significantly on a per-residue basis, but the residues in spatial proximity tend to have similar values15. Interestingly, we discovered linear relationships in the log k vs. log K and log k′ vs. log K plots10,15. In contrast to the conventional LFERs, the data points (log K, log k) and (log K, log k′) in our LFER are derived from different positions in one polypeptide chain. Therefore, we refer to the new type of LFER as residue-based LFER (rbLFER).
Here, we performed a literature search to collect residue-specific equilibrium and kinetic constants of proteins, to determine the applicability of rbLFER in various protein equilibriums with diverse interconversion time scales. A substantial number of the REFER plots exhibited good linearity. Among the successful cases, the HX (hydrogen exchange) study of apomyoglobin folding intermediates is particularly interesting16. The majority of the amino acid residues are on a straight line in the REFER plot, but some residues deviate from the line. We found that these outlier residues precisely correspond to the transient translocation of an α-helix in the apomyoglobin folding intermediates, which were first discovered a decade-and-a-half ago by other methods17,18. The excellent agreement between the past and present independent analyses demonstrates that rbLFER can reveal the structural and energetic aspects of the dynamic states of protein molecules.
Results
Residue-based LFER examples
Extensive literature searches led to the collection of reports on residue-specific equilibrium constants and residue-specific kinetic constants of proteins (Table 1). We recovered the data from the tables and figures and generated the corresponding REFER plots (Fig. 1). The techniques used and the phenomena under consideration are quite diverse. The first category, including nukacin ISK-1, is the EXSY NMR analyses of slow exchanges between two sets of cross peaks (Fig. 1a, b)10,15,19,20, and the second category is the relaxation dispersion (RD) NMR analyses of the binding of an IDP (intrinsically denatured polypeptide) to a target protein (Fig. 1c)21,22. In the case of an IDP, only one set of cross peaks was observed due to the fast exchange between two or more states. Since the state-specific differences in the R1 and R2 relaxation rates of 1H and 15N nuclei are averaged out, the information on the exchange process can be extracted from the averaged single cross peaks. The same situation is applied to the structural fluctuations of folded-state proteins studied by RD NMR (Fig. 1d)23,24,25,26,27,28. The HX experiment also provides information on the structural fluctuations of folded proteins (Fig. 1e)29,30,31,32. Note that the NMR in the HX studies is used for the quantitation of the proton occupancy and does not directly observe the HX phenomena. Indeed, mass spectrometry is applicable in place of NMR33. Overall, the majority of the REFER plots showed residue-based linear relationships.
Residue-based REFER plots based on the literature data listed in Table 1. (a) Nukacin ISK-1. (b) N-terminal SH3 domain from Drosophila drk protein (drk SH3N). The drk SH3N is in an exchange between unstructured state U and native folded state N. There are different data sets from the two reports. (c) Myb32 and pKID are intrinsically disordered polypeptides that bind to the KIX domain. (d) Structural fluctuations of native states were investigated by the relaxation dispersion (RD) NMR method. The SH3 domains are derived from the Fyn and Abp1 proteins. The mutations in the SH3 domains markedly increased the folding rate despite their destabilization of the folding state, and have suitable properties for the RD studies34. The STARD (steroidogenic acute regulatory-related lipid transfer domain) from the STARD6 protein. The PDZ (PSD-95/Dlg/ZO-1) domain from the Tiam2 (T cell lymphoma invasion and metastasis 2) protein. A dual-phosphorylated (2P-ERK2) form of the ERK2 (extracellular signal-regulated kinase 2) protein. (e) Structural fluctuations of native states investigated by the HX method. There are two measurement conditions for ubiquitin and OMTKY3 (turkey ovomucoid third domain 3). In (a)–(e), the least-square lines and data points associated with the forward direction are colored blue, and those associated with the backward direction are orange. The least-square lines with interpretable slopes between 0 and 1 are depicted as solid lines, whereas those with uninterpretable slopes less than 0 or greater than 1 are depicted as dashed lines. No least-square lines are drawn if the correlations are considered insignificant. The concentric circle represents a basin-shaped energy landscape of the structural fluctuations around the native state, N, in equilibrium with the open state, Nop.
Here, we discuss the interpretation of the slopes of the REFER plots, by focusing on the forward direction (right-pointing arrows) depicted by the blue lines and their associated data points (Fig. 1). According to a generally accepted interpretation4,35,36,37, the slope represents the structural and energetical similarity between the initial state and the transition state, and hence the value must be between 0 and 1. In the case of structural fluctuations of folded-state proteins (Fig. 1d, e), the blue lines are nearly horizontal, and the slopes are almost zero in many instances. This situation indicates the high similarity of the transition state to the folded state. This is a convincing result, considering that the interactions that stabilize the native folded state must be disrupted at the beginning of the fluctuation. The least-square lines with negative slopes and slopes greater than 1 are difficult to interpret. These cases are depicted by dashed lines. In some cases, particularly for large proteins, the data points are scattered, and no least-square lines are shown. The assumption of the two-state exchange probably does not hold in the case of failure. Understandably, the REFER plots based on the literature data, including those with interpretable slopes, must be properly assessed in the future.
Alternative representation of residue-based LFER
The physical interpretation of the REFER plot is clear: the two axes, log K and log k, are proportional to the changes in the corresponding free energy terms. However, the two axes are not independent due to the equation, K = k/k′, i.e., log K = log k − log k′, which could generate an artificial linear relationship in the REFER plot (see the next section). To address this issue, we must check a correlation between log k and log k′ for the proper assessment of rbLFER. Figure 2 shows the type classifications of log k vs. log k′ plots, and Fig. 3 shows the log k vs. log k′ plots of the real examples listed in Table 1. The classification types are defined according to the distribution pattern of the data points. Type N is referred to as the negative correlation between log k and log k′, which leads to the blue least-square lines with the slope of 0 < ρ < 1 in the REFER plot (cf. Equation (9) in the previous paper10). In extreme cases, when the distribution of data points in the log k vs. log k′ plot has a flattened shape, the least square lines have a slope of 0 or 1 in the REFER plot. According to the orientation of the oval-shaped distribution, vertical and horizontal, their types are defined as V and H, respectively. Since either log k or log k′ is rather constant, the two log terms are uncorrelated in types V and H. Consequently, the Pearson's correlation coefficient R is zero in the log k vs. log k′ plot, and one of the two least-square lines with a zero slope has an almost zero R2-value in the REFER plot. This fact indicates that the R and R2 values in the two plots are not always good indicators of rbLFER. Instead, 95% confidence ellipses are drawn to quantify the flat distributions (Fig. 3). The closer flatness of the distribution to 1 reflects the higher linearity of the rbLFER.
Relationships between log k and log k′ as the basis of rbLFER. Several types are defined according to the data point distributions. Type N shows a negative correlation, and types V and H show flattened distributions of data points with zero correlations. The vertically flattened distribution provides two least-square lines with the slopes ρ of 0 (blue) and − 1 (orange), and the horizontally flattened distribution provides those with the slopes ρ of 0 (orange) and 1 (blue) in the REFER plots. Types P and P′ are positive correlations between log k and log k′. Type nr has no relation between log k and log k′, and the REFER plot may show a weak, artificial correlation trend.
Datapoint distributions in the log k vs. log k′ plots. In each panel, the category type defined in Fig. 2, a 95% confidence ellipse, and the flatness of distribution are shown. The flatness of the distribution is defined by f = 1-b/a, where a is the long axis and b is the short axis of the confidence ellipse. The axis ranges are set equally for the proper interpretation of the flatness of the confidence ellipses.
Next, we consider the case of positive correlations between log k and log k′. If the degree of variation of log k′ is larger than that of log k, the type is P, and if the degree of variation of log k′ is smaller than that of log k, the type is P′. Because the slopes of the blue least-square lines become negative or greater than 1 according to the type, the slopes are not physically meaningful. Such anomalous slope values occur if the exchange process cannot be described by a simple two-state model. For example, the 15N relaxation dispersion studies of various mutants of the Fyn SH3 domain revealed the presence of about 1% of the transient intermediate state I in the three-state model, N ⇄ I ⇄ U23,24,27. Even though the percentage is small, the assumption of the two-state model is not strictly valid. Another possible cause is unintended measurement biases. The final type is nr (no relation). This is probably due to large measurement errors or accidental problems (see the next section).
Risk of fake linearity
As already mentioned, the triadic relationship among K and two k’s could generate artificial correlations in the REFEP plots. This could lead to misidentification and even doubt about the validity of rbLFER. We start with an extreme example. Fifteen k and 15 k′ values are generated as uniformly distributed random numbers between 3 and 7 and between 8 and 12, respectively. We can choose any other residue number and numerical ranges for the random numbers. Note that single K, k, and k′ values for all residues are a hidden assumption. The log k vs. log k′ plot is type nr, but the REFER plot shows good linearity (Fig. 4b). This is fake, however, caused by the assumption of unnecessarily large measurement errors. This gedankenexperiment tells us the proper control and assessment of measurement errors (i.e., add error bars) is a prerequisite to avoiding fake linearity in the REFER plots. As the number of observations increases, the data points in the REFER plot converged around the averages (Fig. 4c), but some linearities within narrow ranges remain in the REFER plot (although significant enlargement is necessary to recognize them). Thus, simple increase in the number of experimental measurements does not help solve the problem. Instead, it is necessary to simultaneously observe the three correlations between the log K, log k, and log k′ terms to identify a true rbLFER. As a real example, the experimental results of nukacin ISK-1 are shown with error bars (Fig. 4a). The data points corresponding to different residues are well distributed and correlated in the REFER plot and the log k vs. log k′ plot even after repeated NMR measurements (N = 12 for K, and N = 24 for k and k′)15.
Risk evaluation of linearity overestimation in the REFER plots. (a) REFER plot and log k vs. log k′ plot of nukacin ISK-115 as a reference. The error bars represent one standard error. (b) REFER plot and log k vs. log k′ plot artificially generated using a synthetic dataset. Assuming a 15-residue protein, 15 k and k′ values are generated as uniformly distributed random numbers between 3 and 7 and between 8 and 12, respectively. The numerical ranges used are shown as the rectangular shape in the log k vs. log k′ plot. (c) The random number generation per residue was repeated 30 times (N = 30). The error bars represent one standard error of the mean. Note that one standard deviation is 5.5 (the square root of 30) times larger than one standard error of the mean.
We recovered the error estimates of residue-specific K, k, and k values (Table 1) and added them in the REFER plots (Supplementary Fig. S1) and the log k vs. log k′ plots (Supplementary Fig. S2). We must treat the error estimates with enough care because of the different definitions (e.g., standard error or standard deviation) and the different methods (e.g., curve fitting error or Monte Carlo estimation). In some cases, the errors appear too large (drk SH3N 2001, STAD6, 2P-ERK2, OMTKY3 pH 6–10, and OMTKY3 pH 10–12), but significant dispersions of log K, log k, and log k′ values are observed in all the cases.
We must also pay attention to measurement biases. The imbalance in the number of experimental values to be obtained and parameters to be determined is a serious problem in the accurate and precise determinations of the residue-specific equilibrium and residue-specific rate constants. As for 1H–15N NMR, the resonance- and state-specific NMR parameters, such as the relaxation rates, R1 and R2, of 1H and 15N nuclei must be considered. Global fitting is a solution, but only the average value over many residues is available. Alternatively, an appropriate assumption can be introduced to reduce the number of fitting parameters. For example, some parameters are supposed to remain unchanged under different measurement conditions (Table 1). Therefore, we must pay attention to the risk that unexpected adverse effects caused by obligatory assumptions could generate an artificial linear relationship in REFER plots. In fact, too good correlations in the log k vs. log k′ plots are questionable in the Fyn SH3 triple mutant and Abp1 SH3 cases (Supplementary Fig. S2). However, it is unreasonable to attribute all LFERs in Fig. 1 to measurement biases because a wide variety of methods were used.
In summary, the influences of measurement-specific biases and measurement errors must be considered seriously. The moderate linearity in the REFER plots does not simply prove a direct connection between the equilibrium constants and rate constants. The correlations in the log k vs. log k′ plot must be examined to avoid such a misinterpretation (Fig. 3; Supplementary S2). In this context, as independent evidence, a special insight revealed by the REFER plot can be tested by the results obtained from other experiments. The retrospective analysis of apomyoglobin folding intermediates in the next section provides a clear illustration of this point.
HX experiment of apomyoglobin
Information on the structural fluctuations of proteins can be obtained by monitoring the hydrogen/deuterium exchange of backbone amide protons with bulk water. The exchange mechanism consists of two processes: a two-state exchange of structural conversion and the exchange of isotopes38.
where NH(closed) is a folded state in which amide protons are protected from the exchange, and NH(open) is an open state in which exchange occurs. The H/D exchange rate, kint, is highly dependent on the pH of the solution. Usually, a single high pH pulse is used in the EX1 regime (kint ≫ kcl) to simplify the analysis. Alternatively, a wide pH range of labeling pulses can be used. Since the pH dependence of kint is well known, kop and kcl can be determined without assuming the exchange mechanism, either EX1 (kint ≫ kcl) or EX2 (kint ≪ kcl). After a hydrogen/deuterium exchange reaction, NMR is used to measure the proton occupancy of each residue in an acidic solution. Mass spectrometry is also used after protein fragmentation by protease digestion.
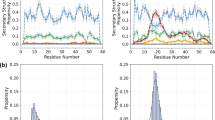
Sperm whale myoglobin is a popular model protein for understanding protein folding39,40. Myoglobin is a globular protein consisting of eight α-helices, designated A to H. The apo form of the protein has almost the same structure as the heme-bound holo form. Within the initial burst phase of apomyoglobin refolding, two kinetic intermediates, designated as Ia and Ib, are sequentially formed41. In the state Ia structure, the major portions of helices A, G, and H and part of helix B are established. Subsequently, parts of helices C, D, and E are formed and added to the already-existing helices in the state Ib structure39,40. Wright's group performed quenched-flow hydrogen exchange experiments, using a continuous-flow mixer, to determine the residue-specific kinetic parameters, kop and kcl, of the folding intermediates16. The kop and kcl values were each assumed to remain unchanged in the two labeling pulse durations of 0.4–4.0 ms and 6.0–9.6 ms, and simultaneous numerical fitting was performed to obtain a more accurate estimation of the rate constants. Consequently, the rate constants are averaged values of Ia (0.4–4.0 ms) and Ib (6.0–9.6 ms). We collected the kop and kcl data and associated errors from the literature16 and constructed the REFER plot. We found that the (log K, log kop) and (log K, log kcl) data points were modestly aligned around straight lines (Fig. 5a). Then, we performed a robust linear regression to iteratively calculate the weight of each data point. Outlier residues were identified by robust regression as a data point with a small weight value (Supplementary Fig. S3) in a statistically objective manner. Seven outlier residues (A134, L135, E136, R139, D141, I142, and A143) were found and removed (green and magenta, Fig. 5b) to redraw the least-square lines. Due to the large measurement errors (Fig. 5a), the exceptional handling may not be convincing in the revised REFER plot (Fig. 5b), but the outlier residues are outside of the 95% confidence ellipse in the log k vs. log k′ plot (Fig. 5c).
REFER plot and log k vs. log k′ plot of apomyoglobin folding intermediates. (a) REFER plot using all observed residues with estimated fitting uncertainties16. The data points and least square lines of the log kop vs. log K plot and the log kcl vs. log K plot are blue and orange, respectively. (b) Replot. Outlier residues (green and magenta) were removed to redraw the least-square lines (blue and orange). See Supplementary Fig. S4 for details. (c) Log k vs. log k′ plot. The yellow dots are the residues contributing to the least-square lines, and the purple dots are the outlier residues in (b). The yellow group belongs to type N. The yellow dots are enclosed by a 95% confidence ellipse.
The outlier residues were mapped on the native-state structure of apomyoglobin. All outlier residues are located on one face of helix H (Fig. 6, magenta). Interestingly, the Wright group showed that the intermediate Ib is a mixed state of two conformations, with one containing the translocation of helix H by one helical turn toward its N-terminus relative to helix G (Fig. 6, inset). They drew this conclusion from the HX study of amino acid mutants17 and the combination of the HX study with fluorescence quenching and FRET (Förster resonance energy transfer) measurements18. The translocated helix H is not present in the folded state N, and thus they referred to the translocated form of helix H as a non-native structure. Strikingly, the region highlighted by the outlier residues precisely coincides with the amino acid residues involved in the helix translocation.
Mapping of the outlier residues in the REFER plot on the N-state structure of myoglobin. The native holo-structure (PDB ID 2JHO) is used as the best alternative to the intermediate structures. The residues on the least-square lines in Fig. 5b are colored cyan and the outlier residues are magenta. The other residues without information are colored white. These unprobed residues include parts of helices A, G, and H due to the full protection of the amide protons, and helix F and the loops due to the lack of local secondary structures in the intermediate states. The inset shows the helical topology of the kinetic intermediate Ib. The major portions of helices A, B, G, and H are formed. The half-translucent cylinders represent partially formed helices C, D, and E. The state of helix F is unclear in the folding intermediate states because helix F is not stably packed in the apo state of apomyoglobin. The white arrow indicates the translocation of helix H in the intermediate states, Ib.
Discussion
Our retrospective analysis showed that the linear relationship between residue-specific log K (the logarithm of the equilibrium constant) and residue-specific log k (the logarithm of the rate constant) in the REFER plot holds for the structural changes of many proteins (Fig. 1). The analytical methods include EXSY NMR, dispersion relaxation NMR, and hydrogen/deuterium exchange measurements. The residue-based LFER is seen in the two-state slow exchange (Fig. 1a) and structural fluctuations (Fig. 1d, e) of monomeric small proteins, and in two-molecule systems, such as IDP-protein interactions (Fig. 1c). Disappointingly, rbLFER is not seen in the dynamic equilibrium between the unfolded (U) and folded (N) states of the drk SH3 domain (Fig. 1b). In the original report, specially designed pulse sequences were used for the cancellation of the different relaxation properties of magnetization associated with the U and N states20, but the correction is only valid for the reverse INEPT step and seems insufficient.
The substantial number of rbLFER instances indicates the applicability of rbLFER to a wide variety of protein-related phenomena. In this context, the inadvertent use of “two-state exchange” is potentially confusing. Traditionally, “two-state exchange” is used for systems exhibiting the property of cooperativity. Due to the assumption of ideal perfect cooperativity among residues, single K, k, and k′ values suffice for the description of the two-state exchange from a macroscopic standpoint. Under the rbLFER concept, however, the K, k, and k′ values are different on a per-residue basis, and in other words, one macroscopic state looks different from one residue to another. We propose the use of “two-state exchange with reduced cooperativity” as a near-term solution to distinguish from the traditional “two-state exchange”. We expect that the “two-state exchange” will naturally include the residue-level heterogeneity, with an increased interest in the rbLFER concept in the future.
The linearity of the REFER plot is a measure of the deviation from the ideal smooth structural changes. In particular, the reanalysis of the HX study of apomyoglobin16 is intriguing. We found that the outlier residues deviated from the least-square lines in the REFER plot of the apomyoglobin folding intermediates (Fig. 5). The distribution of the outlier residues in the three-dimensional structure is in good agreement with the transient translocation of helix H in the intermediate state Ib (Fig. 6). This unexpected outcome demonstrates that the rbLFER is a practical method to study the dynamic aspects of proteins. The outlier data points appear to form second lines that are almost parallel to the first least-square lines (Fig. 5b; Supplementary Fig. S4b), which suggest a collective motion of the outlier residues. The transient translocation of helix H detected in other experiments is a suitable mechanism for collective motion. The hydrogen bond breaks caused by the translocation of helix H accelerate the hydrogen exchange rates of amide protons. The rate increase was about 1000 s−1, considering the rise in the intercept values (Supplementary Fig. S4b). Note that the REFER plot (Fig. 5) is about the structural fluctuations of the apomyoglobin folding intermediate Ib, whereas the translocation of helix H (Fig. 6) was detected in the folding intermediate state during the entire folding process of apomyoglobin. The two phenomena must be closely related, but further theoretical and experimental studies are necessary.
The rbLFER indicates that the per-residue thermodynamic and kinetic energy terms are closely related throughout a polypeptide chain. We suggest that the rbLFER is a physicochemical basis for smooth folding and conformational changes of protein molecules. In application, the rbLFER provides a useful tool for studying the structures and energetics of the dynamic states (in particular, the transition states) of protein molecules.
Methods
We performed a literature search to collect residue-specific equilibrium and residue-specific rate constants of proteins, mainly in the PubMed literature database (http://www.ncbi.nlm.nih.gov/pubmed/). The keywords included ‘two states’, ‘two sets of cross peaks’, ‘exchange spectroscopy’, ‘residue-specific’, LFER, etc., and their combinations. The linear regression analyses of the REFER plots and log k vs. log k′ plots were performed in the Excel files. To identify outlier data points in REFER plots, robust regression was performed in MATLAB R2020b using the ‘fitlm’ command with the ‘RobustOpts’ option. The Excel files and the MATLAB source code are available as Supplementary Datasets S1 to S5. The protein cartoon was generated with the program PyMOL, version 2.4.2 (Schrödinger). The cartoon image of the apomyoglobin was generated using the PDB ID 2JHO.
Data availability
All data needed to evaluate the conclusions in the paper are presented in the paper and the supplementary information.
References
Kingery, D. A. & Strobel, S. A. Analysis of enzymatic transacylase Brønsted studies with application to the ribosome. Acc. Chem. Res. 45, 495–503 (2012).
Hansch, C., Leo, A. & Taft, R. W. A survey of Hammett substituent constants and resonance and field parameters. Chem. Rev. 91, 165–195 (1991).
Ashani, Y., Snyder, S. L. & Wilson, I. B. Linear free energy relations in the hydrolysis of some inhibitors of acetylcholinesterase. J. Med. Chem. 16, 446–450 (1973).
Matouschek, A. & Fersht, A. R. Application of physical organic chemistry to engineered mutants of proteins: Hammond postulate behavior in the transition state of protein folding. Proc. Natl. Acad. Sci. 90, 7814–7818 (1993).
Plaxco, K. W. et al. The folding kinetics and thermodynamics of the Fyn-SH3 domain. Biochemistry 37, 2529–2537 (1998).
Song, B., Cho, J. H. & Raleigh, D. P. Ionic-strength-dependent effects in protein folding: Analysis of rate equilibrium free-energy relationships and their interpretation. Biochemistry 46, 14206–14214 (2007).
Fersht, A. R., Matouschek, A. & Serrano, L. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding. J. Mol. Biol. 224, 771–782 (1992).
Fersht, A. R. & Sato, S. Φ-value analysis and the nature of protein-folding transition states. Proc. Natl. Acad. Sci. USA 101, 7976–7981 (2004).
Fujinami, D. et al. The lantibiotic nukacin ISK-1 exists in an equilibrium between active and inactive lipid-II binding states. Commun. Biol. 1, 150 (2018).
Fujinami, D., Hayashi, S. & Kohda, D. Residue-specific kinetic insights into the transition state in slow polypeptide topological isomerization by NMR exchange spectroscopy. J. Phys. Chem. Lett. 12, 10551–10557 (2021).
Miloushev, V. Z. et al. Dynamic properties of a type II cadherin adhesive domain: Implications for the mechanism of strand-swapping of classical Cadherins. Structure 16, 1195–1205 (2008).
Palmer, A. G. Chemical exchange in biomacromolecules: past, present, and future. J. Magn. Reson. 241, 3–17 (2014).
Hu, K., Westler, W. M. & Markley, J. L. Simultaneous quantification and identification of individual chemicals in metabolite mixtures by two-dimensional extrapolated time-zero 1H–13C HSQC (HSQC0). J. Am. Chem. Soc. 133, 1662–1665 (2011).
Hu, K., Ellinger, J. J., Chylla, R. A. & Markley, J. L. Measurement of absolute concentrations of individual compounds in metabolite mixtures by gradient-selective time-zero 1H–13C HSQC with two concentration references and fast maximum likelihood reconstruction analysis. Anal. Chem. 83, 9352–9360 (2011).
Hayashi, S. & Kohda, D. The time-zero HSQC method improves the linear free energy relationship of a polypeptide chain through the accurate measurement of residue-specific equilibrium constants. J. Biomol. NMR 76, 87–94 (2022).
Uzawa, T. et al. Hierarchical folding mechanism of apomyoglobin revealed by ultra-fast H/D exchange coupled with 2D NMR. Proc. Natl. Acad. Sci. USA 105, 13859–13864 (2008).
Nishimura, C., Dyson, H. J. & Wright, P. E. Identification of native and non-native structure in kinetic folding intermediates of apomyoglobin. J. Mol. Biol. 355, 139–156 (2006).
Aoto, P. C., Nishimura, C., Dyson, H. J. & Wright, P. E. Probing the non-native H helix translocation in apomyoglobin folding intermediates. Biochemistry 53, 3767–3780 (2014).
Farrow, N. A., Zhang, O., Forman-Kay, J. D. & Kay, L. E. Comparison of the backbone dynamics of a folded and an unfolded SH3 domain existing in equilibrium in aqueous buffer. Biochemistry 34, 868–878 (1995).
Tollinger, M., Skrynnikov, N. R., Mulder, F. A. A., Forman-Kay, J. D. & Kay, L. E. Slow dynamics in folded and unfolded states of an SH3 domain. J. Am. Chem. Soc. 123, 11341–11352 (2001).
Arai, M., Sugase, K., Dyson, H. J. & Wright, P. E. Conformational propensities of intrinsically disordered proteins influence the mechanism of binding and folding. Proc. Natl. Acad. Sci. USA 112, 9614–9619 (2015).
Sugase, K., Dyson, H. J. & Wright, P. E. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature 447, 1021–1025 (2007).
Korzhnev, D. M. et al. Low-populated folding intermediates of Fyn SH3 characterized by relaxation dispersion NMR. Nature 430, 586–590 (2004).
Korzhnev, D. M., Neudecker, P., Zarrine-Afsar, A., Davidson, A. R. & Kay, L. E. Abp1p and Fyn SH3 domains fold through similar low-populated intermediate states. Biochemistry 45, 10175–10183 (2006).
Létourneau, D. et al. STARD6 on steroids: Solution structure, multiple timescale backbone dynamics and ligand binding mechanism. Sci. Rep. 6, 1–16 (2016).
Liu, X. et al. Conformational dynamics and cooperativity drive the specificity of a protein–ligand interaction. Biophys. J. 116, 2314–2330 (2019).
Korzhnev, D. M., Orekhov, V. Y. & Kay, L. E. Off-resonance R1ρ NMR studies of exchange dynamics in proteins with low spin-lock fields: An application to a Fyn SH3 domain. J. Am. Chem. Soc. 127, 713–721 (2005).
Xiao, Y. et al. Phosphorylation releases constraints to domain motion in ERK2. Proc. Natl. Acad. Sci. USA 111, 2506–2511 (2014).
Sivaraman, T., Arrington, C. B. & Robertson, A. D. Kinetics of unfolding and folding from amide hydrogen exchange in native ubiquitin. Nat. Struct. Biol. 8, 331–333 (2001).
Rodriguez, H. M., Robertson, A. D. & Gregoret, L. M. Native state EX2 and EX1 hydrogen exchange of Escherichia coli CspA, a small β-sheet protein. Biochemistry 41, 2140–2148 (2002).
Arrington, C. B., Teesch, L. M. & Robertson, A. D. Defining protein ensembles with native-state NH exchange: Kinetics of interconversion and cooperative units from combined NMR and MS analysis. J. Mol. Biol. 285, 1265–1275 (1999).
Arrington, C. B. & Robertson, A. D. Microsecond to minute dynamics revealed by EX1-type hydrogen exchange at nearly every backbone hydrogen bond in a native protein. J. Mol. Biol. 296, 1307–1317 (2000).
Masson, G. R. et al. Recommendations for performing, interpreting and reporting hydrogen deuterium exchange mass spectrometry (HDX-MS) experiments. Nat. Methods 16, 595–602 (2019).
Di Nardo, A. A. et al. Dramatic acceleration of protein folding by stabilization of a nonnative backbone conformation. Proc. Natl. Acad. Sci. 101, 7954–7959 (2004).
Settanni, G., Rao, F. & Caflisch, A. Φ-Value analysis by molecular dynamics simulations of reversible folding. Proc. Natl. Acad. Sci. 102, 628–633 (2005).
Sánchez, I. E. & Kiefhaber, T. Non-linear rate-equilibrium free energy relationships and Hammond behavior in protein folding. Biophys. Chem. 100, 397–407 (2003).
Sánchez, I. E. & Kiefhaber, T. Hammond behavior versus ground state effects in protein folding: Evidence for narrow free energy barriers and residual structure in unfolded states. J. Mol. Biol. 327, 867–884 (2003).
Krishna, M. M. G., Hoang, L., Lin, Y. & Englander, S. W. Hydrogen exchange methods to study protein folding. Methods 34, 51–64 (2004).
Dyson, H. J. & Wright, P. E. How does your protein fold? Elucidating the apomyoglobin folding pathway. Acc. Chem. Res. 50, 105–111 (2017).
Nishimura, C. Folding of apomyoglobin: Analysis of transient intermediate structure during refolding using quick hydrogen deuterium exchange and NMR. Proc. Japan Acad. Ser. B Phys. Biol. Sci. 93, 10–27 (2017).
Jamin, M. & Baldwin, R. L. Two forms of the pH 4 folding intermediate of apomyoglobin. J. Mol. Biol. 276, 491–504 (1998).
Acknowledgements
This work was partly performed in the Medical Research Center Initiative for High Depth Omics, of the Medical Institute of Bioregulation, Kyushu University. This work was supported by the Japan Society for the Promotion of Science (JSPS, Japan), KAKENHI Grant Number JP21H02448, and the Mitsubishi Foundation (Japan) Research Grants in the Natural Sciences, Grant Number 202110017, to D.K.
Author information
Authors and Affiliations
Contributions
Conceptualization, D.F. and D.K.; Investigation, D.F., H.S., and D.K.; Writing—Original Draft, D.K.; Writing—Review & Editing, D.F. and S.H.; Funding Acquisition, D.K.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fujinami, D., Hayashi, S. & Kohda, D. Retrospective study for the universal applicability of the residue-based linear free energy relationship in the two-state exchange of protein molecules. Sci Rep 12, 16843 (2022). https://doi.org/10.1038/s41598-022-21226-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-21226-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.