Abstract
Effective measures to improve road accessibility during storms are required as traffic congestion caused by storm floods increasingly constrains the efficiency of urban commuting. However, flood impacts on urban road connectivity are not yet well assessed due to inaccurate simulation of flood processes in urban areas where high-resolution data for drainage networks and gauged hydrological data are insufficient. Thus, this study assesses flood impacts on road network connectivity in an urban area of southern China through joint modeling of 1-D hydrodynamic processes in drainage networks and 2-D flood inundation processes on roads using MIKE Urban and MIKE 21. High-resolution DEM images of 5 m and a drainage network of 5635 pipelines were used for urban hydrological simulation. Flood depths were gauged for model calibration and validation by recruited volunteers in the context of citizen science. The results show that road network connectivity decreases as rainfall increases. More than 40% of road connectivity is lost in the study area when a 1-in-100-year return period rainfall occurs. The study results can help to inform more adaptive strategies for local flood control. The study methods are also applicable to improving urban hydrological modeling in broader regions.
Similar content being viewed by others
Introduction
Floods are causing increasing damage and losses to human society in this era of global climate change1,2,3. The negative effects of floods are more intense in urban areas because of the intensive land use changes4,5. Over the past several decades, urban floods have considerably increased in frequency and severity due to changes in urban hydrological processes caused by climate and land use changes6,7. Flood control plays a critical role in urban security management8, especially in developing countries experiencing rapid urbanization, as in China9,10,11.
Flooding has significant impacts on various aspects of human society12,13. Understanding the complex nature of flood losses provides a foundation for effective flood management14,15. Generally, there are two types of losses from floods: direct and indirect16,17. Direct damages are those that occur due to physical contact of flood water with humans, property, or other objects16. Indirect damages are wide-ranging, including interruption of traffic that may lead to disruptions in enterprise production and financial losses18. In urban areas, indirect losses from floods may be more widespread, because high-rise buildings and other places of refuge could reduce people’s direct contact with floodwaters, while infrastructure in low-lying areas such as roads, water and gas pipelines, underground subway stations as well as parking lots are flooded, also causing substantial indirect losses19,20,21.
Storm floods that occur due to heavy rainfall are the major type of urban flooding22. Extreme rainfall combined with acceleration of runoff yield caused by increased impervious surfaces in urban areas has caused urban floods to occur increasingly quickly23,24. Urban infrastructure may be flooded in a very short time. As an example, a storm-induced flood devastated Zhengzhou, a city in the central region of China, in July 2021, with maximum 24-h rainfall reaching 663.9 mm25. Water depth on major flooded roads surpassed 1 m after just several hours, causing flood damage to 400,000 cars, about 40.9 billion Yuan in losses. Moreover, the water depth in some subway tunnels exceeded a typical person's chest height in just dozens of minutes, directly claiming the lives of those with insufficient time to escape. Low-lying traffic infrastructure has become a hotspot of inundation losses due to insufficient time for people or cars to evacuate during rapid flooding25.
Models have been developed to improve urban flood management through simulation of urban hydrological processes26,27. For example, Bhattacharjee, et al.28 established a storm water management model to analyze flood peak flow and the flooding extent of Bhubaneswar City, India, using elevation, slope, land use/land cover and storm water drain infrastructure data. Jamali, et al.29 developed RUFIDAM to rapidly estimate flood extent, depth, and associated damage. RUFIDAM was tested in Melbourne, and the resulting prediction of flood extent and accumulated damage cost showed acceptable accuracy. In addition, simulation time was reduced compared to MIKE FLOOD. Quan, et al.30 analyzed the impact of land use/cover change on surface runoff and evaluated flood risk in Shanghai through a simplified urban waterlogging model. These authors found that surface runoff depth increased by 13.19 mm from 1994 to 2006 due to urbanization.
These studies contribute to improved flood management in urban areas, especially for urban road networks. Transportation infrastructure is a key component of the economic growth and development of urban areas31,32,33,34. However, such infrastructure may comprise the major assets affected by inundation, causing not only infrastructure damage but also transportation disruption35. Existing studies assess the vulnerability and accessibility of roads during floods by jointly applying the rainfall–runoff model, the 2-D hydrodynamic model, and road network analysis36,37. For example, Klipper, et al.38 evaluated the accessibility of road networks to hospitals during floods in Jakarta using urban hydraulic models. Katya, et al.18 analyzed the impacts of flooding on traffic in St Maarten, the Netherlands, by integrating a flood model (MIKE Flood) and a traffic model (SUMO). Singh, et al.39 found that more than 40% of road length across the Indian road network becomes impassable when a 1-in-100-year rainfall event occurs, via simulation of road flooding processes.
Road inundation maps in the context of various rainfall events can be generated using methods from the above studies to identify roads at flood risk. However, knowledge gaps remain in that an overall or holistic assessment method for evaluating the performance of inundation maps is lacking. This causes difficulty in comparing different road inundation maps under various flood scenarios. An integrated index, such as one representing changes in road network connectivity across different flood scenarios, is then required to further inform urban flood management by comparing the overall effects of floods.
Accordingly, a comprehensive method for road flood analysis is proposed in this study by jointly applying 2-D flood modeling and road inundation and road network connectivity assessment. Dongguan City, Guangdong Province, China, is adopted as the case study area. The main goals include: (a) assessing flood impacts on urban road connectivity in the case study area; and (b) identifying the relationship between the return periods of rainfall and road network connectivity. This paper proceeds as follows. “Methods” section introduces our method, and “Study area and data” section introduces the data and the data processing. “Results” and “Discussion” sections present the results and discussion. Finally, “Conclusion” section sets forth our conclusions.
Methods
Methodological framework
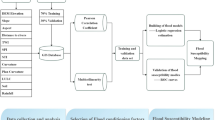
The methodological framework is shown in Fig. 1, in which three calculation steps are represented to assess connectivity changes in the flooded road network under various rainfall scenarios. In the first step, the inundated areas and their water depths in the case area are calculated by simulating urban rainfall–runoff processes using hydrologic and hydrodynamic models. Then, inundated road segments are extracted from inundated urban areas based on the road network map in the study area. It is assumed that inundated segments with water depths over 0.15 m are unavailable for vehicles and pedestrians to pass through. The connectivity of the road network during floods is calculated from the un-flooded roads, which are defined as road segments for which the inundated water depth is less than 0.15 m. The un-flooded road network is obtained by removing road segments with water depth over 0.15 m from the original road network. Finally, in the third step, the connectivity of the road network is assessed using three indicators: Link-Node Ratio (LNR), Intersection Density (ID), and Road Network Density (RND), based on previous studies on road network connectivity40,41,42.
Methodological framework. This graph was generated with Microsoft PowerPoint version 2206(https://www.office.com/).
Hydraulic models
The software packages of MIKE Urban, MIKE 21, and MIKE Flood, developed by the Danish Institute of Hydraulics, are used to model the rainfall–runoff and flood processes in the case area.
MIKE urban
MIKE Urban is applied to calculate the volume of surface runoff by deducting the infiltrated and drained water underground from the rainfall amount. Data on urban land use and drainage networks are used in MIKE Urban. The hydraulic processes in the drainage pipelines are simulated according to the 1-D Saint–Venant equations43, which are as follows:
where Eqs. (1) and (2) represent mass conservation and momentum conservation, respectively. Q, x, A, and t represent the flow (m3/s), distance (m), area of cross-section (m2), and calculation time (s), respectively. g, C, and R represent the acceleration of gravity (m/s2), Chézy coefficient (m1/2·s-1), and hydraulic radius (m), respectively.
MIKE 21
MIKE 21 is used to calculate inundated areas and water depths of surface runoff through hydraulic simulation based on 2-D continuity and momentum equations44, as follows:
where Eq. (3) represents the continuity equation in which h represents the water depth of the wave (m). h = d + η, where d is the steady state water depth (m), and η is the height between the wave surface and still water level (m). t represents the calculation time step (s), and \(\overline{u}\) and \(\overline{v}\) are the flow velocities in the x and y directions (m/s), respectively. S is the water flow from source points. Equations (4) and (5) are momentum equations in the x and y directions, in which f is the Coriolis force coefficient. g, \(\rho , \rho_{0}\), and \(p_{a}\) are the acceleration of gravity (m/s2), water density (kg/m3), reference water density (kg/m3), and atmospheric pressure (Pa), respectively. \(s_{xx} , s_{xy}\), \(s_{yx} , s_{yy}\) are stresses from wave radiation (N). \(T_{xx} , T_{xy}\), \(T_{yx} , T_{yy}\) are shear stresses (N). \(u_{s} , v_{s}\) are flow velocities at the source point (m/s).
MIKE flood
MIKE Flood is applied as a module that couples the 1-D hydrodynamic model (MIKE Urban) and the 2-D model (MIKE21) for joint simulations of rainfall–runoff and flood processes45.
The flow rate and water level in the drainage pipe were calculated by 1-D hydrodynamic model (MIKE Urban) using the land surface runoff as the inflow to the pipe. The surface runoff was obtained by hydrological simulations in the sub- catchments which were divided according to the spatial distribution and the ground elevations of the pipes. Based on these, the overflow from the pipe to the ground was calculated using the model of orifice outflow in MIKE Flood. Finally, the inundated water depth of an area near the overflow point was calculated through 2-D hydrodynamic model (MIKE21) using the terrain data of the area.
Road connectivity assessment
Connectivity refers to the ability to complete links between nodes in transport networks46,47. A higher level of connectivity plays a critical role in improving the accessibility of a transport system, which could provide more effective routes to destinations48. Connectivity is measured by evaluating the intensity of connections between road segments using the number of links, intersections, and dead ends of a road network46. An integrated indicator for assessing road connectivity in the case area is established through normalizing and averaging three sub-indexes: the LNR, ID, and RND, which are widely used for road connectivity assessment in previous studies49,50,51. The LNR is defined as an index equal to the number of links divided by the number of nodes within a road network, as shown in Eq. (6). Links are defined as roadway or pathway segments between two nodes. Nodes are intersections or the end of a road49,52. ID is defined as the number of intersections per unit area53, as shown in Eq. (7). RND is defined as the linear road length per area of the network41, as shown in Eq. (8). A more comprehensive indicator, the Road Network Connectivity Index (RNCI), is established through integrating these three indexes, as shown in Eq. (9). According to previous studies, a larger RNCI represents stronger connectivity of the road network.
where LNRi, IDi, and RNDi represent the Link-Node Ratio, Intersection Density, and Road Network Density, respectively, of un-inundated road segments under rainfall event i. NLi, NPi, and LRi are the number of roadway segments, the number of intersections, and the total length of roadway segments, respectively. S represents the total area of the road network. RNCIi is the connectivity of the road network during rainfall event i. LNRmax, IDmax, and RNDmax represent the maximum value of LNRi, IDi, and RNDi, respectively.
Consent to participate
The authors declare that all the listed authors participate in this article.
Study area and data
Study area
Shatian Town, with an area of 111.5 km2, in Guangdong Province, China, was selected as the case study area. The mean annual rainfall of the area is 1861.6 mm/a. Shatian Town is a highly urbanized area located between Guangzhou and Shenzhen, which are the two biggest metropolises in southern China. As a transportation junction connecting the two metropolises, Shatian Town plays an important role in the commuting of millions of people every year. However, in recent years, it has been facing traffic congestion caused by frequent storm floods. Assessing road connectivity changes during storms is required to implement more efficient and adaptive traffic management in the area.
Data and processing
Rainfall
Rainfall data were obtained from a meteorological station (latitude 22.91, longitude 113.87) in the case area. The meteorological station was established by Dongguan University of Technology; it has measured rainfall for the case area at 30-min intervals since 2018. The gauged rainfall from 17:00 to 22:00 on May 31, 2021 was used for model calibration and validation.
Urban drainage network
The urban drainage network map was obtained from the relevant municipal department of the case area. After data processing and cleaning using CAD and ArcGIS software, a drainage network consisting of 5635 pipes with a total length of 198 km, 5487 nodes, and 269 drainage outlets was selected.
DEM
DEM data with a spatial resolution of 5 m were applied. This high-resolution DEM image was generated from 147,640 elevation points measured on-site by the local municipal department in 2019. Instead of using satellite DEM data, high-resolution ground observation data were used; this is helpful in increasing the accuracy of the hydraulic simulation.
Urban land use
The land use data for the case area at a spatial resolution of 1 m were obtained by reading the boundary data of the object from remote sensing images of Google Earth.
The types of objects including buildings, roads, grasslands, and water bodies were then recognized by manually visual identification.
Road network
Road data was obtained from the OpenStreetMap (https://www.openstreetmap.org/) rather than Google Earth because the geographic information of the roads can be extracted directly from the OpenStreetMap without efforts of manually visual identification. The road data was compared and calibrated with the Google Earth’s map to ensure its spatial consistency with the land use data. The length of roads in the study area is 153.47 km, or 3.57 km per square kilometer. The data on land use, drainage network, DEM, and area road network are shown in Figs. 2 and 3.
Location of and land uses in the case area. This map was generated with ArcMap Version 10.0. (https://www.esri.com/en-us/arcgis/products/arcgis-desktop/overview).
Data for modeling simulation: (a) urban drainage network; (b) DEM data of case area; (c) road network. This map was generated with ArcMap Version 10.0. (https://www.esri.com/en-us/arcgis/products/arcgis-desktop/overview).
Climate scenarios
Six scenarios of rainfall processes consisting of rainfall return periods of 2a, 5a, 10a, 20a, 50a, and 100a were adopted. The return period of a rainfall event refers to the average time interval between the occurrence of a rainstorm with intensity greater than or equal to a particular value54. A longer return period means a larger amount of precipitation.
Rainfall duration of 2 h and a rain peak coefficient of 0.367 were used to graph rainfall events through a Chicago rain type generator55 based on the "Rainstorm Intensity Formula and Calculation Chart (2016)" of the local area according to previous studies56. The rainfall scenarios are shown in Table 1 and Fig. 4.
Two-hour rainfall process of adopted return periods. This graph was generated with OriginPro 2021 (Learning Edition)(https://www.originlab.com/).
Results
Results of model calibration and validation
The models were calibrated by comparing the calculated and observed water depths during a rainfall event in the case area. Water depths at 10 key locations were measured manually from 17:00 to 22:00 on May 31, 2021, during which the total rainfall over 5 h reached 51.44 mm. The rainfall process is shown in Fig. 5. As there are no hydrographic monitoring stations in the case area, flood depths were gauged manually using rulers and on-site photos. Residents were recruited to provide photos or videos of flooding near them, from which the changes in water depths at residents’ locations during a rainfall event were estimated. Based on this, the maximum water depths during rainfall were adopted for model calibration and validation. The observed and simulated maximum water depths at the 10 locations in the case area are shown in Fig. 6.
Rainfall event in the case area on May 31, 2021. This graph was generated with OriginPro 2021 (Learning Edition)(https://www.originlab.com/).
Comparison of observed and simulated water depth. This graph was generated with OriginPro 2021 (Learning Edition)(https://www.originlab.com/).
Changes in flooded areas under various rainfall scenarios
Changes in flooded areas in the case region across the above rainfall scenarios are shown in Table 2. Note that the flooded area increased as rainfall increased from the return period of 2a to 100a. During the 100a rainfall, the flooded area reached 20.42 km2, accounting for 47.51% of the total area of the case region. Moreover, data on flooded areas with various water depths are provided in Table 2, also showing significant positive relationships with rainfall.
The flooded areas are divided into two parts according to water depth, including areas with an average water depth above 0.15 m and 0.30 m. During the 2a rainfall, the area with a water depth over 0.15 m accounted for 6.16% of the total flooded area, and the area with a water depth over 0.30 m accounted for 0.34% of the total flooded area. During the 100a rainfall, the area with water depths beyond 0.15 m and 0.30 m reached 28.55% and 2.84% of the total flooded area, respectively. Water depth thresholds of 0.15 m and 0.30 m were adopted in this study to represent details of the flood changes, as the passage of pedestrians and vehicles may be significantly affected in areas with water depths beyond these values according to previous studies57. However, the results show that the area with water depth beyond 0.30 m occupied a small part of the region.
Further, maximum flood depths in the study area varied from 1.110 to 1.268 m as rainfall increased. This insignificant change in maximum flood depth implied that areas with higher water depths were concentrated in a small region consisting of hotspots significantly affected by urban flooding.
The spatial distribution of maximum water depths is depicted in Fig. 7. Two hotspots of flooding can be recognized in the northwest and the southern part of the region, indicated by the dotted line. At the first hotspot in the northwest, the area with over 0.30 m flood depth emerged during the 2a rainfall return period and increased as rainfall increased. The maximum water depth of this area ranges from 0.527 to 0.605 m across the rainfall scenarios. For the second hotspot in the south, water depths began to exceed 0.30 m from the 10a rainfall period. The maximum water depth increases to 0.841 m under the 100a rainfall.
Flooded area under different rainfall return periods including (a) Return Period = 2a; (b) Return Period = 5a; (c) Return Period = 10a; (d) Return Period = 20a; (e) Return Period = 50a; (f) Return Period = 100a. This map was generated with ArcMap Version 10.0. (https://www.esri.com/en-us/arcgis/products/arcgis-desktop/overview).
Figure 8 shows the changes of water depths at the northwest and southern hotspots across various return periods of the rainfall. As shown in the figure, the water depths of both the spots increased and reached the peaks exceeding 40 cm in the first hour of the modeling. After that, the water depths decreased. In addition, there were higher levels of inundated water at those spots when the return periods of rainfall increased.
Changes of water depths at (a) the northwest spot and (b) the southern spot. This graph was generated with OriginPro 2021 (Learning Edition)(https://www.originlab.com/).
Impact of urban flooding on the road network
The characteristics of the un-flooded road network under various rainfall scenarios are shown in Table 5. The un-flooded road network was shown in Fig. 9. The characteristics of the un-flooded road network under various rainfall scenarios are shown in Table 3. Un-flooded roads are defined as road segments for which inundated water depth is less than 0.15 m. The un-flooded road network, shown in Fig. 9, was then obtained by removing road segments with water depth over 0.15 m from the original road network.
Un-flooded road network under different rainfall scenarios: (a) Rainfall Return Period = 2a; (b) Rainfall Return Period = 5a; (c) Rainfall Return Period = 10a; (d) Rainfall Return Period = 20a; (e) Rainfall Return Period = 50a; (f) Rainfall Return Period = 100a. This map was generated with ArcMap Version 10.0. (https://www.esri.com/en-us/arcgis/products/arcgis-desktop/overview).
As shown in Table 3, the number of un-flooded road segments, intersections, and endpoints decreased along with increasing rainfall. More and more road segments were flooded when the return periods of rainfall increased. Under the 100a rainfall return period, the length of un-flooded roads accounted for only 36.24% of the original road network not affected by flooding. More than half the roads were flooded with a water depth above 0.15 m when the rainfall return period of the area reached 100a. Moreover, in Fig. 9, note that roads in the southern part of the case area were more affected by floods because un-flooded roads significantly decreased as rainfall increased. This is consistent with the flooding hotspots discussed in “Changes in flooded areas under various rainfall scenarios” section.
Changes in road network connectivity
Connectivity changes in un-flooded road networks are shown in Table 4. As shown in the table, the values of LNR, ID, RND, and RNCI decreased as rainfall increased. The RNCI of the case area was only 0.57 during the 100a rainfall return period, which shows that more than 40% of road connectivity can be lost because of heavy storm flooding. This explicitly demonstrates the extent to which storm rainfall can reduce urban road connectivity in the case area.
Figure 10 shows the relationship between the road connectivity index and the rainfall return periods. Observe that the declining trend of LNR, ID, and RNCI tended to stabilize after the rainfall return period exceeds 20a. The RNCI in the case area declined to 0.67 in the 20a rainfall return period. This showed that the rainfall return period of 20a was a critical point in reducing road connectivity of the case area. For rainfall events in which the return period was less than this critical point, such as rainfall of 2a, 5a, and 10a, road connectivity declined more dramatically as rainfall increased, and thus, more adaptive traffic management is required to address the resulting flooding. This also implies that floods of moderate amounts such as those of 10a and 20a are more critical in influencing road connectivity in the case area and thus require more attention.
Relationship between road connectivity and rainfall. This graph was generated with OriginPro 2021 (Learning Edition)(https://www.originlab.com/).
Discussion
This study assesses changes in road network connectivity caused by urban floods of various rainfall intensities through urban hydrological simulation using MIKE Urban and MIKE 21 in a case area of southern China. Flood maps of the study area with inundated segments and water depths were generated via GIS technologies. The network connectivity of un-flooded roads was then calculated through three indicators: the LNR, ID, and RND to explore the impacts of urban floods on urban traffic. However, urban flood simulation is quite challenging as flood processes are affected by numerous factors including climate, topography, hydraulics, land use, and urban infrastructure. The impacts of topography and drainage networks on urban flood modeling are discussed to provide more detailed implications on the nature of flood processes in urban areas.
Impacts of geographic and hydraulic factors on urban floods
Impacts of the micro-terrain in urban areas
Compared with catchment hydrologic modeling in mountain areas, urban hydrologic simulation is more challenging due to the requirement for micro-topographic data to include the strong spatial heterogeneity of urban land surfaces intensively manipulated by human activities. Thus, we employ a DEM image with a high resolution of 5 m from massive on-site measured elevation data at 147,640 points in the case area. These high-resolution DEM data play an important role in increasing the accuracy of urban hydrologic modeling, although such detailed data are not always available in many cities.
Figure 11 shows the DEM data of the case area and the inundated areas with water depths during the 100a rainfall return period. Note that areas that are deeply inundated, such as the area marked by the dotted circle in the figure, are generally located in low-lying regions surrounded by higher objects, such as buildings or highways. This demonstrates that the locations of storm-induced waterlogging areas are not only related to the low-lying terrain of the area but are also affected by the higher elevations of surrounding regions, which could accelerate surface flow from the higher region to its adjacent low-lying spot, resulting in more severe flooding. These were supported by the study of Nobre et al.58, which developed a static approach for mapping the potential extent of inundation using the height above the nearest drainage terrain. They found the relative vertical distances from the higher spots to the nearest river is an effective distributed predictor of flood potential.
DEM and inundated areas of the case region: (a) DEM data; (b) inundated areas of the DEM image. This map was generated with ArcMap Version 10.0. (https://www.esri.com/en-us/arcgis/products/arcgis-desktop/overview).
The decrease of road connectivity in the flooding hotspot which are circled by the dotted line in the Fig.11 are shown in Fig.12. The road connectivity in this area during the rainfall event was much smaller than that of the whole case area. Nearly 50% of the road connectivity was lost during the rainfall of 100-year return period. The micro-terrain feature of this area which can be recognized by the high-resolution DEM data had a significant impact on the modeling of road connectivity in the context of urban floods.
Relationship between road connectivity and rainfall in the flooding hotspot of the case area. This graph was generated with OriginPro 2021 (Learning Edition)(https://www.originlab.com/).
Figure 13 show the changes of road network connectivity in the case area during the first two hours of the rainfall events with various given return periods. The changes of LNR, ID, RND, and RNCI under the rainfalls from 5 to 100a return periods were calculated by those indicator’s relative values to the 2a rainfall. Therefore, the values of indicators under the rainfall of 2a return period were 1.0 in the figures. As shown in the Fig. 13d, the road connectivity decreased and reached the lowest point until 75–105 min after the rainfall began. In addition, at the end of the rainfall event with the return period of 100a, the road connectivity of the case area was 70% of the connectivity at the same time during the 2a rainfall. Moreover, as shown in the Fig. 13a–c, the impacts of the urban flood on reducing the Intersection Density (ID) and the Road Network Density (RND) of the road network were larger than the impact on reducing the Link-Node Ratio (LNR). The ID and RND were reduced to approximately 60% during the 100a rainfall comparing with the 2a rainfall, while the LNR was only reduced to 85%. This means that the number of flooded roads and the number of flooded intersections were increased simultaneously when the rainfall increased, casing the similar extents of decreases of ID and RND in the un-flooded road network. This also led to a relatively smaller reduction of LNR, which was the ratio of the number of roads and the number of intersections in the un-flooded road network.
Changes of road connectivity in the case area: (a) Link-Node Ratio; (b) Intersection Density; (c) Road Density; (d) Road Network Connectivity. This graph was generated with OriginPro 2021 (Learning Edition)(https://www.originlab.com/).
Figure 14 show the changes of road network connectivity in the flooding hotspot of the case area. Comparing with the changes of LNR, ID, RND, and RNCI in whole case area (Fig. 13), the changes of these indicators in the flooding hotspot were larger, showing a higher level of the flood impact in this spot. For example, at the end of the rainfall event with the return period of 100a, the road connectivity at this spot was only 60% of the connectivity at the same time during the 2a rainfall. Moreover, there were sharper declines of the road connectivity during the rainfall events at the flooding hotspot, comparing with the reductions of the road connectivity in the whole case area. This means that the roads and intersections in this spot were flooded faster, thus requiring more timely and rapid response measures for the flood control.
Changes of road connectivity in the hotspot of the case area: (a) Link-Node Ratio; (b) Intersection Density; (c) Road Density; (d) Road Network Connectivity. This graph was generated with OriginPro 2021 (Learning Edition)(https://www.originlab.com/).
Impacts of urban drainage networks
Another challenge of urban flood modeling is the requirement for data on underground drainage pipelines, including pipeline maps, elevations, and diameters, to calculate the amount of water discharged from the surface into the ground. This study considered 5635 pipelines with a total length of 198 km, 5487 nodes, and 269 drainage outlets for a 1-D hydraulic simulation of the drainage process. The impacts of the underground drainage network on urban floods were explored by comparing the diameters of pipelines in areas with different inundated water depths in the context of various rainfall scenarios. For this, the differences of inundated water depths between 2a rainfall and 100a rainfall were calculated and divided into three grades, including 0.00–0.15 m, 0.15–0.30 m, and beyond 0.30 m. Within each grade, the areas and their underground pipelines corresponding to those water depth differences are depicted in Fig. 15. The length and average diameter of these pipelines are shown in Table 5.
Distribution of (a) inundated areas and (b) pipelines where the differences in water depth between 2 and 100a rainfalls are greater than 0.15 m. This map was generated with ArcMap Version 10.0. (https://www.esri.com/en-us/arcgis/products/arcgis-desktop/overview).
As shown in Fig. 15, areas with water depth differences over 0.15 m and 0.30 m were concentrated in the northwest part of the case region, which was a hotspot significantly affected by flooding as rainfall increases. However, the average diameter of the pipelines in this area was 0.676 m, the same as pipelines in other areas, as shown in Table 5. This could be a major limitation on flood control in this hotspot as the pipelines were as small as in other areas not significantly affected by floods. More engineering measures such as new drainage pipelines with larger diameter are required in this area to improve its drainage capacity. This is consistent with recent flood control initiatives of the local government, which regards this area as the one of the most vulnerable spots for flooding across the whole city. The local government invested more than RMB 6 million on updating drainage pipelines in 201759.
Challenges of model calibration and validation for urban flood simulation
Model calibration and validation are another major challenge in urban hydrological simulation. It directly affects the accuracy and applicability of models. Generally, gauged water levels and discharges in river courses are used to calibrate and verify the hydrological model. However, these data are not always available in many cities as there are insufficient hydrological gauge stations in urban areas, which leads to difficulties in urban hydrological simulation.
Previous studies used quantitative and qualitative methods to calibrate and verify urban hydrological models60,61,62. The data adopted for quantitative methods of calibration consist of gauged discharges at the outlets of the drainage pipelines63, gauged water level and river runoff64, and measured flood depth65,66. However, these gauged data are difficult to obtain, especially real-time flood depths in urban areas during rainfall events, as workable methods of measuring flood depth across a large urban area are currently rare. Qualitative methods verify urban hydrological models through comparing the locations of high flood-depth points calculated by models with flood hotspots identified by the local government’s experience or field surveys67,68. Empirical locations of flood hotspots are relatively easy to obtain. However, the amount of such data is small, especially long-term time series data. Consequently, it is nearly impossible to quantitatively calibrate model parameters using these location data. In any case, the costs of calibration and verification of urban hydrological models are substantial due to the limited gauge data. More efficient methods are required to obtain more data for model calibration and verification.
In this study, model verification uses data on flood depth obtained by on-site measurement using rulers and photo-based estimations. In addition to manually measuring water depth at various sites during rainfall events, flood photos and videos taken by volunteers were adopted to estimate the water depth. Several volunteers, including convenience store attendants and factory security guards, were recruited to photograph floods in their surrounding area during a selected rainfall event, using their smartphones. Photo shooting time and the GPS coordinates of the shooting location were also recorded and sent to the study authors. These pictures and videos were then used to estimate the water depth at these locations.
The rainfall event in the case area from 17:00 to 22:00 on May 31, 2021 was selected for model verification. Maximum water depths during the rainfall at 10 locations were measured and estimated. Although only limited water depth data were obtained due to high labor requirements and costs of measurement, this provided a new method to estimate urban flood water depth in the context of citizen science. Citizens sharing their local situation in real time is becoming a rich source of data in the era of smart phones and the Internet69. Measurement points and photos of flooding are shown in Fig. 16.
Measurement points and photos of flooding in the case area. This map was generated with ArcMap Version 10.0. (https://www.esri.com/en-us/arcgis/products/arcgis-desktop/overview).
Conclusion
This study assesses changes in road network connectivity caused by urban floods under various rainfall intensities through urban hydrological simulation using MIKE Urban and MIKE 21 in a case area of southern China. Maps of flooded roads and their water depths are generated via GIS technologies. The network connectivity of un-flooded roads is then calculated using three indicators: the LNR, ID, and RND to explore the impacts of urban flooding on urban traffic.
Results indicate that road network connectivity decreases as rainfall increases. The negative relationship between road connectivity and rainfall return period demonstrates the impact of urban storm floods on road traffic. Moreover, a threshold of rainfall increases reducing road network connectivity is identified in the form of the rainfall return period. For rainfalls with a return period less than 20a, road network connectivity of the case area will be significantly affected by floods. In that case, more than 30% of road connectivity will be lost in the case area. For rainfall events with a return period less than 20a, road connectivity will decline more dramatically as rainfall rises, and thus, more adaptive traffic management is required to address such storms in the case area.
In addition, two hotspots vulnerable to floods in the case area are identified by analyzing the impacts of micro-topography and urban drainage networks on urban flood processes. Our results can inform more adaptive strategies for local flood and traffic management in the case area. The methods established here for hydrological model validation are applicable in broader regions as alternatives to obtain richer data for more effective urban hydrological simulation.
Data availability
The data that support the finding of this study are available from the corresponding author upon reasonable request.
References
Barredo, J. I. Major flood disasters in Europe: 1950–2005. Nat. Hazards 42, 125–148. https://doi.org/10.1007/s11069-006-9065-2 (2006).
Johnson, C. & Blackburn, S. (United Nation Office for Risk Reduction, 2012).
Rogers, D. P. Global Assessment Report on Disaster Risk Reduction. United nations office for disaster risk reduction (2011).
Pall, P. et al. Anthropogenic greenhouse gas contribution to flood risk in England and Wales in autumn 2000. Nature 470, 382–385. https://doi.org/10.1038/nature09762 (2011).
Hammond, M. J., Chen, A. S., Djordjević, S., Butler, D. & Mark, O. Urban flood impact assessment: A state-of-the-art review. Urban Water Journal 12, 14–29. https://doi.org/10.1080/1573062x.2013.857421 (2013).
IPCC. The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. Summary for Policymakers. In: Climate Change 2021 (2021).
Lin, N., Emanuel, K., Oppenheimer, M. & Vanmarcke, E. Physically based assessment of hurricane surge threat under climate change. Nat. Clim. Chang. 2, 462–467. https://doi.org/10.1038/nclimate1389 (2012).
Hegger, D. L. T. et al. Assessing stability and dynamics in flood risk governance. Water Resour. Manage 28, 4127–4142. https://doi.org/10.1007/s11269-014-0732-x (2014).
Bradshaw, C. J. A., Sodhi, N. S., Peh, K. S. H. & Brook, B. W. Global evidence that deforestation amplifies flood risk and severity in the developing world. Glob. Change Biol. 13, 2379–2395. https://doi.org/10.1111/j.1365-2486.2007.01446.x (2007).
Hong, H. et al. Application of fuzzy weight of evidence and data mining techniques in construction of flood susceptibility map of Poyang County, China. Sci. Total Environ. 625, 575–588. https://doi.org/10.1016/j.scitotenv.2017.12.256 (2018).
Muis, S., Guneralp, B., Jongman, B., Aerts, J. C. & Ward, P. J. Flood risk and adaptation strategies under climate change and urban expansion: A probabilistic analysis using global data. Sci. Total Environ. 538, 445–457. https://doi.org/10.1016/j.scitotenv.2015.08.068 (2015).
Di Baldassarre, G. et al. Socio-hydrology: Conceptualising human-flood interactions. Hydrol. Earth Syst. Sci. 17, 3295–3303. https://doi.org/10.5194/hess-17-3295-2013 (2013).
Chen, Y., Syvitski, J. P., Gao, S., Overeem, I. & Kettner, A. J. Socio-economic impacts on flooding: A 4000-year history of the Yellow River, China. Ambio 41, 682–698. https://doi.org/10.1007/s13280-012-0290-5 (2012).
Merz, B. et al. Floods and climate: Emerging perspectives for flood risk assessment and management. Nat. Hazard. 14, 1921–1942. https://doi.org/10.5194/nhess-14-1921-2014 (2014).
Nedkov, S. & Burkhard, B. Flood regulating ecosystem services—Mapping supply and demand, in the Etropole municipality, Bulgaria. Ecol. Ind. 21, 67–79. https://doi.org/10.1016/j.ecolind.2011.06.022 (2012).
Merz, B., Kreibich, H., Schwarze, R. & Thieken, A. Review article "Assessment of economic flood damage". Nat. Hazard. 10, 1697–1724. https://doi.org/10.5194/nhess-10-1697-2010 (2010).
Meyer, V. et al. Review article: Assessing the costs of natural hazards—state of the art and knowledge gaps. Nat. Hazard. 13, 1351–1373. https://doi.org/10.5194/nhess-13-1351-2013 (2013).
Katya, P. et al. Flood impacts on road transportation using microscopic traffic modelling technique. Phys. Rev. https://doi.org/10.1007/978-3-319-33616-9_8 (2015).
Koetse, M. J. & Rietveld, P. The impact of climate change and weather on transport: An overview of empirical findings. Transp. Res. Part D: Transp. Environ. 14, 205–221. https://doi.org/10.1016/j.trd.2008.12.004 (2009).
Forero-Ortiz, E., Martínez-Gomariz, E., Cañas Porcuna, M., Locatelli, L. & Russo, B. Flood risk assessment in an underground railway system under the impact of climate change—A case study of the barcelona metro. Sustainability 12, 5291. https://doi.org/10.3390/su12135291 (2020).
Mallakpour, I., Sadegh, M. & AghaKouchak, A. Changes in the exposure of California’s levee-protected critical infrastructure to flooding hazard in a warming climate. Environ. Res. Lett. 15, 064032. https://doi.org/10.1088/1748-9326/ab80ed (2020).
Jongman, B. et al. Increasing stress on disaster-risk finance due to large floods. Nat. Clim. Chang. 4, 264–268. https://doi.org/10.1038/nclimate2124 (2014).
Miller, J. D. et al. Assessing the impact of urbanization on storm runoff in a peri-urban catchment using historical change in impervious cover. J. Hydrol. 515, 59–70. https://doi.org/10.1016/j.jhydrol.2014.04.011 (2014).
Zhou, F. et al. Hydrological response to urbanization at different spatio-temporal scales simulated by coupling of CLUE-S and the SWAT model in the Yangtze River Delta region. J. Hydrol. 485, 113–125. https://doi.org/10.1016/j.jhydrol.2012.12.040 (2013).
Su, A. et al. The basic observational analysis of “7.20” extreme rainstorm in Zhengzhou. Torrential Rain Disasters 40, 445–454. https://doi.org/10.3969/j.issn.1004-9045.2021.05.001 (2021).
Ouma, Y. & Tateishi, R. Urban flood vulnerability and risk mapping using integrated multi-parametric AHP and GIS: Methodological overview and case study assessment. Water 6, 1515–1545. https://doi.org/10.3390/w6061515 (2014).
Sampson, C. C. et al. A high-resolution global flood hazard model. Water Resour. Res. 51, 7358–7381. https://doi.org/10.1002/2015WR016954 (2015).
Bhattacharjee, S., Kumar, P., Thakur, P. K. & Gupta, K. Hydrodynamic modelling and vulnerability analysis to assess flood risk in a dense Indian city using geospatial techniques. Nat. Hazards 105, 2117–2145. https://doi.org/10.1007/s11069-020-04392-z (2020).
Jamali, B. et al. A rapid urban flood inundation and damage assessment model. J. Hydrol. 564, 1085–1098. https://doi.org/10.1016/j.jhydrol.2018.07.064 (2018).
Quan, R. S. et al. Waterlogging risk assessment based on land use/cover change: A case study in Pudong New Area, Shanghai. Environ. Earth Sci. 61, 1113–1121. https://doi.org/10.1007/s12665-009-0431-8 (2010).
Donaldson, D. Railroads of the Raj: Estimating the impact of transportation infrastructure. Am. Econ. Rev. 108, 899–934. https://doi.org/10.1257/aer.20101199 (2018).
Chandra, A. & Thompson, E. Does public infrastructure affect economic activity? Evidence from the rural interstate highway system. Reg. Sci. Urban Econ. 30, 457–490. https://doi.org/10.1016/S0166-0462(00)00040-5 (2000).
Chang, H. et al. Potential impacts of climate change on flood-induced travel disruptions: A case study of Portland, Oregon, USA. Ann. Assoc. Am. Geograph. 100, 938–952. https://doi.org/10.1080/00045608.2010.497110 (2010).
Praharaj, S., Chen, T. D., Zahura, F. T., Behl, M. & Goodall, J. L. Estimating impacts of recurring flooding on roadway networks: A Norfolk, Virginia case study. Natl. Hazards 107, 2363–2387. https://doi.org/10.1007/s11069-020-04427-5 (2021).
Yin, J., Yu, D., Yin, Z., Liu, M. & He, Q. Evaluating the impact and risk of pluvial flash flood on intra-urban road network: A case study in the city center of Shanghai, China. J. Hydrol. 537, 138–145. https://doi.org/10.1016/j.jhydrol.2016.03.037 (2016).
Lyu, H.-M., Shen, S.-L., Yang, J. & Yin, Z.-Y. Inundation analysis of metro systems with the storm water management model incorporated into a geographical information system: A case study in Shanghai. Hydrol. Earth Syst. Sci. 23, 4293–4307. https://doi.org/10.5194/hess-23-4293-2019 (2019).
Coles, D., Yu, D., Wilby, R. L., Green, D. & Herring, Z. Beyond ‘flood hotspots’: Modelling emergency service accessibility during flooding in York, UK. J. Hydrol. 546, 419–436. https://doi.org/10.1016/j.jhydrol.2016.12.013 (2017).
Klipper, I. G., Zipf, A. & Lautenbach, S. Flood Impact assessment on road network and healthcare access at the example of Jakarta, Indonesia. AGILE: GISci. Ser. 2, 1–11. https://doi.org/10.5194/agile-giss-2-4-2021 (2021).
Singh, P., Sinha, V. S. P., Vijhanic, A. & Pahujad, N. Vulnerability assessment of urban road network from urban flood. Int. J. Disaster Risk Reduct. 28, 237–250. https://doi.org/10.1016/j.ijdrr.2018.03.017 (2018).
Chin, G. K., Van Niel, K. P., Giles-Corti, B. & Knuiman, M. Accessibility and connectivity in physical activity studies: The impact of missing pedestrian data. Prev. Med. 46, 41–45. https://doi.org/10.1016/j.ypmed.2007.08.004 (2008).
Jennifer Dill, P. D. in 84 Th Meeting of the Transportation Research Board 11–15 (2004).
Winters, M., Brauer, M., Setton, E. M. & Teschke, K. Built environment influences on healthy transportation choices: Bicycling versus driving. J. Urban Health 87, 969–993. https://doi.org/10.1007/s11524-010-9509-6 (2010).
Dhi, D. H. I. MIKE URBAN user's manual. (2008).
Dhi, D. H. I. MIKE 21 flow model: Hydrodynamic module user guide. (2007).
Dhi, D. H. I. MIKE Flood User Manual. (2007).
Chen, A., Yang, H., Lo, H. K. & Tang, W. H. Capacity reliability of a road network: An assessment methodology and numerical results. Transp. Res. Part B: Methodol. 36, 225–252. https://doi.org/10.1016/S0191-2615(00)00048-5 (2002).
Daniel, C. B., Saravanan, S. & Mathew, S. in Transportation Research Lecture Notes in Civil Engineering Ch. Chapter 17, 213–226 (2020).
Sreelekha, M. G., Krishnamurthy, K. & Anjaneyulu, M. V. L. R. Interaction between road network connectivity and spatial pattern. Procedia Technol. 24, 131–139. https://doi.org/10.1016/j.protcy.2016.05.019 (2016).
Handy, S., Paterson, R. G. & Butler, K. S. Planning for street connectivity: Getting from here to there. Apa Planning Advisory Service Reports, 1–75 (2003).
Xue, H., Cheng, X., Jia, P. & Wang, Y. Road network intersection density and childhood obesity risk in the US: A national longitudinal study. Public Health 178, 31–37. https://doi.org/10.1016/j.puhe.2019.08.002 (2020).
Ye, C., Chen, Y. & Li, J. Investigating the influences of tree coverage and road density on property crime. ISPRS Int. J. Geo Inf. 7, 101. https://doi.org/10.3390/ijgi7030101 (2018).
Ewing, R. H. & Deanna, M. B. Best Development Practices: Doing the Right Thing and Making Money at the Same Time. (1996).
Kerr, J. et al. Active commuting to school: Associations with environment and parental concerns. Med Sci. Sports Exerc. 38, 787–793. https://doi.org/10.1249/01.mss.0000210208.63565.73 (2006).
Wang, Z. (China Architecture Publishing House (In Chinese), 1998).
Cen, G., Shen, J. & Fan, R. Research on rainfall pattern of urban design storm. Adv. Water Sci. 9, 41–46 (1998) (in Chinese).
Liao, W., Wang, C., Zhou, X. & Wang, Z. in International Conference on Mechatronics, Electronic, Industrial and Control Engineering 370–374 (2014).
Choo, K.-S., Kang, D.-H. & Kim, B.-S. Impact assessment of urban flood on traffic disruption using rainfall–depth–vehicle speed relationship. Water 12, 926. https://doi.org/10.3390/w12040926 (2020).
Nobre, A. D. et al. HAND contour: A new proxy predictor of inundation extent. Hydrol. Process. 30, 320–333. https://doi.org/10.1002/hyp.10581 (2016).
The People's Government of Shatian Town, D. C. Announcement of Tender for Waterlogging Remediation Project of Gangkou Avenue (Shidong Oil Depot Section) and Lianjian Road, http://www.dg.gov.cn/zwgk/zfxxgkml/stz/zdlyxxgk/ggzypzly/gcjsxmzbtbly/content/post_2509184.html# (2017).
Patro, S., Chatterjee, C., Singh, R. & Raghuwanshi, N. S. Hydrodynamic modelling of a large flood-prone river system in India with limited data. Hydrol. Process. 23, 2774–2791. https://doi.org/10.1002/hyp.7375 (2009).
Karim, F. et al. Impact of climate change on floodplain inundation and hydrological connectivity between wetlands and rivers in a tropical river catchment. Hydrol. Process. 30, 1574–1593. https://doi.org/10.1002/hyp.10714 (2016).
Teng, J., Vaze, J., Dutta, D. & Marvanek, S. Rapid inundation modelling in large floodplains using LiDAR DEM. Water Resour. Manage 29, 2619–2636. https://doi.org/10.1007/s11269-015-0960-8 (2015).
Barco, J., Wong, K. M. & Stenstrom, M. K. Automatic calibration of the US EPA SWMM model for a large urban catchment. J. Hydraul. Eng. 134, 466–474. https://doi.org/10.1061/(ASCE)0733-9429(2008)134:4(466) (2008).
Saghafian, B., Farazjoo, H., Bozorgy, B. & Yazdandoost, F. Flood Intensification due to changes in land use. Water Resour. Manage 22, 1051–1067. https://doi.org/10.1007/s11269-007-9210-z (2008).
Anni, A. H., Cohen, S. & Praskievicz, S. Sensitivity of urban flood simulations to stormwater infrastructure and soil infiltration. J. Hydrol. 588, 125028. https://doi.org/10.1016/j.jhydrol.2020.125028 (2020).
Dewan, A. M., Islam, M. M., Kumamoto, T. & Nishigaki, M. Evaluating flood hazard for land-use planning in greater dhaka of bangladesh using remote sensing and GIS techniques. Water Resour. Manage 21, 1601–1612. https://doi.org/10.1007/s11269-006-9116-1 (2007).
Papaioannou, G., Loukas, A., Vasiliades, L. & Aronica, G. T. Flood inundation mapping sensitivity to riverine spatial resolution and modelling approach. Nat. Hazards 83, 117–132. https://doi.org/10.1007/s11069-016-2382-1 (2016).
Mosquera-Machado, S. & Ahmad, S. Flood hazard assessment of Atrato River in Colombia. Water Resour. Manage 21, 591–609. https://doi.org/10.1007/s11269-006-9032-4 (2007).
Liu, H., Hao, Y., Zhang, W., Zhang, H. & Tong, J. Online urban-waterlogging monitoring based on a recurrent neural network for classification of microblogging text. Nat. Hazard. 21, 1179–1194. https://doi.org/10.5194/nhess-21-1179-2021 (2021).
Acknowledgements
This study was funded by the National Natural Science Foundation of China (Nos. 51909035, 52179009, and U2040206).
Funding
The National Natural Science Foundation of China (Nos. 51909035, 52179009 and U2040206).
Author information
Authors and Affiliations
Contributions
R.Z.: Modeling setup; analyzing the experimental results; writing- initial draft preparation, Text editing and draft preparations; H.Z.: Development of the original concepts, scope of the work; writing, review and editing; Y.L.: Data acquisition and preparation; G.X.: Data preprocessing; W.W.: Analyzing and validating of the experimental results. The authors declare that they all agree to the publication of this article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhou, R., Zheng, H., Liu, Y. et al. Flood impacts on urban road connectivity in southern China. Sci Rep 12, 16866 (2022). https://doi.org/10.1038/s41598-022-20882-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-20882-5
This article is cited by
-
Impact on urban river water quality and pollution control of water environmental management projects based on SMS-Mike21 coupled simulation
Scientific Reports (2024)
-
Comprehensive investigation of flood-resilient neighborhoods: the case of Adama City, Ethiopia
Applied Water Science (2024)
-
From Safety Against Floods to Safety at Floods*: Theory of Urban Resilience to Flood Adaptation and Synergy with Mitigation
Anthropocene Science (2023)
-
Evaluating the hydrological performance of integrating PCSWMM and NEXRAD precipitation product at different spatial scales of watersheds
Modeling Earth Systems and Environment (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.