Abstract
This study aimed to analyze anthropometrics and mechanomyography (MMG) signals as forearm flexion, pronation, and supination torque predictors. 25 young, healthy, male participants performed isometric forearm flexion, pronation, and supination tasks from 20 to 100% maximal voluntary isometric contraction (MVIC) while maintaining 90° at the elbow joint. Nine anthropometric measures were recorded, and MMG signals from the biceps brachii (BB), brachialis (BRA), and brachioradialis (BRD) muscles were digitally acquired using triaxial accelerometers. These were then correlated with torque values. Significant positive correlations were found for arm circumference (CA) and MMG root mean square (RMS) values with flexion torque. Flexion torque might be predicted using CA (r = 0.426–0.575), a pseudo for muscle size while MMGRMS (r = 0.441), an indication of muscle activation.
Similar content being viewed by others
Introduction
Mechanomyography (MMG) is a non-invasive technique for recording low-frequency oscillations in active skeletal muscle fibers1. MMG offers notable benefits, which include but not limited to, minimal skin preparation, negligible effect of skin impedance, and lower susceptibility to external noise2,3. Another benefit, which makes this technique more suitable than its electrical counterpart, surface electromyography (sEMG), is the information related to muscle contractile properties carried in the signal’s frequency content4.
The sEMG is a well-developed technique that has been applied in various areas related to muscle physiology including muscle assessment, prosthetics and exoskeleton development, and fatigue analysis5. These studies reveal that sEMG signals are found to be sensitive to exercise intensity6, speed variation7, and cognitive behavior8, among others. While MMG has been only recently researched for some of the above-mentioned areas, its results have been found promising and its application is gaining traction. The ability of MMG to quantify muscle functions using non-invasive means allows its potential usage for clinical applications5. It has been shown that contractile properties of muscles, which are directly related to the composition and fiber type of muscles, can be better estimated by using MMG frequency parameters. Furthermore, advanced multi-domain applications, such as neuromuscular functions, have also been characterized by MMG, like sEMG9.
A variety of transducers have been used to sense MMG signals. When the muscle is contracted, either through voluntary or simulated motor unit activity, dimensional changes occur within muscle fibers resulting in mechanical vibrations or oscillations9. The oscillatory effects of these contractions travel to the skin surface and are captured by MMG transducers. To get the most optimal MMG signal, muscle mass and sensor weight are the key considerations10. Several types of transducers including accelerometers, piezoelectric contact sensors, condenser microphones, and laser displacement sensors have been considered for acquiring MMG signals. As the transducer records surface oscillations on the skin, the risk of potential disturbances is quite high, hence lightweight MEMS accelerometers can be considered one of the best options for MMG signal acquisition10.
Torque estimation is one of the most important research areas in muscle assessment studies, specifically in those cases where it is difficult to estimate torque using direct methods or during activities that involve gross movements. There is evidence from the literature on the application of MMG as a tool for muscle torque estimation9. In one research study, time and frequency domain parameters of MMG signals have been plotted against torque produced by elbow flexor muscles11. It was found that time and frequency domains of MMG signal may reflect the dissimilarity in motor control startegies that regulate isometric and dynamic torque. Another work concluded that MMG can serve as a suitable approach for the estimation of muscle torque under those conditions where direct measurement of torque is not feasible, such as for sustained contractions under fatiguing conditions12. We believe the findings pertaining to torque estimation have the potential to benefit the research community working in the design and control of prosthetics. Further, these findings may also be useful in predicting overuse injury development in workplace settings that use repetitive joint maneuvers or high torque tasks13.
The elbow flexion movement is contributed by the three elbow joint flexors namely biceps brachii (BB), brachialis (BRA), and brachioradialis (BRD)14. All three muscles are considered in this study for the acquisition of MMG signals during sustained isometric forearm flexion, pronation, and supination tasks. The supination and pronation postures of the forearm are related to the BB and the BRA muscles15. The BB can be further subdivided into two muscle–tendon units. The lateral area of the BB and BRA is related to the pronation posture, and the medial area of the BB is related to the supination posture.
The ability of the forearm to produce muscle torque about the elbow joint is an important measure to gauge the ability to perform related workplace tasks. This outcome depends on both muscle activation levels and muscle cross-sectional area13. Suffice to say, anthropometric measures were observed to be predictive of elbow flexion strength16. Researchers found that forearm circumference and sEMG amplitude were observed to influence wrist torque13. Although, our previous study suggested MMGRMS to be invariant to anthropometrics17, the analysis of anthropometrics and MMG signals as torque predictors is still in its infancy stage, and much remains to be uncovered. This paper aims to analyze anthropometrics and MMG signal parameters as predictors of forearm flexion, pronation, and supination torques. It was hypothesized that anthropometrics and MMG signal activation would exhibit positive correlations which could improve the estimation of torque in elbow flexor muscles.
Methods
MMG sensor and signal recording
MMG signals were collected using three triaxial accelerometers (ADXL335, Analogue Devices, USA; full-scale range = ± 3 g; typical frequency response = 0.5–500 Hz; sensitivity = 330 mVg-1; size = 15 mm × 15 mm × 1.5 mm; weight < 1.5 g). The design of experiment and procedures followed, were similar to our previous studies1,17,18. During the flexion task, accelerometers were placed on muscle bellies and attached using double-sided adhesive tape. This was done with the forearm in the supinated position and flexed at 90°. For the pronation and supination tasks, accelerometers were placed with the forearm in the neutral position and flexed at 90° (Fig. 1). The anatomical position of each muscle belly was determined according to19: BB—into the bulk of the muscle in the middle of the arm; BRA—two finger breadths proximal to the elbow crease along and just lateral to the tendon and bulk of the biceps; and BRD—midway between the biceps tendon and lateral epicondyle along the flexor crease. The x, y, and z axes of each accelerometer were positioned along the estimated longitudinal, lateral, and transverse directions of the muscle fibers, respectively. MMG signals recorded in the transverse axis of the accelerometer were utilized for further processing, as analysis in this direction is least influenced by crosstalk, an undesired effect18. The output from each of the sensors was connected to a data acquisition unit (NI cDAQ 9191 coupled with the NI 9205 module to yield an output at 16-bit resolution with CMRR of 100 dB, National Instruments, Austin, TX, USA), which was connected to a personal computer over Wi-Fi. The acquired MMG signals were digitally sampled at 1 kHz. Data acquisition and storage were performed using custom-made programs in LabVIEW™ (version 2016, National Instruments, Austin, TX, USA)1,17,18,20.
Subjects
Twenty-five young, healthy, untrained, and right-handed male subjects (mean ± SD: age = 25.523 ± 4.545 years, weight = 68.219 ± 9.658 kg, height = 167.523 ± 3.172 cm) with no history of neuromuscular injury participated in the experiment. Written informed consent was taken from the subjects. The study was approved by the local Medical Research and Ethics Committee (MREC), Ministry of Health, Malaysia, and adhered to the guidelines established by the Declaration of Helsinki. A medical officer was present on site to aid the researchers and handle any emergency.
Recording of anthropometric measurements
Anthropometrics such as arm length (LA), arm circumference (CA), age, weight, height, BMI, and skin fold thickness (ST) were considered in this study as torque predictors. The recording of these anthropometrics commenced through a familiarization session. The familiarization session was initiated by conducting a short briefing session about the experiments followed by taking written consent from the participants. Subsequently, during the first round, personal details and anthropometric measurements were noted by the experimenter. Later, during the second round, the same anthropometric measurements of all the participants were noted again in another experiment with a gap of at least 24 h between both rounds. The experimenter who recorded the anthropometrics underwent training, under the supervision of a medical officer, to accurately collect more than 150 test readings before taking the actual measurements required for this study. The CA, LA, and ST were measured using the same procedures as described in our previous study17. The details of these anthropometrics along with other parameters of all the subjects are given in Table 1.
Determination of MVIC
Each participant completed the experiment in two sessions. In the first session, maximal voluntary isometric contractions (MVIC) were determined for all three isometric tasks. Three trials were performed for each task with a gap of 2 min between trials and 10 min between tasks. Each participant followed postural settings similar to those described in our previous study17.
The maximum weight (in the form of dumbbells) that a participant could isometrically sustain for 2–3 s in proper posture and forearm in a supinated position, was considered as MVIC for the flexion task. The participant held a wrist dynamometer (Baseline™ Evaluation Instruments, Fabrication Enterprises Inc., NY, USA) for MVIC determination in the pronation and supination tasks. The wrist was maintained at a neutral position and MVIC was determined as the maximum effort the participant could produce for 2–3 s of forearm pronation or supination. Only trials with variations less than ± 5% from the expected values were acceptable. Participants were strongly encouraged verbally to produce their maximum effort for MVIC determination in all three tasks.
Submaximal to maximal tasks
In the second session, subjects performed warmups, followed by submaximal tasks using similar postural settings. Subjects were asked to perform three isometric tasks (flexion, pronation, and supination) at 20%, 40%, 60%, 80%, and 100% MVIC for at least 6 s, with an inter- and intra-task rest of at least 10 min and 2 min, respectively. However, our recordings show that for 100% MVIC, most of the participants could hold only for at most 4 s, which was nevertheless considered sufficient for data processing. All the trials per task were randomized in terms of levels of effort to avoid any risk of biasness in the data. Subjects were not informed of the order prior to the commencement of the task. Trials were repeated if the observed torque levels presented a deviation of ± 5% of the expected values. During the trials, proper posture, off-axis precautionary measures, maximum ± 5% variations, announcement of elapsed time, and verbal encouragement were observed. The generated signals were recorded on a personal computer for further analysis.
Data analysis
The data stored on a personal computer were digitally bandpass filtered (4th-order Butterworth) at 5–100 Hz to obtain the MMG signals. Only those collected signals that provided a signal-to-noise ratio > 10 dB were used for further processing. The 2-s long MMG signals from the middle of each isometric contraction were then extracted to avoid transient phenomenon when the muscle passes from rest to activity and vice versa, as recommended by21. These segments were then used to quantify RMS.
Statistical analysis
Statistical analyses were performed using IBM SPSS (version 20, IBM SPSS Statistics, NY, USA). Data normality was checked using Shapiro–Wilk’s test and the acquired data from the experiments was found to be normally distributed. Thus, parametric analyses were employed in all subsequent computations. Linear regression was performed to determine the estimated relationship of the torque values with RMS and anthropometric parameters. Pearson’s correlation coefficients (r) at a significance level of 0.05 were used to describe the correlation between the variables as follows: 0.00 to ± 0.30 = negligible; ± 0.30 to ± 0.50 = low; ± 0.50 to ± 0.70 = moderate; ± 0.70 to ± 0.90 = high; ± 0.90 to ± 1.00 = very high22.
Results
Tables 2, 3, 4 summarize Pearson’s correlation coefficient (r), goodness of fit (r2), and root mean squared error (RMSE), for torque against the twelve anthropometric parameters and MMGRMS, during flexion, pronation, and supination tasks.
During all three isometric tasks at five different submaximal to maximal effort levels, the values of r, r2 and RMSE varied from − 0.396 to 0.575, 0.000 to 0.331, and 1.832 to 17.674 respectively. The value of r was during all three isometric tasks observed to vary from – 0.122 to 0.175 for LA, 0.159 to 0.575 for CA, − 0.175 to 0.039 for age, − 0.077 to 0.236 for weight, − 0.028 to 0.187 for height, 0.018 to 0.290 for BMI, − 0.086 to 0.232 for ST BB, − 0.119 to 0.026 for ST BRA, − 0.077 to 0.198 for ST BRD, − 0.010 to 0.370 for RMS BB, − 0.007 to 0.386 for RMS BRA and − 0.017 to 0.441 for RMS BRD. The overall range of r for isometric tasks was noted as − 0.362 to 0.575, − 0.293 to 0.294, and − 0.399 to 0.29 during isometric flexion, pronation, and supination tasks respectively.
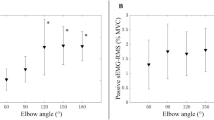
Positive correlations were observed for torque with CA (r = 0.159 to 0.575) and torque with BMI (r = 0.018 to 0.290) during all three isometric tasks. Pearson's correlation of torque with CA were observed to be significant (r = 0.426 to 0.575, r2 = 0.181 to 0.331, RMSE = 2.361 to 5.755) during isometric flexion task at 40–100% MVIC. Scatter plots in Fig. 2 show the linear regression line for torque against CA. The values of r between torque and RMS was found significant (r = 0.441, r2 = 0.194, RMSE = 1.832) for BRD at 20% MVIC. The values of r2 varied from 0.000–0.331, 0.000–0.086, and 0.000–0.157 during isometric flexion, pronation, and supination tasks respectively. Significant and low positive correlations were observed for CA and RMS BRD against torque. It was observed from the scatter plots of CA against muscle torque that positive correlation was exhibited between the two parameters as indicated by their linear regression line. However, the points in the scatter plots for lower submaximal effort levels, specifically at 20 and 40% MVIC, were observed to be rather concentrated at a few torque values.
RMSE was observed to be increasing with ascending levels of effort from 20 to 100% MVIC in all three isometric tasks. RMSE was observed to range from 1.832–2.041, 2.361–2.886, 4.385–4.847, 4.626–5.573 and 6.489–6.751 at 20%, 40%, 60%, 80% and 100% MVIC respectively, during the isometric flexion task. Similarly, RMSE varied from 3.461–3.529, 6.848–7.157, 10.378–10.696, 13.679–14.076 and 16.936–17.674 at 20%, 40%, 60%, 80% and 100% MVIC respectively, during the isometric pronation task. Finally, RMSE ranged from 2.468–2.540, 5.11–5.279, 7.611–7.900, 10.115–10.569 and 12.689–13.186 at 20%, 40%, 60%, 80% and 100% MVIC, respectively during the isometric supination task.
Discussion
From an ergonomics point of view, anthropometrics23 and strength capabilities24 play important roles in workplace design towards the prevention of injury, specifically in the case of workers performing repetitive tasks involving forearm pronation and supination, and elbow joint flexion. Thus, this study was designed to analyze anthropometrics and MMG signals as forearm flexion, pronation, and supination torque predictors. We hypothesized that a few anthropometrics and MMG signal parameters will serve as torque predictors among the elbow flexors. In order to test this hypothesis, correlations of torque, at five submaximal to maximal levels of effort, with nine anthropometrics, and MMGRMS from the BB, BRA and BRD muscles were analyzed. Among the nine investigated anthropometrics, only CA observed the highest correlation with muscle torque during the isometric flexion task at 40% through 100% MVIC (r = 0.426–0.575). The maximum regression values (r2 = 0.181–0.331) observed during the submaximal to maximal isometric flexion task provided evidence of CA being an acceptable torque predictor. These findings support our hypothesis that there is substantial influence by the circumferential measurements of the arm and MMGRMS on flexion torque.
Literature indicates that CA is a measure of muscle size and provides an indication of the amount of contractile tissue25,26,27. While this is true, the findings in this study reveal that CA is more influential in generating muscle torque during the elbow joint flexion tasks, as compared to the forearm pronation and supination tasks. Nevertheless, we do not deny that the participation of all three investigated muscles during the elbow joint flexion might be the reason CA appeared as a significant torque predictor. Significant Pearson’s correlation was observed between MMGRMS from the BRD and joint torque (r = 0.441) during the elbow flexion task. Thus, we can conclude that the acquired MMG signal contains information on muscle activation, and the torque produced at the elbow joint is a result of that activation levels, similar to the conclusions obtained in28. This observation further strengthens our findings on anthropometrics, specifically on CA, to being a prominent torque predictor of the elbow flexion task.
Relationships between muscle size and torque generation have been used in musculoskeletal modeling studies to predict individual muscle forces. Our study observes CA having a weak to moderate positive correlation with muscle torque (r = 0.426–0.575). This finding concurs with similar correlations observed in other studies29,30. Further, moderate correlations were observed at four distinguished levels of effort (40%, 60%, 80% and 100% MVIC). We believe that this observation signifies that muscle torque prediction would not be limited to only low or high levels of effort. Musculoskeletal modeling is conducted, more than often, by purposefully determining individual muscle forces and not the maximum joint force. Thus, having information on the correlation between torque and CA, as revealed by our study, could provide an alternative way towards efficient modeling by being able to estimate individual muscle contributions. In addition, insights into how torque is correlated to anthropometrics and MMG signals have the potential to improve the control and design of prosthetics.
The contribution of muscle activation toward muscle torque prediction has been assessed through sEMG RMS in the past13,16. In this work, MMGRMS from the BRD and muscle torque during the elbow flexion task were observed to have significant correlation (r = 0.441). We believe this correlation, between MMG signal parameters and torque prediction, could be largely improved by including an analysis of the antagonistic coactivation muscles. In addition, a digital dynamometer may be utilized during the isometric flexion task to obtain torque measurements at higher resolutions. This would certainly improve the scatter of acquired data, specifically at the lower effort levels (20 and 40% MVIC), as shown in the regression lines drawn in Fig. 2. The observed accumulation of data points in the scatter plots of low effort levels might be due to the low resolution in the measured torque values. Hence, a protocol designed with a different and sophisticated experimental setup, including fatiguing contractions7, agonistic and antagonistic muscle coactivations5, and participants from both genders, might add more clarity to torque prediction through anthropometrics and MMG signal.
Conclusion
Significant positive correlations were found for flexion torque with CA (r = 0.426–0.575) and MMGRMS (r = 0.441). This observation leads us to conclude that muscle torque is a predictor or pseudo for muscle size and activation levels measured through CA and MMGRMS respectively. These findings on torque correlated with anthropometrics and MMG signals might be useful for workplace design towards injury prevention in the field of ergonomics, and prosthetics design in the field of biomedical engineering and robotics. Our future experiments will involve the engagement of participants having more diverse anthropometrics, which would improve the accuracy and reliability of our findings, and add more clarity on the generation, behavior, and prediction of muscle torque.
Data availability
The datasets generated during and/or analyzed during the study are available from the corresponding author on request.
References
Talib, I., Sundaraj, K. & Lam, C. K. Crosstalk in mechanomyographic signals from elbow flexor muscles during submaximal to maximal isometric flexion, pronation, and supination torque tasks. J. Biomech. Eng. 143, 011001 (2021).
Ma, M. In MMG Sensor for Muscle Activity Detection: Low Cost Design, Implementation and Experimentation: A Thesis Presented in Fulfilment of the Requirements for The Degree of Masters of Engineering In Mechatronics, Massey University, Auckland, New Zealand, Massey University (2010).
Xie, H.-B., Zheng, Y.-P. & Guo, J.-Y. Classification of the mechanomyogram signal using a wavelet packet transform and singular value decomposition for multifunction prosthesis control. Physiol. Meas. 30, 441 (2009).
Beck, T. W. et al. Does the frequency content of the surface mechanomyographic signal reflect motor unit firing rates? A brief review. J. Electromyogr. Kinesiol. 17, 1–13 (2007).
Talib, I., Sundaraj, K., Lam, C. K., Hussain, J. & Ali, M. A. A review on crosstalk in myographic signals. Eur. J. Appl. Physiol. 119, 9–28 (2019).
Hussain, J., Sundaraj, K., Subramaniam, I. D. & Lam, C. K. Analysis of fatigue in the three heads of the triceps brachii during isometric contractions at various effort levels. J. Musculoskelet. Neuronal Interact. 19, 276 (2019).
Hussain, J., Sundaraj, K., Subramaniam, I. D. & Lam, C. K. Muscle fatigue in the three heads of triceps brachii during intensity and speed variations of triceps push-down exercise. Front. Physiol. 11, 112 (2020).
Hussain, J., Sundaraj, K. & Subramaniam, I. D. Cognitive stress changes the attributes of the three heads of the triceps brachii during muscle fatigue. PLoS ONE 15, e0228089 (2020).
Talib, I., Sundaraj, K., Lam, C. K. & Sundaraj, S. A systematic review of muscle activity assessment of the biceps brachii muscle using mechanomyography. J. Musculoskelet. Neuronal Interact. 18, 446 (2018).
Talib, I., Sundaraj, K. & Lam, C. K. Choice of mechanomyography sensors for diverse types of muscle activities. J. Telecommun. Electron. Comput. Eng. 10, 79–82 (2018).
Beck, T. W. et al. Mechanomyographic amplitude and mean power frequency versus torque relationships during isokinetic and isometric muscle actions of the biceps brachii. J. Electromyogr. Kinesiol. 14, 555–564 (2004).
Tarata, M. T. J. Mechanomyography versus electromyography, in monitoring the muscular fatigue. Biomed. Eng. Online 2, 1–10 (2003).
Chimera, N. J., Holmes, M. W. & Gabriel, D. A. Anthropometrics and electromyography as predictors for maximal voluntary isometric wrist torque: Considerations for ergonomists. Appl. Ergon. 97, 103496 (2021).
Staudenmann, D. & Taube, W. J. Brachialis muscle activity can be assessed with surface electromyography. J. Electromyogr. Kinesiol. 25, 199–204 (2015).
Murray, W. M., Buchanan, T. S. & Delp, S. L. The isometric functional capacity of muscles that cross the elbow. J. Biomech. 33, 943–952 (2000).
Green, L. A. & Gabriel, D. A. Anthropometrics and electromyography as predictors for maximal voluntary isometric arm strength. J. Sport Health Sci. 1, 107–113 (2012).
Talib, I., Sundaraj, K. & Lam, C. K. Association of anthropometric parameters with amplitude and crosstalk of mechanomyographic signals during forearm flexion, pronation and supination torque tasks. Sci. Rep. 9, 1–12 (2019).
Talib, I., Sundaraj, K. & Lam, C. K. Analysis of the crosstalk in mechanomyographic signals along the longitudinal, lateral and transverse axes of elbow flexor muscles during sustained isometric forearm flexion, supination and pronation exercises. J. Musculoskelet. Neuronal Interact. 20, 194 (2020).
Perotto, A. O. Anatomical Guide for the Electromyographer: The Limbs and Trunk (Charles C Thomas Publisher, 2011).
Talib, I., Sundaraj, K., Lam, C. & Nabi, F. G. Development of a standalone application to measure crosstalk in MMG signals from forearm muscles during wrist postures. J. Telecommun. Electron. Comput. Eng. 10, 103–106 (2018).
Beck, T. W., DeFreitas, J. M. & Stock, M. S. An examination of cross-talk among surface mechanomyographic signals from the superficial quadriceps femoris muscles during isometric muscle actions. Hum. Mov. Sci. 29, 165–171 (2010).
Mukaka, M. M. A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 24, 69–71 (2012).
Del Prado-Lu, J. L. J. I. J. O. I. E. Anthropometric measurement of Filipino manufacturing workers. Int. J. Ind. Ergon. 37, 497–503 (2007).
Kunelius, A., Darzins, S., Cromie, J. & Oakman, J. Development of normative data for hand strength and anthropometric dimensions in a population of automotive workers. Work 28, 267–278 (2007).
Qazi, S. et al. Relationship of body anthropometric measures with skeletal muscle mass and strength in a reference cohort of young finnish women. J. Musculoskelet. Neuronal Interact. 17, 192 (2017).
Scanlan, J., Ballmann, K., Mayhew, J. & Lantz, C. D. Anthropometric dimensions to predict 1-RM bench press in untrained females. J. Sports Med. Phys. Fitness. 39, 54 (1999).
Rassier, D. E., MacIntosh, B. & Herzog, W. Length dependence of active force production in skeletal muscle. J. Appl. Physiol. 86, 1445–1457 (1999).
Talib, I., Sundaraj, K., Lam, C. K., Ali, M. A. & Hussain, J. Mechanomyography: An insight to muscle physiology. In Intelligent Manufacturing and Mechatronics (Lecture Notes in Mechanical Engineering) 129–137 (Springer, 2020)
Sale, D., MacDougall, J., Alway, S. & Sutton, J. R. Voluntary strength and muscle characteristics in untrained men and women and male bodybuilders. J. Appl. Physiol. 62, 1786–1793 (1987).
Mayhew, J. et al. Relationships of structural dimensions to bench press strength in college males. J. Sports Med. Phys. Fitness 31, 135–141 (1991).
Acknowledgements
The authors would like to acknowledge the Director General of Health Malaysia for giving us permission to publish this article and the Medical Research and Ethics Committee (MREC) of Malaysia for providing ethical approval for the collection of the data used in this study.
Author information
Authors and Affiliations
Contributions
I.T, K.S and J.H conceived, designed and performed the experiments and analyzed the data. All authors contributed reagents/materials/analysis tools and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Talib, I., Sundaraj, K., Hussain, J. et al. Analysis of anthropometrics and mechanomyography signals as forearm flexion, pronation and supination torque predictors. Sci Rep 12, 16086 (2022). https://doi.org/10.1038/s41598-022-20223-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-20223-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.