Abstract
Human interactions and perceptions about health risk are essential to understand the evolution over the course of a pandemic. We present a Susceptible-Exposed-Asymptomatic-Infectious-Recovered-Susceptible mathematical model with quarantine and social-distance-dependent transmission rates, to study COVID-19 dynamics. Human activities are split across different location settings: home, work, school, and elsewhere. Individuals move from home to the other locations at rates dependent on their epidemiological conditions and maintain a social distancing behavior, which varies with their location. We perform simulations and analyze how distinct social behaviors and restrictive measures affect the dynamic of the disease within a population. The model proposed in this study revealed that the main focus on the transmission of COVID-19 is attributed to the “home” location setting, which is understood as family gatherings including relatives and close friends. Limiting encounters at work, school and other locations will only be effective if COVID-19 restrictions occur simultaneously at all those locations and/or contact tracing or social distancing measures are effectively and strictly implemented, especially at the home setting.
Similar content being viewed by others
Introduction
Severe acute respiratory syndrome coronavirus (SARS CoV-2) is a highly transmissible coronavirus that emerged in December 2019 in Wuhan, China causing a devastating disease worldwide named coronavirus disease (COVID-19)1,2,3. It has spread overwhelmingly beyond its predecessors SARS and MERS, in terms of infected figures worldwide and geographical coverage1. SARS CoV-2 is transmitted through respiratory droplets emitted by coughing, sneezing or talking, allowing the virus to enter the respiratory system of the susceptible agent4. Moreover, the virus can cause infection through contaminated hands that make contact with mucous membranes of the eyes, mouth, and nose.
As of July 27, 2021, globally, the number of confirmed cases exceeds 194 million and more than 4 million people have died from COVID-19. On the other hand, as of July 26, 2021, a total of 3,696,135,440 vaccine doses have been administered in the population5. The highest number of cases confirmed is found in the Americas (76,182,529), followed by Europe (59,312,787), South East Asia (37,755,175), Eastern Mediterranean (12,255,849), Africa (4,813,735) and Western Pacific (4,287,201). The 12 countries with the highest number of confirmed cases of COVID-19 to this date are: United States of America (34,256,255); India (31,440,951); Brazil (19,688, 663), Russian Federation (6,172,812); France (5,876,269); United Kingdom (5,722,302); Turkey (5,618,417); Argentina (4,846,615); Colombia (4,727,846); Spain (4,342,054); Italy (4,320,530) and Germany (3,758,401).
In early 2020, the development of vaccines against SARS-CoV-2 began. Several were authorized for emergency use in different countries by the end of 2020 and the beginning of 20216, such as the Pfizer-BioNTech BNT162b2 vaccine7, the Oxford-AstraZeneca vaccine8, the Moderna vaccine9 or the SinoVac-CoronaVac vaccine10,11,12. Even with vaccination campaigns in roll-out, non-pharmaceutical interventions such as keeping social distance, wearing face-masks, and avoiding large gatherings remain mostly recommended and are essential to control the burden of the pandemic13, especially considering the thread of potentially immune-escaping variants14. Additional to social distancing measures, a way to prevent local outbreaks in workplaces, schools, and other locations is implementing effective testing, contact tracing, and quarantine procedures15,16,17.
During the current pandemic, it has become more evident that the spread of COVID-19 primarily depends on factors that strongly relate to human behavior, individual lifestyles, and ways in which people socialize18,19. Considering the relaxation of self-care rules plays an important role when modeling and forecasting the spread of COVID-1920. Hence, while the world is experiencing a global pandemic, the dynamics of social behavior and human contacts have reached a new level of importance. Close contacts are responsible for the transmission of a wide range of diseases18, as well as differences in contacting others become crucial to understand disease dynamics. In fact, social activities and cultural networks play a fundamental role when analyzing contact behavior and contact dynamics that are sensitive to people’s daily activities21. For instance, individuals’ type of social encounters differ when going shopping or spending time at work. In particular, a European large-scale cross-sectional pre-pandemic survey revealed detailed contact patterns22, showing that the number of close contacts per person per day significantly vary depending on the location, including home, work, school, etc., and also differ per country, showing for instance, that the contact rate of a person from Italy almost triples the rate from a German. Additionally, a study conducted in the United States that aimed to determine the prevalence and treatment of latent Tuberculosis, revealed the importance of accounting for the number of contacts made at different workplaces daily23. This study showed that a good percentage of workplaces involved around 20 or more contacts per day; the largest number of reported contacts was 124 within a bank. A further relevant issue is a difference between countries regarding teachers/pupils ratios that affect the contact dynamics in educational facilities. The average U.S. pupil/teacher ratio in public schools is approximately 15.324. Nevertheless, the pupil/teacher ratio of primary and secondary education in developing countries such as the Middle East/North Africa, Sub-Saharan, Latin America, and others Caribbean in conjunction with East and South Asian countries range from 21 to 35 on average25. According to UNESCO, the pupil-teacher ratio (PTR), computed as the total number of pupils in a particular school divided by the total number of teachers, was calculated for public primary schools in Nigeria, revealing a worse scenario with PTRs greater than 5026. Those contact differences between individuals is a crucial element for understanding how diseases are transmitted18.
Intervention measures that reduce social distancing can reduce effective contacts for disease transmission at any location27. In fact, it has been observed that the probability of infection between susceptible and infectious decreases with distance28. In every population, in the absence of disease, there is a natural social distance that is culture and location-dependent (home, work, school, etc.). Theories on human behaviors state that environmental factors, psycho-social aspects, and cultural backgrounds influence those distances that individuals maintain to each other in their daily lives29,30,31,32,33. However, social distances between individuals change from their natural ones in the presence of a pandemic situation34. Under such circumstances, individuals change their awareness by controlling their social distancing and contacting behavior, either spontaneously for protecting themselves or complying to government-mandatory interventions34,35,36.
Social science support in the field of human behavior is needed to align with epidemiological recommendations and to better understand the evolution of COVID-19. In this respect, different perspectives have been presented by the authors in37 for identifying insights regarding social and behavioral approaches during the current pandemic. Such findings show that a strong fear might change the behavior of the people, only if they feel a sense of efficacy in the measure taken. This study revealed a bias optimism among certain people: some of them belief that bad things are unlikely to happen to them which on one hand could avoid negative thoughts, but on the other hand could underestimate the impact of the disease. Consequently, depending of their perception about health risk, people might return to “normal life” by relaxing their protective measures from increased social distancing to their natural distancing and contacting behavior, providing favorable conditions for disease transmission38. Furthermore, scientific studies regarding dispositional resistance to change have been studied in different parts of the world39,40 revealing cultural differences amongst groups of people in terms of strong or weak resistance to change.
Another important issue that needs to be clarified is how people across the world spend their time and where they gather. Evidences suggest that time spent at each location (e.g. work, school, leisure activities, etc.) also depend on cultural practices41,42. A multicultural study conducted by the University of Oxford, revealed information referred to paid work and study hours distributed per week and weekends42 using a big data set that included information from: Belgium, Finland, Germany, Italy, Norway, Spain, Sweden, Bulgaria, Estonia, Latvia, Lithuania, Poland, Slovenia, Japan, Brazil and United States. In addition the American Time Use Survey (ATUS)41 determined the amount of time individuals in the United States spend on various activities, such as: home-activities, work, educational and leisure activities. From those studies, it can be concluded that individuals from Asian countries, Baltic states and the United States are the ones who spend greater time at work compared to other countries. Also, a report made by Data Quality Experian43 detailed the scheduled time Americans spend throughout the day (24 h) via an infographic picture. Based on this information, it can be said, for instance, that the largest number of people in the United States go to sleep at 3:00 a.m.; between 6:00 to 8:00 a.m., there is a sharp rise of people working or performing educational activities. Another digital source of the database is Statista44, reporting that a US citizen’s average daily time shopping is around 29 min. Finally, a recent platform for local mobility provides information about people’s mobility, clustered by types of activities for different communities around the world during COVID-19 times45. This mobility information shows a percentual reduction/increment of mobility for each activity type compared to a baseline pre-pandemic mobility index.
Current literature evidences many mathematical models that explain, characterize, and project the evolution of different infectious diseases that affect human beings46,47,48,49,50. In particular, plenty of mathematical models for COVID-19 dynamics have been developed recently51,52,53,54. Many of the constructed models are extensions of the classical Kermack-McKendrick Susceptible-Infectious-Recovered (SIR) epidemic model55, considering additionally asymptomatic cases53,56, hospitalized individuals, quarantine strategy56,57,58 and/or disease induced deaths53.
The complexity in capturing infectious diseases spread has lead us to incorporate human interactions and reactions within epidemic models18. Most classical models have assumed that all parameters related to human behavior such as contact rates are static, omitting that individuals are likely to change their behavior once they are exposed to the risk of acquiring a potentially deadly or dangerous disease38. In particular, it has been previously suggested to incorporate social-behavioral factors within mathematical disease models to understand better how personal interactions in a society affect disease transmissions, such as physical contact, social distancing behavior, and social mapping of activities38. As a result, a wide range of models that extend the classical approach include dynamic transmission rates, which often depend on the evolution of infectious individuals and human behavioral variables59,60,61,62,63,64,65,66,67,68. In particular, recent scientific evidence has acknowledged the use of incorporating changing human behavior within the mechanisms of transmission of the novel SARS-CoV-251,53,54,57. Some other models account for human behavior by dividing the population into different risk groups to consider disease awareness, risk, or fear levels, among others69,70,71,72,73,74,75,76,77,78. For instance, in77, the authors show a deterministic mathematical model of differential equations and an agent-based model that incorporates the dynamics of “fear” to acquire a disease, showing that when fear subsides, it can produce multiple new waves of infection. In78, the authors include behavioral change by studying disease dynamics, including active and less active groups of people, showing that disease dynamics are sensitive to the transfer rate between both groups. Another study79 incorporates social behavior in a compartmental form by presenting the competing dynamics between a resident pathogenic strain and a mutant strain with higher virulence using imitation dynamics80. In addition, a mathematical model, which quantifies the epidemiological impact of the size of groups of individuals, who do or do not follow responsible behavior, can be found in75. Moreover, in the context of COVID-19, an agent-based model was presented by the authors in81, which study non-pharmaceutical intervention scenarios by reducing contact rates in specific settings/locations, but without considering adaptive behavior due to disease presence. In82, the authors describe the importance of non-pharmaceutical interventions, particularly the use of face-masks, based on a model of ordinary differential equations, modeling face-mask use as a proportion that lowers the probability of transmission of the entire population. Finally, a modeling study in17 combined a model of individual-level transmission stratified by setting, strategies of self-isolation, testing, contact tracing, and also physical distancing to ensure the effectiveness of interventions against SARS-CoV-2 . The aforementioned study showed that only self-isolation of symptomatic cases reduced the transmission rate up to 29%, whilst adding household quarantine increased the transmission reduction to 37%. This leads us to think that a stratified mathematical modeling approach aggregated by different settings such as household, work, school, and others, might provide a more accurate scenario for disease control.
We complement the existing literature by extending a compartmental model of ordinary differential equations by considering three main locations where individuals make contacts: home (h), work (w), school (c), and other locations (o), for instance, those destined to leisure activities. At each location, we propose a disease progression according to a Susceptible-Exposed-Infectious-Recovered (SEIR) model, where infectious individuals are divided into symptomatic and asymptomatic, and those infectious individuals in conjunction with individuals that are encountered by them, become quarantined for a certain period of time. Additionally, we incorporate social distancing at each location as a dependent variable described by a differential equation. The focus of this dynamic might depend on two opposite drives: the fear that people perceive due to the point prevalence of the disease as opposed to the resistance individuals experience to change social distancing behavior. All under the premise of a population that is culturally accustomed to behave following a certain natural distance. In addition, the transmission rate of a disease depends on the proximity of contacts between one susceptible and one infectious individual18. Hence, in the proposed model, a transmission rate function will depend on the dynamics of the social distancing variable described before. The behavioral parameters in the present formulation will reflect how people behave daily, considering: (1) where individuals choose to go each day; (2) average time spent at the chosen location; and (3) behavioral aspects of fear and resistance to change, which affect social distancing dynamics at each location and consequently affect disease transmission.
To the best of our knowledge, no studies have been conducted using epidemiological modeling, structured by location and location-dependent social distancing dynamics, which is governed by disease perception and awareness. This study intends, first, to understand how different location-targeted restrictive measures applied overall or at different daily time-blocks affect disease dynamics; second, how a change in location-dependent social distancing affects disease dynamics; and third, how a policy measure of quarantining a person upon a close contact with an infected person might affect disease propagation at different locations.
Methodology
Model in the absence of disease
In this subsection we present the model in the absence of disease. Without considering demographic factors, we assume a population of constant size N. We stratify the population according to different settings: home (h), work (w), school (c) and other (o), such that \(N_h\), \(N_w\), \(N_c\) and \(N_o\) are respectively the number of individuals at each setting, i.e. \(N=N_{h}+\sum _{x \in X}N_{x}=\sum _{y\in Y}N_{y}\) is the total population size, where \(X=\{w,c,o\}\) and \(Y=\{h,w,c,o\}\).
We assume that individuals that are at home leave home at a rate \(\delta\) in order to visit places in X, distributed such that a proportion \(\alpha _x \ge 0\) goes from home to location \(x\in \{w,c,o\}\) and \(\sum \alpha _{x}=1\). Once an individual visits location \(x\in \{w,c,o\}\), the average time spent at that location is \(\sigma _x\), and hence, the exit rate from location x back to home is \(1/\sigma _x\). It is important to notice that the base location is home, i.e. there are no transitions between locations \(x\in \{w,c,o\}\). The mobility dynamic can be represented by the following system of differential equations:
Considering that the time-unit is days, it is reasonable to assume that the rate \(\delta\) and the proportions of how the location settings are distributed, \(\alpha _x, x\in\) \(\{w,c,o\}\), differ according to the day of the week (e.g. weekday or weekend) and also according to dynamics that occur during a day (e.g. daytime or night). In that sense, we divide each day in six consecutive time-blocks of equal duration \(H=\{1{st},\,2{nd},\,3{rd},\,4{th},\,5{th},\,6{th}\}\) and the week in 7 days a week \(W=\{Mon,\,Tue,\,Wed,Thu,\,Fri,\,Sat,\,Sun\}\), such that the notation
determines the value of each parameter in each time block according to i, and each day of the week according to j.
Figure 1 shows the mobility dynamics of the population in the absence of disease, at the locations home (blue), work (red), school (c) and other locations (purple) with time. Figure 1a shows the mobility for five consecutive weeks, starting on a Monday, with everybody at the home setting. We can observe a weekly periodic pattern, where the home location is the most visited. We see during the weekend an increase in home visits and a decrease in school and work locations, as expected. The zick-zack pattern represents the six time blocks per day, at which mobility dynamics change. Figure 1b depicts the dynamics between a Friday and the coming Monday, for each of the six daily time-blocks at each setting. The figure shows clearly, for instance, the decrease in work and school activities starting Saturday and lasting till Monday morning, while leisure and home activities increase during that time. Table 1 shows the parameter values at each time-block and day of the week used for Fig. 1.
Daily distribution of the population in the spatial compartments of h-home, w-work, c-educational facilities, and o-other activities. In (a) the dynamics for five consecutive weeks. In (b) the dynamics during 4 days from Friday to Monday to differentiate workday and weekend, depicting within each day six time-blocks. The parameters involved are detailed in Table 1 with a total population size \(N=100{,}000\).
Model in the presence of disease
Here we extend the simple mobility model from the previous subsection by including disease dynamics. In particular, we present a model for COVID-19 dynamics with quarantine, mobility and distancing behavior that differs according to location. The model splits the population into six epidemiological classes: Susceptible (S), Latent (E), Asymptomatic (A), Infectious (I), Quarantined (Q) and Recovered (R). We assume that latent individuals cannot transmit the disease, that asymptomatic do not show symptoms and that infectious individuals are symptomatic, and that asymptomatic individuals and infectious individuals are capable of transmitting the disease.
We assume for the classes S, E, A and I, that individuals spend their time at home (h), work (w), educational facilities (c) and doing other leisure activities (o). We assume that susceptible, latent and asymptomatic individuals that are at home leave their home at a rate \(\delta\), such that a proportion \(\alpha _x\) goes from home to location \(x\in \{w,c,o\}\). This proportion does not change according to if the person is susceptible, latent or asymptomatic, since at those stages individuals may not even realize that they are infected and hence wouldn’t change their behavior. Infectious individuals that are at home leave their home at a rate \(\delta ^i<\delta\), where a proportion \(\alpha _x^i\) visits location \(x\in \{w,c,o\}\). Once an individual—of any of the epidemiological classes—visits location x, the time spent at that location is \(\sigma _x\), and hence, the exit rate from location x is \(1/\sigma _x\). Figure 2 describes the behavioral flow of individuals, between home and location x.
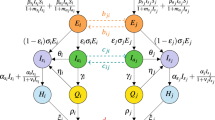
Schematics showing the flow between Susceptible (S), Latent (E), Infectious (I), Asymptomatic (A) individuals, between the home location represented by the subscript h, and other locations represented by the subscript x, where \(x\in \{w,c,o\}\), such that w represents work, c educational facilities, and o other locations for example for leisure activities. The black dotted arrows represent transition rates that are due to disease dynamics and are described in Fig. 3. See Table 2 for the description of the parameters of this diagram.
We assume that individuals change their interaction distance with others depending on where they are located. We denote that interaction distance by \(D_y(t)\), where \(y\in \{h,w,c,o\}\) represents home, work, school and others, respectively, whose dynamics is described by the equation
where \(\lambda _1\) represents the rate of resistance to change with respect to the natural distance \(D^*_y\) that people keep from each other in the absence of disease; \(\lambda _2^y\) represents the per capita rate of change of the distance as a reaction to the number of infectious individuals; and N the total population size.
The diagram in Fig. 3 shows the flow between the epidemiological classes. This disease dynamics holds for any location \(y\in \{h,w,c,o\}\).
Schematics showing the flow between Susceptible (\(S_y\)), Latent (\(E_y\)), Infectious (\(I_y\)), Asymptomatic (\(A_y\)), Recovered (R) and Quarantined (\(Q_i\), \(Q_{e,a}\), \(Q_s\)) individuals, for each location \(y\in \{h,w,c,o\}\), such that h represents home, w work, c educational facilities, and o other locations for example for leisure activities. The read arrows represent rates that depend upon a contact with infectious individuals \(I_y\). The dashed-dotted purple arrow just holds when \(y=h\). See Table 3 for the description of the parameters.
Susceptible individuals can become latent when contacting an infectious or asymptomatic from the same location, according to the following force of infection
where \(\beta _a^y(D_y,\Theta _{y})\) and \(\beta _i^y(D_y,\Theta _{y})\) represent, respectively, the transmission rates upon a contact of a susceptible with an asymptomatic (subscript a) and with an infectious (subscript i) individual. In particular, the transmission rate at home (\(y=h\)) is defined as:
where \(D_h^*\) is the natural distance held at home and \(\Theta _h\) a parameter that considers the reduction in transmission at home due to home-exit restrictions. More specifically, observe that the transmission rate decreases when \(D_h(t)\) increases from the natural distance \(D_h^*\). When \(D_h(t)\) is equal to \(D_h^*\), the disease gets transmitted at a base line transmission rate \(\beta _z^h\), times the parameter \(\Theta _h\). The latter represents the reduction in the home-transmission rate when reducing by \(Red_x\) the proportions \(\alpha _x^*\), \(x\in \{w,c,o\}\), which are the proportions by which people leave the home (h) location under normal conditions. This way, \(\Theta _h\) is defined as
Equivalently, the transmission rates at work (\(y=w\)), school (\(y=c\)), and other locations (\(y=o\)) are defined as
where the respective reductions in the transmission rates at those locations, due to home-exit restrictions, are
From the definitions of the parameters \(\Theta _y\), \(y\in \{h,w,c,o\}\), observe that we assume that the home-transmission-rate gets reduced whenever people choose not to go to any of the other locations; while the transmission-rate at work, school, or other locations, get reduced only when people choose not to go to that specific location, i.e. work, school, other locations, respectively.
Individuals exit the latent class at a rate \(\phi _y\), of which a proportion \(\rho _y\) becomes asymptomatic and a proportion \(1-\rho _y\) becomes infectious (symptomatic). Infectious individuals become quarantined at a rate \(\psi _y^i\), entering the \(Q_i\) class, and then die from the disease at a rate d or recover at a rate \(\gamma\). Asymptomatic individuals become infectious at a rate \(\mu _y\). Asymptomatic and latent individuals become quarantined upon a close contact with an infectious person, entering the \(Q_{e,a}\) class, both at a rate \(\psi _yI_y/N_y\), and then recover at a rate \(\gamma\). Susceptible individuals become quarantined also at a rate \(\psi _y I_y/N_y\) upon a close contact with an infectious person, entering the class \(Q_s\), and then return home at a rate \(\nu\). Recovered individuals may loose immunity and return home as susceptible individuals at a rate \(\epsilon\).
Using the schematics in Figs. 2 and 3 and the above description, we obtain the following system of ordinary differential equations governing the dynamics of the disease:
where \(x\in \{w,c,o\}\), \(y\in \{h,w,c,o\}\), \(N_{y}=S_{y}+E_{y}+A_{y}+I_{y}\), and \(N=\displaystyle \sum _{y}N_y.\)
Numerical results
We present in this section simulations that describe the effect on the number of active cases of different restrictive measures implemented at different locations and time-blocks. We also describe results on how increasing the natural distancing behavior in the home setting or improving close-contacts tracing at different locations affect disease dynamics. The code for these simulations is available in84.
Location-targeted restrictive measures and its effect on the number of active cases
Figures 4 and 5 show the dynamics of the number of active cases \((A(t)+I(t))\) (see subfigures (a.i), i \(=1-4\)) and the transmission rate (see subfigures (b.i), i \(=1-4\)) at each of the locations: home (h, blue), work (w, red), school (c, green), other (o, pink), and for all locations combined (T, black); and under different restrictive measures for attending specific locations. To restrict the attendance to a location (work, school, other), we reduced the proportion of individuals going from home to that location. In the model, that proportion is represented by \(\alpha _x\) for non-infectious individuals at home and \(\alpha _x^i\) for infectious individuals at home, \(x\in \{w,c,o\}\). We study in this section the effect on the number of active cases of the following restrictive measures: (1) reducing the proportion of individuals going from home to work by \(25\%\), capturing the percentage of jobs that can be performed from home that varies within the interval \(20-34\%\) from country to country85, (2) reducing the proportion of individuals going from home to school by \(73\%\), representing a scenario of closing school activities for children older than 4 years of age, who represent \(73\%\) of the child population in the United States86; (3) reducing the proportion of individuals going from home to other locations by \(30\%\), motivated by data showing that a \(15{-}30\%\) growth in consumers in the United States has been observed, who purchase online for most categories post COVID-19 as compared to before87.
Figure 4a.1,b.1 show the base case scenario without any restrictive measures, while Fig. 4a.2–a.4 and b.2–b.4 show the dynamics when restricting the attendance to work, school, and other locations respectively, one at a time. We observe that neither of the single restrictions pictured produce a significant reduction in the total number of active cases as compared to the base case (see black curve in Fig. 4a.1–a.4). We observe that the first peak of the active cases at home shifts slightly to the left when work and other locations attendance is restricted (Fig. 4a.2 and a.4), while it slightly flattens out when school attendance is restricted (Fig. 4a.3), being this restriction the one reducing the number of active cases the most. Additionally, we can observe that the number of active cases at school decrease when school attendance is restricted and becomes the location with the least number of active cases (Fig. 4a.3), while otherwise it can be seen that school is the location (excluding the home location) with the largest number of active cases during weekdays (Fig. 4a.1,a.2,a.4). Also, the number of active cases at other locations become as well the least (compared to work and school) when attendance to other locations is restricted (Fig. 4a.4). On the other hand, when work attendance is restricted, during weekdays the number of active cases at work still remains above the number at other locations (Fig. 4a.2).
We can observe form Fig. 4b.1–b.4 how the transmission rate at home is impacted by the restrictions at different locations that affect the transmission rate at those locations as well. The figures picture the value of the transmission rate at each location for different time blocks within each day from day 7 to 21 (which is the time frame of the first peak). We identify the school attendance restriction (Fig. 4b.3) to be the measure that mostly reduces the transmission rate at home (blue), especially around midday during weekdays, but transmission at home remains mostly high during the weekend (day 13 and 14, 20 and 21). Additionally, we can see that restricting work attendance reduces the transmission rate at work overall (Fig. 4b.2), but does not produce much variation in transmission between time-blocks at work. Nevertheless, the measure reduces the transmission rate at home, especially during the day on workdays. Finally, reducing leisure activities (other) produce a similar effect (Fig. 4b.4), and especially generates a reduction in the transmission rate at home and at other locations at specific times during the weekend.
The figures (a.i), i = 1–4 depict the number of active cases (\(A(t)+I(t)\))—the infectious population—at each location: home (h, blue), work (w, red), school (c, green) and other (o, pink); as well as the total number of active cases (T, black). The curves are pictured for a base case without restrictions and under one restrictions at a time to attend a specific location: (a.1) base case, (a.2) work, (a.3) school, (a.4) other. For each case, the figures (b.i), i = 1–4 show the respective transmission rates at each location, pictured for time blocks within each day, from day 7 to day 21. The restrictions are obtained by reducing the parameters \(\alpha _x\) and \(\alpha _x^i\), \(x\in \{w,c,o\}\), by: \(25\%\) for work, \(73\%\) for school, \(30\%\) for other activities. The parameter values used are as in Table 4.
Figure 5a.1 and b.1 show the base case scenario without any restrictive measures, while Fig. 5a.2–a.4 and b.2–b.4 show the dynamics when restricting the attendance to more than one location at once. For all scenarios pictured we reduced school attendance since it was the single measure that in Fig. 4 showed the largest impact on reducing active cases. As expected, we verify that the more restrictions are implemented the more reduction in the number of active cases can be seen. We observe that when school and one more restriction—either to attend work or attend other activities—are in place (Fig. 5a.2 and a.3), the number of active cases at home at the first peak slightly flattens out and reduces significantly as compared to the base case. The peak of the home cases reduces even more and slightly shifts to the right when attendance to work, school and other activities are restricted (Fig. 5a.4). In all of the combined scenarios of restrictive measures (Fig. 5a.2–a.4), the number of active cases at school is the least as compared to the cases at home, work or other activities. On the other hand, in any restrictive case, including the single location restrictions from Fig. 4, the number of active cases during weekends at other locations exceeds the number of cases at work, while during weekdays it is the opposite, though the latter is least pronounced when work and school attendance is reduced (Fig. 5a.2). Our results reflect the natural behavior of individuals to attend more leisure activities during the weekend and hence it is at these other locations where the majority of active cases are located when leaving the home setting. On the other hand, during weekdays and outside the home setting, without any restrictions (Fig. 5a.1) or only when restricting either work or other locations (Fig. 4a.2 and a.4), it is the school location where most of the active cases are located, whereas when applying combined restrictive measures (Fig. 5a.2–a.4) or just restricting school attendance (Fig. 4a.3) it is the work location where active cases prevail the most.
All measures pictured reduce the transmission rate at the restricted location and also have an effect on the transmission rate at home (Fig. 5b.1–b.4). The most dispersal of the transmission rate at home at different time-blocks per day is observed when restricting work and school attendance (Fig. 5b.2), reducing the home transmission rate during weekdays significantly, but in general maintaining it high during weekends. The latter is also observed for certain weekend time-blocks, when restricting attendance to school and other locations (Fig. 5b.3) and when restricting attendance to all three: work, school and other (Fig. 5b.4).
The figures (a.i), i = 1–4 depict the number of active cases (\(A(t)+I(t)\))- the infectious population- at each location: home (h, blue), work (w, red), school (c, green) and other (o, pink); as well as the total number of active cases (T, black). The curves are pictured for a base case without restrictions, and under several restrictions to attend locations applied at once: (a.1) base case, (a.2) work and school, (a.3) school and other, (a.4) work, school and other. For each case, the figures (b.i), i=\(1-4\) show the respective transmission rates at each location, pictured for time blocks within each day, from day 7 to day 21. The restrictions are obtained by reducing the parameters \(\alpha _x\) and \(\alpha _x^i\), \(x\in \{w,c,o\}\), by: \(25\%\) for work, \(73\%\) for school, \(30\%\) for other activities. The parameter values used are as in Table 4.
Time-blocks and location targeted restrictive measures and its effect on the number of active cases
Figure 6 depicts the dynamics of the number of active cases \((A(t)+I(t))\) at each of the locations: home (h, blue), work (w, red), school (c, green), other (o, pink), and for all locations combined (T, black) under restrictive measures that target specific time-blocks during the day. Figure 6a shows the base case without restrictions. Figure 6b shows a scenario of night quarantine, where the proportions of individuals leaving the home setting—represented by \(\alpha _x\) and \(\alpha _x^i\), \(x\in \{w,c,o\}\)—are reduced to zero for the time-blocks between 9:00 p.m. and 5:00 p.m. On the other hand, Fig. 6c represents the restrictive measure of reducing work and school hours in the afternoon, reducing by half the times spent at work and school (represented by the parameters \(\sigma _w\) and \(\sigma _c\)) during the time-blocks from 1:00 p.m. and 5:00 p.m. and from 5:00 p.m. to 9:00 p.m.
We can observe from Fig. 6b that if night quarantine is fully met, that is, nobody leaves the home setting, the first peak of active cases decreases at all locations and slightly flattens out in the home setting. On the other hand, no decline in the total number of active cases is observed in Fig. 6c when reducing work and school hours in the afternoon by half. On the contrary, there is a slight increase in the size of the first peak of the total number of active cases as compared to the base case without restrictions (5894 cases vs 5852, respectively). Nevertheless, a reduction in infectious cases is observed at work and school, which are probably shifted to the home setting due to individuals staying in the home setting instead of going to work or school and due to the aforementioned observed increase of total active cases in the population.
The figure depicts in each subplot the number of active cases (\(A(t)+I(t)\))—the infectious population—at each location: home (h, blue), work (w, red), school (c, green) and other (o, pink); as well as the total number of active cases (T, black). The subplots show the curves under: (a) the base-case without restrictions; (b) a strict night-quarantine, obtained by reducing the parameters \(\alpha _x\) and \(\alpha _x^i\), \(x\in \{w,c,o\}\) to zero for the time-blocks between 9:00 p.m. and 5:00 p.m.; (c) a restrictive measure reducing the time spent at work and school (represented by the parameters \(\sigma _w\) and \(\sigma _c\)) in the afternoon by half during the time-blocks from 1:00 p.m. and 5:00 p.m. and from 5:00 p.m. to 9:00 p.m. The parameter values used are as in Table 4.
Natural-distancing in the home setting \(D_h^*\) and its effect on the number of active cases
Figure 7 shows how different natural distance values \(D_h^*\) at home affect disease dynamics under the measure that restricts mobility from home to work, school and other locations. When comparing Fig. 7a–d we observe that, the greater the natural distance \(D_h^*\) at home is, the later occurs the first peak of total cases and the smaller is its size, such that large \(D_h^*\) values eventually flatten out the infection curve of total cases (see Fig. 7d). Hence, increasing the natural distance at home may reduce the number of active cases significantly. In particular, Fig. 7 shows that the average physical natural distance at home \(D_h^*\) represents a serious threat for disease transmission when kept low, and on the contrary, it positively impacts disease reduction when kept high (see Fig. 7a,b vs 7c,d). Finally, changing the natural distance at home does not affect the dynamics between locations, being work the location with most of the cases during weekdays and being other activities locations the ones with the highest infectious population during weekends. Nevertheless, reducing natural distancing in the home setting also reduces the number of infectious cases at each of the other locations. Therefore, the inclusion of a responsible behavior at home is essential to reduce the infection curve as a whole.
The sub-figures show the dynamics of active cases for different natural distances at home, under the measure where simultaneously going to work, school, and other locations is restricted. The parameter values used are as in Table 4.
Close-contacts tracing and its effect on the number of active cases
Figures 8 and 9 show point prevalence levels at each location, when quarantine measures of infectious individuals and of non-infectious due to close contacts with infected are more efficiently enforced. That efficiency is represented by an increase in the rates \(\psi _y\) and \(\psi _y^i\), \(y\in \{h,w,c,o\}\), representing the transition rates to quarantine at each location: home (h), work (w), school (c), other (o), either due to a close contact with an infected at the given location or due to being infectious. Figure 8 depicts an increase of 20%, 40% and 60% in all transition rates to quarantine. As expected, we observe that the higher that increase is, the less is the point prevalence level of the disease overall (black curve) and also at each location, when compared to the base line case. Hence, measures that make quarantine measures more efficient, such as stricter tracing of close contacts and enforcement of quarantines, reduce the number of active cases (point prevalence) significantly.
Addition (in percentage) to the transition rate leading to quarantine upon a close contact at every location. The parameter values used are as in Table 4.
On the other hand, Fig. 9 depicts the effect of stricter close contact tracing and quarantine enforcement in only one location, when increasing the transition rates \(\psi _y\) and \(\psi _y^i\) to quarantine by 60% for (a) home, (b) work, (c) school and (d) other. As compared to the base line case depicted in Fig. 8, we observe that stricter quarantine enforcement in the home setting has the biggest effect on reducing the number of total active cases and especially cases at home, while reducing the active cases at other locations as well. On the other hand, we observe that stricter quarantine enforcement only at work, school or others decreases the number of active cases only slightly. These results enforce the importance of implementing strict quarantine measures in the home setting. We observe that strict close contact tracing in the home setting (friends and family) in order to implement quarantine measures is essential to control disease spread. Even if those strict measures are implemented at other locations such as work, school and other, it may not be enough to lower the number of active cases if they are not implemented in the home setting.
Addition (in percentage) to the transition rate leading to quarantine upon a close contact at a specific location. The parameter values used are as in Table 4.
Discussion and conclusions
Social science support in the field of human behavior is needed to align with epidemiological recommendations and to better understand the evolution of COVID-19. In this respect, different perspectives have been presented by the authors in37 for identifying insights regarding social and behavioral approaches during the current pandemic. Such findings show that a strong fear might change the behavior of the people if they feel a sense of efficacy in the measure taken, but nevertheless also a bias optimism among certain people can be observed.
Consequently, depending of their perception on health risk, individuals might return to normal life by relaxing their protective measures from increased social distancing to natural distancing and contacting behaviors, providing favorable conditions for disease transmission40. Some studies have even shown evidence of dispositional resistance to change across different countries40,41,42, revealing cultural differences amongst groups of people in term of strong or weak resistance to change. To account for changes in distancing behavior, our model includes a dynamic resistance- and fear-dependent distancing behavior that affects disease transmission, and specifically, our results show the importance of distancing behavior in the home setting that is essential even under strict mobility restrictions (see Fig. 7). In particular, increasing the natural distance in the home setting may decrease significantly the number of active cases overall. In practice, reducing the number of visits from relatives and/or friends, avoiding long time exposure with them and also preventing crowded gatherings, can serve as handy measures to prevent infection. These findings reveal the importance of promoting family awareness through social distancing as a way to mitigate COVID-19 transmission, even while mobility to work, school and other activities may be restricted and social distancing there may be mandatory.
Another critical issue that affects disease transmission is how people spend their time and where they gather. Evidence suggests that time spent at different locations (e.g., work, school, other leisure activities, etc.) also depends on cultural practices43,44. A multicultural study conducted by the University of Oxford revealed information referred to paid work and study hours distributed per week and weekends44, using an extensive data set that included information from Belgium, Finland, Germany, Italy, Norway, Spain, Sweden, Bulgaria, Estonia, Latvia, Lithuania, Poland, Slovenia, Japan, Brazil, and United States. In addition, the American Time Use Survey (ATUS)43 determined how much time individuals in the United States spend on various activities, such as home activities, work, educational, and leisure activities. Also, a report made by Data Quality45, detailed the scheduled time Americans spend on different activities throughout the day (24 h), via an infographic picture. Finally, a recent platform for local mobility was searched to complete a set of information required to better understand people’s mobility, clustered by the type of activities that different communities around the world established to combat COVID-1945. This information is obtained when comparing with baseline pre-pandemic mobility indices.
Based on information from the previously mentioned studies, we structured our model including home, school, work and other location settings; and considered mobility from home to these settings. Our results show that in general restricting mobility from home to only one location does not impact significantly the number of active cases overall, each measure does though reduce the cases at that specific location. In particular, we observe that restricting school attendance reduces the transmission rate at home the most, especially during weekdays, but not during weekends. We observe a similar but less pronounced effect when restricting work attendance. Restricting other leisure activities reduces home transmission specifically at certain time blocks during weekends. These results show again the importance of the transmission in the home setting (which is the highest among locations), and how measures restricting the mobility from home to only one individual location may not be enough to control the disease overall, since under such a restriction, transmission at home may remain high at certain times during the week (see Fig. 4). Hence, a combination of restrictive measures needs to be considered to really reduce disease transmission. Indeed, we present simulations considering several restrictive measures applied at once, which produce a larger impact on case reduction overall (see Fig. 5). Our results show that if simultaneously school and work attendance is reduced, the most reduction in home transmission during the day on weekdays can be observed, but still remaining high during weekends, unless mobility to other locations is restricted as well. This shows the importance of complementing with other type of protective measures, such as keeping social distance or mask use to reduce overall transmission. Social distancing shows to be particularly important during weekend activities with family and friends (home setting), which indeed has a large impact according to Fig. 7 as discussed before. Therefore, our results conclude that safety at work and school—either by implementing online activities (keeping people at home) or social distancing—may not be enough to reduce active cases to a desired level, if safety measures in the home setting are neglected.
Another important safety measure to prevent disease spread is quarantining individuals after being in close-contact with an infectious person or isolating infectious individuals88. It is worth to highlight that, whether a non-infected person must go into quarantine depends on the definition of close-contact and how well in practice this definition is implemented. We incorporated classes of quarantined individuals, which get there either through the infectious class (go into isolation) or due to having been in close contact with an infectious. Our results show that, when quarantines due to close-contact with an infectious are more efficiently enforced and strict contact tracing is implemented, a significant decrease in infectious cases can be observed. We can see this effect especially if this is done in the home setting, while stricter quarantine enforcement only at work or school just slightly reduces the number of cases overall. This highlights the importance of strictly following and eventually hardening the close-contact definition, especially at home, in order to control the disease.
The new complexity on the transmission of infectious diseases has lead us to incorporate human interactions and reactions to improve the modeling course of the epidemics18. Scientific evidence has highlighted changes in the mechanisms of transmission of this novel SARS-CoV-2, when individuals modify their behavior48,51. Likewise a similar approach has been implemented for modelling the spread of other infectious diseases48,75 targeted to propose more effective control measures to mitigate the spread of the disease. Also, it has been previously suggested to incorporate social, behavioral factors within mathematical disease models to better understand how personal interactions in a society affect disease transmissions; in particular physical contact, social distancing behavior, and social mapping of activities38. We believe that our work contributes to the existing literature by including these aspects in a novel way, implementing the simple idea presented in54—that connects disease transmission with social distancing—, while incorporating it into a location-dependent and time-block-dependent structure, essential for mobility of individuals.
In general, the strength of the present study is the integration of multiple mobility scenarios based on a mathematical approach of Susceptible-Exposed-Asymptomatic-Infectious-Recovered-Susceptible model, with quarantine and social distance dependent transmission rates to study COVID-19 dynamics. Nevertheless, our model shows the limitations intrinsic to extended SIR type models, and is not an exception when considering the difficulties that need to be overcome when analyzing model uncertainty. Before fitting the model to real data, much work needs to be done in conjunction with human behavior scientists, epidemiologists and statisticians, to better understand human behavioral factors used in our model and to obtain data regarding these. Future work entails an interdisciplinary study of this kind. Finally, our model allows to study a variety of potential scenarios using combination of parameters (such as, the ones related to mobility restrictions, average time spent at each location, distribution of activities, cultural factors, close contact definition, etc.), which provides a vast framework for future studies connecting human behavioral factors and disease transmission.
References
Hu, B., Guo, H., Zhou, P. & Shi, Z.-L. Characteristics of SARS-CoV-2 and COVID-19. Nat. Rev. Microbiol. 19, 1–14 (2020).
Coronavirus disease (COVID-19) pandemic, world health organization. https://www.who.int/emergencies/diseases/novel-coronavirus-2019 (2021).
What you should know about COVID-19 to protect yourself and others, centers for disease control and prevention (CDC). https://www.cdc.gov/coronavirus/2019-ncov/downloads/2019-ncov-factsheet.pdf (2020).
Wang, M.-Y. et al. SARS-CoV-2: Structure, biology, and structure-based therapeutics development. Front. Cell. Infect. Microbiol. 10, 587269 (2020).
Who coronavirus (COVID-19) dashboard. https://covid19.who.int (2021).
Status of COVID-19 vaccines within who EUL/PQ evaluation process, World Health Organization (WHO). https://extranet.who.int/pqweb/sites/default/files/documents/Status_COVID_VAX_07April2021.pdf (2021).
Polack, F. P. et al. Safety and efficacy of the BNT162b2 mRNA COVID-19 vaccine. N. Engl. J. Med. 383, 2603–2615 (2020).
Voysey, M. et al. Safety and efficacy of the ChAdOx1 nCoV-19 vaccine (AZD1222) against SARS-CoV-2: An interim analysis of four randomised controlled trials in Brazil, South Africa, and the UK. Lancet 397, 99–111 (2021).
Baden, L. R. et al. Efficacy and safety of the mRNA-1273 SARS-CoV-2 vaccine. N. Engl. J. Med. 384, 403–416 (2021).
Wu, Z. et al. Safety, tolerability, and immunogenicity of an inactivated SARS-CoV-2 vaccine (CoronaVac) in healthy adults aged 60 years and older: A randomised, double-blind, placebo-controlled, phase 1/2 clinical trial. Lancet Infect. Dis. 21, 803–812 (2021).
Zhang, Y. et al. Safety, tolerability, and immunogenicity of an inactivated SARS-CoV-2 vaccine in healthy adults aged 18–59 years: A randomised, double-blind, placebo-controlled, phase 1/2 clinical trial. Lancet Infect. Dis. 21, 181–192 (2021).
Bueno, S. M. et al. Interim report: Safety and immunogenicity of an inactivated vaccine against SARS-CoV-2 in healthy Chilean adults in a phase 3 clinical trial. medRxiv (2021).
Interim public health recommendations for fully vaccinated people, centers for disease control and prevention (CDC). https://www.cdc.gov/coronavirus/2019-ncov/vaccines/fully-vaccinated-guidance.html (2021).
About variants of the virus that causes COVID-19, centers for disease control and prevention (CDC). https://www.cdc.gov/coronavirus/2019-ncov/transmission/variant.html (2021).
Aleta, A. et al. Modelling the impact of testing, contact tracing and household quarantine on second waves of COVID-19. Nat. Hum. Behav. 4, 964–971 (2020).
When to quarantine, centers for disease control and prevention (CDC). https://www.cdc.gov/coronavirus/2019-ncov/if-you-are-sick/quarantine.html (2021).
Kucharski, A. J. et al. Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: A mathematical modelling study. Lancet Infect. Dis. 20, 1151–1160 (2020).
Funk, S. et al. Nine challenges in incorporating the dynamics of behaviour in infectious diseases models. Epidemics 10, 21–25 (2015).
Di Renzo, L. et al. Eating habits and lifestyle changes during COVID-19 lockdown: An Italian survey. J. Transl. Med. 18, 1–15 (2020).
Bertozzi, A. L., Franco, E., Mohler, G., Short, M. B. & Sledge, D. The challenges of modeling and forecasting the spread of COVID-19. Proc. Natl. Acad. Sci. 117, 16732–16738 (2020).
Carrasco, J. A., Miller, E. J. & Wellman, B. How far and with whom do people socialize? Empirical evidence about distance between social network members. Transp. Res. Rec. 2076, 114–122 (2008).
Mossong, J. et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 5, e74 (2008).
Davidow, A. L. et al. Workplace contact investigations in the United States. Int. J. Tuberc. Lung Dis. 7, S446–S452 (2003).
Chingos, M. M. & Whitehurst, G. J. Class Size: What Research Says and What It Means for State Policy. (Brookings Institute, 2011) (Accessed 5 June 2016).
Barro, R. J. & Lee, J. W. International measures of schooling years and schooling quality. Am. Econ. Rev. 86, 218–223 (1996).
Opanuga, A. A., Okagbue, H. I., Oguntunde, P. E., Bishop, S. A. & Ogundile, O. P. Learning analytics: Issues on the pupil-teacher ratio in public primary schools in Nigeria. Int. J. Emerg. Technol. Learn. 14 (2019).
Ahmed, F., Zviedrite, N. & Uzicanin, A. Effectiveness of workplace social distancing measures in reducing influenza transmission: A systematic review. BMC Public Health 18, 1–13 (2018).
Ster, I. C. & Ferguson, N. M. Transmission parameters of the 2001 foot and mouth epidemic in Great Britain. PLoS ONE 2, e502 (2007).
Acosta, C. A. Cuatro preguntas para iniciarse en cambio organizacional. Revista colombiana de psicología 9–24 (2002).
Amaoka, T., Laga, H., Saito, S. & Nakajima, M. Personal space modeling for human-computer interaction. In International Conference on Entertainment Computing, 60–72 (Springer, 2009).
González Pérez, U. El modo de vida en la comunidad y la conducta cotidiana de las personas. Revista Cubana de Salud Pública 31, 0 (2005).
Hall, E. T. et al. Proxemics [and comments and replies]. Curr. Anthropol. 9, 83–108 (1968).
Sorokowska, A. et al. Preferred interpersonal distances: A global comparison. J. Cross-Cult. Psychol. 48, 577–592 (2017).
Maharaj, S. & Kleczkowski, A. Controlling epidemic spread by social distancing: Do it well or not at all. BMC Public Health 12, 1–16 (2012).
Jarvis, C. I. et al. Quantifying the impact of physical distance measures on the transmission of COVID-19 in the UK. BMC Med. 18, 1–10 (2020).
Salje, H., Cummings, D. A. & Lessler, J. Estimating infectious disease transmission distances using the overall distribution of cases. Epidemics 17, 10–18 (2016).
Van Bavel, J. J. et al. Using social and behavioural science to support COVID-19 pandemic response. Nat. Hum. Behav. 4, 460–471 (2020).
Ferguson, N. Capturing human behaviour. Nature 446, 733 (2007).
Boada-Cuerva, M., Boada-Grau, J., Prizmic-Kuzmica, A. J., de Diego, N. G. & Vigil-Colet, A. Rtc-11: Adaptación de la escala de resistencia al cambio en dos países (españa y argentina). Anales de Psicología/Annals of Psychology 34, 360–367 (2018).
Oreg, S. et al. Dispositional resistance to change: Measurement equivalence and the link to personal values across 17 nations. J. Appl. Psychol. 93, 935 (2008).
American time use survey (ATUS). https://www.bls.gov/tus/#data (2020).
Fisher, K. & Robinson, J. Average weekly time spent in 30 basic activities across 17 countries. Soc. Indic. Res. 93, 249–254 (2009).
How Americans spend their time. https://www.edq.com (2021).
Infographics. https://www.statista.com (2021).
COVID-19 community mobility report, google. https://www.google.com/covid19/mobility/index.html?hl=en (2021).
Hethcote, H. W. The mathematics of infectious diseases. SIAM Rev. 42, 599–653 (2000).
Allen, L. J., Brauer, F., Van den Driessche, P. & Wu, J. Mathematical Epidemiology Vol. 1945 (Springer, 2008).
Brauer, F. & Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology Vol. 2 (Springer, 2012).
Roddam, A. W. Mathematical epidemiology of infectious diseases: Model building, analysis and interpretation: O diekmann and jap heesterbeek, 2000, 303. ISBN 0-471-49241-8 (Wiley, 2001).
Chowell, G., Sattenspiel, L., Bansal, S. & Viboud, C. Mathematical models to characterize early epidemic growth: A review. Phys. Life Rev. 18, 66–97 (2016).
Harjule, P., Tiwari, V. & Kumar, A. Mathematical models to predict COVID-19 outbreak: An interim review. J. Interdiscip. Math. 24, 259–284 (2021).
D’angelo, D. et al. Strategies to exiting the COVID-19 lockdown for workplace and school: A scoping review. Saf. Sci. 134, 105067 (2020).
Gumel, A. B., Iboi, E. A., Ngonghala, C. N. & Elbasha, E. H. A primer on using mathematics to understand COVID-19 dynamics: Modeling, analysis and simulations. Infect. Dis. Model. 6, 148–168 (2021).
Cabrera, M., Cordova-Lepe, F., Gutierrez-Jara, J. P. & Vogt Geisse, K. An sir type epidemiological model that integrates social distancing as a dynamic law based on point prevalence and socio-behavioral factors. Sci. Rep. 11, 1–16 (2021).
Kermack, W. Q. & McKendrick, A. G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 115, 700–721 (1927).
Efimov, D. & Ushirobira, R. On an interval prediction of COVID-19 development based on a SEIR epidemic model. (2020).
Fredj, H. B. & Chrif, F. Novel corona virus disease infection in Tunisia: Mathematical model and the impact of the quarantine strategy. Chaos Solitons Fractals 138, 109969 (2020).
Bhadauria, A. S., Pathak, R. & Chaudhary, M. A SIQ mathematical model on COVID-19 investigating the lockdown effect. Infect. Dis. Model. 6, 244–257 (2021).
Capasso, V. & Serio, G. A generalization of the Kermack-McKendrick deterministic epidemic model. Math. Biosci. 42, 43–61 (1978).
Wang, X., Gao, D. & Wang, J. Influence of human behavior on cholera dynamics. Math. Biosci. 267, 41–52 (2015).
Kolokolnikov, T. & Iron, D. Law of mass action and saturation in sir model with application to coronavirus modelling. Infec. Dis. Model. 6, 91–97 (2021).
van den Driessche, P. & Watmough, J. A simple sis epidemic model with a backward bifurcation. J. Math. Biol. 40, 525–540 (2000).
Kochańczyk, M., Grabowski, F. & Lipniacki, T. Dynamics of COVID-19 pandemic at constant and time-dependent contact rates. Math. Model. Nat. Phenomena 15, 28 (2020).
Taghvaei, A., Georgiou, T., Norton, L. & Tannenbaum, A. Fractional sir epidemiological models. Sci. Rep. 10, 20882 (2020).
Ruan, S. & Wang, W. Dynamical behavior of an epidemic model with a nonlinear incidence rate. J. Differ. Equ. 188, 135–163 (2003).
Reluga, T. C. Game theory of social distancing in response to an epidemic. PLoS Comput. Biol. 5, e1000793 (2010).
d’Onofrio, A. & Manfredi, P. Information-related changes in contact patterns may trigger oscillations in the endemic prevalence of infectious diseases. J. Theor. Biol. 256, 473–478 (2009).
Pedro, S. A. et al. Conditions for a second wave of COVID-19 due to interactions between disease dynamics and social processes. medRxiv (2020).
Greenhalgh, D. et al. Awareness programs control infectious disease—Multiple delay induced mathematical model.. Appl. Math. Comput. 251, 539–563 (2015).
Poletti, P., Ajelli, M. & Stefano, M. The effect of risk perception on the 2009 H1N1 pandemic influenza dynamics. PLoS ONE 6, e16460 (2011).
Teslya, A. et al. Impact of self-imposed prevention measures and short-term government-imposed social distancing on mitigating and delaying a COVID-19 epidemic: A modelling study. PLoS Med. 17, e1003166 (2020).
Mummert, A. & Weiss, H. Get the news out loudly and quickly: The influence of the media on limiting emerging infectious disease outbreaks. PLoS ONE 8, e71692 (2013).
Agaba, G., Kyrychko, Y. & Blyuss, K. Mathematical model for the impact of awareness on the dynamics of infectious diseases. Math. Biosci. 286, 22–30 (2017).
Zhao, S. et al. Imitation dynamics in the mitigation of the novel coronavirus disease (COVID-19) outbreak in Wuhan, China from 2019 to 2020. Ann. Transl. Med. 8 (2020).
Córdova-Lepe, F., Cabrera Hernández, M. & Gutiérrez-Jara, J. P. Modeling the epidemiological impact of a preventive behavioral group. Medwave 18 (2018).
Karlsson, C.-J. & Rowlett, J. Decisions and disease: A mechanism for the evolution of cooperation. Sci. Rep. 10, 1–9 (2020).
Epstein, J. M., Parker, J., Cummings, D. & Hammond, R. A. Coupled contagion dynamics of fear and disease: Mathematical and computational explorations. PLoS ONE 3, e3955 (2008).
Del Valle, S., Hethcote, H., Hyman, J. M. & Castillo-Chavez, C. Effects of behavioral changes in a smallpox attack model. Math. Biosci. 195, 228–251 (2005).
Pharaon, J. & Bauch, C. The influence of social behavior on competition between virulent pathogen strains. bioRxiv 293936 (2018).
Bauch, C. T. Imitation dynamics predict vaccinating behaviour. Proc. R. Soc. B Biol. Sci. 272, 1669–1675 (2005).
Ferguson, N. et al. Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce covid19 mortality and healthcare demand. (2020).
Ngonghala, C. N. et al. Mathematical assessment of the impact of non-pharmaceutical interventions on curtailing the 2019 novel coronavirus. Math. Biosci. 325, 108364 (2020).
Situación nacional de covid-19 en chile, ministerio de salud, gobierno de chile. https://www.gob.cl/coronavirus/cifrasoficiales/ (2021).
Working from home: Estimating the worldwide potential, international labour organization. https://www.ilo.org/global/topics/non-standard-employment/publications/WCMS_743447/lang--en/index.htm (2021).
Child population by age group in the united states, kids count data center. https://datacenter.kidscount.org/data/tables/101-child-population-by-age-group (2021).
The great consumer shift: Ten charts that show how us shopping behavior is changing. https://www.mckinsey.com/business-functions/marketing-and-sales/our-insights/the-great-consumer-shift-ten-charts-that-show-how-us-shopping-behavior-is-changing# (2021).
Quarantine and isolation, CDC. https://www.cdc.gov/coronavirus/2019-ncov/your-health/quarantine-isolation.html (2021).
Funding
This work was partially funded by Proyecto Ingeniería 2030 14ENI2-26865 from the Facultad de Ingeniería y Ciencias at Universidad Adolfo Ibáñez, a project financed by the Chilean economic development agency CORFO.
Author information
Authors and Affiliations
Contributions
J.G. proposed the initial model. J.G., K.V., M.C. and F.C. developed the presented model, analyzed results and edited the main text. J.G. developed simulations. K.V., M.C. and M.M. developed the introduction and discussion. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gutiérrez-Jara, J.P., Vogt-Geisse, K., Cabrera, M. et al. Effects of human mobility and behavior on disease transmission in a COVID-19 mathematical model. Sci Rep 12, 10840 (2022). https://doi.org/10.1038/s41598-022-14155-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-14155-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.