Abstract
We demonstrate the formation of a two dimensional Airy beam soliton in a photorefractive crystal. By simply varying the nonlinearity strength we identify several scenarios showing the coexistence between an Airy beam and the emerging soliton. The soliton output profile behaves according to the theoretical soliton existence curve and can be tailored by the nonlinearity strength even without modifying the input Airy beam shape. This last feature makes this Airy soliton distinct from the Gaussian beam generated photorefractive soliton.
Similar content being viewed by others
Introduction
The Airy beam has been extensively studied in the last fifteen years since its first experimental observation in 20071. The Airy beam originated from the domain of quantum mechanics in 1979 with the work of Berry and Balazs2 who found a shape-preserving accelerating solution to the potential-free Schrödinger equation in the form of an ideal Airy function. The paraxial wave equation is a mathematical equivalent of the Shrödinger potential-free equation, which allowed the same solution in optics. Due to the infinite tail of the Airy function and the impossibility to create infinitely large beams, the Airy beam profile is actually an exponentially truncated form of the analytic Airy function. Still, the truncated Airy beam shows characteristics of self-regeneration3, acceleration (or curved trajectory) and to a certain extent non-diffraction. The parabolic trajectory of the Airy beam has been studied4 as well as modified using dynamically varying linear index potentials5. Beams derived from the one-dimensional Airy beam are now being explored such as optical Airy bullets6, abruptly auto-focusing waves7, circular Airy beams8 or super-Airy beams9. These properties have led to a number of interesting applications such as curved plasma channel generations10, light-sheet microscopy11, particle manipulation12, plasmons13, material processing14 or all-optical routing15,16,17.
Airy beam propagation in nonlinear media has suggested interesting dynamics such as soliton-like behaviors and interactions of co- and counter-propagating Airy beams18,19,20,21,22. As a reminder, self-trapping of light beams has been originally observed by compensating the natural diffraction of light by using the focusing effect of nonlinear media23,24. Theoretically, the generation of stable 2D \(\chi\) \(^2\) solitons using a nonlinear frequency conversion phenomenon from Airy waves has been predicted in25; following this study, in similar quadratic optical media, the dynamics and interactions of 2D Airy waves and solitons emerging from a frequency conversion process has also been studied26. By using saturable nonlinear media such as photorefractive crystals, two dimensional self-trapping is also possible, meaning the beam self-traps in both axes transverse to the propagation axis27. In similar focusing nonlinear conditions the Airy beam may split into a weak accelerating structure and an “off-shooting soliton” (OSS) that propagates along the medium without transverse acceleration21,28. The analysis of the one-dimensional Airy beam propagation has proven that the OSS may behave as the expected photorefractive spatial soliton22. Still, there is so far neither theoretical and experimental evidence of a two-dimensional soliton emerging from an Airy beam nor any experimental study of two dimensional Airy beam propagating in a self focusing nonlinear medium. The understanding of such dynamics are of particular interest for the engineering of all-optical waveguides16,17.
In this paper we study experimentally the propagation of a 2D Airy beam inside a photorefractive strontium barium niobate (SBN) crystal for different values of light power and bias electric field applied on the crystal. We demonstrate the formation of a two dimensional Airy beam soliton. Several scenarios are identified showing the transition from the Airy beam to the soliton when increasing the nonlinearity strength of the medium. We show that the soliton output profile behaves according to the theoretical soliton existence curve and that it can be tailored through the nonlinearity strength even without modifying the input Airy beam shape. Hence, this feature distinguishes the Airy beam soliton from the Gaussian beam generated photorefractive soliton. In addition, the Airy soliton is formed at a distinct transverse coordinate than the expected linear Airy output, and this transverse splitting is interesting for the soliton analysis and its applications.
Two dimensional Airy soliton
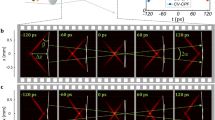
(a) Transverse power profile of the input Airy beam, \(2.8\ \mu\)W. (b–d) Transverse power profile of the output for different applied external field, \(E_{ext}=0\) V/cm, \(E_{ext}= 800\) V/cm, and \(E_{ext}=1200\) V/cm, the soliton position is represented by a dotted white circle. (e) Schematic of the experimental setup. (f–g) power profiles along the x and y axis at the soliton coordinates, centered at the dotted white circle position.
The Airy beam profile injected inside the crystal (Fig. 1a) is obtained by modulating the phase of a Gaussian beam using a spatial light modulator (SLM). The SLM displays a 2D quadratic phase superimposed with a diffraction grating. Figure 1e shows a schematic of our experiment. We propagate a 2D Airy beam, of wavelength \(\lambda = 532\) nm, through a photorefractive Cerium doped (0.01%) SBN:61 crystal (\(n_{SBN}=2.3\)) with dimensions 5 mm * 20 mm * 5 mm along 100, 010, 001 axis. The c axis of the crystal is placed along one of the 5 mm edge along the tetragonal axis and perpendicular to the propagation direction (20 mm edge) : it permits to exploit the dominant electro-optic coefficient of our SBN sample via a linearly polarized incident laser beam along c. Figures 1b–d shows the output face of the crystal for different values of externally applied electric field. After propagation through the SBN crystal the Airy beam seen in Fig. 1b is slightly diffracted and shifted due to the acceleration of the Airy beam. The Airy beam’s truncation parameter is chosen in function of the crystal’s length: it must be weak enough to preserve the Airy beam characteristics across the crystal, but strong enough to enable the observation of nonlinear effects on the beam’s propagation after a 2 cm propagation. When an external electric field is applied (Fig. 1c–d), the light focuses into a soliton-like beam that presents almost no shift in position when compared to the input Airy beam’s main lobe position (see the white circle). The dynamic of spatial light distribution in a photorefractive media is due to the interaction of light and matter and can be explained using the Kukhtarev band transport model29. The light propagation affects the refractive index variations and vice versa. This dynamic results in a focusing effect that, if sufficiently strong (Fig. 1c–d), modifies the profile of the propagating beam into a soliton.
When increasing the external field, the transition is gradual from Airy beam to soliton at the output face of the crystal. However we can distinguish two steps. The first step is the focusing along the preferential c-axis which is collinear to the applied external field and to the x-axis. Figure 1f (respectively (g)) shows the horizontal (respectively vertical) transverse output power profiles for applied fields of 800 V/cm and 1200 V/cm displayed in Fig. 1c,d. In Fig. 1c–d the light has focused horizontally along the x-axis to form an Airy soliton (Fig. 1f). This soliton is similar to the one-dimensional Airy soliton that would be induced by a one dimensional Airy beam22. However, with two dimensional Airy beams, a one-dimensional Airy beam structure is obtained along the vertical y-axis and competes with the Airy soliton (Fig. 1g). The second step occurs when focusing also takes place along the vertical y-axis, and this requires a stronger nonlinearity. Indeed, when further increasing the applied electric field, the light previously confined in the Airy beam structure transfers into a soliton-like structure as can be seen in Fig. 1g, and ultimately leads to the two dimensional Airy soliton. The process appearing in two steps will be explained in more details in the section entitled discussion and soliton analysis. To sum up, analysing the Airy beam focusing profile versus the applied electric field, different focusing strengths and soliton formation steps in x and y-axis are observed : this can be explained by the anisotropy of the crystal and the asymmetry of the electric field.
In order to compare the Airy beam soliton profile to the theoretical soliton profile, we test the theory developed for a one-dimensional steady state bright screening soliton profile which is described by the following reduced wave equation30:
whose first integral is
and where \(u(\xi )\) is the soliton amplitude divided by the square root of the effective background intensity (defined as the sum of the background and dark intensities induced respectively by an external homogeneous illumination of the crystal and the intrinsic thermal excitation of charges inside the crystal), \(\xi =x/d\) is the transverse coordinate normalized by \(d=(k^2n_b^2r_{eff}E_{ext})^{-1/2}\), \(u_0\) is the maximum amplitude of the soliton at \(\xi =0\), \(k=2\pi n_b/\lambda\) is the wave vector, \(n_b\) is the unperturbed refractive index, \(\lambda\) is the wavelength, \(r_{eff}\) is the effective component of the electro-optic tensor, \(E_{ext}=V/l\) with V the voltage applied onto the crystal and l the crystal’s width. As detailed in22, Eq. (2) is solved numerically using a Runge-Kutta method for an electric field applied along the x-axis and therefore gives the one-dimensional theoretical soliton profile along x. In practice, for (i) a different applied electric field \(E_{ext}\) corresponding to a different d coefficient and (ii) a maximum soliton amplitude \(u_0\), a different soliton profile is obtained. When we fix d and \(u_0\) in our experiment (\(n_b=2.3\), \(r_{eff}=235\,\)pm/V and \(E_{ext}=800\) or 1200 V/cm), we therefore calculate the corresponding theoretical soliton profile. We then compare the superimposed soliton profile plots to the experimental profiles observed at the output face of our crystal in Fig. 1f, and both horizontal profiles along \(x-axis\) fit perfectly. The profile along the vertical axis in Fig. 1g is slightly broader due to the elliptic shape of the soliton31.
Tailoring the Airy soliton shape
In order to show the effect of nonlinear strength on propagation behavior, Fig. 2 shows a panel of different output profiles after propagating through the SBN-crystal for different input powers and externally applied electric fields. The input power ranges from \(1.4\,\upmu \hbox {W}\) to \(6.4\,\upmu \hbox {W}\), the background lighting is constant at 35 mW and the applied electric field ranges from 0 V to 2000 V/cm. Figure 2a shows profiles for an input Airy beam with an acceleration direction along the negative x-axis and positive y-axis whereas for Fig. 2b the profile of the input Airy beam has a positive x-axis and negative y-axis acceleration direction. The same exposure time and attenuation in front of the camera are used for images belonging to the same row, but different attenuation and exposure time are used in the different rows. The image is taken once the Airy soliton is formed or when the output has stabilized. The soliton position is circled in white for the first row (light power of \(1.4\,\upmu\)W) for both Fig. 2a,b.
In Fig. 2a, when no electric field is applied, the 2D-Airy beam profile is unchanged. When an electric field of 400 V/cm is applied, the profile resembles a vertical 1D-Airy beam profile at the position in x where the soliton will form. Additionally, we notice the 1D-Airy beam profile appears more clearly at higher power (\(6.4\,\upmu\)W). When the applied electric field increases to 800 V/cm the residual vertical 1D-Airy beam profile is in competition with the soliton: for low power values (\(1.4\,\upmu\)W) the profile resembles a vertical 1D-Airy beam, whereas for higher power values (\(6.4\,\upmu\)W), both the 1D-Airy beam and the soliton are clearly discerned. When an electric field of 1200 V/cm is applied the 1D-Airy beam is still in competition with the soliton: for a beam power of \(1.4\,\upmu\)W both the 1D-Airy beam and soliton are discerned, whereas for a beam power of \(6.4\,\upmu\)W the 1D-Airy profile has almost disappeared to the benefit of the soliton. When an electric field of 1600 V/cm or 2000 V/cm is applied the soliton is very intense and other few off-shooting beams (OSB) of low power are discerned.
In Fig. 2b, when no electric field is applied, the 2D-Airy beam profile has already changed in comparison to the linear Airy beam propagation: all of the power has shifted to the main lobe along the x-axis. The asymmetry between Fig. 2a,b is to be expected: as explained in reference32, diffusion of carriers along the c-axis causes the light power to shift to the Airy beam’s main lobe. When an electric field of 400 V/cm is applied, the light focuses more strongly in the Airy beam’s main lobe. When an electric field of 800 V/cm is applied, light power starts to shift from the Airy beam’s main lobe position in x to the soliton position. When light shifts to the position of the soliton position in x, for \(6.4\,\upmu\)W, a residual vertical 1D-Airy beam is in competition with the soliton. When an electric field of 1200 V/cm is applied the light in the Airy beam’s main lobe focuses in an OSB and is in competition with the 1D-Airy beam and the soliton: for a beam power of \(1.4\,\upmu\)W to \(5.5\,\upmu\)W, three structure can be observed (Airy and soliton to the left, OSB to the right), whereas for a beam power of \(6.4\,\upmu\)W the OSB is no longer visible. When an electric field of 1600 V/cm is applied the Airy beam, soliton and OSB are still in competition: the three structures are discerned for light powers of \(1.4\,\upmu\)W to \(2.8\,\upmu\)W and only the soliton is very intense for light powers of \(5.5\,\upmu\)W and \(6.4\,\upmu\)W. When an electric field of 2000 V/cm is applied only the soliton remains. When comparing Fig. 2a,b, the differences in light propagation behavior occur mainly at low applied electric field when diffusion is a significant effect, but the behaviors become similar when a higher electric field is applied (greater or equal to 1200 V/cm).
The nonlinear effect can be increased by increasing the applied electric field and/or the light power injected in the crystal. In both Fig. 2a,b, increasing the nonlinear effect yields similar behaviors. The Airy beam profile disappears, replaced by a focused and centered soliton. Indeed, for a given injected light power and when increasing the applied external field, the output light power when propagating is focused first horizontally from 400 to 1200 V/cm and secondly is focused both horizontally and vertically from 1200 to 2000 V/cm. Similarly for a given externally applied electric field, for example 1200 V/cm, increasing the light power from 1.4 to \(6.4\,\upmu\)W allows focusing previously only along the x-axis to be focusing along both x and y axes. The c-axis of the SBN-crystal and the applied external field are both along the x-axis, explaining the stronger horizontal focusing effect and a two step focusing dynamic. Figure 2a,b present slightly different behaviors that can be due to different factors. The main identified factor is the diffusion effect as it is unidirectional and along the horizontal c-axis. It can be observed at 0 V/cm and the resulting profiles coincide with what can be expected in literature32.
When no voltage is applied in Fig. 2a the light shifts along the x-axis towards the soliton position, and in Fig. 2b the light distribution shifts along the x-axis to the position of the Airy beam’s main lobe. When the externally applied field is turned on an additional drift effect must be added to the diffusion effect. The shift increases with the value of the applied external field and light power, and causes the soliton to shift position at the output of the crystal or “bend” similarly to previous works with Gaussian solitons33. The bending effect is not apparent in Fig. 2 because the bending occurs after the soliton is formed, on a time scale ranging from a few dozen seconds to a few minutes. Time measurements show that the bending is faster when the light power or externally applied field increases.
Discussion and soliton analysis
Regarding the soliton formation theory and the related nonlinear propagation equation, a 1D or 2D soliton generation needs a perfect balance between a nonlinear focusing process and the natural diffraction appearing when light propagates inside a medium34,35. Thanks to the photorefractive effect, focusing processes may occur when the travelling light induces by itself gradients of charges that redistribute themselves due to drift and/or diffusion effect in ferroelectric medium such as SBN crystals. As such, self bending of the resulting soliton can also be observed33. Furthermore, in 1D, self-localized beams can nevertheless be observed thanks to carrier diffusion effects and a smart tailoring of the accelerating component of the Airy structure32. In order to annihilate the bending trajectory of such a self-focused Airy beam, an external electric field applied along the appropriate direction (ferroelectric c-axis of the crystal) is necessary. Nevertheless, the SBN crystal electro-optic tensor, its anisotropy and the asymmetry of the applied electric field lead to an asymmetry in the charges redistribution in x (c-axis) and perpendicular y axis. As already explained in part II, this results in different focusing strengths and soliton formation along the x and y transverse axis explaining how the focusing behaviors in Figs. 1 and 2 appear in two steps. The horizontal c-axis, along which the voltage is applied, focuses more strongly than the vertical axis. Due to the saturation nature of the photorefractive effect, the focusing will saturate for both transverse axis but at different values of the applied electric fields. Before saturation is reached for both axis the beam is elliptic, once saturation is reached along both axis the soliton is circular. However, due to the strong applied electric field needed for saturation to be reached, the soliton also tends to self-bend in the direction of the applied electric field.
Theoretical soliton existence curve in red and experimental measures corresponding to Fig. 2a.
To further understand the dynamic of the Airy beam soliton behavior we can look at the soliton profile along the c-axis (x-axis) by plotting the full width at half maximum (FWHM) as a function of the maximum amplitude and superimposing it to the theoretical soliton existence curve. Indeed, equation (2) is solved numerically for different values of \(u_{0}\). The FWHM of the amplitude profile \(u(\xi )\) as a function of \(u_0\) is represented in Fig. 3 in red. The experimental horizontal FWHM of the Airy soliton and the corresponding max amplitude from Fig. 2a are plotted as diamonds in Fig. 3. The experimental measures are scattered along the existence curve represented in red, and follow the same trend as the soliton existence curve for \(u_0<1.5\) (orange area on Fig. 3) confirming the solitonic nature of the 1D observed focused beam (as predicted in22). Whereas the existence curve concerns only the 1D soliton theory, this curve is a good indicator of the expected Airy beam soliton propagation behavior: indeed, experimental measures corresponding to \(u_0<1.5\) are for unidimensional horizontal focusing in agreement with the one-dimensional soliton theory, whereas experimental values corresponding to \(u_0>1.5\) are for two dimensional focusing (green area on Fig. 3). Above \(u_0>1.5\), the experimental values corresponding to the measured profiles for external applied fields \(E_{ext}\) from 400V to 1200 V/cm (green, blue and pink diamonds in Fig. 3) follow the curve trend and starts slightly diverging from the fundamental curve for \(E_{ext}\) equal to 1600 V/cm to 2000 V/cm (light blue and yellow diamonds in Fig. 3). The ones for \(u_0>3\) lead to overfocusing or strong drift effects after a dozen seconds, showing less stable Off Shooting Solitons. Indeed, for high nonlinearities (\(E_{ext}>1500\) V/cm or \(u_0>3\)), solitons are no more steady-state because of overfocusing phenomena accompanied by bending effect: we are in presence of quasi-steady or transient soliton. The different scenarii are illustrated in Fig. 3 where we represent the different steps in the observation of the solitonic behaviours: stable 1D and 2D solitons and quasi steady overfocused and drifted beams (orange and green areas on Fig. 3).
Conclusions
In summary we have performed an in-depth experimental analysis of a two-dimensional Airy beam inside a photorefractive nonlinear medium. The nonlinearity strength can be changed by modifying the externally applied electric field and/or the Airy beam’s power. With weak nonlinearity, the two-dimensional input Airy beam turns into a one-dimensional output Airy beam. With moderate nonlinearity, the one dimensional Airy beam coexists with the soliton. With high nonlinearity the two-dimensional Airy beam converts completely into a two dimensional soliton. The soliton output profile behaves according to the theoretical soliton existence curve. When thinking about all-optical interconnects using soliton interactions, these different light propagation behaviors can be seen as different waveguiding configurations. The different configurations and soliton shape are obtained for the same Airy beam profile contrarily to Gaussian generated solitons that require the Gaussian beam to have an initial profile very close to the expected theoretical soliton profile.
Data availability
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Siviloglou, G. A. & Christodoulides, D. N. Accelerating finite energy Airy beams. Opt. Lett. 32, 979 (2007).
Berry, M. V. & Balazs, N. L. Nonspreading wave packets. Am. J. Phys. 47, 264 (1979).
Broky, J., Siviloglou, G. A., Dogariu, A. & Christodoulides, D. N. Self-healing properties of optical Airy beams. Opt. Exp. 16, 12880 (2008).
Siviloglou, G. A., Broky, J., Dogariu, A. & Christodoulides, D. N. Ballistic dynamics of Airy beams. Opt. Lett. 33, 207 (2008).
Efremidis, N. K. Airy trajectory engineering in dynamic linear index potentials. Opt. Lett. 36, 3006 (2011).
Bongiovanni, D., Wetzel, B., Hu, Y., Chen, Z. & Morandotti, R. Optimal compression and energy confinement of optical Airy bullets. Opt. Exp. 24, 26454 (2016).
Efremidis, N. K. & Christodoulides, D. N. Abruptly autofocusing waves. Opt. Lett. 35, 4045 (2010).
Chremmos, I., Efremidis, N. K. & Christodoulides, D. N. Pre-engineered abruptly autofocusing beams. Opt. Lett. 36, 1890 (2011).
Singh, B. K., Remez, R., Tsur, Y. & Arie, A. Super-Airy beam: Self-accelerating beam with intensified main lobe. Opt. Lett. 40, 4703 (2015).
Polynkin, P., Kolesik, M., Moloney, J. V., Siviloglou, G. A. & Christodoulides, D. N. Curved plasma channel generation using ultraintense Airy beams. Science 324, 229 (2009).
Vettenburg, T. et al. Light-sheet microscopy using an Airy beam. Nat. Methods 11, 541 (2014).
Baumgartl, J., Mazilu, M. & Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photonics 2, 675 (2008).
Zhang, P. et al. Plasmonic Airy beams with dynamically controlled trajectories. Opt. Lett. 36, 3191 (2011).
Mathis, A. et al. Micromachining along a curve: Femtosecond laser micromachining of curved profiles in diamond and silicon using accelerating beams. Appl. Physi. Lett. 101, 071110 (2012).
Rose, P., Diebel, F., Boguslawski, M. & Denz, C. Airy beam induced optical routing. Appl. Phys. Lett. 102, 101101 (2013).
Wiersma, N., Marsal, N., Sciamanna, M. & Wolfersberger, D. All-optical interconnects using Airy beams. Opt. Lett. 39, 5997 (2014).
T. Bouchet, N. Marsal, M. Sciamanna, & D. Wolfersberger, Light-induced interconnects using nonlinear Airy beam interactions. J. Phys. Photo. (2018).
Panagiotopoulos, P. et al. Nonlinear propagation dynamics of finite-energy Airy beams. Phys. Rev. A 86, 013842 (2012).
Kaminer, I., Segev, M. & Christodoulides, D. N. Self-accelerating self-trapped optical beams. Phys. Rev. Lett. 106, 213903 (2011).
Zhang, Y. et al. Interactions of Airy beams, nonlinear accelerating beams, and induced solitons in Kerr and saturable nonlinear media. Opt. Exp. 22, 7160 (2014).
Wiersma, N., Marsal, N., Sciamanna, M. & Wolfersberger, D. Airy beam self-focusing in a photorefractive medium. Sci. Rep. 6, 35078 (2016).
Bouchet, T., Marsal, N., Sciamanna, M. & Wolfersberger, D. Solitonic characteristics of Airy beam nonlinear propagation. Phys. Rev. A 97, 051801 (2018).
Barthelemy, A., Maneuf, S. & Froehly, C. Propagation soliton et auto-confinement de faisceaux laser par non linearité optique de Kerr. Opt. Commun. 55, 201 (1985).
Aitchison, J. et al. Observation of spatial optical solitons in a nonlinear glass waveguide. Opt. Lett. 15, 471 (1990).
Mayteevarunyoo, T. & Malomed, B. A. Two-dimensional \(\chi\)2 solitons generated by the downconversion of Airy waves. Opt. Lett. 41, 2919 (2016).
Mayteevarunyoo, T., Prasatsap, U., Mayteevarunyoo, T. & Malomed, B. A. Two-dimensional airy waves and three-wave solitons in quadratic media. J. Opt. 24, 055501 (2022).
Duree, G. C. Jr. et al. Observation of self-trapping of an optical beam due to the photorefractive effect. Phys. Rev. Lett. 71, 533 (1993).
Hu, Y. et al. Reshaping the trajectory and spectrum of nonlinear Airy beams. Opt. Lett. 37, 3201 (2012).
Kukhtarev, N., Markov, V., Odulov, S., Soskin, M. & Vinetskii, V. Holographic storage in electrooptic crystals I. Steady state. Ferroelectrics 22, 949 (1978).
Kos, K. et al. One-dimensional steady-state photorefractive screening solitons. Phys. Rev. E 53, R4330 (1996).
Zozulya, A. A., Anderson, D. Z., Mamaev, A. V. & Saffman, M. Self-focusing and soliton formation in media with anisotropic nonlocal material response. Europhys. Lett. 36, 419 (1996).
Jia, S., Lee, J., Fleischer, J. W., Siviloglou, G. A. & Christodoulides, D. N. Diffusion-trapped Airy beams in photorefractive media. Phys. Rev. Lett. 104, 253904 (2010).
Petter, J., Weilnau, C., Denz, C., Stepken, A. & Kaiser, F. Self-bending of photorefractive solitons. Opt. Commun. 170, 291 (1999).
Chen, Z., Segev, M. & Christodoulides, D. N. Optical spatial solitons: historical overview and recent advances. Rep. Prog. Phys. 75, 086401 (2012).
Fressengeas, N., Wolfersberger, D., Maufoy, J. & Kugel, G. Build up mechanisms of (1+ 1)-dimensional photorefractive bright spatial quasi-steady-state and screening solitons. Opt. Commun. 145, 393 (1998).
Acknowledgements
We wish to acknowledge the support of the AIRBUS-GDI Simulation, Metz Métropole, Conseil Départemental de Moselle, Conseil Régional Grand-Est, Préfecture de Région Grand-Est, FEDER, CentraleSupélec, Fondation Supélec through the funding of the Chair in Photonics.
Author information
Authors and Affiliations
Contributions
N.M., M.S. and D.W. supervised the experiments and theoretical calculations. T.B. performed the measurements. All the authors contributed to the data analysis and to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bouchet, T., Marsal, N., Sciamanna, M. et al. Two dimensional Airy beam soliton. Sci Rep 12, 9064 (2022). https://doi.org/10.1038/s41598-022-12758-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-12758-5
This article is cited by
-
New types of transverse electric nonlinear waves propagating along a linearly graded-index layer in a medium with Kerr nonlinearity
Optical and Quantum Electronics (2023)
-
Formation characteristics of dark solitons in photorefractive crystals having both linear and quadratic electro-optic effect simultaneously
Optical and Quantum Electronics (2023)
-
Traveling wave solutions for explicit-time nonlinear photorefractive dynamics equation
Nonlinear Dynamics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.