Abstract
The structural and magnetic properties of the ThCr2Si2-type solid solution LaMn2(Ge1−xSix)2 (x = 0.0 to 1.0) have been investigated employing a combination of X-ray diffraction, magnetization and neutron diffraction measurements, which allowed establishing a magnetic composition-temperature phase diagram. Substitution of Ge by Si leads to a compression of the unit cell, which affects the magnetic exchange interactions. In particular, the magnetic structure of LaMn2(Ge1−xSix)2 is strongly affected by the unit cell parameter c, which is related to the distance between adjacent Mn layers. Commensurate antiferromagnetic layers and a canted ferromagnetic structure dominate the Si-rich part of the solid solution, whilst an incommensurate antiferromagnetic flat spiral and a conical magnetic structure are observed in the Si-poor part.
Similar content being viewed by others
Introduction
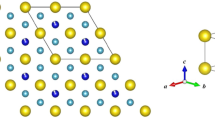
Materials belonging to the AM2X2 (A = alkali, alkaline-earth, or a rare-earth element, M = transition metal, X = a main group element) family of compounds are known to show a wide spectrum of intriguing physical phenomena including magnetism, superconductivity, heavy fermions, quantum critical points and Kondo behavior1,2,3,4. Its members preferentially crystallize in the ThCr2Si2-type structure (space group I4/mmm) in which the A, M and X atoms occupy the 2a, 4d and 4e crystallographic sites, respectively. This atomic arrangement leads each of the three elements to form square nets stacked along the crystallographic c axis in the order A-X-M-X-A, c.f. Figure 1. The structure can also be described as being composed of layers of edge-sharing XM4 square pyramids of alternating orientation between square nets of A atoms. A third structure description is as layers of edge-sharing MX4 tetrahedra alternating with square nets of the A metal. Illustrations of the latter two crystal structure description can be found in the Supplementary Fig. S1.
The subgroup of manganese silicides and germanides, REMn2X2 (RE = rare-earth metal, X = Si, Ge) has gained particular attention for their interesting physical properties. Giant magnetoresistance (GMR) was observed in REMn2Ge2 (RE = La, Sm)5,6,7, magnetocaloric behavior in REMn2Si2 (RE = Ho, Er, Tb)8,9,10 and REMn2Ge2 (RE = Ce, Tb)11,12 and skyrmionic bubbles in REMn2Ge2 (RE = Ce, Pr, Nd)13. Recently, LaMn2Ge2 has been shown to demonstrate a topological Hall effect (THE)14.
The wide range of behavior exhibited by the REMn2X2 materials is related to the rich diversity of collinear and non-collinear magnetic states that can be realized in this atomic arrangement15,16,17,18,19,20,21,22,23,24,25,26. Magnetic ordering temperatures between 300 and 714 K have been observed for all compounds of this type1,27, and many of them undergo several magnetic transitions upon cooling before they reach their magnetic ground state. Previous studies on various solid solutions based on REMn2X2 indicated that the Mn–Mn distances play a major role in the formation of different magnetic structures. At intra-planar nearest-neighbor Mn–Mn distances dintra < 2.84 Å, the magnetic moments within the Mn-layers order in a ferromagnetic out-of-plane arrangement while adjacent square nets couple antiferromagnetically. When dintra surpasses the critical distance of 2.84 Å a transition from the ferromagnetic out-of-plane arrangement to an antiferromagnetic in-plane one takes place. At the same time, the coupling between the planes remains antiferromagnetic11,28,29,30. A further increase to dintra > 2.87 Å results in a second transition in which the intra-layer arrangement remains unchanged but the inter-layer coupling evolves from antiferromagnetic to ferromagnetic11,28,29,30,31.
The ternaries LaMn2X2 (X = Si, Ge) both exhibit magnetic structures with ferromagnetic inter-layer coupling. Adopting the nomenclature commonly used in the literature (the detailed description follows below)11,28,29,31,32,33, LaMn2Si2 exhibits a magnetic structure referred to as antiferromagnetic layers (AFl) below 470 K15,34,35 and undergoes a transition to the ferromagnetic mixed commensurate (Fmc) structure at 310 K on cooling15,35,36. Additional incommensurate modulation peaks occur below 40 K and remain down to low temperatures, which was interpreted as co-existence of the ferromagnetic mixed incommensurate (Fmi) and ferromagnetic mixed commensurate (Fmc) structures15,35. In contrast, LaMn2Ge2 is reported to adopt the antiferromagnetic flat spiral (AFfs) below 425 K. On cooling, a transition into the Fmi structure occurs at TC = 325 K, and this state is preserved down to 2 K15,28,34,36.
The Fmc and Fmi structures observed in LaMn2Si2 and LaMn2Ge2, respectively, share some similarities: Both exhibit a ferromagnetic out-of-plane magnetic moment component as well as an identical checkerboard in-plane spin arrangement within the Mn nets. The incommensurability for the Fmi structure of LaMn2Ge2 results from a rotation of the magnetic moments in the adjacent square nets with respect to each other along the tetragonal c axis. In the case of the commensurate Fmc structure observed for LaMn2Si2, the magnetic moments in neighboring planes are rotated by 180° along c. Previous studies on the solid solution LaMn2(Si1−xGex)2 (x = 0, 0.2, 0.4, 0.6, 0.8, 1) using Perturbed Angular Correlation (PAC) spectroscopy with 111In(111Cd) and 140La(140Ce) as probe nuclei have shown that the Curie and Neél temperatures in both ternaries can be tuned by Si/Ge mixing34,36. This indicates that different compositions of the solid solution LaMn2(Si1−xGex)2 will exhibit magnetic behavior similar to that of the ternary compounds and that the magnetic transition temperatures can be tuned by the composition. Thus, a study of the influence of the amount of Si/Ge mixing on the magnetic incommensurability and co-existing magnetic phases becomes necessary. Furthermore, the physical properties relevant for potential application of the LaMn2X2 compounds (X = Si, Ge) are directly linked to their magnetism. For this purpose, we investigated the effect of the substitution of Ge by Si in the solid solution LaMn2(Ge1−xSix)2 on the structural and magnetic properties by magnetization, X-ray and neutron diffraction measurements.
Results
Powder X-ray diffraction measurements
Rietveld refinements of the PXRD data indicate that all samples of LaMn2(Ge1−xSix)2 crystallize in the ThCr2Si2-type structure. The lattice parameters a and c of the ternary compounds are in good agreement with the values reported in the literature15. Table 1 lists the lattice parameters of all samples. The quaternary samples are labelled according to their refined compositions. The composition dependence of a, c, the cell ratio c/a and the unit cell volume V is plotted in Fig. 2. The partial substitution of Ge by Si leads to a compression of lattice parameters at room temperature. The lattice parameter a follows Vegard’s law37 (Fig. 2 top) over the whole composition range. In contrast, the c parameter exhibits deviations from a linear behavior (dashed lines). A steeper decline of c is observed in the Ge-rich part of LaMn2(Ge1−xSix)2. This anomaly is also reflected in the behavior of the c/a ratio (Fig. 2 bottom). The change in slope of c is correlated to the magnetic properties, vide infra. The z component of the crystallographic site of Si/Ge (0, 0, z) remains at a nearly constant value of about 0.38 throughout the whole solid solution.
Composition dependence of the LaMn2(Ge1–xSix)2 lattice parameters a and c (top), cell ratio c/a and unit cell volume V (bottom) at room temperature. The data points of the samples synthesized by furnace annealing (x = 0, 0.05, 0.33, 0.47) are highlighted by filled symbols, the ones prepared by arc melting (x = 0.18, 0.58, 0.78, 1) by empty symbols. The compression of a follows Vegard’s law (top, solid lines), but c deviates from this linear trend (top, dashed line). The same anomalous behavior is also observable in the cell ratio c/a (bottom). In order to compensate possible errors from the different sample preparation techniques, the c and c/a values of the samples prepared by arc melting and solid state synthesis were fitted separately. All error bars are shown and represent 1σ. However, the error bars may be smaller than the symbol.
Magnetization measurements
Temperature dependence of the DC magnetic susceptibility χDC for ternary LaMn2Ge2 and LaMn2Si2 between 2 and 400 K is plotted in Fig. 3. Both compounds undergo a ferromagnetic-like transition at their respective Curie temperatures TC = 326.22(3) K and 308.53(3) K. Above TC, the inverse susceptibilities χDC−1(T) do not follow a linear behavior (not shown) up to 400 K and suggest that LaMn2Ge2 and LaMn2Si2 do not fully enter the paramagnetic regime up to the highest measured temperature. This is also supported by the powder neutron diffraction data presented below. Similar behavior of the DC magnetic susceptibility was also observed for the quaternary samples (Supplementary Fig. S3). TC decreases from LaMn2Ge2 to LaMn2Si2 as a function of the Ge/Si mixing (Table 1). The Curie temperatures of all samples were determined by fitting the first derivative of the susceptibility dχDC/dT with a Gaussian peak function (Supplementary Fig. S4a,b). The transition temperatures extracted from our data are in fair agreement with the literature36. Thus, the TC values reported in previous studies go from 323.3(2) K in LaMn2Ge2 to 308.5(2) K in LaMn2Si2.
The isothermal magnetization curves of the ternary LaMn2Ge2 and LaMn2Si2 measured at 2 K and 250 K between − 6 and 6 T exhibit typical ferromagnetic behavior (Fig. 3 insets). For LaMn2Ge2, the M(H) curve reaches Msat = 1.3005(1) µB/Mn at 2 K and Msat = 1.0976(1) µB/Mn at 250 K. In contrast, the M(H) curve of LaMn2Si2 shows no saturation under the same applied magnetic fields at 2 K, but reaches saturation with Msat = 0.99823(4) µB/Mn at 250 K. A similar behavior to LaMn2Si2 is also observed for the Si-rich quaternary samples with the composition x = 0.58 and 0.78 (Supplementary Fig. S3): They reach saturation at 250 K, but not at 2 K. This lack of saturation possibly indicates the presence of an antiferromagnetic component38. Furthermore, the low saturation magnetization observed for all compositions points toward a magnetic structure different from that of a simple ferromagnet, which will be discussed below. Hysteresis loops were observed for all compositions. Supplementary Fig. S5a,b highlight the isothermal magnetization of all samples between − 1 and 1 T. On raising the temperature from 2 to 250 K, the coercive field Hc of the samples with compositions x = 0.33, 0.47, 0.58, 0.78 and 1 decreases clearly whereas Hc remains nearly constant for x = 0, 0.05 and 0.18 (Supplementary Table S1). The change of the coercive field on warming hints at a magnetic phase transition occurring between 2 and 250 K which is also confirmed by the PND data presented below. The different coercive fields between samples are attributed to variations in particle size39. The magnetization data observed here are in line with the literature15,38,40,41. As the samples only contain small amounts of impurities, we believe the impurities do not affect the magnetization data in a significant way.
Powder neutron diffraction measurements
Powder neutron diffraction (PND) patterns were collected for a series of samples with the composition LaMn2(Ge1−xSix)2 (x = 0, 0.05, 0.18, 0.33, 0.47, 0.58, 0.78, 1). Following previous works11,28,29,31,32,33,42, we will describe the observed magnetic structures based on elementary magnetic components. The latter can be readily identified from characteristic magnetic reflections:
-
1.
The antiferromagnetic flat spiral (AFfs) can be described as an antiferromagnetic alignment of magnetic moments within the square lattice for each Mn layer. The spin motive of each layers is the same but the moments are rotated by an angle φ in adjacent layers, by 2φ in case of the next-nearest layer and so on. Therefore, the magnetic moments in AFfs form a flat spiral along the c-axis. (Fig. 4a) The incommensurate propagation vector (0, 0, kz) describes the length of the spiral or how many crystal unit cells are necessary until the magnetic moments have reached a full rotation. In the diffraction patterns, the AFfs can be identified by pairs of low intensity, magnetic modulation peaks appearing around reflections with the diffraction condition h + k = 2n + 1: e.g. satellite reflections (101)−/(101)+ and (103)−/(103)+ around (101) and (103), respectively.
-
2.
The structure of antiferromagnetic layers (AFl) consists of the same antiferromagnetic arrangement of magnetic moments within the square lattice as in the case of AFfs. However, the moments in adjacent layers are rotated by 180° along c. (Fig. 4b) The magnetic reflections of AFl can be indexed with a k-vector of (0, 0, 0) and add intensity to nuclear Bragg peaks with the reflection condition h + k = 2n + 1. The magnetic signal of the AFl contribution is especially visible for (101) and (103).
-
3.
In the ferromagnetic (FM) component, all magnetic moments are aligned along c (Fig. 4c). The FM contribution is found on nuclear Bragg peaks fulfilling the reflection conditions h + k = 2n and l = 2n. Therefore, the FM Bragg peaks increase the intensity of nuclear Bragg peaks. This is most noticeable for the reflections (002) and (112).
Before presenting the results of the PND studies, we would like to provide some general comments about the magnetic structures:
Reflection condition (1) points to incommensurate magnetic modulation (IC), while conditions (2) and (3) indicate commensurate magnetic reflections (C). The Bragg markers corresponding to the magnetic phases in the PND patterns presented below are separated into IC and C contributions. The sets of magnetic peaks corresponding to either of the magnetic components (1) or (2) can be observed in PND patterns in the absence of other magnetic reflections, suggesting that these two elementary components represent actual magnetic structures. In addition, more complex magnetic arrangements result from combinations of the elementary contributions listed above:
-
4.
The ferromagnetic mixed incommensurate structure (Fmi) is a superposition of the in-plane component (1) and the out-of-plane component (3), and is characterized by a conical magnetic structure with the cone axis parallel to c (Fig. 4d). This type of structure is referred to as conical as the magnetic moments appear to rotate in a conical fashion. Due to the FM contribution to Fmi, all magnetic moments lie parallel to c which results in an overall non-zero net moment. Additionally, there is the non-zero contribution of the AFfs with an antiferromagnetic arrangement in the basal plane. Similar to AFfs, the magnetic moments of Fmi are rotated by an angle φ from layer to layer.
-
5.
The ferromagnetic mixed commensurate state (Fmc) is a superposition of (2) and (3)—the resulting structure is similar to AFl with the same antiferromagnetic in-plane arrangement and antiferromagnetic coupling between neighboring layers, but the magnetic moments are canted out-of-plane. Thus, Fmc exhibits an additional ferromagnetic coupling along c (Fig. 4e).
Figure 4 Models for the spin arrangements of the five diffraction conditions observed in LaMn2(Ge1−xSix)2: (a) antiferromagnetic flat spiral (AFfs), (b) antiferromagnetic layers (AFl), (c) ferromagnetic contribution (FM), (d) ferromagnetic mixed incommensurate (Fmi) and (e) ferromagnetic mixed commensurate (Fmc). The circles in (a) and (d) indicate the full rotation of the spins along (c) in the incommensurate AFfs and Fmi. FM does not exist as an independent phase but contributes to Fmi and Fmc.
It should be noted that the FM component (3) is only observed in combination with AFfs (1) and AFl (2) in the Fmi and Fmc structures, and thus, is not an independent magnetic structure of LaMn2(Ge1−xSix)2. The superposition of magnetic components can be understood as an addition of vectors. Adding an out-of-plane and an in-plane magnetic component will result in a canted magnetic structure. The canting angle of such a non-collinear structure is defined by the ratio of the vector lengths. The individual components are therefore projections onto either the ab-plane (AFfs and AFl) or the c-axis (FM). Figure 4 illustrates the spin arrangements for all three diffraction conditions and the two observed superpositions of the elementary magnetic contributions.
LaMn2Ge2
Neutron diffraction data of the ternary LaMn2Ge2 were collected between 28 and 500 K. Refinements confirm that LaMn2Ge2 is paramagnetic at 430 K. Below 420 K, magnetic satellite peaks consistent with diffraction condition (1) occur around the (101) and (103) reflections (Fig. 5). They can be indexed with the propagation vector (0, 0, kz), and their intensities as well as kz increase with decreasing temperatures. The magnetic structure is a pure antiferromagnetic flat spiral (AFfs)28 (Fig. 4a). The ordering temperature observed here is in good agreement with previous studies28,34. At 330 K, slightly above a ferromagnetic-like transition observed in the magnetic susceptibility, the nuclear peaks following reflection condition (3) gain intensity. This increase is most clearly visible on the (112) reflection, as its nuclear contribution is negligible. Diffraction condition (3) describes the ferromagnetic contribution (FM), in which the moments align parallel to c (Fig. 4c). The magnetic signal attributed to FM co-exists with the satellite peaks (101)−/(101)+ and (103)−/(103)+ of AFfs down to low temperatures. As discussed above, the superposition of an in-plane AFfs and an out-of-plane FM contribution forms the ferromagnetic mixed incommensurate structure (Fmi, Fig. 4d), reported previously15.
Figure 6a shows the temperature dependence of the total magnetic moment µtot of LaMn2Ge2 and its partial components µAFfs and µFM derived from the data refinements. The magnetic transition temperatures from PND were defined where an abrupt drop in the magnetic moment is observed, as can be seen in Fig. 6 and is indicated by the vertical dash-dotted line. The same methodology was applied to all samples. As it is an approximate value, error propagation is not considered. At 28 K, LaMn2Ge2 reaches magnetic moments of µtot ≈ 3.13(3) µB, µAFfs ≈ 2.68(2) µB and µFM ≈ 1.61(4) µB per Mn with a propagation vector of kz ≈ 0.2983(2). At this temperature, the magnetic moment is canted from the c-axis by an angle of α ≈ 59.1(4)°. The value of µFM refined from the PND data is slightly larger than the Msat value of 1.3005(1) observed in the isothermal magnetization but is in line with the approximately 1.5 µB/Mn reported in the literature15,40,43,44,45. The lower value of Msat determined here might be explained by a non-magnetic amorphous impurity or hindered domain wall motion preventing complete saturation of the magnetization. µtot decreases for increasing temperatures, makes a stronger downturn close to TC before it vanishes abruptly at 430 K. The intermediate dip at TC also occurs in µAFfs and kz (Fig. 6a inset). Figure 6b depicts the evolution of the lattice parameters a and c, the unit cell volume V and the cell ratio c/a as a function of temperature. The cell ratio c/a exhibits a stronger temperature dependence in the region TC < T < TN. This anomalous behavior hints at a strong coupling of the thermal expansion of the crystal lattice to the Mn–Mn inter-layer interactions of the Mn moments. Similar effects have also been observed in CeMn2(Ge1−xSix)211, PrMn2(Ge1−xSix)231 and Pr(Mn1−xFex)2Ge232.
Magnetic and structural parameters of LaMn2Ge2 derived from PND data refinements: (a) Temperature dependence of the total magnetic moment µtot, its partial components µAFfs, µFM, and the propagation vector kz (inset). (b) Change of the lattice parameters a and c, the unit cell volume V and the cell ratio c/a as a function of temperature. All error bars are shown and represent 1σ. However, the error bars may be smaller than the symbol. The dashed lines connecting neighboring points were added to guide the eye. The vertical dash-dotted lines indicate the magnetic transition temperatures.
LaMn2(Ge0.95Si0.05)2
The introduction of marginal amounts of Si already leads to a significant change in the magnetic properties (Fig. 7a). LaMn2(Ge0.95Si0.05)2 is paramagnetic at 500 K. At 450 K, an increased intensity of the (101) reflection, consistent with diffraction condition (2), can be observed, indicating that LaMn2(Ge0.95Si0.05)2 orders in the AFl structure. Additional magnetic modulation peaks (101)−/(101)+ appear at \({T}_{N1}^{c/i}\) ≈ 420 K, signaling the emergence of the AFfs structure, while the magnetic contribution to the (101) reflection does not disappear. That points to a co-existence of the AFl and AFfs phases below 420 K. Thus, \({T}_{N1}^{c/i}\) indicates the transition temperature from a purely AFl component to the co-existing AFfs and AFl and will be used throughout the text. The magnetic moment of the AFl component is significantly smaller than of the AFfs and, therefore, contributes only little to µtot of LaMn2(Ge0.95Si0.05)2. The prevalence of the AFfs phase, detected in the ternary LaMn2Ge2 in a similar temperature region, is in line with the small amount of Si in the solid solution. Below TC ≈ 320 K, three magnetic scattering components fulfilling the conditions (1)–(3) co-exist down to \({T}_{N2}^{c/i}\) ≈ 300 K. In line with the terminology used above, \({T}_{N2}^{c/i}\) marks the transition from the co-existing AFfs and AFl contributions to the pure AFfs. The addition of the FM component in this temperature range corresponds to transformation of the AFl and AFfs phases into Fmc and Fmi, respectively. The co-existence of Fmi and Fmc phases was previously reported for the ternary LaMn2Si215,35. In contrast to related solid solutions with a co-existence of the Fmc structure and the antiferromagnetic mixed commensurate phase (AFmc)11,29,31,33,46, a co-refinement of the Fmi and Fmc structures could not be performed for LaMn2(Ge0.95Si0.05)2. Since both these magnetic phases share the FM contribution, FM could not be unambiguously partitioned between Fmi and Fmc. Instead, the elementary AFfs, AFl, and FM components were refined individually.
(a) PND patterns of LaMn2(Ge0.95Si0.05)2 at 14 K, 300 K, 330 K and 430 K (from bottom to top). The Bragg markers indicate the positions of the nuclear (N), commensurate (C) and incommensurate magnetic (IC) reflections. The asterisk (*) highlights the position of a peak of the impurity La9.3((Si1−xGex)O4)6O247. (b) Temperature dependence of the total magnetic moment µtot, its partial components µAFfs, µFM, µAFl, and the propagation vector kz (inset) derived from the PND refinements. All error bars are shown and represent 1σ. However, the error bars may be smaller than the symbol. The dashed lines connecting neighboring points were added to guide the eye. The vertical dash-dotted lines indicate the magnetic transition temperatures.
Below 300 K, the AFl contribution vanishes, and only the Fmi magnetic structure remains. The Mn magnetic moment obtained from the refinements at 14 K drops with respect to LaMn2Ge2 down to µtot ≈ 2.99(4) µB and µAFfs ≈ 2.52(3) µB. Similarly, the refined value of kz ≈ 0.2907(3) is marginally smaller than the value observed in LaMn2Ge2. The ferromagnetic moment, on the other hand, stays relatively constant at µFM ≈ 1.61(6) µB, which leads to a slightly smaller angle α ≈ 57.5(6)°. The temperature dependence of µtot, µAFfs and kz shows a strong resemblance to the ternary LaMn2Ge2 (Fig. 7b). In the temperature region of the co-existing AFl and AFfs phases, µtot was numerically calculated from µAFl and µAFfs and the refinement errors were estimated using the error propagation formula. The in-plane moment of the co-existing µAFl and µAFfs were calculated by averaging over the vector sum using the integral:
The integral averages over all possible angles ω between µAFl and µAFfs. For the co-existing Fmi and Fmc phases, the in-plane component calculated using the integral above was combined with the ferromagnetic out-of-plane µFM component using the Pythagorean equation.
LaMn2(Ge1−xSix)2 (x = 0.18, 0.33, 0.47, 0.58)
A further increase in the Si fraction in LaMn2(Ge1−xSix)2 leads to a continuous increase of TN and the disappearance of the AFfs structure. In the samples with compositions LaMn2(Ge1−xSix)2 (x = 0.18, 0.33, 0.47, 0.58), only AFl could be observed above TC (Fig. 8). LaMn2(Ge0.67Si0.33)2 retains this magnetic structure up to at least 475 K. In LaMn2(Ge0.53Si0.47)2, the paramagnetic regime was not reached even at 500 K. For the other two samples (x = 0.18, 0.58) no data were collected at such high temperatures. The composition-dependent increase of the Néel temperature follows the trend previously detected by Perturbed Angular Correlation (PAC) spectroscopy34.
PND patterns of (a) LaMn2(Ge0.82Si0.18)2 at 3 K, 320 K and 350 K and (b) LaMn2(Ge0.53Si0.47)2 at 29 K, 225 K, 300 K and 320 K (from bottom to top). The Bragg markers indicate the positions of the nuclear (N), commensurate (C) and incommensurate (IC) magnetic reflections. LaMn2(Ge0.53Si0.47)2 also contains the minor impurity Mn5(Ge1–xSix)3 (I).
In LaMn2(Ge0.82Si0.18)2, the simultaneous appearance of the satellite peaks (101)−/(101)+ and the intensity increase of the (112) reflection below 320 K indicate a transition to the Fmi structure below TC (Fig. 8a). However, as the magnetic scattering contribution on the (101) reflection does not disappear at the same time, the Fmi co-exists with the Fmc phase down to at least 290 K. Finally, LaMn2(Ge0.82Si0.18)2 transforms into the Fmi structure at even lower temperatures. Since only a few data points were collected for this sample, the exact transition temperature is not known but it occurs somewhere between 200 K < \({T}_{N2}^{c/i}\) < 290 K. Taking the transition temperatures of the neighboring samples into account, \({T}_{N2}^{c/i}\) is expected to be at around 250 K.
Below TC, the samples with the compositions x = 0.33, 0.47, 0.58 undergo a transition to the Fmc phase, identified by magnetic peaks consistent with diffraction conditions (2) and (3). Below 275 K, 250 K and 210 K, respectively, modulation peaks following condition (1) appear, which suggests co-existence of the Fmc and Fmi structures. Interestingly, the temperature range in which this co-existence is observed increases with the amount of Si in LaMn2(Ge1−xSix)2: at 275 K < T < 250 K for x = 0.33, at 250 K < T < 200 K for x = 0.47, and at 210 K < T < 70 K for x = 0.58. Figure 8b shows the PND patterns of LaMn2(Ge0.53Si0.47)2 at 320 K, 300 K, 225 K and 29 K.
The total magnetic moment of LaMn2(Ge0.53Si0.47)2 reaches µtot ≈ 2.66(4) µB per Mn atom, with partial components of µAFfs ≈ 2.24(3) µB and µFM ≈ 1.44(5) µB at 29 K and a resulting angle of α ≈ 59.2(6)°. Thus, both magnetic contributions drop compared to the Ge-richer samples. In a similar fashion, a lower kz value of 0.1983(3) is observed. The temperature dependence of µtot, the partial magnetic moments µAFfs, µAFl, µFM, and kz are plotted in Fig. 9a. It is noteworthy that µAFl rises while µAFfs drops in the temperature region where Fmi and Fmc co-exist. Meanwhile, µFM appears to be unperturbed. Thus, the co-existence occurs in the temperature region where the phase transition from Fmc to Fmi takes place. In comparison to LaMn2Ge2 and LaMn2(Ge0.95Si0.05)2, kz decreases less abruptly in LaMn2(Ge0.53Si0.47)2 (Fig. 9a inset). Figure 9b shows the change of the lattice parameters as a function of temperature. The non-linear behavior of c/a with a slope increase around TC noted earlier for LaMn2Ge2 can also be seen in LaMn2(Ge0.53Si0.47)2 but becomes less pronounced with increasing Si-concentration.
Magnetic and structural parameters of LaMn2(Ge0.53Si0.47)2 derived from the refinements of the PND data: (a) Temperature dependence of the total magnetic moment µtot, its partial components µAFfs, µFM, and the propagation vector kz (inset). (b) Change of the lattice parameters a and c, the unit cell volume V and the cell ratio c/a as a function of temperature. All error bars are shown and represent 1σ. However, the error bars may be smaller than the symbol. The dashed lines connecting neighboring points were added to guide the eye. The vertical dash-dotted lines indicate the magnetic transition temperatures.
LaMn2(Ge1−xSix)2 (x = 0.78, 1)
PND patterns of the samples LaMn2(Ge0.22Si0.78)2 and LaMn2Si2 were collected between 3 and 295 K. At room temperature, both adopt the Fmc structure, identified by magnetic peaks following conditions (2) and (3). LaMn2(Ge0.22Si0.78)2 preserves this structure down to 150 K. At lower temperatures, the (101)−/(101)+ reflections of the incommensurate AFfs emerge, in addition to the magnetic peaks satisfying conditions (2) and (3). Thus, the co-existence of Fmi and Fmc structure is also observed in LaMn2(Ge0.22Si0.78)2 and retained down to 3 K.
Interestingly, LaMn2Si2 orders in the same magnetic structures as LaMn2(Ge0.22Si0.78)2: LaMn2Si2 remains in the Fmc phase down to 70 K, and the co-existence of Fmi and Fmc sets in at 50 K (Fig. 10a). In previous PND measurements of LaMn2Si2, the satellite reflections (101)−/(101)+ were detected as a broadening at the foot of the (101) peak15,35. We can clearly distinguish the satellite peaks thanks to the higher resolution of our data. The incommensurate peaks were refined with kz ≈ 0.0710(5) at 3 K which is even smaller than the value of 0.09 reported earlier15,35. The temperature dependence of the total magnetic moment µtot and its partial components µAFfs, µAFl and µFM is shown in Fig. 10b. The magnetic moments vary substantially from previous studies. The value for µAFfs derived from our refinements is 1.35(3) µB at 3 K, which is significantly larger than the 0.8 µB and 0.5 µB published by Venturini et al.15 and Hofmann et al., respectively35. µFM ≈ 1.72(4) µB is in line with their results but µAFl ≈ 1.43(3) µB is slightly lower. Nevertheless, µtot reaches similar values in all cases. We attribute the discrepancies between the partial moments to our improved data resolution. As we were able to resolve the modulation peaks, it is much easier to refine the accurate values of kz and the partial magnetic moments.
(a) Powder neutron diffraction patterns of LaMn2Si2 at 3 K (bottom) and 70 K (top). The Bragg markers indicate the positions of the nuclear (N), commensurate (C) and incommensurate magnetic (IC) reflections (from top to bottom). (b) Temperature dependence of the total magnetic moment µtot and its partial components µAFfs, µAFl and µFM. All error bars are shown and represent 1σ. However, the error bars may be smaller than the symbol. The dashed lines connecting neighboring points were added to guide the eye. The vertical dash-dotted line indicate the magnetic transition temperatures.
The compositional and thermal variation of the magnetic phases is plotted in Fig. 11. Below TC, the Ge-rich part of the solid solution is dominated by the Fmi phase, the Si-rich—by Fmc. In-between, the co-existence of Fmi and Fmc originally observed in LaMn2Si215,35 spreads from low Si concentrations at high temperatures to the Si-rich compositions at low temperatures. Fmi and Fmc co-exist in every quaternary sample as well as in LaMn2Si2. As the FM component vanishes at TC, the magnetic moments align within the plane of the Mn square net. The AFl phase prevails for a wide range of compositions at TC < T < TN, while AFfs is favored by LaMn2Ge2. In the narrow Si-poor window around x = 0.05, AFfs and AFl co-exist above TC. As the AFfs contribution vanishes faster than the AFl, the pure AFl structure is detected at higher temperatures. The thick black lines in Fig. 11 sketch the phase edges. The composition dependence of TC was plotted using the values in Table 1. Supplementary Fig. S6 presents another version of the same magnetic x-T phase diagram where all measured temperature points are displayed.
x-T magnetic phase diagram of the solid solution LaMn2(Ge1-xSix)2: Paramagnetic (PM), antiferromagnetic flat spiral (AFfs), antiferromagnetic layers (AFl), ferromagnetic mixed incommensurate (Fmi), ferromagnetic mixed commensurate (Fmc). The magnetic phase boarders were determined from the PND data. The slight composition-dependent shift of TC was established from the magnetic susceptibility.
Discussion
Co-existence of different magnetic phases is frequently observed in solid solutions. In the ThCr2Si2-type structure alone it has been found for, e.g., La1−xYxMn2Si229,46,48, La1−xPrxMn2Si233, CeMn2(Ge1−xSix)211 and PrMn2(Ge1−xSix)231. In all these examples, such co-existence is reported in a limited composition region. LaMn2(Ge1−xSix)2 sets itself apart from all these cases as the co-existence occurs in all quaternary samples and the ternary LaMn2Si2. In the literature, the origin of magnetic phase co-existence is usually explained by a chemical phase separation of the quaternary samples into regions with nearly identical compositions and, thus, nearly identical lattice parameters. In CeMn2(Ge1−xSix)2, for example, compositional inhomogeneity was suggested based on high-resolution synchrotron PXRD studies11. In La1−xYxMn2Si2, a peak splitting could even be observed in the PND data48. The coexistence of two or more magnetic phases found in the PND measurements is supported by the non-saturation of the isothermal magnetization found for LaMn2Si2 and some of the quaternary samples at 2 K under 6 T external field. This behavior of the isothermal magnetization indicates the existence of more than one magnetic component, as explained above.
In the quaternary samples in our study, a broadening of certain peaks in the PXRD data at room temperature can be detected, which likely indicates a somewhat inhomogeneous distribution of Si and Ge. Since this behavior is especially visible for some (hkl) reflections with non-zero l, these small inhomogeneities must have a stronger impact on c. Figure 12 shows the PXRD patterns in the 2θ region around the (105) reflection. The peak broadening and the asymmetry is pronounced in some of the quaternary samples. In LaMn2(Ge0.82Si0.18)2 and LaMn2(Ge0.42Si0.58)2, the (105) reflection even appears to be split. LaMn2Si2, however, exhibits the smallest reflection width, rendering any significant chemical inhomogeneity (such as related to intrinsic defects) improbable. Future high-resolution PXRD measurements at a synchrotron source may shed light on the crystal structural origin of the co-existing magnetic phases in LaMn2Si2.
The partial substitution of Ge by Si leads to a minor decrease of TC from 326.10(4) K in LaMn2Ge2 to 308.37(6) K in LaMn2Si2 and was reported previously36. The values for TC we observe from magnetization and PND measurements are in agreement with each other and match those from the literature28,36,49. Considering the strong composition and temperature dependence of the AFfs and AFl components (Fig. 11 and Supplementary Fig. S6) it is noteworthy that FM, and therefore TC, remains nearly constant throughout the solid solution. A similar effect was also noted for TN, which increases monotonically with increasing Si content from approximately 420 K in LaMn2Ge234 to 470 K in LaMn2Si2 according to the literature34,35,49,50. The Neél temperature of LaMn2Ge2 is in line with the values reported earlier28,34. Although we did not investigate the high temperature behavior for all samples, the three quaternary samples (x = 0.05, 0.33, 0.47) for which we collected PND data up to 500 K confirm the trend observed earlier: TN increases with increasing Si content34. Our data suggests, however, that the actual ordering temperatures may be higher than reported previously34,35,50. This is especially visible for the sample with the composition x = 0.47 which did not even reach the paramagnetic regime up to 500 K. Additional measurements at elevated temperatures may be required to confirm if TN is indeed higher than the values reported in the literature.
The x-T phase diagram of LaMn2(Ge1−xSix)2 exhibits certain similarities to those of La1−xYxMn2Ge228, CeMn2(Ge1−xSix)211 and PrMn2(Ge1−xSix)231. In all these solid solutions, the Fmc structure is observed in a similar composition range as Fmi. Analysis of the unit cell and magnetic phase evolution indicates that the Fmi structure dominates the samples with longer lattice parameters and at lower temperatures, while Fmc is found for the samples with shorter lattice parameters and at higher temperatures11,28,31. The same tendency is observed in LaMn2(Ge1−xSix)2 and suggests a correlation to the lattice dimensions. In previous studies, the intra-planar Mn–Mn distance was proposed as one of the important crystal structure parameters that help rationalize the magnetic phase diagram of the REMn2X2 systems, as was discussed in the Introduction. We note, however, that the distance between adjacent Mn square nets also appears to be a significant factor for stabilization of certain magnetic phases. As the composition dependence of c does not follow Vegard’s law but appears to make a kink in Ge-rich side of the solid solution (Fig. 2), the composition region where magnetic incommensurability is most pronounced even above room temperature (Fig. 11), the transition from incommensurate to commensurate structure must be governed by the Mn–Mn interlayer spacing dinter. Figure 13 shows the dinter-T phase diagram of the different magnetic structures in LaMn2(Ge1−xSix)2 which can be assigned to clearly defined regions. The data points of the co-existing phases were excluded for this consideration. Published results for other solid solutions series were added to the phase diagram in order to put the dinter-T trend found from our data into perspective. Interestingly, each data point from these other solid solutions fits perfectly into the dinter-T phase diagram of LaMn2(Ge1−xSix)2. Thus, the occurrence of the commensurate Fmc and incommensurate Fmi structures can be directly correlated to the inter-planar Mn–Mn distances and the temperature. Therefore, Fig. 13 represents a “universal” phase diagram for the REMn2X2 systems. Although it may not enable prediction of all possible magnetic phases in these materials, the uncovered relationship between the magnetism and the crystal structure can be used to target magnetic incommensurability, which can be of significance for design of functional magnetic materials.
Universal magnetic dinter-T phase diagram of the REMn2X2 systems. Colored regions are based on the data of the solid solution LaMn2(Ge1-xSix)2. Additional data points for Fmc (filled circle), Fmi (filled square) and AFl (filled star) from other solid solutions were added for comparison11,28,29,31,33,38.
Conclusions
The influence of the substitution of Ge by Si in LaMn2(Ge1−xSix)2 on the structural and magnetic properties has been investigated by PXRD, magnetization and PND measurements between 3 and 500 K, which allowed establishing a magnetic phase diagram. Replacing Ge with Si leads to a compression of the unit cell. The non-linear lattice contraction in the Ge-richer samples at room temperature suggests strong magnetovolume effects.
The magnetic structures of LaMn2(Ge1−xSix)2 are strongly affected by the change of the unit cell parameter c, which is reflective of the interlayer separation. In the x-T phase diagram, the commensurate Fmc and AFl structures dominate the Si-richer part of the solid solution mostly at higher temperatures, while the incommensurate Fmi and AFfs prevail in the Si-poorer part at lower temperatures. Thus, the transition from commensurate to incommensurate phases is linked to a combination of both inter-planar Mn–Mn distances and temperature. Co-existence of magnetic phases is observed in all quaternary samples and LaMn2Si2. Peak broadening of certain reflections in the PXRD pattern of the quaternary samples suggests the existence of compositional inhomogeneities as a result of the Ge/Si mixing. This effect could be the origin of the magnetic phase co-existence in the quaternary compositions. However, the same cannot be true for LaMn2Si2. High-resolution PXRD measurements might shed light on the origin of the co-existence of magnetic phases in LaMn2Si2. Comparison of the data on the LaMn2(Ge1−xSix)2 series and related solid solutions reported in the literature allows construction of a universal phase diagram relating the emergence of magnetic incommensurability to the inter-planar Mn–Mn distance.
Methods
Synthesis
LaMn2(Ge1−xSix)2 samples with the composition x = 0, 0.05, 0.33, 0.47 were produced at the Department for Materials and Environmental Chemistry at Stockholm University by first preparing the LaGe precursor through arc-melting of a 1:1 stoichiometric mixture of the elements (La 99.99% purity, Ge 99.999%). To synthetize the respective LaMn2(Ge1−xSix)2 compositions, LaGe was mixed with the appropriate amounts of elemental Mn (99.95%), Si (99.999%), and Ge. The nominal compositions corresponded to x = 0, 0.1, 0.4, and 0.5. The mixtures were thoroughly ground, pelletized, and wrapped in Mo foil. The pellets were then enclosed in evacuated fused silica tubes under a pressure of approximately 0.1 Pa and annealed at 1273 K for 2 weeks in a tube furnace with several intermediate regrinding/repelletizing steps. After each annealing step, the samples were allowed to cool to room temperature naturally by shutting-off the furnace.
LaMn2(Ge1−xSix)2 samples with x = 0.18, 0.58, 0.78, 1 were prepared in the Hyperfine Interactions Laboratory at the Instituto de Pesquisas Energéticas e Nucleares (IPEN). Starting elements were molten in an argon atmosphere purified with a hot titanium getter. La pieces with 99.9% of purity and Mn, Ge and Si pieces with 99.999% of purity were added in the stoichiometric ratio. A little excess of Mn (around 5% by mass fraction) was used to compensate the weight loss by evaporation during reaction. After melting, the resulting ingot of each sample was sealed in an evacuated fused silica tube under reduced pressure of 10–2 Pa and annealed at 1073 K for 24 h.
The sample composition was confirmed by powder X-ray diffraction (PXRD) and revealed, aside from the targeted pseudo ternary, small amounts of impurities for the samples with the composition x = 0, 0.05, 0.33, 0.47 and 0.58, thus resulting in slight deviations of the major phase composition from the nominal one. The following impurities were identified: La2O351 in x = 0 [0.92(5) % by mass fraction]; La9.3((Si1−xGex)O4)6O247 in x = 0.05 [0.84(9) % by mass fraction], 0.33 [1.47(8) % by mass fraction] and 0.47 [1.20(9) % by mass fraction]; Mn5(Ge1–xSix)352,53 in x = 0.33 [3.18(13) % by mass fraction] and 0.47 [3.03(14) % by mass fraction]; La5(Ge1–xSix)454 in x = 0.58 [1.49(19) % by mass fraction]. The compositions for the respective LaMn2(Ge1−xSix)2 samples were refined from the PXRD data and are used throughout the text to identify the samples.
Powder X-ray diffraction (PXRD)
Powder X-ray diffraction patterns were collected at room temperature using a Panalytical X’Pert PRO diffractometer (Panalytical, Netherlands) operated in Bragg-Brentano geometry. The instrument is equipped with a Johansson Ge monochromator to generate pure Cu Kα1 radiation (λ = 1.54059 Å). The samples were measured on zero-background Si sample holders. Rietveld refinements of the PXRD patterns were performed by Fullprof55. Phase analysis yielded only small amounts of impurities. Three representative PXRD patterns of the samples with the composition x = 0, 0.47 and 1 are plotted in Supplementary Fig. S2a–c.
Magnetic measurements
Magnetization was measured utilizing a Quantum Design Physical Property Measurement System (PPMS, Quantum Design, USA). A Vibrating Sample Magnetometer (VSM) option was employed to collect zero-field cooled (ZFC) and field-cooled (FC) magnetization data between 2 and 400 K in static magnetic fields (DC). Isothermal magnetization was measured at 2 K and 250 K up to 6 T. Polycrystalline samples were loaded into polypropylene (PP) sample containers which were subsequently mounted in brass sample holders.
Powder neutron diffraction (PND)
Powder neutron diffraction patterns were acquired during two beamtimes at the neutron sources of the Canadian Neutron Beam Centre (CNBC, Chalk River, Ontario, Canada) and the Center for High Resolution Neutron Scattering (CHRNS) at the National Institute of Standards and Technology (NIST Center for Neutron Research (NCNR), Gaithersburg, MD, USA), respectively. At the CNBC, diffraction patterns for the LaMn2(Ge1−xSix)2 samples with x = 0.18, 0.58, 0.78 and 1 were collected on the High Resolution Powder Diffractometer C2 in the angular range 2θ between 18.9° to 99° with a neutron wavelength of λ = 2.3722(17) Å in a He-cryostat (3 K to 290 K) and a dedicated furnace (320 K to 380 K). At NCNR, the measurements with the compositions x = 0, 0.05, 0.33 and 0.47 took place at the High Resolution Neutron Powder Diffractometer BT-156 equipped with 32 3He detectors covering an angular range of 3° ≤ 2θ ≤ 166° with a step size of 0.050°. The data were collected using a Ge (311) monochromator wavelength of λ = 2.0787(2) Å and in pile collimation of 60 min per arc. Closed Cycle Refrigerators (CCRs) were used to cover the temperature range of 14 K to 500 K. Rietveld refinements of the PND patterns were carried out for magnetic structure determination employing Fullprof for all samples55.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Shatruk, M. ThCr2Si2 structure type: The “perovskite” of intermetallics. J. Solid State Chem. 272, 198–209. https://doi.org/10.1016/j.jssc.2019.02.012 (2019).
Jia, S. et al. Ferromagnetic quantum critical point induced by dimer-breaking in SrCo2(Ge1−xPx)2. Nat. Phys. 7, 207–210. https://doi.org/10.1038/nphys1868 (2011).
Friedemann, S. et al. Detaching the antiferromagnetic quantum critical point from the Fermi-surface reconstruction in YbRh2Si2. Nat. Phys. 5, 465–469. https://doi.org/10.1038/nphys1299 (2009).
Rotter, M., Tegel, M. & Johrendt, D. Superconductivity at 38 K in the iron arsenide Ba1−xKxFe2As2. Phys. Rev. Lett. 101, 107006. https://doi.org/10.1103/PhysRevLett.101.107006 (2008).
Mallik, R., Sampathkumaran, E. V. & Paulose, P. L. Large positive magnetoresistance at low temperatures in a ferromagnetic natural multilayer, LaMn2Ge2. Appl. Phys. Lett. 71, 2385–2387. https://doi.org/10.1063/1.120036 (1997).
Di Napoli, S. et al. Magnetic structure and transport properties of noncollinear LaMn2X2 (X=Ge, Si) systems. Phys. Rev. B 70, 174418. https://doi.org/10.1103/PhysRevB.70.174418 (2004).
Brabers, J. H. V. J. et al. Giant magnetoresistance in polycrystalline SmMn2Ge2. J. Alloys Compd. 199, L1–L3. https://doi.org/10.1016/0925-8388(93)90419-N (1993).
Debnath, J. C. & Wang, J. Magnetocaloric effect in HoMn2Si2 compound with multiple magnetic phase transitions. Intermetallics 78, 50–54. https://doi.org/10.1016/j.intermet.2016.09.002 (2016).
Li, L. et al. Giant reversible magnetocaloric effect in ErMn2Si2 compound with a second order magnetic phase transition. Appl. Phys. Lett. 100, 152403. https://doi.org/10.1063/1.4704155 (2012).
Maji, B., Ray, M. K., Suresh, K. G. & Banerjee, S. Large exchange bias and magnetocaloric effect in TbMn2Si2. J. Appl. Phys. 116, 213913. https://doi.org/10.1063/1.4903770 (2014).
Md Din, M. F. et al. Tuneable magnetic phase transitions in layered CeMn2Ge(2–x)Six compounds. Sci. Rep. 5, 11288–11288. https://doi.org/10.1038/srep11288 (2015).
Fang, C. et al. New insight into magneto-structural phase transitions in layered TbMn2Ge2-based compounds. Sci. Rep. 7, 45814. https://doi.org/10.1038/srep45814 (2017).
Hou, Z. et al. Emergence of room temperature stable skyrmionic bubbles in the rare earth based REMn2Ge2 (RE = Ce, Pr, and Nd) magnets. Mater. Today Phys. 17, 100341. https://doi.org/10.1016/j.mtphys.2021.100341 (2021).
Gong, G. et al. Large topological Hall effect near room temperature in noncollinear ferromagnet LaMn2Ge2 single crystal. Phys. Rev. Mater. 5, 034405. https://doi.org/10.1103/PhysRevMaterials.5.034405 (2021).
Venturini, G., Welter, R., Ressouche, E. & Malaman, B. Neutron diffraction studies of LaMn2Ge2 and LaMn2Si2 compounds: Evidence of dominant antiferromagnetic components within the Mn planes. J. Alloys Compd. 210, 213–220. https://doi.org/10.1016/0925-8388(94)90141-4 (1994).
Welter, R., Venturini, G., Ressouche, E. & Malaman, B. Neutron diffraction study of CeMn2Ge2, PrMn2Ge2 and NdMn2Ge2: Evidence of dominant antiferromagnetic components within the (001) Mn planes in ferromagnetic ThCr2Si2-type manganese ternary compounds. J. Alloys Compd. 218, 204–215. https://doi.org/10.1016/0925-8388(94)01378-0 (1995).
Venturini, G., Malaman, B. & Ressouche, E. Magnetic ordering in ternary RMn2Ge2 compounds (R = Tb, Ho, Er, Tm, Lu) from neutron diffraction study. J. Alloys Compd. 240, 139–150. https://doi.org/10.1016/0925-8388(96)02272-4 (1996).
Tomka, G. J. et al. Magnetic structure and transitions of SmMn2Ge2. Phys. B 230–232, 727–730. https://doi.org/10.1016/S0921-4526(96)00820-4 (1997).
Granovsky, S. A. et al. The magnetic order of GdMn2Ge2 studied by neutron diffraction and X-ray resonant magnetic scattering. J. Phys. Condens. Matter 22, 226005. https://doi.org/10.1088/0953-8984/22/22/226005 (2010).
Kobayashi, H., Ohashi, M., Onodera, H., Ono, T. & Yamaguchi, Y. Magnetic phase transitions in DyMn2Ge2 studied by neutron diffraction. J. Magn. Magn. Mater. 140–144, 905–906. https://doi.org/10.1016/0304-8853(94)01478-7 (1995).
Fernandez-Baca, J. A., Hill, P., Chakoumakos, B. C. & Ali, N. Neutron diffraction study of the magnetic structures of CeMn2Ge2 and CeMn2Si2. J. Appl. Phys. 79, 5398–5400. https://doi.org/10.1063/1.362317 (1996).
Welter, R., Venturini, G., Fruchart, D. & Malaman, B. Magnetic structures of PrMn2Si2 and NdMn2Si2 from neutron diffraction studies. J. Alloys Compd. 191, 263–270. https://doi.org/10.1016/0925-8388(93)90075-X (1993).
Campbell, S. J. et al. Magnetic order in YbMn2Si2—neutron scattering investigation. J. Korean Phys. Soc. 63, 314–319. https://doi.org/10.3938/jkps.63.314 (2013).
Kolenda, M., Leciejewicz, J., Szytula, A., Stüsser, N. & Tomkowicz, Z. Magnetic transition in TbMn2Si2. J. Alloys Compd. 241, L1–L3. https://doi.org/10.1016/0925-8388(96)02333-X (1996).
Gerasimov, E. G. et al. Easy-plane magnetic anisotropy in layered GdMn2Si2 compound with easy-axis magnetocrystalline anisotropy. J. Alloys Compd. 818, 152902. https://doi.org/10.1016/j.jallcom.2019.152902 (2020).
dos Reis, D. C. et al. Magnetic and magnetocaloric properties of DyMn2Si2 compound with multiple magnetic phase transition. J. Magn. Magn. Mater. 424, 84–88. https://doi.org/10.1016/j.jmmm.2016.10.019 (2017).
Ryan, D. H., Rejali, R., Cadogan, J. M., Flacau, R. & Boyer, C. D. Europium and manganese magnetic ordering in EuMn2Ge2. J. Phys. Condens. Matter 28, 166003. https://doi.org/10.1088/0953-8984/28/16/166003 (2016).
Venturini, G., Malaman, B. & Ressouche, E. The x–T magnetic phase diagram of the La1−xYxMn2Ge2 system by neutron diffraction study. J. Alloys Compd. 241, 135–147. https://doi.org/10.1016/0925-8388(96)02310-9 (1996).
Ijjaali, I., Venturini, G., Malaman, B. & Ressouche, E. Neutron diffraction study of the La1−xYxMn2Si2 solid solution (0≤x≤1). J. Alloys Compd. 266, 61–70. https://doi.org/10.1016/S0925-8388(97)00487-8 (1998).
Di Napoli, S., Llois, A. M., Bihlmayer, G. & Blügel, S. Magnetic order in RMn2Ge2 (R=Y, Ca) compounds and their solid solutions with LaMn2Ge2. Phys. Rev. B 75, 104406. https://doi.org/10.1103/PhysRevB.75.104406 (2007).
Wang, J. L. et al. Magnetism and magnetic structures of PrMn2Ge2−xSix. J. Phys. Condens. Matter 25, 386003. https://doi.org/10.1088/0953-8984/25/38/386003 (2013).
Wang, J. L. et al. Magnetic structures and phase transitions in PrMn2−xFexGe2. J. Appl. Phys. 104, 103911. https://doi.org/10.1063/1.3021096 (2008).
Dincer, I., Elerman, Y., Elmali, A., Ehrenberg, H. & André, G. Neutron diffraction study of the La1-xPrxMn2Si2 (x=0.4, 0.7 and 1) compounds and the general description of the magnetic behavior of Mn in RMn2Ge2 and RMn2Si2. J. Magn. Magn. Mater. 313, 342–353. https://doi.org/10.1016/j.jmmm.2006.12.032 (2007).
Bosch-Santos, B., Carbonari, A. W., Cabrera-Pasca, G. A. & Saxena, R. N. Magnetic behavior of LaMn2(Si(1–x)Gex)2 compounds characterized by magnetic hyperfine field measurements. J. Appl. Phys. 115, 17E124. https://doi.org/10.1063/1.4864439 (2014).
Hofmann, M., Campbell, S. J., Kennedy, S. J. & Zhao, X. L. A neutron diffraction study of LaMn2Si2 (10–473 K). J. Magn. Magn. Mater. 176, 279–287. https://doi.org/10.1016/S0304-8853(97)00532-5 (1997).
Bosch-Santos, B., Carbonari, A. W., Cabrera-Pasca, G. A., Costa, M. S. & Saxena, R. N. Effect of Ge substitution for Si on the magnetic hyperfine field in LaMn2Si2 compound measured by perturbed angular correlation spectroscopy with 140Ce as probe nuclei. J. Appl. Phys. 113, 17E124. https://doi.org/10.1063/1.4795419 (2013).
Vegard, L. Die Konstitution der Mischkristalle und die Raumfüllung der Atome. Z. Phys. 5, 17–26. https://doi.org/10.1007/BF01349680 (1921).
Pandey, S., Siruguri, V. & Rawat, R. Effect of Tb substitution in naturally layered LaMn2Si2: Magnetic, magnetocaloric, magnetoresistance and neutron diffraction study. J. Phys. Condens. Matter 32, 035807. https://doi.org/10.1088/1361-648X/ab4b3b (2019).
Jammalamadaka, S. N., Das, S. D., Chalke, B. A. & Sampathkumaran, E. V. Magnetic behavior of nanocrystalline LaMn2Ge2. J. Magn. Magn. Mater. 320, L129–L131. https://doi.org/10.1016/j.jmmm.2008.05.021 (2008).
Shigeoka, T., Iwata, N., Fujii, H. & Okamoto, T. Magnetic properties of LaMn2Ge2 single crystal. J. Magn. Magn. Mater. 53, 83–86. https://doi.org/10.1016/0304-8853(85)90133-7 (1985).
Gerasimov, E. G., Kurkin, M. I., Korolyov, A. V. & Gaviko, V. S. Magnetic anisotropy and ferro-antiferromagnetic phase transition in LaMn2Si2. Phys. B 322, 297–305. https://doi.org/10.1016/S0921-4526(02)01196-1 (2002).
Welter, R., Ijjaali, I., Venturini, G., Ressouche, E. & Malaman, B. Investigations of the La1−xCaxMn2Ge2 (0≤x≤1) solid solution by magnetic measurements and neutron diffraction. J. Magn. Magn. Mater. 187, 278–292. https://doi.org/10.1016/S0304-8853(98)00147-4 (1998).
Narasimhan, K. S. V. L., Rao, V. U. S., Bergner, R. L. & Wallace, W. E. Magnetic properties of RMn2Ge2 compounds (R=La, Ce, Pr, Nd, Cd, Tb, Dy, Ho, Er, and Th). J. Appl. Phys. 46, 4957–4960. https://doi.org/10.1063/1.321480 (1975).
Szytuła, A. & Leciejewicz, J. Handbook on the Physics and Chemistry of Rare Earths Vol. 12, 133–211 (Elsevier, 1989).
Kolmakova, N. P., Sidorenko, A. A. & Levitin, R. Z. Features of the magnetic properties of rare-earth intermetallides RMn2Ge2 (review). Low Temp. Phys. 28, 653–668. https://doi.org/10.1063/1.1511711 (2002).
Hofmann, M., Campbell, S. J. & Kennedy, S. J. Competing magnetic interactions in La0.8Y0.2Mn2Si2-coexistence of canted ferromagnetism and antiferromagnetism. J. Phys. Condens. Matter 12, 3241–3254. https://doi.org/10.1088/0953-8984/12/14/303 (2000).
Masubuchi, Y., Higuchi, M., Takeda, T. & Kikkawa, S. Oxide ion conduction mechanism in RE933(SiO4)6O2 and Sr2RE8(SiO4)6O2 (RE=La, Nd) from neutron powder diffraction. Solid State Ionics 177, 263–268. https://doi.org/10.1016/j.ssi.2005.09.015 (2006).
Kennedy, S. J., Kamiyama, T., Oikawa, K., Campbell, S. J. & Hofmann, M. Mixed magnetic phases in La0.85Y0.15Mn2Si2—High resolution diffraction. Appl. Phys. A 74, s880–s882. https://doi.org/10.1007/s003390201368 (2002).
Nowik, I., Levi, Y., Felner, I. & Bauminger, E. R. New multiple magnetic phase transitions and structures in RMn2X2, X = Si or Ge, R = rare earth. J. Magn. Magn. Mater. 147, 373–384. https://doi.org/10.1016/0304-8853(95)00015-1 (1995).
Campbell, S. J., Cadogan, J. M., Zhao, X. L., Hofmann, M. & Hong-Shuo, L. Magnetic transitions in La1-xYxMn2Si2—Mössbauer investigation (4.2–520 K). J. Phys. Condens. Matter 11, 7835. https://doi.org/10.1088/0953-8984/11/40/310 (1999).
Müller-Buschbaum, H. & Schnering, H. G. V. Zur Struktur der A-Form der Sesquioxide der Seltenen Erden. Strukturuntersuchungen an La2O3. Z. Anorg. Allg. Chem. 340, 232–245. https://doi.org/10.1002/zaac.19653400503 (1965).
Yusupov, R. G. et al. Mavlyanovite, Mn5Si3: A new mineral species from a lamproite diatreme, Chatkal Ridge, Uzbekistan. Mineral. Mag. 73, 43–50. https://doi.org/10.1180/minmag.2009.073.1.43 (2009).
Castelliz, L. Kristallstruktur von Mn5Ge3 und einiger ternärer Phasen mit zwei Übergangselementen. Monatshefte für Chemie und verwandte Teile anderer Wissenschaften 84, 765–776. https://doi.org/10.1007/BF00902776 (1953).
Yang, H. F. et al. The crystal structure of La5Si4 and Nd5Si4. J. Alloys Compd. 334, 131–134. https://doi.org/10.1016/S0925-8388(01)01753-4 (2002).
Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B 192, 55–69. https://doi.org/10.1016/0921-4526(93)90108-I (1993).
Santoro, A. Past and present crystallographic work at the NBS/NIST reactor. J. Res. Natl. Inst. Stand. Technol. 106, 921–952. https://doi.org/10.6028/jres.106.046 (2001).
Acknowledgements
We acknowledge the support of the National Institute of Standards and Technology, U. S. Department of Commerce, in providing the neutron research facilities used in this work. This research is funded in part by the Swedish Foundation for Strategic Research (SSF) within the Swedish national graduate school in neutron scattering (SwedNess). AVM would like to thank also Energimyndigheten for funding through grant no. 48699-1 and the Royal Swedish Academy of Sciences for support through the Göran Gustafsson award in chemistry. Financial support for this work was partially provided by Fonds Québécois de la Recherche sur la Nature et les Technologies, and the Natural Sciences and Engineering Research Council (NSERC) Canada. Partial financial support for this work was provided by Fundação de Amparo a Pesquisa do Estado de São Paulo (FAPESP) under grants 2012/11104-9 and 2013/05552-1. The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology. We would like to thank Katharina V. Dorn for experimental support during the PND beamtime at NCNR.
Funding
Open access funding provided by Stockholm University.
Author information
Authors and Affiliations
Contributions
The manuscript was written through the contributions of all authors. All authors have approved the final version of the manuscript. Conceptualization and supervision, A.-V.M.; experimental work, S.S., A.O., B.B.S., G.A.C-P. and A.C.; writing S.S., A.O., B.B.S., G.A.C-P., A.C., D.R. and A.-V.M. The samples with the composition x = 0.18, 0.58, 0.78 and 1 were synthesized by B.B-S. The PND experiments at CNBC were performed by G.A.C-P. Both happened under the supervision of A.C. The samples with the composition x = 0, 0.05, 0.33 and 0.47 were synthesized by A.O. The PND experiments at NCNR were performed by S.S. Both happened under the supervision of A.-V.M.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Siebeneichler, S., Ovchinnikov, A., Bosch-Santos, B. et al. Magnetic phase diagram of the solid solution LaMn2(Ge1−xSix)2 (0 ≤ x ≤ 1) unraveled by powder neutron diffraction. Sci Rep 12, 9248 (2022). https://doi.org/10.1038/s41598-022-12549-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-12549-y
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.