Abstract
In this article, a symmetric split ring resonator (SRR) based metamaterial (MTM) is presented that exhibits three resonances of transmission coefficient (S21) covering S, C, and X-bands with epsilon negative (ENG) and near zero index properties. The proposed MTM is designed on an FR4 substrate with the copper resonator at one side formed with two square rings and one circular split ring. The two square rings are coupled together around the split gap of the outer ring, whereas two split semicircles are also coupled together near the split gaps. Thus, gap coupled symmetric SRR is formed, which helps to obtain resonances at 2.78 GHz, 7.7 GHz and 10.16 GHz with desired properties of the MTM unit cell. The MTM unit cell's symmetric nature helps reduce the mutual coupling effect among the array elements. Thus, different array of unit cells provides a similar response to the unit cell compared with numerical simulation performed in CST microwave studio and validated by measurement. The equivalent circuit is modelled for the proposed MTM unit cell in Advanced Design System (ADS) software, and circuit validation is accomplished by comparing S21 obtained in ADS with the same of CST. The effective medium ratio (EMR) of 10.7 indicates the compactness of the proposed MTM. A test antenna is designed to observe the effect of the MTM over it. Numerical analysis shows that the proposed MTM have an impact on the antenna when it is used as the superstrate and helps to increase the gain of the antenna by 95% with increased directivity. Thus, compact size, high EMR, negative permittivity, near zero permeability and refractive index makes this MTM suitable for S, C and X band applications, especially for antenna gain with directivity enhancement.
Similar content being viewed by others
Introduction
Metamaterial express exotic optical and electromagnetic properties when an interaction occurs with electromagnetic wave. Negative permeability, permittivity and refractive index are some exclusive properties of the metamaterial that can be used for various applications in communication systems of microwave frequencies. Antenna performance improvement1,2,3, radiation reduction4,5, design of absorber6,7, sensors8,9, high-frequency communications10,11, solar energy harvesting12,13, electromagnetic shielding14, metamaterial lenses15, etc. are some prominent applications of the metamaterial. Metamaterials can be classified as either single negative or double negative based on the fact that any one of permeability or permittivity is negative or both are negative. Artifical metamaterial can be constructed with metalic rings in association with splits. Geometrical structure of the MTM is an important parameter that governs resonance frequency along with the existance of negative permeability and permittivity.
Metamaterial (MTM) is extensively investigated by researchers to improve the performance of the antenna targeting various applications. In recent works, Sakli et al. has designed ultra-wideband antenna with MIMO configurations in which a complementary split-ring resonator is used to create isolation between antenna elements. By using this MTM, the transmission coefficient between two antennas decreases to − 43 dB, which is 1.87 times less compared to the same without using MTM. Moreover, the presented MIMO system with MTM helps to achieve size reduction and good diversity gain16. In another work, a metamaterial with near zero index is used to improve gain of a multiband antenna using MTM as a superstrate17. The metamaterial is also utilized by Das et al. to increase the bandwidth and gain of monopole antenna18, whereas Ke et al. have proposed a dielectric ring resonator(DRR) based quasi-Yagi antenna targeting broadband filtering applications in which good gain response is obtained by using wideband near-zero index characteristics of the metamaterial19. Moreover, in another article, an antenna is presented that involves metamaterial as superstrate for improving different parameters in antenna such as gain and bandwidth11. In this work, the metamaterial is used as radome to enhance the strength of the overall structure. Frequency can be reconfigured using diode switches in the metamaterial. In another article, the directivity of the antenna has been increased by using near zero permeability metamaterial20. Moreover, metamaterial helps to reduce the overall dimension of the antenna by about 11.4%. Moussa et al. proposes slotted metamaterial that helps to reduce mutual coupling between the antennas in MIMO system21. Moreover, metamaterial also helps to reduce the inter-element gaps. In another work, a metamaterial absorber is introduced with a four-element circularly polarized (CP) antenna array to reduce the mutual coupling effect. In this design, double-sided MTM absorbers walls having slotted cross patches are vertically placed between the antenna array elements that exhibit about 8 dB mutual coupling reduction22. A metasurface comprising with periodic metamaterial suspended over the MIMO antenna array for boosting up the antenna gain si present by Luo et al. the system provides 3 dB gain enhancement with mutula coupling redcution using neutralization line decouling element plance on feeding line23. Mishra et al. persented fractal antenna loading with metamaterial in which MTM helps to improve the bandwidth24. Jabire et al. describes a monopole antenna in which metamaterial is loaded to improve the bandwidth with reduction of mutual coupling25. Thus, metamaterials play a vital role in controlling different performance parameters of the antenna. A number of metamaterial structures have also been explored in various literature intending the applications in various fields in the microwave region28,29,30. Computational metamaterials providing the feasibility of wave-based computations in analog form with the massive parallel operation have been explored by Nejad et al.31. Dalgac et al. presents a chiral metamaterial as a sensor constructed with square and circular shaped resonator and works in X band and exhibits high sensitivity and selectivity to determine the quality of car lubricant oil32. On the other hand, a millimeter-wave range sensor based on metamaterial is presented by Qureshi et al. to characterize cooking oils, which show high transmission coefficient shifting when operating at 30 GHz33. A dual-function metamaterial is presented by Lu et al. that can be applied for vibration isolation along with energy harvesting34. Coskuner et al. has presented an impedance matching network based on a metamaterial-based transmission line to improve energy harvesting system operating around 2.4 GHz and 5 GHz35. A fabricated antenna loaded with metamaterial is presented by Ashyap et al. The metamaterial helps to diminish frequency detuning influence and attenuate backward radiation36. A metamaterial based antenna is presented in Ref.26 where a transmission line having negative permittivity and a splitted ring resonator are incorporated. Image theory is exercised to obtain impedance and the measured result exhibits impedance bandwidth of 16.36% having a gain of 5.62 dBi with an average efficiency of 72.1%. On the other hand, Ameen et al. presented a circularly polarized (CP) antenna with V-shaped metasurface27. This CP antenna exhibits a good gain of 5.76 dBi and it can be utilized for small satellite applications.
This article presents a metamaterial that is axis-symmetric and split rings or parts of the rings coupled near the split gaps intending to obtain the S21 resonances at S, C, and X-bands. These three bands cover the frequency ranges 2–4 GHz, 4–8 GHz, and 8–12 GHz for S, C, and X band, respectively, for various applications such as Radar, satellite Multimedia communications, etc. Particularly, the ISM band (2.4–2.45 GHz) is used for unlicensed devices such as cordless phones, wireless electronic devices, blue tooth, Wi-Fi communications. Moreover, in some countries, direct home to satellite television utilizes frequency band 2.5 to 2.7 GHz. For X-band satellite communication, 7.9–8.4 GHz is used for uplink, and 7.25–7.75 is used for the downlink. On the other hand, 10 to 10.5 GHz is allocated by ITU for amateur radio operations, whereas 10.45 to 10.5 GHz for amateur satellite operations. In our present design, we focus on the fact that the MTM can help to increase the antenna gain of a particular frequency band. For this purpose, we tried to keep the resonances of MTM around the frequency as mentioned above bands so that proposed MTM, when implemented with the microwave devices, can boost up the performances of those.
The proposed MTM exhibits three resonances of S21 at frequencies of 2.78 GHz, 7.7 GHz, and 10.16 GHz with − 10 dB bandwidth in the frequency ranges 2.38–3.1 GHz, 6.6–8.33 GHz, and 9.5–11 GHz, respectively, which can effectively influence to enhance the performance of microwave devices of our targeted frequency bands. The specific properties of the proposed MTM are: (i) Structural design of unit cell is simple, (ii) coupling between two outer layers from both ends of the split gaps of the outmost ring, named as gap coupling aids to adjust resonance frequencies at the target bands maintaining negative permittivity with near zero permeability and refractive index, (iii) The obtained EMR value of 10.7 indicates its compactness and makes it suitable for small-sized devices, (iv) The unit cell is symmetric about the two perpendicular axes through the center of the structure. Due to symmetric structure, the mutual coupling effect is reduced that provides similar resonances for different arrays, (iv) it exhibits good antenna gain enhancement properties when used as a superstrate with the antenna. A test antenna is designed, and the performance of the MTM on this antenna is examined through numerical simulation that provides about 2.45 dBi gain increment with boosting of the directivity of the antenna when the MTM array is used as the superstrate. The antenna is essentially a rectangular patch with slots. Two ground plane slots with the rectangular patch establish the resonances, but the overall shape of the antenna in both top and bottom perspectives is new. Furthermore, two inverted L-shaped parasitic elements at the bottom side help to modify the resonance frequency, and bandwidth as its length significantly affects both. The proposed antenna shows a wide bandwidth with marginal gain. But, when the proposed metamaterial is used with the antenna, significant gain enhancement is achieved within a broad bandwidth, verified through the experiments.
Design of metamaterial and equivalent circuit modeling
This section includes a discussion on the proposed MTM that consists of the substrate material properties, resonating patch structure, simulation set up, step by step design process of MTM with the change of transmission and reflection coefficient. Furthermore, since the MTM unit cell exhibits multiband resonances indicating that the unit cell acts as LC resonance circuit, the equivalent circuit is also modeled and designed with validation using ADS in this section.
Design and simulation of the proposed MTM
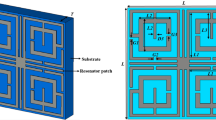
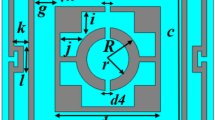
The proposed metamaterial(MTM) unit cell is designed on FR-4 substrate of 1.6 mm thick having a dielectric constant value of 4.3 with a loss tangent value of 0.025. The resonating patch is constructed at one side of the substrate using a copper metal having 0.035 mm thick. The MTM is originated on the substrate having a dimension of 10 × 10.5 mm2. As shown in Fig. 1a, the resonating patch is constructed with three split rings, the outer two are square-shaped, and the innermost one is circular. Two outer rectangular SRRs are coupled together by using metal strips at both ends of the split gaps of the outermost ring, as shown in Fig. 1a. Moreover, parallel inductive paths are created by coupling two ends of split gaps of the innermost circular ring. All these couplings contribute significantly to the resonances when electromagnetic waves are imposed on the MTM. Each SRR ring's dimension is selected, and the slip gaps and coupling metal strips are so positioned that the whole structure becomes axis-symmetric. The symmetric nature of the MTM helps to eliminate the harmonics and mutual coupling effect between the array elements when an array of the unit cells are employed for different uses. Table 1 presents the parameter values of different segments of the proposed MTM of Fig. 1a. The parameter values shown in Table 1 are finalized with numerous numerical simulations performed for the frequency ranges 2–12 GHz in CST microwave studio suite-2019 to obtained triple-band resonances of transmission coefficient (S21). The simulation arrangement in CST is presented in Fig. 1b, where two waveguide ports are used in Z-axis. In this arrangement, transverse electromagnetic (TEM) signal transmitted from one waveguide port incidents perpendicularly on the resonating patch. After transmitting through the MTM, the transmitted signal is received by another port. The electrical boundary is employed in X-axis in the simulation arrangement, on the other hand, the magnetic boundary is used in the Y-axis.
(a) Schematic layout of the unit cell and (b) simulation arrangement (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
The TEM waves represent a particular class of guided waves with neither E field component nor H filed component in the direction of propagation, meaning that Ez = Hz = 0 along the Z-axis. When this wave is incident upon the metamaterial, the response of the material depends on its properties such as permittivity, permeability. The time varying electric and magnetic flux densities in the material can be interrelated with the time varying electric and magnetic field using the mathmetical relations presented in Ref.37 which helps to understand the impact of the medium on some important parameters such as refractive index, wavenumber, and wave impedance. Electromagnetic field coupling occurs in a medium as time-varying electric charges are the sources of the magnetic fields, generating electric fields varied with time. These relations can be expressed through Maxwell’s equations presented in the differential form in Ref.37. The Maxwell’s equations indicate the coexistance of oscillating electric and magnetic fields, which initiates electromagnetic waves that travel through the medium. Now, when the incident wave is imposed upon the MTM, electromagnetic induction occurs and resonating phenomena is experienced as the split rings of it acts as resonantor. Thus the split ring resonator (SRR) can be demonstrated by an equivalent resonant circuit containg inductance, L and capacitance, C that offers resonances at some frequencies of SRR.
The proposed MTM is designed through numerous numerical simulations with the modification of the length and width of different rings, and split gap distances since these parameters have an dominating impact on the resonance phenomena of the MTM. Moreover, inter ring distances and their interconnections are modified through trial and error basis to obtain the expected outcomes. Thus, the design finalization of the proposed MTM unit cell undergoes several design steps started with a square copper ring having two split gaps at vertical arms as displayed in design 1 of Fig. 2. This single ring causes a resonance of transmission coefficient (S21) taking place at 4.02 GHz, as shown in Fig. 3a. In design two, another square split ring is added that holds two splits at horizontal arms and square blocks at each corner, as illustrated in design 2 of Fig. 2. This insertion causes another addition resonance of S21 holding at 13.3 GHz. Moreover, owing to the mutual coupling between these two rings, primary resonance shifts slightly to 4.1 GHz. In the next step, one additional circular-shaped split ring is introduced (presented in design 3 of Fig. 2) that includes other resonances along with frequency shifts of the previous two resonances as consisted at 4.02 GHz, 11.43 GHz, and 14.5 GHz, as shown in Fig. 3a. In the succeeding step, two half circles of the innermost rings are coupled near the split gaps by using shunt copper strips as shown in design 4 of Fig. 2 with an effect of shifting of mid and high-frequency resonances at 10.02 GHz and 13.2 GHz as depicted in Fig. 3a. In the final step, two outermost rings are coupled adjoining the outmost ring’s gaps as illustrated in the proposed MTM of Fig. 2 with a formation of gap coupled symmetric split ring resonator MTM. This gap coupling causes shifting in the resonances at 2.78 GHz, 7.7 GHz and 10.16 GHz with an increasing effective medium ratio. Thus, the proposed MTM provides triple-band resonances within C, S, X-bands. The S21 response of the MTM for all design phases are also mentioned in Table 2, whereas reflection coefficients (S11) plots are presented in Fig. 3b for various design steps.
Scattering parameters for different design steps: (a) coefficiens of transmission (S21), (b) coefficients of reflection (S11). (c). Sufrace current, magnetic field and electric field distribution at 4.02 GHz for various design steps to the proposed MTM. (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
The effect of different design steps is further analyzed through field analysis (magnetic and electric) and study of current at MTM at a particular frequency of 4.02 GHz, where resonance for design 1 occurs. As expressed in Fig. 3c shown in design 1, the horizontal sides of the outermost ring is susceptible to the magnetic field, and magnetic dipoles are created when electromagnetic waves are incident on the SRR, which in turn creates the current dipole with current flowing clockwise and anticlockwise through this two edges of outer ring. Electric field spreading is oriented in the vertical sides and forms an electric dipole. Therefore, magnetic and electric dipoles are linked to each other, and electromagnetic resonances of S21 occur at 4.02 GHz. In design 2, as extra ring is inserted inside earlier ring, this not only causes an additional resonance at 13.3 GHz but also modifies earlier resonance at 4.1 GHz. This is because of the mutual inductance and co-planar capacitance presented in Eqs. (7) and (8), respectively. This effect is evident from Fig. 3c, as it is noticed the opposite flowing currents through the inner ring compared to the outer ring. This opposition effect is dominant at four corners. Thus, this current causes a mutual inductance to the outer ring causing the modification of the total inductance and resonance frequency to 4.2 GHz. The electric field and magnetic field distribution for design 2 in Fig. 3c also exhibits the change compared to the same distribution of design 1. In design 3, an additional inner ring causes to reduce the mutual coupling effect on the outer ring; thus first resonance is restored at 4.02 GHz, whereas it has an impact on the second ring as shown electric and magnetic field distribution in design 3 of Fig. 3c. Design 4 has less impact on the field distribution at 4.02 GHz whereas, gap coupling in the proposed design modifies the current, electric field and magnetic field distribution drastically, and electric and magnetic dipole no longer exist in the outer ring and resonance shifts from this frequency to another frequency of 2.78 GHz.
Equivalent circuit modeling of the proposed MTM
The equivalent circuit of the MTM can be drawn, considering it as analogous to LC resonance circuit39 as copper strips of the resonator exhibits inductive effect whereas split gaps have inductive effects. Due to these effects, various segments of the MTM exhibit different values of inductances and capacitances. Figure 4 shows the approximated equivalent circuit in which the inductances of different segments of the outer ring is represented by L1, L2, L11, L12, L13, L14, whereas C1 and C2 are the capacitances due to the split gaps of this ring. The effect of the middle ring is expressed by the L–C pairs L7 & C3 and L8 & C4, whereas L9, L10, L15, and L16 are the inductances and C5, C6 split gap capacitances for the innermost ring. L3, L4, L5, and L6 are the inductances due to the coupling of the two outermost rings. C7 and C8 are coupling capacitances between the innermost and outer rings. This circuit is then designed in Advanced Design Software (ADS) to check whether it resembles the proposed MTM structure or not by comparing the transmission coefficients (S21) obtained from the equivalent circuit and from the structure. Two ports are connected at the left and right sides of the equivalent circuit; those act as source and receiving ports. These transmitting and receiving ports are terminated with 50 Ω impedances. The simulation in ADS is started with the nominal values for the inductors and capacitors with 1 nH for each inductor and 1 pF for each capacitor. The component values are then adjusted using the tuning module in ADS as the tuning option provides the flexibility to enable the changing of one or more component values with a quick observation of the effect without emulating the circuit again. Thus, circuit parameter values are finalized through numerous tuning of the components when the obtained S21 exhibits resonance frequency closer to the S21 resonance in CST. A comparison of the S21 response obtained from the equivalent circuit with the same obtained in CST is shown in Fig. 5. As shown in Fig. 5, S21 of the equivalent circuit is well matched with the S21 of the MTM unit cell obtained in CST. As shown in Fig. 5, the bandwidth of resonances obtained from the equivalent circuit is narrower than the MTM response in CST. This is due to the fact that in the proposed MTM the inductance and capacitance are distributed all over the design domain. In contrast, in the equivalent circuit model, the components are considered lumped. Moreover, the resistive effects of the copper strips and inter-ring capacitances are ignored, which is distributive in nature.
Result analysis of the proposed MTM
This section comprises various property analyses of the proposed MTM along with electromagnetic field and current distribution studies. Moreover, array performance is also studied as cluster of MTM cells arranged in a regualar pattern is utilized in many applications. Furthermore, the obtained result in measurement is also conferred, and an analysis is made on the presented MTM in comparison with other recent works on the MTM.
Effective parameter analysis
The MTM property has been extracted by using CST post processing template that uses transmission (S21) and reflection coefficient (S11) coefficients to calculate permittivity, permeability and refractive index with the help of robust method where scattering parameters are concerned with by40:
where (.)′ is real part, (.)″ is the imaginary part, m is an integer associated to real part of refractive index. Two other effective parameter permeability and permittivity can be calculated by using the equations:
By using Eqs. (7)–(9) the effective parameters are determined using post processing module in CST. The result obtained from the CST related to scattering parameters, permeability, permittivity and refractive index are depicted in Fig. 6a–d. As expressed in Fig. 6a, three resonances of transmission coefficient occur at 2.78 GHz, 7.7 GHz and 10.16 GHz, whereas S11 resonances occurred at 3.86 GHz and 8.85 GHz. It is witnessed that real component of the permittivity is negative within frequency ranges 2.78–3.75 GHz, 7.77–8.76 GHz and 10.17–12.74 GHz and obtained bandwidths are 0.97 GHz, 0.99 GHz and 12.57 GHz, respectively as expressed in Fig. 6b. Thus, comparatively wider bandwidth is obtained for negative values of permittivity for three different bands within S, C, X bands. The permeability plot depicted in Fig. 6c show near zero permeability with a magnitude less than 0.1 in the vicinity of 2.5–3.05 GHz, 7.27–8.3 GHz and 9.9–11.2 GHz which indicates wide bandwidth for near zero permeability. Minimum values of permeability are 0.04, 0.03 and 0.025 at 2.85 GHz, 7.94 GHz and 10.53 GHz, respectively. Additionally, as depicted in Fig. 6d, real component of the refractive index shows negative values within the negative permittivity frequency regions and near zero magnitudes is noticed in the vicinities of frequencies 2.82 GHz, 3.63 GHz, 7.84 GHz, 8.65 GHz, 10.25 GHz and 12.3 GHz. Thus, the proposed MTM reveals epsilon negative (ENG) behavior with both permeability and refractive index near zero, making it suitable for antenna applications for gain enhancement.
Surface current, electric field and magnetic field analysis
The interaction of the electromagnetic wave with the metamaterial and its effects on resonances can be realized by analyzing various fields (electromagnetic) and current. Figure 7 shows the surface current spreading at 2.78 GHz and 10.16 GHz. In contrast, magnetic field and electric field distribution at these frequencies are presented in Figs. 8 and 9, respectively. The interrelation between various fields and currents can be explained with the help of Maxwell’s equations37. As shown in Fig. 7a, a strong surface current flows through the outermost ring at 2.78 GHz. The lower and upper halves of these ring currents form a circular current with the second ring though the current density in the second ring is low. The upper current loop forms circulating current in the anticlockwise direction, whereas the lower loop bears current in clockwise current. These currents induce a strong magnetic field surrounding the outer ring, as displayed in Fig. 8a. Likely, Fig. 9a shows the corresponding electric field distribution, indicating that a strong electric field exists at two vertical arms forming the electric dipoles triggering the resonance at 2.78 GHz. At this frequency, a strong magnetic field also exists at different portions of the middle ring and nearest portions of the middle and inner rings. At 10.16 GHz, the surface current is strong at the boundaries of the innermost ring, and lower and upper half current flows in the opposite directions, as shown in Fig. 7b. This surface current induces magnetic fields at the periphery of the innermost ring, as depicted in Fig. 8b. A strong electric field exists adjacent to the horizontal sides and gap coupling stips of the innermost ring (shown in Fig. 9b), indicating the contribution of the innermost ring for the resonance at 10.16 GHz.
Surface current distribution for two different frequencies of S21 resonances: (a) 2.78 GHz, (b) 10.16 GHz (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
Magnetic field distribution for two different frequencies of S21 resonances: (a) 2.78 GHz and (b) 10.16 GHz (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
Electric field distribution for two different frequencies of S21 resonances: (a) 2.78 GHz and (b) 10.16 GHz (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
Array analysis and measurement
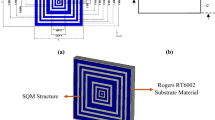
As in many pragmatic cases, the array of the unit cells works together for particular applications rather than solitary unit cell and so, outcomes of array is analyzed using 2 × 2 and 4 × 4 arrays of MTM cells. The S21 and S11 obtained from this study are depicted in Fig. 10a,b, respectively. Comparing the array performances with the unit cell indicates that array results are well matched with the unit cell. The substantial similarity is owing to the fact that the MTM cell is symmetric in the structure; thus, when several cells are organized in a regular pattern in an array, the electromagnetic field near the adjacent side does not affect much. Therefore, it avoids harmonics and resonance frequency shifts. Since unit cell response and array response of the metamaterial are similar, so measurement result is taken by fabricating a 2 × 2 array. The fabricated prototype is shown in Fig. 11a, whereas measurement arrangement is presented in Fig. 11b. In the measurement setup in Fig. 11b, two waveguide ports are employed as a transmitter and receiver of the electromagnetic waves that are coupled to the vector network analyzer (VNA). MTM array is positioned between two ports. As displayed in Fig. 12, the measured result shows three significant resonances of S21 at 2.72 GHz, 7.82 GHz and 10.21 GHz with a magnitude of − 36.9 dB, − 48.9 dB, − 39.8 dB, respectively. It is also observed from this figure that some amount of noise and harmonics exist at the low and mid-frequency in the measured S21. Moreover, measured S21 deviates from simulation one in terms of resonance frequencies and magnitude at resonance, but this mismatching is not significant. Fabrication tolerances, coupling effect in the waveguide ports and calibration errors in VNA are the reasons for this mismatching. Despite minor mismatch and harmonics, the measured result is well agreed with the simulation results covering the S, C and X-bands.
Comparative analysis
A comparison is made of the proposed MTM unit cell with some recent works where MTMs are designed to target various applications, summarized in Table 3. In this comparison, physical and electrical dimensions of the applied MTM, Transmission coefficient resonance frequencies, effective medium ratio (EMR), covering bands are considered major parameters. Moreover, special features along with the applications are also discussed in this comparison. EMR is calculated at the lowest resonance frequency of S21 using the relation, \(\mathrm{EMR }=\uplambda /L\), where \(\uplambda\) is the wavelength at the lowest resonance frequency of S21 and L is the highest dimension of the MTM unit cell. From Table 3, it is observed that in Refs.1,28,41,42,43, the sizes of the listed MTMs are small compared with our proposed MTM, but all these MTMs bear lower values of the EMR compared to our present work. Moreover, Refs.1,41,42,43 covers only a single band, limiting their applications to a specific range of frequencies. Although MTM in Ref.28 covers X, C and Ku bands, no particular application is presented. All the other MTMs presented in Refs.44,45,46,47 in Table 3 lag behind physical size, EMR values, and the number of covering bands. Thus, the proposed MTM covers multiples bands with high EMR values within its moderate dimension that provides the flexibility of application in small dimension devices in wireless communication with a diversity of operating in the wider frequency range. Moreover, its negative permittivity property with near zero refractive index and permeability makes it suitable for gain enhancement verified with numerical analysis in the next section.
Design and simulation of the test antenna
A monopole antenna is designed consisting of a slotted patch with partial ground and parasitic elements in the backside, as shown in Fig. 13. The designed antenna is initiated on an FR4-substrate with 1.6 mm thickness and 4.3 dielectric constant. The overall dimension of the antenna is 40 × 41 mm2 and has a patch of 22 × 26 mm2. At the same time, a feedline of width 2.96 mm is used to match the impedance to 50 Ω. Various slots in the patch are used to control the current flowing through the patch to obtain the wideband response with sufficient gain and efficiency of the antenna48. Figure 13a shows the geometry of the patch of the antenna, whereas Fig. 13b shows the structural geometry of the ground plane. The different parameter values of the various slots and segments in patch and grounds are listed in Table 4. The partial ground structure helps to obtain an omnidirectional radiation pattern, whereas slots in the ground plane along with the inverted L shaped parasitic elements help to improve the bandwidth. Figure 14a shows the reflection coefficient of the antenna that expresses the bandwidth extended from 2.5 to 4.24 GHz, with two resonances occurring at 2.6 GHz and 3.77 GHz. Moreover, the efficiency and gain presented in Fig. 14b indicates that the average efficiency is more than 80% within this band, and the antenna's average gain is 2 dBi with maximum efficiency of 88% and a maximum gain of 2.95 dBi. The slots inside the patch modify the direction of the current flow and lessen the patch's dimension49 or help to improve the impedance bandwidth50. The effects of various slots on resonance phenomena surface current analysis can be done for two different frequencies of resonances at 2.6 GHz and 3.77 GHz. Figure 15 shows the current distribution at the patch and ground side of the antenna. As expressed in Fig. 15a, it is noticed that current is more concentrated near the vertical edges of the patch and edges of the inner slots. Larger current path due to inner slot helps to increase the effective inductive reactance. Thus, it causes to obtain the resonance frequency at 2.6 GHz. On the other hand, a study of ground side current (in Fig. 15a) for this frequency of resonance shows that parasitic elements have a high concentration of currents. In contrast, the ground plane offers a lower dense current. Unlikely, as shown in Fig. 15b, at 3.77 GHz, patch current is mainly concentrated at the vertical edges of the patch, whereas surrounding the inner slot, the current is drastically reduced compared to the current of earlier resonance. Due to the reduced current path, the inductance associated with the patch is lessened, which ultimately affects the resonance at this frequency. A closer look at the ground plane current (in Fig. 15b) shows that current density at both parasitic elements is significantly higher compared with the current through the same elements at 2.6 GHz. A high-intensity current is noticed in the ground plane at the top horizontal edges and through slots in the ground plane. Moreover, all over the ground plane, the current density is high as compared to the current flowing through the ground at 2.6 GHz. Thus, it can be concluded that the current surrounding the inner slot of the patch contributes significantly to the resonance at 2.6 GHz. In contrast, resonance at 3.77 GHz is mainly governed by the current flowing through the backplane slots.
(a) Front view of the antenna (b) back view (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
Surface current distributions at patch and ground side at (a) 2.60 GHz and (b) 3.77 GHz (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
Gain enhancement of antenna using MTM superstrate with antenna
A metamaterial array is introduced, having a 4 × 4 array with the overall dimension of 41 mm × 40 mm to use it as a superstrate. This array element provides the same area of the designed antenna that covers the total surface of the antenna. Thus, it interacts with the most emitted radiation of the antenna, which ultimately helps to improve the gain of the antenna. Figure 16 shows the MTM with the antenna in which MTM array is placed as superstrate at the ground side of the antenna at spacing of 30 mm. The space is selected by parametric study targeting that position of MTM array will not affect the bandwidth of the antenna much rather it will increase the gain. Figure 17 shows the parametric study for various distances between antenna and MTM cover. The S11 response of the antenna showed in Fig. 17a for different distances between antenna and MTM. As shown in Fig. 17a, the antenna shows dual-band resonances when h = 10 mm for the low distance. As the value of h increases, lower band resonance frequency seems to maintain a constant value with increasing magnitude with distance. But in the case of the upper band, magnitude and resonance frequency shift with increasing the distance. As the distance increases, the upper band resonance frequency decreases gradually with the increasing distance. Eventually, two different bands come closer and combine, and a wideband response is perceived when h = 30 mm or higher. A comparison of antenna gain with MTM for different values of h is made, and the gain plots are depicted in Fig. 17b. As expressed in Fig. 17b, high gain is observed when the distance between the antenna and MTM is low and decreases gradually with the increasing distance. It is because when the distance between the antenna and MTM is low, most of the radiated field impinges on the MTM. Thus more directional radiation is obtained due to the near zero property of the MTM. As the distance increases, more radiated field propagates through the free space and thus, MTM faces less radiation to make its direction, resulting in a decreased gain. Therefore, from this parametric analysis, an optimum distance of 30 mm is considered that provides a considerable bandwidth extended from 2.5 to 3.96 GHz with a moderate amount of enhanced gain. A comparison of S11 of the antenna with and without MTM is presented in Fig. 18a. It is observed that bandwidth is decreased for the antenna with MTM with a downward shift of upper cutoff frequency. It can be explained by using the impedance matching of the equivalent circuit of the antenna as impedance, Z and frequency, f of resonance can be expressed51 as, \(Z=\frac{1}{j\omega C+1/1/j\omega L}\) and \(f=\frac{1}{2\pi \sqrt{L{C}}}\) respectively, in which L corresponds to total inductance and C is the capacitance. Introducing the MTM with antenna causes a modification of the total capacitance, thus resonance frequency shifts. As the distance between antenna and MTM is low, MTM causes the reduction of the total capacitance of the antenna equivalent circuit, which eventually causes the higher resonance frequency, as shown in Fig. 17a. Contrarily, an increasing distance effects as changing resonances towards lower frequencies.
Antenna with MTM superstrate (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
A comparison of the gain for the antenna with and without MTM superstrate is shown in Fig. 18b that indicates a high gain with MTM superstrate. MTM cover provides a maximum gain of around 4.95 dBi, whereas bared antenna offers a maximum gain of around 2.5 dBi, indicating a gain enhancement by 95%. The gain enhancement can be explained with the help of the electric field (E) distribution in space and on the antenna. This distribution of the E fields at 3.77 GHz is presented in Fig. 19a,b, respectively. Figure 19a shows that electric field strength increases significantly surrounding the antenna when metamaterial is introduced. Moreover, when a radiated field is exposed over MTM, it emits radiation due to its NZI property which is normal to the surface of the MTM. Additionally, EM waves that incidents on the MTM contain a sideward E component that becomes more directional due to the NZI property, which added an extra field in a particular direction. Thus, antenna gain increases significantly. A comparison of the E field distribution over the antenna is shown in Fig. 19b. This figure shows a strong E field induced at the top of the antenna when MTM is used with the antenna. This strong E field is also the contributor to the gain enhancement. Thus, MTM superstrate causes to increase the directionality as well as radiated power that combinedly enhances the overall gain of the antenna. Figure 20a shows the 3D radiation pattern at 3.77 GHz for the antenna without MTM that is omnidirectional in nature. When MTM superstrate is used, the radiation pattern becomes directional as shown in Fig. 20b. The radiation is more concentrated in the Z direction, increasing the antenna's directional gain when MTM superstrate is used.
Electric field distribution at 3.77 GHz with and without MTM: (a) at XZ plane surrounding antenna, and (b) on the surface of antenna and MTM superstarte (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
3D radiation pattern at 3.77 GHz for: (a) antenna without MTM and (b) antenna with MTM superstarte (CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite)38.
The result obtained in the simulation is verified by fabricating the antenna and taking the measurement for S11 and gain. Figure 21a shows the front view of the antenna prototype, whereas Fig. 21b exhibits the back view. Morevoer, antenna with metamaterial superstrate arrangement is presented in Fig. 21c where 4 × 4 array of unit cells of the proposed MTM is seperated from the antenna using a 30 mm thick polystyrene block. The experimental arrangement for S11 is depicted in Fig. 22a, in which a vector network analyzer (VNA) is used for measuring this parameter. The measured values of the S11 for antenna with and without metamaterial is depicted in Fig. 23a in comparison with outcomes of simulation. From Fig. 23a, it is noticed that measured results of the antennas with and without metamaterail exhibits close similarity. The measured − 10 dB impedance bandwidth of the test antenna without MTM is exteded from 2.56 to 4.2 GHz with a resonance peak at 3.5 GHz having magnitude of − 17 dB. When MTM is used as the superstrate − 10 dB bandwidth is observed extending from 2.58 to 4.1 GHz with resonance peak of – 24 dB at 3.67 GHz. In both cases, the bandwidth is slightly less than the simulation result, but the deviations are less than 5%. This slight variation is associated with fabrication tolerances, calibration errors involved in VNA, and loss incurred in the cable connecting VNA and the antenna prototype. But neglecting these errors fabricated antenna provides good bandwidth when metamaterial superstrate is used. Figure 22b shows the Satimo nearfield measurement setup for the antenna with MTM superstrate to determine the performance parameters, including gain and radiation pattern. Corresponding gain data is plotted in Fig. 23b to compare measured gain with an antenna without MTM and simulation results. This result shows that measured antenna gain with and without metamaterial is slightly varied compared to the simulation result. This mismatching is due to fabrication tolerances of the antenna and calibration errors associated with the Satimo near field measurement system. Measured antenna gain is less compared compared to the simulated gain except the frequency range 3.2–3.8 GHz where the measured gain well above the simulated gain. But, comparing measured gain between antenna without metamaterail and antenna with metamaterial it is observed that metamaterial exhibits its dominant impact on the antenna and helps to boost up the antenna gain. Figures 24 and 25 display the measured 2D radiation pattern of the designed antenna and antenna with metamaterial array for E and H plane at 2.6 GHz and 3.76 GHz respectively. From Fig. 24, it can be stated that the radiation pattern shows an omnidirectional type for the antenna with low cross-polarization. On the otherhand, for antenna with metamaterial presented in Fig. 25, the pattren shows slightly directional towards + z directions with low cross polarizations due to gain enhancement by using metamaterial array.
The performance of the proposed antenna with MTM superstrate is compared with some other recently published MTM loaded antennas, and the comparison outcomes are presented in Table 5. From Table 5, it is observed that the antenna with MTM superstrate presented in Ref.52 provides a good maximum gain of 6.56 dBi with an operating resonance frequency at 2.4 GHz. But the overall dimension of the antenna system is large compared to our proposed antenna system. Moreover, the bandwidth of this antenna system is low compared, and metamaterial helps to increase the gain by 22.37%. As is viewed from this Table 5, Ref.53 shows a comparatively high gain with good percentage enhancement due to the MTM superstrate. But the overall dimension of the MTM array and antenna is high, and this gain is achieved by using four layers of MTM superstrates. Moreover, this antenna operates at a high frequency with a comparatively low bandwidth. In Ref.54, the triangular-shaped antenna array is used for two ports MIMO system that exhibits the highest gain of 14.05 dBi. But, this high gain is due to an antenna structure of large size. In this antenna system, a comparatively low gain enhancement is acquired when MTM array is used as a superstrate. Contrary to this, the dimension of the antenna system presented in Ref.55 exhibits lower dimension, moderate antenna gain, with good gain enhancement due to MTM superstrate. But the high gain within the lower dimension is achieved by using two layers of superstrate. Thus, comparing these antenna systems with MTM superstrate, our proposed MTM provides good gain enhancement within its small dimension with a broader bandwidth. Thus, the proposed MTM can be used for developing compact-sized high gain broadband antenna system. The antenna presented in this article exhibits − 10 dB S11 response from 2.58 to 4.1 GHz having a bandwidth of 1.52 GHz. With MTM superstrate, it exhibits maximum gain of 5.5 dBi. This broadband compact high gain antenna can be used for broadband wireless applications like microwave based energy harvesting from WiMAX, WLAN or from sub-6 GHz 5G sources.
Conclusion
This paper presents a metamaterial consisting of a resonator patch of a symmetric split ring resonator coupling around the split gaps. This proposed MTM provides three resonances at 2.78 GHz, 7.7 GHz, and 10.16 GHz covering S, C, and X-bands. Due to symmetric structure, mutual coupling between the array elements is reduced, and the array shows a similar S21 response of the unit cell. The simulated result is evaluated with the experiment, and the measured result is well matched with the simulation. The equivalent circuit of the MTM is modeled in ADS and validated by comparing the S21 response with CST that provides close similarity. The MTM characteristics are also analyzed that show negative permittivity, near zero permeability, and refractive index. The contribution of the different parts of the MTM unit cell in resonance is also studied through the electric field, magnetic field and surface current analysis. The calculated EMR value of 10.7 indicates the compactness of the proposed MTM for application in various small microwave devices. A test antenna having − 10 dB bandwidth of S11 extending from 2.5 to 3.95 GHz with maximum gain around 2.5 dBi is designed, and MTM influence is observed by using a 4 × 4 array of MTM as superstrate. MTM superstrate over the test antenna provides a maximum gain of 4.95 dBi with an increment by 95% when the distance between antenna and MTM is 30 mm. NZI property of the proposed ENG metamaterial increases the directionality of the radiation in the XZ plane, which is studied through E field and radiation pattern analysis. The antenna gain enhancement is validated by measuring the performance of the antenna with and without metamaterials. Due to its compactness with high EMR, negative permittivity, near zero permeability and refractive index, proposed MTM can be utilized with various wireless devices in microwave applications, especially to enhance gain and directivity of the antenna.
References
Shabbir, T. et al. 16-port non-planar MIMO antenna system with near-zero-index (NZI) metamaterial decoupling structure for 5G applications. IEEE Access 8, 157946–157958 (2020).
Hussain, N., Jeong, M.-J., Abbas, A., Kim, T.-J. & Kim, N. A metasurface-based low-profile wideband circularly polarized patch antenna for 5G millimeter-wave systems. IEEE Access 8, 22127–22135 (2020).
Iyer, A. K., Alù, A. & Epstein, A. Metamaterials and metasurfaces—Historical context, recent advances, and future directions. IEEE Trans. Antennas Propag. 68, 1223–1231 (2020).
Il Kwak, S., Sim, D.-U., Kwon, J. H. & Yoon, Y. J. Design of PIFA with metamaterials for body-SAR reduction in wearable applications. IEEE Trans. Electromagn. Compat. 59, 297–300 (2016).
Wang, M. et al. Investigation of SAR reduction using flexible antenna with metamaterial structure in wireless body area network. IEEE Trans. Antennas Propag. 66, 3076–3086 (2018).
Moniruzzaman, M., Islam, M. T., Muhammad, G., Singh, M. S. J. & Samsuzzaman, M. Quad band metamaterial absorber based on asymmetric circular split ring resonator for multiband microwave applications. Results Phys. 19, 103467 (2020).
Wang, B.-X., He, Y., Lou, P. & Zhu, H. Multi-band terahertz superabsorbers based on perforated square-patch metamaterials. Nanoscale Adv. 3, 455–462 (2021).
Loh, L. Y. W. et al. 3D printed metamaterial capacitive sensing array for universal jamming gripper and human joint wearables. Adv. Eng. Mater. 23, 2001082 (2021).
Liu, W. et al. Suspended silicon waveguide platform with subwavelength grating metamaterial cladding for long-wave infrared sensing applications. Nanophotonics 10, 1861–1870 (2021).
Rammyaa, B. & Vishvaksenan, K. CPW fed metamaterial loaded dual-band roof-top antenna for vehicular communications. Int. J. RF Microw. Comput. Aided Eng. 31, e22740 (2021).
Sumathi, K., Lavadiya, S., Yin, P., Parmar, J. & Patel, S. K. High gain multiband and frequency reconfigurable metamaterial superstrate microstrip patch antenna for C/X/Ku-band wireless network applications. Wirel. Netw. 27, 2131–2146 (2021).
Wang, Z., Duan, G. & Duan, H. Optimization of the perfect absorber for solar energy harvesting based on the cone-like nanostructures. AIMS Energy 9, 714–726 (2021).
Hossain, I. et al. Polarization-independent broadband optical regime metamaterial absorber for solar harvesting: A numerical approach. Chin. J. Phys. 71, 699–715 (2021).
Mishra, R. K., Gupta, R. D. & Datar, S. Metamaterial microwave absorber (MMA) for electromagnetic interference (EMI) shielding in X-band. Plasmonics 16, 1–11 (2021).
Lu, C. et al. GRIN metamaterial generalized Luneburg lens for ultra-long acoustic jet. Appl. Phys. Lett. 118, 144103 (2021).
Sakli, H., Abdelhamid, C., Essid, C. & Sakli, N. Metamaterial-based antenna performance enhancement for MIMO system applications. IEEE Access 9, 38546–38556 (2021).
Moniruzzaman, M. et al. Inductively tuned modified split ring resonator based quad band epsilon negative (ENG) with near zero index (NZI) metamaterial for multiband antenna performance enhancement. Sci. Rep. 11, 1–29 (2021).
Das, S., Gupta, A. & Sahu, S. Metamaterial based fractal-ground loaded frequency-reconfigurable monopole-antenna with gain-bandwidth enhancement. AEU Int. J. Electron. Commun. 132, 153593 (2021).
Ke, Y.-H., Yang, L.-L., Zhu, Y.-Y., Wang, J. & Chen, J.-X. Filtering quasi-yagi strip-loaded DRR antenna with enhanced gain and selectivity by metamaterial. IEEE Access 9, 31755–31761 (2021).
Shaw, T. & Mitra, D. Design of highly directive slot antenna using metamaterial structure under optimal condition. Int. J. RF Microw. Comput. Aided Eng. 31, e22791 (2021).
Moussa, K. H., Amar, A. S., Mabrouk, M. & Mohamed, H. G. Slotted E-shaped meta-material decoupling slab for densely packed MIMO antenna arrays. Micromachines 12, 873 (2021).
Zhang, J., Li, J. & Chen, J. Mutual coupling reduction of a circularly polarized four-element antenna array using metamaterial absorber for unmanned vehicles. IEEE Access 7, 57469–57475 (2019).
Luo, S., Li, Y., Xia, Y. & Zhang, L. A low mutual coupling antenna array with gain enhancement using metamaterial loading and neutralization line structure. Appl. Comput. Electromagn. Soc. J. 34, 411–418 (2019).
Mishra, P., Pattnaik, S. S. & Dhaliwal, B. S. Square-shaped fractal antenna under metamaterial loaded condition for bandwidth enhancement. Prog. Electromagn. Res. C 78, 183–192 (2017).
Jabire, A. H. et al. Metamaterial based design of compact UWB/MIMO monopoles antenna with characteristic mode analysis. Appl. Sci. 11, 1542 (2021).
Ameen, M. & Chaudhary, R. Metamaterial circularly polarized antennas: Integrating an epsilon negative transmission line and single split ring-type resonator. IEEE Antennas Propag. Mag. 63, 60–77 (2020).
Ameen, M. & Chaudhary, R. Metamaterial-based wideband circularly polarised antenna with rotated V-shaped metasurface for small satellite applications. Electron. Lett. 55, 365–366 (2019).
Moniruzzaman, M. et al. Cross coupled interlinked split ring resonator based epsilon negative metamaterial with high effective medium ratio for multiband satellite and radar communications. Results Phys. 18, 103296 (2020).
Moniruzzaman, M., Islam, M. T., Islam, M. R., Misran, N. & Samsuzzaman, M. Coupled ring split ring resonator (CR-SRR) based epsilon negative metamaterial for multiband wireless communications with high effective medium ratio. Results Phys. 18, 103248 (2020).
Misran, N., Yusop, S. H., Islam, M. T. & Ismail, M. Y. Analysis of parameterization substrate thickness and permittivity for concentric split ring square reflectarray element. Jurnal Kejuruteraan J. Eng. 23, 11–16 (2012).
Zangeneh-Nejad, F., Sounas, D. L., Alù, A. & Fleury, R. Analogue computing with metamaterials. Nat. Rev. Mater. 6, 207–225 (2021).
Dalgaç, Ş et al. Chiral metamaterial-based sensor applications to determine quality of car lubrication oil. Trans. Inst. Meas. Control. 43, 1640–1649 (2021).
Qureshi, S. A. et al. Millimetre-wave metamaterial-based sensor for characterisation of cooking oils. Int. J. Antennas Propag. 2021, 1–10 (2021).
Lu, Z.-Q., Zhao, L., Ding, H. & Chen, L.-Q. A dual-functional metamaterial for integrated vibration isolation and energy harvesting. J. Sound Vib. 509, 116251 (2021).
Coskuner, E. & Garcia-Garcia, J. J. Metamaterial impedance matching network for ambient RF-energy harvesting operating at 2.4 GHz and 5 GHz. Electronics 10, 1196 (2021).
Ashyap, A. Y., Zainal Abidin, Z., Dahlan, S. H., Majid, H. A. & Saleh, G. Metamaterial inspired fabric antenna for wearable applications. Int. J. RF Microw. Comput. Aided Eng. 29, e21640 (2019).
Bait-Suwailam, M. M. Electromagnetic Fields and Waves (IntechOpen, 2019).
Systemes, D. CST STUDIO SUITE 2019, https://www.3ds.com/products-services/simulia/products/cst-studio-suite/?utm_source=cst.com&utm_medium=301&utm_campaign=cst. Accessed 29 Mar 2022.
Garg, R., Bhartia, P., Bahl, I. J. & Ittipiboon, A. Microstrip Antenna Design Handbook (Artech House, 2001).
Chen, X., Grzegorczyk, T. M., Wu, B.-I., Pacheco, J. Jr. & Kong, J. A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 70, 016608 (2004).
Khajeh-Khalili, F., Honarvar, M. A., Naser-Moghadasi, M. & Dolatshahi, M. Gain enhancement and mutual coupling reduction of multiple-intput multiple-output antenna for millimeter-wave applications using two types of novel metamaterial structures. Int. J. RF Microw. Comput. Aided Eng. 30, e22006 (2020).
Rosaline, I. A triple-band antenna with a metamaterial slab for gain enhancement and specific absorption rate (SAR) reduction. Prog. Electromagn. Res. C 109, 275–287 (2021).
Asif, M. et al. Design of a dual band SNG metamaterial based antenna for LTE 46/WLAN and Ka-band applications. IEEE Access 9, 71553–71562 (2021).
Rezapour, M., Rashed-Mohassel, J. A., Keshtkar, A. & Moghadasi, M.-N. Suppression of mutual coupling in rectangular dielectric resonator antenna arrays using Epsilon-Negative metamaterials (ENG). J. Electromagn. Waves Appl. 33, 1211–1223 (2019).
Gao, B., Yuen, M. M. & Ye, T. T. Flexible frequency selective metamaterials for microwave applications. Sci. Rep. 7, 1–7 (2017).
Hoque, A. et al. A polarization independent quasi-TEM metamaterial absorber for x and ku band sensing applications. Sensors 18, 4209 (2018).
Sabah, C. & Nesimoglu, T. Design and characterization of a resonator-based metamaterial and its sensor application using microstrip technology. Opt. Eng. 55, 027107 (2016).
Alharbi, K. H. et al. Ultra-wideband monopole antenna with U and L shaped slotted patch for applications in 5G and short distance wireless communications. Int. J. Appl. Electromagn. Mech. 66, 1–22 (2021).
Kossiavas, G., Papiernik, A., Boisset, J. & Sauvan, M. The C-patch: A small microstrip element. Electron. Lett. 25, 253–254 (1989).
Huynh, T. & Lee, K.-F. Single-layer single-patch wideband microstrip antenna. Electron. Lett. 31, 1310–1312 (1995).
Guo, Y., Zhao, J., Hou, Q. & Zhao, X. Broadband omnidirectional patch antenna with horizontal gain enhanced by near-zero-index metamaterial cover. IET Microw. Antennas Propag. 14, 671–676 (2020).
Saravanan, M. & Umarani, S. Gain enhancement of patch antenna integrated with metamaterial inspired superstrate. J. Electr. Syst. Inf. Technol. 5, 263–270 (2018).
Borazjani, O., Naser-Moghadasi, M., Rashed-Mohassel, J. & Sadeghzadeh, R. Design and fabrication of a new high gain multilayer negative refractive index metamaterial antenna for X-band applications. Int. J. RF Microw. Comput. Aided Eng. 30, e22284 (2020).
Ojo, R. et al. A triangular MIMO array antenna with a double negative metamaterial superstrate to enhance bandwidth and gain. Int. J. RF Microw. Comput. Aided Eng. 30, e22320 (2020).
Ameen, M. & Chaudhary, R. K. Multilayered and low-volume cavity resonator antenna using metasurface reflector and superstrate for airborne application. Trans. Indian Natl. Acad. Eng. 6, 491–506 (2021).
Funding
This work was supported by the Universiti Kebangsaan Malaysia, Malaysia research grant code DIP-2021-027. This work was also supported by Taif University Researchers Supporting Project number (TURSP-2020/206), Taif University, Taif, Kingdom of Saud Arabia.
Author information
Authors and Affiliations
Contributions
Conceptualization, M.M., M.S. and M.T.I.; data curation, M.M., S.H.A.A.. N.M.S. and M.S.M.; formal analysis. M.M., M.S.I. and M.T.I.; funding acquisition, H.A., M.S.S., M.S.I. and M.T.I.; investigation, M.M., N.M.S., S.S.A. and M.T.I.; methodology, M.M., M.S., and M.S.M.; visualization, S.H.A.A., H.A. and M.T.I.; writing—original draft, M.M., M.S. and M.T.I.; writing—review and editing, M.M., M.S., H.A., N.M.S., M.S.I. and M.T.I.; software and resources, M.T.I.; supervision, M.T.I.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moniruzzaman, M., Islam, M.T., Samsuzzaman, M. et al. Gap coupled symmetric split ring resonator based near zero index ENG metamaterial for gain improvement of monopole antenna. Sci Rep 12, 7406 (2022). https://doi.org/10.1038/s41598-022-11029-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-11029-7
This article is cited by
-
Compact metamaterial-based single/double-negative/near-zero index resonator for 5G sub-6 GHz wireless applications
Scientific Reports (2024)
-
Machine learning-based technique for gain and resonance prediction of mid band 5G Yagi antenna
Scientific Reports (2023)
-
H-shaped modifiers loaded mirror symmetric resonator based double negative metamaterial for multi-band wireless communications
Scientific Reports (2023)
-
Electromagnetic characterization of mirror symmetric resonator based metamaterial and frequency tuning: a dielectric based multilayer approach
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.