Abstract
We present a particle-in-cell (PIC) analysis of terahertz (THz) radiation by ultrafast plasma currents driven by relativistic-intensity laser pulses. We show that, while the I0 \({\lambda }_{0}^{2}\) product of the laser intensity I0 and the laser wavelength λ0 plays the key role in the energy scaling of strong-field laser-plasma THz generation, the THz output energy, WTHz, does not follow the I0 \({\lambda }_{0}^{2}\) scaling. Its behavior as a function of I0 and λ0 is instead much more complex. Our two- and three-dimensional PIC analysis shows that, for moderate, subrelativistic and weakly relativistic fields, WTHz(I0 \({\lambda }_{0}^{2}\)) can be approximated as (I0λ02)α, with a suitable exponent α, as a clear signature of vacuum electron acceleration as a predominant physical mechanism whereby the energy of the laser driver is transferred to THz radiation. For strongly relativistic laser fields, on the other hand, WTHz(I0 \({\lambda }_{0}^{2}\)) closely follows the scaling dictated by the relativistic electron laser ponderomotive potential \({\mathscr{F}}_{{\text{e}}}\), converging to WTHz ∝ \({I}_{0}^{1/2}{\lambda }_{0}\) for very high I0, thus indicating the decisive role of relativistic ponderomotive charge acceleration as a mechanism behind laser-to-THz energy conversion. Analysis of the electron distribution function shows that the temperature Te of hot laser-driven electrons bouncing back and forth between the plasma boundaries displays the same behavior as a function of I0 and λ0, altering its scaling from (I0λ02)α to that of \({\mathscr{F}}_{{\text{e}}}\), converging to WTHz ∝ \({I}_{0}^{1/2}{\lambda }_{0}\) for very high I0. These findings provide a clear physical picture of THz generation in relativistic and subrelativistic laser plasmas, suggesting the THz yield WTHz resolved as a function of I0 and λ0 as a meaningful measurable that can serve as a probe for the temperature Te of hot electrons in a vast class of laser–plasma interactions. Specifically, the α exponent of the best (I0λ02)α fit of the THz yield suggests a meaningful probe that can help identify the dominant physical mechanisms whereby the energy of the laser field is converted to the energy of plasma electrons.
Similar content being viewed by others
Introduction
Terahertz (THz) radiation is a powerful resource for biomedical applications1,2,3, molecular spectroscopy3,4,5, remote sensing1,6, wireless communications7, and time-resolved studies of ultrafast charge-carrier dynamics in metals and semiconductors8,9,10,11,12,13. Ultrashort THz field waveforms help coherently control over the dynamics of spins14, molecular rotations9,15,16, vibrations of crystal lattices17, and evolution of free- and bound-state electron wave packets9,10,11,12,13,18. In strong-field ultrafast optics, THz generation provides means for particle acceleration19, laser-wakefield characterization20,21, external-field-assisted high-harmonic generation11,12,13,22, and electron bunch diagnostics at particle-accelerator, synchrotron, and free-electron laser (FEL) facilities23,24.
Strong-field optics not only lends a rapidly growing area for applications of THz photonics, but also provides powerful means for high-brightness THz generation, opening ways toward unprecedented levels of THz output energy25,26,27,28,29,30,31,32. Standing out as one of the most promising strong-field scenarios for high-yield THz generation is coherent transient radiation (CTR)—secondary radiation emitted by relativistic electrons traversing dielectric discontinuities33,34. Laser-driven CTR has been shown to provide a powerful source of THz radiation25,26,27,28,29,30,31,32,35,36, enabling the generation of terawatt-level ultrashort pulses of coherent THz radiation with field strengths at the level of 10 GV/m28,29 and pulse energies as high as tens of millijoules30,32.
Identifying the physical limits of this method of THz generation would provide a deeper understanding of the fundamental aspects of relativistic laser–plasma electrodynamics and would help answer an urgent call of optical science for the development of high-power THz sources. Specifically, the generic I0 \({\lambda }_{0}^{2}\) scaling of the kinetic energy that electrons tend to pick up from the driver field with intensity I0 and wavelength λ0 gives grounds to expect that longer-λ0 driver pulses, such as those available as an idler-wave output of high-peak power optical parametric chirped-pulse amplifiers (OPCPAs)37,38,39, could help enhance THz generation in relativistic laser–plasma settings. However, relativistic-intensity laser fields can give rise to a complex interplay of concurrent highly nonlinear motions of charged particles in a plasma target. This complex dynamics imprints itself onto a highly sophisticated picture of secondary radiation27,28,29,30,31,40,41,42,43,44, giving rise to long-wavelength radiation with widely different spatial, spectral, temporal and polarization properties. The intensity of THz emission in this complex laser–plasma interaction scenario depends on a variety of factors whose relevance to THz generation is sometimes difficult to assess and whose significance is often difficult to quantify. The actual behavior of the THz yield as a function of I0 and λ0 in such settings can significantly differ from the naïve I0 \({\lambda }_{0}^{2}\) expectation45,46,47,48. Many of the pressing questions related to the brightness scaling of relativistic laser-plasma THz sources, including the scaling of the THz yield as a function of I0 and λ0, remain to be answered.
Here, we seek to address these questions by resorting to a particle-in-cell (PIC) analysis of laser–plasma interaction dynamics driven by relativistic-intensity ultrashort laser pulses in a metal-film target. We show that, while the I0 \({\lambda }_{0}^{2}\) product of the laser intensity I0 and the laser wavelength λ0 plays the key role in the energy scaling of strong-field laser-plasma THz generation, the THz output energy, WTHz, does not follow the I0 \({\lambda }_{0}^{2}\) scaling. Its behavior as a function of I0 and λ0 is instead much more complex. Our two- and three-dimensional PIC analysis shows that, for moderate, subrelativistic and weakly relativistic fields, WTHz(I0 \({\lambda }_{0}^{2}\)) can be approximated as (I0λ02)α, with a suitable exponent α, as a clear signature of vacuum electron acceleration as a predominant physical mechanism whereby the energy of the laser driver is transferred to THz radiation. For strongly relativistic laser fields, on the other hand, WTHz(I0 \({\lambda }_{0}^{2}\)) closely follows the scaling dictated by the relativistic electron laser ponderomotive potential \({\mathscr{F}}_{{\text{e}}}\), converging to WTHz ∝ \({I}_{0}^{1/2}{\lambda }_{0}\) for very high I0, thus indicating the decisive role of relativistic ponderomotive charge acceleration as a mechanism behind laser-to-THz energy conversion. Analysis of the electron distribution function shows that the temperature Te of hot laser-driven electrons bouncing back and forth between the plasma boundaries displays the same behavior as a function of I0 and λ0, altering its scaling from (I0λ02)α to that of \({\mathscr{F}}_{{\text{e}}}\), converging to WTHz ∝ \({I}_{0}^{1/2}{\lambda }_{0}\) for very high I0. These findings provide a clear physical picture of THz generation in relativistic and subrelativistic laser plasmas, suggesting the THz yield WTHz resolved as a function of I0 and λ0 as a meaningful measurable that can serve as a probe for the temperature Te of hot electrons in a vast class of laser–plasma interactions. Specifically, the α exponent of the best (I0λ02)α fit of the THz yield suggests a meaningful probe that can help identify the dominant physical mechanisms whereby the energy of the laser field is converted to the energy of plasma electrons.
The physical model and numerical setting
We consider a high-intensity laser pulse with a central wavelength λ0 that drives a plasma slab (Fig. 1a, b) with a width lx = 16λ0, a variable depth ly, and initial electron density n0 = 4nc, where nc = meω02/(4πe2) is the critical plasma density, ω0 = 2πc/λ0 is the central frequency of the laser driver, c is the speed of light in vacuum, me and e are the electron mass and charge. The initial electron velocity distribution inside the plasma slab is Maxwellian with an electron temperature of 230 eV. Such parameters are representative of plasmas generated on thin solid targets by high-intensity ultrashort laser pulses40,49,50,51.
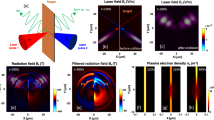
(a–j) Spatial distributions of (a–e) the overall field \({\mathscr{B}}\)z(x, y) and (f–j) the THz-filtered field \({B}\)z(x, y) and (k–o) electron y–py phase-space distributions f(y, py) for a plasma slab with ly = 4λ0 driven by a p-polarized field with a0 = 1 and τ0 = 80 fs at t = 0 (a, f, k), 15T0 (b, g, l), 30T0 (c, h, m), 40T0 (d, i, n), and 50T0 (e, j, o).
We simulate the solutions to the Maxwell–Vlasov equations for this laser–plasma interaction setting40,52 using a 2D Smilei PIC code53. The solutions to the Maxwell equations are computed in this code with the finite-difference time-domain method in a two-dimensional configuration space and three-dimensional momentum space (2D3V) with the electromagnetic field discretized on a Yee grid with space steps Δx = Δy = λ0/128 along the x and y coordinates chosen, respectively, within the plane of the target and along the normal to this plane. Each grid cell contains 49 electrons and 49 protons, totaling to over 107 particles of each sort within the entire simulation domain. Time derivatives in the Maxwell equations were computed on a time grid with a step Δt = T0/256, T0 being the driver field cycle.
The driver field in our simulations is taken in the form of an ultrashort Gaussian pulse with a pulse width τ0, an electric field amplitude E0, central frequency ω0, and variable polarization. The laser beam makes an angle φ0 = 450 with the normal to the plasma surface (Fig. 1a, b) and is focused into a beam waist with a diameter d0 = 4λ0 on the plasma surface. Providing a meaningful quantifier of the significance of relativistic effects in this laser–plasma interaction setting is the normalized vector potential a0 = eE0/(meω0c), which can be viewed as a ratio of the velocity v0 = eE0/(meω0) of nonrelativistic laser-driven electron quiver motion to the speed of light. The driver field is injected into the simulation domain via the Silver–Müller-type boundary conditions. PIC simulations were performed using graphic-processor-unit laboratory clusters54, as well as a shared research facility of high-performance supercomputing resources at M.V. Lomonosov Moscow State University55.
THz supercontinua and high-harmonic radiation
As it drives the plasma target, the laser field gives rise to intense radial waves of secondary emission (Fig. 1a–j). The low-frequency part of this radiation field (Ex, Ey, Bz) is isolated in our calculations by applying a super-Gaussian filter \({\mathscr{F}}_{{\text{e}}}\)(ω) = exp[− (ω/ωc)q] to the total, driver + secondary radiation field (\({\mathscr{E}}\)x, \({\mathscr{E}}\)y, \({\mathscr{B}}\)z) as shown in Fig. 1a–e. We set q = 12 and ωc = ω0/4 in calculations presented here to provide a steep passband edge at νc = ωc/(2π) ≈ 20 THz. Fully capturing the field structure of low-ω secondary radiation in 2D3V simulations is the Bz field component, whose xy-plane maps are shown in Fig. 1f–j.
As the high-intensity laser pulse reaches the plasma surface at around t ≈ 15T0 (Fig. 1b), the laser field starts to drive plasma electrons, modulating the electron density ne(x, y, t) inside the plasma and giving rise to signature ripples on the front surface of the plasma target (Fig. 2a). The ponderomotive force induced by the laser pulse drives electron oscillations, making plasma electrons bounce back and forth between the plasma boundaries. In Fig. 2a, b, we follow several oscillatory electron y(t) traces that start at different (y, t) space–time points at the center of the plasma target, x = 0. Shown against the map of the electron density, ne(x = 0, y, t), these traces illustrate how the amplitude of electron oscillations tends to grow as the electrons pick more energy toward the trailing edge of the pulse, following a similar behavior of the amplitude of the ripples in ne(x = 0, y, t).
Oscillatory electron y(t) traces that start at different (y, t) space–time points, (–0.05λ0, 7.8T0), (–0.06λ0, 8.9T0), (–0.02λ0, 8.9T0), (–0.09λ0, 10.7T0), (–0.03λ0, 10.8T0), and (–0.07λ0, 13.0T0), at the center of the plasma target, x = 0, against the map of the electron density, ne(x = 0, y, t) for a0 = 1 and ly = 4λ0.
Each time the laser-driven electrons leave or re-enter the plasma target as a part of their oscillatory motion (e.g., at around t/T0 ≈ 21 and 30 in Fig. 2b), they emit ultrashort bursts of secondary radiation (Fig. 1h–j), giving rise to bright THz supercontinua along with an intense short-wavelength output, dominated by high-order harmonics (HH) of the driver. To calculate the spectrum of this radiation, we choose to work in polar coordinates r and θ, such that x = rcosθ and y = rsinθ, fix r at r = 30λ0, and integrate over the r = 30λ0, y > 0 semi-circumference, S(ω) = \({\int }_{0}^{\pi }|F\)[Q(t, r = 30λ0, θ)]|2dθ, where F[∙] is the Fourier transform and Q(t, r, θ) = \({\mathscr{B}}\)z(t, r, θ) and \({\mathscr{E}}\)z(t, r, θ) for p- and s-polarized field, respectively. The spectrum S(ω) spans the entire THz, infrared, and visible regions, extending deep into the ultraviolet range. In the spatial maps of the THz-filtered field Bz(x, y) (Fig. 1f–j), this process shows up as the first wave of THz radiation, whose emission starts as soon as the driver pulse strikes the plasma surface (cf. Fig. 1b, c, g, h).
Presented in Fig. 3a, b are the temporal traces of specular-reflected THz radiation (blue line) and the overall, THz + HH field (green line) whose xy-plane snapshots are shown in Fig. 3e, g. The troughs of the first-wave bursts of THz radiation (blue line) are highlighted in these traces with pink arrows. As can be seen from these traces and the spatial field structure, emission of the first THz burst is accompanied by HH generation (HHG). The HH field is emitted in the form of a train of attosecond pulses, tightly confined to the central, most intense part of the laser pulse. Polarization properties of the HH field are in full obedience to the selection rules for relativistic HHG40,56—a p-polarized driver generates p-polarized even- and odd-order HHs; an s-polarized driver gives rise to s-polarized odd HHs and p-polarized even harmonics, and a circularly polarized driver generates even and odd harmonics in both p and s polarization states.
(a, b) Temporal traces of specular-reflected THz radiation (blue line) and the overall, THz + HH field (green line), (c, d) spectra of specular-reflected THz radiation, and (e–g) the snapshots of the spatial distribution of the THz-filtered field Bz(x, y) taken at t = 50T0 (e, f) and 65T0 (g) for a plasma slab with ly = 4λ0 (a, c, e, f) and 6λ0 (b, d, g) driven by a p-polarized laser pulse with a0 = 1 and τ0 = 80 fs in (a–e, g) a full PIC simulation and (f) PIC simulation where electron recirculation is suppressed by halting all the electrons reaching the rear plasma boundary. Shown with arrows in the temporal traces are the instantaneous THz + HH bursts of secondary radiation (pink arrows) and recurring CTR waves (blue arrows).
Subcycle CTR waves
The spectral properties and the spatiotemporal structure of broadband radiation in Figs. 1, 2 and 3 are understood in terms of a physical scenario that combines CTR by electrons traversing the plasma boundary23,24,25,26,27,28,30,31 with HHG by laser-driven relativistic electrons near the front plasma surface32,37,38,39. In this study, we focus on the THz part of broadband radiation emitted as a part of this complex laser–plasma interaction scenario. Central to THz generation is the ponderomotive force induced by the laser driver, which accelerates plasma electrons, making them move toward the rear surface of the plasma slab. While the laser-driven oscillatory motion of relativistic electrons near the plasma surface gives rise to attosecond pulses of HH radiation, the ponderomotive force induced by the laser driver accelerates plasma electrons, making them move toward the rear surface of the plasma slab. This process is readily discernible in the electron y − py phase-space distribution f(y, py) as shown in Fig. 1k–o for a0 = 1. Specifically, at t ≈ 15T0 (Fig. 1l), some of the electrons near the front surface of the plasma slab at y = 0 are seen to start gaining momentum from the laser driver (marked with an arrow in Fig. 1l), which has just reached the y = 0 plasma surface. Because the laser ponderomotive force pushes electrons toward the inside of the plasma slab, i.e., toward negative y, the momentum gained by the electrons in Fig. 1l is negative. Accordingly, at later t, the electrons that have picked up their momentum from the laser driver are found deeper within the plasma target (Fig. 1m), with their energy further increased via the action of the laser ponderomotive force.
Near the rear surface of the plasma slab, however, the electrostatic sheath field gradually decelerates and eventually reflects some of these electrons, preventing them from leaving the plasma slab. This effect is readily visible in Fig. 1m, where electrons with positive py appear near the rear surface of the plasma slab at y = −4λ0 and move toward its front side, in accordance with the positive sign of py, building up their momentum and gaining their kinetic energy in the process of this motion (the arrow in Fig. 1m). By the time these electrons reach the front surface of the plasma target at y = 0, the energy of some of these electrons is high enough to overcome the binding forces that tend to keep the electrons within the plasma. When such electrons cross the plasma boundary, they emit an outgoing radial CTR wave, clearly visible in Fig. 1i, j. The electrons whose energy is not sufficient to make it to the other side of the plasma boundary are reflected, once again, to continue their circulation within the plasma (the arrow in Fig. 1n). Such recirculating electrons give rise to recurring subcycle bursts of THz radiation in the y > 0 semi-space (highlighted with blue arrows in Fig. 3a, b) each time they approach the y = 0 plasma boundary with a sufficiently high kinetic energy.
The spatiotemporal structure of the THz field (Figs. 1f–j, 3a, b, e, g) is fully consistent with this picture of THz generation. While the first burst of THz radiation is generated as soon as the driver pulse strikes the plasma surface (cf. Figure 1b, g), the highest intensity of THz radiation in the direction of specular reflection is achieved not within, but in the wake of the laser pulse, at the trough of the first radial subcycle CTR wave (Fig. 1i, j), emitted at t1 ≈ 0.70 ps (blue arrow in Fig. 3a), as a completion of the first cycle of electron recirculation within the plasma target driven by a laser pulse with λ0 = 3.9 μm. This first burst of CTR is followed by a second CTR wave, which is observed as a well-resolved subcycle waveform in the temporal trace of the THz field in Fig. 3a with a trough at t2 ≈ 0.88 ps. As can be seen in the spatial maps of Bz(x, y) in Figs. 1j and 3e, this trough is separated by Δr ≈ 17.5λ0 from the trough of the first CTR wave. When the thickness of the plasma slab is increased by a factor of 1.5, both the spatial separation Δr between the troughs of the first and second CTR waves (Figs. 3e, 3g) and the delay time δt = t2 − t1 between these troughs in the temporal trace of the THz field (Fig. 3a, b) increase by a factor of ≈1.5.
Because THz CTR waves are emitted within time intervals when laser-driven electrons traverse plasma boundaries, the visibility of the spatial crest-and-trough structure of the THz output is sensitive to the sharpness of the plasma boundaries. To quantify this effect, Fig. 4a–d present the spatial maps of the THz radiation field calculated for a plasma slab with the initial electron density profile defined as ne(x, y, t = 0) = n0 for − 4λ0 ≤ y ≤ 0 and ne(x, y, t = 0) = n0 exp(− y/L) for y ≥ 0 (Fig. 4a). As the extension of the plasma transition layer L (plasma gradient length scale) increases from L = 0 to L = λ0/20, the essential features in the crest-and-trough structure of the THz output show little to no variation. This suggests a rather comfortable margin of L within which simulations performed within the approximation of infinitely sharp plasma boundaries continue to provide an adequate physical picture of THz radiation. While for gas targets, steep plasma profiles with L ≤ λ0/20 are hard to achieve, in laser–plasma experiments with solid targets, plasma density profiles with L ≤ λ0/100 have been repeatedly demonstrated57,58,59 and even plasma gradients as steep as L ≈ λ0/200 have been achieved60.
(a) Electron density profiles used in simulations. (b–d) The spatial distribution of the THz-filtered field Bz(x, y) at t = 40T0 for (g, h) and 65T0 (i) for a plasma slab with L = 0 (b), λ0/50 (c), and λ0/20 (d) driven by a p-polarized laser pulse with τ0 = 80 fs, λ0 = 3.9 μm, and a0 = 1. (e) THz output intensity as a function of the plasma depth ly for a p-polarized laser driver with τ0 = 80 fs, λ0 = 3.9 μm, and a0 = 1.
In the frequency domain, the recurring bursts of THz radiation manifest themselves as clearly resolved fringes in the spectrum of THz radiation (Fig. 3c, d). Unlike the field intensity of the THz laser-plasma output, which is found, in close agreement with earlier studies31, to be a very weak function of the plasma depth ly (Fig. 4e), the spacing between the fringes in THz spectra is defined by the time interval δt between the CTR bursts, or the separation Δr between the CTR waves, Δν = c/Δr, and is therefore highly sensitive to ly. Specifically, for a plasma target with ly = 4λ0, the CTR waves are separated by Δr ≈ 17.5λ0, giving rise to fringes with Δν ≈ 4.4 THz in the spectrum of THz radiation (Fig. 3c). As ly is increased up to 6λ0, the spacing between the fringes in the THz spectrum decreases by a factor of ≈1.5, becoming Δν ≈ 3.0 THz (Fig. 3d).
As a useful verification of the role of recirculating electron currents for THz generation, we performed a series of PIC simulations in which electron recirculation was suppressed by artificially halting all the electrons reaching the rear plasma boundary. Any artificial THz emission that such a halting of electrons may cause does not disturb the THz field outside the plasma, because the plasma, whose plasma frequency is in the 100-THz range in this regime, totally screens such artificial radiation. Specifically, with all the electrons reaching y = −4λ0 brought to a halt, the most intense component of THz radiation, as is readily seen from a comparison of Fig. 3e, f, is completely suppressed.
The I 0 λ 0 2 scalability of the THz output and the electron energy distribution function
We now focus on the behavior of the THz yield in the considered laser–plasma setting as a function of the driver wavelength λ0 and field intensity I0. To this end, we set a detection point at ξ = 30λ0 along the ξ-axis in the direction of specular reflection (Fig. 1a, b, f) and define the field intensity as ITHz = [c/(2μ0)][B0(ξ = 30λ0)]2, where B0 is the peak Bz field at the trough of the first CTR wave (blue arrows in Fig. 3a, b) and μ0 is the magnetic permeability. In Fig. 5a, the THz intensity ITHz is plotted as a function of the driver field intensity I0 for two values of the driver wavelength, representing two types of relativistic-intensity short-pulse laser sources—Ti: sapphire lasers, λ0 = 0.8 μm61,62, and high-peak-power mid-infrared OPCPAs, λ0 = 3.9 μm63,64,65. Simulations here are performed for a laser driver with a pulse width τ0 = 80 fs and a beam-waist diameter d0 = 4λ0. The laser slab in these simulations has an initial electron density n0 = 4nc, a width lx = 16λ0, and a depth ly = 4λ0. The laser and plasma parameters τ0, d0, n0, lx, and ly are thus defined in such a way that they change with the driver wavelength λ0. Specifically, the pulse width τ0 = 80 fs corresponds to ≈ 30 field cycles for a laser driver with λ0 = 0.8 μm and ≈ 6 field cycles for a λ0 = 3.9 μm driver.
(a) The field strength (right axis) and field intensity (left axis) of THz radiation at ξ = 30λ0 as a function of the driver field intensity I0 for a p-polarized (green and blue boxes) and s-polarized (purple triangles) laser driver with τ0 = 80 fs and λ0 = 0.8 μm (green circles) and λ0 = 3.9 μm (blue boxes and purple triangles). Also shown is the ∝ Φ(I0λ02) scaling, as dictated by the relativistic electron laser ponderomotive potential \({\mathscr{F}}_{{\text{e}}}\) for λ0 = 0.8 μm (green dotted lines) and λ0 = 3.9 μm (blue and purple dotted lines). (b) Energy distribution function of the recirculating electrons at the moment of time when these electrons reach the y = 0 plasma boundary versus the best Maxwellian fits of their high-energy tails (pink lines) for I0λ02 increasing from top to bottom: I0λ02 = 1.4 × 1018 W μm2/cm2 (blue curve), 2.2 × 1019 W μm2/cm2 (wine curve), 8.8 × 1019 W μm2/cm2 (green curve), and 1.4 × 1020 W μm2/cm2 (grey curve). (c) The field intensity of THz radiation at ξ = 30λ0 (left axis, blue filled circles) and the temperature of CTR-emitting electrons Te (right axis, red open circles) as a function of I0λ02. Also shown are the ∝ Φ(I0λ02) scaling (blue dotted line) and the best (I0λ02)α fit for Te(I0λ02) with α = 1.2 (green dash–dotted line) and 1/2 (purple dash–dotted line). Shown by dashed vertical lines are the driver intensities I0 (a) and the I0λ02 product (c) corresponding to a0 = 1. Simulations are performed for a laser driver with two central wavelengths (λ0 = 0.8 and 3.9 μm), a pulse width τ0 = 80 fs, and a beam-waist diameter d0 = 4λ0. The laser slab has an initial electron density n0 = 4nc, a width lx = 16λ0, and a depth ly = 4λ0.
For both driver wavelengths, the growth of the THz intensity as a function of I0 is seen to significantly slow down as the driver field intensity approaches the a0 = 1 relativistic borderline (the vertical dashed lines in Fig. 5a). Simulations performed within the range of laser pulse widths τ0 from 30 to 250 fs, initial electron densities n0 from 4 to 80nc, and plasma slab depths ly from 0.8λ0 to 15λ0 show that, when varied within these ranges, neither of these parameters has any significant effect on the behavior of ITHz as a function of I0 and λ0 (Fig. 4e). In agreement with earlier studies66,67, an increase in n0 was found to give rise to a growth of computational noise.
To gain insights into this behavior of ITHz(I0), we resort to the analysis of the energy distribution function of the recirculating electrons at the moment of time when these electrons reach the y = 0 plasma boundary. In Fig. 5b, we present such energy distribution functions for I0λ02 ranging from 1.4 × 1018 W μm2/cm2 (a0 ≈ 1) to 1.4 × 1020 W μm2/cm2 (a0 ≈ 10). We then define the temperature of CTR-emitting electrons, Te, by fitting the high-energy tails of these functions with Maxwellian distribution functions (shown by the pink lines in Fig. 5b). Remarkably, in the limit of a0 > 1, the temperature Te obtained via such a procedure tends to follow the same scaling as a function of I0λ02 as the THz intensity ITHz (cf. blue filled circles and red open circles in Fig. 5c). Moreover, both ITHz(I0λ02) and Te(I0λ02) are seen to converge in the high-a0 limit to the scaling of Φ(I0λ02) = \({\mathscr{F}}_{{\text{e}}}\)/(mec2) (dotted line in Fig. 5a, c), as dictated by the laser pondermotive potential \({\mathscr{F}}_{{\text{e}}}\) = mec2(γ − 1) of a relativistic electron with rest energy mec2 and relativistic Lorentz factor γ.
To relate these tendencies in the behavior of the THz intensity to the physical picture of THz generation, we search for the best (I0λ02)α fit for Te(I0λ02), allowing α to take different values below and above the a0 = 1 relativistic borderline. As shown in earlier studies66,67,68,69,70, for high, yet nonrelativistic driver intensities, with a0 ≤ 1 or a0 ~ 1, the temperature of hot electrons, Te, tends to scale as (I0λ02)α, with α depending on the plasma gradient scale length and the incidence angle of the laser beam, varying from its lower bound at 1/3 to α > 1 in the case of laser vacuum heating68,69. However, for driver intensities well above the relativistic borderline of a0 = 1, the energy of laser radiation is absorbed predominantly via a ponderomotive acceleration of electrons, leading to a Te ∝ (I0λ02)1/2 scaling69,70. The α exponent is thus a meaningful probe that can help identify the physical scenario whereby THz radiation is generated as a part of ultrafast laser–plasma electrodynamics.
In Fig. 5c, we plot the intensity of THz radiation as a function of I0λ02 along with two best (I0λ02)α fits for the a0 ~ 1 and a0 > > 1 regimes. That the best (I0λ02)α fit for ITHz(I0λ02) near the a0 = 1 borderline (shown by dashed vertical lines in Fig. 5a, c) regime is achieved with α = 1.2 (green dash–dotted line) is indicative of the predominance of laser vacuum heating as a mechanism of laser electron acceleration in our laser–plasma setting. For a0 > > 1, on the other hand, a search for the best (I0λ02)α fit for ITHz(I0λ02) converges to α = 1/2 (purple dash–dotted line), as expected for CTR-emitting electrons generated mainly by the laser ponderomotive force66,67,68,69,70. Both the electron temperature Te and the THz yield are seen to monotonically increase with λ0 (Figs. 5a, 5c). At I0 ≈ 8 × 1017 W/cm2, the THz field in the trough of the first CTR wave induced by a λ0 = 3.9 μm driver is seen to be an order of magnitude higher than the respective THz field from laser plasmas driven by λ0 = 0.8 μm laser pulses (Fig. 5a). As the THz yield continues to grow with I0 in the a0 > 1 regime, THz fields with amplitudes above 0.2 MV/m can be generated from laser plasmas driven by mid-infrared pulses with a sufficiently high field intensity (I0 ≥ 7 × 1018 W/cm2 for λ0 = 3.9 μm in Fig. 5a). While the THz yield and the electron temperature Te in subrelativistic, a0 < 1 plasmas with L ≤ λ0/20 follows the (I0λ02)α scaling with α > 1 (Fig. 5a, c), as an indication of laser vacuum heating68,69, for plasmas with significantly longer L, with L being as long as a few λ0, plasma electrons gain much of their energy via resonant absorption40, leading to Te ∝ (I0λ02)α with α ≈ 1/340,66. For strongly relativistic plasmas, on the other hand, with a0 > > 1, both the THz yield and the electron temperature Te are found to show little to no deviations from the (I0λ02)1/2 scaling regardless of L.
While a p-polarized laser field can drive plasma electrons via both the ponderomotive force and vacuum heating, an s-polarized driver does not provide an effective field component that would induce vacuum-heating acceleration. The intensity of THz radiation from laser plasmas driven by a moderate-a0 s-polarized laser pulse is therefore much lower (purple triangles in Fig. 5a) than the intensity of THz radiation generated by a p-polarized driver with the same a0 (blue boxes in Fig. 5a). Yet, in the high-a0 regime, where a ponderomotive acceleration dominates over vacuum heating, ITHz(I0λ02) is seen to converge to the scaling of Φ(I0λ02) = \({\mathscr{F}}_{{\text{e}}}\)/(mec2) (blue and purple dotted lines in Fig. 5a) regardless of the polarization of the driver.
Three-dimensional analysis
The purpose of the analysis presented in this section is to show that the key tendencies in the behavior of the THz laser-plasma output as a function of the parameters of the laser driver, such as I0 and λ0, are in no way limited to the specific 2D oblique-incidence laser–plasma interaction geometry examined in the previous sections, but should be viewed instead as signatures of laser-driven plasma electrodynamics representative of a vast, rather general class of laser–plasma interaction settings. To reach this goal, we resort to a 3D PIC modeling of laser–plasma interactions driven by a relativistic-intensity laser driver propagating along the normal to the plasma surface. Due to its cylindrical symmetry, the field of such a driver can be decomposed into azimuthal modes53. With the y-axis chosen along the field propagation direction (Fig. 6a, b), as in the previous sections, a laser-driver field polarized along the z-axis is recognized as a pure azimuthal mode of order m = 1. Such a field is conveniently described in cylindrical coordinates r, θ, y (Fig. 6a) and is fully defined by m = 1 azimuthal-mode components \({\mathscr{E}}\)1y(y, r), \({\mathscr{E}}\)1r(y, r), \({\mathscr{E}}\)1θ(y, r), \({\mathscr{B}}\)1y(y, r), \({\mathscr{B}}\)1r(y, r), and \({\mathscr{B}}\)1θ(y, r). As such a laser field drives ultrafast electron oscillations within a plasma target, it gives rise to a pure m = 0 azimuthal-mode of THz radiation53 with cylindrical field components E0y(y, r), E0r(y, r), E0θ(y, r), B0y(y, r), B0r(y, r), and B0θ(y, r). The azimuthal-mode decomposition of the fields and electron currents for laser–plasma interactions of such a symmetry thus helps to substantially reduce the computation complexity of the problem while preserving its 3D nature53,71. The plasma target in these simulations is taken in the form of a ly x lr = 2.5λ0 × 25λ0 cylinder with ne = 5nc (Fig. 6b), supporting the overall cylindrical symmetry of the problem.
(a) The driving laser field (blue line) and its components against the Cartesian (black) and cylindrical coordinates (pink) used in 3D PIC simulations. (b) An ry-map of the laser field approaching the plasma target. (c–e) Spatial distributions of the E0y(y, r) (c), E0r(y, r) (d), and B0θ(y, r) (e) components of the THz field for t = 90T0 and a0 = 1. The dashed line is the FWHM radius of the driver laser beam propagating in space with no plasmas. Also shown is laser-driven electric charge separation in shielding plasma currents (red and blue coding is for the positive and negative charges, respectively), giving rise to antenna-like emission of THz radiation from plasma edges.
In Fig. 6c–e, we present typical ry-maps of the E0y(y, r), E0r(y, r), and B0θ(y, r) field components in the THz laser—plasma output. Clearly seen in these maps are two forward-propagating THz CTR waves, emitted by the rear plasma boundary, and one backward THz CTR wave, radiation by the front plasma boundary. Also readily discernible are spherical THz waves emitted by plasma edges. Radiation of THz waves of this class has been earlier identified as antenna-like emission by shielding electron currents flowing along the plasma surfaces as a part of laser-driven ultrafast charge-carrier dynamics inside the plasma31. Charge separation arising as a result of such dynamics is shown by red and blue coding in Fig. 6c–e. Similar to electric currents in an impulsively driven antenna72, such electron currents provide a source of outgoing spherical waves of electromagnetic radiation (clearly seen in Fig. 6c–e, as well as in Fig. 7a–j) as they are brought to a halt near the edges of the plasma target31.
(a–j) Spatial distributions of the THz field B0θ(y, r) at t = 85T0 for a0 as specified in the panels. The dashed line is the FWHM radius of the driver laser beam propagating in space with no plasmas. (k, l) THz output energy (k) and laser-to-THz energy conversion efficiency (l) as functions of a0: (green circles) the CTR component, (pink circles) antenna-like plasma emission, and (blue circles) overall THz output. The ∝ Φ(I0λ02) scaling is shown by the dashed line.
Shown in Fig. 7a–j are the ry-maps of the B0θ(y, r) field component in THz radiation from the plasmas driven by a laser field with the laser vector potential ranging from a0 = 1 in Fig. 7a to = 10 in Fig. 7j. As a0 increases, antenna-like THz emission of laser-driven plasmas is seen to become more and more isolated in space from THz CTR waves, allowing an accurate separation of radiation energies, W1 and W2, in the antenna-emission and CTR-wave components of the THz laser-plasma output. In Fig. 7k, we present these energies along with the total energy of the THz output, WTHz = W1 + W2, as functions of a0. The THz output energy is seen to grow with a0, reaching the level above 10 mJ for a0 ~ 10.
The key tendencies in the behavior of WTHz as a function of a0, are fully consistent, as a comparison of Figs. 5a, b, 7k, l shows, with the behavior of the THz radiation output in the 2D laser–plasma interaction geometry. Similar to the 2D laser–plasma setting, THz radiation in 3D simulations is emitted in both forward direction and in reflection. However, because the THz energy cannot be calculated in a 2D setting, where one dimension is missing, 2D scaling laws are formulated for the THz intensity rather than the THz energy. In the 3D setting, on the other hand, where the full THz radiation energy WTHz can be calculated, analysis of the THz energy as a function of I0 and λ0 becomes possible.
Similar to the THz output in 2D simulations (Fig. 5a, b), the THz energy WTHz in Fig. 7k is seen to rapidly grow with a0 in the range of moderate a0, indicating vacuum heating as a predominant physical mechanism whereby the energy of the laser driver is transferred to THz radiation via electron acceleration. As a0 grows above the a0 > 1 level, WTHz slows its growth, converging to a much more gently sloping Φ(I0λ02) asymptotics (shown by the dashed line in Fig. 7k), thus showing once again a close similarity with 2D simulations (cf. Figures 5a, b and 7k). As the laser-driver field approaches the a0 ~ 10 level, WTHz(a0) follows the ∝ \({I}_{0}^{1/2}{\lambda }_{0}\) scaling with a very high accuracy, indicating, in full agreement with the 2D analysis, the decisive role of relativistic ponderomotive charge acceleration as a physical mechanism behind laser-to-THz energy conversion.
Conclusion
To summarize, we have shown that, while the I0 \({\lambda }_{0}^{2}\) product of the laser intensity I0 and the laser wavelength λ0 plays the key role in the energy scaling of strong-field laser-plasma THz generation, the THz output energy, WTHz, does not follow the I0 \({\lambda }_{0}^{2}\) scaling. Its behavior as a function of I0 and λ0 is instead much more complex. Our two- and three-dimensional PIC analysis shows that, for moderate, subrelativistic and weakly relativistic fields, WTHz(I0 \({\lambda }_{0}^{2}\)) can be approximated as (I0λ02)α, with a suitable exponent α, as a clear signature of vacuum electron acceleration as a predominant physical mechanism whereby the energy of the laser driver is transferred to THz radiation. For strongly relativistic laser fields, on the other hand, WTHz(I0 \({\lambda }_{0}^{2}\)) closely follows the scaling dictated by the relativistic electron laser ponderomotive potential \({\mathscr{F}}_{{\text{e}}}\), converging to WTHz ∝ \({I}_{0}^{1/2}{\lambda }_{0}\) for very high I0, thus indicating the decisive role of relativistic ponderomotive charge acceleration as a mechanism behind laser-to-THz energy conversion. Analysis of the electron distribution function shows that the temperature of hot laser-driven electrons bouncing back and forth between the plasma boundaries displays the same behavior as a function of I0 and λ0, altering its scaling from (I0λ02)α to that of \({\mathscr{F}}_{{\text{e}}}\), converging to WTHz ∝ \({I}_{0}^{1/2}{\lambda }_{0}\) for very high I0. Specifically, as can be seen from the comparison of THz yields attainable from laser-plasma sources driven with 0.8- and 3.9-μm laser pulses (green and blue boxes in Fig. 5a along with the respective Φ(I0λ02) asymptotes), the use of a 3.9-μm, sub-100-fs output of the latest-generation high-power OPCPAs37,38,39,63,64,65 can significantly enhance THz generation from relativistic laser–plasma settings relative to plasmas driven by standard, 0.8-μm Ti: sapphire laser pulses. Relativistic field intensities have been already achieved for such sources63,64. The work to even higher I0 is in progress. These findings provide a clear physical picture of THz generation in relativistic laser plasmas, suggesting the THz yield WTHz resolved as a function of I0 and λ0 as a meaningful measurable that can serve as a probe for the temperature Te of hot electrons in a vast class of laser–plasma interactions.
Data availability
All data generated or analyzed during this study are included in this published article.
References
Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 1, 97–105. https://doi.org/10.1038/nphoton.2007.3 (2007).
Blanchard, F., Doi, A., Tanaka, T. & Tanaka, K. Real-time, subwavelength terahertz imaging. Annu. Rev. Mater. Res. 43, 237–259. https://doi.org/10.1146/annurev-matsci-071312-121656 (2013).
Jepsen, P. U., Cooke, D. G. & Koch, M. Terahertz spectroscopy and imaging—Modern techniques and applications. Laser Photon. Rev. 5, 124–166. https://doi.org/10.1002/lpor.201000011 (2011).
Beard, M. C., Turner, G. M. & Schmuttenmaer, C. A. Terahertz spectroscopy. J. Phys. Chem. B 106, 7146–7159. https://doi.org/10.1021/jp020579i (2002).
Baxter, J. B. & Guglietta, G. W. Terahertz spectroscopy. Anal. Chem. 83, 4342–4368. https://doi.org/10.1021/ac200907z (2011).
Liu, J., Dai, J., Chin, S. L. & Zhang, X.-C. Broadband terahertz wave remote sensing using coherent manipulation of fluorescence from asymmetrically ionized gases. Nat. Photonics 4, 627–631. https://doi.org/10.1038/nphoton.2010.165 (2010).
Koenig, S. et al. Wireless sub-THz communication system with high data rate. Nat. Photonics 7, 977–981. https://doi.org/10.1038/nphoton.2013.275 (2013).
Ulbricht, R., Hendry, E., Shan, J., Heinz, T. F. & Bonn, M. Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy. Rev. Mod. Phys. 83, 543–586. https://doi.org/10.1103/RevModPhys.83.543 (2011).
Kampfrath, T., Tanaka, K. & Nelson, K. A. Resonant and nonresonant control over matter and light by intense terahertz transients. Nat. Photonics 7, 680–690. https://doi.org/10.1038/nphoton.2013.184 (2013).
Zaks, B., Liu, R. B. & Sherwin, M. S. Experimental observation of electron–hole recollisions. Nature 483, 580–583. https://doi.org/10.1038/nature10864 (2012).
Vampa, G. et al. Strong-field optoelectronics in solids. Nat. Photonics 12, 465–468. https://doi.org/10.1038/s41566-018-0193-5 (2018).
Schubert, O. et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nat. Photonics 8, 119–123. https://doi.org/10.1038/nphoton.2013.349 (2014).
Lanin, A. A., Stepanov, E. A., Fedotov, A. B. & Zheltikov, A. M. Mapping the electron band structure by intraband high-harmonic generation in solids. Optica 4, 516–519. https://doi.org/10.1364/OPTICA.4.000516 (2017).
Kampfrath, T. et al. Coherent terahertz control of antiferromagnetic spin waves. Nat. Photonics 5, 31–34. https://doi.org/10.1038/nphoton.2010.259 (2011).
Fleischer, S., Zhou, Y., Field, R. W. & Nelson, K. A. Molecular orientation and alignment by intense single-cycle THz pulses. Phys. Rev. Lett. 107, 163603. https://doi.org/10.1103/PhysRevLett.107.163603 (2011).
Fedotov, I. V., Savvin, A. D., Fedotov, A. B. & Zheltikov, A. M. Controlled rotational Raman echo recurrences and modulation of high-intensity ultrashort laser pulses by molecular rotations in the gas phase. Opt. Lett. 32, 1275–1277. https://doi.org/10.1364/OL.32.001275 (2007).
Feurer, T., Vaughan, J. C. & Nelson, K. A. Spatiotemporal coherent control of lattice vibrational waves. Science 299, 374–377. https://doi.org/10.1126/science.1078726 (2003).
Greenland, P. T. et al. Coherent control of Rydberg states in silicon. Nature 465, 1057–1061. https://doi.org/10.1038/nature09112 (2010).
Xu, Z. et al. Driving positron beam acceleration with coherent transition radiation. Commun. Phys. 3, 191. https://doi.org/10.1038/s42005-020-00471-6 (2020).
van Tilborg, J. et al. Temporal characterization of femtosecond laser-plasma-accelerated electron bunches using terahertz radiation. Phys. Rev. Lett. 96, 014801. https://doi.org/10.1103/PhysRevLett.96.014801 (2006).
Leemans, W. P. et al. Observation of terahertz emission from a laser-plasma accelerated electron bunch crossing a plasma-vacuum boundary. Phys. Rev. Lett. 91, 074802. https://doi.org/10.1103/PhysRevLett.91.074802 (2003).
Balciunas, T. et al. Optical and THz signatures of sub-cycle tunneling dynamics. Chem. Phys. 414, 92–99. https://doi.org/10.1016/j.chemphys.2012.02.007 (2013).
Esarey, E., Schroeder, C. B. & Leemans, W. P. Physics of laser-driven plasma-based electron accelerators. Rev. Mod. Phys. 81, 1229–1285. https://doi.org/10.1103/RevModPhys.81.1229 (2009).
van Tilborg, J. et al. Terahertz radiation as a bunch diagnostic for laser-wakefield-accelerated electron bunches. Phys. Plasmas 13, 056704. https://doi.org/10.1063/1.2187957 (2006).
Liao, G.-Q. et al. Demonstration of coherent terahertz transition radiation from relativistic laser-solid interactions. Phys. Rev. Lett. 116, 205003. https://doi.org/10.1103/PhysRevLett.116.205003 (2016).
Jin, Z. et al. Highly efficient terahertz radiation from a thin foil irradiated by a high-contrast laser pulse. Phys. Rev. E 94, 033206. https://doi.org/10.1103/PhysRevE.94.033206 (2016).
Schroeder, C. B., Esarey, E., van Tilborg, J. & Leemans, W. P. Theory of coherent transition radiation generated at a plasma-vacuum interface. Phys. Rev. E 69, 016501. https://doi.org/10.1103/PhysRevE.69.016501 (2004).
Déchard, J., Debayle, A., Davoine, X., Gremillet, L. & Bergé, L. Terahertz pulse generation in underdense relativistic plasmas: from photoionization-induced radiation to coherent transition radiation. Phys. Rev. Lett. 120, 144801. https://doi.org/10.1103/PhysRevLett.120.144801 (2018).
Déchard, J., Davoine, X. & Bergé, L. THz generation from relativistic plasmas driven by near- to far-infrared laser pulses. Phys. Rev. Lett. 123, 264801. https://doi.org/10.1103/PhysRevLett.123.264801 (2019).
Liao, G. et al. Multimillijoule coherent terahertz bursts from picosecond laser-irradiated metal foils. Proc. Natl. Acad. Sci. 116, 3994–3999. https://doi.org/10.1073/pnas.1815256116 (2019).
Déchard, J., Davoine, X., Gremillet, L. & Bergé, L. Terahertz emission from submicron solid targets irradiated by ultraintense femtosecond laser pulses. Phys. Plasmas 27, 093105. https://doi.org/10.1063/5.0013415 (2020).
Liao, G.-Q. et al. Towards terawatt-scale spectrally tunable terahertz pulses via relativistic laser-foil interactions. Phys. Rev. X 10, 031062. https://doi.org/10.1103/PhysRevX.10.031062 (2020).
Frank, I. M. & Ginzburg, V. L. J. Radiation of a uniformly moving electron due to its transition from one medium to another. Phys. USSR 9, 353–362 (1945).
Landau, L. D. & Lifshitz, E. M. Electrodynamics of Continuous Media (Pergamon, 1960).
Liao, G. Q. et al. Intense terahertz radiation from relativistic laser–plasma interactions. Plasma Phys. Control. Fusion 59, 014039. https://doi.org/10.1088/0741-3335/59/1/014039 (2017).
Herzer, S. et al. An investigation on THz yield from laser-produced solid density plasmas at relativistic laser intensities. New J. Phys. 20, 063019. https://doi.org/10.1088/1367-2630/aaada0 (2018).
Mitrofanov, A. V. et al. Mid-infrared laser filaments in the atmosphere. Sci. Rep. 5, 8368. https://doi.org/10.1038/srep08368 (2015).
Mitrofanov, A. V. et al. Subterawatt few-cycle mid-infrared pulses from a single filament. Optica 3, 299–302. https://doi.org/10.1364/OPTICA.3.000299 (2016).
Liang, H. et al. High-energy mid-infrared sub-cycle pulse synthesis from a parametric amplifier. Nat. Commun. 8, 141. https://doi.org/10.1038/s41467-017-00193-4 (2017).
Teubner, U. & Gibbon, P. High-order harmonics from laser-irradiated plasma surfaces. Rev. Mod. Phys. 81, 445–479. https://doi.org/10.1103/RevModPhys.81.445 (2009).
Mikhailova, J. M. et al. Isolated attosecond pulses from laser-driven synchrotron radiation. Phys. Rev. Lett. 109, 245005. https://doi.org/10.1103/PhysRevLett.109.245005 (2012).
Dromey, B. et al. Coherent synchrotron emission from electron nanobunches formed in relativistic laser–plasma interactions. Nat. Phys. 8, 804–808. https://doi.org/10.1038/nphys2439 (2012).
Borot, A. et al. Attosecond control of collective electron motion in plasmas. Nat. Phys. 8, 416–421. https://doi.org/10.1038/nphys2269 (2012).
Poye, A. et al. Physics of giant electromagnetic pulse generation in short-pulse laser experiments. Phys. Rev. E 91, 043106. https://doi.org/10.1103/PhysRevE.91.043106 (2015).
Colosimo, P. et al. Scaling strong-field interactions towards the classical limit. Nat. Phys. 4, 386–389. https://doi.org/10.1038/nphys914 (2008).
Fuchs, J. et al. Laser-driven proton scaling laws and new paths towards energy increase. Nat. Phys. 2, 48–54. https://doi.org/10.1038/nphys199 (2006).
Serebryannikov, E. E. & Zheltikov, A. M. Quantum and semiclassical physics behind ultrafast optical nonlinearity in the midinfrared: the role of ionization dynamics within the field half cycle. Phys. Rev. Lett. 113, 043901. https://doi.org/10.1103/physrevlett.113.043901 (2014).
Zheltikov, A. M. & Nevels, R. D. Intensity and wavelength scaling of laser-driven electron transition radiation: Toward a table-top source of electromagnetic pulses. Laser Phys. Lett. 16, 015401. https://doi.org/10.1088/1612-202X/aae788 (2019).
Theobald, W. et al. Electron densities, temperatures, and the dielectric function of femtosecond-laser-produced plasmas. Phys. Rev. E 59, 3544–2553. https://doi.org/10.1103/PhysRevE.59.3544 (1999).
Dobosz, S. et al. Probing hot and dense laser-induced plasmas with ultrafast XUV pulses. Phys. Rev. Lett. 95, 025001. https://doi.org/10.1103/PhysRevLett.95.025001 (2005).
Chen, H., Wilks, S. C., Kruer, W. L., Patel, P. K. & Shepherd, R. Hot electron energy distributions from ultraintense laser solid interactions. Phys. Plasmas 16, 020705. https://doi.org/10.1063/1.3080197 (2009).
Pukhov, A. & Meyer-ter-Vehn, J. Relativistic magnetic self-channeling of light in near-critical plasma: three-dimensional particle-in-cell simulation. Phys. Rev. Lett. 76, 3975–3978. https://doi.org/10.1103/PhysRevLett.76.3975 (1996).
Derouillat, J. et al. Smilei: a collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comput. Phys. Commun. 222, 351–373. https://doi.org/10.1016/j.cpc.2017.09.024 (2018).
Voronin, A. A. & Zheltikov, A. M. Nonlinear dynamics of high-power ultrashort laser pulses: exaflop computations on a laboratory computer station and subcycle light bullets. Phys.-Usp. 59, 869–877. https://doi.org/10.3367/UFNe.2016.02.037700 (2016).
Glek, P. B., Voronin, A. A., Panchenko, V. . Ya. . & Zheltikov, A. M. Relativistic electron bunches locked to attosecond optical field waveforms: An attosecond light–matter bound state. Laser Phys. Lett. 17, 55–401 (2020).
von der Linde, D. & Rzàzewski, K. High-order optical harmonic generation from solid surfaces. Appl. Phys. B 63, 499–506. https://doi.org/10.1007/BF01828947 (1996).
Tarasevitch, A., Lobov, K., Wünsche, C. & von der Linde, D. Transition to the relativistic regime in high order harmonic generation. Phys. Rev. Lett. 98, 103902. https://doi.org/10.1103/PhysRevLett.98.103902 (2007).
Tarasevitch, A. et al. High order harmonic generation from solid targets: Towards intense attosecond pulses. Phys. Rev. A 62, 023816. https://doi.org/10.1140/epjst/e2009-01114-7 (2000).
Kahaly, S. et al. Direct observation of density-gradient effects in harmonic generation from plasma mirrors. Phys. Rev. Lett. 110, 175001. https://doi.org/10.1103/PhysRevLett.110.175001 (2013).
Malvache, A., Borot, A., Quéré, F. & Lopez-Martens, R. Coherent wake emission spectroscopy as a probe of steep plasma density profiles. Phys. Rev. E 87, 035101. https://doi.org/10.1103/PhysRevE.87.035101 (2013).
Mourou, G. A., Tajima, T. & Bulanov, S. V. Optics in the relativistic regime. Rev. Mod. Phys. 78, 309–371. https://doi.org/10.1103/RevModPhys.78.309 (2006).
Di Piazza, A., Müller, C., Hatsagortsyan, K. Z. & Keitel, C. H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 84, 1177–1228. https://doi.org/10.1103/RevModPhys.84.1177 (2012).
Woodbury, D. et al. Laser wakefield acceleration with mid-IR laser pulses. Opt. Lett. 43, 1131–1134. https://doi.org/10.1364/OL.43.001131 (2018).
Mitrofanov, A. V. et al. High-order harmonic generation from a solid-surface plasma by relativistic-intensity sub-100-fs mid-infrared pulses. Opt. Lett. 43, 5571–5574. https://doi.org/10.1364/OL.43.005571 (2018).
Mitrofanov, A. V. et al. Chirp-controlled high-harmonic and attosecond-pulse generation via coherent-wake plasma emission driven by mid-infrared laser pulses. Opt. Lett. 45, 750–753. https://doi.org/10.1364/OL.45.000750 (2020).
Cui, Y., Wang, W., Sheng, Z., Li, Y. & Zhang, J. Laser absorption and hot electron temperature scalings in laser–plasma interactions. Plasma Phys. Control. Fusion 55, 085008. https://doi.org/10.1088/0741-3335/55/8/085008 (2013).
Ding, W. J., Sheng, Z. M. & Koh, W. S. High-field half-cycle terahertz radiation from relativistic laser interaction with thin solid targets. Appl. Phys. Lett. 103, 204107. https://doi.org/10.1063/1.4831684 (2013).
Forslund, D. W., Kindel, J. M. & Lee, K. Theory of hot-electron spectra at high laser intensity. Phys. Rev. Lett. 39, 284–288. https://doi.org/10.1103/PhysRevLett.39.284 (1977).
Wilks, S. C., Kruer, W. L., Tabak, M. & Langdon, A. B. Absorption of ultra-intense laser pulses. Phys. Rev. Lett. 69, 1383–1386. https://doi.org/10.1103/PhysRevLett.69.1383 (1992).
Haines, M. G., Wei, M. S., Beg, F. N. & Stephens, R. B. Hot-electron temperature and laser-light absorption in fast ignition. Phys. Rev. Lett. 102, 045008. https://doi.org/10.1103/PhysRevLett.102.045008 (2009).
Lifschitz, A. F. et al. Particle-in-cell modelling of laser-plasma interaction using Fourier decomposition. J. Comput. Phys. 228, 1803–1814. https://doi.org/10.1016/j.jcp.2008.11.017 (2009).
Smith, G. S. Teaching antenna radiation from a time-domain perspective. Am. J. Phys. 69, 288–300. https://doi.org/10.1119/1.1320439 (2001).
Acknowledgements
This research was supported in part by the Russian Science Foundation (Project No. 20-12-00088—ultrabroadband optical science), Ministry of Science and Higher Education of the Russian Federation (Project 075-15-2020-801), and the Welch Foundation (grant A-1801-20180324). Research by P.B.G. is partially supported by the “BASIS” Foundation (Grant No. 20-2-10-2-1).
Author information
Authors and Affiliations
Contributions
P.B.G. performed numerical simulations and analyzed the data. A.M.Z. oversaw the project, analyzed the data, and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Glek, P.B., Zheltikov, A.M. Enhanced coherent transition radiation from midinfrared-laser-driven microplasmas. Sci Rep 12, 7660 (2022). https://doi.org/10.1038/s41598-022-10614-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-10614-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.