Abstract
In this study, Galerkin Finite Element Method or GFEM is used for the modeling of mixed convection with the entropy generation in wavy lid-driven porous enclosure filled by the CNT-water nanofluid under the magnetic field. Two different cases of boundary conditions for hot and cold walls are considered to study the fluid flow (streamlines) and heat transfer (local and average Nusselt numbers) as well as the entropy generation parameters. Richardson (Ri), Darcy (Da), Hartmann angle (γ), Amplitude (A), Number of peaks (N), Volume fraction (φ), Heat generation factor (λ), Hartmann number (Ha) and Reynolds number (Re) are studied parameters in this study which results indicated that at low Richardson numbers (< 1) increasing the inclined angle of magnetic field, decreases the Nu numbers, but at larger Richardson numbers (> 1) it improves the Nu numbers.
Similar content being viewed by others
Introduction
The rapid development of electronic devices, solar collectors, heating elements, heat exchangers, drying and lubricant techniques, it pushes us to find an effective way to increase the efficiency of heat transfer effectively and to reach that effectiveness it became necessary to use the combined method (passive-active). Using nanofluid and porous medium is an active method while the wall modification with sinusoidal style is the passive method. Lots industrial applications that depend on its work of lid-driven cavity such as chemical etching, film coating, industrial drying process, industrial coating, short dwell coaters utilizing for the manufacturing of high quality photographic films and papers, roll coating, several color printings, polymer processing apparatus design, Bingham plastics flow, dryers and solar collectors. Free and forced convection of heat transfer from nanofluids such as CNT-water has many applications such as cooling processes in industries which motivated the researchers to work on this phenomena1. Furthermore, different ways and techniques such as magnetic field applying and porous media usage is used to improve or control the heat transfer amount in those applications1,2. Hamida and Hatami3 used the electrical field in their square light emitting diode modeling to improve the cooling process from microchannel filled by nanofluid. Ghasemi et al.4 and Hamzah et al.5 used the magnetic field to improve the heat transfer in the solar radiation application and immersed rotating cylinder, respectively. Behzadnia et al.6,7 modeled the super-critical nanofluid flow for improving the cooling process in reactors and Hatami8, and Hatami and Safari9 improved the nanofluid heat transfer from cavities by using heated fins and cylinders, respectively. Recently, Nakhchi et al.10 investigated the CuO-water heat transfer from heat exchanger using the novel perforated turbulators as external devices.
Many researchers tried to improve the heat transfer of nanofluids using new technologies. Shaker et al.11 used the non-uniform magnetic field for the mixed convection of open cavity and found maximum 57.07% Nu improvements by magnetic number. Wang et al.12 used the porous twisted tapes for heat transfer improvement of silica-water (SiO2–H2O) nanofluids in rounds and triangular tubes. Al-Farhany and Abdulsahib13 considered the mixed convection of nanofluid in porous medium over a rotating cylinder and found the higher Darcy number and clockwise rotation causes a maximum Nusselt number. Nong et al.14 used the control volume finite element (CVFE) method to study the Lorentz force effect on the free convection of a wavy cavity and concluded that nanoparticles shape insignificantly influences the average Nusselt number. Abbas et al.15 used magnetic field and Ag/Ni-water hybrid nanofluids to improve the heat transfer over a cylinder, analytically. Electrical field applying to the nanofluids heat trasnfer is another technique which recently is used by researchers such as Chen et al.16, numerically. They concluded that the electric field forces modify the velocity field and temperature.
Among the studies on the external fields, magnetic field is more used by researchers than an electric field due to its more effect on the nanoparticles. Recently, Aly et al.17 investigated the effect of magnetic field on the finned cavity, including a rotating rectangle and reported that mean rates of heat and mass transfer decreased by increasing the Hartmann number. Berrahil et al.18 applied the magnetic field on the Al2O3/water, natural convection in an annular enclosure and found that the rate of the average Nu number, decrement caused by the magnetic field, is greater as the radius ratio λ decreases. Mourad et al.19 used the uniform magnetic field for the thermal performance of a wavy cavity filled by Fe3O4-MWCNT hybrid nanofluid and confirmed that Nu improves by Darcy and porosity number, while it reduced by Ha number. Alsabery et al.20 used at the same time magnetic field and rotating cylinders in a wavy surface and stated that rotation of the cylinders can enhance the Nu number up to 315%. Also, Zhang and Zhang21 studied the effect of magnetic field direction on the heat transfer of Fe3O4-water nanofluid, numerically. They described that 8% increase in convective heat transfer is observed when the magnetic direction was perpendicular to the flow direction. Also, in another study, they22 confirmed that the convective heat transfer coefficient increases with the increase of alternating frequency for the magnetic field, experimentally. Not only the magnetic field is used for heat transfer of nanofluids in cavities23, but also porous media are considered as a wavy of heat transfer improvement as seen in the literature24. Sara et al.25 in this review study deals with natural convection in multi-shapes cavities and effective parameters such as magnetic field, nanoparticle, porosity, obstruction body and inclination angle of the cavity. Mohammad et al.26 the aim of this work focused an enhance heat transfer in the helical tube heat exchanger having non-Newtonian nanofluid taking into account the following factors such as cost, dimensions, and thermal system energy storage. The result shows that maximum performance can reduce to 28%. Hamid et al.27 in the current study, an inclusive review was made of the utilized of nanofluid in heat pipe thermosyphon. The execution of thermosyphon relies on many factors such as types of nanofluid and its concentration, using of surfactant and the amount of heat supplied. Also the study deals with of nanofluid thermosyphon implementation is systems of energy. Ahmed et al.28 in the current work a very valuable historical review that deals with nanofluids, types of nanomaterial, base fluid and surfactant. Application in different energy systems, advantage and disadvantage in a very detailed and accurate manner. Sara et al.29 the study deals with the influence of using sound waves of measuring viscosity of ethylene glycol with SiO2 nanofluid. Many factors were student like temperature, mass fraction, rate of shear and time of a sound wave and its effect on viscosity by two method step. Quyan et al.30,31,32,33 in this works, a numerical investigation was used to simulate heat transfer, fluid flow and entropy generation in three different channels, the first one is double pipe wavy wall heat exchanger, the second one is corrugated wall with triangular shape and the third is a microchannel injection from top wall. The working fluid, a novel admixture of FMWNT-water (Functionilized Multi-Walled Carbon Nano-Tubes) based water is exercised as the working fluid. The flow is subjected to magnetic strength with constant value. The results show that using magnetic flux with this type of nanofluid was effective in improving heat transfer and reducing the entropy generation. Masoud et al.34 during this search, controlling heat transfer by applying the magnetic field technique to the conductive electrical fluid (melting gallium) in circular enclosure was displayed. Many parameters are studied, magnetic field angle, Rayleigh number, magnetic strength and inner to outer radius ratio, The results indicated that increasing magnetic field angle, Rayleigh and radius ratio lead to increase the heat transfer Nusselt number. Ehsan et al.35 calculated the thermal conductivity and viscosity of FMWCN (Functionalized Multi-Walled Carbon Nanotubes) from experimental results and using this properties to simulate heat transfer and fluid flow of non-Newtonian fluid in circular pipe and constant heat flux. Results indicate that this type of nanoparticles was more convenient with great shear fluid rate. Liang et el.36 the aim of this study is to make a comparison between the common rectangular channel and corrugated one in the presence of discrete heat sources in the upper straight surface. The results display that when the discrete heat source near the peak of undulation surface has more effective than other cases.
Abanoub et al.37 in the recent current study, the problem of lid-driven of two dimensional incompressible flow using a finite difference technique. In this work, most of industrial applications in which it is possible to be noticed the phenomenon of mixed convection by lid-driven.
So, in this study, it is trying to do a complete study on the mixed convection heat transfer of nanofluids under the magnetic field in a porous medium which has a movable wavy wall with different boundary conditions, numerically. The study goes for the first time that dealing with lid-drive having wavy in shape and movement with presence of many factors such as CNT-nanomaterial, porous medium, heat generation, effect of magnetic field and its angle.
Mathematical description of the problem
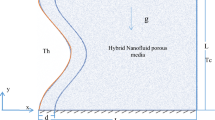
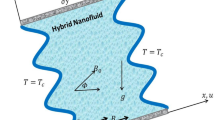
The problem geometry is schematically explained in Fig. 1, it is two dimensional porous cavity of similar length and height equal to unity filled by CNT-nanofluid. CNT are non-Newtonian fluids, whose high viscosity obstructs convection and leads to acceptable heat transfer coefficient under mixed convection, despite their high thermal conductivity. The upper and lower boundaries are insulated where the straight right and wavy left walls are in cold and hot temperatures in two different cases. The right wall is wavy with a number of peaks (N) and amplitude (A), this wavy wall is moved to upward with the velocity of U = 1. A magnetic field which strength of B0 and angle of γ is applied to the cavity. Uniform heat generation (qʺ) was applied entire the cavity. The assumptions of this model are incompressible, steady state, laminar flow, homogenous isotropic porous medium, single phase nanofluid. The model of porous media is a Darcy Brinkman model. The parameters neglected are radiation effect and viscous dissipation. Under the above assumptions, the conservation of mass, and in the case of mixed convection, and also the conservation of momentum energy equations can be written as2:
where (\(\nabla u\)) shows the velocity vector and K denotes the permeability of porous media, J is electrical current and B* refers to external magnetic field. Ω is the electric potential, and σnf is the electrical conductivity. More information on the parameters can be found in2. Chamkha et al.2 showed that the expressed equations are:
Also, they showed that by considering the following non-dimentional parameters:
The non-dimentional form of governing equation will be in the form of:
where
The local Nusselt number will be
and the non-dimensional entropy generation, (S), can be written as2
where Sh, Sv, and Sj are the dimensionless local entropy generation rate due to heat transfer, the fluid fraction, and the Joule heating, respectively. Θ is the irreversibility factor which represents the ratio of the viscous entropy generation to thermal entropy generation
The Bejan number, Be, defined as the ratio between the entropy generation due to heat transfer by the total entropy generation:
More details of defined parameters such as average Nusselt number, boundary conditions, and nanofluid properties in the governing equations can be found in2.
The density, heat capacity, thermal expansion, thermal diffusivity, thermal conductivity, viscosity and the electrical conductivity are explained by the following equations:
where \(\delta =\frac{{\sigma }_{nf}}{{\sigma }_{f}}\).
Numerical method
In this study, Galerkin weighted residual FEM (GFEM) is used for the explanation of the governing equations and the boundary conditions by the software package COMSOL Multiphysics 5.6 [https://www.comsol.com/release/5.6]. At the beginning, thus named Galerkin weighted residual is progressed by conquest appropriate grid number of elements ad a gradation of lattices is intended from the rough grid at G1. The next grid of next mesh is repeated for smooth grid G2 by rising number of elements as can noticed in Table 2. So, the full domain is divided into non-mapping elements \({\Omega }_{R}\), \(R\in N\) at every mesh grid. So as to realize the shape function on every element \({\Omega }_{R}\), a domestic sign coordinate system (ξ, η) is inserted. Here, the nanofluid considered single-phase and incompressible, by laminar flow (spf) module and the heat transfer in the media (ht) are used for the modeling of Eqs. (11)–(14) with nanofluid properties of Table 1. To model the magnetic field, the source terms of the governing equations have changed in the software in this demonstrating. Additionally, to state the stability of the solution, Galerkin least-squares method and P2-P1 Lagrange elements were used. In the present numerical solution, the convergence criteria are defined by the error estimation setting to \(\left| {M^{m + 1} - M^{m} } \right| \le 10^{ - 5}\), where m shows the iteration number during the solution and M refers to \((u,v,T,V)\) parameters as the general dependent variables.
Results and discussion
As discussed above, in this manuscript the effect of mixed convection of CNT-water nanofluid in a wavy porous cavity is investigated under the magnetic field. As shown in Fig. 1, the wavy wall is moved by a unit velocity and two cases are considered for the temperature boundary layers. In case 1 the straight left hand side wall is at high temperature (Th) while the wavy right hand side is a low temperature (Tc). For Case 2, the Th and Tc temperatures are replaced as shown in Fig. 1. Table 1 shows the CNTs thermal properties obtained from1. To reach a grid independence study, Table 2 is studied for different grid numbers. Five different grid numbers are tested and results of an average Nusselt number, time of the solution and ψmin were presented. As seen, G5 and G6 elements have excellent results which are more close to each other, but G5 due to lower time of solution can be chosen as the suitable grind number for this study. To have a validation study, the results of the present numerical method are compared with those of Chamkha et al.2 in a square cavity as shown in Fig. 2a,b. As seen, the current results have excellent agreement with those of Chamkha et al.2 for Isotherms, Streamlines, Entropy generations and Bejan numbers contours. In the next steps, effects of different parameters which are presented by their values in Table 3, are investigated on the results. Richardson (Ri), Darcy (Da), Hartmann angle (γ), Amplitude (A), Number of peaks (N), Volume fraction (φ), Heat generation factor (λ), Hartmann number (Ha) and Reynolds number (Re) are the considered parameters in this study. Following the results of the two cases are presented.
Case 1
Figure 3 demonstrates the effect of Da and Ri on the streamlines and isotherms at (Re = 100, λ = 5, φ = 0.02, Ha = 25, γ = 45, A = 0.1, N = 3). As seen, lower Darcy numbers have more uniform temperature and streamlines. Also, for greater Richardson numbers, the flow patterns are more complicated due to natural convection effects in greater numbers, but isotherm lines of the larger Ri numbers are uniform since the forced convection in this condition has minor effect. Figure 4 shows the effect of geometry parameters of wavy wall (A and N) on the streamlines and temperature values when Da = 1e−3, Re = 100, λ = 5, φ = 0.03, Ha = 25, γ = 45, Ri = 10 and Fig. 5 demonstrates the same contour for a greater Re number equal to 200. As seen, Nuave for the case of square cavity is 12.668 while for all wavy wall its value is increased. It is evident that by increasing the both A and N, the surface of heat transfer is increased and consequently Nu improved in these situations. Table 4 compares these values for better perception on these figures. Tables 5 and 6 compares the results of an average Nusselt number by increasing the Ri and Da numbers at different geometries of wavy wall through changing the A and N parameters. As seen, by increasing the Ri, Nu number is increased significantly due to the natural convection effect, also increasing the Darcy number, improves the Nu number due to more porosity effect on the heat transfer. Figure 6 shows the local Nusselt number of heated wall at different parameters. As seen the maximum local Nusselt numbers occurs for the cases with Ri = 100 and D = 0.1, 0.01 which confirms the discussed issues. Entropy analysis of these cases is presented through Fig. 7 and Table 7 by presenting the different terms of entropy generations and Bejan numbers. To find the effect of nanoparticle volume fraction, Fig. 8 is depicted to see the difference between the two cases. As seen for a greater nanoparticle volume fraction two vortexes are presented in the streamlines which affects the heat transfer as seen in Table 8 and Fig. 9. As seen, increasing the φ has not a significant effect on Nu numbers, but at greater Ri numbers, it reduced the Nu values. Also, Fig. 9 shows the effect of Re, inclined angle and generation parameter in the local Nusselt number. It is observable the Re, γ improves the Nu by their increment, but greater Nu numbers occurs for λ = − 5 compared to λ = 0, 5. Figure 10 investigates the effect of Reynolds number on the streamlines, isotherms and entropy generation parameters.
Case 2
By changing the Th and Tc positions, case 2 results are obtained and presented here. Table 9 shows the effect of geometry parameters on the average Nusselt number. As seen in this case, all wavy walls have smaller Nu than the square cavity with Nu = 5.7461, and increasing the A and N reduces the Nu number, significantly. Table 10 confirms that in the second case the treatment of Ri and Da increment is the same of Case 1 and improve the Nu number. Figure 11 shows the isotherms and streamlines of second case which is depicted at different Da and Ri numbers. Greater Richardson number causes more uniform isothemlines due to natural convection, while smaller values have more turbulent lines due to more forced convection in heat transfer. Figures 12 and 13 is presented to find the effect of amplitude and number of peaks of wavy wall on the temperatures and streamlines. Table 11 is presented to show the entropy analysis of second case and Table 12 shows the effect of the different nanoparticle volume fraction on the Nu number which have the same treatment of Case 1. Figure 14 is depicted based on the entropy analysis and Bejan number and Sgen numbers are presented at different Ri and Da numbers. Finally, the effect of Ri and Da numbers on the local Nu numbers over the wavy wall is depicted in Fig. 15 for case 2. As seen the greatest values of Nu is related to cases with Da = 0.1 or Ri = 100. To have a comparison between the two tested cases, Tables 13, 14, 15 and 16 are presented. Table 13 compared them at different Ri and λ numbers which confirm the same treatments, but greater values are observed for the Case 1. Table 14 says that increasing the Hartmann number has a negative effect on heat transfer and reduce the Nu values. For the effect of the inclined angle of the magnetic field, Table 15 approves that at low Ri numbers (< 1) increasing the inclined angle, decreases the Nu numbers, but at larger Ri numbers (> 1) it improves the Nu numbers. About the Reynolds number, Table 16 demonstrates that Re number increment can improve the heat transfer of both cases, significantly.
Conclusion
In this paper, GFEM was used for modeling the CNT-water nanofluids in a wavy porous cavity with movable and different boundary conditions under the magnetic field. Richardson (Ri), Darcy (Da), Hartmann angle (γ), Amplitude (A), Number of peaks (N), Volume fraction (φ), Heat generation factor (λ), Hartmann number (Ha) and Reynolds number (Re) effects were studied on the results of entropy generation and Nu numbers. Results indicated that by increasing the Ri, Nu number is increased significantly due to the natural convection effect, also increasing the Darcy number, improves the Nu number due to more porosity effect on the heat transfer. The presence of the wavy wall increases the Nusselt number, thus it reinforces heat transfer, this reinforcement, increasing with the increase of both number of undulation and its amplitude. Also, greatest values of Nu are occurring for the case with Da = 0.1 or Ri = 100.
Abbreviations
- A:
-
Amplitude (m)
- B* :
-
External Magnetic field
- Bo :
-
Magnetic field strength (T)
- Be:
-
Bejan number
- Cp :
-
Specific heat at constant pressure (KJ/kg K)
- Da:
-
Darcy number
- g:
-
Gravitational acceleration (m/s2)
- Ha:
-
Hartman number
- k:
-
Thermal conductivity (W/m K)
- K :
-
Permeability of porous medium (m2)
- L:
-
Length and height of the cavity (m)
- N:
-
Number of peaks
- Nu s :
-
Local Nusselt number
- Nuave :
-
Average Nusselt number
- p :
-
Pressure (Pa)
- P:
-
Dimensionless pressure (\(\frac{p}{{\rho }_{nf}{V}_{o}^{2}}\))
- Pr:
-
Prandtl number (νbf/αbf)
- Q:
-
Heat generation source (W/m2)
- Ra:
-
Rayleigh number \((g{\beta }_{bf}{L}^{3}({T}_{h}-{T}_{\mathrm{c}})/{\nu }_{bf}{\alpha }_{bf})\)
- Ri:
-
Richardson number (Ri = Gr/Re2)
- S:
-
Entropy generation (W/K m3)
- S1, ST :
-
Dimensionless partial slip parameters
- T :
-
Temperature (K)
- Tc :
-
Wall with cold temperature
- Th :
-
Wall with hot temperature
- To :
-
Reference Temperature
- u, v:
-
Components velocity in Cartesian coordinates (m/s)
- \(\nabla u\) :
-
Velocity vector
- \(U, V\) :
-
Dimensionless velocity component
- \({V}_{o}\) :
-
Velocity of lid-driven (m/s)
- X, Y:
-
Dimensionless coordinate
- x, y :
-
Cartesian coordinates (m
- α:
-
Thermal diffusivity (m2/s)
- \(\beta \) :
-
Thermal Expansion coefficient (1/K)
- \(\theta \) :
-
Dimensionless temperature (T − Tc/Th − Tc)
- \(\lambda \) :
-
Heat generation factor
- \(\Psi \) :
-
Dimensionless stream function
- μ:
-
Dynamic viscosity (kg s/m)
- \(\sigma \) :
-
Electrical conductivity
- ν:
-
Kinematic viscosity (μ/ρ)(Pa s)
- γ:
-
Hartman angle
- φ:
-
Nanoparticle volume fraction (%)
- \(\Theta \) :
-
Irreversibility factor
- \(\varnothing \) :
-
Basic function
- Ω:
-
Electrical potential
- ρ:
-
Density (kg/m3
- c:
-
Cold
- f :
-
Base Fluid (pure)
- sp:
-
Solid particle
- nf :
-
Nanofluid
- so:
-
Conductive solid cylinder
- h:
-
Hot
- Cond.:
-
Conduction
- GFEM:
-
Galerkin finite elements method
- Conv.:
-
Convection
- CNT:
-
Carbon nano-tube
References
Selimefendigil, F. & Öztop, H. F. Corrugated conductive partition effects on MHD free convection of CNT-water nanofluid in a cavity. Int. J. Heat Mass Transf. 129, 265–277 (2019).
Chamkha, A. J., Rashad, A. M., Mansour, M. A., Armaghani, T. & Ghalambaz, M. Effects of heat sink and source and entropy generation on MHD mixed convection of a Cu-water nanofluid in a lid-driven square porous enclosure with partial slip. Phys. Fluids 29(5), 2001 (2017).
Hamida, M. B. B. & Hatami, M. Optimization of fins arrangements for the square light emitting diode (LED) cooling through nanofluid-filled microchannel. Sci. Rep. 11(1), 1–22 (2021).
Ghasemi, S. E. & Hatami, M. Solar radiation effects on MHD stagnation point flow and heat transfer of a nanofluid over a stretching sheet. Case Stud. Thermal Eng. 25, 100898 (2021).
Hamzah, H. K., Ali, F. H., Hatami, M., Jing, D. & Jabbar, M. Y. Magnetic nanofluid behavior including an immersed rotating conductive cylinder: finite element analysis. Sci. Rep. 11(1), 1–21 (2021).
Behzadnia, H., Jin, H., Najafian, M. & Hatami, M. Geometry optimization for a rectangular corrugated tube in supercritical water reactors (SCWRs) using alumina-water nanofluid as coolant. Energy 221, 9850 (2021).
Behzadnia, H., Jin, H., Najafian, M., & Hatami, M. Investigation of super-critical water-based nanofluid with different nanoparticles (shapes and types) used in the rectangular corrugated tube of reactors. Alex. Eng. J. (2021).
Hatami, M. Numerical study of nanofluids natural convection in a rectangular cavity including heated fins. J. Mol. Liq. 233, 1–8 (2017).
Hatami, M. & Safari, H. Effect of inside heated cylinder on the natural convection heat transfer of nanofluids in a wavy-wall enclosure. Int. J. Heat Mass Transf. 103, 1053–1057 (2016).
Nakhchi, M. E., Hatami, M., & Rahmati, M. Effects of CuO nano powder on performance improvement and entropy production of double-pipe heat exchanger with innovative perforated turbulators. Adv. Powder Technol. (2021).
Shaker, H., Abbasalizadeh, M., Khalilarya, S. & Motlagh, S. Y. Two-phase modeling of the effect of non-uniform magnetic field on mixed convection of magnetic nanofluid inside an open cavity. Int. J. Mech. Sci. 207, 106666 (2021).
Wang, Y., Qi, C., Ding, Z., Tu, J. & Zhao, R. Numerical simulation of flow and heat transfer characteristics of nanofluids in built-in porous twisted tape tube. Powder Technol. 392, 570–586 (2021).
Al-Farhany, K. & Abdulsahib, A. D. Study of mixed convection in two layers of saturated porous medium and nanofluid with rotating circular cylinder. Prog. Nuclear Energy 135, 103723 (2021).
Nong, H. et al. Numerical modeling for steady-state nanofluid free convection involving radiation through a wavy cavity with Lorentz forces. J. Mol. Liquids 336, 116324 (2021).
Abbas, N. et al. Models base study of inclined MHD of hybrid nanofluid flow over nonlinear stretching cylinder. Chin. J. Phys. 69, 109–117 (2021).
Chen, Y., Luo, P., He, D. & Ma, R. Numerical simulation and analysis of natural convective flow and heat transfer of nanofluid under electric field. Int. Commun. Heat Mass Transfer 120, 105053 (2021).
Aly, A. M., Mohamed, E. M. & Alsedais, N. Double-diffusive convection from a rotating rectangle in a finned cavity filled by a nanofluid and affected by a magnetic field. Int. Commun. Heat Mass Transfer 126, 105363 (2021).
Berrahil, F. et al. Numerical investigation on natural convection of Al2O3/water nanofluid with variable properties in an annular enclosure under magnetic field. Int. Commun. Heat Mass Transfer 126, 105408 (2021).
Mourad, A. et al. Galerkin finite element analysis of thermal aspects of Fe3O4-MWCNT/water hybrid nanofluid filled in wavy enclosure with uniform magnetic field effect. Int. Commun. Heat Mass Transfer 126, 461 (2021).
Alsabery, A. I., Ismael, M. A., Gedik, E., Chamkha, A. J. & Hashim, I. Transient nanofluid flow and energy dissipation from wavy surface using magnetic field and two rotating cylinders. Comput. Math. Appl. 97, 329–343 (2021).
Zhang, X. & Zhang, Y. Heat transfer and flow characteristics of Fe3O4-water nanofluids under magnetic excitation. Int. J. Thermal Sci. 163, 106826 (2021).
Zhang, X. & Zhang, Y. Experimental study on enhanced heat transfer and flow performance of magnetic nanofluids under alternating magnetic field. Int. J. Thermal Sci. 164, 106897 (2021).
Zhang, X. et al. Numerical study of mixed convection of nanofluid inside an inlet/outlet inclined cavity under the effect of Brownian motion using Lattice Boltzmann Method (LBM). Int. Commun. Heat Mass Transfer 126, 105428 (2021).
Baïri, A. Porous materials saturated with water-copper nanofluid for heat transfer improvement between vertical concentric cones. Int. Commun. Heat Mass Transfer 126, 105439 (2021).
Rostami, S. et al. A review on control parameters of natural convection in different shape cavities with and without nanofluid. Processes 8, 1011 (2020).
Ibrahim, M. et al. Assessment of economic thermal and hydraulic performances a corrugated helical heat exchanger filled with non-Newtonian nanofluid. Sci. Rep. 11, 11568 (2021).
Ghorabaee, H., Emami, M. R. S., Moosakazemi, F. & Kerimi, N. The use of nanofluid in thermosyphon heat pipe: A comprehensive review. Powder Technol. 394, 250–269 (2021).
Pordanjani, A. H., Aghakhan, S., Afrand, M. & Shrifpur, M. Nanofluids: Physical phenomena, applications in thermal systems and environment effects: A critical review. J. Clean. Prod. 320, 128573 (2021).
Rostami, S. et al. Effect of silica nano-materials on the viscosity of ethylene glycol: An experimental study by considering sonication duration effect. J. Mater. Res. Technol. 9(5), 11905–11917 (2020).
Nguyen, Q., Baharami, D., Kalbasi, R. & Karimipour, A. Functionlized multi-walled carbon nano tubes nanoparticles dispersed in water through an magneto hydro dynamic nonsmooth duct equipped with sinusoidal-wavy wall: Diminshing vortex intensity via nonlinear Navir-Stock equations. Math. Method Appl. Sci. 1, 1–18 (2020).
Nguyen, Q., Baharami, D., Kalbasi, R. & Bach, Q. Nanofluid through microchannel with a triangular corrugated wall: Heat transfer enhancement against entropy generation intensification. Math. Method Appl. Sci. 1, 1–14 (2020).
Karimipour, A., Bahrami, D., Kalbasi, R. & Marjani, A. Diminishing vortex intensity and improving heat transfer by applying magnetic field an an injectable slip microchannel containing FMWNT/water nanofluid. J. Therm. Anal. Calorim. 144(6), 2235–2246 (2021).
Afrand, M., Karimipour, A., Nadooshan, A. A. & Akbari, M. The variations of heat transfer and slip velocity of FMWNT-water nano-fluid along the micro-channel in the lack and presence of a magnetic field. Phys. E 84, 474–481 (2016).
Afrand, M., Faraht, S., Nezhad, A. H., Sheikhzadeh, G. A. & Sarhaddi, F. Numerical simulation of electrically conducting fluid flow and free convective heat transfer in an annulus on applying a magnetic field. Heat Transfer Res. 45(8), 749–766 (2014).
Applicable for use in heat exchangers. Shahsavani, E., Afrand, M., Kalbasi., R. Using experimental data to estimate heat transfer and pressure drop of non-Newtonian nanofluid flow through a circular tube. Appl. Therm. Eng. 129, 1573–1581 (2018).
Cheng, L. et al. Role of gradients and vortexes on suitable locations of discrete heat sources on a sinusoidal-wall microchannel. Eng. Appl. Comput. Fluid Mech. 15(1), 1126–1190 (2021).
Kamel, A. G., Haraz, E. H. & Hanna, S. N. Numerical simulation of three sided lid-driven square cavity. Eng. Rep. 2, 1–22 (2020).
Author information
Authors and Affiliations
Contributions
All authors participated in modeling and writing sections.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hamzah, H.K., Ali, F.H. & Hatami, M. MHD mixed convection and entropy generation of CNT-water nanofluid in a wavy lid-driven porous enclosure at different boundary conditions. Sci Rep 12, 2881 (2022). https://doi.org/10.1038/s41598-022-06957-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-06957-3
This article is cited by
-
Entropy optimization of lid-driven micropolar hybrid nanofluid flow in a partially porous hexagonal-shaped cavity with relevance to energy efficient storage processes
Scientific Reports (2024)
-
Entropy generation and thermal analysis in quadratic translation of sodium alginate with MHD and porosity effects
Journal of Thermal Analysis and Calorimetry (2024)
-
Numerical analysis of magnetohydrodynamic (MHD) convection using CNT-based nanofluids in a wavy-shaped enclosure with a double lid
Journal of Thermal Analysis and Calorimetry (2024)
-
Influence of magnetic field on MHD mixed convection in lid-driven cavity with heated wavy bottom surface
Scientific Reports (2023)
-
The behaviour of ethylene glycol-based rotating nanofluid flow with thermal radiation and heat generation
Pramana (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.