Abstract
According to the predictive coding (PC) theory, the brain is constantly engaged in predicting its upcoming states and refining these predictions through error signals. Despite extensive research investigating the neural bases of this theory, to date no previous study has systematically attempted to define the neural mechanisms of predictive coding across studies and sensory channels, focussing on functional connectivity. In this study, we employ a coordinate-based meta-analytical approach to address this issue. We first use the Activation Likelihood Estimation (ALE) algorithm to detect spatial convergence across studies, related to prediction error and encoding. Overall, our ALE results suggest the ultimate role of the left inferior frontal gyrus and left insula in both processes. Moreover, we employ a meta-analytic connectivity method (Seed-Voxel Correlations Consensus). This technique reveals a large, bilateral predictive network, which resembles large-scale networks involved in task-driven attention and execution. In sum, we find that: (i) predictive processing seems to occur more in certain brain regions than others, when considering different sensory modalities at a time; (ii) there is no evidence, at the network level, for a distinction between error and prediction processing.
Similar content being viewed by others
Introduction
According to the theory of predictive coding (PC)1,2,3,4,5, our brain constantly attempts to model the probability of its own future states, with the goal of minimizing uncertainty4. More specifically, the brain is considered a hierarchically organized system where, at each level of processing, higher layers try to predict the latent causes of the sensory input coming from lower layers6,7. Thus, neurons at higher levels encode predictions about the upcoming signal, which is continuously compared with the effective signal received from lower levels. Through this comparison, the brain either reinforces existing predictions or it updates them, if these do not match the incoming signal8. When predictions are violated, a prediction error signal5,9,10 is fed back to the neurons encoding predictions. These recursive loops of predictions and error signals ultimately allow the individual to maintain up-to-date representations about its own internal states11 and the surrounding external stimuli. Over the past two decades, PC theory has received extensive support from a vast range of theoretical and experimental studies, both in relation to primary sensory processes5,12,13,14 and higher level cognitive processes15,16, such as decision making and naturalistic speech comprehension14,17,18. Moreover, evidence has been obtained with a variety of methods, mostly with functional magnetic resonance imaging (fMRI), but also electroencephalography19,20,21, computational simulations22, transcranial magnetic stimulation23, and physiological recordings of single neurons (for a review, see24).
Since 1999, when Rao and Ballard published their seminal simulation work on predictive coding in the visual cortex5, there has been a proliferation of attempts to implement PC in the human brain. Initially, it was argued that predictive processing occurs at the cellular level25, where the activity of neural populations is modulated by higher-order predictions and units signalling precision of those predictions. According to Bastos and colleagues26, PC is a typical property of the human cerebral neocortex because its structure suits a hierarchical signal exchange between cortical layers. In particular, error signals seem to be computed in the granular layers (especially layer IV), while predictions would be encoded in layers II and III26. These mechanisms have been identified in a large set of brain areas, including the primary sensory and motor cortices, motor association cortices, dorsal and ventral prefrontal cortices, parietal cortex, anterior cingulate cortex, insula, hippocampus, amygdala, basal ganglia, thalamus, hypothalamus, cerebellum and the superior colliculus27,28. However, in all these regions, neuronal units producing error signals and those encoding predictions of future states are functionally separated29. This separation has been found empirically through computational modelling, where neurons encoding predictions were found to be located in cortical layers II/III and prediction error neurons in layer IV22. Based on these considerations and a previous study30, in this work we consider the functions of prediction encoding and violation in two separate conditions.
Current views conceive brain functions as a product of the co-activity of distributed brain networks31,32. This shift has also influenced implementations of PC in the brain. Specifically, while earlier formulations ground PC mechanisms in different layers of the human cortex, more recent models of PC attribute functions of error computation and prediction encoding to discrete brain regions and their long-range interconnections33,34,35. However, such models describe PC-related networks in isolated domains, such as face processing33. Thus, the question of whether the same network structure exists for the encoding of predictions and transmission of error signal across sensory modalities, domains and experimental paradigms remains open. To our knowledge, no previous study has addressed the existence of a predictive network with meta-analytic functional connectivity methods. In addition, compared to previous studies (e.g.30), we aim to include a wider variety of experimental paradigms and sensory modalities. First, we performed a coordinate-based meta-analysis, then we calculated the functional connectivity of the regions which were activated in the original studies. We formulated the following hypotheses:
-
(a)
At least some of the regions involved in predictive activity might be functionally connected, revealing a spatially defined network. Moreover, given the dense interchange of prediction and error signals in the human cortex26,29, and the heterogeneous nature of our datasets, our network might involve mostly higher order regions.
-
(b)
As regards the brain areas generally involved in predictive processing, we might only partially replicate the results from a recent meta-analysis30, principally due to the diversity of selection criteria. While Siman-Tov and colleagues30 include studies pertaining to three specific domains, we include a wider range of effects and sensory modalities.
-
(c)
As for the areas involved in prediction error computation, a recent meta-analysis9 highlighted the role of striatum, insula, thalamus and fronto-medial structures, while others36 reported other regions (the bilateral ventral striatum, the thalamus, the left frontal operculum, the left caudate and the left IFG). We therefore aimed to verify whether, with different selection and categorization criteria, these results on prediction error computation could be replicated.
Results
Selection of studies
Following the criteria (a–f) described in “Selection of studies”, 106 articles were collected (see Fig. 1). Data from these articles were classified in a table specifying the study identification code, year of publication, first author’s last name, title, scientific journal, number of experimental subjects, experimental task, sensory modality investigated, experimental contrast, type of stimuli. A further selection based on criteria (g) and (h) led to 70 articles. All the peak coordinates listed for the experimental contrast, which were classified as Prediction Encoding or Prediction Violation, were reported in a separate table. The classification of each reported contrast in the two conditions can be found in the Supplementary Tables S1 and S2. When necessary, we converted the peak coordinates to the Montreal Neurological Institute (MNI) space, using the icbm_spm2tal transform on GingerALE37,38 (http://www.brainmap.org/icbm2tal/).
Activation likelihood estimation
A detailed explanation of how each contrast was classified as reflecting the effect of prediction encoding and violation is reported in “Selection of studies”. As a first step, we performed ALE meta-analyses singularly on the two main conditions: Prediction Violation (45 experiments, 511 foci and 939 subjects) and Prediction Encoding (39 experiments, 444 foci, 750 subjects). Afterwards, we run an ALE meta-analysis on a unified dataset, derived by pooling the coordinates relative to the two conditions (70 experiments, 930 foci of activation and 1419 participants). We refer to these analyses as General Prediction. Figure 2 shows the results of the ALE analyses at FWE, p < 0.05. Further details of the ALE results are reported in Table 1.
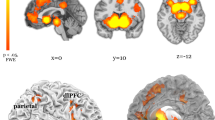
Activation Likelihood Estimation results at a FWE-corrected voxel-level threshold (p < 0.05). Green: condition of General Prediction; Red: condition of Prediction Violation. Two clusters are in common between the two conditions, one in the left anterior insula/claustrum and the other in the left inferior frontal gyrus/precentral gyrus. The General Prediction condition also shows clusters in the right insula, right and left inferior parietal lobule, one in the cuneus and one in the right middle frontal gyrus.
Prediction violation
Two significant clusters were related to the violation of predictions (Fig. 2, red color). The larger cluster included the left inferior frontal gyrus, while a smaller cluster was found over the left anterior insular cortex, partially overlapping with the claustrum.
Prediction encoding
No significant cluster was found for Prediction Encoding at the typically applied, conservative threshold of FWE, p < 0.05. Lowering the threshold to FDR, p < 0.01 still did not produce any significant convergence. However, at an exploratory level, we report the results obtained at a more liberal threshold (Uncorrected, p < 0.0005). At this threshold, fourteen clusters emerged. These included the right superior and left inferior parietal lobules, the right superior, right middle and left inferior frontal gyri, the bilateral fusiform gyri and the right amygdala, and a few clusters with a size inferior to 200 mm3 (including the left amygdala, the left precuneus and the right cuneus, the right insula and the right superior temporal gyrus).
General prediction
Overall, the ALE analysis of the whole dataset returned a set of cortical regions in the frontal and parietal lobes (Fig. 2, green). These include the left inferior frontal gyrus, the insulae bilaterally, the right superior frontal gyrus, the bilateral inferior parietal lobules, and the left precuneus.
Seed-voxel correlations consensus
This technique highlights the regions showing correlated activity with those that were active during the tasks tapping into predictive processing (see “Seed-voxel correlations Consensus”). Overall, the results from all the three conditions are remarkably similar, thus we focus on the results of the General Prediction condition (\({SIM}_{General/Encoding}=0.78\); \({SIM}_{General/Violation}=0.93\); \({SIM}_{Encoding/Violation}=0.68\)). Peaks are located in the left inferior frontal gyrus, the superior temporal gyrus bilaterally, the left thalamus, the left hippocampus and the left cerebellum. Significant voxels are shown in warm colors. The network emerging from negative correlations (cold colors) includes the right cerebellum (uvula), the left precentral gyrus and the post-central gyri bilaterally, and the right middle occipital gyrus (Fig. 3; see Table S2 for more details). Finally, the network relative to Encoding is substantially overlapping with that of the other two conditions, although the map of positive values appeared to be less extended. The major regions of differential connectivity between this and the map of Prediction Encoding include the left insula, the left middle frontal gyrus, the left anterior cingulate gyrus and the inferior frontal gyrus bilaterally (Fig. S3).
Surface, medial and cerebellar mapping of the SVC Consensus analysis revealing the “predictive network” for the condition of General Prediction. Note that this and the Prediction Violation areas overlap entirely. The network that shows the Prediction Encoding areas is presented in the Supplementary Materials (Fig. S2). Warm colors represent positive t-values (range: 4.37–14.17), cold colors are for negative t-values (range: 4.37–19.61), shown in arbitrary units.
Although the SVC Consensus maps indicate regions that are significantly connected to the activation foci reported in the literature, the relation between these foci and such maps needs to be clarified. In fact, on one hand it is possible that only a few foci are responsible for the connectivity maps. On the other hand, these maps might show areas that are not reported in the literature (thus are not primarily considered to be involved in predictive processing), but are systematically connected to the predictive regions, possibly providing input or output to them. To investigate the relation between the foci and their connectivity, we overlapped the SVC Consensus of the General Prediction condition to the corresponding unthresholded ALE map. Here, the unthresholded map can be seen as an indicator of all the activated regions in the literature. We found out that there is a substantial overlap between the two maps (Fig. 4), suggesting that the activated areas tend to be interconnected and to form a coherent functional network (\(SIM = 0.56\)). Lastly, to exclude the possibility of bias due to local connectivity, the SVC Consensus analysis was repeated excluding proximal connections between close areas from the SVC maps. The resulting maps were extremely similar to those obtained with the original SVC Consensus maps, suggesting that activation foci are connected not only to the spatially closer areas, but also to the more distal ones (Fig. S1).
Fail-safe technique
To test the impact of potential selection bias, we performed a fail-safe analysis39 (“Fail-safe technique”). In the General Prediction condition, the analysis shows that at least one of the clusters remains significant up to the introduction of 250% random data, suggesting their robustness against selection bias (Fig. 5). The analysis of the Prediction Violation dataset suggests an even greater robustness (the clusters remain significant up to the inclusion of 425% random data). In general, both fail-safe tests suggest the robustness to bias of the two clusters that are in common for the two conditions, i.e. the left IFG/precentral gyrus and the left insula/claustrum.
Coronal sections showing the results of the fail-safe analysis. Upper row: General Prediction; lower row: Prediction Violation. The color scales represent gradually increasing added random data in percentage. The warmer the color of the pixels, the more random noise (representing potentially unpublished results) is tolerated.
Leave-N-out
This analysis tests the heterogeneity of a dataset, or whether all the studies in a dataset contribute to the results similarly (Section 4.5). It was performed on the condition of Prediction Encoding due to the lack of convergence. Figure 6 shows the results from the leave-N-out analysis. The y axis indicates the number of papers, while the x axis the energy (1-quadratic error/total N experiments). The diagrams show the distribution of energy obtained by removing 3, 5, 7, 9 and 11 articles at each run separately. When removing less than 7 random articles at a time, no important changes are visible in the distribution. Since 7/39 (removed articles/total) equals to 18% of the included experiments, this suggests that the condition of Prediction Encoding is mostly homogeneous. Thus, it is unlikely that the absence of convergence is due to the heterogeneity in the experiments. Instead, it may be due to the spatial distributedness of the activation coordinates per se.
Diagram relative to the results of the leave-N-out analysis on the articles included in the Prediction Encoding condition. In each section, the y-axis shows the number of articles, and the x-axis shows the energy (1-quadratic error/total N experiments). To calculate the standard error, each run with removal and reinsertion of ‘N’ articles was repeated 10 times. Since removing up to 7 articles at a time (18% or the total dataset) still did not introduce important changes in the distribution of energy, we conclude that the dataset is homogeneous. See Section 4.5 for more details.
Discussion
In this study, we partially replicate convergence results from previous meta-analyses. In addition, we provide evidence for the existence of a network involved in PC across sensory modalities and a variety of tasks. This spatially extended and bilateral network overlaps with known large-scale networks supporting attention and task execution. Finally, although the separation between error, weighting and encoding units is supported by our ALE results and previous work, our findings suggest that the regions that are engaged during prediction violation and encoding tend to be functionally connected with the same network.
The ALE results show convergence across tasks targeting predictive processing in a set of cortical regions, in both the Violation and the General condition. However, we did not find convergence in the Encoding condition, even at more liberal thresholds. As suggested by the results of the leave-N-out analysis, this spatial heterogeneity does not seem to be due to the disproportionate contribution of few studies, but rather to the large variability in the localization of foci. A qualitative inspection further indicates that this spatial distributedness is not due to a larger heterogeneity in the selected tasks either. Rather, it likely reflects a wider range of effects, due to our definition of prediction encoding. In fact, while the Violation condition mainly includes effects of surprise and stimulus randomness, that of Encoding reflects effects of item repetition, habituation/adaptation, belief updating, memory, high probability and, in some cases, an explicit effort to predict upcoming stimuli. However, we cannot exclude that the spatial heterogeneity is an intrinsic property of the process itself. For instance, it was found that the effect of belief updating, one of the effects we included in the Encoding dataset, did not replicate between different methods40. If other effects suffered from the same issue, this could perhaps explain their wide spatial distributedness. Another potential reason for the lack of convergence is that one of the typical effects we included is that of repetition suppression, which is defined as a decrease in brain activity in task-related areas41. Therefore, this effect is probably at least partially more task-dependent in nature, thus leading to reduced convergence. It is challenging to compare this result to that by Siman-Tov et al., since only results from a subtraction between violation and formation of prediction are reported30. Nevertheless, we compared a meta-analysis on visual repetition suppression42 with the results of a subgroup analysis on a subset of studies employing visual stimuli from the Encoding condition. While Kim et al. report a network including visual cortices, frontal and parietal regions and the caudate, we again obtained no significant convergence, at the same threshold. This further strengthens the idea that the effects included in the Prediction Encoding condition show strong task-dependency. Although we preferred not to compare such effects systematically due to low power, future meta-analyses may quantitatively compare different aspects of prediction encoding.
One expected site of convergence that we have not found is the cerebellum, especially when analysing the violations of predictions. In fact, this structure has been reported in previous works as an important hub processing the comparison between an internal model and the current sensory input, and as a region that supports procedural and perceptual learning mechanisms43,44,45. However, there are two main reasons why few neuroimaging meta-analyses are able to detect convergence in the cerebellum46. First, there could be technical difficulties associated with the detection of BOLD signal from the cerebellum, principally dependent on experiments targeting climbing fibres, which are poorly coupled to this signal46. Second, some experimental paradigms tend to promote rapid habituation in this area, which in turn produces lower neural responses46.
Overall, our analyses of the Prediction Violation condition confirm previous findings9,30,36 regarding the insula and the IFG, while the involvement of others, such as the striatum and the thalamus, are not replicated. Both the insula and the IFG have been related to the violation of predictions in previous works. In particular, the anterior insulae have been related to the processing of bodily sensations and awareness of subjective feelings47. Moreover, insular regions compute prediction error signals, especially in the interoceptive modality35,48,49. Considering that only a small number of included studies explicitly targeted bodily sensations, this finding deserves special attention. A tentative interpretation is that, regardless of the nature of the specific expectations that are violated in each task, these tend to produce an error broadly related to the self50. The insular cluster also extends to include the left claustrum, which produces prediction error signals in Pavlovian classical conditioning paradigms51. Notably, these involve a component of automatic learning, which probably most of the tasks we included contain, to some degree. The second cluster was located in the IFG, which is involved in risk aversion52, and in detecting a mismatch between expectations and decisions53. Recent studies indicate that this region plays a role in the violation of expectations. For instance, a correlation was found between both IFG and insula activity with a prediction error model during bi-stable perception, which is a paradigm inducing strong violations of visual expectations54. Moreover, ERP components in both which are associated with surprise were larger than those related to belief updating the right IFG and the bilateral insulae55. Lastly, intrinsic connectivity between the IFG and the insula was predicted by the degree of intolerance of uncertainty, which further indicates their sensitivity to error signals56. Together, these findings and our results suggest that the insula and the IFG, and their connectivity during prediction violation across modalities, are a worthy avenue for further research.
The General Prediction condition was designed to tap into the general effects of predictive processing, that arise from the mere fact of performing a task eliciting predictions or prediction errors. Thus, we expected the brain regions emerging here to be related either to one or the other process, or to both. First, convergence was found in two larger clusters, one in the inferior frontal gyrus/precentral gyrus, and the other bilaterally in the insula. Strikingly, both regions also emerged in the meta-analysis of Siman-Tov et al., who similarly pooled together the effects of prediction encoding and violation30. This strengthens the plausibility of this result in other domains than those of music, action and language perception. Further supporting the double role of both the IFG and the insula in PC, activity in these areas represents the building of an expectation, analysing the conjunction across somatosensory, visual and auditory stimulus modality57. However, evidence about the IFG is somewhat more mixed. In fact, its activity does not always seem to depend on the predictability of a situation58. Moreover, whereas some authors describe it as an area involved in the processing of “expectancy input”59, others report increased activity in the IFG when the stimulus probability is low, leading to larger prediction error signal60. As regards the anterior insulae, notably these are an important hub of the salience network61. It is plausible that this hub is more activated in surprising situations driving attention62, which also involve an increased gain in error signal computation (the relationship between predictive and attentional processes is extensively discussed in the following paragraphs). Lastly, the role of precuneus in the General Prediction condition is more difficult to relate to the existing literature. In general, it is involved in self-related cognition, episodic memory and mental imagery63. Interestingly, this region was responsive to deviant stimuli even during sleep64, which may indicate a selective sensitivity to prediction error during different states of consciousness. However, belief updating modulates activity in this region as well40. Overall, these studies support our findings, and suggest that the IFG and the insula might be involved in both the encoding and the violation of predictions. More evidence on prediction violation than encoding exists in both cases, and the sensitivity of the IFG (and the less discussed precuneus) to stimulus probability may more strongly depend on specific task characteristics.
The SVC Consensus analysis was conducted to highlight the brain regions that tend to provide input or output to those involved in prediction violation and encoding. Since the resulting network is largely similar between conditions, we focus on the General Prediction condition.
An important aspect is that the maps relative to the Prediction Violation and Prediction Encoding conditions are highly similar (\(SIM=0.68\), Fig. S2). This means that the regions involved in prediction cross-modally tend to exchange information with the same, broad set of areas during task execution. This finding is surprising for several reasons. First, as previously discussed, the Prediction Encoding condition reflects a greater diversity of effects than that of Violation. Second, a study examining functional connectivity during temporal and spatial predictions found that prediction violation and fulfilment modulate connectivity in distinct networks65. Lastly, this finding seems to contradict the fact that prediction violation and encoding are functionally separated6,26,29. Our ALE results further support this functional separation. Notably, all the regions differentially connected during the violation of predictions (Prediction Violation > Prediction Encoding) have been reported in a meta-analysis on prediction error during reinforcement learning51, an experimental paradigm designed to provoke a strong error signal. Still, despite minor differences between these two maps (Figs. S2 and S3), our results strongly suggest that the same network supports both functions.
A key feature of the network that we obtained in all conditions is its remarkable similarity to the so-called task-positive network (TPN66). The TPN is a set of areas involved in task execution, and is usually divided into three large-scale brain networks related to salience processing61 and the dorsal and the ventral attentional networks67,68.
The fact that the regions which are more involved in prediction are also part of attentional networks replicates the findings by Siman-Tov and colleagues30 and is of key theoretical importance. An increasing body of research considers prediction and attention as dissociable but strongly interdependent processes (for empirical evidences, see69,70,71; for further readings see72,73,74,75). Attention adjusts the computational weight (precision) of prediction error units via synaptic gain enhancement7,76,77, leading to increased error signals. While attention enhances the processing of relevant information and regulates the overall cortical responsiveness78,79,80, prediction allows the brain to take prior information into account81. Moreover, prediction “anchors” attentional processing, meaning that computing predictions is necessary to subsequent attention orientation71. Thus, the overlap between our map and the TPN could be interpreted in several ways. First, despite being distinct processes82,83,84,85, they may share a common neural territory. Considering that this network relies on the original coordinates of brain activations during task performance, it is clearly possible that both attention to the actual stimuli and the prediction of future stimuli were working simultaneously. Second, when multiple modalities are considered together, the activity of prediction and error computation might specifically involve attentional networks more than other brain regions. This has never been observed before because, for obvious practical reasons, only a limited set of modalities are investigated at a time, often in a rather constrained experimental setting. Finally, a third possibility is that the TPN emerged from our analyses merely for the effect of participants’ engagement in any attention-demanding task, and the selected contrasts do not reflect predictive processing at all. It is difficult to rule this possibility out completely, as we did not analyse an arguably non-predictive neutral control condition86. However, as we performed a careful selection of neuroimaging contrasts targeting the effects of interest, the overlap with the canonical attentional networks might imply some relationship between the two processes.
Finally, our predictive network appears to be negatively correlated with the default mode network (DMN; for example, see Fig. 3, negative values). Activity patterns of the DMN and those of the TPN are anticorrelated87, and possibly involved in different forms of cognition. In particular, the DMN is typically reported to be more activated during rest and mind-wandering88. Considering recent work suggesting that this network creates and updates internal predictive models about the self89, and that it is engaged when stimuli are temporally predictable90, the lack of connectivity within its key hubs is rather unexpected, especially in the Encoding condition (cf.40). Moreover, since the DMN is located at the extreme end of a continuum of integration and hetero-modal functioning within the human connectome91,92, it is even more surprising that it did not result from our functionally heterogeneous dataset. A possible reason for its absence could be that, under the hypothesis that the DMN is responsible for the integration of predictions in prior internal models—acting in a sort of “autopilot mode”93,94—almost no included experimental paradigm tested this kind of automatic activity. High temporal resolution techniques, computational, and meta-analytic approaches to functional neuroimaging data can be valuable tools to investigate the role of the DMN in predictive processing in the future.
While we have highlighted the theoretical relevance of our results in the previous paragraphs, the finding of a predictive network could also be meaningful in the clinical context. Debilitating clinical conditions seem to stem from alterations in the production of prediction error signals (e.g. schizophrenia, anxiety95,96,97,98), hyper-rigidity of prior information or inflexible precision of prediction error (e.g. autism99,100,101). Since psychopathology tends to spread in the brain exploiting existing functional connectivity patterns102,103,104,105, and our network is thought to reflect the connectivity between regions involved in cross-modal prediction, investigating this network in different psychiatric samples should be fruitful.
One potential limitation of the current work is that the selection, classification and coding of the articles was conducted manually by one author only. However, the coded dataset was independently cross-checked by another author. Moreover, a section of notes was included in the database with the aim to make the interpretation and selection processes more transparent, as suggested by recent guidelines106. Another potential flaw is caused by the heterogeneity of the definition of “prediction” in the literature. In fact, the concepts of prediction, anticipation and expectation are often used interchangeably107 and how they are operationalized in each study can potentially lead to confusion with other processes81,108. Lastly, the strong presence of studies employing visual or audio-visual tasks may have also limited the validity of the current results (Table S4). However, the absence of early visual areas in both the ALE and the SVC Consensus results may suggest that the impact of this imbalance is nevertheless limited.
Methods
Selection of studies
We searched for publications (Pubmed, https://www.ncbi.nlm.nih.gov/pubmed/) up to January 2019. Articles were chosen using the keywords “predictive coding” AND “fMRI”, OR “functional magnetic imaging” OR “functional brain imaging” in the title or in the abstract of the articles. The decision to choose the only term “predictive coding” instead of a variety of related terms had two purposes: on one hand, to select only articles explicitly explaining their results under this framework; on the other hand, we did not include terms as “prediction error”, “expectation” or “Bayesian brain” so that articles describing the role of expectancy in psychology without referring to PC could be excluded.
In the initial selection stage, the following primary inclusion criteria were applied. We included studies:
-
(a)
which employed fMRI;
-
(b)
which provided the peak coordinates of significant activation in stereotactic brain space (MNI, TAL). In some cases, we included coordinates derived from model fit or correlations with model parameters reflecting the effect of interest. Peak coordinates reflecting functional connectivity were excluded;
-
(c)
which were original experimental works. We excluded reviews or other meta-analytic studies;
-
(d)
which reported whole-brain analysis for the contrasts of interest (i.e., contrasts which were based on a priori regions of interests (ROI analyses) were excluded);
-
(e)
which were based on a healthy adult sample;
-
(f)
which were written in English.
Additional, more specific criteria for inclusion were the following:
-
(g)
the articles had to explicitly support the PC theory, regardless of the sensory modality and the process investigated (i.e., only studies bringing evidence in favour of the framework were considered);
-
(h)
the articles had to include experimental contrasts which reflect the violation of a prediction or the creation, updating or maintenance of a predictive internal model.
First, we collected the contrasts fulfilling these criteria from each experiment. Afterwards, we assigned the coordinates to two conditions. The first condition, that we label Prediction Violation, includes tasks where the expectations of participants are unfulfilled. This effect is reflected in contrasts comparing, for instance, a deviant condition with an expected one, a mismatch condition with a match one, or a random condition with a regular one. Other studies similarly investigated prediction violation, by fitting a statistical model designed to represent the same effect. In general, such experimental conditions might cause a sense of surprise and increase prediction error signals9. The second condition, labelled as Prediction Encoding, contains a variety of effects, reflecting the neural encoding of expectations about upcoming stimuli or the learning of their statistical regularities109. Typically, these included contrasts between a learned and an unfamiliar condition/event, or between an expected and an unexpected condition. However, others target the effect of consciously trying to predict future scenes, those of adaptation to repeated stimuli or the comparison between high and low probability conditions. Finally, in order to investigate the regions involved in prediction encoding and violation, we created a third condition (General Prediction), obtained by merging the datasets of the other two conditions.
Importantly, since it is frequent that coordinates related to the error or the encoding effect are reported in the same experiments from different contrasts, we did not classify the individual studies according to the two conditions, but the single contrasts reported in each study. In other words, the unit of analysis was each individual contrast, and not the study. Furthermore, this classification not only considered the performed task, but also the interpretation of the results that was provided by the authors. For instance, a reduced response in some brain areas, related to the repetition of stimuli, is often interpreted as repetition suppression (RS), hence this effect would be included in our Prediction Encoding category (for a review on how PC may explain RS, see33). Finally, although some authors pointed out that the effects of repetition and expectation suppression are different86, note that we merge both effects under the category of Prediction Encoding. Figure 1 shows a flowchart representing the described steps of the selection process. For a detailed list of the contrasts included in the study and the classification of their reflected effect, see Tables S1 and S2.
Activation likelihood estimation
Activation Likelihood Estimation (ALE) is a meta-analytic technique which detects areas of convergence across peak coordinates of significant activations from functional neuroimaging studies110,111,112. In short, the current version of this algorithm models a Gaussian kernel for each activation peak, considering these as fixed-effects within each study, whereas studies are treated as random-effects. The width of the kernels accounts for between-subject and between-lab variations leading to spatial uncertainty, and it is based on the number of participants in each study110. Then, one Modelled Activation (MA) map is calculated for each study, unifying all the modelled peaks. Afterwards, a union of all the MA maps is performed, where each voxel contains an ALE score. In order to test for statistical significance, the algorithm compares the ALE scores of the obtained union map with a null-distribution of ALE scores, reflecting random spatial association between studies. Specifically, such distribution reflects the null hypothesis that the activation foci are randomly distributed throughout the brain, leading to convergence only by pure chance. Lastly, a correction for multiple comparisons is applied. We used GingerALE version 3.0 (http://www.brainmap.org/) to perform the above meta-analysis. The threshold for detecting significant convergence was set at voxel-level p < 0.05, with 1000 permutations with the family-wise error correction method (FWE), and the analyses were performed in the MNI152 coordinate space. Coordinates reported in TAL in the original study were converted using the icbm2tal transform prior to the ALE analysis38. When more contrasts in one study reflected the effect of interest in each condition (e.g. two contrasts reflecting different aspects of encoding), we merged their respective coordinates. This ensured that participants were not included in the analyses twice106.
Seed-voxel correlations consensus
To investigate the connectivity patterns of the areas involved in predictive processing, we performed a Seed-Voxel Correlations (SVC) Consensus technique, adapted to functional data. This type of connectivity detects the brain regions providing input or output to those activated in the original studies. This technique was originally developed by Boes and colleagues113 to map the connectivity of brain lesions. It consists of overlapping several SVC maps, to verify if they tend to connect to a set of shared areas. The explicit aim of this method was to test if the spatial heterogeneity of brain lesion of a given deficit could be reduced to a common functional network114. Similarly, in the present work we aimed to evaluate the spatial variability of regions associated with predictive processing. Specifically, we hypothesized that the diverse activation foci which were reported in the literature might belong to a single brain network, and thus that they tend to be connected to each other. To do so, each peak that entered the ALE meta-analysis was searched in the Neurosynth resting-state database to obtain a functional connectivity map. This means that the voxel corresponding to a given coordinate of activation was taken as the seed of each SVC. Neurosynth (http://www.neurosynth.org) is an online database of functional meta-data which allows to easily obtain SVC maps calculated on the 1000 subjects of the Brain Genomics Superstruct Project (https://dataverse.harvard.edu/dataverse/GSP). Each SVC map was then considered as an individual subject in a second-level analysis. Then, the overlap of those maps was assessed by the means of a one-sample t-test on SPM12, (http://www.fil.ion.ucl.ac.uk/spm/software/spm12/) with a FWE-corrected threshold of p < 0.05. Both the positive and the negative contrasts were calculated, thus obtaining a map related to the shared positive correlations and one related to the negative ones. This analysis was carried out separately for the datasets of the three conditions (Violation, Encoding and General; for details see below). To facilitate the comparison between the conditions of Prediction Encoding and Violation, we perform a two-sample t-test on the two SVC Consensus maps (see Table S4, Fig. S3).
It should be noted that functional connectivity is partly influenced by physical closeness, so that spatially closer voxels tend to be connected more strongly115. As we worked with a large number of foci (930 in total), it may be argued that many of the seeds were close to each other, and thus their maps would display a high degree of overlap. Therefore, the SVC Consensus results could be biased because of the mere spatial closeness of a high number of peaks. To test this hypothesis, we repeated the SVC Consensus analysis of the General Prediction condition using only the distant connectivity of each seed, defined as all the voxels in each SVC map that were at least 14 mm3 far from the seed115. Hence, local connectivity of a seed is the volume within the radius of 14 mm around it. For this test, all the voxels around the seed in each of the SVC maps were set to 0, before recalculating the t-test.
Fail-safe technique
The fail-safe technique allows the verification of the potential presence of selection bias in the dataset39. The so-called “file-drawer problem” indicates the possibility that there might have been studies that were not published because of null results or findings that were not consistent with the authors’ expectations. This problem affects both neuroimaging and standard effect-size meta-analyses116, so that unpublished studies are likely to contradict the results of the meta-analysis. The fail-safe analysis39 aims to detect selection biases, estimating how many of these studies would make the results of the meta-analysis non-significant. This is performed in two steps. First, we introduced in our datasets a number of maps with similar features to those included in the meta-analysis, but random foci location (spatial noise). These maps represent potentially unpublished neuroimaging studies. Second, we performed the ALE analysis on the original dataset multiple times, using the same threshold and correction settings of the main analysis, but each time with an increasing number of spatial noise maps. We performed this analysis on the conditions of Prediction Violation and General Prediction. Since no significant cluster emerged from the condition of Prediction Encoding at voxel-level FWE p < 0.05, we did not perform the fail-safe analysis in this case. The results of this procedure are generally considered robust if the convergence results are maintained after adding more than 200% of random data.
Leave-N-out
The leave-N-out method is a cross-validation method to test the heterogeneity of a set of data. In the present study, it was employed on the dataset of the Prediction Encoding condition, to check if the reason behind the absence of significant clusters could be the particular impact of a study or group of studies in the meta-analysis. This method gives us the possibility to weight the contribution of each experiment (or group of experiments) and estimate the presence of “outliers”, i.e. studies which contribute to the result disproportionately, driving the outcome to a certain direction117. This analysis has been performed by calculating the ALE results each time omitting a growing number of ‘N’ experiments with reinsertion after each run. Each ‘leave-N-out’ iteration has been repeated 10 times to calculate the standard error. The calculation of 1—quadratic error divided by the total number of experiments that are removed from the analysis and reinserted at each step is a measure called energy. This value can be interpreted as a measure of the extent to which ALE results are affected by the removal of the articles, indicating how much the dataset is homogeneous. In our dataset, the level of energy that seemed to be associated with a change in its distribution is 0.6, thus the procedure at each leave-N stopped when this threshold was reached.
Overlap between the unthresholded ALE map and the SVC Consensus map
In order to test the overall robustness of the network, obtained with the SVC Consensus technique, we created the overlap of the General Prediction Consensus and the unthresholded General ALE maps. An overlap between these maps shows brain regions that are functionally connected to each other. We tested the degree of overlap both by visually analysing the map and by calculating the Cosine Similarity Index (SIM). This is a widely used metric to assess the similarity between two vectors, which is unsensitive to their magnitude. It is calculated as the dot product of two vectors (in our case, the two maps) divided by the product of the two vectors' magnitudes. Then, the similarity between the two maps was calculated with the following formula:
where \({A}_{i}\) and \({B}_{i}\) represent the two maps’ vectors, and n the number of voxels. This index ranges from 0 to 1, where 1 indicates, in our case, complete similarity. We calculate the SIM to compare the SVC Consensus maps between each other, to quantify their overall degree of overlap.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Clark, A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav. Brain Sci. 36, 181–204 (2013).
Friston, K. The free-energy principle: a unified brain theory?. Nat. Rev. Neurosci. 11, 127–138 (2010).
Huang, Y. & Rao, R. P. N. Predictive coding. Wiley Interdiscip. Rev. Cogn. Sci. 2, 580–593 (2011).
Knill, D. C. & Pouget, A. The Bayesian brain: The role of uncertainty in neural coding and computation. Trends Neurosci. 27, 712–719 (2004).
Rao, R. P. & Ballard, D. H. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 2, 79–87 (1999).
Mumford, D. On the computational architecture of neocortex. Biol. Cybern. 65, 135–145 (1991).
Feldman, H. & Friston, K. Attention, uncertainty and free-energy. Hum. Neurosci. 4, 1–23 (2010).
Friston, K. A theory of cortical responses. Philos. Trans. R. Soc. B 360, 815–836 (2005).
D’Astolfo, L. & Rief, W. Learning about expectation violation from prediction error paradigms: A meta-analysis on brain processes following a prediction error. Front. Psychol. 8, 1–11 (2017).
Malekshahi, R. et al. Differential neural mechanisms for early and late prediction error detection. Nat. Publ. Gr. https://doi.org/10.1038/srep24350 (2016).
Barrett, L. F. & Simmons, W. K. Interoceptive predictions in the brain. Nat. Rev. Neurosci. 16, 419–429 (2015).
Hosoya, T., Baccus, S. A. & Meister, M. Dynamic predictive coding by the retina. Nature 436, 71–77 (2005).
Rauss, K., Schwartz, S. & Pourtois, G. Top-down effects on early visual processing in humans: A predictive coding framework. Neurosci. Biobehav. Rev. 35, 1237–1253 (2011).
Osterhout, L. E. E. & Holcomb, P. J. Journal of memory and language 2002. Lang. Cogn. Process. 8, 439–483 (1993).
Deco, G., Jirsa, V. K. & McIntosh, A. R. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nat. Rev. Neurosci. 12, 43–56 (2011).
Hohwy, J., Roepstorff, A. & Friston, K. Predictive coding explains binocular rivalry: An epistemological review. Cognition 108, 687–701 (2008).
Jessup, R. K., Busemeyer, J. R. & Brown, J. W. Error effects in anterior cingulate cortex reverse when error likelihood is high. J. Neurosci. 30, 3467–3472 (2010).
Shain, C., Blank, I. A., van Schijndel, M., Schuler, W. & Fedorenko, E. fMRI reveals language-specific predictive coding during naturalistic sentence comprehension. Neuropsychologia 138, 107307 (2020).
Gordon, N., Koenig-Robert, R., Tsuchiya, N., Van Boxtel, J. J. A. & Hohwy, J. Neural markers of predictive coding under perceptual uncertainty revealed with hierarchical frequency tagging. Elife 6, 1–17 (2017).
Stefanics, G. & Czigler, I. Automatic prediction error responses to hands with unexpected laterality: An electrophysiological study. Neuroimage 63, 253–261 (2012).
Friston, K. J. Waves of prediction. PLOS Biol. 17, 1–7 (2019).
Wacongne, C., Changeux, J. P. & Dehaene, S. A neuronal model of predictive coding accounting for the mismatch negativity. J. Neurosci. 32, 3665–3678 (2012).
Cretu, A. L., Ruddy, K., Germann, M. & Wenderoth, N. Uncertainty in contextual and kinematic cues jointly modulates motor resonance in primary motor cortex. J. Neurophysiol. 121, 1451–1464 (2019).
Carbajal, G. V. & Malmierca, M. S. The neuronal basis of predictive coding along the auditory pathway: From the subcortical roots to cortical deviance detection. Trends Hear. 22, 1–33 (2018).
Shipp, S. Neural elements for predictive coding. Front. Psychol. 7, 1–21 (2016).
Bastos, A. M. et al. Canonical microcircuits for predictive coding. Neuron 76, 695–711 (2012).
Friston, K., FitzGerald, T., Rigoli, F., Schwartenbeck, P. & Pezzulo, G. Active inference: A process theory. Neural Comput. 29, 1–49 (2017).
Owens, A. P., Allen, M., Ondobaka, S. & Friston, K. J. Interoceptive inference: From computational neuroscience to clinic. Neurosci. Biobehav. Rev. 90, 174–183 (2018).
Keller, G. B. & Mrsic-Flogel, T. D. Predictive processing: A canonical cortical computation. Neuron 100, 424–435 (2018).
Siman-Tov, T. et al. Is there a prediction network? Meta-analytic evidence for a cortical-subcortical network likely subserving prediction. Neurosci. Biobehav. Rev. https://doi.org/10.1016/j.neubiorev.2019.08.012 (2019).
Bressler, S. L. & Menon, V. Large-scale brain networks in cognition: Emerging methods and principles. Trends Cogn. Sci. 14, 277–290 (2010).
Raichle, M. E. A paradigm shift in functional brain imaging. J. Neurosci. 29, 12729–12734 (2009).
Grotheer, M. & Kovacs, G. Z. Can predictive coding explain repetition suppression?. Cortex 80, 113–124 (2016).
Kilner, J. M., Friston, K. J. & Frith, C. D. Predictive coding: An account of the mirror neuron system. Cogn. Process. 8, 159–166 (2007).
Seth, A. K., Suzuki, K., Critchley, H. D., Frith, C. & Trust, W. An interoceptive predictive coding model of conscious presence. Cogn. Process. 2, 1–16 (2012).
Chase, H. W., Kumar, P., Eickhoff, S. B. & Dombrovski, A. Y. Reinforcement learning models and their neural correlates: An activation likelihood estimation meta-analysis. Cogn. Affect. Behav. Neurosci. 15, 435–459 (2015).
Laird, A. R. et al. Comparison of the disparity between Talairach and MNI coordinates in functional neuroimaging data: validation of the Lancaster transform. Neuroimage 51, 677–683 (2010).
Lancaster, J. L. et al. Bias between MNI and Talairach coordinates analyzed using the ICBM-152 brain template. Hum. Brain Mapp. 28, 1194–1205 (2007).
Acar, F., Seurinck, R., Eickhoff, S. B. & Moerkerke, B. Assessing robustness against potential publication bias in Activation Likelihood Estimation (ALE) meta-analyses for fMRI. PLoS ONE 13, 1–23 (2018).
Visalli, A., Capizzi, M., Ambrosini, E., Mazzonetto, I. & Vallesi, A. Bayesian modeling of temporal expectations in the human brain. Neuroimage 202, 116097 (2019).
Grill-Spector, K., Henson, R. & Martin, A. Repetition and the brain: Neural models of stimulus-specific effects. Trends Cogn. Sci. 10, 14–23 (2006).
Kim, H. Brain regions that show repetition suppression and enhancement: A meta-analysis of 137 neuroimaging experiments. Hum. Brain Mapp. 38, 1894–1913 (2017).
Boyden, E. S., Katoh, A. & Raymond, J. L. Cerebellum-dependent learning: The role of multiple plasticity mechanisms. Annu. Rev. Neurosci. 27, 581–609 (2004).
Deluca, C. et al. The cerebellum and visual perceptual learning: Evidence from a motion extrapolation task. Cortex 58, 52–71 (2014).
Schultz, W. & Dickinson, A. Neuronal coding of prediction errors. Annu. Rev. Neurosci. 23, 473–500 (2000).
Johnson, J. F., Belyk, M., Schwartze, M., Pinheiro, A. P. & Kotz, S. A. The role of the cerebellum in adaptation: ALE meta-analyses on sensory feedback error. Hum. Brain Mapp. https://doi.org/10.1002/hbm.24681 (2019).
Craig, A. D. How do you feel? Interoception: The sense of the physiological condition of the body. Nat. Rev. Neurosci. 3, 655–666 (2002).
Bossaerts, P. Risk and risk prediction error signals in anterior insula. Brain Struct. Funct. 214, 645–653 (2010).
Ishida, H., Suzuki, K. & Grandi, L. C. Predictive coding accounts of shared representations in parieto-insular networks. Neuropsychologia 70, 442–454 (2015).
Seth, A. K. & Tsakiris, M. Being a beast machine: The somatic basis of selfhood. Trends Cogn. Sci. 22, 969–981 (2018).
Garrison, J., Erdeniz, B. & Done, J. Prediction error in reinforcement learning: A meta-analysis of neuroimaging studies. Neurosci. Biobehav. Rev. 37, 1297–1310 (2013).
Christopoulos, G. I., Tobler, P. N., Bossaerts, P., Dolan, R. J. & Schultz, W. Neural correlates of value, risk, and risk aversion contributing to decision making under risk. J. Neurosci. 29, 12574–12583 (2009).
Sherman, M. T., Seth, A. K. & Kanai, R. Predictions shape confidence in right inferior frontal gyrus. J. Neurosci. 36, 10323–10336 (2016).
Weilnhammer, V., Stuke, H., Hesselmann, G., Sterzer, P. & Schmack, K. A predictive coding account of bistable perception: A model-based fMRI study. PLoS Comput. Biol. 13, 1–21 (2017).
Visalli, A., Capizzi, M., Ambrosini, E., Kopp, B. & Vallesi, A. Electroencephalographic correlates of temporal Bayesian belief updating and surprise. Neuroimage 231, 117867 (2021).
DeSerisy, M., Musial, A., Comer, J. S. & Roy, A. K. Functional connectivity of the anterior insula associated with intolerance of uncertainty in youth. Cogn. Affect. Behav. Neurosci. 20, 493–502 (2020).
Langner, R. et al. Modality-specific perceptual expectations selectively modulate baseline activity in auditory, somatosensory, and visual cortices. Cogn. Affect. Behav. Neurosci. https://doi.org/10.1093/cercor/bhr083 (2011).
Jin, H. et al. Involvement of the left inferior frontal gyrus in predictive inference making. Int. J. Psychophysiol. 71, 142–148 (2009).
Heilbron, M. & Chait, M. Great expectations: is there evidence for predictive coding in auditory cortex?. Neuroscience 389, 54–73 (2018).
Vassena, E., Krebs, R. M., Silvetti, M., Fias, W. & Verguts, T. Neuropsychologia Dissociating contributions of ACC and vmPFC in reward prediction, outcome, and choice. Neuropsychologia 59, 112–123 (2014).
Uddin, L. Q. Salience processing and insular cortical function and dysfunction. Nat. Rev. Neurosci. 16, 55–61 (2015).
Touroutoglou, A., Hollenbeck, M., Dickerson, B. C. & Feldman Barrett, L. Dissociable large-scale networks anchored in the right anterior insula subserve affective experience and attention. Neuroimage 60, 1947–1958 (2012).
Cavanna, A. E. & Trimble, M. R. The precuneus: A review of its functional anatomy and behavioural correlates. Brain 129, 564–583 (2006).
Strauss, M. et al. Disruption of hierarchical predictive coding during sleep. Proc. Natl. Acad. Sci. USA. 112, E1353–E1362 (2015).
Ciullo, V., Vecchio, D., Gili, T., Spalletta, G. & Piras, F. Segregation of brain structural networks supports spatio-temporal predictive processing. Front. Hum. Neurosci. 12, 1–14 (2018).
Fox, M. D. et al. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci. USA. 102, 9673–9678 (2005).
Corbetta, M. & Shulman, G. L. Control of goal-directed and stimulus-driven attention in the brain. Nat. Rev. Neurosci. 3, 201–215 (2002).
Fox, M., Corbetta, M., Snyder, A., Vincent, J. & Raichle, M. Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proc. Natl. Acad. Sci. USA. 103, 10046–10051 (2006).
Chennu, S. et al. Expectation and attention in hierarchical auditory prediction. J. Neurosci. 33, 11194–11205 (2013).
Thillay, A. et al. Sustained attention and prediction: distinct brain maturation trajectories during adolescence. Front. Hum. Neurosci. 9, 3389 (2015).
Hsu, Y.-F., Hamalainen, J. & Waszak, F. Both attention and prediction are necessary for adaptive neuronal tuning in sensory processing. Front. Hum. Neurosci. 8, 152 (2014).
Andermane, N., Bosten, J. M., Seth, A. K. & Ward, J. Individual differences in the tendency to see the expected. Conscious. Cogn. 85, 102989 (2020).
Jones, A., Hughes, G. & Waszak, F. The interaction between attention and motor prediction. An ERP study. Neuroimage 83, 533 (2013).
Marzecová, A., Widmann, A., SanMiguel, I., Kotz, S. A. & Schröger, E. Interrelation of attention and prediction in visual processing: Effects of task-relevance and stimulus probability. Biol. Psychol. 125, 76–90 (2017).
Smout, C. A., Tang, M. F., Garrido, M. I. & Mattingley, J. B. Attention promotes the neural encoding of prediction errors. PLoS Biol. 17, 1–22 (2019).
Kok, P., Rahnev, D., Jehee, J. F. M., Lau, H. C. & De Lange, F. P. Attention reverses the effect of prediction in silencing sensory signals. Cereb. Cortex 22, 2197–2206 (2012).
Clark, A. Surfing Uncertainty: Prediction, Action, and the Embodied Mind (Oxford University Press, 2015).
Schroeder, C. E. & Lakatos, P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 32, 9–18 (2009).
Lakatos, P., Karmos, G., Mehta, A. D., Ulbert, I. & Schroeder, C. E. Entrainment of neuronal oscillations as a mechanism of attentional selection. Science 320, 110–113 (2008).
Busch, N. A. & VanRullen, R. Spontaneous EEG oscillations reveal periodic sampling of visual attention. Proc. Natl. Acad. Sci. 107, 16048–16053 (2010).
Schröger, E., Marzecová, A. & Sanmiguel, I. Attention and prediction in human audition: A lesson from cognitive psychophysiology. Eur. J. Neurosci. 41, 641–664 (2015).
Aitchison, L. & Lengyel, M. With or without you: Predictive coding and Bayesian inference in the brain. Curr. Opin. Neurobiol. 46, 219–227 (2017).
Nahum, L., Barcellona-Lehmann, S., Morand, S., Sander, D. & Schnider, A. Intrinsic emotional relevance of outcomes and prediction error: Their influence on early processing of subsequent stimulus during reversal learning. J. Psychophysiol. 26, 42–50 (2012).
Ransom, M., Fazelpour, S. & Mole, C. Attention in the predictive mind. Conscious. Cogn. 47, 99–112 (2017).
Summerfield, C. & Egner, T. Expectation (and attention) in visual cognition. Trends Cogn. Sci. 13, 403–409 (2009).
Feuerriegel, D., Vogels, R. & Kovács, G. Evaluating the evidence for expectation suppression in the visual system. Neurosci. Biobehav. Rev. 126, 368–381 (2021).
Fox, K. C. R., Spreng, R. N., Ellamil, M., Andrews-Hanna, J. R. & Christoff, K. The wandering brain: Meta-analysis of functional neuroimaging studies of mind-wandering and related spontaneous thought processes. Neuroimage 111, 611–621 (2015).
Buckner, R. L., Andrews-Hanna, J. R. & Schacter, D. L. The brain’s default network: Anatomy, function, and relevance to disease. Ann. N. Y. Acad. Sci. 1124, 1–38 (2008).
Klarić, K. The world according to my predictions: human brains’ default mode network in the context of predictive coding. Ann. N. Y. Acad. Sci https://doi.org/10.13140/RG.2.2.23541.01767 (2018).
Carvalho, F. M., Chaim, K. T., Sanchez, T. A. & de Araujo, D. B. Time-perception network and default mode network are associated with temporal prediction in a periodic motion task. Front. Hum. Neurosci. 10, 268 (2016).
Margulies, D. S. et al. Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc. Natl. Acad. Sci. USA. 113, 12574–12579 (2016).
Tomasi, D. & Volkow, N. D. Functional connectivity hubs in the human brain. Neuroimage 57, 908–917 (2011).
Vatansever, D., Menon, D. K. & Stamatakis, E. A. Default mode contributions to automated information processing. Proc. Natl. Acad. Sci. USA. 114, 12821–12826 (2017).
Pezzulo, G., Zorzi, M. & Corbetta, M. The Secret Life of Predictive Brains: What’s Spontaneous Activity For? (Springer, 2020).
Horga, G., Schatz, K. C., Abi-Dargham, A. & Peterson, B. S. Deficits in predictive coding underlie hallucinations in schizophrenia. J. Neurosci. 34, 8072–8082 (2014).
Schmack, K., Schnack, A., Priller, J. & Sterzer, P. Perceptual instability in schizophrenia: Probing predictive coding accounts of delusions with ambiguous stimuli. Schizophr. Res. Cogn. 2, 72–77 (2015).
Wacongne, C. A predictive coding account of MMN reduction in schizophrenia. Biol. Psychol. 116, 68–74 (2016).
Paulus, M. P. & Stein, M. B. An insular view of anxiety. Biol. Psychol. 1, 383–387. https://doi.org/10.1016/j.biopsych.2006.03.042 (2006).
de Cruys, S. et al. Precise minds in uncertain worlds: predictive coding in autism. Psychol. Rev. 121, 649 (2014).
de Cruys, S., der Hallen, R. & Wagemans, J. Disentangling signal and noise in autism spectrum disorder. Brain Cogn. 112, 78–83 (2017).
Constant, A., Bervoets, J., Hens, K. & de Cruys, S. Precise worlds for certain minds: An ecological perspective on the relational self in autism. Topoi 39, 611–622 (2020).
Manuello, J. et al. The pathoconnectivity profile of alzheimer’s disease: a morphometric coalteration network analysis. Front. Neurol. 8, 739 (2018).
Cauda, F. et al. Hubs of long-distance co-alteration characterize brain pathology. Hum. Brain Mapp. 41, 3878–3899 (2020).
Crossley, N. A. et al. The hubs of the human connectome are generally implicated in the anatomy of brain disorders. Brain 137, 2382–2395 (2014).
Cauda, F. et al. Brain structural alterations are distributed following functional, anatomic and genetic connectivity. Brain 141, 3211–3232 (2018).
Müller, V. I. et al. Ten simple rules for neuroimaging meta-analysis. Neurosci. Biobehav. Rev. 176, 100–106 (2016).
Roepstorff, A. Interactively human: Sharing time, constructing materiality. Behav. Brain Sci. 36, 224–225 (2013).
Feuerriegel, D. Selecting appropriate designs and comparison conditions in repetition paradigms. Cortex 80, 196–205 (2016).
Summerfield, C., Monti, J. M., Trittschuh, E. H., Mesulam, M. & Egner, T. Neural repetition suppression reflects fulfilled perceptual expectations. Nat. Neurosci. 11, 1004–1006 (2008).
Eickhoff, S. B. et al. Coordinate-based activation likelihood estimation meta-analysis of neuroimaging data: A random-effects approach based on empirical estimates of spatial uncertainty. Hum. Brain Mapp. 30, 2907–2926 (2009).
Turkeltaub, P. E., Eden, G. F., Jones, K. M. & Zeffiro, T. A. Meta-analysis of the functional neuroanatomy of single-word reading: Method and validation. Neuroimage 16, 765–780 (2002).
Eickhoff, S.B., Bzdok, D., Laird, A.R., Kurth, F., Fox, P.T. Activation likelihood estimation meta-analysis revisited. NeuroImage 59(3) 2349–2361. https://doi.org/10.1016/j.neuroimage.2011.09.017 (2012).
Boes, A. D. et al. Network localization of neurological symptoms from focal brain lesions. Brain 138, 3061–3075 (2015).
Darby, R. R., Joutsa, J. & Fox, M. D. Network localization of heterogeneous neuroimaging findings. Brain 142, 70–79 (2019).
Sepulcre, J. et al. The organization of local and distant functional connectivity in the human brain. PLoS Comput. Biol. 6, 1–15 (2010).
Rosenthal, R. The ‘file Drawer problem’ and tolerance for null results. Psychol. Bullettin 686, 638–641 (1979).
Gee, T. Capturing study influence: The concept of ‘gravity’ in meta-analysis. Couns. Psychother. Health 1, 52–75 (2005).
Acknowledgements
We are thankful to Isaac Stead, who proofread our manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
L.F. conceptualized the research idea, designed the study, curated the dataset, performed part of the statistical analyses, and created data visualizations. L.M. contributed to the conceptualization of this research work, provided methodological knowledge, and performed statistical analyses. D.L. devised the Supplementary Material and provided feedback on study design and dataset building. J.M., T.C. and A.T. curated substantial part of the methodology, by supporting, performing and validating the present statistical analyses. G.Z.K. provided research materials, contributed valuable input for study conceptualization, and revised the manuscript. S.D and F.C. provided organizational and methodological support, revised and corrected the manuscript. The manuscript was primarily written by L.F., L.M. and G.Z.K., and it was approved by all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ficco, L., Mancuso, L., Manuello, J. et al. Disentangling predictive processing in the brain: a meta-analytic study in favour of a predictive network. Sci Rep 11, 16258 (2021). https://doi.org/10.1038/s41598-021-95603-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-95603-5
This article is cited by
-
Active Inference and Social Actors: Towards a Neuro-Bio-Social Theory of Brains and Bodies in Their Worlds
KZfSS Kölner Zeitschrift für Soziologie und Sozialpsychologie (2024)
-
Neural correlates of hierarchical predictive processes in autistic adults
Nature Communications (2023)
-
Schema-Centred Unity and Process-Centred Pluralism of the Predictive Mind
Minds and Machines (2022)
-
Prediction learning in adults with autism and its molecular correlates
Molecular Autism (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.