Abstract
Cardiorespiratory fitness (CRF) is associated with mortality and cardiovascular disease, but assessing CRF in the population is challenging. Here we develop and validate a novel framework to estimate CRF (as maximal oxygen consumption, VO2max) from heart rate response to low-risk personalised exercise tests. We apply the method to examine associations between CRF and health outcomes in the UK Biobank study, one of the world’s largest and most inclusive studies of CRF, showing that risk of all-cause mortality is 8% lower (95%CI 5–11%, 2670 deaths among 79,981 participants) and cardiovascular mortality is 9% lower (95%CI 4–14%, 854 deaths) per 1-metabolic equivalent difference in CRF. Associations obtained with the novel validated CRF estimation method are stronger than those obtained using previous methodology, suggesting previous methods may have underestimated the importance of fitness for human health.
Similar content being viewed by others
Introduction
Maximal oxygen consumption (VO2max) is the gold-standard measure of cardiorespiratory fitness (CRF) and a powerful predictor of all-cause and cause-specific mortality1,2,3 and morbidity4,5,6,7. VO2max is rarely directly measured in population studies due to cost and safety concerns. Alternative methods have been developed to indirectly measure VO2max from heart rate (HR) response to incremental submaximal exercise tests8. Screening procedures are generally used to exclude high-risk individuals from CRF testing, causing selection bias. Ironically, excluded individuals are more likely to experience incident disease events, making it harder to examine relationships between measured CRF and disease outcomes.
Exercise tests typically used in population studies are broadly classified as steady-state tests or ramped tests. Steady-state tests consist of several stepwise work rate (WR) increments every 4–6 min, allowing HR and VO2 to stabilise at each WR. Methods for estimating VO2max from submaximal HR response to steady-state testing are well-studied and validated9. Steady-state testing can be long and inefficient, however, depending on the number of WR increments and impractical for populations with low exercise tolerance10. Ramped tests continuously increase WR in small increments. This allows HR and VO2 response to be characterised over a wider range of WR values in less time and enables the rate at which WR is increased (i.e. ramp rate) to be individualised to the participant’s ability and contraindications to exercise. Ramped tests present an analytic challenge: at a given ramped WR, HR and VO2 values will be less than those measured during a steady-state test at an equivalent WR11. Thus, VO2max estimates from ramped tests may be biased if the HR- or VO2-ramp response is extrapolated from submaximal to maximal levels using methods validated for steady-state tests. Alternative methods for estimating VO2max from HR- or VO2-ramp response may be valid for common ramp rates but are insufficient for tests individualised across a wide range of ramp rates12,13,14.
We designed a ramped submaximal cycle ergometer test to assess CRF in 80,000 participants from the UK Biobank (UKB) study. The UKB-CRF test had relatively low WR and was individualised depending on presumed ability and a preliminary health risk assessment, resulting in 11 sets of protocols for men and women (22 in total). Previous attempts at estimating VO2max from UKB-CRF test data have assumed no difference in estimation bias between different test protocols, and some use only a small proportion of available test data15,16,17,18,19,20,21. These approaches may broadly rank individuals by CRF level, but external data are required to verify their internal validity and establish absolute validity against directly measured VO2max.
Here we develop and validate a novel CRF estimation method for the UKB-CRF test using exercise test data from a validation study of participants, age-, sex- and BMI-matched to the UKB sample. We first devise a hierarchical CRF estimation framework using ramped and steady-state HR response features to estimate VO2max. We then demonstrate the validity of VO2max estimates against direct measurements, apply the framework to estimate CRF in UKB participants, and conduct survival analyses to examine associations between CRF and prospective health outcomes. Finally, we compare our findings with previous methods used to estimate CRF in UKB.
Results
Development and validation of CRF estimation method for the UKB-CRF test
We recruited 105 female (mean age: 54.3y ± 7.3) and 86 male (mean age: 55.0y ± 6.5) validation study participants (Supplemental Fig. 1). Participants completed a series of UKB-CRF tests and a submaximal steady-state test to characterise exercise HR response across different test protocols. VO2max was directly measured during an independent maximal exercise test (Fig. 1A). All participants contributed submaximal exercise test data. Some maximal exercise test data were excluded due to missing HR and VO2 response data (n = 25) and failure to achieve predefined maximal exercise threshold criteria (n = 33). Participant characteristics were generally similar in these subsamples.
Conceptual framework and design for validation study. (A) Overview of the five exercise tests performed by validation study participants (3 UKB-CRF tests (flat protocol, low ramp protocol, high ramp protocol), 1 steady-state test unique to the validation study, and 1 maximal exercise test to measure VO2max). X-axes: Time; Y-axes: Work rate (WR). Tests were completed consecutively, and work rates were individualised according to standardised criteria (See `Experimental procedure and equipment’ in Methods). UKB-CRF test and steady-state test data were used for method development. Maximal exercise test data were withheld from method development and used for validation purposes only. (B) Conceptual plot of WR-to-VO2 response during steady-state and ramped exercise tests. VO2 increases linearly at a rate proportional to the rate of change in WR (i.e. ramp rate) until VO2max is reached (in an exhaustive test). The WR-to- VO2 relationship (line slope) changes depending on the ramp rate of the test. As ramp rate decreases, the WR when VO2max is achieved approaches the maximal WR for an exhaustive steady-state test. Note that VO2 is extrapolated to maximal values for demonstrative purposes, but in the validation study ramped and steady-states tests were non-exhaustive. (C) Exemplar HR data (blue scatter and grey line; upper panel), WR data (red line; lower panel), and test phase annotation for ramp test. (D,E) Feature extraction for ramp phase using simple linear regression model and for recovery phase using first-order exponential decay model (see Supplemental Methods).
HR response features derived from the UKB-CRF test vary with ramp rate of the assigned protocol and, if unaccounted for, will result in biased CRF estimates (Fig. 1B). HR response features may also be of poor quality or missing, a common situation in exercise testing. We addressed these issues by integrating UKB-CRF test and steady-state test HR response features (Fig. 1C–E) into a multilevel CRF estimation framework (Supplemental Table 1). The framework uses these features to estimate the HR–WR relationship that would be established if a longer steady-state test had been completed instead of the short ramped UKB-CRF test. Maximal WR is then estimated by extrapolation to age-predicted maximal HR (HRmax). This framework approach minimises bias introduced by protocol assignment of ramp rate. It also enables the application of different estimation models to different data availability scenarios. We derived several estimation models, notated as M1 through M5 in order of comprehensiveness. The highest-level model (M1) used more HR response features to estimate CRF, while lower-level models (M2 through M5) used fewer.
An accepted method for estimating VO2max from submaximal cycle ergometry is to estimate maximal steady-state WR from HR response and convert the estimated maximal steady-state WR to VO2max using the American College of Sports Medicine (ACSM) metabolic equation for cycling9. Before applying this equation, we verified that maximal WR estimated from the UKB-CRF test by the multilevel framework corresponded to maximal steady-state WR by comparing WR estimates with WR measured at the respiratory compensation point (RCP) from the maximal exercise test. The WR at RCP is equivalent to maximal steady-state WR and is the WR above which anaerobic metabolism is needed to sustain exercise until exhaustion. Figure 2 shows agreement with WR at RCP using the most comprehensive model for each test type (M1: ramp tests; M4: flat tests). Agreement for remaining estimation models is shown in Supplemental Table 2. Across estimation models (M1 through M5), estimated WR were strongly correlated with WR at RCP (Pearson’s r range 0.81–0.86) with no significant mean bias (Bias range in women: − 3.7 to 3.8 W; in men: − 5.2 to 0.1 W). Mean bias also did not differ between low and high ramped tests, but root-mean-square error was generally lower for flat tests. Correlations were higher when WR was computed using features from ramp- and recovery-phase data (models M1 through M3) compared to using only flat-phase data (models M4 and M5), although all models were relatively precise. We also compared estimated WR with WR measured at the lactate threshold (Supplemental Table 3) and WR measured at VO2max (Supplemental Table 4).
Scatterplots (top row) and Bland–Altman plots (bottom row) demonstrating agreement between work rates measured at the respiratory compensation point (RCP) and work rates estimated from flat ramp tests (left column), low ramp tests (middle column), and high ramp tests (right column) using the most comprehensive prediction equation from the multilevel framework (M1 for ramp tests; M4 for flat test). r: Pearson’s correlation coefficient, rho: Spearman’s rank correlation coefficient. RMSE: Root-mean-square error.
After confirming that WR computed from the multilevel framework corresponded to WR at RCP, we estimated VO2max by applying the ACSM metabolic equation. We then compared these VO2max estimates with VO2max directly measured from the maximal exercise test. Figure 3 demonstrates VO2max agreement using the most comprehensive estimation model for each test type (M1: ramp tests; M4: flat test). Agreement for remaining estimation models is shown in Supplemental Table 5. Estimated VO2max was correlated with measured VO2max (Pearson’s r range 0.68–0.74) with no significant mean bias (Bias range in women: − 0.8 to 0.4 ml O2 kg−1 min−1; in men: − 0.3 to 0.3 ml O2 kg−1 min−1), establishing the multilevel framework’s absolute validity. We also quantified the proportion of bias emerging from uncertainty when using age-predicted versus measured HRmax in the multilevel framework (Supplemental Table 6); agreement improved only slightly when using measured HRmax. As a sensitivity analysis, we also evaluated agreement between estimated and directly measured VO2max in all participants with usable maximal test data and relaxing the criteria for maximal effort (n = 178). Estimated and directly measured VO2max were not statistically significantly different across all comparisons in this analysis.
Scatterplots (top row) and Bland–Altman plots (second row) demonstrating agreement between directly measured VO2max and VO2max estimated from flat tests (left column), low ramp tests (middle column), and high ramp tests (right column) using the most comprehensive equation from the multilevel framework (M1 for ramp tests; M4 for flat test). Below these (bottom row), the box plot demonstrates agreement across all ramp rates tested using estimates from the multilevel framework, the simple linear regression method, and the two-point estimation method. r: Pearson’s correlation coefficient, rho: Spearman’s rank correlation coefficient. RMSE: Root-mean-square error.
We next addressed whether the multilevel framework would yield similar CRF estimates from different UKB-CRF test protocols completed by the same validation study participant (i.e. internal validity). Within-participant, we compared VO2max estimates from low and high ramp tests across estimation models M1–M3 and M5, as well as between flat tests across M4 and M5 (Supplemental Table 7). VO2max estimates from different UKB-CRF test protocols were highly correlated across estimation models (Pearson’s r range: 0.91–0.99). While mean bias was minimal across all comparisons (Bias range: − 0.6 to 0.0 ml O2 kg−1 min−1), some were statistically significantly different from zero mean bias. We also examined differential bias by protocol ramp rate (from 0 W min−1 for flat tests and 7.5–25 W min−1 for ramp tests), finding mean bias to be minimal across all ramp rates tested (Fig. 3, lower panel).
For method-comparison purposes, we also assessed the absolute and internal validity of a simple linear regression CRF estimation method used previously by our group and a two-point CRF estimation method used by other groups working with UKB data. These latter two methods relate exercise HR response to WR without accounting for protocol ramp rate. Both methods demonstrated overestimation bias and low precision when applied to ramped tests but had low bias when applied to flat tests (Supplemental Fig. 2).
To assess measurement consistency of the UKB-CRF test, we evaluated short-term test–retest reliability in validation study participants and long-term test–retest reliability in UKB participants (Fig. 4). In validation study participants with short-term repeat tests (within 2 weeks, n = 87), estimated VO2max values from the first and second UKB-CRF tests were highly correlated (r = 0.91) with no mean difference. Agreement was nearly as strong (λ = 0.79) in UKB participants with long-term repeat tests (about 2.8 years between tests, n = 2877).
Scatterplots (top row) and Bland–Altman plots (bottom row) demonstrating short- and long-term test–retest reliability. r: Pearson’s correlation coefficient, rho: Spearman’s rank correlation coefficient. RMSE: Root-mean-square error. Lamda: Regression-dilution coefficient. SE: Standard error. Short-term reliability data are from the validation study (n = 87, follow-up ~ 10 days) and long-term reliability data are from the repeat-measures sub-study in UK Biobank (n = 2877, follow-up ~ 2.8 years).
Application of VO2max estimation method in UKB cohort
After establishing the absolute validity, internal validity, and test–retest reliability of the multilevel framework for interpreting UKB-CRF test data, we applied the framework to estimate CRF in UKB (Supplemental Fig. 3 and Supplemental Table 8) and examined prospective associations with health outcomes. In total, 42,351 women and 37,650 men from UKB were considered in this analysis. Baseline participant characteristics are shown by sex-specific and age-adjusted CRF tertiles, across half-decade age groups, in Supplemental Table 9. Estimated VO2max was higher in men compared to women, and in younger versus older adults. Participants in the middle and higher CRF tertiles also had better baseline measures of heart and lung function, lower body weight, and better self-perceived health than participants in the lower tertile.
To examine associations between CRF and prospective health outcomes in UKB, we used Cox proportional hazards regression to estimate hazard ratios per 1-metabolic equivalent difference in CRF (METs; 1 MET = 3.5 ml O2 kg−1 min−1) for fatal and nonfatal events, excluding those experiencing the event in question in the first 2 years of follow-up. In total, 2670 participants died during a median 9.9 years (interquartile range 9.7–10.0) of follow-up (746,377 person-years). After adjustment for potential confounders, each 1-MET difference in CRF was associated with approximately 8% (95%CI 5–11%) lower all-cause mortality (Fig. 5); this equates to a difference in mortality of about 23% between top and bottom CRF tertiles. Associations were stronger for deaths from respiratory disease (RD; 14% lower per 1-MET, 95%CI 8–19%) and similar for deaths from cardiovascular disease (CVD; 9%, 95%CI 4–14%), and cancers (8%, 95%CI 5–12%). Higher CRF was more strongly associated with lower mortality risk in obese compared to non-obese participants (Supplemental Fig. 4).
Hazard ratio and 95% confidence interval (CI) for prospective log-linear associations (Cox regression) between fatal and non-fatal outcomes in the UK Biobank with cardiorespiratory fitness in metabolic equivalents (METs, per 3.5 ml O2·kg−1 min−1) computed from the multilevel framework and simple linear regression methods. Event-rate per 100,000 person-years. AF: atrial fibrillation; COPD: chronic obstructive pulmonary disease; CVD: cardiovascular disease; IHD: ischaemic heart disease; RD: respiratory disease. COPD incidence mostly reflects severe COPD since only ~ 25% of cases end up in hospital. Mortality and incidence event-rates differ between fitness prediction methods owing to different inclusion criteria at the estimation level.
Analyses of incident disease outcomes combined fatal and non-fatal events from hospital admissions data over 6.9 (interquartile range 6.7–7.0) years of follow-up. Risk of chronic obstructive pulmonary disease (COPD; 10% lower per 1-MET, 95%CI 4–16%) and heart-failure (11%, 95%CI 3–19%) were more strongly associated with CRF than stroke (3%, 95%CI − 5 to 10%), ischaemic heart disease (IHD; 2%, 95%CI − 2 to 5%), and atrial fibrillation (AF; − 7%, 95%CI − 1 to − 12%). Associations with CRF were not significant in obese participants for these endpoints (Supplemental Fig. 4).
For method comparison purposes, associations were also examined for CRF computed using the simple linear regression CRF estimation method. Associations were generally shallower and estimated with less uncertainty using simple linear regression, an analysis which also included fewer participants compared to the analysis using the multilevel framework.
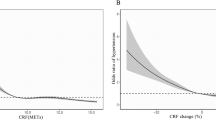
We used cubic spline regression to examine natural variation and potential nonlinearity in dose–response associations between CRF and prospective health outcomes (Fig. 6; obesity-stratified result in Supplemental Fig. 5). For method comparison purposes, separate sets of dose–response curves were modeled for CRF when computed with the multilevel framework and when using the simple linear regression method. For mortality outcomes, CRF was inversely associated with death from all causes, CVD, RD, and cancer in the CRF range of 3–11 METs. Relationships were steeper at the low end of that range and shallower at higher CRF levels. The shape of estimated CRF dose–response relationships varied considerably across incident disease outcomes. In the range of 3–8 METs, CRF was inversely associated with incidence of IHD, heart-failure, AF, stroke, and COPD, but disease associations flattened (IHD, heart failure, COPD) or became positive (AF, stroke) above 8 METs. Differences between these associations and those observed using the simple linear regression to estimate CRF were most evident at the tails of the distributions.
Hazard ratio and 95% confidence interval (CI) for nonlinear associations (cubic splines, Cox regression) between fatal and non-fatal outcomes in the UK Biobank with cardiorespiratory fitness in metabolic equivalents (METs, per 3.5 ml O2·kg−1·min−1) computed from the multilevel framework and simple linear regression methods. Hazard ratios were computed relative to a fitness reference point of 8.0 METs. AF: atrial fibrillation; COPD: chronic obstructive pulmonary disease; CVD: cardiovascular disease; IHD: ischaemic heart disease; RD: respiratory disease. Mortality and incidence counts (superimposed histograms) differ between fitness estimation methods owing to different inclusion criteria at the estimation level.
We performed several sensitivity analyses to determine whether health associations with CRF computed from the multilevel framework were altered by restricting the analytical sample or by using different estimation models in the multilevel framework to compute CRF. Compared to the main analysis, health associations with CRF were slightly weaker but estimated dose–response curves were qualitatively similar when the analytic sample was restricted so as to be matched with the sample used when the simple linear regression method was applied (Supplemental Figs. 6 and 7). To examine differences in health associations by estimation models in the multilevel framework, we split the analytic sample into two separate sets of analyses for those who either performed a ramp test (Supplemental Figs. 8 and 9) or a flat test (Supplemental Fig. 10). In the ramp test analysis, associations were generally stronger using more comprehensive estimation models (M1–3) compared to less comprehensive models (M5). Estimated dose–response curves were qualitatively similar for all outcomes. The association with incident AF, however, was a positive monotonic relationship at all estimation models in the ramp test subsample (event rate 217 per 100,000 person-years), rather than the U-shaped relationship found in the main analysis. In the subsample allocated a flat test (Supplemental Fig. 10), the association with incident AF was positive, non-significant, and at a higher event rate (460 per 100,000 person-years). The analysis in the flat test subsample is primarily a comparison of associations for CRF estimated by M4 and M5. Associations were generally similar between the two estimation models but non-significant due to the small sample size. We did not estimate dose–response curves in the flat test subsample for the same reason.
Discussion
We have developed a novel multilevel CRF estimation method based on HR response to short, individualised submaximal exercise tests and applied it in one of the largest and most inclusive population-based studies of CRF. We establish the validity and reliability of this new method in an independent validation study and demonstrate advantages over other methods applied in previous population studies.
The multilevel framework method estimates VO2max by modeling maximal steady-state exercise capacity from HR response to the UKB-CRF test. This approach minimises CRF estimation bias that may be introduced by the UKB-CRF test individualisation process. We demonstrate that for each 1-MET difference in CRF estimated using the multilevel method, all-cause mortality was 8% lower and CVD mortality was 9% lower; associations nearly twice as strong as those estimated when using a method that did not use external data to map between ramped and steady-state exercise15. Improvements in CRF estimation validity and disease outcome characterisation may have broad implications for future research in UKB.
We have reported on a range of associations between CRF and prospective health outcomes in UKB, demonstrating the protective effects of CRF on all-cause and cause-specific mortality and morbidity. Our findings are largely in agreement with numerous other populations-based studies1,2,3, however associations between CRF and non-fatal incidence rates of IHD, stroke, and AF were not significant. In previous work, dose–response associations were J-shaped for stroke22 and U-shaped for AF23. Another study with longer follow-up time and more incident events reported inverse relationships between CRF and AF24. As for cancer mortality, we found an inverse relationship between CRF and all-cancer mortality, in agreement with previous studies25,26. Additional follow-up time is warranted to investigate CRF associations with site-specific cancers in UKB. Additional follow-up would, however, also increase the probability that participants may change their CRF level over time, which would dilute observed associations between a single baseline measure of CRF and health outcomes. The Cox proportional hazards model estimates the difference in hazards of the outcome in question by baseline exposure level, and if this exposure level is very stable over time, the estimated association will be a more accurate reflection of the importance of that exposure than if it were more variable. We show in this work that CRF has a long-term reliability of around 0.80, indicating good stability. However, if we were to formally apply correction for the element of instability using regression dilution bias methods, the point estimate of hazard ratios would be about 20% stronger than what we report here but with wider confidence intervals.
We have developed a novel multilevel estimation framework that optimises the validity of VO2max estimates from the UKB-CRF test. The key strengths of the framework are that it: (1) uses HR response features across all test phases to infer the relationship between HR and exercise intensity; (2) is flexible to the availability or absence of HR response features due to data quality issues; and (3) harmonises the inferential modeling of HR response features to the within-person invariant relationship between steady-state HR and exercise intensity. For these reasons, predicted CRF values and health associations we have presented diverge from previous reports of CRF in UKB. In a previous analysis15, we estimated CRF by using simple linear regression to establish the relationship between ramp test HR response and WR. This approach is currently the most common in the field but does not account for the protocol individualisation process of ramp rates used in UKB. Using external validation data, we show that this approach overestimates VO2max differentially by test protocol, thus limiting the ability to validly compare VO2max estimates from different UKB-CRF tests. Lacking protocol comparison data, previous work could only partially address the impact of this by a meta-analytic approach. Our new approach resolves this issue at the individual level and demonstrates stronger associations with all-cause and cause-specific mortality and morbidity compared to this previous non-validated method. We can have more confidence in these associations because validity of the exposure is now documented.
Other approaches also use simple linear regression, but establish the relationship between HR and exercise capacity by relating resting HR to only a single measurement of HR during the test16,17,19,20,21,27,28,29,30. HR measurement noise will greatly decrease precision of this approach, and resulting CRF estimates are still subject to bias that will differ by protocol ramp rate. Another reported approach18,31,32,33 is to use the maximally achieved WR to infer CRF. As most participants completed their test, this approach merely reflects the protocol that participants were assigned according to age, sex, body size, resting HR, and exertional chest pain risk, with the latter feature most indicative of test risk-stratification. While prospective associations of such an exposure measure with CVD endpoints do to a degree validate the stratification of risk, it is not possible to interpret these results solely as associations with CRF. At best, it is a composite score of exercise capacity and cardiac risk.
Our CRF estimation approach may also have implications for exercise prescription in clinical environments. CRF testing in UKB has demonstrated that it is safe to obtain valid VO2max estimates in a population setting while including some individuals with contraindications to exercise. In practice, such individuals would be prescribed a less strenuous exercise test that could contain less information about their physiological state compared to a more strenuous test. The multilevel framework approach we describe in this work for interpreting such test results yields unbiased estimates of CRF, addressing a well-recognised limitation of exercise testing34. Future research is warranted to investigate whether the multilevel framework can be generalised to other ramp-style exercise tests.
The strengths of our study include independent validation work for our VO2max estimation approach prior to estimating dose–response relationships with disease outcomes in the UK Biobank. There are also some limitations. The exercise capacity of validation study participants was slightly higher than the average capacity of UKB participants. Furthermore, the comparatively relaxed testing conditions in the validation study may not directly match those in UKB, where testing was conducted in large testing centres and where a variety of additional exposures were examined under stringent time constraints. We also did not directly evaluate the validity of UKB-CRF test protocols with ramp rates at 2.5 and 5.0 W min−1. Agreement for ramp rates above and below these untested rates were unbiased, however. Finally, we examined non-fatal health outcomes using only hospitalisation data; this does not necessarily capture all disease events in a given category.
Conclusions
We have demonstrated the absolute validity, internal validity, and test–retest reliability of a novel VO2max estimation method for individualised ramped exercise tests that can be safely and efficiently applied in population studies. Our analytic approach uses a generalised multilevel modeling framework that bridges the gap between steady-state and ramped incremental exercise, addressing a persistent problem in exercise physiology and prescription. CRF estimated in this way is more strongly associated with mortality and other disease endpoints than previous methodology, strengthening the case for promoting CRF in the general population.
Methods
UKB-CRF test description
The UKB-CRF test protocol design and individualisation process are described in detail by the most recent test manual35. Briefly, participants were categorised into separate risk levels according to questions adapted from the Rose-Angina questionnaire. Participants with “minimal” and “small” risk completed an individualised ramp test, those with “medium” risk completed a flat test, and those with “high” risk did not complete an exercise test. Ramped tests began with a 2-min flat-phase at a single WR (30 W for females, 40 W for males) followed by a 4-min ramp-phase where WR increased continuously to a pre-specified target WR. The target WR was calculated as a risk-adjusted percentage (50% for those with “minimal” risk, 35% for “small” risk) of the maximal WR predicted from an equation derived from maximal exercise (cycle ergometer) testing data collected in the Danish Health Examination Survey 2007–200836. The computed value for target WR was combined with participant sex (“F” for female, “M” for male) to notate different exercise protocols. For example, a male participant with “minimal” risk and predicted WR at VO2max of ~ 200 W would have a target work rate of 100 W and be individualised to UKB protocol “M100”. Flat tests consisted of a single 6-min flat-phase. Participants cycled at a 60-rpm cadence while WR and heart rate (HR) were monitored. All tests ended with a 1-min recovery-phase where participants sat quietly and motionless on the ergometer. No adverse events were reported when this test was applied in UKB.
Validation of UKB-CRF test
Validation study participants
We recruited a subsample of participants from the Fenland study, a population-based study in Cambridgeshire, UK37, using an age-, sex- and BMI-stratified random sampling procedure (Supplemental Table 10). Exclusion criteria were: heart pacemaker; unable to walk without aid; history of angina pectoris; blood pressure greater than 180/110 mm Hg; musculoskeletal injury that would impair cycling on the ergometer; pregnancy; and currently taking cardioactive drugs (e.g. beta-blockers, aspirin). Ethical approval was obtained by the University of Cambridge Human Biology Research Ethics Committee (Ref: HBREC/2015.16). All participants provided written informed consent.
Experimental procedure and equipment
Validation study participants were screened according to standardised procedures used for the UKB-CRF test35. Then, participants completed the UKB flat test, two UKB ramped tests at different ramp rates, a steady-state test (unique to the validation study), and another ramped test (validation only) to elicit VO2max (Fig. 1A). Tests were conducted consecutively, separated by at least 15 min of rest, and were specified according to the test that the participant would have been assigned had they been part of UKB (see Supplemental Table 11). The target (highest) WR for the second ramped test was at least 30 W greater than the first; thus, each participant completed a “low” and “high” ramped UKB test. The steady-state test consisted of four incremental 4-min flat-phases with each WR increment ranging from 10 to 20 W. For the ramped max test, participants were fitted with a face mask to measure respiratory ventilation and gas exchange and cycled while WR increased until exhaustion. VO2max was considered reached if two of the following criteria were met: a respiratory exchange ratio exceeding 1.20; no VO2 increase despite increasing WR (< 2.5 ml O2 kg−1 min−2); and no HR increase despite increasing WR. During data analysis, the levelling-off criterion was confirmed by inspecting whether the first differential of HR and VO2 data approached zero over the last 1-min period of the maximal test.
VO2max was expressed as the average of the two highest VO2 measurements in the last forty-five seconds of the maximal exercise test. WR values were measured at VO2max (i.e. maximal work rate achieved on the test, WRmax), at the lactate threshold (LT), and at the respiratory compensation point (RCP). The work rate at LT was measured at the point when both ventilatory equivalent of oxygen (VE/VO2) and end-tidal pressure of oxygen (PETO2) increased with no increase in ventilatory equivalent of carbon dioxide (VE/VCO2). The work rate at RCP was measured at the point when both VE/VO2 and VE/VCO2 increased and end-tidal pressure of carbon dioxide (PETCO2) decreased (see Supplemental Fig. 11)38. Directly measured WR at LT and RCP were determined visually by three independent investigators, blinded to all other measures except the variables above needed for making direct measurements. The median value among investigators was considered the final value.
Cycling was performed on an electromagnetically-braked stationary bike (eBike ergometer, GE) while electrocardiography (ECG) was recorded using 4-lead ECG (Cardiosoft) on the forearms and a Actiwave Cardio device (CamNtech, Papworth, UK) on the chest with sampling frequency of 128 Hz. The 4-lead ECG leads were placed on the cubital fossa and ventral wrist of the left and right arms (mimicking the UKB protocol). Cycling WR were controlled by computer software. Respiratory gas measurements were conducted using a computerised metabolic system with Hans Rudolph face masks (Oxycon Pro, Erich Jaeger GmbH, Hoechberg, Germany) as validated elsewhere39.
All ECG signals were processed using the Physionet Toolkit implementation of the SQRS algorithm40, which applies a digital filter to the measured ECG and identifies the downward slopes of the QRS complexes41. The resulting inter-beat-intervals were converted to beats-per-minute values using the “ihr” package in the PhysioNet Toolkit, as described previously15. Pulmonary gas exchange data were sampled breath-by-breath. All data were linearly interpolated to derive quasi-continuous HR response and respiratory measures at 1 s time resolution. Sections of linearly interpolated HR data greater than 1 s in duration were removed prior to analysis.
CRF estimation framework: conceptual and modeling framework
Our approach for estimating VO2max from UKB-CRF test HR response is illustrated in Fig. 1B–E. Here we first describe a VO2max estimation method for HR response to steady-state exercise. We then adapt this method to the UKB-CRF test by using a multilevel hierarchical framework of linear models to harmonise HR response features extracted from flat and ramped UKB-CRF tests to those extracted from steady-state exercise.
Conceptual framework
VO2max can be estimated from HR response to exercise at steady-state WR increments using linear extrapolation of the submaximal HR-to-WR relationship42. For this approach, an individual exercises at two or more submaximal WR increments while HR is recorded. The steady-state HR response at each test increment is then regressed against WR to establish a line-of-best fit for the observed HR-to-WR relationship (W bpm−1). This relationship can be represented as:
where \(WR_{t}\) and \(HR_{t}\) are paired measurements at several test increments, \(\beta_{{1_{ss} }}\) is the linear regression slope representing the steady-state HR-to-WR relationship, and \(\beta_{{0_{ss} }}\) is the intercept of that regression. The regression line is extrapolated to age-predicted maximal HR (HRmax)43 to estimate the maximal steady-state WR that would be achieved if the exercise test was completed to exhaustion. VO2max is then estimated by converting the extrapolated maximal steady-state WR value to net VO2 using a caloric equivalent of oxygen and adding an estimate of resting VO2 plus the VO2 required for unloaded cycling44.
The HR-to-WR linear extrapolation approach presents challenges when applied to ramped exercise HR response. Assuming HR and VO2 responses are linearly related, the principal methodological issues are45,46,47: (1) within-participant, the VO2-to-WR relationship and total time delay for VO2 response to achieve linearity after ramped exercise onset will vary across ramped tests as a function of ramp rate; (2) The ramped VO2-to-WR relationship decreases asymptotically with ramp rate and, as ramp rate approaches zero, becomes similar to values determined from steady-state exercise; (3) the VO2-to-WR relationship has high test–retest variability; and (4) the VO2-to-WR relationship diverges from linearity above RCP. Thus, the HR-to-WR linear extrapolation approach will induce VO2max overestimation bias as a function of ramp rate, demonstrate low test–retest reliability, and have poor precision if the WR computed at age-predicted HRmax is greater than the WR at RCP.
Modeling framework
We addressed these methodological issues by constructing a multilevel CRF estimation framework that computes a participant’s steady-state HR-to-WR relationship using features extracted from HR response to flat or ramp UKB-CRF test protocols. The framework was derived using a three-stage hierarchical linear model. The first stage equates WR computed from steady-state test HR response (Eq. 1) with WR computed from dynamic regression coefficients that vary between and within individual participants as a function of lower-stage hierarchical features. Within every ith individual participant, each having completed a set of p exercise protocols:
Stage-1 (base-stage equating steady-state test HR response with UKB-CRF flat and ramped HR response):
where (1) \({\beta }_{{0}_{p[ss]i}}\) and \({\beta }_{{1}_{p[ss]i}}\) are linear regression coefficients estimated from the steady-state protocol (p[ss]); (2) \({HR}_{tp[ss]i}\) is a sequence of t simulated steady-state HR values, equally spaced and spanning the submaximal intensity range; (3) \({WR}_{tp[ss]i}\) is a sequence of t steady-state WR values computed with \({\beta }_{{0}_{p[ss]i}}\), \({\beta }_{{1}_{p[ss]i}}\), and \({HR}_{tp[ss]i}\) (thus, a matrix representation of the line defined by Eq. 1); and (4) \({\beta }_{{0}_{p[UKB]i}}\) and \({\beta }_{{1}_{p[UKB]i}}\) are dynamic regression coefficients that, while unique to each UKB protocol (p[UKB]) and individual, converge to the values of \({\beta }_{{0}_{p[ss]i}}\) and \({\beta }_{{1}_{p[ss]i}}\) by their linkage with \({WR}_{tp[ss]i}\). \({\beta }_{{0}_{p[UKB]i}}\) and \({\beta }_{{1}_{p[UKB]i}}\) are estimated at the second stage using combinations of HR-response and protocol-based features:
Stage-2 (HR-response and protocol features extracted from flat and ramped UKB-CRF tests):
where (1) \({\gamma }_{{0x}_{i}}\) and \({\gamma }_{{1x}_{i}}\) are sets of a fixed regression coefficients for HR-response and protocol-level features \({P}_{{x}_{p[UKB]i}}\); and (2) \({\gamma }_{{00}_{i}}\) and \({\gamma }_{{10}_{i}}\) are the mean intercept and slope for the ith individual participant. \({\gamma }_{{00}_{i}}\) and \({\gamma }_{{10}_{i}}\) are estimated at the third stage:
Stage-3 (pretest participant characteristics):
where (1) \({\delta }_{00x}\) and \({\delta }_{10x}\) are sets of b fixed regression coefficients for participant characteristics \({I}_{{x}_{i}}\); and (2) \({\delta }_{000}\) and \({\delta }_{100}\) are the model-invariant intercept and slope. \({\beta }_{{0}_{p[UKB]i}}\) and \({\beta }_{{1}_{p[UKB]i}}\) can be estimated using different sets of HR-response and protocol features \({(P}_{{x}_{p[UKB]i}})\) as well as different sets of participant characteristics \(({I}_{{x}_{i}})\). We leveraged this adaptability to derive five WR estimation models (notated as M1–M5; Supplemental Table 1), each using different combinations of HR response feature sets, so that our approach was robust to different data quality scenarios encountered when analysing HR response data in UKB. Additional details regarding the extraction of feature sets included in \({P}_{{x}_{p[UKB]i}}\) and \({I}_{{x}_{i}}\) are provided in Supplemental Methods.
Application of multilevel framework
VO2max was estimated from the multilevel framework by extrapolating the linear fit defined by \({\beta }_{{0}_{p[UKB]i}}\) and \({\beta }_{{1}_{p[UKB]i}}\) to age-predicted HRmax43 and converting the resultant maximal steady-state WR value to VO2max using the American College of Sports Medicine metabolic equation for cycling9. We also estimated WR and VO2max values using a simple linear regression approach15, a two-point estimation method19, and an approach for steady-state tests15 (see ‘Prediction of VO2max using alternative methods’ in Supplemental Materials).
Agreement analyses
We used Bland–Altman analysis48 to quantify agreement between estimated WR and VO2max values with those directly measured during the maximal exercise test. Correlations between estimated and directly measured values were quantified using Pearson’s r and Spearman’s rho. One-sample t-tests were performed to determine whether mean biases were statistically significantly different from zero mean bias. Estimation model precision was expressed as the root mean square error (RMSE) between estimated and directly measured values. ANOVA repeated measures were used to test differences between estimated and directly measured values across estimation models.
Short-term test–retest reliability
To assess short-term test–retest reliability, a subsample of 87 validation study participants completed a second UKB-CRF test within 2 weeks after main testing, identical to either the low or high ramped test at the main visit. Estimated VO2max values from first and second tests were compared using agreement analysis.
Estimation of VO2max and associations with prospective health outcomes in UKB
UKB participants
The UKB is a prospective cohort study of 502,625 older adults. Baseline data collection was conducted between 2006 and 2010 where a variety of physical measurements, biological samples, and health questionnaires were administered; repeat-measures visits were conducted between 2012 and 2013. The UKB-CRF test was offered approximately 100,000 times (last 79,209 participants from baseline and 20,218 from the repeat-measures visit). The study was approved by the North West Multicentre Research Ethics Committee and participants provided written informed consent.
Implementation of CRF estimation in UKB
VO2max values were estimated in UKB participants, largely as described above for the validation study. Supplemental Fig. 12 describes specific criteria used to assign the multilevel framework estimation models for the primary analysis. Age-predicted HRmax was reduced by 20 beats-per-minute in those taking beta-blockers49.
Long-term test–retest reliability of CRF
To assess long-term test–retest reliability, we compared estimated VO2max values at baseline and the first follow-up test in those UKB participants with repeat tests (n = 2877, mean follow-up time 2.8 years). The follow-up UKB-CRF test protocol was re-individualised at the time of testing and therefore may have differed from the baseline protocol.
Health characteristics across CRF levels in UKB
Health characteristics were described across age-adjusted and sex-specific CRF categories50. We age-stratified the UKB cohort in half-decades as < 50, 50–54, 55–59, 60–64, and ≥ 65 years, defined CRF categories by tertiles (“lower”, “middle”, and “higher”) of estimated VO2max levels from each age group, and combined CRF categories from each age group to form CRF categories for the entire UKB cohort. Health characteristics were compared across CRF tertiles for men and women separately.
Survival analyses
Cox regression with age as the underlying timescale was used to estimate log-linear associations between estimated VO2max levels (in METs; 1 MET = 3.5 ml O2 kg−1 min−1) and mortality and incident disease outcomes. We compared prospective associations between two VO2max estimation approaches: the multilevel framework developed in this study and the previously described method using simple linear regression. Vital status and hospital episodes of UKB participants were established by linkage to national registry data obtained from the Health and Social Care Information Centre (now NHS Digital) for England and Wales and the Information Services Department (ISD) for Scotland. The censoring date for mortality outcomes was 31st March 2020. Censoring dates for incident disease outcomes were 31st January 2018 in England and Wales, and 30th November 2016 in Scotland. International Classification of Diseases (ICD) 10th edition (ICD-10) codes were used to define health outcomes; heart failure (I50, I11.0, I13.0, I13.2), stroke (I60-166), ischaemic heart disease (IHD; I20-I25), atrial fibrillation (AF; I48), and chronic obstructive pulmonary disease (COPD; J44). Fatal outcomes were all-cause mortality, cardiovascular disease mortality (CVD; I5-I9, I10-I89), respiratory disease mortality (RD; J00-J99), and cancer mortality (C00-97 and D00-D49).
Models were adjusted for age, sex, body weight, ethnicity, smoking status, employment status, Townsend index of deprivation, alcohol consumption, red meat intake, medication use (beta blockers, calcium channel blockers, ACE inhibitors, diuretics, bronchodialators, lipid-lowering agents, iron deficiency agents), hypertension, diabetes, and pre-baseline self-report and hospital episodes of cancer. When analysing fatal outcomes, models were additionally adjusted for pre-baseline self-report and hospital episodes of heart failure, IHD, stroke, AF, and COPD. When analysing specific incident disease outcomes (combined non-fatal and fatal), however, participants were excluded if these pre-baseline events were reported. Potential residual confounding by obesity was addressed in stratified analyses. Participants experiencing disease events in the first two years of follow-up were excluded (analysis specific). Nonlinear associations between estimated VO2max levels and each of the health outcomes were evaluated using a cubic spline regression model with three knots placed at the 25th, 50th, and 75th percentiles of the VO2max distribution. Spline models were adjusted using all covariates listed above; these models were used to estimate dose–response curves for the association between CRF and hazard ratios of the disease outcomes, using 8.0 METs as the reference exposure point.
This study complied with the items listed in the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) guidelines. All methods were performed in accordance with relevant guidelines and regulations including the Declarations of Helsinki.
Statistical software
All analyses were performed in Stata/SE 15.1 (StataCorp, Texas, USA). Statistical significance was set at p < 0.05.
Change history
17 October 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41598-023-44856-3
References
Blair, S. N. et al. Influences of cardiorespiratory fitness and other precursors on cardiovascular disease and all-cause mortality in men and women. JAMA 276, 205–210 (1996).
Kodama, S. et al. Cardiorespiratory fitness as a quantitative predictor of all-cause mortality and cardiovascular events in healthy men and women: A meta-analysis. JAMA 301, 2024–2035 (2009).
Berry, J. D. et al. Lifetime risks for cardiovascular disease mortality by cardiorespiratory fitness levels measured at ages 45, 55, and 65 years in men. J. Am. Coll. Cardiol. 57, 1604–1610 (2011).
Carnethon, M. R. et al. Cardiorespiratory fitness in young adulthood and the development of cardiovascular disease risk factors. JAMA 290, 3092–3100 (2003).
Katzmarzyk, P. T., Church, T. S., Janssen, I., Ross, R. & Blair, S. N. Metabolic syndrome, obesity, and mortality: Impact of cardiorespiratory fitness. Diabetes Care 28, 391–397 (2005).
Wei, M. et al. The association between cardiorespiratory fitness and impaired fasting glucose and type 2 diabetes mellitus in men. Ann. Intern. Med. 130, 89–96 (1999).
Sui, X. et al. A prospective study of cardiorespiratory fitness and risk of type 2 diabetes in women. Diabetes Care 31, 550–555 (2008).
Noonan, V. & Dean, E. Submaximal exercise testing: Clinical application and interpretation. Phys. Ther. 80, 782–807 (2000).
Pescatello, L. S., Arena, R., Riebe, D., Thompson, P. D. & American College of Sports Medicine Health-related physical fitness testing and interpretation. In ACSM’s Guidelines for Exercise Testing and Prescription (eds Pescatello, L. S. et al.) 88–93 (Lippincott Williams & Wilkins, 2014).
Questad, K. A. & Alquist, A. Exercise assessment in clinical practice. Phys. Med. Rehabil. Clin. N. Am. 5, 243–253 (1994).
Keir, D. A., Paterson, D. H., Kowalchuk, J. M. & Murias, J. M. Using ramp-incremental VO2 responses for constant-intensity exercise selection. Appl. Physiol. Nutr. Metab. 43, 882–892 (2018).
Hansen, J. E., Sue, D. Y., Oren, A. & Wasserman, K. Relation of oxygen uptake to work rate in normal men and men with circulatory disorders. Am. J. Cardiol. 59, 669–674 (1987).
Adami, A., Sivieri, A., Moia, C., Perini, R. & Ferretti, G. Effects of step duration in incremental ramp protocols on peak power and maximal oxygen consumption. Eur. J. Appl. Physiol. 113, 2647–2653 (2013).
Kokkinos, P., Kaminsky, L. A., Arena, R., Zhang, J. & Myers, J. A new generalized cycle ergometry equation for predicting maximal oxygen uptake: The fitness registry and the importance of exercise national database (FRIEND). Eur. J. Prev. Cardiol. 25, 1077–1082 (2018).
Kim, Y. et al. The combination of cardiorespiratory fitness and muscle strength, and mortality risk. Eur. J. Epidemiol. 33, 953–964 (2018).
Steell, L. et al. Dose-response associations of cardiorespiratory fitness with all-cause mortality and incidence and mortality of cancer and cardiovascular and respiratory diseases: The UK Biobank cohort study. Br. J. Sports Med. https://doi.org/10.1136/bjsports-2018-099093 (2019).
Celis-Morales, C. A. et al. Walking pace is associated with lower risk of all-cause and cause-specific mortality. Med. Sci. Sports Exerc. https://doi.org/10.1249/MSS.0000000000001795 (2018).
Tikkanen, E., Gustafsson, S. & Ingelsson, E. Associations of fitness, physical activity, strength, and genetic risk with cardiovascular disease: Longitudinal analyses in the UK Biobank Study. Circulation 137, 2583–2591 (2018).
Yates, T. et al. Association of walking pace and handgrip strength with all-cause, cardiovascular, and cancer mortality: A UK Biobank observational study. Eur. Heart J. 38, 3232–3240 (2017).
Yates, T. et al. Reaction time, cardiorespiratory fitness and mortality in UK Biobank: An observational study. Intelligence 66, 79–83 (2018).
Laukkanen, J. A. et al. Prognostic relevance of cardiorespiratory fitness as assessed by submaximal exercise testing for all-cause mortality: A UK Biobank prospective study. Mayo Clin. Proc. 95, 867–878 (2020).
Hooker, S. P. et al. Cardiorespiratory fitness as a predictor of fatal and nonfatal stroke in asymptomatic women and men. Stroke 39, 2950–2957 (2008).
Abdulla, J. & Nielsen, J. R. Is the risk of atrial fibrillation higher in athletes than in the general population? A systematic review and meta-analysis. Europace 11, 1156–1159 (2009).
Qureshi, W. T. et al. Cardiorespiratory fitness and risk of incident atrial fibrillation: Results from the Henry Ford exercise testing (FIT) project. Circulation 131, 1827–1834 (2015).
Robsahm, T. E. et al. Measured cardiorespiratory fitness and self-reported physical activity: Associations with cancer risk and death in a long-term prospective cohort study. Cancer Med. 5, 2136–2144 (2016).
Laukkanen, J. A. et al. Cardiorespiratory fitness, lifestyle factors and cancer risk and mortality in Finnish men. Eur. J. Cancer 46, 355–363 (2010).
Celis-Morales, C. A. et al. Associations of discretionary screen time with mortality, cardiovascular disease and cancer are attenuated by strength, fitness and physical activity: Findings from the UK Biobank study. BMC Med. 16, 77 (2018).
Celis-Morales, C. A. et al. Do physical activity, commuting mode, cardiorespiratory fitness and sedentary behaviours modify the genetic predisposition to higher BMI? Findings from a UK Biobank study. Int. J. Obes. 43, 1526–1538 (2019).
Hillreiner, A. et al. Association between cardiorespiratory fitness and colorectal cancer in the UK Biobank. Eur. J. Epidemiol. https://doi.org/10.1007/s10654-019-00575-6 (2019).
Sillars, A. et al. Association of fitness and grip strength with heart failure. Mayo Clin. Proc. 94, 2230–2240 (2019).
Tikkanen, E. et al. Biological insights into muscular strength: Genetic findings in the UK Biobank. Sci. Rep. 8, 1–9 (2018).
Pan, F. et al. Association between musculoskeletal pain at multiple sites and objectively measured physical activity and work capacity: Results from UK Biobank study. J. Sci. Med. Sport 22, 444–449 (2019).
Raichlen, D. A., Klimentidis, Y. C., Bharadwaj, P. K. & Alexander, G. E. Differential associations of engagement in physical activity and estimated cardiorespiratory fitness with brain volume in middle-aged to older adults. Brain Imaging Behav. https://doi.org/10.1007/s11682-019-00148-x (2019).
Balady, G. J. et al. Clinician’s guide to cardiopulmonary exercise testing in adults: A scientific statement from the American Heart Association. Circulation 122, 191–225 (2010).
UK Biobank Cardio Assessment Manual Version 1.0. https://biobank.ctsu.ox.ac.uk/crystal/crystal/docs/Cardio.pdf (2011).
Eriksen, L., Grønbæk, M., Helge, J. W., Tolstrup, J. S. & Curtis, T. The Danish health examination survey 2007–2008 (DANHES 2007–2008). Scand. J. Public Health 39, 203–211 (2011).
Lindsay, T. et al. Descriptive epidemiology of physical activity energy expenditure in UK adults (The Fenland study). Int. J. Behav. Nutr. Phys. Act. 16, 126 (2019).
Lucia, A., Hoyos, J., Perez, M. & Chicharro, J. Heart rate and performance parameters in elite cyclists: A longitudinal study. Med. Sci. Sports Exerc. 32, 1777–1782 (2000).
Rietjens, G., Kuipers, H., Kester, A. D. M. & Keizer, H. A. Validation of a computerized metabolic measurement system (Oxycon-Pro®) during low and high intensity exercise. Int. J. Sports Med. 22, 291–294 (2001).
Goldberger, A. L. et al. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 101, e215–e220 (2000).
Engelse, W. A. H. & Zeelenberg, C. A single scan algorithm for QRS-detection and feature extraction. Comput. Cardiol. 6, 37–42 (1979).
Maritz, J. S., Morrison, J. F., Peter, J., Strydom, N. B. & Wyndham, C. H. A practical method of estimating an individual’s maximal oxygen intake. Ergonomics 4, 97–122 (1961).
Tanaka, H., Monahan, K. D. & Seals, D. R. Age-predicted maximal heart rate revisited. J. Am. Coll. Cardiol. 37, 153–156 (2001).
Whipp, B. J. The bioenergetic and gas exchange basis of exercise testing. Clin. Chest Med. 15, 173–192 (1994).
Boone, J. & Bourgois, J. The oxygen uptake response to incremental ramp exercise: Methodogical and physiological issues. Sports Med. 42, 511–526 (2012).
Iannetta, D., de Almeida Azevedo, R., Keir, D. A. & Murias, J. M. Establishing the VO2 versus constant-work-rate relationship from ramp-incremental exercise: Simple strategies for an unsolved problem. J. Appl. Physiol. 127, 1519–1527 (2019).
Swanson, G. D. & Hughson, R. L. On the modeling and interpretation of oxygen uptake kinetics from ramp work rate tests. J. Appl. Physiol. 65, 2453–2458 (1988).
Bland, J. M. & Altman, D. G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 8, 135–160 (1999).
Wonisch, M. et al. Influence of beta-blocker use on percentage of target heart rate exercise prescription. Eur. J. Cardiovasc. Prev. Rehabil. 10, 296–301 (2003).
Kokkinos, P. et al. Cardiorespiratory fitness and health outcomes: A call to standardize fitness categories. Mayo Clin. Proc. 93, 333–336 (2018).
Acknowledgements
We thank the participants of both the validation study and the UK Biobank study for their time. We are also grateful to all members of the MRC Epidemiology Unit functional groups, including field epidemiology, physical activity technical team, IT and data management for their contribution to the validation study, as well as the UK Biobank principal investigators and study teams. We thank Youngwon Kim for early discussions around the design of the validation study and Thomas White for implementation of the heart beat detection algorithms from Physionet. The present analyses of UK Biobank data use application #408. This work was funded by the UK Medical Research Council (MC_UU_12015/3 and MC_UU_00006/4) and the NIHR Biomedical Research Centre in Cambridge (IS-BRC-1215-20014). UK Biobank is acknowledged for contributing to the costs of the validation fieldwork. The funders had no role in the design, conduct, analysis, and decision to publish results from this study.
Author information
Authors and Affiliations
Contributions
T.G. and S.B. defined the research question. K.W., N.J.W., and S.B. designed the fitness component in UK Biobank. K.W., S.H., Jo.J., D.C., and S.B. contributed to the validation study design. T.G. conducted the main study analyses. T.G. prepared all tables and figures. T.G., T.S. and S.B. wrote the main manuscript text. All authors approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this Article was revised: The original version of this article contained errors in Supplementary Information Table 1 and Table 12. Full information regarding the corrections made can be found in the correction for this Article.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gonzales, T.I., Westgate, K., Strain, T. et al. Cardiorespiratory fitness assessment using risk-stratified exercise testing and dose–response relationships with disease outcomes. Sci Rep 11, 15315 (2021). https://doi.org/10.1038/s41598-021-94768-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-94768-3
This article is cited by
-
Cardiorespiratory responses: Pilates compared to different walking speeds in healthy adults
Irish Journal of Medical Science (1971 -) (2024)
-
Proteomic analysis of cardiorespiratory fitness for prediction of mortality and multisystem disease risks
Nature Medicine (2024)
-
Observational and genetic associations between cardiorespiratory fitness and cancer: a UK Biobank and international consortia study
British Journal of Cancer (2024)
-
Causal associations between cardiorespiratory fitness and type 2 diabetes
Nature Communications (2023)
-
Equipment-free, unsupervised high intensity interval training elicits significant improvements in the physiological resilience of older adults
BMC Geriatrics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.