Abstract
Nuclear radiation shielding capabilities for a glass series 20Bi2O3 − xPbO − (80 − 2x)B2O3 − xGeO2 (where x = 5, 10, 20, and 30 mol%) have been investigated using the Phy-X/PSD software and Monte Carlo N-Particle transport code. The mass attenuation coefficients (μm) of selected samples have been estimated through XCOM dependent Phy-X/PSD program and MCNP-5 code in the photon-energy range 0.015–15 MeV. So obtained μm values are used to calculate other γ-ray shielding parameters such as half-value layer (HVL), mean-free-path (MFP), etc. The calculated μm values were found to be 71.20 cm2/g, 76.03 cm2/g, 84.24 cm2/g, and 90.94 cm2/g for four glasses S1 to S4, respectively. The effective atomic number (Zeff)values vary between 69.87 and 17.11 for S1 or 75.66 and 29.11 for S4 over 0.05–15 MeV of photon-energy. Sample S4, which has a larger PbO/GeO2 of 30 mol% in the bismuth-borate glass, possesses the lowest MFP and HVL, providing higher radiation protection efficiency compared to all other combinations. It shows outperformance while compared the calculated parameters (HVL and MFP) with the commercial shielding glasses, different alloys, polymers, standard shielding concretes, and ceramics. Geometric Progression (G-P) was applied for evaluating the energy absorption and exposure buildup factors at energies 0.015–15 MeV with penetration depths up to 40 mfp. The buildup factors showed dependence on the MFP and photon-energy as well. The studied samples' neutron shielding behavior was also evaluated by calculating the fast neutron removal cross-section (ΣR), i.e. found to be 0.139 cm−1 for S1, 0.133 cm−1 for S2, 0.128 cm−1 for S3, and 0.12 cm−1 for S4. The results reveal a great potential for using a glass composite sample S4 in radiation protection applications.
Similar content being viewed by others
Introduction
γ-Rays emitting radionuclides are found to be useful in many fields like industrial (to detect defects in metal casting), medical (to treat malignant and cancerous tumors), agriculture (to control the degree of ripeness and extend the shelf life of fruits and vegetables) and space applications, etc.1,2,3. γ-Rays are high-frequency electromagnetic radiation that easily transmit through a thick wall, which may produce greater occupational exposures in nuclear facilities if not shielded adequately. Using suitable shielding may ensure better safety of radiation workers against its harmful dosages. Consequently, many researchers have been paid a great effort to develop and design well-formed radiation shielding materials4,5,6.
In this view, a range of materials, including concrete, lead, oxide glass, etc., have been developed and used to shield radiation1,2,4. Concrete has been formed from a loosely compacted mass of small fragments or particles4,7. It has several limitations to be used as shielding in a nuclear reactor. Due to its non-transparent characteristics, it is not possible to observe/monitor the internal environment. Moreover, variation in water quantity in concrete often exhibits unwanted fluctuations in attenuation coefficients8,9. To overcome such limitations, several glass-based materials have been processed. Being transparent in visible light, their properties can be modified by changing the components and preparation methods8,10,11. As a result, a number of researchers studied the γ-rays attenuation parameters for a variety of glasses like bismuth borate glasses12, lead borate glasses13, lead fluoroborate glasses14, bismuth borosilicate glasses15, alkali borosilicate glasses16, barium borosilicate glasses17, calcium–strontium-borate glasses18, lead silicate glasses19 and lead/barium phosphate glasses20, etc. In these glasses12,13,14,15,16,17,18,19,20, B2O3 is a common component that gives glass-forming of a lower melting point with good thermal stability and transparency. Smaller B3+ ionic size provides high bond strength3,11. Heavier cations used in different dosages promote glasses of varied shielding capabilities. Radiation shielding of glass structures can be developed by adding some high-density materials like heavy metal oxides (HMO).
The glass structures made with HMO (Pb, Ba, and Bi) show characteristics like high refractive index, high infrared transparency, and high nonlinear optical susceptibility21,22,23, all of which are favorable for a material to be used as an effective γ-rays shielding. Heavy metal oxides PbO, Bi2O3, BaO, etc. play a key role in enhancing an average product density. A required characteristic of a good radiation shielding material is its chemical homogeneity made over its high density24,25,26. Generally, PbO containing high-density glasses offer high optical nonlinearity. A reasonably high PbO solubility is required to make a suitable glass for γ-rays' attenuation27. Bi2O3 doped borate glasses find wide applications in various fields like fast optical switching, photonic devices, and infrared transmission components, with high refractive index, large optical susceptibility, large polarizability, and high optical basicity28. Boro-germanate glasses offer high solubility to dissolve heavy metals, extending resistance to moisture, low melting point, good transparency, and excellent thermal stability29.
The main goal of this work is to evaluate the γ-rays shielding parameters of glasses 0.2Bi2O3 − xPbO − (0.8 − 2x)B2O3 − xGeO2, x = 0.05, 0.1, 0.2 and 0.3 mol %, as given in Table 1. The densities of the present samples have been taken from Knoblochova et al.30. The μm values, as determined using the XCOM dependent Phy-X/PSD program and MCNP computer code, were used to calculate the other shielding parameters like linear attenuation coefficient (µ), electron density, mean-free-path (MFP), half-value layer (HVL), and radiation protection efficiency (RPE). The exposure buildup factor (EBF) and energy absorption buildup factor (EABF) were evaluated using the geometric progression (GP) fitting method within a 0.015–10 MeV energy range. The interaction of the neutrons with the present glasses is studied in terms of fast neutron removal cross-sections.
Theoretical approach on attenuating γ-rays
The MFP is defined as an average distance λ (in cm) traveled by the photons before being absorbed in a particular material. It has been calculated as31,32,33, MFP = μ−1, where μ (cm−1) denotes a linear attenuation coefficient of the medium. When a narrow beam of radiation of initial intensity I0 moves through a specific medium of thickness t, the number of photons (I) that can transmit the medium is given by the Lambert–Beer law34,35,36, I = I0e−μt. Also, the mixture rule is a suitable relation used to determine μm (or µ/ρ, where ρ is the material density) for an absorber27,28, µm = ∑ωi (µm)i. The HVL used to describe the material thickness diminishes the intensity I to be 0.5 I013, HVL = 0.693 µ−1. The μm quantities helps in evaluating the total molecular cross-section (σt,m)13,36, σt,m = µm(M/NA), NA is the Avogadros’ number. The σt,m used to calculate the average atomic cross-section (σt,a)12,36, σt,a = σt,m (∑nj)−1. The fractional abundance fi, atomic mass Ai, and atomic weight Zi were used to calculate the average electronic cross-section (σt,el), where σt,el = (NA)−1∑fi Ai (µm) (Zi)−1. The calculated quantities σt,a and σt,el utilized to calculate Zeff, Zeff = σt,a (σt,el)−1. The radiation protection efficiency (RPE) of an attenuator is determined in a relation, RPE = (1 − e−µt) × 100.
The equivalent atomic number (Zeq) is interpolated by matching the ratio, R = (μm)comp/(μm)total. Beside, the Zeq, geometric progression (G-P) fitting parameters (b, c, a, Xk and d), (EABF), and (EBF) were calculated using the Phy-X/PSD program37.
On the other hand, a (∑R) represents the probability of a neutron undergoing certain reaction per unit length of moving through a certain medium, which can be calculated using the mass removal cross-section (∑ER) and fractional abundance ω for ith constituent, ∑R (cm−1) = ∑ωi (∑ER)i.
Simulations of shielding parameters
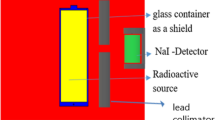
The shielding parameters have been obtained using the user-friendly online Photon Shielding and Dosimetry (Phys-X/PSD) software. Several articles recently reported shielding properties against γ-rays, X-rays, and neutrons using simulation codes such as Geant, Fluka, and MCNP 38,39,40. Previously mentioned codes were used as alternative methods for the experimental measurements. The shielding parameters were evaluated using MCNP-5 code for the glasses 20 Bi2O3 − xPbO − (80 − 2x)B2O3 − xGeO2, with x = 5, 10, 20, and 30 mol %. As presented in Fig. 1, the simulation processes started with creating an input file, containing all information required to introduce the shielding material (density and chemical composition), γ-rays source (energy and its distribution), detector, and the geometry (cell and surface cards). A disk γ-source with a diameter of 2 cm and thickness of 0.5 cm was placed inside a lead collimator. The NPS card is set to stop running the simulation after 106 particle. The sample was placed at mid-distance between the collimator and γ-rays detector, so that the γ-rays transmit via the sample and transmited part is directed to the detector. The simulation process aims to estimate the average track length (ATL) of γ-photons; thus, Tally (F4) was used. MCNP-5 is a helpful code supported by continuous-energy nuclear and atomic data libraries. The cross-section data sources used in the MCNP-5 nuclear database are ENDF/B-VI.8, ACTI, ENDL, ACTI, and T-16 files41.
Results and discussion
The μm values of the glasses simulated utilizing MCNP-5 code and calculated using the Phy-X/PSD in the energy range 0.015–15 MeV, as presented in Table 2. Both the μm values (MCNP-5 and Phy-X/PSD) are found to be in good agreement. Their variations with incident photon energies for all the glasses are displayed in Fig. 2. The μm values for sample S1 (71.20–1.288 cm2/g), S2 (76.03–1.34 cm2/g), S3 (84.24–1.43 cm2/g) and S4 (90.94–1.50 cm2/g) decrease sharply up to 15 keV, with a maximum over 71.20–90.94 cm2/g.
An abrupt change in μm is observed in the lower energy region in the Pb/Bi modified glasses, which have their K—absorption edges. The highest μm value is shown in S4 what is it required for a good shielding. In this energy region, the photoelectric process (PE) is the dominant process, which has the Z-dependence of Z4–5. The μm values for all samples (~ 0.08 cm2/g) are found to be nearly constant in the energy range 0.08 MeV on predominating Compton scattering, which varies linearly with Z, falling down on higher energies. The μm is found to increase slowly above 1 MeV on prevailing pair production process in this region, i.e., an order of Z2. It is found to be 0.037–0.041 cm2/g in S1, 0.038–0.043 cm2/g in S2, 0.039–0.045 cm2/g in S3, and 0.039–0.047 cm2/g in S4 in the energy range of 4–15 MeV. The linear attenuation coefficients can easily be obtained from the μm values, following a similar trend with the energy as presented in Fig. 342. Table 2 shows a comparison of these values closely lying one another. The diff (%) calculated between the two programs is ≤ 5%.
Figure 4 plots the Zeff changes with the energy in the different samples, varied over 69.87–17.11 for S1 and 75.66–29.11 for S4 in the energy range of 0.05–15 MeV. The Zeff is found to decrease up to 1.5 MeV on dominance of the photoelectric absorption process in this region, which has Z-dependence of Z4–5. It arises sharply beyond 3 MeV, attributing to dominance of pair production process, which depends on Z2. At 15 MeV, it is found to be 29.83 for S1, 32.86 for S2 39.01 for S3, and 45.30 for S4. A maximum value are used in S4 over S1 in a duly increased PbO dose. A low value 17.11–17.60 for S1 and 29.11–29.89 for S4 in a medium 1–3 MeV energy region is contributed by the dominant Compton scattering in this region, which has a linear Z-dependence responsible for duly increased Zeff in the high-energy regions43.
The Ne values, calculated for present samples at different γ-rays energies using Eq. (9), are ploted with energy in Fig. 5. These are 1.33 × 1024 e/g (i.e. electrons/g) for S1 and 7.05 × 1023 e/g for S4 at 15 keV. The values of S1 (2.94 × 1023 e/g) and S4 (2.84 × 1023 e/g), with a minimum at 1.5 MeV, fall down sharply up to 1 MeV. A pretty smaller value is found for S1 of 3.09 × 1023–3.18 × 1023 e/g, while 2.99 × 1023–3.07 × 1023 e/g for S4 in the medium 1–3 MeV energy region, and then increases beyond 3 MeV. The Zeff values at 15 MeV are 5.39 × 1023 and 4.65 × 1023 e/g for glass samples S1 and S4, respectively.
Figure 6 presents how HVL is varied with photon energy. It is significantly lower and stationary below 0.1 MeV and then arises sharply above 0.1 MeV, having the values 0.002 and 0.001 cm at 15 keV, while 0.034 and 0.024 cm at 0.1 MeV for S1 and S4, respectively. It becomes 3.24, 3.01, 2.73 and 2.51 cm at 6 MeV, while 2.857, 2.688, 2.303 and 2.088 cm at 15 MeV for S1, S2, S3 and S4, respectively. A minimum value shown in glass S4 thus characterizing it to be the best shielding material42,43 among all the four glasses studied here.
The MFP values, as calculated from μ at several energies, vary from 0.015 to 15 MeV, as plotted in Fig. 7. Evidently, MFP varies with energy due to dominance of photons interactions. All the four S1–S4 glasses have a value 0.02 cm at 15 keV energy. A sharp peak is marked at 80 keV, showing 0.109, 0.101, 0.085 and 0.075 cm values (MFP) for S1, S2, S3, S4, respectively. Significantly lower (nearly steady) values stand below 0.1 MeV, namely, 0.04 cm, 0.04 cm, 0.03 cm and 0.03 cm at 0.1 MeV for the respective samples, following the dominance of photoelectric effect, and quickly arise over 0.3–6 MeV energy on Compton scattering dominates. Those become 4.681 cm, 4.474 cm, 3.928 cm, and 3.626 cm respectively at 6 MeV. Above 6 MeV, almost constant MFP prolongs on dominance of pair production, namely, 4.121 cm, 3.878 cm, 3.323 cm and 3.012 cm, respectively, at 15 MeV42. The shielding effectiveness is thus better in the lower energies, i.e. glass S4 is the best attenuator.
Further, the HVL and MFP of sample S4 have been compared to that of traditionally used shielding materials such as five types of glasses fabricated by SCHOTT AG, steels such as stainless steel-403 (SS403), cupero-nickel (CN), carbon steel-516 (CS516), inconel-600 (IL600), and monel-400 (MN400) alloys44, several types of concretes45 and ceramics such as CaSi2, Mg2Si, MgB2, CaB6, Al2O3, or TiO2, as shown in Figs. 8a–e and 9a–e respectively. Usefully, our glass S4 possesses better HVL and MFP values compared to that of traditionally used shielding materials. Values of both HVL and MFP for alloys are higher than the sample S4 values, except at 1.5 and 2 MeV (Figs. 8b and 9b). Moreover, Figs. 8c,d and 9c,d show lower HVL and MFP values of sample S4 as compared to alloys and concretes. Thus, S4 possess better shielding ability compared to the commercial glasses, concretes, alloys (excluding at 1.5 and 2 MeV energies), or ceramics.
The values of other parameters studied for the present glasses are given in Table 3. The changes in EBF and EABF studied with energy at several penetration depths of 1, 2, 5, 10, 15, 20, 25, 30, 35 and 40 mfp are plotted in Figs. 10, 11, 12 and 13, 14, 15, 16 and 17 respectively. Both EBF and EABF of the studied samples possess low values in low and high-energy regions, but assume higher values in the moderate energy regions. At 0.015 and 0.15 MeV energies, EBF and EABF values are more dependent on sample contents and increase with decreasing Zeq in these glasses. The Zeq is maximum in S4, while minimum in S1. Both EBF and EABF in low-energies of 0.015–0.3 MeV are small and nearly equal to one for all penetration depths since the photons are totally absorbed/removed through photoelectric absorption in dominant interaction process up to 0.3 MeV. Those progressively increase with energy due to multiple Compton scattering (the degradation of photon energy), which dominates in the intermediate-energies (0.3–3 MeV). The EABF reduces in high-energy region (E > 3 MeV) in absorption behavior of the pair production process. After that, for gamma photon energies higher than 3 MeV, the buildup factors have high increase with increasing the incident energy. Also, EBF has a peak at 0.02 MeV in the K-absorption edge of high Z-elements present in these glasses46. The EBF values are the highest for 40 mfp and lowest for the penetration depth of 1 mfp due to the multiple scattering events for large penetration depths. Therefore, both EBF and EABF are increasing to reach a maximum for all S1, S2, S3, and S4 samples for penetration depth at 40 mfp. But, the buildup factors are maximum/minimum for S1/S4 at penetration depths of 1, 2, 5, 10, 15, 20, 25, 30, 35 and 40 mfp for incident energies up to 3 MeV. By contrast, at E > 3 MeV, S4 has maximum EBF and S1 has the least EBF.
Calculated RPE for S1-S4 glasses and their variation with energy is portrayed in Fig. 18, where RPE is stationary up to 0.1 MeV. This means the incident photons can totally penetrate at 0.1 MeV, then RPE sharply decreases over 0.1 to 3 MeV energies, showing 23.29, 23.58, 26.00, and 27.28% residual values in respective glasses, which stay constant up to 8 MeV. About 21% of incident photons penetrate at 15 MeV. Glasses S1 and S4 have 32.83% and 38.20% values at 1 MeV, respectively, in a due effect of PbO–GeO2 additives of suppressing the attenuation properties. Thus, sample S4 can shield better than the other glasses. A composite glass has the property of removing more neutrons if it owes high Z elements. Low-Z elements may also remove neutrons if one using a combination of high-Z elements with low-Z elements. As portrayed in Fig. 19, the ΣR value varies as 0.139, 0.133, 0.128 and 0.12 cm−1 in the respective glasses. There is only a minor variation in this parameter. The amount of Z-elements like B and O may increase the neutron shielding capability in such glasses.
Conclusions
Major γ-rays shielding parameters are studied over a multicomponent glass series, 20Bi2O3 − xPbO − (80 − 2x)B2O3 − xGeO2, with x-values varied in small steps up to 30 mol%, in precisely determining how sensitively the PbO/GeO2 additives tailor the features. The additives promptly facilitate proportional behavior for µ, Zeff and RPE in the doped glasses on duly suppressed HVL and MFP values. A sample S4 is found to possess the highest value of the effective atomic number and the sample S1 is found to possess the lower values of effective atomic number among the selected glasses beyond 0.05 MeV, anticipating a synergic PbO role of improving the shielding capability in this series. The HVL and MFP of this sample S4 have been compared to those of traditionally used shielding glasses, such as SCHOTT AG glasses, steels, polymers, concretes, and ceramics. This specific glass S4 possesses suitably lowered HVL and MFP values (excluding at 1.5 and 2 MeV energies), over all these traditionally materials being used for this purpose. This work reveals a great potential of selected lead borate glasses to shield ionizing radiations in nuclear environment. The future scope of the presently selected glass series is to explore the structural and the mechanical properties.
References
Kirdsiri, K., Kaewkhao, J., Pokaipisit, A., Chewpraditkul, W. & Limsuwan, P. Gamma-rays shielding properties of xPbO:(100 − x)B2O3 glasses system at 662 keV. Ann. Nucl. Energy 36, 1360–1365 (2009).
Kumar, A. et al. Physical, structural, optical and gamma ray shielding behavior of (20 + x) PbO – 10 BaO – 10 Na2O – 10 MgO – (50–x) B2O3 glasses. Physica B Condens. Mater. 552, 110–118 (2019).
Sayyed, M. I. et al. Evaluation of radiation shielding features of Co and Ni-based superalloys using MCNP-5 code: potential use in nuclear safety. Appl. Sci. 10–21, 7680 (2020).
Srinivasan, K. & Samuel, E. J. Evaluation of radiation shielding properties of the polyvinyl alcohol/iron oxide polymer composite. J. Med. Phys. 42–4, 273–278 (2017).
Al-Hamarneh, I. F. Investigation of gamma-ray shielding effectiveness of natural marble used for external wall cladding of buildings in Riyadh, Saudi Arabia. Results Phys. 7, 1792–1798 (2017).
Zayed, A. M. et al. Influence of heavyweight aggregates on the physico-mechanical and radiation attenuation properties of serpentine-based concrete. Constr. Build. Mater. 260, 120473 (2020).
Mahmoud, K. A., Tashlykov, O. L., El Wakil, A. F. & El Aassy, I. E. Aggregates grain size and press rate dependence of the shielding parameters for some concretes. Prog. Nucl. Energy 1181, 103092 (2020).
Singh, N., Singh, K. J., Singh, K. & Singh, H. Comparative study of lead borate and bismuth lead borate glass systems as gamma-radiation shielding materials. Nucl. Instrum. Methods Phys. Res. B 225, 305–309 (2004).
Kaur, S. & Singh, K. J. Investigation of lead borate glasses doped with aluminium oxide as gamma ray shielding materials. Ann. Nucl. Energy 63, 350–354 (2014).
Singh, K. et al. Gamma-ray attenuation coefficients in bismuth borate glasses. Nucl. Instrum. Methods Phys. Res. B 194, 1–6 (2002).
Sayyed, M. I. et al. Investigation on gamma and neutron radiation shielding parameters for BaO/SrO–Bi2O3–B2O3 glasses. Radiat. Phys. Chem. 145, 26–33 (2018).
Sayyed, M. I. et al. Borate multicomponent of bismuth rich glasses for gamma radiation shielding application. Radiat. Phys. Chem. 161, 77–82 (2019).
Kumar, A. Gamma ray shielding properties of PbO–Li2O–B2O3 glasses. Radiat. Phys. Chem. 136, 50–53 (2017).
Singh, K. J., Singh, N., Kaundal, R. S. & Singh, K. Gamma-ray shielding and structural properties of PbO–SiO2 glasses. Nucl. Instrum. Methods Phys. Res. B 266, 944–948 (2008).
Singh, V. P., Badiger, N. M., Chanthima, N. & Kaewkhao, J. Evaluation of gamma-ray exposure buildup factors and neutron shielding for bismuth borosilicate glasses. Radiat. Phys. Chem. 98, 14–21 (2014).
Salama, E., Maher, A. & Youssef, G. M. Gamma radiation and neutron shielding properties of transparent alkali borosilicate glass containing lead. J. Phys. Chem. Solids 131, 139–147 (2019).
Ruengsri, S., Insiripong, S., Sangwaranatee, N. & Kaewkhao, J. Development of barium borosilicate glasses for radiation shielding materials using rice husk ash as a silica source. Prog. Nucl. Energy 83, 99–104 (2015).
Sharma, R., Sharma, V., Singh, P. S. & Singh, T. Effective atomic numbers for some calcium–strontium-borate glasses. Ann. Nucl. Energy 45, 144–149 (2014).
Rahimi, R. A., Raisali, G., Sadrnezhaad, S. K. & Alipour, A. Chemical corrosion and gamma-ray attenuation properties of Zr and Ti containing lead silicate glasses. J. Nucl. Mater 385, 527–532 (2009).
Kharita, M. H., Jabra, R., Yousef, S. & Samaan, T. Shielding properties of lead and barium phosphate glasses. Radiat. Phys. Chem. 81, 1568–1571 (2012).
Ram, S., Chakravorty, D. & Bahadur, D. Effect of nucleating agents on the crystallisation behaviour of barium hexaferrite in a borate glass. J. Magn. Magn. Mater. 62, 221 (1986).
Ram, S., Bahadur, D. & Chakravorty, D. Crystallisation of W-type hexagonal ferrites in an oxide glass with As2O3 as nucleation catalyst. J. Magn. Magn. Mater. 67, 378 (1987).
Ram, S. & Ram, K. Infrared reflectance spectra and formalism of precipitation of acicular magnetic particles in network glasse. Infrared Phys. Technol. 37, 457 (1996).
Ram, S., Bahadur, D. & Chakravorty, D. Magnetic glass-ceramics with hexagonal lead ferrites. J. Non-Cryst. Solids. 88, 311 (1986).
Ram, S. & Narayan, K. A. Controlled crystallization of lead oxide-chromium oxide-boron oxide (PbO–Cr2O3–B2O3) glasses and a catalytic effect of alumina for the growth of lead chromate (Pb2CrO5) microcrystals. Ind. Eng. Chem. Res. 26, 1051 (1987).
Ram, S. & Ram, K. IR and Raman studies and effect of γ radiation on crystallization of some lead borate glasses containing Al2O3. J. Mater. Sci. 23, 4541 (1988).
Manohara, S. R., Hanagodimath, S. M. & Gerward, L. Photon interaction and energy absorption in glass: a transparent gamma ray shield. J. Nucl. Mater. 393, 465–472 (2009).
Yasaka, P., Pattanaboonmee, N., Kim, H. J., Limkitjaroenporn, P. & Kaewkhao, J. Gamma radiation shielding and optical properties measurements of zinc bismuth borate glasses. Ann. Nucl. Energy 68, 4–9 (2014).
Al-Hadeethi, Y., Sayyed, M. I. & Rammah, Y. S. Fabrication, optical, structural and gamma radiation shielding characterizations of GeO2–PbO–Al2O3–CaO glasses. Ceram. Int. 46, 2055–2062 (2020).
Knoblochova, K., Ticha, H., Schwarz, J. & Tichy, L. Raman spectra and optical properties of selected Bi2O3–PbO–B2O3–GeO2 glasses. Opt. Mater. 31, 895–898 (2009).
Kumar, A. Studies on effective atomic numbers and electron densities of nucleobases in DNA. Radiat. Phys. Chem. 127, 48–55 (2016).
Biswas, R., Sahadath, H., Mollah, A. S. & Huq, M. F. Calculation of gamma-ray attenuation parameters for locally developed shielding material: Polyboron. J. Radiat. Res. Appl. 9, 26–34 (2016).
Al-Hadeethi, Y., Sayyed, M. I., Mohammed, H. & Rimondin, L. X-ray photons attenuation characteristics for two tellurite based glass systems at dental diagnostic energies. Ceram. Int. 46, 251–257 (2020).
Singh, H. et al. ZnO–PbO–B2O3 glasses as gamma-ray shielding materials. Nucl. Instrum. Methods Phys. Res. B 207, 257–262 (2003).
Yasmin, S., Barua, B. S., Khandaker, M. U., Rashid, M. A. & Bradley, D. A. Studies of ionizing radiation shielding effectiveness of silica-based commercial glasses used in Bangladeshi dwellings. Results Phys. 9, 541–549 (2018).
Cheewasukhanont, W., Limkitjaroenporn, P., Kothan, S., Kedkaew, C. & Kaewkhao, J. The effect of particle size on radiation shielding properties for bismuth borosilicate glass. Radiat. Phys. Chem. 172, 108791 (2020).
Erdem, Ş, Özgür, F., Al, B., Sayyed, M. I. & Kurudirek, M. Phy-X / PSD : Development of a user friendly online software for calculation of parameters relevant to radiation shielding and dosimetry. Radiat. Phys. Chem. 166, 108496 (2020).
Askin, A., Sayyed, M. I., Dal, M., El-Mallawanye, R. & Kacal, M. R. Investigations of the gamma ray shielding parameters of (100–x)[0.5Li2O–0.1B2O3–0.4P2O5] − xTeO2 glasses using Geant4 and FLUKA codes. J. Non-Cryst. Solids 521, 11989 (2019).
Lakshminarayana, G. et al. Li2O–B2O3–Bi2O3 glasses: gamma-rays and neutrons attenuation study using ParShield/WinXCOM program and Geant4 and Penelope codes. Mater. Sci. Process. Appl. Phys. A 126, 249 (2020).
Al-Hadeethi, Y. & Sayyed, M. I. BaO–Li2O–B2O3 glass systems: Potential utilization in gamma radiation protection. Prog. Nucl. Energy 129, 103511 (2020).
X-5 Monte Carlo Team, MCNP-A General Monte Carlo N-Particle Transport Code, Version 5, Los Alamos Controlled Publication. LA-CP-03–0245 (2003).
Sayyed, M. I. et al. Evaluation of gamma-ray and neutron shielding features of heavy metals doped Bi2O3–BaO-Na2O–MgO-B2O3 glass systems. Prog. Nucl. Energy 118, 103118 (2020).
Al-Hadeethi, Y. & Sayyed, M. I. A comprehensive study on the effect of TeO2 on the radiation shielding properties of TeO2–B2O3–Bi2O3–LiF–SrCl2 glass system using Phy-X/PSD software. Ceram. Int. 46, 6136–6140 (2020).
Singh, V. P. & Badiger, N. M. Gamma ray and neutron shielding properties of some alloy materials. Ann. Nucl. Energy 64, 301–310 (2014).
Bashter, I. I. Calculation of radiation attenuation coefficients for shielding concretes. Ann. Nucl. Energy 24, 1389–1401 (1997).
Manohara, S. R., Hanagodimath, S. M., Gerward, L. & Mittal, K. C. Exposure buildup factors for heavy metal oxide glass: a radiation shield. J. Korean Phys. Soc. 59–2, 2039–2042 (2011).
Acknowledgements
This work has been supported by the Research Universiti Grant, Universiti Kebangsaan Malaysia, Geran Universiti Penyelidikan (GUP), code: 2018-134.
Author information
Authors and Affiliations
Contributions
Conceptualization, A.K.; methodology, A.J.; software, F.L.; validation, M.I.S. and K.A.M.; formal analysis, A.K.; investigation, A.K. and A.J.; resources, M.I.S.; data curation, M.I.S.; writing—original draft preparation, A.K., A.J. and M.I.S.; writing—review and editing, M.U.K.; visualization, F.L.; supervision, M.I.S.; project administration, M.R.I.F.; funding acquisition, M.R.I.F. All authors have read and agreed to the published version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kumar, A., Jain, A., Sayyed, M.I. et al. Tailoring bismuth borate glasses by incorporating PbO/GeO2 for protection against nuclear radiation. Sci Rep 11, 7784 (2021). https://doi.org/10.1038/s41598-021-87256-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-87256-1
This article is cited by
-
Zirconium tungstate (Zr4W8O32)-doped zirconium dioxide (ZrO2) for gamma ray shielding: an in-depth examination of fabrication, characterizations, and gamma ray attenuation properties
Journal of Materials Science (2024)
-
Synthesis and Characterization of La2O3–BaO–Na2O–SiO2–Bi2O3 Glass as a Potent Shield Against Ionizing Radiation
Arabian Journal for Science and Engineering (2024)
-
Loading of rubber nanocomposites by lead nanoparticles for gamma radiation shielding
Optical and Quantum Electronics (2024)
-
Effect of Bi2O3 on the Structural, Mechanical, and Radiation Gamma Shielding Properties of the Boro-Silica-Phosphate Glasses
Silicon (2023)
-
Carbon Nanostructure-based Glass Composites: A Review
Transactions of the Indian Institute of Metals (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.