Abstract
The state of Selangor, in Malaysia consist of urban and peri-urban centres with good transportation system, and suitable temperature levels with high precipitations and humidity which make the state ideal for high number of dengue cases, annually. This study investigates if districts within the Selangor state do influence each other in determining pattern of dengue cases. Study compares two different models; the Autoregressive Integrated Moving Average (ARIMA) and Ensemble ARIMA models, using the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) measurement to gauge their performance tools. ARIMA model is developed using the epidemiological data of dengue cases, whereas ensemble ARIMA incorporates the neighbouring regions’ dengue models as the exogenous variable (X), into traditional ARIMA model. Ensemble ARIMA models have better model fit compared to the basic ARIMA models by incorporating neighbuoring effects of seven districts which made of state of Selangor. The AIC and BIC values of ensemble ARIMA models to be smaller compared to traditional ARIMA counterpart models. Thus, study concludes that pattern of dengue cases for a district is subject to spatial effects of its neighbouring districts and number of dengue cases in the surrounding areas.
Similar content being viewed by others
Introduction
Dengue is a vector-borne disease, transmitted by two types of mosquito vectors; the Aedes Aegypti and Aedes Albopictus, where the life-cycle of the vector and transmission of the disease are closely related to climate variables1. Dengue is endemic in tropical and subtropical regions worldwide, and this includes Malaysia, specifically the state of Selangor2. Of the total number of 120,836, 101,357 and 83,849 dengue cases that occurred in Malaysia, during the years of 2015, 2016, and 2017 respectively, 52.30%, 50.96% and 54.00% of these cases occurred in the state of Selangor3. The state level health authorities would alert all the districts in the abovementioned states (namely, Petaling, Klang, Hulu Selangor, Hulu Langat, Kuala Selangor, Gombak, Sepang, Kuala Langat and Sabak Bernam) if there is/are always hotspot(s) or many confirmed dengue cases being identified within these localities4.
These Aedes mosquito vector populations are difficult to control and to eliminate as their eggs can mature and hatch even after a prolonged drought1. However, control against the mosquito vectors is known to be the best measure for curbing the rise of dengue cases at present. Vaccination for this disease is still under study as the efficacy of the vaccine has yet to yield reliable outcomes. One such example is dengue vaccine named Dengvaxia which has been developed by Sanofi Pasteur Ltd, but further investigations has found this vaccine was only effective for those who have been infected previously with dengue, however may cause a more severe disease and hospitalization to those who are sero-negative (not being infected prior)5.
In view of these developments, forecasting increases in dengue cases is still relevant and important for health authorities in Malaysia. Dengue prediction models are an important complementary tools to determine when an increase in dengue cases will occur and thereby to deploy methods of controlling the vector population early.
In looking into possible factors to be included in dengue prediction models, a previous study6 emphasized six factors contributing to dengue increase: serotype shift, climate change, human behavior, poor environmental sanitation, mobility of population and the ineffectiveness of the vector control activities. Therefore, these factors mentioned should be considered while building the dengue forecasting models as studies have suggested that the circulating serotype contributes to the rising trend of dengue cases7,8,9. However determining the circulating serotype requires laboratory testing which is time consuming compared to the climate factors. Moreover weather based dengue early warning surveillance systems are considered as simple, low cost, and more efficient systems10. Several dengue affected countries also have studied dengue-climate relationships and incorporated climate variables into their dengue forecasting models9.
Besides the climate, several studies have also discussed the spatial aspects of dengue patterns in developing effective prediction models. These studies discussed the global dengue prediction models11,12 and also spread across states13, districts14,15 and at localized levels16,17,18. Studies have shown that dengue prediction models are best to be localized to distribution of the mosquito vector populations that varies with biological and environmental factors15. Several different scales of localization have been used by previous studies, for example one study investigated dengue patterns with a range of only 100 m within houses of children suspected to have fever18, which represents the distance that female Aedes Aegypti mosquitoes could fly up to. Further expanding this distance, previous studies have clustered dengue incidences as hotspots within a range of 100 m–1 km19,20. Here, the direct chain of dengue transmission, flight range of the mosquito, human movement within localities and the similar serotype-specified immunity acquired by the respective residents were considered as contributing factors.
Movement of dengue-infected individuals would result in increasing the size of the outbreak clusters where many studies have instead considered localization at district levels instead of localities. A study carried out in Southern Vietnam found that high and low numbers of dengue cases occurred at time points close to each other for districts located within 100km2 radius, with villages located at a shorter distance of 52km2 radius of each other having more temporal coorelations15. In addition, a study in Taiwan suggested that temporal coorelations in neighbouring areas can be used to determine the risk of a dengue outbreak occuring in future21. The authors reported that the risk of an outbreak occuring in a area corresponds to the the probability of its neighbouring areas having a higher number of dengue cases. This possibility is measured as indices over time (temporal indices) and a total of three indices are used, consisting of probability for dengue occurrences, duration of an epidemic and the intensity of an endemic. Therefore, with these examples, it can be suggested that dengue cases are subject to spatial effect too, that is, the pattern of dengue cases in an area can be influenced by the cases in neighbouring areas. Considering the importance of neighbouring regions, this study aims to investigate spatial effects for the selected study area. For this purpose, this study applies two Box-Jenkins based model structures, the Autoregressive Integrated Moving Average (ARIMA) and its extension, Autoregressive Integrated Moving Average with Exogenous variable (ARIMAX) models (described as Ensemble ARIMA for this study) for predicting dengue cases22,23.
Thus, specifically this study consists of three research objectives. First, is to build a single ARIMA dengue prediction model. The next step is to build an ensemble ARIMA model that incorporates the spatial effects of neighboring regions which represents an ARIMAX model structure with the ARIMA representing own regions’ dengue estimation model, and the external variables (X) from the neighboring regions’ dengue estimation models. Finally, the third objective is to compare and select the optimum dengue prediction models for each study region for single and ensemble model using AIC (Akaike Information Criterion) and BIC (Bayes Information Criterion) model selection tools.
Materials methods
Study region
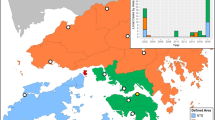
The study region consists of seven districts in the state of Selangor, Malaysia. These districts are, Hulu Selangor, Petaling, Klang, Kuala Selangor, Hulu Langat, Gombak and Sepang. Data on dengue cases were obtained from the Ministry of Health (MoH), Malaysia. The data used is on a weekly basis and was collected from the years 2009–2013, consisting of 260 weeks. Since the dengue trajectories are non-stationary, first order differencing with d = 1 is applied to convert dataset to stationary time series. The ARIMA and ARIMAX methodologies were then applied to the resulting differenced and stationary time series. It is found that d = 1 was sufficient to achieve stationarity and thus, higher order differencing was not needed. Figure 1 shows the study districts whereas the neighbouring regions for each study district which is needed to develop the ensemble models as in Eq. (2), is described in Table 1. These neighboring districts are aligned with a previous study emphasizing dengue cases within regions around 52km2 in average, are more likely to be correlated and their patterns may influence one area to another15. Thus, this study considered districts within 52km2 as the neighbouring districts and the distance on road are computed.
ARIMA and ensemble ARIMA models for dengue prediction
In order to determine best dengue prediction model, a comparison study is carried out between models with (i) dengue cases of own region only and (ii) dengue cases of own region together with dengue models of neighbouring regions. These models are represented as the ARIMA and ensemble ARIMA (which can be viewed as ARIMAX extension) models, respectively, and developed using the Box-Jenkins (BJ) approach consisting of three stages: Model Identification, Parameter Estimation and Residual Diagnostics.
Both ARIMA and Ensemble ARIMA models can be represented as Eqs. (1) and (2) respectively.
where: \({\widehat{Y}}_{t-1}^{{\prime}}\) is the observation at time \((t-1)\) obtained from its own region’s dengue model, \({X}_{i}^{{{\prime}}(l)}\) are the observation obtained from the i-indexed dengue models of \(\left(l\right)\) number of neighbouring regions’ dengue models and \(\widehat{{\varepsilon }_{t}}\) is the error value at time \(t\) obtained from its own region dengue model. The vectors \(\underset{\_}{\phi }=\left({\phi }_{1}, {\phi }_{2},\dots ,{\phi }_{p}\right)\), \(\underset{\_}{\theta }=\left({\theta }_{1},{\theta }_{2},\dots ,{\theta }_{q}\right)\) and \(\underset{\_}{\beta }=\left({\beta }_{1}^{l}, {\beta }_{2}^{l}, \dots ,{\beta }_{i}^{l}\right)\) are the total \(\left(p+q+l\right)\) unknown parameters to be estimated with each \({\phi }_{i}\in \mathfrak{R}\) in Eqs. (1) and (2) representing the correlation for previous dengue cases, \({\theta }_{i}\in \mathfrak{R}\) in Eqs. (1) and (2) representing the correlation for moving average of previous error terms to be included and finally \({\beta }_{i}\in \mathfrak{R}\) representing the correlation coefficient for the neighbouring regions’ dengue models considering each \(\left(l\right)\). The parameters are estimated using the Maximum Likelihood (ML) approach, and residual diagnostics are carried out on the obtained models to ensure the errors are white-noise. The developments of ARIMA and Ensemble ARIMA models are illustrated in Fig. 2a,b, respectively.
Akaike Information Criterion (AIC) and Bayes Information Criterion (BIC)
As two models are obtained for each study region, the optimum model needs to be identified, and therefore, the AIC and BIC values are used as the model selection tools. The best model would be the one with lowest AIC and BIC values. Since AIC safeguards against underfitting and BIC against overfitting, by considering both these AIC and BIC values, the selected model will have good prediction capability and will be parsimonious24.
The AIC and BIC values25 are defined as in Eqs. (3) and (4) respectively:
where \(\mathrm{log} \,L\) is the model likelihood, \(k\) is the number of model parameters and \(N\) is the number of observations in the time series data. The notation \(k\) is used as follows: \(k={k}_{0}+1\), where \({k}_{0}\) is the number of significant non-zero \(\underset{\_}{\upphi }\) and \(\underset{\_}{\uptheta }\) coefficients in the ARIMA \({\left(\mathrm{p},\mathrm{d},\mathrm{q}\right)}^{*}\) model (see Fig. 2a), the \(\underset{\_}{\upphi }\) coefficients are represented by at most \(p\) non-zero values and the \(\underset{\_}{\uptheta }\) coefficients are represented by at most \(q\) non-zero values. The extra \(\left("+1"\right)\) corresponds to the variance parameter, \({\upsigma }^{2}\). For the Ensemble ARIMA \(\left(p,d,q,l\right)\) model, the value of k is \(\mathrm{k}={\mathrm{k}}_{0}+\mathrm{m}+1\) since there are \(m\) number of \(\beta\)-coefficients of neighbouring regions’ dengue models and one variance parameter,\({\sigma }^{2}\).
Results
Data description
The data descriptions of dengue cases for each study district are given in Table 2.
Prior to model building and selection, the value of dengue cases of each study region is normalized into the same range (0–1): Letting \(A\) represent a generic notation for a variable which represents number of cases, normalization entails the formula given in Eq. (5).
Single dengue prediction models
Phase I: ARIMA model development
The development of the dengue prediction model is illustrated for Petaling district in Figs. 3, 4 and 5. Figure 3 shows the weekly dengue case trajectory for Petaling district during years of 2009–2013 which shows clearly the cases are not stationary as they have many noticeable peaks. First order differencing (d = 1) was carried out and visible lag orders are identified using the ACF and PACF plots. The PACF plot in Fig. 4 shows significant peaks at p = 1 and p = 2, hence, ARIMA (2,1,0) model is selected as a viable option. Figure 5 shows the ACF and PACF plots which depicts residuals from the fitted model have no significant peaks outside the 95% confidence intervals for the first three lags, indicating that the residuals are possibly white noise. Hence, ARIMA (2,1,0) model structure is set for dengue cases of Petaling district (taking the case for a district).
Ensemble ARIMA model development
Single dengue models are enlarged by including its neighbouring districts’ (as in Table 1), forming the ensemble dengue models. Single models are built using dengue cases time series from its own district, whereas ensemble models are built based on combining own district, and neighbouring districts’ dengue models. The ensemble ARIMA model, by taking the example of Petaling district is described as in Eq. (6).
where \(ARIMA {\left(\mathrm{2,1},0\right)}_{P}\) is the ARIMA (2,1,0) model using observations from the dengue prediction model of Petaling district, the exogenous (X) part is built using observations from the four neighbouring regions’ ARIMA dengue prediction models of Hulu Langat, Gombak, Kuala Selangor and Klang: \(\widehat{HL}, \widehat{G},\) \(\widehat{KS}\) and \(\widehat{K}\), respectively. These observations are obtained from the respective single models, which are the ARIMA (1,1,2) * model for Hulu Langat district, ARIMA (2,1,0) model for both Gombak and Klang districts and finally ARIMA (3,1,0) for Kuala Selangor district. Parameters \(\alpha , \beta ,\) \(\gamma\) and \(\delta\) are the coefficients of the respective dengue prediction models.
Comparisons between single and ensemble ARIMA dengue prediction models
Figure 6 shows the results obtained for single (AIC-S and BIC-S) and ensemble ARIMA model (AIC-E and AIC-E) comparisons. The results obtained indicate that ensemble models have lower AIC and BIC values in all of the seven districts considered (refer to Table 3). This explains that across all seven study districts, ensemble models have better fit and predicts dengue cases better compared to single dengue models.
Discussion
This finding explains that the pattern of dengue cases at neighbouring districts influences and suggests that human movements and contact between neighbouring districts is a factor in dengue transmission and the spread of the disease. Human mobility is neighbouring areas allows for the possibility of an infected person to transmit dengue virus to the surrounding areas26. Previous studies have shown that urban areas with high population densities and with increased movement of infected individuals contributes to increase spread of the disease27,28,29. Sources for human mobility can be obtained from the geo-location information in mobile phone data30,31,32 and from data on the use of public transportation33,34, air travel patterns and data on human mobility35. In all these studies, authors managed to conclude that inclusion of human mobility data enhanced the dengue prediction models which is shown as ensemble of neighbouring regions in this study.
Conclusion
Firstly, modelling dengue cases using ARIMA models in this study, is considered crucial and appropriate since these models can incorporate feedback information. Feedback information is necessary for modelling infectious disease trajectories, such as dengue, whose current values are strongly correlated to past values. In order to fit ARIMA models to dengue trajectories which are typically non-stationary, one has to first apply differencing in order to convert these times series into stationary ones36,37.
Based on the single-ensemble model comparisons, this study concludes that dengue cases are subject to spatial effects, that is, patterns of dengue cases in neighboring areas do influence dengue case pattern of the study area.
Among the limitation of this study is that besides spatial effects, there are many other factors that may influence dengue cases. These include climate, new serotypes, herd immunity and strain-cross immunity, impact of vector control programs that have been carried out and finally mosquito vector densities38,39. A better fit model can be obtained by including all these factors.
Finally, dengue prediction models in this study are only built for seven districts in Selangor as incorporating larger area may not yield an optimal model given that the dengue prediction models are localized, where they only describe their own respective district’s dengue case patterns. Future work shall investigate other districts in other states in Malaysia, especially Wilayah Persekutuan, Kuala Lumpur and Johor which have reported high number of dengue cases39.
References
Ebi, K. L. & Nealon, J. Dengue in a changing climate. Environ. Res. 151, 115–123 (2016).
Selvarajoo, S. et al. Knowledge, attitude and practice on dengue prevention and dengue seroprevalence in a dengue hotspot in Malaysia: a cross-sectional study. Sci. Rep. 10(1), 1–3 (2020).
Kei, H. M. Percentages of dengue fever cases by states, Malaysia 2015 and 2016 (2017).
Salim, N. et al. Prediction of dengue outbreak in Selangor Malaysia using machine learning techniques. Sci. Rep. 11(1), 939 (2021).
Fatima, K. & Syed, N.I. Dengvaxia controversy: impact on vaccine hesitancy. J. Global Health 8 (2018).
Díaz-Robles, L. A. et al. A hybrid ARIMA and artificial neural networks model to forecast particulate matter in urban areas: the case of Temuco, Chile. Atmos. Environ. 42, 8331–8340 (2008).
Lee, K.-S. et al. Dengue virus surveillance for early warning, Singapore. Emerg. Infect. Dis. 16, 847 (2010).
Recker, M., Blyuss, K. B., Simmons, C. P., Hien, T.T., Wills, b. & Farrar, J. et al. Immunological serotype interactions and their effect on the epidemiological pattern of dengue. In Proceedings of the Royal Society of London B: Biological Sciences, p. rspb. 2009.0331 (2009).
Xu, H.-Y. et al. Statistical modeling reveals the effect of absolute humidity on dengue in Singapore. PLoS Negl. Trop. Dis. 8, e2805 (2014).
Hii, Y. L., Zaki, R. A., Aghamohammadi, N. & Rocklöv, J. Research on climate and dengue in Malaysia: a systematic review. Curr. Environ. Health Rep. 3, 81–90 (2016).
Bhatt, S. et al. The global distribution and burden of dengue. Nature 496, 504–507 (2013).
Hales, S., De Wet, N., Maindonald, J. & Woodward, A. Potential effect of population and climate changes on global distribution of dengue fever: an empirical model. The Lancet 360, 830–834 (2002).
Cheong, Y. L., Burkart, K., Leitão, P. J. & Lakes, T. Assessing weather effects on dengue disease in Malaysia. Int. J. Environ. Res. Public Health 10, 6319–6334 (2013).
Cummings, D. A. et al. Travelling waves in the occurrence of dengue haemorrhagic fever in Thailand. Nature 427, 344 (2004).
Cuong, H. Q. et al. Spatiotemporal dynamics of dengue epidemics, southern Vietnam. Emerg. Infect. Dis. 19, 945 (2013).
Dom, N. C., Hassan, A. A., Latif, Z. A. & Ismail, R. Generating temporal model using climate variables for the prediction of dengue cases in Subang Jaya, Malaysia. Asian Pac. J. Trop. Dis. 3, 352–361 (2013).
Rosli, A. C. et al. Spatial mapping of dengue incidence: a case study in Hulu Langat District, Selangor, Malaysia. Int. J. Hum. Soc. Sci. 5, 410–414 (2010).
Mammen, M. P. Jr. et al. Spatial and temporal clustering of dengue virus transmission in Thai villages. PLoS Med. 5, e205 (2008).
Liebman, K. A. et al. Spatial dimensions of dengue virus transmission across interepidemic and epidemic periods in Iquitos, Peru (1999–2003). PLoS Negl. Trop. Dis. 6, e1472 (2012).
Salje, H. et al. Revealing the microscale spatial signature of dengue transmission and immunity in an urban population. Proc. Natl. Acad. Sci. 109, 9535–9538 (2012).
Wen, T.-H. et al. Spatial–temporal patterns of dengue in areas at risk of dengue hemorrhagic fever in Kaohsiung, Taiwan, 2002. Int. J. Infect. Dis. 14, e334–e343 (2010).
Jing, Q. et al. Imported cases and minimum temperature drive dengue transmission in Guangzhou, China: evidence from ARIMAX model. Epidemiol. Infect. 146, 1226–1235 (2018).
Rubaya, A. K., Kusnanto, H., Lazuardi, L. & Satoto, T. B. T. ARIMA models of dengue cases in Kartamantul, based on area risk classification. Jurnal Medicoeticolegal dan Manajemen Rumah Sakit 7(3), 119–126 (2018).
Dziak, J. J., Coffman, D. L., Lanza, S. T., Li, R. & Jermiin, L. S. Sensitivity and specificity of information criteria. bioRxiv, p. 449751 (2019).
Nau, R. Statistical forecasting: notes on regression and time series analysis. https://people.duke.edu/~rnau/411home.htm. Access date: 30 December 2017.
W. H. Organization, S. P. f. Research, T. i. T. Diseases, W. H. O. D. o. C. o. N. T. Diseases, W. H. O. Epidemic, and P. Alert, Dengue: guidelines for diagnosis, treatment, prevention and control: World Health Organization (2009)
Ashmore, P. et al. Spatiotemporal and Socioeconomic Risk Factors for Dengue at the Province Level in Vietnam, 2013–2015: clustering Analysis and Regression Model. Trop. Med. Infect. Dis. 5(2), 81 (2020).
Tao, H. et al. A comprehensive framework for studying diffusion patterns of imported dengue with individual-based movement data. Int. J. Geogr. Inf. Sci. 34, 604–624 (2020).
Wen, T.-H., Lin, M.-H. & Fang, C.-T. Population movement and vector-borne disease transmission: differentiating spatial–temporal diffusion patterns of commuting and noncommuting dengue cases. Ann. Assoc. Am. Geogr. 102, 1026–1037 (2012).
Chen, Y. et al. Neighbourhood level real-time forecasting of dengue cases in tropical urban Singapore. BMC Med. 16(1), 1–13 (2018).
Wesolowski, A. et al. Impact of human mobility on the emergence of dengue epidemics in Pakistan. Proc. Natl. Acad Sci. 112(38), 11887–11892 (2015).
Tizzoni, M. et al. On the use of human mobility proxies for modelling epidemics. PLoS Comput. Biol. 10(7), e1003716 (2014).
Saba, H. et al. Relevance of transportation to correlations among criticality, physical means of propagation, and distribution of dengue fever cases in the state of Bahia. Sci. Total Environ. 618, 971–976 (2018).
Bomfim, R. et al. Predicting dengue outbreaks at neighbourhood level using human mobility in urban areas. R. Soc. Interface 17: 2020691
Dalziel, B. D., Pourbohloul, B. & Ellner, S. P. Human mobility patterns predict divergent epidemic dynamics among cities. Proc. R. Soc. 280, 20130763 (2013).
Alain, F. Z. Graham, M. S. Time series analysis. In Analyzing ecological data. New York, USA (2007).
Cressie, N. & Wikle, C. K. Statistics for Spatio-Temporal Data (Wiley, Hoboken, 2015).
Hazrin, M. et al. Spatial distribution of dengue incidence: a case study in Putrajaya. J. Geogr. Inf. Syst. 8, 89 (2016).
Azeem. Malaysia's statistics on dengue fever (2017). https://vase.ai/blog/malaysias-selected-statistics-health-2/
Acknowledgements
Authors would like to thank the Ministry of Health (MoH) for providing the necessary data to conduct this work. Authors also thank PETRONAS and Ministry of Higher Education (MOHE) for providing required funding through the grants below to conduct this research.
Funding
This research was funded by the PRGS grant 015MEO-054 and supported by the YUTP grant 015C0-299.
Author information
Authors and Affiliations
Contributions
Conceptualization, L.T., S.C.D, V.S.A, H.D., and B.S.G; methodology, S.C.D and V.S.A; data curation, S.C.D, V.S.A, and B.S.G; writing—original draft preparation, L.T.; writing—review and editing, S.C.D, H.D., V.S.A. and B.S.G.; supervision, S.C.D, H.D. and V.S.A.; project administration, V.S.A.; funding acquisition, V.S.A.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thiruchelvam, L., Dass, S.C., Asirvadam, V.S. et al. Determine neighboring region spatial effect on dengue cases using ensemble ARIMA models. Sci Rep 11, 5873 (2021). https://doi.org/10.1038/s41598-021-84176-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-84176-y
This article is cited by
-
A method for short-term passenger flow prediction in urban rail transit based on deep learning
Multimedia Tools and Applications (2023)
-
Predictive analysis of the number of human brucellosis cases in Xinjiang, China
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.