Abstract
Photoexcited lead-free perovskite CH3NH3SnI3 based solar cell device was simulated using a solar cell capacitance simulator. It was modeled to investigate its output characteristics under AM 1.5G illumination. Simulation efforts are focused on the thickness, acceptor concentration and defect density of absorber layer on photovoltaic properties of solar cell device. In addition, the impact of various metal contact work function was also investigated. The simulation results indicate that an absorber thickness of 500 nm is appropriate for a good photovoltaic cell. Oxidation of Sn2+ into Sn4+ was considered and it is found that the reduction of acceptor concentration of absorber layer significantly improves the device performance. Further, optimizing the defect density (1014 cm−3) of the perovskite absorber layer, encouraging results of the Jsc of 40.14 mA/cm2, Voc of 0.93 V, FF of 75.78% and PCE of 28.39% were achieved. Finally, an anode material with a high work function is necessary to get the device's better performance. The high-power conversion efficiency opens a new avenue for attaining clean energy.
Similar content being viewed by others
Introduction
In the future, energy demand will be increased drastically. Nowadays, most of the energy consumption is obtained from fossil fuels, and this energy reserve will be depleted in the coming days. Since it pollutes the environment, therefore, the most challenging task is to establish a renewable energy source. The demand for renewable sources of energy is increasing due to industrialization and growing populations. For this, solar energy is an up-and-coming source because it is clean and no adverse effect on the environment1,2,3,4,5,6,7. Solar energy devices after a sustainable solution in global energy are demanded.
Perovskite solar cell (PSC) has garnered tremendous attention to the scientific community due to increased power conversion efficiency (PCE) day by day. Researchers started working on perovskite solar cells in 20098. At that time, efficiency was relatively low (~ 3.8%). This organic–inorganic perovskite solar cell becomes a next-generation device because it showed a step increase in PCE. The state-of-the-art certified PCE of PSC is exceeding 25%5,6,7,9,10. Apart from that, these materials exhibit peculiar features such as high absorption coefficient, good charge carrier mobility, small exciton binding energy and large diffusion length of charge carriers9,11,12,13. Therefore, it is imperative to work on it. This energy can be converted into electricity using a photovoltaic effect14. However, it is cheap and clean energy; hence, it has dominated the Si-based solar cell in the photovoltaic market15. People studied pure and modified methylammonium lead halide as a perovskite material because of their good photovoltaic performance16,17. Nowadays, some of the reports are coming on lead-based materials. However, lead-based electronic devices have been sternly circumscribed by the European Union and other countries as well. These materials showed a high value of power conversion efficiency. However, lead is not eco-friendly, which is harmful to humans and the environment5,18,19,20,21,22,23,24,25.
To overcome this issue and owing to the superior optoelectronic properties lead-free perovskite CH3NH3SnI3 has been explored by many scientists and researchers as a photovoltaic material. This material exhibits a direct band gap of 1.3 eV, a suitable range for the absorber. Recently, several group have successfully fabricated/simulated organic–inorganic perovskites solar cells based CH3NH3SnI3, which yields the good PCE. Freshly, the studied description stated that CH3NH3SnI3 is as favorable as its lead-based counterpart17,26,27,28,29,30. The electron transport layer (ETL) is a crucial component of PSC. TiO2 is a promising candidate material because of its appropriate energy level for electron injection, high electron mobility, chemical stability, low synthesis cost and environmental friendliness31,32,33,34. TiO2 material has an appropriate band gap between diminishing the transportation of holes35. The hole transport layer (HTL) plays a crucial role for getting the high-power conversion efficiency in PSC. HTL needs high hole carrier mobility and should form a less defect at the HTL/absorber layer to minimize the charge carriers recombination at the interface. Recently, Yu et al. reported that Cu2O as an HTL showed high hole mobility, good energy level alignment with CH3NH3PbI3 and a longer lifetime of photo-generated charge carriers33. Cu2O is used as an HTL because of abundant availability on Earth, environmental-friendly, perfectly band alignment with CH3NH3SnI3 and easily synthesized materials. It decreases the barrier height of metal contact and reduces the recombination loss of minority at anode11,36,37. Device simulation provides a strong way to improve PSC's efficiency after the optimization of various physical parameters. Solar cell capacitance simulator (SCAPS) was utilized by many theoreticians to predict the open circuit voltage (Voc), short circuit current density (Jsc), fill factor (FF) and PCE of the perovskite based solar cell27,38,39. Hence, the simulation of lead-free CH3NH3SnI3 as a photoactive material was studied using SCAPS. The impact of rectifying and ohmic contact behaviour on lead-free CH3NH3SnI3 based PSC was also investigated.
Device structure and simulation
In this work, a numerical simulation of a planar heterojunction tin-based perovskite solar cell was performed using SCAPS. To obtain the performance parameters of the device like current density–voltage (J-V) curve, quantum efficiency and energy bands, Poisson Eq. (1) is solved with continuity equation of electron (2) and hole (3). These curves are used to calculate Jsc, Voc, FF and PCE of the solar cell device.
where, G, τn, τp, D, q, Ψ, µn, µp, n (x), p (x), nt (x), pt (x), \({N}_{A}^{-}\left(x\right)\), \({N}_{D}^{+} (x)\) and ξ denote the generation rate, electron life time, hole life time, diffusion coefficient, electron charge, electrostatic potential, electron mobility, hole mobility, concentration of free electrons, concentration of free holes, concentration of trapped electrons, concentration of trapped holes, ionized acceptor concentrations, ionized donor concentrations and electric field, respectively. x denotes the direction along the thickness29.
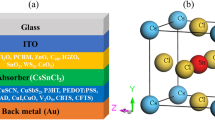
The device's structure in the simulation is transparent conduction oxide (TCO)/buffer (ETL)/interface defect layer 1/absorber/interface defect layer 2/HTL. The simulation was done under the illumination of 1000 W/m2, at 300 K and an air mass of AM 1.5G. The active area of the studied device is 1 cm2. The device's configuration is illustrated in Fig. 1a where, p-type Cu2O is used as an HTL, CH3NH3SnI3 is used as an absorber layer and n-type TiO2 is used as an ETL. In addition, fluorine doped tin oxide (FTO) is selected as the contact material and various materials like Ag, Cu, Au and Pt is selected as an anode. The energy level diagram of the corresponding materials utilized in the device architecture is depicted in Fig. 1b.
The values of the device and material parameters that are adopted from theories, experiments and literature are summarized in Tables 1 and 227,28,29,39. Initially, the thickness of FTO (500 nm), TiO2 (120 nm) and Cu2O (420 nm) were optimized for high PCE, as mentioned in Table 1.
Herein, χ is the electron affinity, Eg is the band gap, εr is the relative permittivity, Nc is the density of state of the conduction band, Nv is the density of state of the valence band, µn is the mobility of electron, µp is the mobility of hole, NA is the acceptor density, ND is the donor density and Nt is the defect density. The thermal velocity of electron and hole are set be 107 cm/s. The absorption coefficient of FTO, Cu2O, CH3NH3SnI3 and TiO2 were extracted from experimental results15,40,41,42. The diffusion lengths of electron and hole were set to 260 nm and 560 nm, respectively, similar to the experimentally observed value of Ma et al.28.
Results and discussion
With these initial parameters in Tables 1 and 2, energy band diagram, J-V characteristic and quantum efficiency of the cell was plotted, as shown in Fig. 2a–c, respectively. After illumination, electron–hole pairs are generated inside the absorber layer. Due to the junction field electrons and holes move towards ETL and HTL, respectively. These electrons and holes are collected at the cathode and anode, respectively and generates a voltage. The Jsc of 39.72 mA/cm2, Voc of 0.66 V, FF of 69.82%, and PCE of 18.31% are obtained. The Jsc of the device depends upon the absorption coefficient, thickness and mobility of the active material. The higher the absorption coefficient, the higher the photo current will be9,12,29,39,43. The second important parameter is the thickness of the absorber. It must be thick enough to absorb the highest cut off wavelength of the incident solar radiation27,29. Apart from that, mobility plays a very crucial role for getting the high Jsc. Ideally, the Jsc is equivalent to solar cell current after illumination. Ma et al. and Stoumpos et al. reported the very high value of mobility of electron (2000 cm2/Vs) and hole (300 cm2/Vs) for CH3NH3SnI3 sample synthesized by open tube method28,44. Similar values of carriers mobilities have been utilized by Lazemi et al. and stated a high value of Jsc (~ 37 mA/cm2)27. In this simulation, the mobility of electron and hole was adopted from recently studied researcher27,28,43,44. Since, current density is linearly proportional to the mobility of charge carriers, and hence the high value of Jsc was achieved. However, Devi et al.45 and Khattak et al.46 have considered the significantly smaller and identical values of electron and hole mobilities, which are 1.6 cm2/Vs and 0.16 cm2/Vs, respectively and reported good Jsc (~ 30 mA/cm2). Another aspect is that diffusion length is proportional to the square root of mobilit45. Hence, diffusion length becomes more for high mobility of charge carrier, and hence recombination of charge carriers decreases. This may be other reasons for getting the comparatively higher value of Jsc as compare to recently reported results45,46. The simulated device performance is auspicious and consistent with the tin-based PSC27,29,39. The quantum efficiency curve covers the entire visible spectrum, which is in good accordance with the recently published results47,48. Further enhancement in photovoltaic performance is possible. Figure 2a displays the energy band diagram of PSC. The positive conduction band offset (CBO) of about 0.36 eV is observed at absorber/ETL interface. Due to this positive CBO, a spike is formed at the absorber/ETL interface. This spike acts as a barrier for photo-generated electron flow towards the electrode49,50,51,52.
Absorber thickness
The absorber layer plays a significant role in the performance of device. The previously published report shows that the photovoltaic parameters such as Jsc, Voc, FF and PCE are influenced by the absorber layer thickness27,39. To get the absorber layer's role in the device simulation, the absorber layer's thickness was varied from 100 to 1000 nm, and other parameters tabulated in a Tables 1 and 2 remain the same. The simulation results, i.e., the variation of photovoltaic parameters concerning the absorber layer's thickness, is shown in Fig. 3. It is observed that Jsc increases steeply up to 700 nm and then varies slowly with thickness. The large value of Jsc was obtained (~ 42.70 mA/cm2) with a thickness 900 nm is mainly due to the large absorption coefficient of the perovskite29. Voc falls off smoothly, which may be attributed to the enhanced recombination of free charge carriers in the thicker absorber27. The decreasing value of FF with respect to absorber thickness may be due to the increased series resistance29,53. In addition, PCE initially increases and reaches a maximum (~ 18.36%) at 500 nm and decreases with a further increase in absorber thickness. Firstly, the absorber thickness is smaller than the diffusion length of charge carriers; therefore, most of the charge carriers reach at the electrodes, and therefore PCE increases. However, recombination occurs for thick absorber layer, and hence PCE decreases with a further increase in thickness27,29,39.
Acceptor carrier concentration (NA) of the absorber
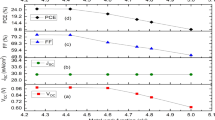
Apart from the absorber layer thickness, the photovoltaic cell's device performance is significantly affected by the acceptor density of holes in the absorber layer. CH3NH3SnI3 oxides in which Sn2+ is converted into Sn4+ (self-doping process) when the device is exposed to air. Unfortunately, this process deteriorates the performance of the device and making it a p-type semiconductor28. Addition of SnO2 suppresses the formation of Sn2+ to Sn4+15,43,54. Feng et al. calculated the dark carrier density of 1014 cm−3 to 1017 cm−3 by Hall- effect measurement55. Takashi et el. found out that the hole concentration in the CH3NH3SnI3 absorber layer can be varied up to 1019 cm−356. Therefore, to get to know how acceptor doping concentration affects the photovoltaic parameters, the acceptor density of the CH3NH3SnI3 layer was varied from 1014 to 1018 cm−3. Figure 4 provides the variation of J-V characteristics and PCE with respect to acceptor densities of the perovskite layer. The slight change in photovoltaic parameters up to 1015 cm−3 acceptor concentration implies that the generation rate of photo-generated carriers does not change with acceptor densities under the incident of the same photon number39. With increasing the acceptor doping concentration, the Fermi energy level of the hole decreases and hence Voc increases, as shown in Fig. 4a. Another aspect is that built-in potential increases with increasing the acceptor doping concentration. Due to this, charge separation promotes and hence Voc increased. However, initially, Jsc decreases slightly up to 1015 cm−3 and then decreases drastically. It may be due to the increase in the recombination rate of charge carriers inside the perovskite absorber layer39. However, PCE drops rapidly when NA exceeds 1015 cm−3. The absorber layer's defect state leads to a considerable drop in power conversion efficiency, as exposed in Fig. 4b.
Defect density (Nt)
The effect of defect density of absorber was also investigated. Defects are inevitable in absorber layer. They exist in the bulk and at surfaces. In perovskite absorber layer, defects present in the form of point defects such as lattice vacancy, interstitial, Schottky and Frenkel defects. Apart from that, the higher order defects like dislocations and grain boundaries may also be present57. The self-doping process, which makes the semiconductor p-type, produces impurity defect in absorber layer15,28,43,55. These defects introduce deep or shallow levels in the energy band gap57. As a result of these defects, charge carriers can trap and facilitate non-radiative electron–hole recombination27,39. It is noted that the diffusion length of charge carriers is increased up to ~ 3 µm in Sn-based perovskite absorber layer using tin-reduced precursor solution58. Since, diffusion length of charge carriers is related to the defect density45. Therefore, in order to see the effect of diffusion length on photovoltaic responses, diffusion length of electron was varied from 0.046 to 4.6 µm by changing defect density from 1018 to 1014 cm−359. Similar change in defect density has also been adopted by Lazemi et al., Du et al. and Hao et al.27,30,39. Based on these studies, the defect density was varied from 1014 to 1018 cm−3 and depicted its variation on photovoltaic properties in PSC, as shown in Fig. 5. It is observed that the performance of the device improved with the reduction of defect density. The absorber layer's initial defect density was set to be 3.029 × 1016 cm−3 (as per Table 2). Because for this value of defect density, the diffusion length of electron and hole is nearly similar to experimentally observed values28. When the defect density is 1015 per cm−3, the cell performance is significantly improved, attaining the Jsc of 40.13 mA/cm2, Voc of 0.81 V, FF of 75.17% and PCE of 24.54%. Now, further decrease of Nt, from 1015 to 1014 cm−3, slight variation is observed in Jsc (40.14 mA/cm2) and FF (75.78%) but considerable changes occurred in Voc (0.93 V) and PCE (28.39%). However, experimentally, it is not easy to synthesize a material with such a low value of defect density39.
The Shockley–Read–hall (SRH) recombination model can be utilized to get information about the influence of the absorber layer's defect density on device performance27,29,52. To get the influence of Nt on the performance of the device acutely, the effect of defect density on the recombination rate based on the SRH recombination model was studied. Figure 6 shows the variation of recombination rate with depth from the surface for different value of Nt. It is detected that with increasing the defect density recombination rate increases, which is the reason for the reduction of cell performance with the increased value of defect density. Since, recombination rate increases with increasing the defect density; therefore, Voc decreases with increasing the defect concentration, as shown in Fig. 5.
According to SRH model, the recombination rate (R) can be expressed like
where, τn,p, n, p, ni, Ei and Et are the lifetime of charge carriers, the density of electron, the density of hole, intrinsic density, intrinsic energy level and energy level of the trap defects, respectively.
Lifetime of charge carriers is given by
where, σn,p, vth and Nt are the capture cross section of charge carriers, velocity of charge carriers, and the absorber layer's defect density, respectively. Therefore, with increasing the defect density, the relaxation time of charge carriers decreases (as per Eq. 5) and hence recombination rate increases (according to Eq. 4) as confirmed by Fig. 6.
The interface recombination depends upon the conduction band offset between the buffer and absorber layer. The interface recombination at the absorber/buffer interface reduces due to the creation of positive CBO49,50,51. Minemoto et al. theoretically studied the effect of CBO at the absorber/buffer interface49. He reported that about 0.3 eV CBO offset minimizes the recombination at the interface due to this photovoltaic parameter increases. Hence, the recombination rate is significantly low at the absorber/ETL interface as compared to previously reported results39,52.
The diffusion length of charge carriers can be written like
where, D is the diffusion coefficient. Since, the diffusion coefficient is proportional to the mobility of charge carriers and the mobility of electron (~ 2000 cm2/Vs) and hole (300 cm2/Vs) is large as experimentally observed by various researchers30,44. Due to the large value of mobility, diffusion length is large, which is why obtaining the very high value of PCE (28.39%). Because of the low recombination rate and large diffusion length, a very high value of PCE was achieved. Hence, the obtained outcomes are found to be better than previously published results27,29,39,60.
Metal electrode work function
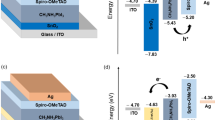
To study the ohmic or rectifying behaviour at metal contact/HTL interface, a work function study was carried out by varying various anode materials. Simulation was done using Ag, Cu, Au and Pt as an anode for PSC. The work function of Ag, Cu, Au and Pt are 4.74 eV, 5.0 eV, 5.1 eV and 5.7 eV, respectively61,62. The energy band diagram with various anode materials is shown in Fig. 7a,b. As clearly shown that the barrier layer for hole increases with decreasing the wave function of contact materials (Fig. 7a). Figure 8a,b presents the anode material's effect on J-V characteristics and photovoltaic properties of PSC. We can see that PCE decreases with decreasing the work function of the anode. In the case of Ag, Cu and Au, the anode's work function is less than the work function of Cu2O61,62. Hence, a rectifying Schottky barrier contact was formed for Ag, Cu and Au anode materials at an anode/Cu2O interface, as indicated by the dashed oval frame in Fig. 7a. This Schottky barrier hinders the hole transport to the anode, decreasing the FF and PCE as confirmed by Fig. 8b29. However, in the case of Pt anode, the work function of Pt is higher than the work function of Cu2O63. The ohmic contact was formed at an anode/Cu2O interface, as indicated by the dashed oval frame in Fig. 7b. The ohmic contact allows the hole transport at the interface62. Therefore, further improvement in Jsc (42.63 mA/cm2) and PCE (19.67%) are observed as shown in Fig. 8.
The surface potential energy barrier (\({\phi }_{B}\)) at the anode/Cu2O interfaces is given by
Here, Eg is the band gap of Cu2O, \(\chi \) is the electron affinity of Cu2O and \({\phi }_{M}\) is the anode's work function. Due to the decrease in the value of work function the surface potential energy barrier increases (as per Eq. 7), hence the FF and PCE decreases.
Conclusion
Lead-free CH3NH3SnI3 perovskite as light harvester is investigated. A planner heterojunction perovskite solar cell with the structure FTO/TiO2/CH3NH3SnI3/Cu2O/anode was numerically analysed. Photovoltaic parameters were optimized with respect to several factors such as absorber layer thickness, acceptor density, defect density and work function of anode materials. The optimized perovskite thickness of 500 nm significantly enhances the PCE (18.36%). Reducing the defect density and improving the Sn2+ stability of absorber layers are the critical issues for future research, which might be resolved by refining the device's fabrication techniques. The results indicated that the appropriate defect density improves the cell performance; however excessive concentration leads to a higher recombination rate of charge carriers and poor cell performance. The Schottky junction was formed at an anode/Cu2O interface for lower work function contact materials; therefore, high work function material is necessary for ohmic contact like Pt. The reported CH3NH3SnI3-based PSC provide a viable path to realizing environmentally benign, low-cost, and high-efficiency PSC.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Markose, K. K. et al. Novel boron-doped p-type Cu2O thin films as a hole-selective contact in c-Si solar cells. Appl. Mater. Interfaces 12, 12972–12981 (2020).
Nocera, D. G. The artificial leaf. Acc. Chem. Res. 50, 616–619 (2017).
Lipomi, D. J. & Bao, Z. Stretchable, elastic materials and devices for solar energy conversion. Energy Environ. Sci. 4, 3314–3328 (2011).
Li, Y. et al. High-performance perovskite solar cells with a non-doped small molecule hole transporting layer. Appl. Energy Mater 2, 1634–1641 (2019).
Huang, H. H., Shih, Y. C., Wang, L. & Lin, K. F. Boosting the ultra-stable unencapsulated perovskite solar cells by using montmorillonite/CH3NH3PbI3 nanocomposite as photoactive layer. Energy Environ. Sci. 12, 1265–1273 (2019).
Yang, W. S. et al. Iodide management in formamidinium-lead-halide-based perovskite layers for efficient solar cells. Science 356, 1376–1379 (2017).
Shih, Y. C. et al. Amino-acid-induced preferential orientation of perovskite crystals for enhancing interfacial charge transfer and photovoltaic performance. Small 13, 1604305–1604314 (2017).
Kojima, A., Teshima, K., Shirai, Y. & Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 131, 6050–6051 (2009).
Kim, H. S., Im, S. H. & Park, N. G. Organolead halide perovskite: New horizons in solar cell research. J. Phys. Chem. C 118, 5615–5625 (2014).
Gao, F. et al. Enhanced performance of tin halide perovskite solar cell by addition of lead thiocyanate. RSC Adv. 8, 14025–14030 (2018).
Lyu, M., Yun, J. H., Chen, P., Hao, M. & Wang, L. Addressing toxicity of lead: Progress and applications of low-toxic metal halide perovskites and their derivatives. Adv. Energy Mater 7, 1602512–1602537 (2017).
Stranks, S. D. et al. Electron–hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 342, 341–344 (2013).
Su, Y. et al. Impermeable barrier films and protective coatings based on reduced graphene oxide. Nat. Commun. 5, 4843–4847 (2014).
Weiss, M., Horn, J., Richter, C. & Schlettwein, D. Preparation and characterization of methylammonium tin iodide layers as photovoltaic absorbers. Phys. Status Solidi A 213, 975–981 (2016).
Noel, N. K. et al. Lead-free organic–inorganic tin halide perovskites for photovoltaic applications. Energy Environ. Sci. 7, 3061–3068 (2014).
Burschka, J. et al. Sequential deposition as a route to high-performance perovskite-sensitized solar cells. Nature 499, 316–319 (2013).
Lee, M. M., Teuscher, J., Miyasaka, T., Murakami, T. N. & Snaith, H. J. Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Science 338, 643–647 (2012).
Liu, D., Li, Q., Hu, J., Jing, H. & Wu, K. Predicted photovoltaic performance of lead-based hybrid perovskites under the influence of a mixed-cation approach: Theoretical insights. J. Mater. Chem. C 7, 371–379 (2019).
Caputo, M. et al. Electronic structure of MAPbI3 and MAPBCl3: Importance of band alignment. Sci. Rep. 9, 15159–15169 (2019).
Santosa, I. M. D. L. et al. Optimization of CH3NH3PbI3 perovskite solar cells: A theoretical and experimental study. Sol. Energy 199, 198–205 (2020).
Guo, N. et al. A simple fabrication of CH3NH3PbI3 perovskite for solar cells using low-purity PbI2. J. Semicond. 38, 014004–014008 (2017).
Li, X. et al. Low-temperature solution-processed ZnSe electron transport layer for efficient planar perovskite solar cells with negligible hysteresis and improved photostability. ACS Nano 12, 5605–5614 (2018).
Noh, J. H., Im, S. H., Heo, J. H., Mandal, T. N. & Seok, S. I. Chemical management for colorful, efficient, and stable inorganic–organic hybrid nanostructured solar cells. Nano Lett. 13, 1764–1772 (2013).
You, J. et al. Low-temperature solution-processed perovskite solar cells with high efficiency and flexibility. ACS Nano 8, 1674–1680 (2014).
Etgar, L. et al. Mesoscopic CH3NH3PbI3/TiO2 heterojunction solar cells. J. Am. Chem. Soc. 134, 17396–17399 (2012).
Liu, M., Johnston, M. B. & Snaith, H. J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 501, 395–398 (2013).
Lazemi, M., Asgharizadeh, S. & Bellucci, S. A computational approach to interface engineering of lead-free CH3NH3SnI3highly-efficient perovskite solar cells. Phys. Chem. Chem. Phys. 00, 1–10 (2018).
Ma, L. et al. Carrier diffusion lengths of over 500 nm in lead-free perovskite CH3NH3SnI3 films. J. Am. Chem. Soc. 138, 14750–14755 (2016).
Lin, L., Jiang, L., Li, P., Fan, B. & Qiu, Y. A modelled perovskite solar cell structure with a Cu2O hole- transporting layer enabling over 20% efficiency by low-cost low-temperature processing. J. Phys. Chem Solids 14, 205–211 (2019).
Hao, F., Stoumpos, C. C., Cao, D. H., Chang, R. P. H. & Kanatzidis, M. G. Lead-free solid-state organic-inorganic halide perovskite solar cells. Nat. Photonics 8, 489–494 (2014).
Guo, Y. et al. Effects of transition metal substituents on interfacial and electronic structure of CH3NH3PbI3/TiO2 interface: A first-principles comparative study. Nanomaterials 9, 966–979 (2019).
Yang, H. Y., Rho, W. Y., Lee, S. K., Kim, S. H. & Hahn, Y. B. TiO2 nanoparticles/nanotubes for efficient light harvesting in perovskite solar cells. Nanomaterials 9, 326–335 (2019).
Yu, W. et al. Ultrathin Cu2O as an efficient inorganic hole transporting material for perovskite solar cells. Nanoscale 00, 1–3 (2015).
Bera, A. et al. Perovskite oxide SrTiO3 as an efficient electron transporter for hybrid perovskite solar cells. J. Phys. Chem. C 118, 28494–28501 (2014).
Zhou, Y. et al. Review on methods for improving the thermal and ambient stability of perovskite solar cells. J. Photonics Energy 9, 040901–040920 (2019).
Khattak, Y. H. et al. Effect of Cu2O hole transport layer and improved minority carrier life time on the efficiency enhancement of Cu2NiSnS4 based experimental solar cell. J. Renew. Sustain. Energy 10, 043502–043513 (2018).
Wang, Y. et al. Towards printed perovskite solar cells with cuprous oxide hole transporting layers: A theoretical design. Semicond. Sci. Tech. 30, 054004–054010 (2015).
Mandadapu, U., Vedanayakam, S. V. & Reddy, M. R. Design and simulation of high efficiency tin halide perovskite solar cell. Int. J. Renew. Energy Res. 7, 1604–1613 (2017).
Du, H. J., Wang, W. C. & Zhu, J. Z. Device simulation of lead-free CH3NH3SnI3 perovskite solar cells with high efficiency. Chin. Phys. B 25, 108802–188809 (2016).
Oku, T., Yamada, T., Fujimoto, K. & Akiyama, T. Microstructures and photovoltaic properties of Zn(Al)O/Cu2O-based solar cells prepared by spin-coating and electrodeposition. Coatings 4, 203–213 (2014).
Yu, S., Li, L., Lyu, X. & Zhang, W. Preparation and investigation of nano-thick FTO/Ag/FTO multilayer transparent electrodes with high figure of merit. Sci. Rep. 6, 20399–20406 (2016).
Dai, S. et al. Preparation of highly crystalline TiO2 nanostructures by acid-assisted hydrothermal treatment of hexagonalstructured nanocrystalline titania/cetyltrimethyammonium bromide nanoskeleton. Nanoscale Res Lett. 5, 1829–1835 (2010).
Hao, F. et al. Lead-free solid-state organic–inorganic halide perovskite solar cells. Nat. Photonics 137, 489–494 (2015).
Stoumpos, C. C., Malliakas, C. D. & Kanatzidis, M. G. Semiconducting tin and lead iodide perovskites with organic cations: Phase transitions, high mobilities, and near-infrared photoluminescent properties. Inorg. Chem. 52, 9019–9038 (2013).
Devi, C. & Mehra, R. Device simulation of lead-free MASnI3 solar cellwith CuSbS2 (copper antimony sulfide). J. Mater. Sci. 54, 5615–5624 (2019).
Khattak, Y. H., Baig, F., Toura, H., Beg, S. & Soucase, B. M. CZTSe kesterite as an alternative hole transport layer for MASnI3 perovskite solar cells. J. Electron. Mater. 48, 5723–5733 (2019).
Shi, X. et al. Efficient formamidinium-based planar perovskite solar cells fabricated through a CaI2−PbI2 precursor. ACS Sustain. Chem. Eng. 8, 4267–4275 (2020).
Peng, H. et al. Structurally reinforced all-inorganic CsPbI2Br perovskite by non-ionic polymer via coordination and hydrogen bond. Sol. RRL 4, 2000216 (2020).
Minemoto, T. & Murata, M. Theoretical analysis on effect of band offsets in perovskite solar cells. Sol. Energy Mater. Sol. Cells 133, 8–14 (2015).
Klenk, R. Characterization and modeling of chalcopyrite solar cells. Thin Solid Films 387, 135–140 (2001).
Gloeckler, M. & Sites, J. Efficiency limitations for wide-band-gap chalcopyrite solar cells. Thin Solid Films 480, 241–245 (2005).
Haider, S. Z., Anwar, H. & Wang, M. A comprehensive device modelling of perovskite solar cell with inorganic copper iodide as hole transport material. Semicond. Sci. Technol. 33, 035001–035012 (2018).
Son, D. Y., Im, J. H., Kim, H. S. & Park, N. G. 11% efficient perovskite solar cell based on ZnO nanorods: An effective charge collection system. J. Phys. Chem. C 118, 16567–16573 (2014).
Zhao, Z. et al. Mixed-organic-cation tin iodide for lead-free perovskite solar cells with an efficiency of 8.12%. Adv. Sci. 4, 1700204–1700210 (2017).
Hao, F. et al. Solvent-mediated crystallization of CH3NH3SnI3 films for heterojunction depleted perovskite solar cells. J. Am. Chem. Soc. 137, 11445–11452 (2015).
Takahashi, Y., Hasegawa, H., Takahashi, Y. & Inabe, T. Hall mobility in tin iodide perovskite CH3NH3SnI3: Evidence for a doped semiconductor. J. Solid State Chem. 205, 39–43 (2013).
Lee, Y. M. et al. Comprehensive understanding and controlling the defect structures: An effective approach for organic-inorganic hybrid perovskite-based solar-cell application. Front. Energy Res. 6, 1–9 (2018).
Lin, R. et al. Monolithic all-perovskite tandem solar cells with 24.8% efficiency exploiting comproportionation to suppress Sn(ii) oxidation in precursor ink. Nat. Energy 4, 864–873 (2019).
Minemoto, T. & Murata, M. Device modeling of perovskite solar cells based on structural similarity with thin film inorganic semiconductor solar cells. J. Appl. Phys. 116, 054505–054510 (2014).
Liu, C., Fan, J., Li, H., Zhang, C. & Mai, Y. Highly efficient perovskite solar cells with substantial reduction of lead content. Sci. Rep. 6, 35705–35712 (2016).
Kevin, M., Ong, W. L., Lee, G. H. & Ho, G. W. Formation of hybrid structures: Copper oxide nanocrystals templated on ultralong copper nanowires for open network sensing at room temperature. Nanotechnology 22, 235701–235710 (2011).
Ming, W., Yang, D., Li, T., Zhang, L. & Du, M. H. Formation and diffusion of metal impurities in perovskite solar cell material CH3NH3PbI3: Implications on solar cell degradation and choice of electrode. Adv. Sci. 5, 1700662–1700671 (2017).
Pierret, R. F. Semiconductor Device Fundamentals, 2nd edn, 477–491 (Addison-Wesley, 1996).
Acknowledgements
The authors would like to acknowledge Dr. Marc Burgelman (University of Gent) for providing the simulation software SCAPS.
Author information
Authors and Affiliations
Contributions
P.K.P.: conceptualization, investigation, formal analysis, data curation, methodology, visualization, software.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Patel, P.K. Device simulation of highly efficient eco-friendly CH3NH3SnI3 perovskite solar cell. Sci Rep 11, 3082 (2021). https://doi.org/10.1038/s41598-021-82817-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-82817-w
This article is cited by
-
Simulation and optimization of 30.17% high performance N-type TCO-free inverted perovskite solar cell using inorganic transport materials
Scientific Reports (2024)
-
Device modeling of high performance and eco-friendly \({\text {FAMASnI}}_{3}\) based perovskite solar cell
Scientific Reports (2024)
-
Performance simulation of the perovskite solar cells with Ti3C2 MXene in the SnO2 electron transport layer
Scientific Reports (2024)
-
Performance optimization of lead-free inorganic perovskite solar cell using SCAPS-1D
Journal of Optics (2024)
-
Performance Optimization of CH3NH3SnI3 based Solar Cell with Graphene Oxide as ETL and Carbazole Pyrene as HTL
Transactions on Electrical and Electronic Materials (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.