Abstract
Strontium isotopic analysis of sequentially formed tissues, such as tooth enamel, is commonly used to study provenance and mobility of humans and animals. However, the potential of 87Sr/86Sr in tooth enamel to track high-frequency movements has not yet been established, in part due to the lack of data on modern animals of known movement and predictive model of isotope variation across the landscape. To tackle this issue, we measured the 87Sr/86Sr in plant samples taken from a 2000 km2 area in the Altai Mountains (Mongolia), and the 87Sr/86Sr in tooth enamel of domestic caprines whose mobility was monitored using GPS tracking. We show that high-resolution, sequential profiles of strontium isotope composition of tooth enamel reliably reflect the high-frequency mobility of domestic livestock and that short-term residency of about 45 days can be resolved. This offers new perspectives in various disciplines, including forensics, ecology, palaeoanthropology, and bioarchaeology.
Similar content being viewed by others
Introduction
The analysis of radiogenic strontium isotope ratios (87Sr/86Sr) in tooth enamel is commonly used to study provenance and mobility of modern-day humans in forensics1,2, past humans in palaeoanthropology3,4, and domestic and wild mammals in ecology and archeology5,6,7,8. In all cases, the rationale is the following. Variations in the radiogenic 87Sr/86Sr in the landscape are associated with the age, chemical composition, and weathering rates of the underlying geological substrate because 87Sr is the stable product of the radioactive 87Rb. Any contribution of mass-dependent fractionation to variability of 87Sr/86Sr is removed by their normalization to a constant stable 88Sr/86Sr; therefore the primitive bedrock 87Sr/86Sr are conserved up the trophic chain, without any possible change. Mammal tooth enamel is no exception, and because it grows incrementally and is not remodeled once fully mineralized, the 87Sr/86Sr in tooth enamel reflects that of the bedrock at the moment of mineralization. The tooth enamel hence holds a 87Sr/86Sr time record that can be documented through sequential sampling along the direction of tooth growth9.
Although it is, in theory, possible to reconstruct rapid mobility using high-resolution 87Sr/86Sr time series in tooth enamel, this has never been formally demonstrated. Several reasons can be put forward to explain this. First, there is a lack of studies using individuals whose mobility is known with precision. Second, the kinetics of Sr incorporation (deposition and maturation) in tooth enamel during mineralization are still not well understood10. Targeting the innermost enamel layer (< 20 μm thickness) has been proposed as the best strategy for measuring any geochemical proxy11,12,13,14,15. This zone is a good prospect because it mineralizes faster than middle and outer enamel11, and thus minimizes the attenuation of environmental variations recorded in this tissue. However, this layer remains difficult to isolate precisely for analysis. In theory, this could be achieved using laser ablation as this approach allows high-resolution analysis of the 87Sr/86Sr ratio and the reconstruction of 87Sr/86Sr time series3,16,17,18.
Finally, the reconstruction of geographical origin and mobility also relies on an acute knowledge of the local bioavailable 87Sr/86Sr. To this end, isoscapes, which are predictive models of isotope variations across a landscape, have been generated using either geostatistical approaches19, multi-source mixing models20, machine learning21, or discrete entities22. Isoscapes can be constructed by taking into account the bedrock lithology only, but this has limitations, notably due to preferential weathering of minerals with distinct 87Sr/86Sr; influence of atmospheric deposition (i.e. dust, precipitation, sea spray); and anthropogenic influences, such as fertilizer or air pollution23,24,25,26,27,28. Constructing isoscapes by measuring the plant 87Sr/86Sr has been demonstrated as the most reliable method for determining local bioavailable 87Sr/86Sr22,26,29.
Here, we test the ability of 87Sr/86Sr to detect high-frequency mobility of domestic animals living in the Altai mountains of western Mongolia. To do this, we compared high-resolution 87Sr/86Sr time series in domestic caprine tooth enamel with predictions derived from a plant 87Sr/86Sr isoscape of the study area. We monitored the animals’ movements for more than 2 years using GPS collars, allowing us to precisely document their mobility. We used this information to predict intra-tooth 87Sr/86Sr from the isoscape. To this end, we (i) measured 87Sr/86Sr in plants from 156 sampling sites; (ii) constructed an isoscape of the bioavailable 87Sr/86Sr of the study area; (iii) constructed the theoretical bioavailable 87Sr/86Sr time series using the GPS data and the 87Sr/86Sr isoscape for four herds; (iv) converted the bioavailable 87Sr/86Sr time series into enamel 87Sr/86Sr time series using the tooth enamel growth model of Passey and Cerling (2002), leading to four predicted time series of 87Sr/86Sr variations in enamel; (v) measured the 87Sr/86Sr in the inner enamel layer of teeth using laser-ablation multi-collector inductively coupled plasma mass spectrometry (LA-MC-ICPMS); (vi) optimized the cross-correlation between the associated 4 predicted and 11 measured time series. The synchronicity of 87Sr/86Sr variations in the predicted and measured time series was used to discuss the ability of 87Sr/86Sr to detect high-frequency mobility of the animals.
Results
Plant 87Sr/86Sr and bioavailable 87Sr/86Sr isoscape
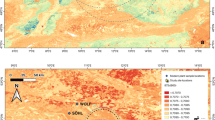
The 87Sr/86Sr in the plant samples ranged between 0.71007 and 0.72340, with an average of 0.71456 ± 0.00537 (± 2SD, N = 156) (SI Appendix, Table S1; Fig. S1A). The study area exhibited a wide range (0.01333) in bioavailable 87Sr/86Sr, 5 times higher than at Köşk Höyük (Central Turkey, 0.002530) and 26 times higher than at Oldupai Gorge (Tanzania, 0.0005231), two areas of similar size (roughly 2000 km2). There was no significant relationship between the plant 87Sr/86Sr and geographic variables (i.e. latitude, longitude, and altitude; SI Appendix, Fig. S2A–C). An ordinary kriging method was used to create the Sr isoscape of the study area. The main advantage of this method over other interpolation methods, is that it takes into account both the distance and the degree of variation between known data points when estimating values in unknown areas and that predictions are based on a spatial statistical analysis of the data. Detailed results are given in SI Appendix (Supplementary Information Text; Table S2; Figs. S3 and S4). The 87Sr/86Sr values predicted by the isoscape ranged from 0.71012 to 0.72251, with a mean value of 0.71457 ± 0.00530 (± 2SD). The isoscape highlighted the spatial heterogeneity of the study area, with the lowest values in the southern part and the highest values in the eastern and western parts (Fig. 1A). The standard error from the model predictions was evenly distributed and started increasing 6–7 km away from the sample locations (Fig. 1B).
Bioavailable 87Sr/86Sr of the study area, near the village of Nogoonnur, western Mongolia. 87Sr/86Sr isoscape (A) and its associated predicted error (B) were created using QGIS 3.2 Bonn51 with the predictive model of bioavailable 87Sr/86Sr built with the kriging function in ArcGIS 10.0 (Environmental Systems Research Institute)52. White circles represent the bioavailable 87Sr/86Sr sampling localities used to create the model. Black dots represent the 16 randomly selected sampling locations that were extracted prior to model development and later used to test the model predictions. Colors indicate areas of lowest bioavailable 87Sr/86Sr (blue) to highest bioavailable 87Sr/86Sr (red) for the top panel and lowest predictive error (light beige) to highest predictive error (brown) for the bottom panel.
Bioavailable 87Sr/86Sr time series inferred by GPS monitoring
We monitored the movements of eight animals (four sheep and four goats) by means of GPS devices over a period of 29 months (SI Appendix, Table S3). Their range overlapped the plant sampling sites (SI Appendix, Fig. S1B). The Lavielle’s segmentation of individual trajectories indicated that the mobility patterns of caprines within the same herd were similar and that they differed from those of the other herds (SI Appendix, Tables S4 and S5; Fig. S5). Three herds (belonging to herders Jk, Kb, and Kj) displayed more or less an East–West mobility and exploited both the eastern depression (1451–1684 m asl) and the western mountain pastures (2540–3102 m asl). In contrast, herder Dl’s animals remained at an elevated altitude of 2364 ± 130 m asl throughout the study period (SI Appendix, Fig. S1B). This was associated with a smaller grazing area (12.5 km2 for Dl versus 18.9–22.3 km2 for the other three herders) and a lower yearly mobility (30 km for Dl versus 161 ± 98 km for the other three herders). The herders nomadized between 8 (Dl) and 13 (Jk) times per year during the study period and used between 5 (Dl) and 11 (Kj) different campsites; the average distance traveled during each nomadization ranged from 4 (Dl) to 17 (Jk) km (Table S4).
To predict daily bioavailable 87Sr/86Sr for a given herd based on its GPS location, we extracted the 87Sr/86Sr from the isoscape raster. For each herd, we then predicted the daily bioavailable 87Sr/86Sr value by calculating the average of the different bioavailable 87Sr/86Sr values for each day. Each herd exhibited temporal variations in bioavailable 87Sr/86Sr, with peaks occurring mostly during the spring and fall seasons (SI Appendix, Fig. S6). Most temporal variations were common to all herds, but some of them were characteristic of only some of them (e.g. the 2017 winter variations for Dl’s and JK’s herds). Sr isotope ratios remained generally stable during 2 months, which is the duration of the short spring and fall seasons, but some other levelling off were shorter, i.e. the 2017 spring levelling off for Dl’s herd, which lasted only 1 month. Most of these temporal variations in Sr isotope ratios corresponded to a nomadization and to a change of pasture by the herder and their herd between two isotopically different areas and extended as long as residence at a given camp lasted. For Dl, the fast decrease during winter 2017 can be linked to the nomadization from camp B to camp A (SI Appendix, Table S5; Fig. S5).
Predicted 87Sr/86Sr time series in tooth enamel
We then converted the bioavailable 87Sr/86Sr time series into predicted 87Sr/86Sr in tooth enamel using Passey and Cerling’s model32. Originally developed for carbon isotopes, this model describes how the isotopic signal is time-averaged in enamel during the mineralization process. Overall, the effect of the mineralization process on the output variations of 87Sr/86Sr in tooth enamel resulted in the dampening of about 56% of the amplitude of variations of the input bioavailable 87Sr/86Sr (SI Appendix, Table S6; Fig. S6).
Measured 87Sr/86Sr time series in tooth enamel
The Sr voltage (approximated by the 88Sr voltage) ranged from ~ 0.4 to ~ 5 V (SI Appendix, Fig. S7). There was no increase in 87Sr/86Sr associated to 88Sr decrease, which has been suggested to be symptomatic of enhanced influence of polyatomic Ca-P-O/Ar-P-O interferences at low Sr intensities18,33,34,35. The SRM-1400 bracketing standard had a Sr concentration of 250 ppm and exhibited a 88Sr voltage of 0.5 V and a reproducibility of 214 ppm (2SD, N = 50). This is more than 60 times lower than the range in plant 87Sr/86Sr of the study area. While the precision of this technique is lower than the resolution of MC-ICP-MS and thermal ionization mass spectrometry (TIMS) of purified strontium solution analyses, it is however, large enough to interpret variations of the bioavailable 87Sr/86Sr in terms of animal mobility.
The 87Sr/86Sr in caprine teeth (N = 11) was measured along a continuous raster as close as possible to the innermost enamel layer. On average, the enamel 87Sr/86Sr was 0.71414 ± 0.00210 (± 2SD), falling within the range of bioavailable strontium predicted by the isoscape (Fig. 2 and SI Appendix, Table S6). The average 87Sr/86Sr, however, differed among individuals and ranged from 0.71200 ± 0.00087 (± 2SD) for Kb-98-M3 to 0.71602 ± 0.00198 (± 2SD) for Kj-369-M3. Intra-individual variability was 0.00143, ranging from 0.00087 (Kb-98-M3) to 0.00198 (Kj-369-M3). Large and significant inter-individual differences (ANOVA, p < 2.2e−16) within the same herd were observed, ranging from 0.00226 (Kj) to 0.00311 (Kb), but a smaller inter-individual difference of 0.00033 (Kb) was found within the same herd. Significant differences were observed in the 87Sr/86Sr means and medians (ANOVA, p < 2.2e−16) and in variance (Bartlett, p < 2.2e−16) between herds. Kb’s herd (n = 3) had the lowest mean value (0.71344 ± 0.00311, ± 2SD), while Kj’s herd (n = 4) had the highest mean value (0.71465 ± 0.00226, ± 2SD).
Sr isotope ratios of modern caprine teeth from western Mongolia. The horizontal brackets delineate the animals belonging to the same herder. Bio-available Sr isotope ratios (estimated in plants—gray boxplot) are reported for comparison. The gray shading represents the mean ± 1 SD of plant 87Sr/86Sr.
Comparison of the predicted and measured time series
To compare measured and predicted values, it was first necessary to anchor the measured 87Sr/86Sr profiles in enamel to time. This required determining the date of birth (DOB) of the animals, the onset of mineralization of the second and third molars (M2 and M3), and the tooth growth rates of these molars. Based on interviews with the herders, a DOB of March 31 was set for all individuals, with an uncertainty of ± 1 month. An average onset of mineralization of 0.3 month and 10.3 months after birth was estimated for M2 and M3, respectively, associated with an uncertainty of approximately 1 month and 2–4 months for M2 and M3, respectively36. Finally, a constant and an exponentially decreasing growth rate were calculated for M2 and M337. For three animals, both their M2 and M3 were analyzed (2017-98, 2017-146, and 2017-124). In these cases, the end of the M2 87Sr/86Sr profiles joined up well with the beginning of the M3 87Sr/86Sr profiles, leading to a continuous 87Sr/86Sr time series of more than 2 years.
Taken together, our analyses led to 4 predicted tooth enamel 87Sr/86Sr time series and 11 measured tooth enamel 87Sr/86Sr time series, which we compared accordingly. Time uncertainties were associated with the results, especially about the DOB of the animals and the growth rate of the teeth, impacting the measured time series, and about the Sr residence time in the body and the enamel maturation effect of Sr, impacting the predicted time series. To take these uncertainties into account, we used a cross-correlation method to optimize the match between the two times series as a function of the displacement (lag) of measured relative to predicted time series. Resulting lag values were generally small, with a median value of + 41 days (n = 11) (SI Appendix, Table S7; Fig. S8). Two larger lags, of + 125 and + 135 days, respectively, were estimated for Kj-369-M3 and Kb-283-M3 (SI Appendix, Table S7), but these lags remained credible considering the potential variation in the DOB and the variation in the development rate of the teeth. In five cases, adding the inferred lag values to the date turned negative correlations between measured and predicted time series into positive ones. In all cases, the correlations were significant (SI Appendix, Table S7; Fig. S8).
The first derivative of the predicted and measured 87Sr/86Sr time series showed that most variations are synchronous (Fig. 3). For Dl’s herd, for which there is only one sample, the synchronicity was obvious for the period during which the GPS data were available (Fig. 3A). For Jk’s herd, the synchronicity was also observable for all the samples (Fig. 3B). For other cases, especially for Kb-98, M2 and M3 seem to have recorded identical variations, but they appear to be offset by about 1 month (Fig. 3C). Finally, in Kj’s herd, the synchronicity was good, but variations in the measured time series were larger than those in the predicted ones (Fig. 3D).
Comparison between the variation of the derivative of the modeling of intra-tooth variations. Variation predicted by the forward model (black line) and the derivative of measured intra-tooth variations of 87Sr/86Sr running mean (colored full line) for animals belonging to (A) Dl, (B) Jk, (C) Kb, and (D) Kj. The time calibration of measured intra-tooth profiles was done using the time lag given by cross-correlation. The date is given as month and year. (W = winter; Sp = spring; Su = summer; A = autumn).
Discussion
The aim of the present work was to evaluate the potential of intra-tooth 87Sr/86Sr variations to track high-frequency mobility independently assessed using GPS data. Most of the first derivative of the 87Sr/86Sr variations of the measured and predicted time series showed synchronicity (Fig. 3). The good agreement between the measured and predicted time series suggests that the time averaging model of Passey and Cerling32, initially developed for C, is adapted for the reconstruction of 87Sr/86Sr time series and that 87Sr/86Sr records are synchronous with those of δ13C.
It also appears that a better fit would be possible with a better knowledge of the DOB, the tooth formation schedule, and the enamel growth rate. Indeed, in the case of Jk’s herd, some of the variations in the predicted time series seem synchronous with those in the measured time series, but some are likely not (Fig. 3B). This observation holds for the other cases, such as for KB-98, for which the variations recorded by M2 and M3 appear to be offset by about 1 month (Fig. 3C). It is noteworthy that we used a tooth growth model with a constant and a decreasing exponential rate for M2 and M3, respectively. The offset suggests that perhaps this model was an oversimplification.
The existence of synchronicity between the measured and predicted time series allows estimation of the sensibility to detect high-frequency mobility. For instance, during mid-December 2015, Jk’s herd undertook a round trip between two areas (#3 and #4), which differed by about 5000 ppm (0.7137 to 0.7183) in 87Sr/86Sr (SI Appendix, Table S5; Fig. S6). The duration of their residence in area #4 was approximately 51 days (SI Appendix, Table S5). This movement resulted in a resolvable 87Sr/86Sr variation of ~ 1000 ppm in the teeth of animals Jk-104 (0.7124 to 0.7135)and Jk-146 (0.7130 to 0.7144) (SI Appendix, Fig. S6). Another example is provided by animal Dl-71 during the winter–spring 2017 nomadization, with a residency lasting 57 and 58 days in each area, respectively (SI Appendix, Table S5). These two examples show that short-term residency of fewer than 2 months can be detected by measuring the 87Sr/86Sr in tooth enamel. The present results emphasize that considering migrations in terms of distance only is not appropriate, because large Sr isotope differences can be found within a short distance. For example, the same 87Sr/86Sr variation of 1000 ppm was recorded during winter 2017 in the enamel of two herds (Jk’s and Dl’s) following a nomadization of 14 and 5 km, respectively. It is also noteworthy that all these movements, and those studied in the field of bioarcheology more generally, were accomplished at human walking speed. Forensic science, in contrast, deals with the movements of humans, who (assuming they are not encumbered by a herd), can potentially migrate faster (including by car or by plane). It is therefore even less appropriate to use 87Sr/86Sr variation as an indication of distance travelled in forensics.
Generally, we found that the measured 87Sr/86Sr in tooth enamel for a given herd are homogeneous and match the predicted ones. However, two animals displayed unexpectedly low (Kb-98) or high (Kj-369) ratios (SI Appendix, Fig. S6). Their average 87Sr/86Sr differed by about 2500 ppm from the expected ratios (SI Appendix, Table S6). Moreover, the animals in these two herds (Kb’s and Kj’s) showed significant inter-individual variability. The issue of inter-individual variability has, to our knowledge, been tackled by only two studies38,39. In the study of Lewis et al.39, the diet was constant and controlled throughout the duration of the experiment. The authors calculated a two standard deviation variability of 100 ppm of the 87Sr/86Sr in pig tooth enamel for all feeding groups. This number, which represents the minimum variation in the tooth enamel 87Sr/86Sr that can be expected from individuals raised on identical diets in the same location, is 25 times lower than the difference observed here for Kb-98 and Kj-369. In the study of Anders et al.38, the pigs were raised under identical conditions, with the same food, but its composition may have varied over time. For their study, an inter-individual variability of about 2000 ppm in tooth enamel 87Sr/86Sr can be calculated, which is the order of magnitude found here. It must hence be pointed out that more knowledge is required on the potential—yet poorly constrained—dietary and physiological factors that could contribute to the inter-individual variability in tooth enamel 87Sr/86Sr of herd animals with similar life histories (e.g., varying contributions of Sr from food versus drinking water, differential digestive efficiency or differential bioavailability of potentially heterogeneous Sr-carrying diet components). Ongoing research involving diet-switch experiments in mammal models should help unraveling these factors40.
The present study demonstrates that tooth enamel 87Sr/86Sr time series of caprines can be used to track high-frequency mobility, potentially with a monthly resolution. Despite a precise knowledge of animal mobility and Sr isotope distribution in the landscape, we sometimes found offsets between measured and predicted tooth enamel 87Sr/86Sr. The role of biological variability also remains to be explained. This could be done by simplified diet shift experiments involving several animals, to take into account potential individual response. For archaeological applications, our results show that the inference of high-frequency mobility using Sr isotope analysis should be treated with an appropriate degree of caution depending on the resolution of the sampling method and the heterogeneity of the bioavailable 87Sr/86Sr isoscape of the studied area. Diagenesis is an additional caveat for archaeological applications especially when sampling near the enamel-dentine junction. This could be overcome by conducting in situ measurements of trace element concentrations in enamel and co-genetic dentine of the same tooth using LA-ICPMS.
Materials and methods
Study area and caprine GPS tracking
The sheep and goats sampled in this study inhabit the district of Nogoonnuur (province of Bayan-Ölgii, Mongolia), on the eastern fringes of the Altai mountain range, at elevations ranging from 1500 m to more than 4000 m (Fig. 1). The climate is strongly continental, with long, cold winters and short, hot summers with extreme temperatures, ranging from + 34 to − 44 °C, and a lower average annual rainfall of 131 mm (meteorological station based at Nogoonnuur village—http://fr.climate.org). Eight caprines (4 sheep and 4 goats) belonging to four different families of Kazakh−Mongolian nomadic pastoralists (shortened here to Dl, Jk, Kb, and Kj), participated in the survey. Caprine mobility was controlled by the herders, and the animals were brought back to the family’s camp every night. Nomadization patterns (seasonal mobility among camps separated by a few km) were monitored precisely using GPS devices fitted on the animals from June 2015 to July 2018 (Globalstar or Iridium collars, Lotek Wireless Inc.—http://www.lotek.com/), programmed to record animal position every 13 and 2 h, respectively (SI Appendix, Table S3). Mobility patterns were described using Lavielle’s segmentation method, which allows determination of changes in animal movement, and discrimination between small-scale movements (within each pasture, in this study) and large-scale movements among pastures, by discriminating series of successive locations (“segments”) during which movements happen at the same spatial scale but between which movements happen at different spatial scales. Due to the nature of the landscape, segmentation was based on altitude, and each segment was considered as a pasture, after visual validation. Only males were sampled, because females may be supplemented with fodder during winter (usually harvested in August and September), potentially overprinting the influence of mobility on enamel 87Sr/86Sr. Animal slaughter was carried out by the herders themselves for their own consumption. Study animals were slaughtered on two different occasions, during their second or third year: September 2016 (n = 4) and November 2017 (n = 4), and 11 molars were sampled for analysis (SI Appendix, Table S3). In order to ensure contemporaneity between GPS records and tooth enamel growth, only M3 was sampled on the animals slaughtered in September 2016 and both M2 and M3 were sampled on the animals slaughtered in November 2017.
Plant sampling to model bioavailable strontium isoscape
In order to build the isoscape of bioavailable Sr, we sampled plants at 156 sites distributed throughout the study area, in September 2016 and November 2017 (Fig. 1 and SI Appendix, Table S1). Sampling localities were selected to cover as much as possible the grazing areas of the animals based on their GPS records, complemented by sites located between grazing areas (SI Appendix, Fig. S1A and B). The distance between neighboring sites was 2.5 km on average, and ranged between 0.2 km and 17.2 km. However, some parts of the study area were difficult to reach due to the presence of an escarpment or the proximity to the Russian border to the north. Each sample represented a mix of plant species present within a circle of ca. 2–3 m diameter. The assemblage was usually dominated by grasses, but also included some forbs and shrubs (SI Appendix, Table S1). In most cases, most collected plant items were plant leaves, but stems, seeds, and fruits were also collected if present. All plant material was air dried and then placed in a loosely sealed paper envelope.
Solution measurement of the 87Sr/86Sr in plants
Strontium purification and 87Sr/86Sr analysis were performed at the Ecole Normale Supérieure in Lyon. Plant samples (N = 156) were crushed using a mixer mill and ashed in a muffle furnace at 850 °C for 10 h. For each ashed plant sample, about 5 mg of ashed sample was digested in a mixture of 1 ml of HNO3 (15 M) and 1 ml of 30% H2O2 in a closed Teflon beaker at 120 °C for 8 h. The solution was evaporated and taken up with 500 μL of HNO3 (2 M). Strontium was separated from the matrix sample using a column filled with the Sr-spec resin (Eichrom). Following several washes with Milli-Q water and the conditioning of the resin with HNO3 (2 M), samples were loaded onto the columns and washed repeatedly with HNO3 (2 M), and Sr was eluted with Milli-Q water. The solution was evaporated and taken up with 1 ml of HNO3 (0.05 M). Then 100 µl was diluted with 9.9 ml HNO3 (0.05 M) marked with 2 ppb of Indium as a calibration and analyzed using a Thermo Scientific iCAP (Thermo Scientific) triple quadrupole inductively coupled plasma mass spectrometer (TQ-ICP-MS) to determine Sr concentrations. Procedural blank levels for plant samples were lower than 0.002 ppb Sr. Finally, samples were diluted with HNO3 (0.05 M) to reach 200 ppb Sr concentrations in 2 ml. This final solution was used for isotopic analysis, using a Nu Plasma 1700 (Nu Instruments) multi-collector inductively coupled plasma mass spectrometer (MC-ICP-MS) and, using an invariant normalization 88Sr/86Sr (8.37521), the exponential fractionation law and a sample-standard bracketing with the NIST SRM-987 reference solution (0.71025 ± 0.00002)41. Additional control was carried within the run with standard material NIST SRM-1400 (0.713139 ± 0.000087)42 bone ash. The repeated measurements (N = 6) of SRM-1400 gave an average 87Sr/86Sr value of 0.71312 ± 0.000033 (± 2SD). 88Sr values (V) obtained for the plant samples were consistent and averaged 0.9642 ± 0.3033 (± 2SD). We tested the potential influence of geographic parameters (i.e. altitude, latitude, and longitude) on plant 87Sr/86Sr, using linear regression with the function lm in the gstat package in R (version 3.4.4)43. Unless noted otherwise, all statistical analyses were conducted using this package, with a threshold of significance at p-value < 0.05.
Spatial modeling of the bioavailable 87Sr/86Sr isoscape
An ordinary kriging method was used to model the bioavailable 87Sr/86Sr isoscape. The kriging method provides a spatially explicit interpolation and variance estimate for a given coordinate location, based on a variogram, which is a statistical model of spatial autocorrelation between pairs of sampled points (here, the plant 87Sr/86Sr). Thus this method allows the spatial behaviour of the data to be taken into account. This variogram model is then used as a basis to interpolate the target variable away from the points. The 87Sr/86Sr isoscape was performed on a training subsample of 90% (n = 140) of the original samples, the remaining 10% (n = 16) being saved as a validation subsample, to test model predictions. First, the variogram model was fit with the functions variogram (cutoff = 0.1) and fit.variogram. The predictive model of bioavailable 87Sr/86Sr across the study area was then built with the kriging function in ArcGIS 10.0 (Environmental Systems Research Institute), using the parameters of the variogram model (cell size = 1.4 × 10–3; SI Appendix, Table S2, Fig. S3A). Moreover, we checked for anisotropy with a directional variogram (Fig. S3B). We tested the reliability of the isoscape by calculating the difference between the field values of the validation subsample and the values predicted in the isoscape for both the training and the validation subsamples (SI Appendix, Fig. S4A and B). We used a normal Q–Q plot to check the distribution of the predicted values (SI Appendix, Fig. S4C). More details are given in the SI Appendix (Supplementary Text).
Predicted 87Sr/86Sr intra-tooth variation
The isoscape raster was used to calculate for each herd its predicted daily bioavailable 87Sr/86Sr, based on the GPS locations of one of its monitored animals (GPS locations of the different animals belonging to the same herd were < 80 m [data not shown], obviating the need to use the location data of the other animals). To this end, for each GPS location covered by the isoscape, we extracted the 87Sr/86Sr from the raster using the function extract (method = “simple”) of the raster package in R (version 3.4.4)44. For the animals equipped with a Globalstar collar, we kept all the GPS data points (including nighttime data points) to partly make up for the lower recording density. For the other animals, we only kept daylight data points. For each herd, we predicted the daily bioavailable 87Sr/86Sr by calculating the average of the different bioavailable 87Sr/86Sr for each day. We then used these daily bioavailable 87Sr/86Sr to predict a hypothetical intra-tooth 87Sr/86Sr profile for each of the four herds, using Passey and Cerling’s model32. Originally, this model was developed for carbon isotopes in continuously growing teeth, but it has also been used to describe the isotopic time averaging in teeth with definite growth, such as ungulate teeth11,14,15,37,45. The main model parameters include the initial mineral content during enamel deposition (fi) and the length of maturation (lm) (corresponding to the length along the tooth over which the maturation stage of the amelogenesis occurs). The model for signal attenuation during enamel formation can be expressed as follows:
Equation (1) implies that the isotope ratio of fully mineralized enamel at position i (δei) reflects a contribution from the appositional layer (with δmi the initial isotope ratio) and a time-integrated contribution of average isotope ratios of the input signal over the length lm. We set a length of maturation spanning more than 4 months (~ 120 days), as proposed by Zazzo et al.45, and a value of 0.25 (fi) for the amount of material incorporated during the secretory stage, based on previous estimates of the mineral content of developing tooth enamel11,32. We kept lm constant for any stage of the crown, hence assuming a constant growth rate of the enamel.
Laser ablation measurement of the 87Sr/86Sr in tooth enamel
The teeth were mounted in polyester resin (BROT LAB) and sliced longitudinally with a diamond disc and polished with silicon carbide powder (F500 and F1000; Escil) to expose the entire dental structure. The 87Sr/86Sr was measured in situ by LA-MC-ICP-MS with a Nu 500 h (Nu Instruments) MC-ICP-MS (multi-collector inductively coupled plasma mass spectrometry), coupled to an Excite (Photon Machines) 193 nm laser ablation system at the Ecole Normale Supérieure in Lyon (SI Appendix, Table S8 and Fig. S9). Sample aerosol was carried to the plasma using a mixture of He and N2. Masses 88, 87, 86, 85, 84, and 83 were measured on Faraday cups to resolve the isobaric interference of 87Rb on 87Sr using 85Rb, and of 84Kr and 86Kr on 84Sr and 86Sr, respectively, using 83Kr. We used a sample-standard bracketing method adapted from the study of Martin et al.46, using the sintered "Bone Ash" reference material NIST SRM-140047. The repeated measurements (N = 45) of the sintered reference material NIST SRM-1400 gave an average 87Sr/86Sr value of 0.71384 ± 0.000214 (± 2SD), which is in good agreement with other laser ablation published values42,46. The sequence procedure and data processing were adapted from Tacail et al.48. Teeth were analyzed in two or three consecutive runs depending on tooth total length. For each sequence, the procedure consisted of the correction of the sample 87Sr/86Sr with that of the NIST SRM-1400 (0.713139). Finally, a centered moving average on 35 individual measurements (~ 2 mm length of enamel) was used to smooth variability of the final profiles. All data are available in SI Appendix Table S9.
Statistic comparison among herds and individuals of 87Sr/86Sr in tooth enamel
In order to compare mean 87Sr/86Sr between herds, we performed one-way ANOVA tests followed by Tukey’s post-hoc HSD tests. Then, in order to compare inter-individual 87Sr/86Sr, for each herd, we performed one-way ANOVA tests followed by Tukey’s post-hoc HSD test. We also conducted Bartlett’s test to compare variances between herds and among individuals within a herd.
Time calibration of measured intra-tooth 87Sr/86Sr profiles
To compare predicted 87Sr/86Sr time series with measured intra-tooth 87Sr/86Sr profiles, it was necessary to associate the position in the tooth with the approximate date in the calendar when this part of the tooth was formed. To do this, it is necessary to know the DOB of the animal, as well as the dental development rate and the growth rate of its molars. However, none of these parameters are known with certainty. Interviews with herders indicated that the season of birth is very restricted, extending from February to April, with slight variations between years and herders, which is in accordance with Fijn49. In the absence of individual information, we chose an arbitrary DOB of March 31 for all the animals. This clearly introduces an uncertainty of ± 1 month in the predicted tooth enamel 87Sr/86Sr time series. We calculated the onset of mineralization of M2 and M3 to be, on average, at 1.3 months and 10.3 months after birth, respectively, based on literature values for caprines (SI Appendix, Table S10). We used these average dental development rates (Table S10) to calculate the duration of formation for each M2 and M3, depending on the state of crown formation (SI Appendix, Table S11).
Finally, we calculated individual tooth growth rates specifically for M2 and M3. For M2, we calculated a constant growth rate (τ) by dividing tooth length (Lmax) by the duration of tooth formation (SI Appendix, Table S10). To convert measured distances along the tooth into time (td) for any point at a distance d from the enamel–root junction in M2, we used the following equation:
For M3, tooth growth rate may decrease exponentially37. Therefore, to convert measured distances along the tooth into time (td) for any point at a distance d from the enamel–root junction in M3, we used the following equation:
where λ is the rate constant of the growth (λ = ln(2)/t1/2), t1/2 is the time taken for the tooth to grow to half of its maximum length (Lmax), and t0 is the time at which the tooth begins to grow. Thus, t0 depends on the DOB and the onset of formation of M3. We set t1/2 to 141 days37. Given the logarithmic characteristics of the model, the last 2–3 mm gave dates tending well beyond the date of the individual’s death, as such these were omitted.
Cross-correlation of time series
Because of the unavoidable imprecision associated with the time calibration of intra-tooth 87Sr/86Sr profiles, there may be a temporal shift between the measured and predicted time series. To detect this shift and readjust the two time series, we used the function ccf (cross-correlation function)50. This function calculates the correlation between two time series for various time lags between them, allowing inferring of the existence and amount of temporal shift between time series. Then, we calculated the Pearson’s correlation coefficient and the linear regression between the 87Sr/86Sr of the measured and predicted times series with the selected lag value. Finally, we also visually evaluated the amount of synchronicity of the readjusted 87Sr/86Sr of the measured and predicted time series, by calculating the first derivatives of the 87Sr/86Sr (d(87Sr/86Sr)/dt), smoothed on 30 days, for each time series, to estimate the slope of the variation.
Data availability
All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
References
Beard, B. L. & Johnson, C. M. Strontium isotope composition of skeletal material can determine the birth place and geographic mobility of humans and animals. J. Forensic Sci. 45, 1049–1061 (2000).
Hu, L., Fernandez, D. P., Cerling, T. E. & Tipple, B. J. Fast exchange of strontium between hair and ambient water: Implication for isotopic analysis in provenance and forensic studies. PLoS ONE 15, e0233712 (2020).
Sillen, A. & Balter, V. Strontium isotopic aspects of Paranthropus robustus teeth; implications for habitat, residence, and growth. J. Hum. Evol. 114, 118–130 (2018).
Lugli, F. et al. Strontium and stable isotope evidence of human mobility strategies across the Last Glacial Maximum in southern Italy. Nat. Ecol. Evol. 3, 905 (2019).
Bendrey, R., Hayes, T. E. & Palmer, M. R. Patterns of iron age horse supply: An analysis of strontium isotope ratios in teeth. Archaeometry 51, 140–150 (2009).
Britton, K., Grimes, V., Dau, J. & Richards, M. P. Reconstructing faunal migrations using intra-tooth sampling and strontium and oxygen isotope analyses: A case study of modern caribou (Rangifer tarandus granti). J. Archaeol. Sci. 36, 1163–1172 (2009).
Chase, B., Meiggs, D., Ajithprasad, P. & Slater, P. A. What is left behind: Advancing interpretation of pastoral land-use in Harappan Gujarat using herbivore dung to examine biosphere strontium isotope (87Sr/86Sr) variation. J. Archaeol. Sci. 92, 1–12 (2018).
Brennan, S. R. et al. Strontium isotopes delineate fine-scale natal origins and migration histories of Pacific salmon. Sci. Adv. 1, e1400124 (2015).
Montgomery, J., Evans, J. A. & Horstwood, M. S. A. Evidence for long-term averaging of strontium in bovine enamel using TIMS and LA-MC-ICP-MS strontium isotope intra-molar profiles. Environ. Archaeol. 15, 32–42 (2010).
Humphrey, L. T., Dean, M. C., Jeffries, T. E. & Penn, M. Unlocking evidence of early diet from tooth enamel. Proc. Natl. Acad. Sci. 105, 6834–6839 (2008).
Blumenthal, S. A. et al. Stable isotope time-series in mammalian teeth: In situ δ18O from the innermost enamel layer. Geochim. Cosmochim. Acta 124, 223–236 (2014).
Müller, W. et al. Enamel mineralization and compositional time-resolution in human teeth evaluated via histologically-defined LA-ICPMS profiles. Geochim. Cosmochim. Acta https://doi.org/10.1016/j.gca.2019.03.005 (2019).
Tafforeau, P., Bentaleb, I., Jaeger, J.-J. & Martin, C. Nature of laminations and mineralization in rhinoceros enamel using histology and X-ray synchrotron microtomography: Potential implications for palaeoenvironmental isotopic studies. Palaeogeogr. Palaeoclimatol. Palaeoecol. 246, 206–227 (2007).
Trayler, R. B. & Kohn, M. J. Tooth enamel maturation reequilibrates oxygen isotope compositions and supports simple sampling methods. Geochim. Cosmochim. Acta 198, 32–47 (2017).
Zazzo, A., Balasse, M. & Patterson, W. P. High-resolution δ13C intratooth profiles in bovine enamel: Implications for mineralization pattern and isotopic attenuation. Geochim. Cosmochim. Acta 69, 3631–3642 (2005).
Balter, V., Braga, J., Télouk, P. & Thackeray, J. F. Evidence for dietary change but not landscape use in South African early hominins. Nature 489, 558–560 (2012).
Balter, V. et al. Analysis of coupled Sr/Ca and 87Sr/86Sr variations in enamel using laser-ablation tandem quadrupole-multicollector ICPMS. Geochim. Cosmochim. Acta 72, 3980–3990 (2008).
Lugli, F., Cipriani, A., Peretto, C., Mazzucchelli, M. & Brunelli, D. In situ high spatial resolution 87Sr/86Sr ratio determination of two Middle Pleistocene (c.a. 580ka) Stephanorhinus hundsheimensis teeth by LA–MC–ICP–MS. Int. J. Mass Spectrom. 412, 38–48 (2017).
Bowen, G. J. & Wilkinson, B. Spatial distribution of δ18O in meteoric precipitation. Geology 30, 315–318 (2002).
Bataille, C. P. & Bowen, G. J. Mapping 87Sr/86Sr variations in bedrock and water for large scale provenance studies. Chem. Geol. 304, 39–52 (2012).
Bataille, C. P. et al. A bioavailable strontium isoscape for Western Europe: A machine learning approach. PLoS ONE 13, e0197386 (2018).
Willmes, M. et al. Mapping of bioavailable strontium isotope ratios in France for archaeological provenance studies. Appl. Geochem. 90, 75–86 (2018).
Crowley, B. E., Miller, J. H. & Bataille, C. P. Strontium isotopes (87Sr/86Sr) in terrestrial ecological and palaeoecological research: Empirical efforts and recent advances in continental-scale models. Biol. Rev. 92, 43–59 (2017).
Frei, K. M. & Frei, R. The geographic distribution of strontium isotopes in Danish surface waters: A base for provenance studies in archaeology, hydrology and agriculture. Appl. Geochem. 26, 326–340 (2011).
Jin, Z. et al. Seasonal contributions of catchment weathering and eolian dust to river water chemistry, northeastern Tibetan Plateau: Chemical and Sr isotopic constraints. J. Geophys. Res. Earth Surf. 116, 4 (2011).
Maurer, A.-F. et al. Bioavailable 87Sr/86Sr in different environmental samples: Effects of anthropogenic contamination and implications for isoscapes in past migration studies. Sci. Total Environ. 433, 216–229 (2012).
Slovak, N. M. & Paytan, A. Applications of Sr isotopes in archaeology. In Handbook of Environmental Isotope Geochemistry (ed. Baskaran, M.) 743–768 (Springer, Heidelberg, 2012).
Widga, C., Walker, J. D. & Boehm, A. Variability in bioavailable 87Sr/86Sr in the North American midcontinent. Open Quat. 3, 4 (2017).
Copeland, S. R. et al. Strontium isotope investigation of ungulate movement patterns on the Pleistocene Paleo-Agulhas Plain of the Greater Cape Floristic Region, South Africa. Quat. Sci. Rev. 141, 65–84 (2016).
Meiggs, D. C., Arbuckle, B. S. & Öztan, A. The Pixelated Shepherd: Identifying Detailed Local Land-Use Practices at Chalcolithic Köşk Höyük, central Turkey, Using a Strontium Isotope (87Sr/86Sr) Isoscape. Isotopic Investigations of Pastoralism in Prehistory 77–95 (Routledge, London, 2017).
Tucker, L. et al. Initial assessment of bioavailable strontium at Oldupai Gorge, Tanzania: Potential for early mobility studies. J. Archaeol. Sci. 114, 105066 (2020).
Passey, B. H. & Cerling, T. E. Tooth enamel mineralization in ungulates: implications for recovering a primary isotopic time-series. Geochim. Cosmochim. Acta 66, 3225–3234 (2002).
Simonetti, A., Buzon, M. R. & Creaser, R. A. In-situ elemental and Sr isotope investigation of human tooth enamel by laser ablation-(MC)-ICP-MS: Successes and pitfalls. Archaeometry 50, 371–385 (2008).
Müller, W. & Anczkiewicz, R. Accuracy of laser-ablation (LA)-MC-ICPMS Sr isotope analysis of (bio)apatite: A problem reassessed. J. Anal. At. Spectrom. 31, 259–269 (2016).
Horstwood, M. S. A., Evans, J. A. & Montgomery, J. Determination of Sr isotopes in calcium phosphates using laser ablation inductively coupled plasma mass spectrometry and their application to archaeological tooth enamel. Geochim. Cosmochim. Acta 72, 5659–5674 (2008).
Upex, B. & Dobney, K. Dental enamel hypoplasia as indicators of seasonal environmental and physiological impacts in modern sheep populations: A model for interpreting the zooarchaeological record. J. Zool. 287, 259–268 (2012).
Zazzo, A. et al. A refined sampling strategy for intra-tooth stable isotope analysis of mammalian enamel. Geochim. Cosmochim. Acta 84, 1–13 (2012).
Anders, D., Osmanovic, A. & Vohberger, M. Intra- and inter-individual variability of stable strontium isotope ratios in hard and soft body tissues of pigs. Rapid Commun. Mass Spectrom. 33, 281–290 (2019).
Lewis, J., Pike, A. W. G., Coath, C. D. & Evershed, R. P. Strontium concentration, radiogenic (87Sr/86Sr) and stable (δ88Sr) strontium isotope systematics in a controlled feeding study. STAR Sci. Technol. Archaeol. Res. 3, 45–57 (2017).
Weber, M. et al. Strontium uptake and intra-population 87Sr/86Sr variability of bones and teeth: Controlled feeding experiments with rodents (Rattus norvegicus, Cavia porcellus). Front. Ecol. Evol. 8, 1–10 (2020).
Brazier, J.-M. et al. Determination of radiogenic 87Sr/86Sr and stable δ88/86SrSRM987 isotope values of thirteen mineral, vegetal and animal reference materials by DS-TIMS. Geostand. Geoanal. Res. 44, 331–348 (2020).
Weber, M., Lugli, F., Jochum, K. P., Cipriani, A. & Scholz, D. Calcium carbonate and phosphate reference materials for monitoring bulk and microanalytical determination of Sr isotopes. Geostand. Geoanal. Res. 42, 77–89 (2018).
Pebesma, E. J. Multivariable geostatistics in S: the gstat package. Comput. Geosci. 1, 683–691 (2004).
Hijmans, R. J. raster: Geographic Data Analysis and Modeling (Springer, New York, 2018).
Zazzo, A. et al. The isotope record of short- and long-term dietary changes in sheep tooth enamel: Implications for quantitative reconstruction of paleodiets. Geochim. Cosmochim. Acta 74, 3571–3586 (2010).
Martin, J. E. et al. Strontium isotopes and the long-term residency of thalattosuchians in the freshwater environment. Paleobiology 42, 143–156 (2016).
Tacail, T., Télouk, P. & Balter, V. Precise analysis of calcium stable isotope variations in biological apatites using laser ablation MC-ICPMS. J. Anal. At. Spectrom. 31, 152–162 (2016).
Tacail, T., Kovačiková, L., Brůžek, J. & Balter, V. Spatial distribution of trace element Ca-normalized ratios in primary and permanent human tooth enamel. Sci. Total Environ. 603–604, 308–318 (2017).
Fijn, N. Living with Herds: Human-Animal Coexistence in Mongolia (Cambridge University Press, Cambridge, 2011).
Venables, W. & Ripley, B. Modern Applied Statistics with S 4th edn. (World. Springer, New York, 2002).
QGIS Development Team. QGIS Geographic Information System: Release 3.2 Bonn. (QGIS Association, 2018). https://www.qgis.org.
Redlands, C. E. S. R. I. ArcGIS Desktop: Release 10. (2011) https://www.esri.com/en-us/home.
Acknowledgements
We would like to thank A. Lamboux (UMR 5276 LGLTPE, ENSL, UCBL) for her help in the preparation of plant and tooth samples prior to analysis. The isotope analyses were performed at the ENSL. Fieldwork was supported by the Joint French-Mongol Archaeological Mission (Ministère des Affaires Etrangères et du Développement International, director S. Lepetz) and by the CNRS. We thank Prof O. Batlai (Natl Univ Mongolia) for her help with plant identification and S. Needs-Howarth for the English editing and the three reviewers for their constructive comments. This research was funded by a Ph.D. grant to NL from the French National Research Agency/Agence Nationale de la Recherche Laboratoires d'Excellence ANR-10-LABX-0003-BCDiv, in the context of the “Investissements d’avenir” ANR-11-IDEX-0004-02, and by an Inalco (Institut National des Langues et Civilisations Orientales) Early Career Research Grant 2017 to CM.
Author information
Authors and Affiliations
Contributions
Conceptualization: A.Z, S.L and A.C. Methodology: N.L, A.C, T.T., V.B. and M.L. Investigation: N.L., A.Z., V.B. and A.C. Writing (original draft): N.L., A.Z., V.B. and A.C. Writing (review and editing): N.L., A.Z., V.B., A.C., T.T., C.M., S.L., N.B. and T.T. Funding acquisition: A.Z., A.C., S.L. and C.M. Supervision: A.Z, S.L and A.C.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lazzerini, N., Balter, V., Coulon, A. et al. Monthly mobility inferred from isoscapes and laser ablation strontium isotope ratios in caprine tooth enamel. Sci Rep 11, 2277 (2021). https://doi.org/10.1038/s41598-021-81923-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-81923-z
This article is cited by
-
Life-history of Palaeoloxodon antiquus reveals Middle Pleistocene glacial refugium in the Megalopolis basin, Greece
Scientific Reports (2024)
-
Limited herbivore migration during the Last Glacial Period of Kenya
Nature Ecology & Evolution (2024)
-
Reindeer prey mobility and seasonal hunting strategies in the late Gravettian mammoth steppe
Archaeological and Anthropological Sciences (2024)
-
Comparison between strip sampling and laser ablation methods to infer seasonal movements from intra-tooth strontium isotopes profiles in migratory caribou
Scientific Reports (2023)
-
Extensive pedigrees reveal the social organization of a Neolithic community
Nature (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.