Abstract
The performance of copper selenide and effectiveness of chemical catalytic reactors are dependent on an inclined magnetic field, the nature of the chemical reaction, introduction of space heat source, changes in both distributions of temperature and concentration of nanofluids. This report presents the significance of increasing radius of nanoparticles, energy flux due to the concentration gradient, and mass flux due to the temperature gradient in the dynamics of the fluid subject to inclined magnetic strength is presented. The non-dimensionalization and parameterization of the dimensional governing equation were obtained by introducing suitable similarity variables. Thereafter, the numerical solutions were obtained through shooting techniques together with 4th order Runge–Kutta Scheme and MATLAB in-built bvp4c package. It was concluded that at all the levels of energy flux due to concentration gradient, reduction in the viscosity of water-based nanofluid due to a higher radius of copper nanoparticles causes an enhancement of the velocity. The emergence of both energy flux and mass flux due to gradients in concentration and temperature affect the distribution of temperature and concentration at the free stream.
Similar content being viewed by others
Introduction
The roles of energy and mass fluxes due to temperature and concentration gradients play major roles in electrochemical processes, dynamics of gases, chemical catalytic reactors, production of copper selenide sequel to the pioneering work by Louis Dufour1; see Ingle and Horne2, Hollinger and Lucke3, Korzhuev4, Kim et al.5, Mahdy6, Anjum Badruddin7. Conservation of energy is capable to unravel the nature of outward flux of energy. Meanwhile, Hort et al.8 once remarked that concentration currents and heat are two driven forces of fluctuations in temperature as in the case of conservation of energy. The effect of energy flux due to concentration gradient on six different gases (\( CO_2+O_2 \), \(N_2+H_2\), \(H_2+CO_2\), \(N_2+O_2\), \(CO_2+N_2\), \(H_2+O_2\)) at various levels of pressure was examined experimentally by Rastogi and Madan9. It was remarked that kinetic theory is useful to determine the Dufour coefficient of each gas and temperature difference within the domain \((T_w - T_\infty )\) is dependent on pressure that maintains the motion of each gas. Formation of energy flux due to temperature gradient is highly significant in gases than in liquids. In fact, the occurrence in a less viscous fluid is 10,000 larger than in high viscous fluid. This fact suggests that the magnitude of the Dufour number is larger for gases (Hort et al.10). Dynamics of peristaltic flow through a channel of width 2a subject to energy flux due to concentration gradient and mass flux due to energy gradient was closely examined by Hayat et al.11. It was shown that temperature distribution is an increasing property of both Dufour and Soret effects. Although, the increase in the temperature distribution is more enhanced near the surface. The reverse is the observed effects of Dufour and Soret phenomena on the concentration as both properties decreases.
Further examination of energy and mass fluxes by Linz12 led to a conclusion that a larger Dufour number was recommended for gaseous mixtures in which energy flux due to concentration gradient is significant. Following the suggestion by Partha et al.15, Lewis number is more appropriate than Schmidt number in characterizing heat and mass transfer due to the significance of energy flux due to concentration gradient and mass flux due to temperature gradient. This led to a robust analysis of the interconnectedness of Lewis number, Dufour number, and Soret number. The results show that when \(L_e = 0.1\) and \(S_r = 0.6\), Nusselt number \(Nu_xRa_x^{-0.5}\) decreases with Dufour effect at the rate of \(-0.076145399\). But, when Lewis number is more higher (i.e. \(L_e = 1\)) and Soret number still remain \(S_r = 0.6\), the same Nusselt number \(Nu_xRa_x^{-0.5}\) decreases with Dufour effect at higher rate of \(-0.585851817\). Energy flux due to concentration gradient was pointed out by Garcia-Colin et al.13 as the most important source of heat conduction within the region where magnetic fields do not exist or even weak. The further associated increase in effective thermal conductivity to growth in Dufour effect. The major reason why temperature increases due to higher magnetic strength were associated with the fact that heat conduction in the perpendicular direction diminishes whenever magnetic field is intensified. The conclusions mentioned above are not affected in the correction published as Ref.14.
Enhancement in the transfer of heat across fluid flow has made experts in thermal engineering embrace the efficiency of nanofluids. The earlier mentioned advancement is based on the nature of the base fluid and nanoparticles. Nanoparticle concentration and temperature effects on the ratio of mass to density and viscosity are some of the physical properties. However, thermal conductivity and specific heat capacity at different levels of concentration of nanoparticles, nanoparticles’ size, and temperature are some of the thermal properties. The concentration of nanoparticles, pressure drop, friction factor, nanoparticles radius are also some of the outlined characteristics of nanofluids as pointed out by Mohamoud Jama16, Narayanan and Rakesh17, Lin and Yang18. Intrinsic magnetic related properties of magnetite vary as to its diameter changes (i.e. higher ratio of surface to volume). As the size of nanoparticles becoming smaller, the superparamagnetic nature of magnetic nano-sized particles even changes19. Ashraf et al.20 remarked that changes in the radius of nanoparticles affect the characteristics of both interphase and nanoparticles. According to Yapici et al.21, the outcome of comparative analysis of ethylene glycol conveying SiO\(_2\) (20–30 nm, 60–70 nm), TiO\(_2\) (30 nm, 50 nm), ZnO (10–30 nm, 35–45 nm, 80–200 nm), CuO (40 nm, 80 nm), and MgO (20 nm, 40 nm) shows that the relative viscosity of these nanofluids is a decreasing property of particle sizes. Vishal et al.22 noted that the viscosity of nanofluid can be greatly influenced by particle size, the nature of energy transfer between fluid’s layer and the surface of the particles. There exist significant changes in the melting point of nanoparticles due to rises in the radius. This conclusion was based on the fact that the melting temperature was seen to be a decreasing property of higher particle size with a significant decreasing rate between spherical and nanoparticles; see Antoniammal and Arivuoli23.
The analysis of Namburu et al.24 indicates that increasing the diameter of silicon dioxide nanoparticles in ethylene glycol and water corresponds to a decrease in the nanofluid’s viscosity. It is worth remarking that the observed decrease in fluid’s viscosity is more significant when the nanofluid is cold (negative temperature). At a larger temperature, the decrease in viscosity with particle size disappears. In the case of a nanofluid parallel to a moving stretchable sheet, platelet shape of molybdenum disulfide (MoS2) nanoparticles was found by Hamid et al.25 to produce a unique heat transfer. In another study, Sheikholeslami et al.26 illustrated the movement of multiple wall carbon nanotube and Iron(iii)oxide nanoparticles in a typical water based nanofluid through a porous medium when Lorentz force is predominant. The dynamics of water conveying alumina and copper nanoparticles over a split lid-driven square cavity was examined by Khan et al.27 and it was shown that higher Nusselt number proportional to the heat transfer rate is attained at the point when both lids meet. In another related report by Khan et al.28, carbon nanotubes and heating of the wall are two factors capable to boost the local Nusselt number in the case of water-based carbon nanotubes over a right-angle trapezoidal cavity. Meanwhile, the local Nusselt numbers are increasing property of solid volume fraction of carbon nanoparticles; Hamid et al.29. The analysis of seven different hybrid nanofluids by Nehad et al.30 shows that optimal Nusselt number is achievable when suction and stretching are significantly large but less dense nanoparticles like silicon dioxide and multiple wall CNT.
Sequel to the aforementioned reviews of related literatures, in the presence of Joule heating and space-dependent heating, it is noteworthy to examine the significance of increasing nanoparticle radius and inclined magnetic field on the dynamics of chemical reactive water conveying copper nanoparticles through a porous medium. The outcome of such study would be very helpful to experts dealing with the performance of copper selenide and effectiveness of chemical catalytic reactors. This study was designed to provide answers to the following related research questions:
-
1.
when energy flux due to concentration gradient and mass flux due to temperature gradient are negligible, what is the significance of increasing radius of nanoparticles on the local skin friction coefficients, heat transfer rate, and mass transfer rate?
-
2.
At various levels of energy flux and mass flux due to gradients in concentration and temperature respectively, how does increasing radius of copper nanoparticles influences the transport phenomena of Cu-water nanofluids?
-
3.
What is the variation in \(Cf_x\sqrt{Re_x}\), \(\frac{Nu_x}{\sqrt{Re_x}}\), and \(\frac{Sh_x}{\sqrt{Re_x}}\), with increasing radius of nanoparticles, Dufour number and Soret number?
Mathematical formulation
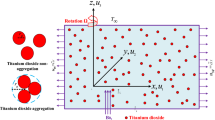
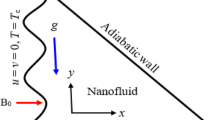
When energy flux due to concentration gradient and mass flux due to temperature gradient are significant, the dynamics of water conveying copper nanoparticles over a horizontal surface subject to magnetic field of strength \(B_o\) inclined at an angle \(\gamma \) was formulated. Due to the stretching at the wall, stretching velocity is assumed to be \(u_w = \lambda U_ox\) where \(\lambda <0\) implies shrinking while \(\lambda >0\) implies stretching at the wall \(y = 0\). The chemical reaction that occurs in the transport phenomenon was model as first order where the rate of the chemical reaction is \(Kc^*\). Following Bachok et al.39, the governing equation suitable to investigate the aforementioned transport phenomenon is
Suitable boundary conditions are
The model proposed by Graham31 and Gosukonda et al.32 for the ratio of dynamic viscosity of the nanofluid to the dynamic viscosity of base fluid defined as
where the radius of nanoparticle is \(d_p\) and the inter-particle spacing is h was adopted. The effective nanofluid properties are given by
where \(\phi \) is the solid volume fraction, \(\mu _f\) is the dynamic viscosity of the base fluid, \(\rho _f\) and \(\rho _s\) are the densities, \((\rho c_p)_f\) and \((\rho c_p)_s\) are the heat capacitance, \(\kappa _f\) and \(\kappa _s\) are the thermal conductivities and \(\sigma _f\) and \(\sigma _s\) are the electrically conductivities of the base fluid and nanoparticles respectively. Prior to one of the conclusions by Buongiorno et al.33 on the thermal conductivity of nanofluids, the model proposed by Maxwell34 was adopted to incorporate the enhancement in the thermal conductivity of Cu-Water nanofluid. Next is to introduce the following variables
where \(D_f\) is the Dufour number, \(S_r\) is the Soret number, Prandtl number \(P_r\), magnetic field parameter M, and porosity parameter P, heat source/sink parameter \(Q_e\), Lewis number \(L_e\), viscous dissipation term \(E_c\), and suction S are defined as
The dimensionless governing equation is now of the form
Subject to
Skin friction coefficient \(Cf_x\), Nusselt number \(Nu_x\), and Sherwood number \(Sh_x\) are defined as
where Reynold number \(\sqrt{Re_x} = \frac{a^{1/2}x}{\vartheta _f^{1/2}}\), shear stress \(\tau _w\), heat flux \(q_w\), mass flux \(q_m\), \(\rho _f = 997.1\), \((Cp)_f = 4179\), \(\kappa _f = 0.613\), \(\sigma _f = 5.5\times 10^{-6}\), \(\rho _s = 8933\), \((Cp)_s = 385\), \(\kappa _s = 401\), and \(\sigma _s = 5.96\times 10^{7}\). These values are extracted from Wakif et al.35, Saidi & Karimi36, Khoshvaght-Aliabadi & Hormozi37, Wan et al.38, and Bachok et al.39. The dimensionless local skin friction, heat transfer rate, and mass transfer rate are
Method of solution, results and discussion
The method of superposition (Na40) was used to obtain the system of first order IVP for Eqs. (10)–(14). The numerical solution of the corresponding IVP was obtained using MATLAB based bvp4c package suggested by Gokhan41, Kierzenka and Shampine42, and Ali Umit Keskin43. Reliability and validity of solution was established by comparing the limiting case of this present study with that of Hamad44 at various values of Prandtl number. As shown in Table 1, good agreement is seen, hence further analysis is reliable. The simulation was carried out for fixed magnetic field strength \(M = 0.5\), inclination of the magnetic field \(\gamma = 30^o\), inter-particle spacing \(h = 1\), Lewis number \(L_e = 0.2\), Prandtl number \(P_r = 6.2\), chemical reaction parameter \(K_c = 0.5\), heat source parameter \(Q_e = 0.5\), intensity of heat source \(n = 0.5\), viscous dissipation term—Eckert number \(E_c = 0.3\), stretching related parameter \(\lambda = 0.5\), and suction \(S = 0.5\). The answer to the remaining research questions was obatined when \(M = 0.5\), \(\gamma = 30^o\), \(h=1\), \(L_e = 0.2\), \(P_r = 6.2\), \(K_c = 0.5\), \(Q_e = 0.5\), \(n = 0.5\), \(E_c = 0.3\), \(\phi = 0.02\), \(S = 0.5\), and \(\lambda = 0.5\). Using the technique called linear regression through the data point suggested by Shah et al.50, Wakif et al.51, and Animasaun et al.52, the analysis presented as Tables 2, 3, 4 and 5 reveal that a larger radius of copper nanoparticles leads to negligible higher local skin friction coefficients. Firstly, when \(S_r = 0.1\) and \(D_f = 0.1\), as \(d_p\) increases, local skin friction coefficients increases at the rate of 0.046678714, higher heat transfer rate of 0.019499889, and higher mass transfer rate of 0.004874409. In order to capture the significance of energy flux due to concentration gradient, the same analysis was carried out for \(D_f = 10\); see Table 3. Percentage increase in \(\frac{Nu_x}{\sqrt{Re_x}}\) with \(d_p\) as \(D_f\) changes from 0.1 to 10 was estimated \(344.286288\%\). Comparative analysis of the data presented as Tables 4 and 5 and figures illustrated as Figs. 1 and 2 confirm that there exists a relationship between energy flux due to concentration gradient and mass flux due to temperature gradient.
When \(S_r = 0.1\), the significance of increasing radius of copper nanoparticles \(d_p\) and energy flux due to concentration gradient \(D_f\) were examined. The outcome of the analysis presented as Figs. 3 and 4 show that the velocity of the transport phenomenon increases with a larger radius of nanoparticles. Meanwhile, an increment in the friction across the layers near the inclined surface is observed through an increase in the radius of nanoparticles as shown in Fig. 5. This can be associated with the fact that increasing the diameter of nanoparticles in water as pointed out by Namburu et al.24 corresponds to a decrease in the nanofluid’s viscosity. Not only that, the outcome of an examination of (i) ethylene glycol and alumina nanoparticles mixture (ii) water and CuO nanoparticles mixture by Pastoriza-Gallego et al.48,49 shows that higher viscosity is bound to occur as particle size diminishes. It is worth deducing from Figs. 3, 4, and 5 that the velocity is the same at all the levels of heat energy flux due to concentration gradient \(D_f\). However, in the case of distribution of temperature illustrated as Fig. 6, decreases negligibly with \(d_p\) when \(D_f\) is small in magnitude. When \(D_f = 5\) and \(D_f = 10\), the observed decrease in the temperature distribution due to the higher radius of nanoparticles is ascertained. Further exploration of temperature distribution for \(0.1 \le D_f \le 10\) was achieved through kriging gridding method package in Surfer plot version 11.1.719 as shown in Figs. 7 and 8. When the transfer of species due to temperature gradient is small in magnitude optimal temperature is seen a few distances away from the inclined surface at larger values of \(D_f\). Now, when mass flux due to temperature gradient is sufficiently large, optimal temperature, although it is small in magnitude is seen at all the levels of energy flux due to the concentration gradient.
Conclusion
Attempt had been made to examine the significance of increasing radius of nanoparticles, energy flux due to concentration gradient, and mass flux due to temperature gradient in the dynamics of chemically reactive fluid subject to suction and inclined magnetic strength. Based on the analysis, it is worth concluding that
-
1.
at all the levels of energy flux due to concentration gradient, reduction in the viscosity of water-based nanofluid due to a higher radius of copper nanoparticles causes an enhancement of the velocity.
-
2.
significance decrease in distribution of temperature across the domain due to increasing radius of copper nanoparticles is achievable when energy flux due to concentration gradient is sufficiently large in magnitude.
-
3.
when mass flux due to temperature gradient is highly negligible, optimal temperature is also observable when energy flux due to concentration gradient is sufficiently large. Reverse is the case when mass flux due to temperature gradient is sufficiently large as optimal temperature is ascertained at all levels of energy flux due to concentration gradient.
-
4.
reduction in the mass transfer rate \(\frac{Sh_x}{\sqrt{Re_x}}\) due to higher radius of copper nanoparticles is guaranteed when the transfer of species (mass) due to temperature gradient is sufficiently large but transfer of heat energy due to concentration gradient is highly negligible.
-
5.
the emergence of both energy flux and mass flux due to gradients in concentration and temperature affect the distribution of temperature and concentration at the free stream.
References
Louis Dufour, H. (1873) Ueber die Diffusion der Gase durch porose Wande und die sie begleitenden Temperaturveranderungen. Annalen der Physik 224(3), 490. https://doi.org/10.1002/andp.18732240311.
Ingle, S. E. & Horne, F. H. The Dufour effect. J. Chem. Phys. 59(11), 5882–5894 (1973). https://doi.org/10.1063/1.1679957..
Hollinger, S. & Lucke, M. Influence of the Dufour effect on convection in binary gas mixtures. Phys. Rev. E 52(1), 642–657 (1995). https://doi.org/10.1103/physreve.52.642..
Korzhuev, M. A. Dufour effect in superionic copper selenide. Phys. Solid State 40(2), 217–219 (1998). https://doi.org/10.1134/1.1130276..
Kim, J., Kang, Y. T. & Choi, C. K. Soret and Dufour effects on convective instabilities in binary nanofluids for absorption application. Int. J. Refriger. 30(2), 323–328 (2007). https://doi.org/10.1016/j.ijrefrig.2006.04.005..
Mahdy, A. MHD non-Darcian free convection from a vertical wavy surface embedded in porous media in the presence of Soret and Dufour effect. Int. Commun. Heat Mass Transf. 36(10), 1067–1074 (2009). https://doi.org/10.1016/j.icheatmasstransfer.2009.07.004..
Anjum Badruddin, I. Heat and mass transfer with Soret/Dufour effect in irregular porous cavity. J. Thermophys. Heat Transf. 33(3), 647–662 (2019). https://doi.org/10.2514/1.t5666..
Hort, W., Linz, S. J. & Lucke, M. Onset of convection in binary gas mixtures: Role of the Dufour effect. Phys. Rev. A 45(6), 3737–3748 (1992). https://doi.org/10.1103/physreva.45.3737..
Rastogi, R. P. & Madan, G. L. Cross-phenomenological coefficients Part 6—Dufour effect in gases. Trans. Faraday Soc. 62(0), 3325–3330 (1966). https://doi.org/10.1039/tf9666203325.
Hort, W., Linz, S. J. & Lucke, M. Onset of Soret and Dufour sriven convection in binary fluid mixtures. Nonlinear Evol. Spatio-Temp. Struct. Dissipative Continuous Syst. 21, 149–153 (1990).
Hayat, T., Abbasi, F. M. & Obaidat, S. Peristaltic motion with Soret and Dufour effects. Magnetohydrodynamics 47(3), 295–302 (2011). https://doi.org/10.22364/mhd.47.3.8.
Linz, S. J. Onset of Dufour-driven convection in binary fluid mixtures: No-slip boundary conditions. Phys. Rev. A 45(2), 1262–1265 (1992). https://doi.org/10.1103/physreva.45.1262..
Garcia-Colin, L. S., Garcia-Perciante, A. L. & Sandoval-Villalbazo, A. Dufour and Soret effects in a magnetized and non-magnetized plasma. Phys. Plasmas 14(1), 012305, (2007). https://doi.org/10.1063/1.2428279..
Garcia-Colin, L. S., Garcia-Perciante, A. L. & Sandoval-Villalbazo, A. Erratum: “Dufour and Soret effects in a magnetized and non-magnetized plasma” [Phys. Plasmas 14, 012305 (2007)]. Phys. Plasmas 14(8), 089901, (2007). https://doi.org/10.1063/1.2748054.
Partha, M. K., Murthy, P. V. S. N. & RajaSekhar, G. P. Soret and Dufour effects in a non-Darcy porous medium. J. Heat Transf. 128(6), 605–610 (2005). https://doi.org/10.1115/1.2188512.
Mohamoud, J., Tejvir, S., Seifelislam, M., Gamaleldin, M., Koc, A., Samara, R.J.I., & Muataz, A.A. Critical review on nanofluids: Preparation, characterization, and applications. J. Nanomater. (2016). https://doi.org/10.1155/2016/6717624.
Narayanan, M. V., & Rakesh, S. G. Nanofluids: A review on current scenario and future prospective. IOP Conf. Ser. Mater. Sci. Eng. 377, 012084 (2018). https://doi.org/10.1088/1757-899x/377/1/012084..
Lin, J. & Yang, H. A review on the flow instability of nanofluids. Appl. Math. Mech. 40(9), 1227–1238 (2019). https://doi.org/10.1007/s10483-019-2521-9..
Sharifi, I., Shokrollahi, H., & Amiri, S. Ferrite-based magnetic nanofluids used in hyperthermia applications. J. Magn. Magn. Mater. 324(6), 903–915 (2012). https://doi.org/10.1016/j.jmmm.2011.10.017..
Ashraf, M. A., Peng, W., Zare, Y., & Rhee, K. Y. Effects of size and aggregation/agglomeration of nanoparticles on the interfacial/interphase properties and tensile strength of polymer nanocomposites. Nanoscale Res. Lett. 13(1), 214 (2018). https://doi.org/10.1186/s11671-018-2624-0..
Yapici, K., Osturk, O. & Uludag, Y. Dependency of nanofluid rheology on particle size and concentration of various metal oxide nanoparticles. Braz. J. Chem. Eng. 35(2), 575–586 (2018). https://doi.org/10.1590/0104-6632.20180352s20160172..
Vishal, C. C., Kanala, R. K., Raju, C. S. K., Madathil, P. K., Saha, P., Rao, B. R., and Sriganesh, G. Sub-micron sized metal oxides based organic thermic fluids with enhanced thermo-physical properties. Appl. Therm. Eng. 163, 114337, (2019). https://doi.org/10.1016/j.applthermaleng.2019.114337..
Antoniammal, P. & Arivuoli, D. Size and shape dependence on melting temperature of Gallium nitride nanoparticles. J. Nanomater. 2012, 1–11 (2012). https://doi.org/10.1155/2012/415797..
Namburu, P. K., Kulkarni, D. P., Dandekar, A. & Das, D. K. Experimental investigation of viscosity and specific heat of silicon dioxide nanofluids. Micro Nano Lett. 2(3), 67 (2007). https://doi.org/10.1049/mnl:20070037..
Hamid, M., Usman, M., Zubair, T., Haq, R. U. & Wang, W. Shape effects of MoS2 nanoparticles on rotating flow of nanofluid along a stretching surface with variable thermal conductivity: A Galerkin approach. Int. J. Heat Mass Transf. 124, 706–714 (2018). https://doi.org/10.1016/j.ijheatmasstransfer.2018.03.108.
Sheikholeslami, M., Hamid, M., Haq, R. U. & Shafee, A. Numerical simulation of wavy porous enclosure filled with hybrid nanofluid involving Lorentz effect. Phys. Scripta 95(11), 115701 (2020). https://doi.org/10.1088/1402-4896/abbcf3.
Khan, Z. H., Khan, W. A., Hamid, M. & Liu, H. Finite element analysis of hybrid nanofluid flow and heat transfer in a split lid-driven square cavity with Y-shaped obstacle. Phys. Fluids 32(9), 093609 (2020). https://doi.org/10.1063/5.0021638.
Khan, Z. H., Khan, W. A., Haq, R. U., Usman, M. & Hamid, M. Effects of volume fraction on water-based carbon nanotubes flow in a right-angle trapezoidal cavity: FEM based analysis. Int. Commun. Heat Mass Transf. 116, 104640 (2020). https://doi.org/10.1016/j.icheatmasstransfer.2020.104640.
Hamid, M., Khan, Z. H., Khan, W. A. & Haq, R. U. Natural convection of water-based carbon nanotubes in a partially heated rectangular fin-shaped cavity with an inner cylindrical obstacle. Phys. Fluids 31(10), 103607 (2019). https://doi.org/10.1063/1.5124516.
Nehad, A. S., Animasaun, I. L., Wakif, A., Koriko, O. K., Sivaraj, R., Adegbie, K. S., Zahra, A., Hanumesh Vaidya, A. F. Ijirimoye & Prasad, K. V. Significance of suction and dual stretching on the dynamics of various hybrid nanofluids: Comparative analysis between type I and type II models. Phys. Scripta 95(9), 095205 (2020). https://doi.org/10.1088/1402-4896/aba8c6.
Graham, A. L. On the viscosity of suspensions of solid spheres. Appl. Sci. Res. 37, 275–286 (1981).
Gosukonda, S., Gorti, V. P. N. S., Baluguri, S. B. & Sakam, S. R. Particle spacing and chemical reaction effects on convective heat transfer through a nano-fluid in cylindrical annulus. Proc. Eng. 127, 263–270 (2015). https://doi.org/10.1016/j.proeng.2015.11.359.
Buongiorno, J., Venerus, D. C., Prabhat, N., McKrell, T., Townsend, J., Christianson, R., & Bang, I. C. A benchmark study on the thermal conductivity of nanofluids. J. Appl. Phys. 106(9), 094312 (2009).
Maxwell, J. C. A Treatise on Electricity and Magnetism. (Clarendon, Oxford, 1873).
Wakif, A., Chamkha, A., Thumma, T., Animasaun, I. L. & Sehaqui, R. Thermal radiation and surface roughness effects on the thermo-magneto-hydrodynamic stability of alumina-copper oxide hybrid nanofluids utilizing the generalized Buongiorno’s nanofluid model. J. Therm. Anal. Calorim.. (in-press) (2020). https://doi.org/10.1007/s10973-020-09488-z.
Saidi, M. & Karimi, G. Free convection cooling in modified L-shape enclosures using copper-water nanofluid. Energy 70, 251–271 (2014). https://doi.org/10.1016/j.energy.2014.03.121.
Khoshvaght-Aliabadi, M. & Hormozi, F. Heat transfer enhancement by using copper-water nanofluid flow inside a pin channel. Exp. Heat Transf. 28(5), 446–463 (2014). https://doi.org/10.1080/08916152.2014.907844.
Wan, Z., Deng, J., Li, B., Xu, Y., Wang, X., & Tang, Y. Thermal performance of a miniature loop heat pipe using water-copper nanofluid. Appl. Therm. Eng. 78, 712–719 (2015). https://doi.org/10.1016/j.applthermaleng.2014.11.010.
Bachok, N., Ishak, A., Nazar, R., & Senu, N. Stagnation-point flow over a permeable stretching/shrinking sheet in a copper-water nanofluid. Bound. Value Probl. 2013(1), 39 (2013). https://doi.org/10.1186/1687-2770-2013-39.
Na, T. Y. Computational Methods in Engineering Boundary Value Problems. (Academic Press, New York, 1979).
Gokhan, F. S. Effect of the Guess function and continuation method on the run time of MATLAB BVP solvers. Clara M. Ionescu (Ed.) 1, (2011).
Kierzenka, J. & Shampine, L. F. A BVP solver based on residual control and the MATLAB PSE. ACM Trans. Math. Softw. (TOMS) 27(3), 299–316 (2001).
Keskin, A. U. Boundary Value Problems for Engineers with MATLAB Solutions. (Springer Nature Switzerland AG, 2019). https://doi.org/10.1007/978-3-030-21080-9.
Hamad M. A. A. Analytical solution of natural convection flow of a nanofluid over a linearly stretching sheet in the presence of magnetic field. Int. Commun. Heat Mass Transf. 38, 487–492 (2011). https://doi.org/10.1016/j.icheatmasstransfer.2010.12.042.
Wang, C.Y. Free convection on a vertical stretching surface. J. Appl. Math. Mech. (ZAMM). 69, 418–420 (1989).
Gorla, R.S.R. and Sidawi, I. Free convection on a vertical stretching surface with suction and blowing. Appl. Sci. Res. 52, 247–257 (1994).
Khana, W.A. & Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 53, 2477–2483 (2010). https://doi.org/10.1016/j.ijheatmasstransfer.2010.01.032.
Pastoriza-Gallego, M., Lugo, L., Legido, J. & Pineiro, M. M. Thermal conductivity and viscosity measurements of ethylene glycol-based Al2O3 nanofluids. Nanoscale Res. Lett. 6(1), 221 (2011). https://doi.org/10.1186/1556-276x-6-221.
Pastoriza-Gallego, M. J., Casanova, C., Legido, J. L., & Pineiro, M. M. CuO in water nanofluid: Influence of particle size and polydispersity on volumetric behaviour and viscosity. Fluid Phase Equilib. 300(1–2), 188–196 (2011). https://doi.org/10.1016/j.fluid.2010.10.015.
Shah, N. A., Animasaun, I. L., Ibraheem, R. O., Babatunde, H. A., Sandeep, N., & Pop, I. Scrutinization of the effects of Grashof number on the flow of different fluids driven by convection over various surfaces. J. Mol. Liq. 249, 980–990 (2018). https://doi.org/10.1016/j.molliq.2017.11.042.
Wakif, A., Animasaun, I. L., & Sarojamma, G. Meta-analysis on thermo-migration of tiny/nano-sized particles in the motion of various fluids. Chin. J. Phys. 68, 293–307 (2019). https://doi.org/10.1016/j.cjph.2019.12.002.
Animasaun, I. L., Ibraheem, R. O., Mahanthesh, B. & Babatunde, H. A. A meta-analysis on the effects of haphazard motion of tiny/nano-sized particles on the dynamics and other physical properties of some fluids. Chin. J. Phys. 60, 676–687. https://doi.org/10.1016/j.cjph.2019.06.007 (2019).
Acknowledgements
This work was supported by Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (No. 20192010107020, Development of hybrid adsorption chiller using unutilized heat source of low temperature).
Author information
Authors and Affiliations
Contributions
Conceptualization, N.A.S.; Methodology, A.W.; Validation, I.L.A.; Formal analysis, C.S.K.R.; Writing-original draft preparation, I.L.A., N.A.S., A.W., F.I.A., C.S.K.R.; Writing-review and editing, I.L.A., N.A.S., J.D.C., A.W., F.I.A., C.S.K.R. Revision, J.D.C.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shah, N.A., Animasaun, I.L., Chung, J.D. et al. Significance of nanoparticle’s radius, heat flux due to concentration gradient, and mass flux due to temperature gradient: The case of Water conveying copper nanoparticles. Sci Rep 11, 1882 (2021). https://doi.org/10.1038/s41598-021-81417-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-81417-y
This article is cited by
-
Comparative study on hybrid-based MoS2-GO hybrid nanofluid flow over a three-dimensional extending surface: A numerical investigation
Colloid and Polymer Science (2024)
-
Dynamical dissipative and radiative flow of comparative an irreversibility analysis of micropolar and hybrid nanofluid over a Joule heating inclined channel
Scientific Reports (2023)
-
Significance of nanoparticle radius on EMHD Casson blood-gold nanomaterial flow with non-uniform heat source and Arrhenius kinetics
Journal of Thermal Analysis and Calorimetry (2023)
-
Synthesis, Attributes and Defect Control of Defect-Engineered Materials as Superior Adsorbents for Aqueous Species: A Review
Journal of Inorganic and Organometallic Polymers and Materials (2022)
-
Improved natural convection in a vertical cylinder using smart fluid for solar heating and off-place cooking applications
Emergent Materials (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.