Abstract
The shrinking global forest area limits the supply of industrially usable raw resources. This, in combination with the ever-increasing consumption of timber due to population growth can lead to the lack of a positive balance between the annual volumetric growth and consumption of wood. An important innovation toward increasing environmental and economic sustainability of timber production is to reduce the volume of wood residues by minimizing the sawing kerf. It results in higher material yield but may impact the dimensional accuracy of derived products. Therefore, the cutting tool geometry as well as the sawing process as a whole must be carefully optimized to assure optimal use of resources. The goal of this study is to better understand the causes of machining errors that occur when sawing wood with saws of varying thickness of kerf, with a special focus on re-sawing thin lamellae performed on the gang saw. Numerical simulations were tested against experimental results, considering influence of diverse components of cutting forces, in addition to the initial and operating stiffness coefficients of the saw blade. It has been demonstrated that asymmetric loads from the cutting process for the scraper saw blade can cause sawing inaccuracies. The simulation methodology developed in this research can be straightforwardly extended towards determination of optimal geometry of other cutting tools, particularly with the reduced sawing kerf. This may lead to more sustainable use of natural resources as well as an increase in economic gain for the wood processing industries.
Similar content being viewed by others
Introduction
The sawing of logs into timber and the following re-sawing of square-sawn timbers into lamellae are the most common basic woodworking operations performed in primary and secondary wood processing plants. The cost structure within a wood processing company is one of the most important factors determining its revenue. The material component associated with the sawn raw material has, in a typical European sawmill, the largest share in the cost structure reaching up to 70%1. Steele et al.2 argue that material costs can amount to even more, exceeding 75% in extreme cases. At the same time, the global forest area is shrinking, limiting the supply of industrially usable raw resources. This, in combination with the ever-increasing consumption of wood because of a growing population, can lead in the coming years to the lack of a positive balance between the annual volumetric growth and consumption of wood3. Projected and actual scarcity of the raw material (logs) availability, increasing competition on the international market, combined with significant and ever-growing production costs compel wood processing plants to dramatically modernize their technologies4,5. An important innovation toward increasing environmental and economic sustainability of timber production is to reduce the volume of wood residues by minimizing the sawing kerf. It results in higher material yield but may have an impact on the dimensional accuracy of derived products. Therefore, the cutting tool geometry as well as sawing process conditions must be carefully optimized to assure optimal use of resources.
The process of cutting wood on band sawing machines was experimentally studied6,7, while the accuracy of the sawing of timber under industrial conditions was evaluated8. Steele et al.2 analysed 266 reports for 6 types of band sawing machines and the accuracy of products obtained from them. Recommendations have been developed for the selection of sawing machines for cutting selected hardwood species, based on the measured values of the total sawing variation9. Barcik6, Lehmann and Hutton10, Tanaka et al.11 and Wong and Schajer12 reported results of their studies on the transverse movement of band saw blades during the cutting of wood. Albrecht and Möhring13 have demonstrated that adaptive control of the cutting of metals using band sawing machines improves the energy efficiency of the process, as well as cutting accuracy and machining productivity. The same research direction was also adopted for the material-efficient processing of wood14.
Ulsoy et al.15 analysed the dynamics and stability of band sawing machines. Similar issues were also addressed by Yang and Mote16, Lehmann and Hutton10,17, Lister and Schajer18 and Okai et al.19. The latter work explains the phenomenon of self-excited vibrations, called “washboarding”. It directly linked resonance frequencies of saw blades with the generated surface topography. Conversely, Orlowski and Wasielewski20 postulated that unwanted surface washboarding effect after cutting on a frame sawing machine is a result of the regeneration of vibrations or trace machining.
Other direction of wood cutting process studies is focused on circular saw blades. These can be fixed in clamp flanges or guided. Natural frequencies of saws and their dependent critical rotational speeds were determined in21,22,23,24. The impact of the design of the circular saw blade on its dynamic characteristics was described by Cheng and others25. The benefits of using circular saw blades running in guides at supercritical rotational speeds have been presented in several works26,27,28,29. In addition to experimental studies, numerical studies were also conducted, such as the computational model proposed by Mohammadpanah and Hutton26 as well as the multi-point pressure tensioning process of the circular saw blade30.
Issues in the production of top layers of adhesive-bonded floors on band sawing and frame sawing machines using saws with small values of the overall saw set (theoretical kerf) were analysed in the work of Orlowski and Walichnowski31. Kujawińska et al.32 and Zywicki et al.33 proposed a model for estimating raw material waste during the production of the middle layers of the 3-layer floorboard. Similarly, the optimization of raw material allowances in the production of thin lamellae from selected European and exotic wood species, by implementing the “wet technology” on band sawing machines was studied by Kujawińska et al.34. The methodology for determining optimal allowances for processing, and application of the methodology in the process of manufacturing oak wood products for the top layer of adhesive-bonded floorboards are described in the article35.
The standard deviations within-lamella, between lamella, and total standard deviations, are accepted as reliable quantifiers of the accuracy of the sawing process9,36. It was evidenced by authors37 that variations in thickness for the external lamellae x1 and x2 were consistently higher than for the middle lamellae x3 (Fig. 1), and increased along the working shift. The accuracy assessment was carried out using the discrete method37, though solutions based on artificial intelligence algorithms could also be used for monitoring the cutting process38. The asymmetric action of the cutting forces on the main cutting edges and the action of the thrust forces on the minor cutting edges of the scraper saw blades are thought to be the main cause of this dimensional inaccuracy of the external lamellae. This phenomenon occurred despite the considerably larger thicknesses of lateral saw blades compared to the middle saws in the gang.
The set of saw blades in the gang with the obtained lamellae (drawing designed in AutoCad 2020 https://www.autodesk.com/products/autocad).
The goal of this study is to better understand the causes of machining errors that occur when sawing wood with saws of varying thickness of kerf. It could lead to the development of a universal protocol for the determination of optimal saw geometry resulting in a minimal amount of generated residues (saw dust) while assuring tolerable dimensional accuracy. The case study presented is a follow-up of the long-term experimental campaign conducted by authors in the past. It includes studies on the effectiveness of frictional narrow-saw blade fastening in the gang39, methods of determining static saw blade stiffness40, washboarding phenomenon and dynamic behaviour of narrow-kerf saw blades while sawing soft and hard woods20, economic analyses of lamellae production methods31, quality of re-sawing process37,41, application of fracture mechanics for determination of energetic effects while wood sawing42,43, and dynamics of the main driving system of the sash gang sawing machine44. This work focuses on an analysis of the re-sawing processes of thin lamellae performed on the gang saw when implementing narrow-kerf saws. Numerical simulations were tested against experimental results, considering influence of diverse components of cutting forces, in addition to the initial and operating stiffness coefficients of the saw blade.
Theoretical background
Stiffness of the saw blade
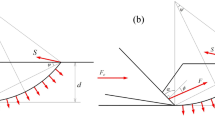
The static stiffness of the saw determined in the machine–chuck–workpiece–tool system, combined with the resistance to wandering in the workpiece, are commonly considered as the basic indicators determining the ability of a saw to properly cut the material10,17,45. Therefore, the saw in the given configuration represents the weakest element of the system. Several attempts were made to predict the behaviour of the tool during the machining5,27. Most of these revealed that the geometrical accuracy of the products being manufactured depends on the transverse displacements of saw blades. Figure 2 shows an arrangement of external forces loading the saw blade, which change their positions depending on the placement of the frame sawing machine sash, when it is driven by a dynamically balanced main drive44.
Loads on the saw during operation; where: FN is the tensioning force (the force stretching the saw blade in the longitudinal direction—Ym axis of the sawing machine’s coordinate system); FcT is the total cutting force; FfT is the total feed force; FpT is the total thrust force to load the saw; L0 is the free saw blade length; hw is the feed roller level; HRP is the saw frame stroke; r is the crank radius in the driving system; s is the saw blade thickness; y(φ) is the position of the point of application of force as a function of the angle of rotation φ of the crank in the main drive of the sawing machine.
The initial static stiffness of the saw blade k0 is determined according to Eq. (1) as the ratio of the thrust force Fp applied in the middle of the free length of the saw blade to the displacement of the saw blade q towards the Xm axis (Fig. 2):
The relationship (1) is non-linear as the stiffness of the saw blade k0 is a nonlinear property. Therefore, the stiffness itself should be assessed as a local stiffness by using the secant method. In that case the ratio of the gain in the thrust force is directly related to the gain in the displacement of the saw blade46. The stiffness of the saw blade is most often analysed by the superposition method, which accounts for the strain of the saw blade resulting from bending (normal strains due to bending) and torsion (shear strains due to torsion)40,47,48,49,50,51. Several analytical methods (the beam and plate models) and/or numerical methods (the finite element method or the rigid finite element method) are frequently used to determine the static stiffness values. However, each of those methods can only be used within the specified range of blade width40. The saw blade width can vary between 20 mm in the case of mini saw blades, up to > 250 mm for high throughput band sawing machines for processing logs.
Factors influencing the saw blade stiffness
An effect of the feed force Ff should be taken into consideration when analysing transverse displacements of the saw. Ff affects the stability of the saw blade and reduces the initial static stiffness coefficient of the saw blade k0 to the value of the operating stiffness coefficient k0w24,49,51. The total loss of saw blade stability occurs when the feed force Ff reaches the critical value (Ff_crit) operating in the plane of the greatest stiffness of the saw blade50,51,52. The critical force Ff_crit corresponds to the force at which the saw blade gets infinitely bent as a result of a small value thrust force Fp11,50,51. In addition, the stiffness of the saw blade can decrease as a result of an increase in the saw blade temperature53. Pahlizch and Puttkammer50, Prokofiev51 and Csanady and Magoss47 proposed the analytical determination of the critical feed-per-tooth force Ff_crit for saws with saw blades wider than 100 mm.
Knowing the value of the critical force Ff_crit, the working stiffness coefficient can be determined from the dependencies proposed by Timoshenko and Gere52 for the general case, or by Prokofiev51 specifically for a wideband sawing machine. Finally, the working stiffness can also be derived from Stakhiev’s equation24.
Estimating values of cutting forces
The cutting forces Fc can be estimated using the empirical classic model which is based on wood specific cutting resistance43,54,55,56. As an alternative, a modern approach considering the fracture toughness and shear yield stress in the cutting zone can be used for the determination of cutting force values43. Although models based on the fracture mechanics theorem allows for predicting energy effects in a highly precise way, the classical empirical method is still widely used in solving practical problems. For this reason, it was adopted for the numerical simulations developed within this research, in which the cutting force Fc was described as in Eq. (2):
where: kc is the coefficient describing the specific cutting resistance [N⋅mm−2], Fc is the cutting force [N]; ADav is the mean cross-section area of the uncut chip [mm2]; St is the total kerf [mm]; hav is the mean uncut chip thickness [mm].
This model shall consider experimentally determined correction coefficients identified to address changes in the factors affecting the cutting process in relation to the basic conditions adopted in56, as summarized in Eq. (3):
where: kφ is the basic specific cutting resistance for Scots pine wood [N·mm-2], cws is the coefficient taking into account the wood species (i.e. cws = 1 for Scots pine wood defined as the reference species); cMC is the coefficient correcting effect of the wood moisture content; cvc is the coefficient taking into account the value of the cutting speed; cδ is the coefficient taking into account the cutting angle defined as the sum of the clearance angle αf and the blade angle βf; cd is the coefficient considering the cutting edge wear; cwT is the coefficient adjusting effect of the temperature of the wood; ch is the coefficient taking into account the value of the uncut chip thickness; cµ is the coefficient taking into account the friction between the wood being cut and the saw blade; cCE is the coefficient taking into account the shape and dimensions of the cutting edge; cp is the factor taking into account the pressure exerted on the workpiece in front of the blade (commonly applied in the production of veneer).
The value of kφ depends on the position of the cutting edge in relation to the direction of the wood grains56. These values take into account the basic cutting directions, along the grains (kII), tangentially to the grains (k#) and perpendicularly to the grains (k⊥), as well as intermediate cutting directions (kII#, kII⊥, k#⊥, kII#⊥). The values of all the correction factors are equal to 1 if the cutting process is carried out under basic reference conditions. In that case, the specific cutting resistance kc corresponds to the basic specific cutting resistance kφ (Eq. 4):
Lateral loads of the saw blade during cutting
Saws with spring setting teeth, especially those with narrow kerfs, are not used for precise cutting as they do not have the symmetry of tooth geometry for the minor cutting edges. Thus, it is important to properly assess the cause of the build-up of the thrust force on saws with swaged teeth. Some of these tools have already been analysed, including circular saw blades57 and frame saw blades51. The causes of build-up of the resultant thrust force on the teeth of the saw with the swaged saw set are presented here in a structured manner, referring to the said works as well as the requirements given in the ISO standards (ISO 3002-1:198258 and ISO 3002-2:198259).
A typical tooth with the swaged saw set is schematically presented in Fig. 3a. The cutting edge angle and the inclination angle of the main cutting edge are κr = 90° and λs = 0°, respectively. The minor cutting edge angles and the rear flank angles on both sides of the blade are the same (κr1' = κr2', αp1' = αp2'). Both thrust forces Fp1 and Fp2 should be balanced in such a configuration of tooth geometry.
Transverse loads of the saw blade as a function of its geometry in the sawing machine’s coordinate system (Xm, Ym, Zm): (a) typical blade with the swaged saw set; (b) effect of the cutting edge angle κr; (c) effect of the angle of inclination of the main cutting edge λs; (d) effect of the difference in the values of the side saw sets s2 > s1; (e) effect of the difference in the values of tool minor cutting edge angles κr1' < κr2'; (f) effect of the difference in the values of the rear angles of clearance αp1’ > αp2’.
Saw blades with a cutting edge angle κr ≠ 90° are additionally loaded with an extra thrust force Fp(κr). Its value depends on the feed force Ff (Fig. 3b) and the additional thrust force Fp(λs) caused by the cutting force Fc (Fig. 3c) when the main cutting edge is tilted at an angle λs ≠ 0°.
Grinding errors in the form of large differences between the values of the side sets s1 and s2 have a significant impact on the resultant thrust force in addition to the assumed geometry of the saw blades. Such an impact is directly related to the presence of an additional thrust force Fp(e), as shown in Fig. 3d.
Another common error occurring during the manufacture of saw blades is the lack of symmetry due to differences in the minor cutting edge angles, κr1' ≠ κr2' (Fig. 3e) and/or in the rear flank angles αp1' ≠ αp2' (Fig. 3f). Each of these errors results in the presence of an additional thrust force Fp(κr’). Fp(αp’), leading to a variable thickness in the generated workpieces.
An additional cause of the asymmetrical forces in the saw working system can be the inaccurate positioning of blades within the saw frame. An additional thrust force will appear when the direction of the feed movement (or the feed force vector Ff) and the Ym-Zm plane of the setting system are divergent60.
It should be stressed, however, that besides the above-listed factors, the natural heterogeneity of the processed material is the driving factor resulting in the unbalance of the thrust forces Fp1 and Fp2. It is especially relevant in the case of processing biological origin materials, such as wood.
Reference case study
The subsequent numerical simulations of the cutting process are an extension of the previously reported experiments where determination of the cutting power42,43, dimensional accuracy37,41 and saw blade stiffness40 were investigated. It corresponded to the thin lamellae re-sawing on the frame sawing machine with the gang configuration as presented in Fig. 1. The list of relevant case study settings is summarized below.
The processed material
Analyses of the stiffness and stability of saw blades were carried out on the frame sawing machine for processing oak wood (Quercus L.). The thickness of re-sawed boards was tb = 24 mm, with 200 mm width and 2000 mm board length. The moisture content of the wood during sawing was MC = 10%, resulting in the proceeding kiln drying process. Three thin lamellae of thickness tl = 6 mm were obtained as a result of the sawing process. The expected tolerance of the thickness deviations was < ± 0.2 mm. Such lamellae are used for manufacturing the top layers for multi-layer adhesive-bonded wooden floorboards.
Sawing machine
Mamuth TR 97 frame sawing machine (Neva, CZ) equipped with a channel system for the simultaneous feeding of boards served as an experimental cutting platform. The basic parameters of the frame sawing machine are summarized in Table 1. The sawed lamellae thickness accuracy analysis was carried out for one of the channels leading the material to be sawn37. The studied channel consisted of two narrow-kerf saw blades (kerf width St = 1.4 mm) and two scraper saw blades (St_sc = 2.9 mm). The thickness of the scraper saw blades was ssc = 2.4 mm, while that of the narrow-kerf saw blades was s = 0.9 mm. Teeth in both saw blade types were stellited and have the same tooth geometry within the set (Table 2). The sawing process was analysed for kinematic parameters used daily in the Łąccy-Kolczygłowy Sp. z o.o. sawmill in Barnowo (Pomerania, Poland). The results are presented in Table 2.
Cutting tools
All the saw blades were fixed together in the gang, using a friction force-based mechanism similar to the solution described in the report39. The procedure for fixing the saw blades included the pre-tensioning of the entire saw blade assembly by providing a force of FN = 9450 N on each blade (Fig. 2). The value of the force was determined assuming the normal tensile stress σN in the narrow-kerf blade corresponding to 300 MPa, following Eq. 5:
where: Ab is the cross-section of the body of the narrow-kerf saw blade calculated as a product of the thickness s and width b.
Bodies of the scraper saw blades were much thicker than those of the narrow-kerf saw blades installed in the centre of the set. Rectangular windows were cut out in scraper saw blades to assure a balanced value of normal tensile stress corresponding to that in the narrow-kerf saws (Fig. 1). The width of the window was bw = 14 mm, and its length was lw = 33 mm. Consequently, the stress in the scrapper saw blades within the smallest cross-section at the window zone was σN_sc = 187.5 MPa.
Given that both types of saw blades (within the same channel) worked under different cutting conditions during the sawing process, it was assumed that (Fig. 4a):
• The two narrow-kerf saw blades located in the middle of the set carried out the cutting process with the entire length of the main cutting edge (St = 1.4 mm), and the load forces were concentrated halfway along the cutting edge of each saw blade (Fig. 4b).
• The two scrapper saw blades located on both sides of the set carried out the cutting process with only half of the length of their main cutting edges (St_sc/2 = 1.45 mm), and the load forces were concentrated in one-quarter of the length of the cutting edge of each saw blade (Fig. 4c).
• Besides the main cutting edges, two minor cutting edges were involved in cutting with narrow-kerf saw blades, while only one minor cutting edge in the case of scrapper saw blades.
Setting the sawing process simulation
Determination of cutting forces when processing experimental samples
The value of the basic specific cutting resistance for the analysed cutting direction (perpendicular to fibres) corresponds to kφ = k⊥ = 53 MPa56. The values of other correction coefficients, as used in Eq. (3) for calculating the value of the specific cutting resistance according to the classic method of Orlicz56 are summarized in Table 3.
Values of the cutting force Fc computed using the above model are summarized in Table 4. These are relevant for the case study configuration and were directly used in the following simulations. Equivalent value of force F*c determined during the real cutting test at a similar machining configuration is presented in Table 4 for comparison. It corresponds to the sawing process of oak wood at a feed speed of 0.5 m min−161,62. It is evident that experimental and modelled values of cutting forces are comparable. However, it ought to be emphasised that energetic effects determined with the classic method are often over-estimated in comparison to experimental results or other models utilizing fracture mechanics theorem43.
Determination of feed and thrust cutting forces when processing experimental samples
Specific values of the analysed feed forces Ff were computed in relation to the mean cutting force Fc_av determined for the mean feed rate simulated in this research (vf = 0.4 m·min−1). It was found in the author’s own studies that the feed forces Ff can reach values equal to the cutting forces Fc or even higher when processing wood on the frame sawing machine. Therefore, the following values of the feed forces Ff were adopted for the numerical analysis: 0.5·Fc_av = 125 N, 1.0·Fc_av = 250 N and 1.5·Fc_av = 375 N.
Similarly, the set of the thrust forces Fp used for the analysis included 10 N, 50 N, 100 N, 150 N, 250 N and 375 N. It enabled numerical analysis to simulate diverse thrust force Fp effects covering a broad range of corresponding cutting force Fc values.
Numerical modelling of saw blades
The numerical analysis of the static stiffness of the saw blades was carried out using the rigid finite element method RFEM software from Dlubal Software GmbH (Tiefenbach, Germany). It performs numerical analysis based on the finite element method, utilizing the iterative Picard algorithm63. This solution can solve non-linear problems and is characterized by improved numerical stability as compared to the Newton-Rapson method64.
Separate numerical models were developed for the analysis of the narrow-kerf saw blade (Fig. 4b) and the scraper saw blade (Fig. 4c). Mechanical properties were modelled using isotropic models with material properties summarized in Table 5 according to65,66. Four-node (quadrangle) and three-node (triangle) finite shell elements of 6 degrees of freedom (DoF) were used to model the body of each saw blade, based on the Mindlin/Reissner theory67. The thickness of the elements was 0.9 mm and 2.4 mm for the narrow-kerf and for the scraper saw blade, respectively. This resulted in a model of the narrow-kerf saw blade consisting of 5218 2D elements combined with 5493 nodes and a model of the scraper saw blade consisting of 3851 2D elements combined with 4393 nodes (Fig. 5).
The 3D model with the global coordinate system (a) and finite element mesh of the analysed saw blades corresponding to the narrow-kerf blade (b) and the scraper saw blade (c) (drawing designed in AutoCad 2020 https://www.autodesk.com/products/autocad and Dlubal https://www.dlubal.com).
All teeth were modelled in both saw variants in the same way as the bodies. Similar shell elements were used, differing only by an element thickness of 1.4 mm or 2.9 mm, respectively. Simulated saw blades were fixed with linear support along their edges on both ends (Fig. 6a,b) to simulate the original attachment to the saw frame. The lower end was fully immobilized to prevent any translation or rotation (Fig. 6c,d). Different support was applied to the upper end, in which displacements in the X and Y directions were blocked. The release in the global direction Z was applied to allow the introduction of the FN force responsible for preloading the saw blades in this direction. The finite element method’s mesh for both saw blades was automatically generated by the software, using the following boundary meshing conditions: the target length of the elements = 2 mm, the maximum diagonal ratio = 1.8, and the maximum angle of tilt of a single quadrilateral element from the plane = 0.5°. The automatically generated mesh was adjusted to the geometry of the model, which greatly reduced the duration of computation.
Boundary conditions for the simulated saw blades: top support for the narrow-kerf (a) and scraper saw blade (b), the bottom support for the narrow-kerf (c) and scraper saw blade (d) (drawing designed in Dlubal https://www.dlubal.com).
Both saw blade models were preloaded by applying the force FN = 9450 N assigned to the upper edge of the saw blade in the longitudinal direction (Z). A stiff 1D element was implemented to achieve an even distribution of the load over the entire width of the free edge of each blade.
Loading configurations of modelled saw blades
Numerical analyses were carried out for each saw blade (Fig. 2) by implementing 78 variants of the loading configuration and corresponding cutting forces (Fc, Ff, Fp) as summarized in Table 6. Loads from individual forces were concentrated at one point on the cutting edge of the medial tooth of the saw blade. This corresponded to the middle of the cutting edge in the case of the narrow-kerf saw blade (Fig. 4b). Alternatively, the point of application of the forces was located at 1/4th of the cutting edge’s width when modelling the scraper saw blade (Fig. 4c).
Results and analysis of the sawing process simulation
Stiffness and stability of the saw blades
The static stiffness values of the narrow-kerf and the scrapper saw blades were determined for loading the saw with the thrust force Fp in the middle of the free length of the saw blade. Additionally, the blade was subjected to the normal tensile force FN = 9450 N. The characteristics of the elasticity of the saw blades linking the thrust force Fp to the strain q produced by this force in the direction of its action is shown in Fig. 746.
Linear relationships for the load in the analysed range of variability of the thrust force Fp were obtained in both models. Therefore, slope factors in the trend line equations can be considered as coefficients of the initial static stiffness k0. It corresponded to k0 = 19.4 N⋅mm−1 and k0 = 60.8 N⋅mm−1 for the narrow-kerf and the scrapper saw blades, respectively. It revealed that the static stiffness of the scraper saw was more than three times higher than that of the narrow-kerf saw blade.
Figure 8 illustrates the operational saw blade stiffnesses OSBS for both the narrow-kerf and scraper saw blades. OSBS is calculated as an apparent result of the feed force Ff. action. This force has a major impact on the stability of the saw blade and reduces the initial static stiffness coefficient k0 to the value of the operating stiffness coefficient k0w. The characteristics shown in Fig. 8 can be used to determine the critical feed forces at which the k0w drops to zero. The critical feed force is equal to Ff_crit = 493 N in the case of the narrow-kerf saw blade. However, the critical force is more than seven times higher in the case of scraper saw blade, reaching Ff_crit = 3640 N.
Computer simulations revealed that the effect of the feed force Ff on changes in the operating stiffness k0w is linear. It was also found that it is possible to determine values of the operating stiffness when the critical feed force Ff_crit is known. It follows the solution proposed by Timoshenko52 and can be expressed as in Eq. (6):
Additional analyses were carried out to determine the effect of the cutting force Fc on the stiffness value of both investigated saw blade types. The results of OSBS numerical simulations are shown in Fig. 9 evidencing that the cutting force Fc does not affect the stiffness value of the saw blade. It confirms previous analyses carried out by Orlowski68 and Prokofiev69.
Analysis of the (extreme) scraper saw blades behaviour during sawing of lamellae
Primary components of the tip total displacement for the saw blade tooth caused by the action of the thrust force Fp are presented in Fig. 10.
The transverse displacement of the saw blade under the action of the thrust force Fp, where: q0 is the displacement resulting from the deflection of the saw blade corresponding to the displacement under the action of the Fp force applied at point O; qs is the torsional displacement of the blade; h is the tooth height; b is the blade width; s is the blade thickness; y is the displacement of the pivotal point relative to the middle of blade O; αb is the saw blade torsion angle; AD and AD’ is the cross-sections of the layers being cut.
The actual pivotal point of the saw blade is located outside point O. It is shifted to O’, which is separated from point O by the distance y. The value of y can be determined from the relationship47 expressed in Eq. (7):
An understanding of the y value is indispensable for proper identification of torques and deflections, especially when cutting with loads applied asymmetrically to the saw blade teeth. It is a typical cutting configuration of the scraper saw that works with the material present only on one side of the blade. It can be assumed following the work40 that the ratio q0/qs = 2/5 when considering narrow-kerf saw blades with a width (b + h) < 50 mm.
The saw blade tooth under analysis is loaded during cutting (in addition to the thrust force Fp) with the feed force Ff applied to the saw blade at a distance e from point A that corresponds to e = St/4 (Fig. 10b). This tooth is in contact with the material along the main cutting edge, with the contact length equal to the width of the layer being cut St/2. The torque from the feed force Ff partially compensates an effect of the thrust force Fp action. It was noticed that the shift of the pivotal point was y = 9 mm in the case of the studied saw blade with b = 35 mm and h = 5 mm. The balance equation for the moments of the force relative to point O’ is therefore dependent on the feed force Ff = 212 N, as shown in Eq. 8:
The maximal thrust force that will not cause any saw blade displacement can be determined using Eq. (8) and corresponds to Fp = 4.88 N. Therefore, the theoretical track of the saw blade will deform when the thrust force increases over that value. It will decrease the dimensional accuracy for the lamellae being cut.
It was demonstrated37 that oak wood lamellae obtained from the outer positions in the frame sawing machine gang are thicker than the medial lamellae, despite the fact that the outer saws are thicker and thus stiffer. This is interpreted as a result of the asymmetric loads occurring on the scraper blades during the process of cutting the wood. An increase in the thickness of the outer lamella (by 0.2 mm for example) can be associated with the presence of natural heterogeneity in the raw material being sawn. The coefficient of working stiffness can be estimated here as in Eq. (9), following Timoshenko’s52 theorem (Eq. 6):
Consequently, the working stiffness coefficient is k0w = 57.24 N⋅mm−1, assuming the initial stiffness coefficient k0 = 60.78 N⋅mm−1 and the feed force Ff = 212 N. The value of the thrust force that will trigger a displacement of 0.2 mm is Fp = 0.2 k0w = 11.45 N. It should be noticed, however, that the contact of the main cutting edge with the workpiece is reduced as a consequence of the saw displacement by 0.2 mm by the same value. It simultaneously results in a proportional decrease of the feed force Ff. The width of the chip being cut drops to dimension St/2 – 0.2 = 1.25 mm, resulting in the feed force Ff = 182.76 N. The point of application of such altered feed force will also change and become e1 = 0.825 mm (Fig. 10c). The load torques M(Fp) and M(Ff) can be determined for this position of the feed force following Eqs. (10) and (11), respectively:
The moment from the thrust force M(Fp) is more than two times higher than that caused by the feed force M(Ff). Moreover, there are no additional external forces within the cutting system which could return the scraper saw blade to its starting position. It is assumed, therefore, that only variations within the structure of the wood being sawn can trigger this phenomenon.
The analysis of the scraper saw blade behaviour and computation of its stiffness coefficients made it possible to explain the processing inaccuracies as observed when re-sawing oak lamellae37. Furthermore, it explains why high values of the feed speed are not used in industrial practice, especially when manufacturing wooden elements requiring high dimensional accuracy. Even though majority of sawing machines are capable of high process velocities, an increase of the feed speed increases the variation in thickness that may exceed accepted tolerances. It is especially noticed for the outer lamellae in the saw set, resulting in unnecessary material loss and a rise in production costs. In the latter case, these excess layers must be removed in the subsequent process steps, such as circumferential planning and/or sanding.
Conclusions
The following conclusions can be drawn based on the results of the theoretical and finite element method analysis of the stiffness of the saw blades:
• The initial static stiffness of the saw blade has a linear course and is a function of the geometric dimensions of the saw blade and its preload or tensioning level.
• The scraper saws have an initial static stiffness that is three times higher than narrow-kerf saw blades when installed in the same gang.
• The feed force has a large effect on the stability of the saw blade and reduces the initial static stiffness of the saw blade to the operating stiffness. The loss of stability of the scraper saw blade can occur at the feed-per-tooth force exceeding Ff_crit = 3640 N. The corresponding critical force for the narrow-kerf saw blade is Ff_crit = 493 N.
• The calculation of the operating stiffness of saws as a function of the feed force can be performed using Timoshenko’s equations.
• The cutting force does not affect the value of the operating stiffness of the saw.
• The effect of asymmetric loads when sawing wood on scraper saw blades can cause severe sawing inaccuracies, particularly in the outer lamellae in the gang.
The simulation methodology developed in this research can be straightforwardly extended towards the determination of optimal geometry of other cutting tools, particularly focusing on kerf reduction. It may lead to more sustainable use of natural resources as well as an increase in economic gain for the wood processing industries.
References
Sandvik. Production, Use and Maintenance of Wood Bandsaw Blades. A Manual from Sandvik Steel. 336. (AB Sandvik Steel, 1999).
Steele, P. H., Wade, M. W., Bullard, S. H. & Araman, P. A. Relative kerf and sawing variation values for some hardwood sawing machines. For. Prod. J. 42(2), 33–39 (1992).
Bowyer, J. & Stockmann, V. E. Agricultural residues: An exciting bio-based raw material for the global panels industry. For. Prod. J. 51(1), 10–20 (2001).
Breinig, L., Broman, O., Brüchert, F. & Becker, G. Optimization potential for perception-oriented appearance classification by simulated sawing of computed tomography-scanned logs of Norway spruce. Wood Mat. Sci. Eng. 10(4), 319–334. https://doi.org/10.1080/17480272.2014.977944 (2015).
Nasir, V. & Cool, J. A review on wood machining: Characterization, optimization, and monitoring of the sawing process. Wood Mater. Sci. Eng. 15(1), 1–16. https://doi.org/10.1080/17480272.2018.1465465 (2020).
Barcik, Š. Experimental cutting on the log band saw. Holz als Roh-und Werkstoff 54, 153–156. https://doi.org/10.1007/s001070050157 (1996).
Okai, R. Influence of vibration coupling between bandsaw frame and feed-carriage system on sawdust spillage and surface quality of workpiece during sawing. Eur. J. Wood Wood Prod. 67, 189–195. https://doi.org/10.1007/s00107-009-0319-z (2009).
Eklund, U. Influencing factors on sawing accuracy in a bandsawmill. Holz als Roh- und Werkstoff 58, 102–106. https://doi.org/10.1007/s001070050394 (2000).
Brown, T. D. Lumber Size Control. Part 2: Size Analysis Considerations. Performance Excellence in the Wood Products Industry. Oregon State University, Extension Service, EM 8731, June. 1–27. (2000).
Lehmann, B. F. & Hutton, S. G. The mechanics of bandsaw cutting. Part II A simulation of the cutting behavior of bandsaws. Holz als Roh- und Werkstoff 55, 35–43. https://doi.org/10.1007/s001070050221 (1997).
Tanaka, C., Shiota, Y., Takahashi, A. & Nakamura, M. Experimental studies on band saw blade vibration. Wood Sci. Technol. 15, 145–159. https://doi.org/10.1007/BF00367860 (1981).
Wong, D. & Schajer, G. Factors controlling bandsaw tracking. Holz als Roh- und Werkstoff 60, 141–145. https://doi.org/10.1007/s00107-001-0269-6 (2002).
Albrecht, D. & Möhring, H.-C. Potentials for the optimization of sawing processes using the example of bandsawing machines. Proc. Manuf. 21, 567–574. https://doi.org/10.1016/j.promfg.2018.02.157 (2018).
Sandak, J. & Tanaka, C. On-line adaptive control of band-saw feed speed using a fuzzy-neural system. For. Prod. J. 53(6), 36–43 (2003).
Ulsoy, A. G., Mote, C. D. & Szymani, R. Principal developments in band saw vibration and stability research. Holz als Roh-und Werkstoff 36, 273–280. https://doi.org/10.1007/BF02610748 (1978).
Yang, B. & Mote, C. D. Vibration control of band saws: Theory and experiment. Wood Sci. Technol. 24, 355–373. https://doi.org/10.1007/BF00227056 (1990).
Lehmann, B. F. & Hutton, S. G. The mechanics of bandsaw cutting. Part I: Modelling the interactions between a bandsaw blade and the workpiece. Holz als Roh- und Werkstoff 54, 423–428 (1996).
Lister, P. F. & Schajer, G. S. The effectiveness of the light-gap method for indicating changes in bandsaw frequency and stiffness. Holz als Roh-und Werkstoff 51, 260–266. https://doi.org/10.1007/BF02629371 (1993).
Okai, R., Kimura, S. & Yokochi, H. Dynamic Characteristics of the Bandsaw 3. Effects of workpiece thickness and its position from the ground on self-excited vibration and washboarding during sawing. Mokuzai Gakkaishi 43(7), 551–557 (1997).
Orlowski, K. & Wasielewski, R. Study washboarding phenomenon in frame sawing machines. Holz Roh Werkst 64, 37–44. https://doi.org/10.1007/s00107-005-0037-0 (2006).
Gogu, G. Critical speeds of circular saw blades. Holz als Roh-und Werkstoff 46, 173–182. https://doi.org/10.1007/BF02619546 (1988).
Merhar, M., Gornik Bučar, D. & Pepelnjak, T. Dynamic behaviour analysis of a commercial roll-tensioned circular sawblade. BioResources 12(3), 5569–5582 (2017).
Orlowski, K., Sandak, J. & Tanaka, C. The critical rotational speed of circular saw: Simple measurement method and its practical implementations. J. Wood Sci. 53, 388–393. https://doi.org/10.1007/s10086-006-0873-5 (2007).
Stakhiev, Y. Today and tomorrow circular sawblades: Russian version. Holz als Roh- und Werkstoff 58, 229–240. https://doi.org/10.1007/s001070050417 (2000).
Cheng, W., Yokochi, H. & Kimura, S. Aerodynamic sound and self-excited vibration of circular saw with step thickness I: Comparison of dynamic characteristics between the common circular saw and the circular saw with step thickness. J. Wood Sci. 44, 177–185. https://doi.org/10.1007/BF00521960 (1998).
Mohammadpanah, A. & Hutton, S. G. Maximum operation speed of splined saws. Wood Mater. Sci. Eng. 11(3), 142–146. https://doi.org/10.1080/17480272.2015.1108998 (2016).
Mohammadpanah, A., Lehmann, B. & White, J. Development of a monitoring system for guided circular saws: An experimental investigation. Wood Mater. Sci. Eng. 14(2), 99–106. https://doi.org/10.1080/17480272.2017.1415970 (2019).
Nasir, V., Mohammadpanah, A. & Cool, J. The effect of rotation speed on the power consumption and cutting accuracy of guided circular saw: Experimental measurement and analysis of saw critical and flutter speeds. Wood Mater. Sci. Eng. 15(3), 140–146. https://doi.org/10.1080/17480272.2018.1508167 (2020).
Schajer, G. & Wang, S. Effect of workpiece interaction on circular saw cutting stability. Holz als Roh- und Werkstoff 59, 388–393. https://doi.org/10.1007/s001070100230 (2001).
Li, B., Zhang, Z., Li, W. & Peng, X. A numerical simulation on multi-spot pressure tensioning process of circular saw blade. J. Wood Sci. 61, 578–585. https://doi.org/10.1007/s10086-015-1508-5 (2015).
Orlowski, K.A. & Walichnowski, A. Analiza ekonomiczna produkcji warstw licowych podłóg klejonych warstwowo. (In Polish: Economic analysis of upper layer production of engineered floorings). Drewno 56(189), 115–125. https://doi.org/10.12841/wood.1644-3985.022.08 (2013).
Kujawinska, A., Diering, M., Rogalewicz. M., Zywicki, K. & Hetman, L. Soft modelling-based methodology of raw material waste estimation. Intelligent systems in production engineering and maintenance—ISPEM 2017. in The Advances in Intelligent Systems and Computing. Vol. 637. 407–417. (Book Series AISC, 2017).
Zywicki, K., Bartkowiak, T. & Kujawinska, A. Application of a simulation model to the prognosis of material loss in wood processing. PLoS ONE 16(2), e0246325. https://doi.org/10.1371/journal.pone.0246325 (2021).
Kujawinska, A., Rogalewicz, M., Diering, M. & Hamrol, A. Statistical approach to making decisions in manufacturing process of floorboard. in Recent Advances in Information Systems and Technologies. Vol. 3. 499–508. (Springer, 2017).
Kujawinska, A. et al. Methodology supporting the planning of machining allowances in the wood industry. in Proceedings SOCO 2017, ICEUTE 2017, CISIS 2017. International Joint Conference SOCO’17-CISIS’17-ICEUTE’17, September 6–8. 338–347. (Springer, 2018).
Brown, T. D. Quality Control in Lumber Manufacturing (Miller Freeman Publisher, 1982).
Orlowski, K. A., Sandak, J. & Chuchala, D. Thickness accuracy of sash gang sawing. BioResources 15(4), 9362–9374 (2020).
Park, J. K., Kwon, B. K., Park, J. H. & Kang, D.-J. Machine learning-based imaging system for surface defect inspection. Int. J. Precis. Eng. Manuf.-Green Technol. 3, 303–310. https://doi.org/10.1007/s40684-016-0039-x (2016).
Orlowski, K., Wasielewski, R. & Blacharski, W. Frictional group fastening effectiveness of mini gang saw blades in the frame sawing machine. Holz als Roh- und Werkstoff 59, 9–12. https://doi.org/10.1007/s001070050464 (2001).
Orlowski, K. Some approaches to the determination of saw blade stiffness. Drvna Industrija 54(4), 207–215 (2003).
Sandak, J., Orlowski, K., Negri, M. & Tanaka, C. Thickness monitoring of thin lamellae by optical measurement method. For. Prod. J. 56(3), 36–40 (2006).
Orlowski, K. A., Ochrymiuk, T., Atkins, A. & Chuchala, D. Application of fracture mechanics for energetic effects predictions while wood sawing. Wood Sci. Technol. 47, 949–963. https://doi.org/10.1007/s00226-013-0551-x (2013).
Orlowski, K. A., Ochrymiuk, T., Hlaskova, L., Chuchala, D. & Kopecky, Z. Revisiting the estimation of cutting power with different energetic methods while sawing soft and hard woods on the circular sawing machine: A Central European case. Wood Sci. Technol. 54, 457–477. https://doi.org/10.1007/s00226-020-01162-9 (2020).
Wasielewski, R. & Orlowski, K. Hybrid dynamically balanced saw frame drive. Holz als Roh- und Werkstoff 60(3), 202–206 (2002).
Bogdanov, F. A. & Ostroumov, I. P. Podgotovka i ekspluatacija ramnych pil. in Lesnaja Promyšlennost, Moskva. (1986).
Wrotny, L.T. Kinematyka i dynamika maszyn technologicznych i robotów przemysłowych. (In Polish: Kinematics and dynamics of technological machines and industrial robots). (Oficyna Wydawnicza Politechniki Warszawskiej, 1996).
Csanady, E. & Magoss, E. Mechanics of Wood Machining. (Springer).
Ivankin, I. I. Teoretičeskije issledovanija načalnoj žetskosti lentočnych pil. (In Russian: Theoretical studies of the initial stiffness of band saws). Lesnoj Žurnal. Izvestija Vysšych Učebnych Zavedenij 3, 115–122 (2000).
Pahlizch, G. & Puttkammer, K. Beurteilungskriterien für die Auslenkungen von Bandsägeblättern. Holz als Roh-und Werkstoff 32, 52–57. https://doi.org/10.1007/BF02607403 (1974).
Pahlitzch, G. & Puttkammer, K. Schnittversuche beim Bandsägen. Holz als Roh-und Werkstoff 33, 181–186. https://doi.org/10.1007/BF02614497 (1975).
Prokofiev, G.F. Intensifikacija pilenija drevesiny ramnymi i lentočnymi pilami. (In Russian: Intensification of sawing wood by frame and band saws). 1–240. (Lesnaja Promyslennost, 1990).
Timoshenko, S.P. & Gere, J.M. Teoria stateczności sprężystej. (in Polish: Theory of elastic stability) Wydawnictwo Arkady, 1963).
Barcík, Š, Očkajová, A., Svoreň, J. & Bahyl, V. The influence of temperature upon the natural static frequencies of saw blades. Holz als Roh- und Werkstoff 58, 191–195. https://doi.org/10.1007/s001070050412 (2000).
Böllinghaus, T. et al. Machining processes (part 7-3 of chapter: manufacturing engineering). in Springer Handbook of Mechanical Engineering (eds. Grote, K.-H., Antonsson, K. K.). 609–656. (Springer, 2009).
Melo, L. E. et al. Study of the physical properties of Corymbia citriodora wood for the prediction of specific cutting force. Sci. For. 44(111), 701–708. https://doi.org/10.18671/scifor.v44n111.16 (2016).
Orlicz, T. Obróbka drewna narzędziami tnącymi. [in Polish: Wood processing with cutting tools]. (Skrypty SGGW-AR w Warszawie, Wydawnictwo SGGW-AR, 1988).
McKenzie, W. Effects of bevelling the teeth of rip saws. Wood Sci. Technol. 34, 125–133. https://doi.org/10.1007/s002260000037 (2000).
ISO 3002-1. Basic Quantities in Cutting and Grinding—Part 1: Geometry of the Active Part of Cutting Tools—General Terms, Reference Systems, Tool and Working Angles, Chip Breakers. (International Organization for Standardization, 1982).
ISO 3002-2. Basic Quantities in Cutting and Grinding—Part 2: Geometry of the Active Part of Cutting Tools—General Conversion Formulae to Relate Tool and Working Angles. (International Organization for Standardization, 1982).
Blokhin, M. A., Podlesny, D. A. & Rodionov, O. A. Solving the problem of reducing the influence of lateral force on the saw blade stability. Lesnoy Z. (Russ. For. J.) 2, 118–128. https://doi.org/10.37482/0536-1036-2020-2-118-128 (2020).
Orlowski K.A. & Wierzbowski M. Fracture toughness and shear yield strength determination of steam kiln–dried wood. in Proceedings of ‘The Future of Quality Control for Wood & Wood Products’, 4–7th May 2010, Edinburgh. The Final Conference of COST Action E53. 584–591. (2010).
Orlowski, K. Materiałooszczędne i dokładne przecinanie drewna piłami (In Polish: Narrow-kerf and accurate sawing of wood). Monografie Nr 40. 1–146. (Politechnika Gdańska, 2003).
Larson, M. G. & Bengzon, F. The Finite Element Method: Theory, Implementation and Applications (Springer, 2013).
Zienkiewicz, O., Taylor, R. & Zhu, J. The Finite Element Method: Its Basis and Fundamentals. 7th edn. https://doi.org/10.1016/C2009-0-24909-9 (Elsevier, 2013).
Davis, J. R. ASM Specialty Handbook: Nickel, Cobalt, and Their Alloys 2013 (ASM International Handbook Committee, 2000).
ISO 4957. Tool Steels. (International Organization for Standardization, 2018).
Schöllhammer, D. & Fries, T. P. Reissner-Mindlin shell theory based on tangential differential calculus. Comput. Methods Appl. Mech. Eng. 352, 172–188. https://doi.org/10.1016/j.cma.2019.04.018 (2019).
Orlowski, K. Why Narrow-Kerf Technologies are Justifiable in Modern Sawmills? 291–295 (Annals of Warsaw Agricultural University, 2002).
Prokofiev, G. F., Tyurin, A. M., Kabakova, MYu. & Kovalenko, O. I. Determination of the initial stiffness of unstretched rolled strip saws. Izvestiâ Vysših Učebnyh Zavedenij Lesnoj Ž. (Russ. For. J.) 3, 143–150. https://doi.org/10.37482/0536-1036-2020-3-143-150 (2020).
Acknowledgements
The authors gratefully acknowledge the Ministry of Science and Higher Education, Poland, for funding the maintenance of scientific and research equipment—PRW15M frame saw (decision no. 21/E-359/SPUB/SP/2019). The authors gratefully acknowledge the financial support of these studies from Gdańsk University of Technology by the DEC-1/2020/IDUB/II.1 grant under the Hydrogenium Supporting Membership in International Networks—‘Excellence Initiative—Research University’ program. The authors would like to acknowledge the sawmill Łąccy—Kołczygłowy spółka z o.o. for its support of the experiment. The authors gratefully acknowledge the European Commission for funding the InnoRenew project (grant agreement #739574 under the Horizon2020 Widespread-2-Teaming program), the Republic of Slovenia (investment funding from the Republic of Slovenia and the European Regional Development Fund) and infrastructural ARRS program IO-0035. Part of this work was conducted during project CLICK DESIGN, “Delivering fingertip knowledge to enable service life performance specification of wood”, (No. 773324) supported under the umbrella of ERA-NET Cofund ForestValue by the Ministry of Education, Science and Sport of the Republic of Slovenia. ForestValue has received funding from the European Union’s Horizon 2020 research and innovation programme.
Author information
Authors and Affiliations
Contributions
K.O. and D.C. performed experimental cuttings and wrote the first draft of the manuscript text. K.O., D.C. and J.S. reviewed and updated theoretical basis for the model of wood cutting process. M.S., W.M. and W.W. designed and executed numerical simulations. All authors reviewed the manuscript and contributed to preparation of figures.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Orlowski, K.A., Chuchala, D., Szczepanski, M. et al. Lateral forces determine dimensional accuracy of the narrow-kerf sawing of wood. Sci Rep 12, 86 (2022). https://doi.org/10.1038/s41598-021-04129-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-04129-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.