Abstract
It is challenging to increase the sensitivity of a hydrogen sensor operating at room temperature due to weak sorption and tiny mass of hydrogen. In this work, an ultrasonic sensor is presented for detecting hydrogen, which is composed of a 128° YX-LiNbO3 substrate and a reduced graphene oxide (RGO) sensitive layer with a platinum catalyzer. By optimizing the depositing parameters of RGO and platinum, a considerably high sensitivity is achieved at room temperature. A frequency shift of 308.9 kHz is obtained in 100 ppm hydrogen mixed with argon, and a frequency shift of 24.4 kHz is obtained in 1000 ppm hydrogen mixed in synthetic air. It is demonstrated that in addition to strong sorption of the sensitive layer, the coaction of mass load and conductivity variation is key to high sensitivity of the sensor. By establishing the original conductivity of the sensitive layer within the “conductivity window” for enhancing electrical response, we improve the sensitivity of the ultrasonic sensor, which is available for detecting hydrogen with an extremely low concentration of 5 ppm.
Similar content being viewed by others
Introduction
Hydrogen (H2) is considered to be a clean and renewable energy source that is promising in various fields as energy battery, chemical production, medical, aerospace and etc. Due to flammability and explosibility, H2 must be strictly monitored in the future application. However, H2 is difficult to detect because of its colorlessness and odorlessness, and thus, to prevent danger induced by H2 leakage, sensors with high sensitivities for detecting early H2 leakage with trace concentrations are required1,2,3,4,5. The majority of H2 sensors work on the basis of sensitive layers for H2 sorption. The performances of these sensors are apt to be influenced by the operating temperature, and the sensitivities decrease remarkably with the decrease of temperature due to weak sorption and tiny mass of H2. Therefore, it is challenging to increase the sensitivity of a H2 sensor operating at room temperature.
Ultrasonic sensors, which are primarily composed of a piezoelectric substrate and a sensitive layer deposited on the substrate, are widely studied for gas sensing owing to distinct advantages of high sensitivities, low detection limits, small bulks, low power dissipation and high integration6. When the sensitive layer sorbs the targeted gas, the acoustic velocity and transmission loss of the ultrasonic wave transmitting in the sensor are changed, and by measuring the shift of the central frequency and/or insert loss of the sensor, the targeted gas can be detected. Because ultrasonic sensors work with high operating frequencies from several Mega to Giga hertz, the central frequency and transmission loss are extremely sensitive to the sorbed matters and the sensitivity increases with the operating frequency7.
To improve performance, ultrasonic sensors for detecting H2 were originally designed to work at high temperatures8, in which metallic oxides, as tungsten trioxide (WO3)9, indium oxide (InOx)10,11, tin dioxide (SnO2)12, were found to be efficient for H2 sensing. The ultrasonic sensors using sensitive layers based on metallic oxides exhibited high performance at high temperatures of 100–200 °C, in which frequency shifts from 100 kHz to over 700 kHz were obtained in H2 with a concentration of 1%9,10,11,12.
Resembling to other types of H2 sensors based on sorption mechanism, the sensitivities of ultrasonic sensors decrease at room temperature because of weak reaction between H2 and sensitive layers13. Nevertheless, in spite of high sensitivities, heating a H2 sensor is an unfavorable way due to explosion danger and energy wastage. Therefore, high-sensitivity hydrogen sensors working at room temperature were given high consideration in the research of ultrasonic sensors. Firstly, H2 sensors working at room temperature were tested in nitrogen14,15,16, and a sensitivity of 67 kHz towards 100 ppm H2 mixed in N2 was obtained based on organometallic conjugated polymers, Pd–DEBP and Pd/Pd–DEBP16. It was more challenging to obtain a high sensitivity when a H2 sensor works in air because the oxygen in air reacts with H2 and reduces the H2 molecules adsorbed by the sensitive layer17,18,19. Layered surface acoustic waves, which are apt to be influenced by the mass load induced by the adsorbed gas, were adopted to increase the sensitivities, in which frequency shifts of 27.9 kHz and 34.6 kHz towards 1% H2 mixed in air were obtained at room temperature with sensitive layers of ZnO nanorods and CSA synthesized polyaniline nanofibers, respectively20,21. Additionally, Rayleigh wave sensors based on Pt modified InOx and WO3 sensitive layers exhibited sensitivities of 20 kHz and 72 kHz in 1% H222,23. However, it is difficult to further increase the sensitivity of an ultrasonic H2 sensor operating in air and at room temperature.
Recently, a new type of material, graphene, attracted great attention due to its unique characteristics24,25,26. It was shown that graphene is also a good sensitive material for H2 sensing owing to its large specific surface area, high carrier mobility and low Johnson noise. On the one hand, good electrical properties of graphene were given high consideration and the majority of H2 sensors using graphene-like sensitive layers worked on account of the variation of conductivity induced by adsorbed H25,27,28,29,30,31. On the other hand, ultrasonic H2 sensors using graphene-like sensitive layers were also presented32,33,34. By adopting Pd as a catalyzer, the sensitivity was increased from 5.8 kHz to 30 kHz towards 1% H2 mixed in air at room temperature36. It can be observed that these ultrasonic H2 sensors using graphene-like sensitive layers exhibited comparative sensitivities to their counterparts with the sensitive layers based on metallic oxides and other nano films20,21,22,23.
In this work, we create an ultrasonic H2 sensor composed of a 128° YX-LiNbO3 piezoelectric substrate and a graphene-like sensitive layer modified by a Pt catalyzer. The sensitive layer on the basis of the reduced graphene oxide (RGO) is characterized by X-ray diffraction (XRD), Fourier transform infrared spectroscopy (FTIR) and scanning electron microscope (SEM), which demonstrates high performance in H2 adsorption. Additionally, owing to the coaction of mass load and conductivity variation induced by the adsorbed H2, we achieve an extremely high sensitivity at room temperature by accurately controlling the original conductivity of the RGO/Pt composite sensitive layer. The sensor exhibits a frequency shift of 302.9 kHz towards 100 ppm H2 mixed in argon, and in the environment of air, a frequency shift of 24.4 kHz is obtained in 1000 ppm H2. Our sensor based on a graphene-like sensitive layer can be available to detect H2 with extremely low concentrations below 5 ppm.
Results
Fabrication and characterization of the sensitive layer
An oxidation–reduction method is adopted to create graphene-like sensitive layer on the surface of a 128° YX-LiNbO3 piezoelectric substrate. First, graphene oxide (GO) is prepared using modified Hummers method24, in which graphite powder is oxidized with strong oxidants and oxygen-containing functional groups (OCFGs) are induced into the layered structure of graphite. Then, the layered structure is exfoliated using an ultrasonic cleaner and an ultrasonic cell pulverizer. To remove the OCFGs, hydrothermal reduction method is adopted to reduce the GO25, and thus, we obtain a solution of reduced graphene oxide. Finally, we drop the solution on the surface of a 128° YX-LiNbO3 substrate with a pair of interdigital transducers and dry it at room temperature. In our experiments, this sedimentation method is more efficient than spin coating or pulling method because the concentration of the RGO solution is low. Using this method, we can rapidly grow sensitive layers on multiple samples. Additionally, it was shown that pure graphene cannot effectively adsorb H232, and catalyzers are required to enhance the reaction between the graphene-like sensitive layer and H2. In our experiments, we deposit Pt as a catalyzer on the RGO layer via magnetron sputtering method (see “Methods” for details).
Figure 1a shows the images of XRD of graphite and GO obtained by the processes of oxidation and exfoliation. It can be observed that graphite exhibits a high and sharp characteristic diffraction peak at 26.5°, which indicates the 002 crystal plane of graphite. In the XRD image of GO, the diffraction peak shifts to 10.6°, and the peak is much lower and wider than the diffraction peak obtained in graphite. Because the OCFGs increase the distance between the crystal planes, the diffraction peak of GO is shifted to a smaller angle. Furthermore, the OCFGs inserted between layers break the ordered structure of graphite, which results in a lower and wider diffraction peak in GO.
Evaluation of the sensitive layer. (a) XRD images for graphite and GO. (b) FTIR spectra for graphite, GO, RGO-120 °C and RGO-180 °C. (c–e) SEM images for (c) GO, (d) RGO-120 °C and (e) RGO-180 °C. (f–i) SEM images with different resolutions for sensitive layers created on LiNbO3 substrates using (f,g) RGO-120 °C and (h,i) RGO-180 °C.
To optimize the RGO obtained by hydrothermal reduction method, we adopted two reaction temperatures, 120 °C and 180 °C, in the reduction. The images of FTIR for different samples, graphite, GO, RGO-120 °C and RGO-180 °C are shown in Fig. 1b. The FTIR spectrum for graphite shows three absorption peaks at 3424 cm−1, 1622 cm−1 and 1384 cm−1, which are induced by the absorbed water molecules in graphite. The absorption peaks arising at 3424 cm−1 are related to the stretching vibration of –OH in a water molecule, while the weak peaks at 1384 cm−1 and 1622 cm−1 originate from the flexural vibration of –OH. For GO, it is observed that the three absorption peaks induced by water molecules (3424 cm−1, 1622 cm−1 and 1384 cm−1) are higher than those obtained in graphite, which demonstrates that GO stores more water than graphite does35. Furthermore, different absorption peaks can be observed in the FTIR spectrum for GO, which are induced by the stretching vibration of distinct OCFGs like C=O (1734 cm−1), C–O–C (1224 cm−1), and C–O (1105 cm−1 or 1053 cm−1). Thus, it is observed that abundant OCFGs are created in the process of oxidation, which enhances hydrophily of GO.
Comparing the FTIR spectra of RGO and GO indicates that the absorption peaks induced by water molecules and OCFGs are weakened in hydrothermal reduction. Furthermore, the absorption peaks at 1224 cm−1, 1105 cm−1 and 1053 cm−1 even vanish in RGO-180 °C. Thus, it is demonstrated that the OCFGs in GO are removed in the reduction process, and the RGO obtained at a higher reduction temperature possesses less OCFGs. Furthermore, in the FTIR spectra of RGO, an absorption peak arises at 1575 cm−1, which cannot be observed in the spectrum of GO. This peak is created by C=C bonds in RGO, demonstrating that the broken π conjugated structure is recovered in the hydrothermal reduction. Additionally, in RGO-180 °C, the absorption peak at 1575 cm−1 is much higher than that in RGO-120 °C, indicating better recovery of the π conjugated structure in RGO-180 °C.
To explore the micro-structures of the sensitive layers, the SEM images of different samples are shown in Fig. 1c–i. Figure 1c–e exhibit the SEM images for GO, RGO-120 °C and RGO-180 °C. Compared to RGO samples, the GO sample possesses larger grain sizes and a small number of folds. The RGO samples exhibit agglomerate because the reduction of GO results in the heterogeneity and increases the porosity as a result of exfoliation and rearrangement of layers36,37,38. Additionally, it was shown that a higher degree of reduction of GO resulted in smaller grains, more folds and larger specific surface areas39. Thus, comparing Fig. 1f–i shows that the grains of the sensitive layer obtained with the solution of RGO-120 °C are much longer than that created using the solution of RGO-180 °C. The sensitive layer of RGO-180 °C exhibits smaller grain sizes and a large number of folds on the surface, which remarkably increase the porosity and specific surface area, providing abundant adsorption points for Pt and H2 molecules. Owing to this feature, the RGO-180 °C sensitive layer exhibits great potentials as a sensitive material for H2 sensing.
H2 sensing
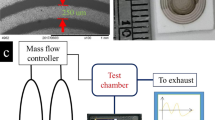
Figure 2a shows our experimental system for H2 sensing. To test the performance of our sensor for detecting H2 with low concentrations, we use two gas bottles, one contains H2 with a concentration of 1000 ppm mixed with a background gas, argon or synthetic air, and the other contains the background gas. The H2 with the concentration of 1000 ppm and the background gas are mixed in a gas distributor and the concentration of the H2 is lowered further. Then, we have H2 with the concentrations from 5 to 1000 ppm. The mixed gas is introduced into a humidification bottle to adjust the humidity. Finally, the gas is tested using our H2 sensor in a closed box. Multiple parameters, the central frequency, insert loss and surface electric conductivity, of the sensor are measured by a network analyzer and a 4-probes resistivity measurement system.
Figure 2b,c show the frequency responses of the sample before and after coating the sensitive layer, respectively. The original central frequency and insert loss are 124 MHz and 10.80 dB, which are shifted to 123.75 MHz and 34.05 dB by depositing the RGO/Pt sensitive layer.
H2 sensing experiments are first conducted in argon and the dynamic responses of the sensor are shown in Fig. 3. As shown in Fig. 3a,b, by introducing 100 ppm H2 mixed with dry argon, we obtain a frequency shift of 303.5 kHz within 10 min. By increasing the relative humidity of the argon to 60%, we obtain a frequency shift of 308.9 kHz. Furthermore, after 10 min, the central frequency of the sensor continues to decrease rapidly, which demonstrates dramatic H2 adsorbability of the sensitive layer. Thus, the sensor exhibits an extremely high sensitivity to H2 with a low concentration. Due to the strong chemical adsorption of H2 in the RGO/Pt sensitive layer, the central frequency of the sensor returns slowly after we stop the mixed gas flow and introduce pure argon. It can be observed in Fig. 3b that the recovery of the sensor is better in an environment with a high humidity.
Frequency shift of the sensor towards H2. (a,b) Shifts of the central frequency of the sensor to 100 ppm H2 mixed in (a) dry argon and (b) argon with a relative humidity of 60%. (c,d) Shifts of the central frequency of the sensor to 1000 ppm H2 mixed in (c) dry air and (d) air with a relative humidity of 60%. (e) Shifts of the central frequencies of the sensors with RGO-120 °C and RGO-180 °C sensitive layers to 100 ppm H2 mixed in argon with a relative humidity of 60%.
Furthermore, we measure the frequency shift of the sensor to H2 mixed in synthetic air. As shown in Fig. 3c,d, the sensor exhibits a frequency shift of 24.1 kHz to 1000 ppm H2 in dry air, and by increasing the relative humidity to 60%, we obtain a frequency shift of 24.4 kHz. Although the sensitivity of the sensor working in air is lower than that of the sensor operating in argon, our sensor is much more sensitive than those using traditional sensitive layers20,21,22,23. Resembling to the experiments obtained in argon, in an environment with a high humidity, the sensor recovers faster when H2 is exhausted. The performance of the H2 sensor is compared to those of the sensors adopting traditional sensitive layers in Table 1.
In Fig. 3e, we compare the performances of the sensitive layers fabricated using RGO-120 °C and RGO-180 °C. It is demonstrated that a much higher sensitivity is achieved with the sensitive layer fabricated using RGO-180 °C with a high reduction degree. The high performance of RGO-180 °C is determined by the optimized micro-structure, small grain sizes, high porosity and numerous folds, resulting in a large surface area, which is exhibited in the FTIR and SEM images shown in Fig. 2.
Discussion
In addition to the high performance of the sensitive layer created using RGO-180 °C, the high sensitivity of our sensor is related to a critical sensing mechanism of ultrasonic gas sensors. Generally, mass load induced by the sorbed matter was considered to be the major factor causing central frequency shift, and thus, the mass sensitivity was defined to be \({S_m} = \mathop {\lim }\limits_{\Delta m \to 0} {{\left( {{{\Delta V} \mathord{\left/ {\vphantom {{\Delta V} V}} \right. \kern-\nulldelimiterspace} V}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\Delta V} \mathord{\left/ {\vphantom {{\Delta V} V}} \right. \kern-\nulldelimiterspace} V}} \right)} {\Delta m}}} \right. \kern-\nulldelimiterspace} {\Delta m}}\)40,41, where \(\Delta m\) is the tiny mass of the sorbed matter and \(\Delta V\) is the mass-induced variation of the velocity V of the ultrasonic wave transmitting in the sensor. However, it was presented that the central frequency of an ultrasonic sensor is also influenced by the variation of the surface conductivity induced by the sorbed matter, and the conductivity sensitivity was thus defined to be \({S_c} = \mathop {\lim }\limits_{\Delta \sigma \to 0} {{\left( {{{\Delta V} \mathord{\left/ {\vphantom {{\Delta V} V}} \right. \kern-\nulldelimiterspace} V}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\Delta V} \mathord{\left/ {\vphantom {{\Delta V} V}} \right. \kern-\nulldelimiterspace} V}} \right)} {\Delta \sigma }}} \right. \kern-\nulldelimiterspace} {\Delta \sigma }}\)42,43,44, indicating the relative velocity variation \({{\Delta V} \mathord{\left/ {\vphantom {{\Delta V} V}} \right. \kern-\nulldelimiterspace} V}\) induced by the conductivity shift \(\Delta \sigma\). Especially, in sensors for detecting a light gas, like H2, the frequency shift induced by the variation of surface conductivity even overwhelms that caused by the mass load, resulting in an abnormal response that the central frequency increased after the sensor sorbed the targeted gas42,43,44,45.
Therefore, to achieve a high sensitivity in an ultrasonic H2 sensor, several conditions must be satisfied. First, the sensitive layer possesses strong sorption to H2. Second, the central frequency of the sensor is shifted to the same direction by the mass load and conductivity variation. Since a mass load always decreases the central frequency of a sensor, the conductivity should be increased by the sorbed gas to decrease the central frequency. The abovementioned two conditions can be satisfied using the RGO/Pt sensitive layer because it was proven that the conductivity of a graphene-like film was increased by H228,30. Finally, because the central frequency of in an ultrasonic H2 sensor is primarily influenced by the variation of the conductivity, the electric response of the sensor must be enhanced to achieve a high sensitivity. Noting that a strong electric response, creating a large frequency shift, can merely be achieved within a narrow conductivity window42,43,44. Thus, we strictly control the initial conductivity of our RGO/Pt sensitive layer in the sensor. The relation between the velocity of the surface acoustic wave and the conductivity of the sensitive layer is calculated using transfer matrix method, which is shown in Fig. 4a,b. Figure 4a shows that in our sensor based on a LiNbO3 piezoelectric substrate, the conductivity window for a high conductivity sensitivity is centered at \({\sigma_m} = 1.6\;\mu S\), with a width from \({\sigma^- } = {10^{ - 1}}{\sigma_m}\) to \({\sigma^+ } = {10^{0.5}}{\sigma_m}\). Furthermore, as shown in Fig. 4b, in the left part of the window, the slope of the curve is larger, indicating a higher conductivity sensitivity. Therefore, the initial conductivity of our RGO/Pt sensitive layer is established at \({\sigma_0} = 0.77\;\mu S\), which is located within the window, as shown in Fig. 4b. In this case, a large frequency shift can be induced by the variation of the surface conductivity in the sensor, which adds to the frequency shift originating from the mass load of the adsorbed H2. This coaction of two mechanisms, mass load and conductivity variation, can be adopted in any other ultrasonic sensors for detecting matters with trace concentrations to increase the sensitivities.
Conductivity variation of the sensor towards H2. (a,b) The velocity V of the Rayleigh wave transmitting in the sensor versus the normalized surface conductivity \({\sigma \mathord{\left/ {\vphantom {\sigma {\sigma_m}}} \right. \kern-\nulldelimiterspace} {\sigma_m}}\). It is observed that the Rayleigh wave velocity varies rapidly with the conductivity in a narrow conductivity window, indicating a high conductivity sensitivity. (c,d) Responses of the conductivity of the sensor to 100 ppm H2 mixed in (c) dry argon and (d) argon with a relative humidity of 60%. (e,f) Responses of the conductivity of the sensor to 1000 ppm H2 mixed in (e) dry air and (f) air with a relative humidity of 60%.
Moreover, to observe electric turbulence induced by the adsorbed H2, we measure the conductivity of the RGO/Pt sensitivity layer using a RTS-8 type 4-probes resistivity measurement system. Figure 4c–f show the relative variation of the surface conductivity of the sensor \({C_r} = {{\sigma_A} \mathord{\left/ {\vphantom {{\sigma_A} {\sigma_0}}} \right. \kern-\nulldelimiterspace} {\sigma_0}}\), which is defined by the conductivity before (\({\sigma_0}\)) and after (\({\sigma_A}\)) exposure to H2. It can be observed that when H2 is introduced into the test box, the conductivity of the sensitive layer increases from its original value \({\sigma_0} = 0.77\;{\mu S}\), resulting in \({\sigma_A} > {\sigma_0}\) and \({C_r} > 1\). It was presented that a increase of the surface conductivity results in a decrease of the central frequency of an ultrasonic sensor42. Thus, the central frequency of our sensor is decreased by both the mass load and variation of surface conductivity, which leads to an extremely high sensitivity.
As shown in Fig. 4c,d, the conductivity of the sample is shifted to 4.63 and 4.21 times after exposure in 100 ppm H2 mixed in dry argon and argon with a humidity of 60%, respectively. For a recovery process of 10 min, \({C_A}\) returns to \(1.52{C_0}\) in dry argon and to \(1.34{C_0}\) in wet argon, which indicates a better recovery in a humid environment. Furthermore, as shown in Fig. 4e,f, in the background gas of air, we obtain \({C_r} = 1.72\) and 1.31 in 1000 ppm H2 mixed in dry and wet air, respectively, which exhibits that the conductivity variation is smaller in air than that obtained in argon. Meanwhile, comparing Fig. 4e,f shows that the recovery of the sensor in wet air is faster and better than that in dry air. Generally, as shown Figs. 3 and 4, the influences of the background gas and humidity on the conductivity variation resemble to their influences on the frequency shift, which demonstrates the importance of electric turbulence in the response of our H2 sensor.
The performances of the sensor in different background gases and humidity conditions can be explained on the basis of the sensing mechanism. As shown in Fig. 5a, in the adsorption process, H2 molecule is dissociated on the sensitive layer on the basis of competing mechanisms28,29, physisorption in which H2 is bounded on the surface of Pt by weak van der Waals forces, and chemisorption in which H2 enters the lattices of Pt, creating platinum hydride Pt/H and changing the work function of Pt28. This process is determined by the sticking coefficient of the platinum catalyst for H2 adsorption46. Additionally, H2 atoms also diffuse through the Pt thin layer30, and the concentration of free carriers in RGO will increase, thus improving the conductivity of RGO/Pt sensitive layer33.
As indicated in Fig. 5c, with the presence of oxygen, the dissociated H2 atoms react with oxygen and form water34,40. Then, the concentration of H2 bounded by the sensitive layer decreases. Moreover, it was found that water decreases the conductivity of the RGO/Pt layer47. Thus, the sensor exhibits a lower sensitivity in air than that in argon.
In the desorption section shown in Fig. 5b, when H2 is exhausted, desorption automatically happens for physically adsorbed H2 atoms, while the chemically bounded H2 cannot be released easily, and thus, the sensor do not return to the original state. Nevertheless, in wet air, as shown in Fig. 5d, the bounded H2 atoms react with oxygen in air, creating water molecules. In a high humidity condition, numerous water molecules stay on the surface of the sensitive layer after the desorption of H2, further decreasing the surface conductivity, which improves the recovery of the sensor.
Finally, we use our sensor to detect H2 with different concentrations from 5 to 100 ppm mixed in argon. To speed up the recovery process, we inlet wet air into the testing box in the desorption section. The dynamic response of the sensor to H2 with different concentrations is shown in Fig. 6a. The sensor exhibits a frequency shift of 8.7 kHz towards H2 with a concentration of 5 ppm, which demonstrates that the sensor is efficient for detecting H2 with an extremely low concentration. Moreover, by introducing wet air in the recovery section, the central frequency of the sensor rapidly return to the original value. It can be observed that the sensor responses swiftly to H2 with low concentrations. Additionally, we measure the response of our sensor to five cycles of H2 flow with a concentration of 100 ppm. As shown in Fig. 6b, the sensor can stably response and recover in the repeated progresses. Furthermore, the insert loss of the sensor is also measured. The frequency shift and insert loss variation measured in H2 with different concentrations are shown in Fig. 6c which show similar tendencies. Finally, we use our sensor to detect ammonia gas (NH3) with a concentration of 100 ppm mixed in argon with a relative humidity of 60%. As shown in Fig. 6d, it can be seen that the central frequency of the sensor decreases by 140.97 kHz in 10 min, which is lower than the frequency shift to H2. Moreover, it is observed that in NH3, the frequency of the sensor marginally changes after 5 min, while in H2, the frequency continues to decrease after 10 min, which demonstrates that our sensor is more sensitive to H2 than to NH3.
Response of the sensor to H2 with different concentrations and NH3. (a) Dynamic responses of the sensor to H2 with different concentrations mixed in argon. (b) Dynamic responses of the sensor to five cycles of H2 of 100 ppm mixed in argon. To speed up the recovery process, we introduce wet air into the text box to exhaust H2 in the experiments. (c) The frequency shift and loss variation versus the concentration of H2. (d) The frequency shift of the sensor to 100 ppm NH3 mixed in argon with a relative humidity of 60%.
In conclusion, we present an ultrasonic H2 sensor on the basis of a LiNbO3 piezoelectric waveguide and a RGO/Pt sensitive layer. RGO solution is prepared using hydrothermal reduction method, and a sedimentation method is adopted to efficiently create multiple samples of the H2 sensors. The images of XRD, FTIR and SEM exhibit that the sensitive layer possesses small grains, high porosities and large specific surface areas, which provide strong adsorbability of H2. In the experiments of H2 sensing, our sensor exhibits an extremely high sensitivity, which is 308.9 kHz towards 100 ppm H2 mixed in argon and 24.1 kHz towards 1000 ppm H2 mixed in air. In addition to the high performance of the RGO/Pt sensitive layer in H2 adsorption, the high sensitivity is primarily achieved owing to the coaction of the mass load and conductivity variation induced by the adsorbed H2. By accurately controlling the initial surface conductivity within the window for strong electric response, the conductivity variation greatly decreases the central frequency, which adds to the frequency shift induced by the mass load and considerably increases the sensitivity of the sensor. Additionally, it is found that oxygen and water molecules speed up the recovery process of the sensor. Thus, our sensor swiftly responses to trace concentrations of H2 and the sensor can be available to detect H2 with a low concentration below 5 ppm. Furthermore, the synergistic effect of two mechanisms, mass load and conductivity variation, adopted in this H2 sensor can be applied in any other ultrasonic sensors for enhancing the performance in detection of matters with trace concentrations.
Methods
RGO preparation
First, graphite powder (325 mesh) and sodium nitrate are stirred into refrigerated concentrated sulfuric acid in an ice bath. Then, potassium permanganate is added into the suspension, which continues to be stirred in the ice bath. The temperature of the suspension is increased to 35 °C and maintained for 30 min. Deionized water is added into the suspension and the temperature increases to over 90 °C. The mixture is kept in a water bath at a temperature of 90 °C for 20 min. The suspension is then diluted with warm deionized water and treated using hydrogen peroxide to eliminate the residual potassium permanganate. The treated suspension is filtered and the filter cake is washed in a centrifuge with hydrochloric acid (4%) and deionized water until the supernatant becomes neutral, and we obtain a suspension of GO. The suspension is dialyzed for two days in a dialysis bag with a molecular weight cut-off of 8000–14,000 and the remained solid is sufficiently dried at 50 °C in a vacuum drying oven. Then, GO sheets are obtained, which are grinded into powder in a agate mortar. The powder is added into deionized water and the suspension is exfoliated in an ultrasonic cleaner for 30 min and in an ultrasonic cell disruptor for 30 min under the condition of ice bath. Next, the exfoliated GO is deoxidized using hydrothermal reduction method. The GO solution is diluted to 0.2 mg/ml and transferred to an autoclave. The solution is heated at 180 °C for 6 h, and then we obtain a solution of RGO. Additionally, to study influence of the reduction degree on the performance of the RGO, we conducted hydrothermal reduction at a different reaction temperature of 120 °C.
Sensitive layer deposition
First, interdigital transducers with a period width of 32 μm is created on a LiNbO3 substrate with lithographic technology. Then, we use a sedimentation method to deposit RGO sensitive layer on the surface of the LiNbO3 substrate. The concentration of the solution is strictly controlled. Generally, using a solution with a high concentration, the deposited sensitive layer is thicker and smoother, while a thick sensitive layer increases the loss of the sensor. Therefore, we dilute the RGO solution to \({0}{\text{.175}}\;{{{\text{mg}}} \mathord{\left/ {\vphantom {{{\text{mg}}} {{\text{ml}}}}} \right. \kern-\nulldelimiterspace} {{\text{ml}}}}\) and drop the solution (120 μl) on the LiNbO3 substrate. The sample is dried for over 12 h at room temperature, and thus, a RGO sensitive layer is achieved. Finally, magnetron sputtering method is used to grow Pt on the surface of the sample. This process is critical to high sensitivity of our sensor. Pt is used as a catalyzer, and moreover, the conductivity of the sensitive layer is also influenced by the Pt layer. We use a sputtering power of 15 W and a sputtering time of 3 s. As a result, the conductivity of our sensitive layer is established to be \(\sigma = 0.77 \mu S\), which accurately locates within the narrow window for a high conductivity sensitivity.
References
Sun, Y. G. & Wang, H. H. High-performance, flexible hydrogen sensors that use carbon nanotubes decorated with palladium nanoparticles. Adv. Mater. 19, 2818–2823 (2007).
Korotcenkov, G., Do Han, S. & Stetter, J. R. Review of electrochemical hydrogen sensors. Chem. Rev. 109, 1402–1433 (2010).
Nasir, M. E., Dickson, W., Wurtz, G. A. & Zayats, A. V. Hydrogen detected by the naked eye: Optical hydrogen gas sensors based on Core/Shell plasmonic nanorod metamaterials. Adv. Mater. 26, 3532–3537 (2014).
Boelsma, C. et al. Hafnium—an optical hydrogen sensor spanning six orders in pressure. Nat. Commun. 8, 15718 (2017).
Anand, K., Singh, O., Singh, M. P., Kaur, J. & Singh, R. C. Hydrogen sensor based on graphene/ZnO nanocomposite. Sens. Actuators B. 195, 409–415 (2014).
Caliendo, C. et al. Advances in SAW-based gas sensors. Smart Mater. Struct. 6, 689–699 (1997).
Seidel, W. & Hesjedal, T. Multimode and multifrequency gigahertz surface acoustic wave sensors. Appl. Phys. Lett. 84, 1407–1409 (2004).
Jakubik, W. P., Urbanczyk, M. W., Kochowski, S. & Bodzenta, J. Bilayer structure for hydrogen detection in a surface acoustic wave sensor system. Sens. Actuators, B. 82, 265–271 (2002).
Ippolito, S. J., Kandasamy, S., Kalantar-Zadeh, K. & Wlodarski, W. Layered SAW hydrogen sensor with modified tungsten trioxide selective layer. Sens. Actuators, B. 108, 553–557 (2005).
Ippolito, S. J. et al. Highly sensitive layered ZnO/LiNbO3 SAW device with InOx selective layer for NO2 and H2 gas sensing. Sens. Actuators, B. 111, 207–212 (2005).
Fechete, A. C. et al. SAW-based gas sensors with RF sputtered InOx and PECVD SiNx films: Response to H2 and O3 gases. Sens. Actuators, B. 118, 362–367 (2006).
Yang, L., Yin, C. B., Zhang, Z. L., Zhou, J. J. & Xu, H. H. The investigation of hydrogen gas sensing properties of SAW gas sensor based on palladium surface modified SnO2 thin film. Mater. Sci. Semicond. Process. 60, 16–28 (2017).
Arsat, R., Yu, X. F., Li, Y. X., Wlodarski, W. & Kalantar-Zadeh, K. Hydrogen gas sensor based on highly ordered polyaniline nanofibers. Sens. Actuators, B. 137, 529–532 (2009).
Caliendo, C., D’Amico, A., Verardi, P. & Verona, E. Presented at ultrasonics symposium surface acoustic wave H2 sensor on silicon substrate. Chicago, IL, USA, (1988).
Huang, F. C., Chen, Y. Y. & Wu, T. T. A room temperature surface acoustic wave hydrogen sensor with Pt coated ZnO nanorods. Nanotechnology. 20, 65501 (2009).
Caliendo, C. et al. Nanostructured organometallic polymer and palladium/polymer hybrid: Surface investigation and sensitivity to relative humidity and hydrogen in surface acoustic wave sensors. Nanotechnology. 18, 125504 (2007).
Jakubik, W. P. & Urbanczyk, M. W. SAW hydrogen sensor with a bilayer structure based on interaction speed. Sens. Actuators, B. 106, 602–608 (2005).
Sadek, A. Z. et al. Polyaniline nanofiber based surface acoustic wave gas sensors—effect of nanofiber diameter on H2 response. IEEE Sens. J. 7, 213–218 (2007).
Sadek, A. Z., Wiodarski, W., Shin, K., Kaner, R. B. & Kalantar-Zadeh, K. A polyaniline/WO3 nanofiber composite-based ZnO/64◦ YX LiNbO3 SAW hydrogen gas sensor. Synth. Met. 158, 29–32 (2008).
Wang, Y. et al. Love wave hydrogen sensors based on ZnO nanorod film/36°YX-LiTaO3 substrate structures operated at room temperature. Sens. Actuators, B. 158, 97–103 (2011).
Atashbar, M. Z. et al. Layered SAW gas sensor based on CSA synthesized polyaniline nanofiber on AlN on 64° YX LiNbO3 for H2 sensing. Sens. Actuators, B. 138, 85–89 (2009).
Wang, C. et al. Highly sensitive Rayleigh wave hydrogen sensors with WO3 sensing layers at room temperature. Chin. Phys. Lett. 28, 110701 (2011).
Wang, C., Wang, Y., Zhang, S. Y., Fan, L. & Shui, X. J. Characteristics of SAW hydrogen sensors based on InOx/128°YX-LiNbO3 structures at room temperature. Sens. Actuators, B. 173, 710–715 (2012).
Geim, A. Graphene: Status and prospects. Science 324, 1530–1534 (2009).
Park, S. & Ruoff, R. S. Chemical methods for the production of graphenes. Nat. Nanotech. 4, 217–224 (2009).
Balandin, A. A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 10, 569–581 (2011).
Schedin, F. et al. Detection of individual gas molecules adsorbed on graphene. Nat. Mater. 6, 652–655 (2007).
Kaniyoor, A., Imran, J. R., Arockiadoss, T. & Ramaprabhu, S. Nanostructured Pt decorated graphene and multi walled carbon nanotube based room temperature hydrogen gas sensor. Nanoscale. 1, 382–386 (2009).
Johnson, J. L., Behnam, A., Pearton, S. J. & Ural, A. Hydrogen sensing using Pd-functionalized multi-layer graphene nanoribbon networks. Adv. Mater. 22, 4877–4880 (2010).
Chu, B. H. et al. Effect of coated platinum thickness on hydrogen detection sensitivity of graphene-based sensors. Electrochem. Sol. St. Lett. 14, 43–45 (2011).
Min, G. C. et al. Flexible hydrogen sensors using graphene with palladium nanoparticle decoration. Sens. Actuators, B. 169, 387–392 (2012).
Arsat, R., Breedon, M., Shafiei, M., Kalantar-zadeh, K. & Wlodarski, W. presented at ICSENS 2008 Graphene-like nano-Sheets/36° LiTaO3 surface acoustic wave hydrogen gas sensor, Lecce, Italy, Dec. 188–191 (2008).
Arsat, R. et al. Graphene-like nano-sheets for surface acoustic wave gas sensor applications. Chem. Phys. Lett. 467, 344–347 (2009).
Ha, N. H. et al. Hydrogen gas sensing using palladium-graphene nanocomposite material based on surface acoustic wave. J. Nanomater. 2017, 9057250 (2017).
Zhang, W. et al. Insight into the capacitive properties of reduced graphene oxide. ACS Appl. Mater. Interfaces. 6, 2248–2254 (2014).
Meyer, J. C. et al. The structure of suspended graphene sheets. Nature 446, 60–63 (2007).
Zhu, Y. et al. Graphene and graphene oxide: Synthesis, properties, and applications. Adv. Mater. 22, 3906–3924 (2010).
Bele, S., Samanidou, V. & Deliyanni, E. Effect of the reduction degree of graphene oxide on the adsorption of Bisphenol A. Chem. Eng. Res. Des. 109, 573–585 (2016).
Nethravathi, C. & Rajamathi, M. Chemically modified graphene sheets produced by the solvothermal reduction of colloidal dispersions of graphite oxide. Carbon 46, 1994–1998 (2008).
Wenzel, W. & White, R. M. Analytic comparison of the sensitivities of bulk-wave, surface-wave and flexural plate-wave ultrasonic gravimetric sensors. Appl. Phys. Lett. 54, 1976–1978 (1989).
Duhamel, R. et al. Sensitivity of a lamb wave sensor with 2 μm AlN membrane. Ultrasonics 44, e893–e897 (2006).
Fan, L. et al. Influence of surface conductivity on sensitivity of acoustic wave gas sensors based on multilayered structures. IEEE Trans. Ultrason. Ferroelec. Freq. Contr. 58, 451–460 (2011).
Fan, L., Ge, H., Zhang, S. Y., Zhang, H. & Zhu, J. Optimization of sensitivity induced by surface conductivity and sorbed mass in surface acoustic wave gas sensors. Sens. Actuators, B. 161, 114–123 (2012).
Fan, L., Zhang, S. Y., Ge, H. & Zhang, H. Theoretical optimizations of acoustic wave gas sensors with high conductivity sensitivities. Sens. Actuators, B. 171, 1272–1276 (2012).
Jakubik, W. P. Investigations of thin film structures of WO3 and WO3 with Pd for hydrogen detection in a surface acoustic wave sensor system. Thin Solid Films 515, 8345–8350 (2007).
Ludwig, J. & Vlachos, D. First principles modeling of dissociative adsorption at crystal surfaces: Hydrogen on Pt (111). Mol. Simulat. 30, 765–771 (2004).
Peng, Y. T., Ye, J. X., Zheng, L. L. & Zou, K. The hydrogen sensing properties of Pt–Pd/reduced graphene oxide based sensor under different operating conditions. RSC Adv. 6, 24880–24888 (2016).
Acknowledgements
This work is supported by National Key Research and Development Project of China No. 2020YFA0211400 and National Natural Science Foundation of China, No. 11774169.
Author information
Authors and Affiliations
Contributions
X.Y.Z., R.H.M., L.S.L. and Y.T.Y. conducted the experiments. X.Y.Z., and L.F. contributed to the writing. L.F. conceived and led the project. L.F. and S.Y.Z. contributed to the revision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, XY., Ma, RH., Li, LS. et al. A room-temperature ultrasonic hydrogen sensor based on a sensitive layer of reduced graphene oxide. Sci Rep 11, 2404 (2021). https://doi.org/10.1038/s41598-020-80875-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-80875-0
This article is cited by
-
Advancing Frontiers: Graphene-Based Nano-biosensor Platforms for Cutting-Edge Research and Future Innovations
Indian Journal of Microbiology (2024)
-
Hydrothermal synthesis of Pd-doped rGO/ZnO-SnO2 nanocomposites for efficient hydrogen detection
Ionics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.