Abstract
Wastewater characterization is the basis for process design and operation optimization of wastewater treatment plants (WWTPs). In this work, a comprehensive study of the respirometry method has been performed to evaluate the biodegradable organic matters of wastewater. First, the optimal initial substrate to biomass ratio (S0/X0) was confirmed. Second, under the optimal S0/X0, the degradation curves of wastewater carbon oxygen demand (COD) components rapidly biodegradable COD (RBCOD) and slowly biodegradable COD (SBCOD) were obtained. Third, the Mann–Kendall test was performed to confirm the time point (t2) when endogenous respiration levels were reached, and the hydrolysis model was used to determine the time point (t1) of the SBCOD degradation stage. Considering the results, an adequate wastewater COD characterization method for RBCOD and SBCOD has been proposed. This study provides strong support to carry out effective and feasible process design, process diagnosis and optimization capability, can help achieve refined and stable operational management of WWTPs.
Similar content being viewed by others
Introduction
With the increase in urbanization and the rapid development of urban China, the amount of wastewater discharge continues to increase, resulting in deterioration of the water environment and serious pollution of water resources1. The wastewater treatment facilities in China have continued to develop at a high speed in the past decade2. In addition, increasingly stringent wastewater treatment discharge standards have been implemented to regulate nutrient removal3,4, that put forward stricter requirements for the refined design and operation of wastewater treatment plants (WWTPs).
At present, the dynamic description of municipal wastewater treatment processes, the change and transformation of wastewater components is mainly based on activated sludge models (ASMs)5,6,7. ASMs divide wastewater COD into biodegradable COD and non-biodegradable COD8,9. Biodegradable COD can be further divided into rapidly biodegradable COD (RBCOD) and slowly biodegradable COD (SBCOD). RBCOD is an easily available COD component that can be absorbed by heterotrophic microorganisms for biosynthesis and energy production, it directly determines the performance of nitrogen and phosphorus removal. SBCOD is divided into colloidal substrate and granular substrates, both of which are biodegradable substrates. These substances are often complex organic molecules and need to be decomposed by extracellular enzymes before they can be used by cells.
The design, control, and operation of a wastewater treatment system are largely dependent on how much is known about the characteristics of wastewater RBCOD and SBCOD components10. Therefore, it is particularly important to establish methods of wastewater characterization. Studies have shown that wastewater RBCOD and SBCOD components cannot be separated by physical–chemical methods11 Respirometric analysis method is a biological method that is widely used in wastewater COD component characterization. The respirometric method was confirmed as an effective method for determining RBCOD and SBCOD concentrations. The difference in biodegradation rate between wastewater RBCOD and SBCOD is reflected in the dynamic index of oxygen uptake rate (OUR)12. However, in the research and engineering practices associated with high-standard wastewater treatment, an increasing number of new phenomena and problems are becoming difficult to explain with conventional wastewater quality indicators, process theory and technical knowledge, among others, which restrict the operation process design, process optimization and regulation and stable operation of WWTPs13.
To meet the demand of high standard wastewater treatment and realize refined operational management, in this research, typical domestic wastewater is studied based on the respirometry method in order to establish a characterization method for wastewater COD components. The first goal of the present study was to analyse the influence of the initial substrate to biomass ratio (S0/X0) ratio on experimental OUR-t curves. Second, the respirometry method was utilized for the evaluation of RBCOD and SBCOD components. Finally, Mann–Kendall trend analysis method and a hydrolysis model were used to confirm the degradation time points of different components. Based on the results obtained in this study, a characterization analysis methodology for RBCOD and SBCOD components was proposed, which can effectively support operational process selection and process control technology research on WWTPs.
Materials and methods
Sampling of activated sludge and wastewater
Fresh activated sludge and raw wastewater were collected from the pilot A2/O system of the Research Center for Low Carbon Technology of Water Environment (Renmin University of China, Beijing). The characteristics of the experimental wastewater are listed in Table 1.
In this study, 10 L activated sludge sample was taken from the aerobic terminal of the A2/O system, washed and concentrated, then the supernatant was removed. This operation was repeated three times. The obtained sample was put in a container and aerated for 3–4 h until the activated sludge exhibited endogenous respiration stage. Moreover, the mixed liquor volatile suspended solids (MLVSS) were adjusted to approximately 2000 mg/L.
Respirometry experiments
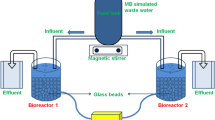
Respiration rates were measured in a Plexiglas reactor with working volumes of 250 mL (Fig. 1). During the experiments, the temperature of the mixed liquid was kept constant at (20 ± 1) °C by placing the reactor in a constant-temperature water bath with magnetic stirring, and the pH was continuously controlled to 7.5 ± 0.3 by adding NaOH and HCl. The dissolved oxygen (DO) concentration was measured in the reactor by means of a WTW Multi3420 oxygen meter (Weilheim, Germany) and was continuously monitored with a paperless recorder14.
For all tests, allyl-thiourea (ATU) was added at a concentration of 20 mg/L to the mixed liquid to suppress nitrification activity14.
Determination of optimal S0/X0
Several respirometry experiments with different S0/X0 ratios were performed to analyse wastewater COD fractions: RBCOD and SBCOD15,16. In this study, according to the ratio of domestic wastewater (the equivalent weight of COD is approximately 400 mg/L) and MLVSS, S0/X0 was divided into five levels, namely, 0.2, 0.4, 0.6, 0.8 and 1.0 mgCOD/mgVSS, and then carried out batch experiments. First, the mixed liquid (200 mL) was added to the 250 mL Plexiglas reactor, with full aeration of the sludge mixture. Second, some ATU solution was added, inserted the DO probe of the WTW-type dissolved oxygen electrode into the Plexiglas reactor, sealed the bottle mouth, placed the bottle on the agitator, and stirred the mixture at a speed of 125 r/min to fully mix the sample. The running cycle was 4 min, the DO value was recorded every 10 s, and DO was continuously monitored with a paperless recorder. Third, the DO value from the good linear relationship of the DO-t curve was obtained, and the slope of the curve was estimated as OUR. An OUR-t curve was constructed and observed by the naked eye using step sample. The organic load of mixed liquid in RBCOD and SBCOD was particularly obvious, and the optimal S0/X0 could be determined.
Test method of COD component
Under the optimal S0/X0, the respirometry method was used for wastewater COD component characterization. The test procedure was as described in “Determination of optimal S0/X0” section, and the COD concentration corresponding to the test time was tested by sampling. During the oxygen uptake rate (OUR) test of the sludge mixture17, when nitrification is inhibited, the ideal OUR curve consists of three stages, namely, the rapidly biodegradable organic matter (RBCOD) degradation stage, slowly biodegradable organic matter (SBCOD) hydrolysis stage and activated sludge endogenous respiration stage, which can be obtained from the OUR-t experimental curve. In the process of OUR tests, 20 mL of mixed liquid was taken out and centrifuged every 5 min, and the supernatant was collected to determine the COD concentration in the wastewater. The time point (t2) when endogenous respiration levels were reached and the time point (t1) of the SBCOD degradation stage were determined and combined with the OUR-t curve. Equation fitting was then performed on the experimental curve and the concentrations of the RBCOD and SBCOD components were calculated by integrating the area of each region for the equation with a higher fitting degree.
Chemical analyses
We analysed the COD concentration of the wastewater samples according to the standard method18. In this study, the organic matter in the wastewater was represented by the total chemical oxygen demand (TCOD), which could be divided into particulate COD (PCOD), colloidal COD (CCOD) and soluble COD (SCOD). The PCOD was the residual COD after filtration through a 1.5 μm filter, the SCOD was the COD that passed through a 0.45 μm filter, and the CCOD was calculated as the difference between TCOD and the sum of PCOD and SCOD19,20.
Ethical standards
This study complied with all ethical standards in all phases of research.
Results and discussion
The optimal S0/X0
Figure 2 illustrates the OUR-t curves of the respirometry experiments performed under different levels of S0/X0, where the variation in the DO concentration data was determined under different operating conditions. As can be seen in Fig. 2, the OUR-t curves of wastewater COD degradation under different S0/X0 ratios showed the same change trend, but there were also obvious differences in segmented points and the resolvability of components. When S0/X0 was 0.2 mgCOD/mgVSS, from 0 to 55 min, the OUR decreased rapidly with reaction time from 32.5 to 7.5 mgO2/(L h). The segmentation was not obvious, which may be related to the low initial matrix concentration and the rapid completion of COD degradation reaction. The results showed that when the S0/X0 ratio was low, it was not conducive to the analysis of COD components. When the S0/X0 ratio was in the range of 0.8 to 1.0, the OUR decreased rapidly from 60 to 8 mgO2/(L h). After 40 min, the reaction exhibited the endogenous respiration level. From 0 to 40 min, the segmentation of the OUR-t curve was not obvious, so it was difficult to analyse the COD components. This may have been due to the high concentration of matrix and the interaction between the degradation and hydrolysis of different COD components. When S0/X0 ranged from 0.4 to 0.6, the OUR-t experimental curve was significantly segmented and could be clearly divided into three stages: the RBCOD degradation stage, SBCOD hydrolysis stage and endogenous respiration stage. The results showed that when the S0/X0 ratio was 0.4 to 0.6, the process of COD degradation could be clearly divided into three reaction stages by the respiration measurement method, and the segmentation was obvious, therefore, meeting the requirements for subsequent analysis of the COD components in wastewater influent.
Whether the OUR curve obtained is clearly segmented and has high resolvability is mainly determined by S0/X0. However, the optimal S0/X0 ratios obtained by applying respirometry experiments are not the same, and it is difficult to determine the optimal state21. When the S0/X0 ratio is higher, owing to the reaction time being sufficient, microorganisms have enough time to oxidize and degrade organic matter, resulting in changes in the maximum specific growth rate of the microorganisms and the degradation rate of the substrate, and further leading to the rapid growth of microorganism via mass multiplication22. Moreover, the slower growth of microorganisms is inhibited, which results in changes in microbial community structure in the activated sludge. When the S0/X0 ratio is lower, the reaction is completed quickly, and it is difficult to observe the rapid oxidation process of wastewater RBCOD components. Hence, the OUR value of the process of microbial degradation is close to the endogenous respiration23, and the component' information cannot be obtained. Some studies have shown that the S0/X0 ratio can be 0.6 mgCOD/mgVSS. However, other studies showed that when the S0/X0 ratio is maintained at 0.45–1.0 mgCOD/mgVSS24, a clear OUR curve can be obtained and the deviation maintained at 5–10%. A reasonable S0/X0 ratio is related to the source and nature of the experimental wastewater and sludge. Therefore, it is very important to determine the optimal S0/X0 ratio through experiments.
Measurement of COD components
According to the optimal S0/X0 determination experiment, we confirmed that the optimal S0/X0 ratio was 0.5 mgCOD/mgVSS, and the OUR-t curve of wastewater COD degradation was shown in Fig. 2. The complete OUR-t curve of COD degradation showed a decreasing trend with reaction time. It was evidently composed of two external respiration (OURex) stages and an endogenous respiration (OURen) stage based on the significant difference in respiration rates. The first stage was the utilization of rapidly biodegradable matrix by microorganisms. Due to the sufficient matrix in this stage, RBCOD and DO were consumed rapidly by microorganisms, and the OUR was at a peak at this time. With the gradual decrease in RBCOD, the OUR decreased continuously. As shown in Fig. 3, in this stage, the OUR decreased rapidly from 46.8 to 22.2 mgO2/(L h). After 15 min of reaction, owing to the RBCOD reaction generally being complete, the system begins to enter the SBCOD degradation stage. Because the hydrolysis reaction is a slow process, the OUR decreased slowly. With the hydrolysis and oxidation of SBCOD, OUR decreased rapidly from 22.2 to 11.8 mgO2/(L h), and the reaction time of the process was approximately 5–7 times longer than the previous stage, approximately 70 min. During this reaction stage, SBCOD is hydrolysed to RBCOD with small molecules, and the OUR response is caused by the degradation of RBCOD. Because the hydrolysis process is relatively slow, the OUR-t curve shows a slow downward trend. After 70 min, the substrate in the wastewater almost completely reacts and begins to enter the endogenous respiration stage. At this time, microorganisms in the activated sludge use only their own stored substances for respiration, and the OUR remained at approximately 11.5 mgO2/(L h), which was close to the level of endogenous respiration measured in the early stage of the experiment. The biological or respirometric component of the characterization method was based on the measurement of the biomass response during substrate degradation in either continuous flow or batch conditions. Based on the respirometry setup, the wastewater RBCOD and SBCOD are easy to measure. During the first stage, this allows the microbial population to consume RBCOD faster and to be detected by the OUR measurement. The profile of fitting can be used to calculate the concentration of RBCOD and SBCOD components. In this experiment, the OUR fitting profile can be described as: y = 8.72 x4 − 0.001 x3 + 0.077 x2 − 2.52 x + 47.81, R2 = 0.98817.
According to the segmentation of the OUR-t curve, the degradation of COD in each stage was analysed. The concentration of COD in the mixture decreased from 387.5 to 108.2 mg/L during the endogenous respiration stage. From 0 to 15 min, the concentration of COD rapidly decreased from 387.5 to 299.6 mg/L, and the degradation rate was approximately 5.86 mg/(L min). From 15 to 70 min, the COD concentration decreased from 299.6 to 122.1 mg/L, and the COD degradation rate was approximately 3.22 mg/(L min). The COD degradation rate was approximately 1.39 mg/(L min) in the 70 to 80 min interval. The results showed that under the optimal S0/X0, the OUR-t curve could be divided into three stages, which may represent different COD components. Similarly, we analysed the PCOD, CCOD and SCOD of wastewater influent. As expected, TCOD is generally divided into three fractions, namely, PCOD, CCOD and SCOD. Moreover, the concentration of three types of COD has a strong correlation with wastewater RBCOD and SBCOD. The wastewater PCOD, CCOD and SCOD fractions were 46.14 ± 11.48%, 36.87 ± 9.71%, and 16.70 ± 5.08%, respectively (Fig. 4).
RBCOD consists of smaller molecules, which are mostly volatile fatty acids (VFAs) and low molecular weight carbohydrates, and is considered soluble organic matter with a particle size less than 0.45 µm. Reports showed that the percentage of the suspended fraction in the TCOD of raw domestic wastewater was 65–79%, while the dissolved fraction was 21–35%8. Biodegradable organic components represent an average of 39% of all organic matter in wastewater, and non-biodegradable components, approximately 61%25. This result is basically in accord with that for the three types of COD.
Methods of characterizing wastewater COD components
In the process of biotransformation, SBCOD needs to be hydrolysed into RBCOD with small molecule and easy biodegradation, before it can be absorbed and utilized by microorganism in activated sludge, finally, realizing the degradation of pollutants. The results showed that the degradation rates of RBCOD and SBCOD differed by 1–2 orders of magnitude, so the two parts could be effectively distinguished theoretically. A complete OUR-t curve of wastewater COD degradation theoretically includes four stages: the RBCOD degradation stage, nitrification stage, SBCOD degradation stage and endogenous respiration stage. The biological inhibitor ATU (20 mg/L) can inhibit nitrification. When nitrification is inhibited, the OUR-t curve can be divided into three stages. Among them, the degradation regulation of RBCOD accords with the Monod equation, and that of SBCOD accords with the hydrolysis rate equation. Therefore, only the time point (t1) of the SBCOD degradation stage and the time point (t2) when endogenous respiration levels were reached can be determined, and RBCOD and SBCOD can be solved quantitatively by an integral equation.
Determination of endogenous respiration levels (the time point (t1))
In this study, after the comparison and selection of the analysis method, the non-parametric Mann–Kendall test26,27,28,29 was used to determine the time point (t2) when the endogenous respiration level was reached. The Mann–Kendall test is used to determine whether a time series has a monotonic upward or downward trend. It does not require that the data be normally distributed or linear, and it is convenient and quick.
In the Mann–Kendall test, the time series {x1, x2, …, xn} represents n individual, independent and uniformly distributed samples of random variables, which are recorded as the null hypothesis H0. The alternative hypothesis H1 is a trend in the two-sided test or an upward (or downward) trend in the one-sided test. For all values of i, when j ≤ n and i ≠ j, the distributions of xi and xj are not the same. The trend test statistic S is calculated as follows:
where Sgn is a symbolic function
where S is a normal distribution, with a mean value of zero and a variance Var(S) = n(n − 1)(2n + 5)/18. When n > 10, the statistic ZMK converges to the standard normal distribution, the null hypothesis is that the sequence has no trend, and the bilateral trend test method is used.
In the bilateral trend test, at a given α confidence level, when {|ZMK|} ≥ Z1 − α/2, the null hypothesis is rejected; that is, at the α confidence level, there is a significant increase or decrease in the OUR series data trend. If ZMK > 0, there is an upward trend, while if ZMK < 0, there is a downward trend. When {|ZMK|} < Z1 − α/2, the null hypothesis that the change trend is not significantly accepted.
In this study, the Mann–Kendall test, the mutation test method, and Excel statistical software were used in combination. The Mann–Kendal test or mutation test was carried out from the end of the obtained OUR curve to the beginning. The portion of the respiratory rate curve without an obvious change trend was the endogenous respiration phase, reflecting the time point (t2) when the endogenous respiration level was reached. The analysis of the Mann–Kendal test results is shown in Table 2.
Note: (1) Z is a positive value that indicates an upward trend, and a negative value indicates a downward trend. (2) When the absolute value of Z is greater than or equal to 1.28, 1.64, and 2.32, it passes the significance test at 90%, 95%, and 99% reliability respectively.
After the calculations, the parameter n is 17, S is − 130, Var(S) is 589, and Z is − 5.3. The results show that |Z|> 2.32 > 0, which passed the significance test at 99% reliability. Since Z = −5.32, the OUR exhibits an upward trend.
In the non-parametric Mann–Kendall test, we set the time series as {x1, x2, …, xn}; Sk represents the cumulative number of the ith sample xi > xj (1 ≤ j ≤ i), and defines the statistic:
Under the assumption of random independence of the time series, the mean and variance of Sk are: E[Sk] = k(k − 1/4), var[Sk] = k(k − 1)(2 k + 5)/72, Among them, 1 ≤ k ≤ n.
After standardizing Sk, we obtain:
The Mann–Kendall test is performed from the end of the obtained OUR-t curve to the beginning, and the point of intersection within the confidence interval was determined as the mutation point t2. The mutation test results from Excel are shown in Tables 3 and 4.
Determination of SBCOD hydrolysis stage (the time point (t1))
Studies have shown that the degradation of SBCOD conforms to the hydrolysis rate equation (Eq. 6). Hydrolysis refers to the process by which SBCOD decomposes into small-molecular organics that can be used by microorganisms in activated sludge24,30,31,32.
The hydrolysis rate equation can be expressed as:
The quantitative relationship between the OUR and matrix is:
Combining the above two equations, we obtain Eq. (8):
where Kh is the maximum specific hydrolysis rate, gCODXs/(gCODXH·d); XH is the concentration of heterotrophic bacteria, mgCOD/L; and YH is the yield coefficient of heterotrophic bacteria, g/g.
To determine the time point (t1) when the SBCOD degradation stage starts, from the time point (t2) onwards, a segment of the OUR sequence is taken, equation fitting of the data is performed, and whether to continue taking OUR data forward is determined according to the fitting error. When the OUR value no longer conforms to the fitting equation, the OUR no longer conforms to the law of hydrolysis, indicating fitting distortion, and the time point when fitting distortion starts is considered the time point (t2).
Quantitative calculation of RBCOD and SBCOD concentrations
The quantitative relationship between the OUR and matrix is shown in Eq. (9), which can be used to calculate the initial concentrations of RBCOD and SBCOD components.
where S is the initial concentration of the substrate, mgCOD/L, and YH is the yield coefficient of heterotrophic bacteria, 0.68 in this study.
The selection of suitable methods for characterizing wastewater components plays a key role in the design, control, and operation of WWTPs10. In this study, based on the above analysis, the characteristic analysis steps of wastewater COD components are summarized as follows:
Step 1: The optimal S0/X0 was confirmed. Under this ratio, we determined the OUR-t curve of the wastewater influent COD component and used the Mann–Kendall test to determine the time point (t2) when the endogenous respiration stage began.
Step 2: The degradation regulation of SBCOD conforms to the hydrolysis model. The hydrolysis model is used for fitting, and the measured data are verified to determine the time point (t1) of the SBCOD degradation stage.
Step 3: After determining the time point (t2) when endogenous respiration levels are reached and the time point (t1) of the SBCOD degradation stage, OUR-t curve fitting is performed, followed by determination of the quantitative relationship between the OUR and matrix degradation to calculate the RBCOD and SBCOD component concentrations.
Conclusions
In this study, the conclusions are as follows:
-
1.
The accuracy of respirometric evaluation of wastewater RBCOD and SBCOD is strongly related to the experimental conditions and S0/X0 ratio. In this work, a satisfactory evaluation of wastewater components was performed with a S0/X0 ratio of approximately 0.5 mgCOD/mgVSS.
-
2.
Using the Mann Kendall test and Hydrolysis model, the time point (t2) when endogenous respiration levels are reached and the time point (t1) of the SBCOD degradation stage were determined. The wastewater RBCOD and SBCOD concentrations were 37.13 and 144.38 mg/L, respectively. The result is basically in accord with that for the three types of COD, and shows the effectiveness of the analytical methods.
-
3.
The analysis steps of wastewater characterization methods are summarized as follows: determine the OUR-t curve under the optimal S0/X0 ratio, use the Mann–Kendall test to determine the time point (t2) of the endogenous respiration phase, and use the hydrolysis model to determine the time point (t1) of the SBCOD degradation stage; then, evaluate the quantitative relationship between the OUR and matrix degradation, and calculate the RBCOD and SBCOD concentrations.
References
Yu, C. et al. Managing nitrogen to restore water quality in China. Nature 567, 516–520 (2019).
Feng, Y., Chiu, Y. & Liu, F. Measuring the performance of wastewater treatment in China. Appl. Sci. 9, 153 (2019).
Chen, X. Analysis of discharge standards of wastewater treatment plants in Yangtze River delta region and consideration of the measures for upgrading. Water Wastewater Eng. 55, 29–32 (2019) (in Chinese).
MOHURD (Ministry of Housing and Urban–Rural Development). Pollutant discharge standard for urban sewage treatment plants (GB18918-2002) (2002). (in Chinese).
Brdjanovic, D., Meijer, S., Lopez-Vazquez, C. Applications of Activated Sludge Models (IWA Publishing, America, 2015).
Brouwer, H., Klapwijk, A. & Keesman, K. J. Modelling and control of an activated sludge process on the basis of respirometry. Br. J. Rheumatol. 29, 189–192 (1994).
Sorour, M. & Bahgat, L. Application of activated sludge models in traditionally operated treatment plants—a software environment overview. Water Qual. Res. J. Can. 39, 294–302 (2004).
Pasztor, I., Thury, P. & Pulai, J. Chemical oxygen demand fractions of municipal wastewater for modeling of wastewater treatment. Int. J. Environ. Sci. Technol. 6, 51–56 (2009).
Shi, H. & Qiu, Y. Modeling and Application for Biological Wastewater Treatment (China Architecture & Building Press, Beijing, 2014) (in Chinese).
Tran, N., Ngo, H., Urase, T. & Gin, K. A critical review on characterization strategies of organic matter for wastewater and water treatment processes. Bioresour. Technol. 193, 523–533 (2015).
Khursheed, A. et al. Dependence of enhanced biological nitrogen removal on carbon to nitrogen and rbCOD to sbCOD ratios during sewage treatment in sequencing batch reactor. J. Clean. Prod. 171, 1244–1254 (2017).
Ai, H., Lu, P. & Long, T. Simultaneous characterization of RBCOD and SBCOD in wastewater by hybrid respirometer. Environ. Sci. 30, 2293–2296 (2008) (in Chinese).
Hu, H. et al. Evaluation of water feature and its application in the wastewater reclamation. Res. Environ. Sci. 32, 725–733 (2019).
Zhang, J. et al. Quantitative analysis on oxygen uptake rate of activated sludge in wastewater treatment plant. Environ. Eng. 36, 25–30 (2018) (in Chinese).
Mahfoud, S., Zamouche-Zerdazi, R., Bencheikh-Lehocine, M. & Menial, A. H. Respirometric evaluation of S0/X0 ratio effect on the kinetic and stoechiometric parameters of activated sludge. Int. J. Hydrog. Energy. 42, 12933–12942 (2017).
Marcela, N., Francisca, G., Aurora, S. & Jose, F. Wastewater COD characterization: analysis of respirometric and physical–chemical methods for determining biodegradable organic matter fractions. J. Chem. Technol. Biotechnol. 85, 536–544 (2010).
Ge, J., Huang, G., Huang, J., Zeng, J. & Han, L. Modeling of oxygen uptake rate evolution in pig manure–wheat straw aerobic composting process. Chem. Eng. J. 276, 29–36 (2015).
APHA. Standard Methods for the Examination of Water and Wastewater, 20th ed. American Public Health Association/American Water Works Association/Water Environment Federation (America: United Book Press, 1998).
Jimenez, J. A., La Motta, E. J. & Parker, D. S. Kinetics of removal of particulate chemical oxygen demand in the activated sludge process. Water Environ. Res. 77, 437–446 (2005).
Mamais, D., Jenkins, D. & Pitt, P. A rapid physical–chemical method for the determination of readily biodegradable soluble COD in municipal wastewater. Water Res. 27, 195197 (1993).
Ekama, G., Dold, P., Marais, G. Procedures for determining influent COD fractions and the maximum specific growth rate of heterotrophs in activated sludge systems. Water Sci. Technol. 18, 91–114 (1986).
Novak, L., Larrea, L., Wanner, J. Estimation of maximum specific growth rate of heterotrophic and autotrophic biomass: A combined technique of mathematical modeling and batch cultivations. Water Sci. Technol. 30, 171–180 (1994).
Sperandio, M., Paul, E. Estimation of wastewater biodegradable COD fractions by combining respirometric experiments in various S0/X0 ratios. Water Res. 34, 1233–1246 (2000).
Orhon, D., Çokgör, E. & Sözen, S. Dual hydrolysis model of the slowly biodegradable substrate in activated sludge systems. Biotechnol. Tech. 12, 737–741 (1998).
Gujer, W. Estimation of kinetic parameters of heterotrophic biomass under aerobic conditions and characterization of wastewater for activated sludge modelling. Water Sci. Technol. 25, 589–596 (1992).
Deb, S. & Sil, B. Climate change study for the meteorological variables in the Barak River basin in North-East India. Urban Climate 30, 100530 (2019).
Isioma, I. N. Non-parametric Mann–Kendall test statistics for rainfall trend analysis in some selected states within the coastal region of Nigeria. J. Civ. Constr. Environ. Eng. 3, 17 (2018).
Zhang, S., Deng, G., Huang, Y. Implement and application of Mann–Kendall test method in Excel. Preprint at http://www.paper.edu.cn (2014). (in Chinese).
Chen, Z., Xin, X. & He, R. The abnormal analysis of seismic data based on the method of Mann–Kendall. China Earthq. Eng. J. 34, 250–255 (2012) (in Chinese).
How, S. et al. Characterization of slowly-biodegradable organic compounds and hydrolysis kinetics in tropical wastewater for biological nitrogen removal. Water Sci. Technol. 81, 71–80 (2020).
Mino, T., San Perdo, D. & Matsuo, T. Estimation of the rate of slowly biodegradable COD (SBCOD) hydrolysis under anaerobic, anoxic and aerobic conditions by experiments using starch as model substrate. Water Sci. Technol. 31, 95–103 (1995).
Morgenroth, E., Kommedal, R. & Harremoës, P. Processes and modeling of hydrolysis of particulate organic matter in aerobic wastewater treatment—a review. Water Sci. Technol. 45, 25–40 (2002).
Author information
Authors and Affiliations
Contributions
J.Z. and Y.S. designed the research and performed the experiments; S.L. analyzed the data; L.Q. and X.X. drafted the manuscript; H.W. and G.L. revised the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, J., Shao, Y., Liu, G. et al. Wastewater COD characterization: RBCOD and SBCOD characterization analysis methods. Sci Rep 11, 691 (2021). https://doi.org/10.1038/s41598-020-80700-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-80700-8
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.