Abstract
Bright, discrete, thin auroral arcs are a typical form of auroras in nightside polar regions. Their light is produced by magnetospheric electrons, accelerated downward to obtain energies of several kilo electron volts by a quasi-static electric field. These electrons collide with and excite thermosphere atoms to higher energy states at altitude of ~ 100 km; relaxation from these states produces the auroral light. The electric potential accelerating the aurora-producing electrons has been reported to lie immediately above the ionosphere, at a few altitudes of thousand kilometres1. However, the highest altitude at which the precipitating electron is accelerated by the parallel potential drop is still unclear. Here, we show that active auroral arcs are powered by electrons accelerated at altitudes reaching greater than 30,000 km. We employ high-angular resolution electron observations achieved by the Arase satellite in the magnetosphere and optical observations of the aurora from a ground-based all-sky imager. Our observations of electron properties and dynamics resemble those of electron potential acceleration reported from low-altitude satellites except that the acceleration region is much higher than previously assumed. This shows that the dominant auroral acceleration region can extend far above a few thousand kilometres, well within the magnetospheric plasma proper, suggesting formation of the acceleration region by some unknown magnetospheric mechanisms.
Similar content being viewed by others
Introduction
Discrete auroral arcs are a manifestation of energy flow from the magnetosphere to the ionosphere1. Auroral light is excited by ~ 1–10 keV electrons precipitating into the ionosphere while carrying an upward field-aligned current—a portion of the magnetosphere–ionosphere current system. Since most magnetospheric electrons cannot reach the ionosphere because of the magnetic mirror force, an electric field that accelerates electrons downward (parallel to the magnetic field) is usually required to satisfy the need for current closure and ensure current continuity2,3. This parallel electric field has been directly measured in-situ in the so-called acceleration region4,5 and also confirmed by other parallel acceleration signatures6,7,8,9 but the generation mechanism of the parallel electric field remains unknown. This mechanism is important for auroral physics and magnetosphere–ionosphere coupling in Earth’s polar ionosphere and other the planetary magnetospheres such as for Jupiter. However, even the altitude extent of this acceleration region is not presently conclusive; thus important observational constraints on its likely generation mechanism are lacking.
A typical representation of the acceleration region observed by previous low altitude satellites is as follows6. Downgoing monoenergetic electrons, whose flux often forms the inverted-V shape in an energy-time spectrogram, indicate that these electrons are accelerated above a satellite prior to precipitating to auroral altitudes. These precipitating electrons could be the main carriers of the upward field-aligned current, which is observed as an azimuthal magnetic field deflection. In the region of those accelerated current carriers, the plasma number density, also known as plasma cavity, is expected to be small. The upgoing proton and converging electric field indicate a U-shape potential drop below a satellite. The lack of upgoing electrons within the loss cone is consistent with accelerated electrons that are lost to the atmosphere while exciting auroral emissions. Since the parallel acceleration makes a pitch angle more field-aligned, in contrast to the mirror force, the electron loss cone width depends on the potential drop below a satellite. Such an acceleration region is assumed to lie in the transition region between ionospheric and magnetospheric plasmas, typically at 1000–20,000 km altitudes1. However, there have been several reports of signatures reminiscent of potential-driven acceleration above 20,000 km, outside the ionosphere-magnetosphere transition region7,8,9,10. It is unclear whether electrons accelerated from such high altitudes can precipitate to the ionosphere and excite auroral emissions, owing to the small loss cone in the region. The high-angular-resolution electron detector equipped on the Arase satellite11 can resolve such a small loss cone, and to the best of our knowledge, there is no observation of the loss cone of electrons accelerated by the potential drop at such high altitudes. Additionally, THEMIS (Time History of Events and Macroscale Interactions during Substorms) ground-based all-sky imagers12,13 have sufficiently high temporal and spatial resolutions, which were not to coordinate with past, the previous high-altitude satellite missions. This study utilizes this unique opportunity to investigate the auroral acceleration properties at high altitudes using comprehensive particle and field observations (including high-angular resolution electron observations)11,14,15,16,17,18 with the Arase satellite19 and the network of THEMIS ground-based imagers.
Results and discussion
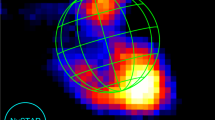
On 15 September, 2017, 02:35–02:42 UT, Arase was at an altitude of ~ 30,000 km, ~ 38° dipole latitude, and ~ 20 h magnetic local time. Arase was magnetically mapped to a thin active auroral arc; the evolution of the arc was captured by the THEMIS all-sky imager at Rankin Inlet (RANK) (Fig. 1 and Supplementary Video S1). As the arc moved equatorward, Arase’s footprint moved poleward and into the arc (Fig. 1a,b), where it remained for the next 7 min; subsequently, it exited slowly thereafter from the poleward side of the arc (Fig. 1c,d). During the 7-min period, the arc brightened (Fig. 1c), then dimmed and broadened in latitude (Fig. 1d). Ionospheric footprints estimated by several state-of-art magnetic field models20,21,22,23 show that the satellite was likely in the flux tube of the arc (Supplementary Fig. S1). This arc variation occurred during the recovery phase of an auroral substorm24, when Arase was located in the plasma sheet boundary layer (PSBL), the transition layer between the plasma sheet and the magnetotail lobe (Supplementary Fig. S2).
Images of the auroral arc around the footprint of Arase. The images were captured at 02:34:00–02:42:30 UT on 15 September, 2017 by the all-sky camera at Rankin Inlet (RANK). The magenta square shows the ionospheric footprint of Arase determined by the Tsyganenko and Andreeva (TA) 15B model. The latitudinal grid shows the magnetic latitude in altitude-adjusted corrected geomagnetic coordinates. The blue line shows the meridian along which the south-to-north cross-sectional time series of auroral intensity were collected for Fig. 2. Supplementary Video S1 shows the full motion of the auroral arc at a 3-s cadence.
Potential-driven acceleration powered the auroral arc; this is depicted by the time series of auroral intensity at the Arase footprint (Fig. 2a) as evidenced by the following: first, monoenergetic downgoing electrons at Arase (accelerated above the satellite) show peak flux energy ~ 1 keV for the period 02:36–02:41 UT (Fig. 2b); second, the upgoing electron flux for the same period is lower than the downgoing electron flux (Fig. 2c), bespeaking of a net upward field-aligned current; third, upgoing monoenergetic protons with energy of 1–10 keV (accelerated below the satellite) are present, while there are very few downgoing protons (Fig. 2d,e), implying that the potential acceleration (upward electric field) region also extends below Arase’s altitude.
Time series data of observations by Arase. (a) Auroral intensity along the south-to-north cross-section at the blue line shown in Fig. 1. Magenta line indicates the magnetic latitude of Arase’s footprint. Differential energy fluxes of: (b) downgoing electrons at the pitch angle of 0°–15°; (c) upgoing electrons at the pitch angle of 165°–180°; (d) downgoing protons at the pitch angle of 0°–15°; and (e) upgoing protons at the pitch angle of 165°–180°. The white region indicates no data in the pitch angle range. (f) Residual east–west magnetic field (azimuthal direction with respect to the Earth’s dipole axis) subtracted by quiet time magnetic field of Tsyganenko 89 model36 at the Kp index of 0. (g) Electric field perpendicular to the magnetic field. Blue and green represent poleward and eastward electric fields, respectively. (h) Spacecraft potential as a proxy of electron density. (i) Estimated potential drops above and below the satellite. (j) Ratio of potential drop above the satellite to the total potential drop. The vertical dashed lines show times when phase space density distributions are shown for Fig. 3.
The east–west magnetic field component variation (Fig. 2f, positive eastward) exhibited a negative deflection (westward) during Arase’s poleward motion across the arc (02:35–02:42UT), indicating traversal of an upward field-aligned current sheet. The electric field perpendicular to the magnetic field is strongly polarized in the latitudinal direction, indicating that the flux tube on the east–west aligned arc is the source of the electric field (Fig. 2g, positive poleward and eastward). The electric field was directed poleward when the satellite was located on the equatorward side of the arc, whereas the field was directed equatorward as the arc approached. Thus, the radial perpendicular electric field converged near the arc, demonstrating the U-shape potential drop in the flux tube of the arc. The spacecraft potential, inversely proportional to the logarithm of the electron plasma density, increased after 02:34 UT and peaked at 02:36 UT (Fig. 2h). The implied decrease in the electron density (a so-called density cavity) is a typical signature of the auroral acceleration region.
The potential drop is estimated both above and below the satellite using the particle data25,26 for the period 02:35:36–02:40:40 UT, which the unidirectional upgoing ions appeared. If the parallel kinetic energy of charged particles originates from acceleration by the parallel electric field, the energy divided by the electric charge can be interpreted as a potential drop. Here we consider the mean energy per particle, the ratio of the energy flux to the number flux, as energy given by a potential drop (Fig. 2i). The potential drop above the satellite estimated from the downgoing electrons is ~ 1 kV while that below the satellite estimated from the upgoing protons is ~ 1–10 kV, and these vary independently. Despite the high altitude of the satellite, the potential drop above the satellite it is often a significant fraction of the total drop, as large as 20–45% (Fig. 2j).
Figure 3 shows snapshots of the phase space density (PSD) distribution of auroral particles. The parallel electric field below the satellite expands the loss cone width and also renders it a function of energy (blue curve in Fig. 3a,b, left). During the event, there is a significant electron PSD within the loss cone in the downgoing direction (precipitating electron); however, there are very few electrons within the loss cone in the upgoing direction. This evidence indicates that accelerated electrons at very high altitudes indeed precipitate and power the visible aurora arc. The proton PSD that has a downward velocity component is quite small, indicating that few protons travelled to the satellite location from the magnetotail region (right panels in Fig. 3a,b); this suggests that most of these protons are repelled by the potential drop above the satellite.
Snapshots of two-spin averaged phase space density (PSD) of auroral electrons and protons. Phase space density distributions of electrons and protons at: (a) 02:37:12 UT and (b) 02:38:32 UT which are labeled by (1) and (2) in Fig. 2, respectively. The positive field-aligned velocity indicates the velocity directed along the magnetic field vector (downward direction). The pitch angle intervals of electron and proton are 3° and 10°, respectively. The white region indicates no data in a pitch angle-energy bin. The magenta line shows the loss cone angle without a potential drop. The blue line shows the loss cone hyperbola in the presence of a potential drop estimated from the proton energy.
The present observation cannot be explained by the conventional mechanisms of electron accelerations in the magnetotail, i.e., kinetic Alfvén waves and PSBL flows by tail reconnection. The time-varying parallel electric field by kinetic Alfvén waves, which have been reported also at high altitudes, contribute not to the monoenergetic acceleration, but the broadband-energy acceleration27,28. The magnitude of the Poynting flux of waves in the 3–180 s period range at the present event is only ~ 0.01 mW/m2, which is two orders smaller than the Alfvén wave events of previous observations at similar altitudes, because of the small magnetic perturbation (Supplementary Fig. S3). The PSBL electron beam, which is often associated with the magnetotail reconnection29,30, has a higher and broader energy range and shorter duration than our electron observations.
Conclusions
Our observations agree with the typical characteristics of the acceleration region observed by previous low altitude satellites. This further compels us to modify our previous representation of the acceleration region6 and extend it to farther than the ~ 30,000 km altitude (Fig. 4) although the potential drop region along the field line above the satellite is not determined. The physical mechanism of the quasi-electrostatic parallel electric field is, however, still unknown. The double layer at the boundary between ionospheric and magnetospheric plasma has been considered as the location of the associated potential drop, residing at low-altitudes31,32. In the Earth’s radiation belts, near the magnetic equator, intense parallel electric fields are short-lived, narrow spatial structures33. This study demonstrates that the parallel electric field accelerating the auroral particle can exist at any height along a field line and is not limited to the transition region where the cold dense plasma from the ionosphere and the hot tenuous plasma from the magnetosphere coexist, suggesting some unknown magnetospheric mechanisms. Understanding the formation mechanism of the quasi-electrostatic parallel electric field is crucial for following the processes of discrete aurora emission and current transport on other planets, including Jupiter and Mars where potential-driven acceleration has been reported34,35.
Methods
Spin-tone noise reduction from the magnetic field
The present 64 Hz magnetic field data from Arase’s MGF instrument (Fig. 2f) include reduction of the spin-tone noise with an amplitude of several nT originating from the satellite spin with a period of ~ 8 s. Spin phase data \(\theta_{s} \left( t \right)\) (\(t\): time index) included in the MGF data product provide an accurate period of the spin-tone noise. The spin-tone noise can be modeled by a linear combination of sinusoidal functions \(A = \left[ {\cos \theta_{s} \left( t \right),\sin \theta_{s} \left( t \right)} \right]\) and arbitrary parameters \({\varvec{x}} = \left[ {C_{1, } C_{2} } \right]^{T }\) that determine the amplitude and initial phase as, \(A{\varvec{x}} = C_{1} \cos \theta_{s} \left( t \right) + C_{2} \sin \theta_{s} \left( t \right).\) We determine the parameters by minimizing the sum of the square differences between \(A{\varvec{x}}\) and the 32-s high-pass filtered magnetic field data \({\varvec{B}}_{hp} \left( t \right)\) by the normal equation method, as \({\varvec{x}} = \left( {A^{T} A} \right)^{ - 1} A^{T} {\varvec{B}}_{hp}\). Because the parameters gradually vary with time, \({\varvec{x}}\) is calculated from data in a 10-min moving window with a time step of 10 min. Then the parameters are interpolated by the time index \(t\). The model spin tone is produced from the spin phase data and the interpolated parameters. Finally, we subtract it from the original magnetic field data.
Perpendicular electric field
The Arase’s EFD instrument observes the electric field in the plane perpendicular to the spin axis. The electric field parallel to the spin axis is complimented by the assumption of relatively small electric fields parallel to \({\varvec{B}}\), as \({\varvec{E}} \cdot {\varvec{B}} \approx 0\), where \({\varvec{E}}\) and \({\varvec{B}}\) are the electric and magnetic field vectors, respectively. The angle between \({\varvec{B}}\) and the spin plane was larger than 25° during the event, which is sufficiently large to use this technique. Then the background corotational and \({\varvec{v}}_{sc} \times {\varvec{B}}\) fields, where \({\varvec{v}}_{sc}\) is the satellite velocity vector, are subtracted from \({\varvec{E}}\). The two orthogonal components of the electric field perpendicular to \({\varvec{B}}\) are defined as follows: the east–west component is parallel to \({\varvec{B}} \times \user2{R }\) where \({\varvec{R}}\) is the outward radial position vector, and the poleward-equatorward component completes the orthogonal right-hand system.
Loss cone hyperbola
The conservation of the first adiabatic invariant gives, \(\frac{{v_{{M \bot^{2} }} }}{{B_{M} }} = \frac{{v_{{I \bot^{2} }} }}{{B_{I} }}\), where \(B\) is the magnetic field strength, and \(v\) is the particle velocity. Suffixes \(I\) and \(M\) donate values at the ionosphere (100 km altitude) and the magnetosphere (satellite location), respectively. The energy conservation of electrons barely reaching the ionosphere gives, \(\frac{1}{2}m_{e} v_{I \bot }^{2} = \frac{1}{2}m_{e} (v_{M \bot }^{2} + v_{M\parallel }^{2} ) + e\Delta \Phi\), where \(m_{e}\) is the electron mass, \(e\) is the electron charge, and \(\Delta \Phi\) is a potential difference. Combining the above equations, we have the loss cone hyperbola \(v_{M \bot }^{2} \left( {\frac{{B_{I} }}{{B_{M} }} - 1} \right) - v_{M\parallel }^{2} = \frac{2e\Delta \Phi }{{m_{e} }}\) 2. In Fig. 3, we use \(B_{M} = 260\) [nT] with the in-situ measurement and \(B_{I} = 55500\) [nT] estimated by the International Geomagnetic Reference Field Model.
Data availability
Data from Arase except for the high-angular resolution electron data used in this study are available from the ERG Science Center18 operated by ISAS/JAXA and ISEE/Nagoya University (https://ergsc.isee.nagoya-u.ac.jp/data_info/index.shtml.en). The present study analyzed L2 definitive orbit v03 data37, LEP-i L2 v03.00 data38 for protons, MGF L2 v03.03 64 Hz39 and spin-fit40 data for the magnetic field data, PWE/EFD L2 v03.00 data for the electric field data41 and v03.01 for the spacecraft potential data42. The pitch angle distribution of the high-angular resolution electron data is generated from fine channel data included LEP-e L1 v6 (calibrated, equivalent to L2) with MGF v03 data. THEMIS-ASI L1 v01 data and THEMIS ground magnetometers L2 v01 data (in Supplementary Fig. S2) are available at http://themis.ssl.berkeley.edu/data_all.shtml. Input parameters for magnetic field models are available at http://geo.phys.spbu.ru/~tsyganenko/modeling.html and https://omniweb.gsfc.nasa.gov/.
Code availability
The software used to read and analyse the data, part of the publicly available SPEDAS software package including ERG plug-in tools (https://ergsc.isee.nagoya-u.ac.jp/analysis/spedas/index.shtml.en), is available at http://themis.ssl.berkeley.edu/software.shtml and can be used without any restriction. The publicly available IDL GEOPACK (v10.6) software (http://ampere.jhuapl.edu/code/idl_geopack.html) is used for calculating the model magnetic fields and performing field line tracings.
References
Karlsson, T. et al. Quiet, discrete auroral arcs—observations. Space Sci. Rev. 216, 16 (2020).
Knight, S. Parallel electric fields. Planet. Space Sci. 21, 741–750 (1973).
Lyons, L. R. The field-aligned current versus electric potential relation and auroral electrodynamics. In Physics of Auroral Arc Formation (Es. Akasofu, S. -I. & Kan J. K.) 252–259 (American Geophysical Union, 2013).
Ergun, R. E. et al. Parallel electric fields in the upward current region of the aurora: Indirect and direct observations. Phys. Plasmas 9, 3685 (2002).
Mozer, F. S. & Kletzing, C. A. Direct observation of large, quasi-static, parallel electric fields in the auroral acceleration region. Geophys. Res. Lett. 25, 1629–1632 (1998).
McFadden, J. P., Carlson, C. W. & Ergun, R. E. Microstructure of the auroral acceleration region as observed by FAST. J. Geophys. Res. Space Phys. 104, 14453–14480 (1999).
Alm, L., Marklund, G. T. & Karlsson, T. In situ observations of density cavities extending above the auroral acceleration region. J. Geophys. Res. Space Phys. 119, 5286–5294 (2014).
Alm, L., Li, B., Marklund, G. T. & Karlsson, T. Statistical altitude distribution of the auroral density cavity. J. Geophys. Res. Space Phys. 120, 996–1006 (2015).
Figueiredo, S. et al. Temporal and spatial evolution of discrete auroral arcs as seen by Cluster. Ann. Geophys. 23, 2531–2557 (2005).
Shiokawa, K. et al. Arase observation of the source region of auroral arcs and diffuse auroras in the inner magnetosphere. J. Geophys. Res. Space Phys. 125, e2019JA027310 (2020).
Kazama, Y. et al. Low-energy particle experiments–electron analyzer (LEPe) onboard the Arase spacecraft. Earth Planets Space 69, 165 (2017).
Angelopoulos, V. The THEMIS mission. Space Sci. Rev. 145, 5. https://doi.org/10.1007/s11214-008-9336-1 (2008).
Mende, S. B. et al. The THEMIS array of ground-based observatories for the study of auroral substorms. Space Sci. Rev. 145, 357. https://doi.org/10.1007/s11214-008-9380-x (2008).
Asamura, K., Kazama, Y., Yokota, S., Kasahara, S. & Miyoshi, Y. Low-energy particle experiments–ion mass analyzer (LEPi) onboard the ERG (Arase) satellite. Earth Planets Space 70, 70 (2018).
Kasahara, Y. et al. The plasma wave experiment (PWE) on board the Arase (ERG) satellite. Earth Planets Space 70, 86 (2018).
Kasaba, Y. et al. Wire Probe Antenna (WPT) and Electric Field Detector (EFD) of Plasma Wave Experiment (PWE) aboard the Arase satellite: Specifications and initial evaluation results. Earth Planets Space 69, 174 (2017).
Matsuoka, A. et al. The ARASE (ERG) magnetic field investigation. Earth Planets Space 70, 43 (2018).
Miyoshi, Y. et al. The ERG Science Center. Earth Planets Space 70, 96 (2018).
Miyoshi, Y. et al. Geospace exploration project ERG. Earth Planets Space 70, 101 (2018).
Tsyganenko, N. A. & Andreeva, V. A. A forecasting model of the magnetosphere driven by an optimal solar wind coupling function. J. Geophys. Res. A: Space Phys. 120, 8401–8425 (2015).
Tsyganenko, N. A. & Sitnov, M. I. Modeling the dynamics of the inner magnetosphere during strong geomagnetic storms. J. Geophys. Res. 110, A03208 (2005).
Tsyganenko, N. A. A model of the near magnetosphere with a dawn-dusk asymmetry. J. Geophys. Res. Space Phys. 107, 1–17 (2002).
Tsyganenko, N. A. Effects of the solar wind conditions in the global magnetospheric configurations as deduced from data-based field models. in International conference on substorms vol. 389 181 (1996).
Akasofu, S. I. The development of the auroral substorm. Planet. Space Sci. 12, 273–282 (1964).
Lin, C. S. & Hoffman, R. A. Characteristics of the inverted-V event. J. Geophys. Res. 84, 1514 (1979).
Reiff, P. H. et al. Determination of auroral electrostatic potentials using high- and low-altitude particle distributions. J. Geophys. Res. 93, 7441 (1988).
Chaston, C. C. et al. Driven Alfven waves and electron acceleration: A FAST case study. Geophys. Res. Lett. 29, 30–1–30–4 (2002).
Wygant, J. R. et al. Evidence for kinetic Alfvén waves and parallel electron energization at 4–6 Re altitudes in the plasma sheet boundary layer. J. Geophys. Res. Space Phys. 107, 1–15 (2002).
Egedal, J., Daughton, W. & Le, A. Large-scale electron acceleration by parallel electric fields during magnetic reconnection. Nat. Phys. 8, 321–324 (2012).
Varsani, A. et al. Simultaneous remote observations of intense reconnection effects by DMSP and MMS spacecraft during a storm time substorm. J. Geophys. Res. Space Phys. 122, 10891–10909 (2017).
Block, L. P. A double layer review. Astrophys. Space Sci. 55, 59–83 (1978).
Ergun, R. E., Carlson, C. W., McFadden, J. P., Mozer, F. S. & Strangeway, R. J. parallel electric fields in discrete arcs. Geophys. Res. Lett. 27, 4053–4056 (2000).
Mozer, F. S. et al. Megavolt parallel potentials arising from double-layer streams in the earth’s outer radiation belt. Phys. Rev. Lett. 111, 1–5 (2013).
Mauk, B. H. et al. Discrete and broadband electron acceleration in Jupiter’s powerful aurora. Nature 549, 66–69 (2017).
Xu, S. et al. Inverted-V electron acceleration events concurring with localized auroral observations at mars by MAVEN. Geophys. Res. Lett. 47, 1–8 (2020).
Tsyganenko, N. A. A magnetospheric magnetic field model with a warped tail current sheet. Planet. Space Sci. 37, 5–20 (1989).
Miyoshi, Y., Shinohara, I. & Jun, C.-W. The Level-2 orbit data of Exploration of energization and Radiation in Geospace (ERG) Arase satellite, v03. https://doi.org/10.34515/DATA.ERG-12000 (2018).
Asamura, K., Miyoshi, Y. & Shinohara, I. The LEPi instrument Level-2 3D flux data of Exploration of energization and Radiation in Geospace (ERG) Arase satellite, v03.00. https://doi.org/10.34515/DATA.ERG-05000 (2018).
Matsuoka, A. et al. The MGF instrument Level-2 high-resolution magnetic field data of Exploration of energization and Radiation in Geospace (ERG) Arase satellite, v03.03. https://doi.org/10.34515/DATA.ERG-06000 (2018).
Matsuoka, A. et al. The MGF instrument Level-2 spinfit magnetic field data of Exploration of energization and Radiation in Geospace (ERG) Arase satellite, v03.03. https://doi.org/10.34515/DATA.ERG-06001 (2018).
Kasahara, Y. et al. The PWE/EFD instrument Level-2 spin-fit electric field data of Exploration of energization and Radiation in Geospace (ERG) Arase satellite, v03.00. https://doi.org/10.34515/DATA.ERG-07000 (2018).
Kasahara, Y. et al. The PWE/EFD instrument Level-2 spin-averaged potential data of Exploration of energization and Radiation in Geospace (ERG) Arase satellite, v03.01. https://doi.org/10.34515/DATA.ERG-07001 (2018).
Acknowledgements
The present study was supported by JSPS KAKENHI 15H05747, 16H06286, 17H00728, 20H01959, and 19K03949. This study was supported by JSPS Bilateral Open Partnership Joint Research Projects. The LEP-e development is supported by the Academia Sinica, the National Cheng Kung University, and also the Ministry of Science and Technology of Taiwan under Contract No. MOST 105-311z1-Y-001-042 and MOST 106-2111-M-001-011. T.-F. Chang acknowledges support from Taiwan grant MOST 109-2635-M-006-001. The authors would also like to extend sincere thanks to all members of the ERG project, the ERG Science Center, the THEMIS team, and contributors to SPEDAS and IDL GEOPACK software.
Author information
Authors and Affiliations
Contributions
S.I. identified the event, analyzed the combined dataset, and wrote the paper. Y.M. oversaw the production of the combined dataset and discussed its interpretation. I.S. oversaw the ERG project and discussed the interpretation of the event. K.S. discussed the interpretation of the event and drafting the paper. Y. Kazama, S-Y.W., S.W.Y.T., T-F.C., B-J.W., and C-W.J. provided the low-energy particle experiments-electron analyser (LEP-e) data. K.A. provided the low-energy particle experiments-ion analyser (LEP-i) data and discussed the interpretation of the event. Y. Kasahara, Y. Kasaba, M.S., S.N., and M.K. provided plasma wave experiment/electric field detector (PWE/EFD) data. A.M., M.T., and S.K., provided MaGnetic Field experiment (MGF) data. V.A. provided ASI/THEMIS data and discussed drafting the paper. T.H. developed the pitch angle sorting tool for LEP-i data and discussed the interpretation of the event. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Supplementary Video 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Imajo, S., Miyoshi, Y., Kazama, Y. et al. Active auroral arc powered by accelerated electrons from very high altitudes. Sci Rep 11, 1610 (2021). https://doi.org/10.1038/s41598-020-79665-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-79665-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.