Abstract
In recent years, non-invasive measurement of tissue stiffness (hardness) using ultrasound elastography has attracted considerable attention. It has been used to evaluate muscle stiffness in the fields of rehabilitation, sports, and orthopedics. However, ultrasonic diagnostic devices with elastography systems are expensive and clinical use of such devices has been limited. In this study, we proposed a novel estimation method for vibration-based shear wave elastography measurement of human skeletal muscle, then determined its reproducibility and reliability. The coefficient of variation and correlation coefficient were used to determine reproducibility and reliability of the method by measuring the shear wave velocities in konjac phantom gels and agar phantom gels, as well as skeletal muscle. The intra-day, day-to-day, and inter-operator reliabilities were good when measuring the shear wave velocities in phantom gels. The intra-day and day-to-day reliabilities were good when measuring the shear wave velocities in skeletal muscle. The findings confirmed adequate reproducibility and reliability of the novel estimation method for vibration-based shear wave elastography. Therefore, the proposed measurement method may be a useful tool for evaluation of muscle stiffness.
Similar content being viewed by others
Introduction
Objective measurement of muscle tissue elasticity can help to confirm the pathological states of various diseases associated with skeletal muscle stiffness and aid in determining treatment efficacy. In clinical practice, muscle spasticity after stroke, spinal cord injury, multiple sclerosis, and myopathy are usually assessed subjectively through manual palpation to characterize muscle tissue. Other characteristics assessed in this manner include tissue stiffness in myofascial pain syndrome, neck–shoulder pain, and low back pain, as well as rehabilitation progress. Muscle characteristics can be measured using ramp-and-hold tests, pendulum tests, and dynamometry; these approaches provide valuable information concerning surrounding tissues but cannot isolate the mechanical properties of individual muscles from those of associated skin, subcutaneous tissues, tendons, neurovascular structures, and joint capsules1,2,3. Although distinct terms are used in different fields of clinical practice, the muscle characteristics described by these terms are related to muscle stiffness. One of the most important parameters used to quantify soft tissue stiffness (or elasticity) is the modulus of elasticity, also known as Young’s modulus; this parameter is defined as the slope of the stress–strain curve of a material in the elastic deformation region, which comprises a local mechanical property of the constituent material. Hence, quantification of elastic modulus distribution could improve the accuracy of muscle stiffness measurement.
A method known as ultrasound strain elastography has been used to assess skeletal muscle stiffness. In this method, an ultrasonic diagnostic probe is held to the body surface and minimal repetitive pressure is applied to tissues. This pressure generates real-time strain images using a transducer. Accordingly, when a consistent amount of pressure is applied, softer tissues demonstrate a greater amount of deformation and therefore experience more strain, compared with stiffer tissues. However, tissue stiffness is measured as a ratio of the amount of actual strain to target strain, indicating that quantitative measurement using Young’s modulus remains impossible, although semiquantitative measurement is possible. At least three cycles of compression and decompression are recommended for optimal measurement4; however, extensive tissue preload through repeated compressions can alter tissue elasticity. Notably, this measurement procedure requires specific technical skills, such that the measurement accuracy depends on the examiner’s experience5,6,7,8.
Recently, an approach that utilizes shear wave elastography has attracted attention as a new method for quantitative estimation of tissue stiffness. Shear wave propagation speed is highly dependent on tissue stiffness; Doppler ultrasonography can be used to measure tissue stiffness because it can measure small propagation-related displacement fluctuations with relatively high accuracy9,10. In ultrasound shear wave elastography, shear waves can be launched in a controlled manner by external mechanical vibrations11,12,13,14,15,16,17,18,19,20,21,22 and acoustic radiation force impulses23,24,25,26,27,28. The use of an external vibrating source is much less common among commercial ultrasound shear wave elastography systems because it is relatively difficult to image the target tissue at appropriate depth; moreover, the required devices can be cumbersome11,22. Most commercial ultrasound shear wave elastography systems (e.g., Philips, GE Healthcare, Siemens, Canon, Mindray, Samsung, and Supersonic) use acoustic radiation force impulse-based techniques to generate ultrasonic shear waves in tissues27,28. This method requires strong ultrasonic waves, but undesirable temperature elevation can occur if bone and surrounding tissues are located near the focal point29. One major limitation of this method is that the detection of shear waves generally requires ultrasound imaging equipment with a high frame rate; these systems are expensive. Therefore, it is difficult to introduce such systems in general clinical practice, rehabilitation facilities, and sports medicine clinics.
Accordingly, external mechanical vibration has been proposed as a cost-effective alternative method for shear-wave induction, with the goal of enabling wider adoption of shear wave elastography14,17,20,22. Recently, there has been considerable progress in developing the technological foundation required for external mechanical vibration-based shear wave elastography imaging16,19,30. Vibro-elastography has found broad clinical applications in prostate cancer detection and liver fibrosis staging20,31,32. To the best of our knowledge, there is no widely available method that can visualize the shear wave wavefront in real time by means of conventional external vibration-based measurement. A shear wave that is reflected from the tissue boundary produces a standing wave in the vicinity of the boundary, which reduces the accuracy of shear wave velocity estimation. The complicated propagation of the shear wave inside tissue also diminishes measurement accuracy. Therefore, we presume that confirmation of the propagation wavefront (i.e., propagation direction, reflection, refraction, and complicated wavefront) of the shear wave and measurement of the shear wave velocity will facilitate quantitative measurements with good reproducibility.
Color Doppler shear wave imaging is a novel wave front imaging method in which ultrasound color flow images are used to detect the wave fronts of shear waves; this approach allows direct, real-time observation of the wave fronts of shear waves33,34,35. Shear wave elastography uses continuous shear waves generated by a mechanical vibrator attached to the tissue surface. The addition of a very simple device system to a traditional ultrasound device allows quantitative visualization of tissue stiffness; this offers an easy-to-use method for evaluation of the viscoelastic properties of superficial tissues. However, the adaptation of this system to skeletal muscle has not yet been investigated in detail. Therefore, this study was performed to examine the reproducibility and reliability of a novel estimation method for vibration-based shear wave elastography measurement of human skeletal muscle.
Results
Evaluation of reproducibility when applying the novel estimation method to vibration-based shear wave elastography measurement of phantom gels
The mean shear wave velocities in konjac yam phantom jelly were 2.21 ± 0.03 m/s (first measurement: coefficient of variation [CV], 1.38%) and 2.21 ± 0.01 m/s (second measurement: CV, 0.38%) on the first day, and 2.21 ± 0.02 m/s (first measurement: CV, 0.83%) and 2.28 ± 0.02 m/s (second measurement: CV, 0.78%) on the second day (Fig. 1). The intra-day, day-to-day, and inter-operator CV values of konjac yam phantom jelly elasticity were 0.2%–0.6%, 0.6%–0.7%, and 0.5%–0.7%, respectively.
In analyses using the agar gel, the shear wave velocity increased as the agar concentration increased from 1 to 8%. Moreover, the agar concentration and shear wave velocity were positively correlated (r = 0.99; Fig. 2). Table 1 shows the CV and intra-class correlation coefficient (ICC) values of the intra-day (CV, < 4.8; ICC, 0.98), day-to-day (CV, < 7.7; ICC, 0.96), and inter-operator reliabilities of agar phantom gel elasticity (CV, < 4.0; ICC, 0.98).
Evaluation of reproducibility when applying the novel estimation method to vibration-based shear wave elastography measurement of skeletal muscle
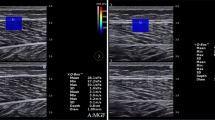
Figure 3 shows the CV and ICC values of the intra-day (CV, < 9.8; ICC, > 0.92) and day-to-day (CV, < 9.6; ICC, > 0.90) reliabilities of shear wave velocity estimation of skeletal muscle stiffness. It also shows example color flow images and shear wave velocity maps for the biceps brachii, flexor carpi radialis, semitendinosus, biceps femoris, medial gastrocnemius, and tibialis anterior.
Intra-day and day-to-day reliabilities of shear wave velocity estimation of skeletal muscle stiffness. (a) B-mode image, (b) color flow image, (c) shear wave velocity map. The right biceps brachii, flexor carpi radialis, semitendinosus, biceps femoris, medial gastrocnemius, and tibialis anterior were measured twice per day for 2 days with a between-measurement interval of 1 day (three measurements per trial). For the semitendinosus and biceps femoris, statistical analysis focused on the upper half of the selected area. Results of skeletal muscle shear wave velocity (mean ± standard deviation) are shown in Supplementary Fig. S1 online.
Discussion
Our study provides evidence of excellent reliability when using our novel estimation method for vibration-based shear wave elastography measurements of phantom elasticity and skeletal muscle stiffness. These observations are clinically important because skeletal muscle stiffness is observed in various conditions, such as myofascial pain syndrome36, neck and shoulder pain27, and low back pain37. Thus, our results suggest that multiple patient groups who experience muscle stiffness may benefit from our proposed method, which is a useful tool for evaluating diseases characterized by muscle stiffness and determining treatment effects; this method is expected to help reduce costs and promote introduction of vibration-based shear wave elastography in general clinical practice.
The proposed estimation method for vibration-based shear wave elastography demonstrated excellent intra-day, day-to-day, and inter-operator reliabilities when measuring phantom elasticity. Konjac gel is used as a phantom for ultrasound imaging38,39 and elastography34. The mean shear wave velocity in konjac phantom gel was 2.2 m/s, which is reasonably consistent with the findings in a previous study34. The CV calculated from the mean and standard deviation of five measurements during one trial was 0.38%–1.38%, indicating excellent repeatability for measurements of phantom elasticity. Therefore, triplicate measurements during each trial were performed in subsequent experiments.
Intra-day and day-to-day reliabilities were measured to evaluate temporal variation. These results revealed that our proposed method was able to reliably measure elasticity at two different time points (intra-day CV, 0.2%–0.6%; day-to-day CV, 0.6%–0.7%). Furthermore, inter-operator reliability was measured to evaluate operator variation; the findings showed that two independent operators produced reliable elasticity measurements using our novel method (inter-operator CV, 0.5%–0.7%).
To verify the effectiveness of our proposed method, agar gels were used because agar is economical and because elasticity can be easily manipulated by modifying the agar concentration34,40. Several attempts were made to produce different concentrations of agar phantom gels, which were prepared based on the recipes described in Table 2. These recipes ensured that the respective components did not separate, powdered agar was dissolved in the solution, and the agar was uniformly solidified. Our results revealed that, as the concentration of agar increased, shear wave velocity increased; moreover, the agar concentration was positively correlated with shear wave velocity. In addition, the CV and ICC measurements were consistent among different agar concentrations, revealing good intra-day, day-to-day, and inter-operator reliabilities. Therefore, our novel estimation method for shear wave elastography may be reliable for measurement of elasticity.
The most striking finding of this study was that our estimation method for shear wave elastography had excellent intra-day and day-to-day reliabilities when measuring the shear wave velocities in the right biceps brachii, flexor carpi radialis, semitendinosus, biceps femoris, medial gastrocnemius, and tibialis anterior. This finding suggests that our method can reliably assess muscle elasticity.
Other authors have proposed alternative techniques to measure muscle stiffness in healthy skeletal muscle by means of ultrasound elastography27,41,42,43,44,45. It is difficult to compare shear wave velocities measured in our study with values measured in previous studies because of inconsistencies in probe positioning, variations in ultrasound elastography techniques, and differences in the methods used to report stiffness. Available shear wave elastography measurement parameters include shear wave speed, elastic modulus, shear elastic modulus, Young’s modulus, and elasticity44,45,46,47. Notably, Ballyns et al.41 measured biceps brachii shear wave velocity by means of external vibrations. Although their probe and vibrator positions, frequencies, and analytical methods differed from our method, the overall approaches were similar in their study and our study; thus, we presumed that their results could be readily compared with our findings. In the study by Ballyns et al., measurements were performed at 60, 110, 160, and 200 Hz; measurements at 276 Hz (the frequency used in our study) were not directly reported. However, the data provided in their publication implied that biceps brachii shear wave velocity at 276 Hz would be approximately 4 m/s, similar to our measured values of 3.02–5.12 m/s (see Supplementary Fig. S1 online). Therefore, the shear wave velocity measured by the proposed method is similar to the value reported in a previous study that involved external vibration measurements.
Our findings are comparable with those of previous studies that have shown good/excellent reliability in measuring muscle elasticity by means of shear wave elastography in resting muscles and during active contraction48,49,50. Lacourpaille et al.48 investigated the reliability of elastic modulus in resting muscles by means of shear wave elastography using supersonic shear wave imaging. They reported good intra-session (n = 20) and inter-day (n = 21) reliabilities (biceps brachii ICC, 0.868 and 0.832, respectively; medial gastrocnemius ICC, 0.950 and 0.922, respectively; and tibialis anterior ICC, 0.811 and 0.809, respectively). Depending on the muscle, the mean temporal variability in the CV over 10 measurements ranged from 2.9% to 5.0%. Dubois et al.49 examined the intra-operator repeatabilities of a measurement protocol to assess shear modulus in the resting lower limb muscles of 10 healthy participants who underwent shear wave elastography using supersonic shear wave imaging. They reported poor repeatability in the biceps femoris (CV, 18%), semimembranosus (CV, 15%), semitendinosus (CV, 20%), and medial gastrocnemius (CV, 9%) muscles. In that study, the CV of shear modulus was calculated and measured six times. Koo et al.50 performed shear wave elastography using supersonic shear wave imaging to estimate muscle elasticity in the resting tibialis anterior of 20 healthy participants, then calculated the CV of shear elastic modulus in triplicate. They observed excellent test–retest reliability (ICC , 0.942).
In this study, we confirmed adequate reproducibility and reliability using our novel estimation method for vibration-based shear wave elastography measurement of skeletal muscle. To verify inter-day and day-to-day reliabilities, we measured participants’ major surface muscles (i.e., biceps brachii, flexor carpi radialis, semitendinosus, biceps femoris, medial gastrocnemius, and tibialis anterior) twice per day for 2 days, with a between-measurement interval of 1 day. For all muscles, the intra-day (CV, < 9.8; ICC, > 0.92) and day-to-day (CV, < 9.6; ICC, > 0.90) reliabilities of the novel estimation method for skeletal muscle were good. Compared with the results of prior studies48,49,50, our findings indicate that the proposed method is a highly reliable approach for estimating major muscle elasticity.
Good reliability in our study may have been achieved through standardization of the scanning site with reference to body landmarks, imaging parameters, and both location and size of the region of interest. In addition, the positions of the probe and excitation point were adjusted to ensure that shear waves propagated in the direction of muscle fibers. Muscle stiffness at rest is perhaps the simplest measurement to capture using ultrasound elastography, but this method must be performed in a standardized manner. In particular, the orientation of the transducer probe affects measurement reliability46. Because our method can directly show shear wave wavefronts in real time, the observer can easily identify the optimal probe orientation and/or excitation point, then reproduce shear wave wavefronts that propagate uniformly in the region of interest; these approaches facilitate good reliability when measuring muscle stiffness.
Limitations
There were several notable limitations in the present study. First, we did not investigate correlations with other quantitative methods in this study, because we previously determined the effectiveness of the new estimation method by comparison with values measured using other instruments. Moreover, we previously showed that shear wave velocity measurements in phantom gels, supraclavicular muscles, and trapezius muscles acquired using the new method were consistent with those acquired by means of other instruments15,33,34,51,52. Comparison of shear wave velocity among skeletal muscle sites and quantitative methods is an important consideration for clinical application of novel skeletal muscle stiffness measurement methods and devices.
Second, all participants were asymptomatic young male volunteers and elasticity was measured in static muscles. Thus, the findings may not be generalizable to a variety of patients or muscles. Nevertheless, the findings provide important support for further validation of this technique’s reliability under different conditions. In particular, this technique should be performed in asymptomatic patients and the findings should be compared with measurements in patients who exhibit various symptoms or pathologies.
Third, only the elasticity of the middle portion of the muscle was examined, on the basis of the recommended placement of surface electrodes for standardized electromyography measurement. Although we focused on sites that are often measured in clinical practice, our results were highly reproducible and reliable in all parts of skeletal muscle measured in this study. Moreover, the results of this study provide important guidance for clinical application of our method. In the future, we plan to investigate areas other than the central section of the muscle, as well as muscle–tendon transition zones, to determine differences in shear elastic modulus among these sites.
Finally, only the elasticity of major surface muscles was examined, largely because these muscles are frequently measured in clinical practice. As noted above, our results were highly reproducible and reliable in the measured muscles. In the future, we plan to investigate other muscles (i.e., deep tissues) to support clinical implementation of our method. As shown in the photograph of the hamstring (Fig. 3), tissues can be readily measured close to the body surface; however, the measurement of deep tissues may be difficult. A previous study51 showed that stable measurement of deeper tissues may be achieved by modifying the shear wave frequency of the actuator with respect to shear wave tissue absorption. However, the feasibility of this approach must be confirmed through additional investigations.
Conclusions
In this experimental study, we assessed phantom gels and volunteers’ skeletal muscles by means of vibration-based shear wave elastography. Our findings confirmed adequate reproducibility and reliability of a novel estimation method for shear wave elastography measurement of skeletal muscle at sites commonly assessed in clinical practice. Depending on the results of additional validation studies in study populations with different ethnicities and disease states, the proposed measurement method may constitute a useful tool for evaluation of muscle stiffness in both clinical and research settings.
Methods
Experimental system
Figure 4 illustrates the experimental system. Our novel estimation method for shear wave elastography was implemented using ultrasound scanners (Xario SSA-660A, Toshiba, Japan). The shear wave imaging method was previously described; quantitative evaluation confirmed a good correlation between the small displacement estimation method and shear wave velocity measured using our new method15,33,34. Notably, shear wave velocity is derived from stiffness by assuming that shear viscosity is negligible. Thus, comparative experiments between these two methods for human supraspinatus muscle, trapezius muscle, and an agar gel phantom have been performed; shear wave velocities measured using our novel estimation method were consistent with measurements performed by means of acoustic radiation force impulses34,51,52. In our novel estimation method, the shear wave frequency is selected from among several frequencies that satisfy the shear wave frequency conditions. The spatial resolution of a shear wave map decreases upon selection of a low frequency. However, determination of shear wave displacement amplitude is difficult because of the limited vibrator output power. Hence, shear wave frequency in this study was set within the frequency range from 235.8 to 296.6 Hz, depending on the pulse repetition frequency of the ultrasound scanner to satisfy the shear wave frequency condition of m = 1.
A short (45 mm) and lightweight (30 g) linear vibration motor, designed to manipulate an electric toothbrush, was adopted for the actuators by generating vibrations with a displacement amplitude of > 400 μm and frequency range of 230–300 Hz. Displacement of the linear vibration motor was measured using a microelectromechanical system accelerometer (ADXL001, Analog Devices, USA) at an accelerometer sampling frequency of 200 kHz; the displacement was derived by two-step integration. Figure 5 shows the vibration displacement when positioned over skeletal muscle. The harmonic distortion was measured by Fourier analysis. Power spectrum analysis showed that the second and third harmonic components of displacement were − 44.5 dB and − 79.9 dB at a vibration frequency of 276 Hz and a displacement amplitude of 300 μm. This result was considered negligible and the harmonic distortion was therefore ignored. Hence, this actuator was presumed to generate a sinusoidal waveform that was suitable for the novel estimation method.
To reconstruct shear wave maps, the color flow image on the ultrasound scanner was recorded as a moving picture for 2 s. Then, the color flow image was fed into a computer by means of a video capture device. Fourier analysis and a directional filter were applied; shear wave phase, velocity, and propagation maps were reconstructed. The central processing unit time required for image reconstruction was < 1 s. In our experimental setup, shear wave maps were reconstructed at intervals of 4 s until the stop button on the computer screen was clicked.
Participants
Fourteen healthy male college students voluntarily participated in the study. Written informed consent was obtained prior to the first measurement and all study procedures related to human participants were approved by the Human Research Ethics Committee of Nihon Fukushi University. All methods were performed in accordance with the relevant guidelines and regulations. Participants were excluded if they: (1) had lower-extremity contracture; (2) had undergone surgery on their back or lower extremities; (3) had neurological disorders; (4) took hormones or muscle-affecting drugs; and/or (5) regularly engaged in competitive sports or resistance, aerobic, or flexibility training. The participants’ mean (± standard deviation) age, height, body mass, and body mass index were 21.7 ± 0.9 years, 170.7 ± 6.6 cm, 63.5 ± 11.2 kg, and 21.8 ± 3.3 kg/m2, respectively. Participants were asked to maintain their normal dietary habits and refrain from vigorous physical activity the day before and immediately before the experiment.
Experimental design
Shear wave velocities were measured in phantom gels (konjac and agar) and skeletal muscles (right biceps brachii, flexor carpi radialis, semitendinosus, biceps femoris, medial gastrocnemius, and tibialis anterior) twice per day for 2 days, with a between-measurement interval of 1 day. During measurement of phantom gels, two investigators measured shear wave velocity. Phantom gels with different concentrations of agar (1%, 2%, 3%, 4%, and 8%) were mixed with sterilized milk (Table 2). The probe of an ultrasonic diagnostic device was placed directly over the measurement point and the excitation point of the vibrator was positioned next to the probe (Fig. 6). Before measurement, the probe position and excitation point were carefully adjusted, while the wave fronts of shear waves were monitored. In addition, the investigator arranged his posture to ensure maintenance of consistent application force to the vibrator and probe during each measurement. In most instances, the investigator’s elbows were placed on the bed to maintain a stable posture. This positioning was maintained and 3–5 measurements were performed. During measurements of skeletal muscle, the probe position and excitation point were parallel to the long axis of the muscle fibers; this positioning was adjusted to ensure that shear waves clearly propagated in the muscle fiber direction. The elasticity of the middle portion of the muscle was examined and adjusted with reference to the recommended placement of surface electrodes for standardized electromyography measurement53,54. The measurement position was determined based on a body surface landmark. If the positions of the probe and vibrator varied between measurements, the measurement location and shear wave propagation would have differed, resulting in inconsistent measurements. Therefore, the positions of the probe and vibrator were marked on the body surface; the probe and vibrator were positioned at the same site for each measurement. Furthermore, a B-mode image acquired during the first measurement was used as a reference image. Measurements were performed on B-mode images; characteristic points of the fascia, bone, nerves, and blood vessels were kept consistent as much as possible.
Statistical analysis
Statistical analyses were performed using the Statistical Package for the Social Sciences version 15.0 (SPSS Inc., USA). Distribution normality was assessed using the Shapiro–Wilk test. CV values were calculated to indicate measurement reproducibility and reliability55. To investigate the relationship between agar gel concentration and shear wave velocity, Pearson’s correlation analysis was performed. Data were compared using a paired t-test. Differences between conditions were considered statistically significant when P values were < 0.05. ICC (1,1) and ICC (2,1) values with 95% confidence intervals were calculated to determine intra-day, day-to-day, and inter-operator reliabilities. Guidelines from Landis and Koch56 were used to interpret reliability values as follows: 0.0–0.2 indicated slight agreement; 0.21–0.40 indicated fair agreement; 0.41–0.60 indicated moderate agreement; 0.61–0.80 indicated substantial agreement; and 0.81–1.0 indicated near-perfect or perfect agreement.
Data availability
All data needed to evaluate the conclusions in the paper are present in the paper, supplementary material, and/or references cited within.
References
Arokoski, J. P., Surakka, J., Ojala, T., Kolari. P. & Jurvelin, J. S. Feasibility of the use of a novel soft tissue stiffness meter. Physiol. Meas. 26, 215–228 (2005).
Bizzini, M. & Mannion, A. F. Reliability of a new, hand-held device for assessing skeletal muscle stiffness. Clin. Biomech. (Bristol, Avon). 18, 459–461 (2003).
Leonard, C. T. et al. Myotonometer intra- and interrater reliabilities. Arch. Phys. Med. Rehabil. 84, 928–932 (2003).
Klauser, A. S., Faschingbauer, R. & Jaschke, W. R. Is sonoelastography of value in assessing tendons?. Semin. Musculoskelet. Radiol. 14, 323–333 (2010).
Drakonaki, E. E., Allen, G. M. & Wilson, D. J. Ultrasound elastography for musculoskeletal applications. Br. J. Radiol. 85, 1435–1445 (2012).
Chino, K., Akagi, R., Dohi, M., Fukashiro, S. & Takahashi, H. Reliability and validity of quantifying absolute muscle hardness using ultrasound elastography. PLoS ONE 7, e45764 (2012).
Muraki, T. et al. Ultrasound elastography-based assessment of the elasticity of the supraspinatus muscle and tendon during muscle contraction. J. Shoulder Elbow Surg. 24, 120–126 (2015).
Ophir, J., Céspedes, I., Ponnekanti, H., Yazdi, Y. & Li, X. Elastography: a quantitative method for imaging the elasticity of biological tissues. Ultrason. Imaging. 13, 111–134 (1991).
Gao, L., Parker, K. J., Lerner, R. M. & Levinson, S. F. Imaging of the elastic properties of tissue—A review. Ultrasound Med. Biol. 22, 959–977 (1996).
Sarvazyan, A. P., Rudenko, O. V., Swanson, S. D., Fowlkes, J. B. & Emelianov, S. Y. Shear wave elasticity imaging: A new ultrasonic technology of medical diagnostics. Ultrasound Med. Biol. 24, 1419–1435 (1998).
Giammarinaro, B., Zorgani, A. & Catheline, S. Shear-wave sources for soft tissues in ultrasound elastography. I.R.B.M. 39, 236–242 (2018).
Eisenscher, A., Schweg-Toffler, E., Pelletier, G. & Jacquemard P. Rhythmic echographic palpation. Echosismography. A new technic of differentiating benign and malignant tumors by ultrasonic study of tissue elasticity. J. Radiol. 64, 255–261 (1983) (in French).
Krouskop, T. A., Dougherty, D. R. & Vinson, F. S. A pulsed Doppler ultrasonic system for making noninvasive measurements of the mechanical properties of soft tissue. J. Rehabil. Res. Dev. 24, 1–8 (1987).
Lerner, R. M., Huang, S. R. & Parker, K. J. “Sonoelasticity” images derived from ultrasound signals in mechanically vibrated tissues. Ultrasound Med. Biol. 16, 231–239 (1990).
Yamakoshi, Y., Sato, J. & Sato, T. Ultrasonic imaging of internal vibration of soft tissue under forced vibration. I.E.E.E. Trans. Ultrason. Ferroelectr. Freq. Control. 37, 45–53 (1990).
Gao, L., Parker, K. J., Alam, S. K. & Lernel, R. M. Sonoelasticity imaging: theory and experimental verification. J. Acoust. Soc. Am. 97, 3875–3886 (1995).
Sandrin, L., Tanter, M., Gennisson, J. L., Catheline, S. & Fink, M. Shear elasticity probe for soft tissues with 1-D transient elastography. I.E.E.E. Trans. Ultrason. Ferroelectr. Freq. Control. 49, 436–446 (2002).
Salcudean, S. E. et al. Viscoelasticity modeling of the prostate region using vibro-elastography. Med. Image Comput. Comput. Assist. Interv. 9, 389–396 (2006).
Hoyt, K., Castaneda, B. & Parker, K. J. Two-dimensional sonoelastographic shear velocity imaging. Ultrasound Med. Biol. 34, 276–288 (2008).
Zhao, H. et al. External vibration multi-directional ultrasound shearwave elastography (EVMUSE): Application in liver fibrosis staging. I.E.E.E. Trans. Med. Imaging. 33, 2140–2148 (2014).
Mellema D. C. et al. Probe oscillation shear elastography (PROSE): a high frame-rate method for two-dimensional ultrasound shear wave elastography. I.E.E.E. Trans. Med. Imaging. 35, 2098–2106 (2016).
Yang, H., Carrascal, C. A., Xie, H., Shamdasani, V. & Anthony, B. W. 2-D ultrasound shear wave elastography with multi-sphere-source external mechanical vibration: Preliminary phantom results. Ultrasound Med. Biol. 46, 2505–2519 (2020).
Nightingale, K., Soo, M. S., Nightingale, R. & Trahey, G. Acoustic radiation force impulse imaging: In vivo demonstration of clinical feasibility. Ultrasound Med. Biol. 28, 227–235 (2002).
Bercoff, J., Tanter, M. & Fink, M. Supersonic shear imaging: a new technique for soft tissue elasticity mapping. I.E.E.E. Trans. Ultrason. Ferroelectr. Freq. Control. 51, 396–409 (2004).
Palmeri, M. L., Wang, M. H., Dahl, J. J., Frinkley, K. D. & Nightingale, K. R. Quantifying hepatic shear modulus in vivo using acoustic radiation force. Ultrasound Med. Biol. 34, 546–658 (2008).
Chen, S. et al. Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity. I.E.E.E. Trans. Ultrason. Ferroelectr. Freq. Control. 56, 55–62 (2009).
Kuo, W. H., Jian, D. W., Wang, T. G. & Wang, Y. C. Neck muscle stiffness quantified by sonoelastography is correlated with body mass index and chronic neck pain symptoms. Ultrasound Med. Biol. 39, 1356–1361 (2013).
Nightingale, K., McAleavey, S. & Trahey, G. Shear-wave generation using acoustic radiation force: In vivo and ex vivo results. Ultrasound Med. Biol. 29, 1715–1723 (2003).
Herman, B. A. & Harris, G. R. Models and regulatory considerations for transient temperature rise during diagnostic ultrasound pulses. Ultrasound Med. Biol. 28, 1217–1224 (2002).
Gonzalez, E. A., Romero, S. E. & Castaneda, B. Real-time crawling wave sonoelastography for human muscle characterization: initial results. I.E.E.E. Trans. Ultrason. Ferroelectr. Freq. Control. 66, 563–571 (2019).
Moradi, M. et al. Multiparametric 3D in vivo ultrasound vibroelastography imaging of prostate cancer: preliminary results. Med. Phys. 41, 073505 (2014).
Mohareri, O. et al. Multi-parametric 3D quantitative ultrasound vibro-elastography imaging for detecting palpable prostate tumors. Med. Image Comput. Comput. Assist. Interv. 17, 561–568 (2014).
Yamakoshi, Y., Kasahara, T., Iijima, T. & Yuminaka, Y. Shear wave wavefront mapping using ultrasound color flow imaging. Ultrason. Imaging. 37, 323–340 (2015).
Yamakoshi, Y. et al. Shear wave imaging of breast tissue by color Doppler shear wave elastography. I.E.E.E. Trans. Ultrason. Ferroelectr. Freq. Control. 64, 340‐348 (2017).
Yamamoto, A. et al. Shear wave velocity measurement of upper trapezius muscle by color Doppler shear wave imaging. J. Med. Ultrason. 2001(45), 129–136 (2018).
Salavati, M. et al. Reliability of the upper trapezius muscle and fascia thickness and strain ratio measures by ultrasonography and sonoelastography in participants with myofascial pain syndrome. J. Chiropr. Med. 16, 316–323 (2017).
Vlaanderen, E., Conza, N. E., Snijders, C. J., Bouakaz, A. & De Jong, N. Low back pain, the stiffness of the sacroiliac joint: A new method using ultrasound. Ultrasound Med. Biol. 31, 39–44 (2005).
Zhou, X., Kenwright, D. A., Wang, S., Hossack, J. A. & Hoskins, P. R. Fabrication of two flow phantoms for Doppler ultrasound imaging. I.E.E.E. Trans. Ultrason. Ferroelectr. Freq. Control. 64, 53–65 (2017).
Meagher, S., Poepping, T. L., Ramnarine, K. V., Black, R. A. & Hoskins, P. R. Anatomical flow phantoms of the nonplanar carotid bifurcation, part II: Experimental validation with Doppler ultrasound. Ultrasound Med. Biol. 33, 303–310 (2007).
Li, C., Guan, G., Cheng, X., Huang, Z. & Wang, R. K. Quantitative elastography provided by surface acoustic waves measured by phase-sensitive optical coherence tomography. Opt. Lett. 37, 722–724 (2012).
Ballyns, J. J. et al. Office-based elastographic technique for quantifying mechanical properties of skeletal muscle. J. Ultrasound Med. 31, 1209–1219 (2012).
Chan, S. T. et al. Dynamic changes of elasticity, cross-sectional area, and fat infiltration of multifidus at different postures in men with chronic low back pain. Spine J. 12, 381–388 (2012).
Shinohara, M., Sabra, K., Gennisson, J. L., Fink, M. & Tanter, M. Real-time visualization of muscle stiffness distribution with ultrasound shear wave imaging during muscle contraction. Muscle Nerve. 42, 438–441 (2010).
Arda, K., Ciledag, N., Aktas, E., Aribas, B. K. & Köse, K. Quantitative assessment of normal soft-tissue elasticity using shear-wave ultrasound elastography. A.J.R. Am. J. Roentgenol. 197, 532–536 (2011).
Leong, H. T., Ng, G. Y., Leung, V. Y. & Fu, S. N. Quantitative estimation of muscle shear elastic modulus of the upper trapezius with supersonic shear imaging during arm positioning. PLoS ONE 8, e67199 (2013).
Gennisson, J. L. et al. Viscoelastic and anisotropic mechanical properties of in vivo muscle tissue assessed by supersonic shear imaging. Ultrasound Med. Biol. 36, 789–801 (2010).
Akagi, R. & Takahashi, H. Acute effect of static stretching on hardness of the gastrocnemius muscle. Med. Sci. Sports Exerc. 45, 1348–1354 (2013).
Lacourpaille, L., Hug, F., Bouillard, K., Hogrel, J. Y. & Nordez, A. Supersonic shear imaging provides a reliable measurement of resting muscle shear elastic modulus. Physiol. Meas. 33, N19–N28 (2012).
Dubois, G. et al. Reliable protocol for shear wave elastography of lower limb muscles at rest and during passive stretching. Ultrasound Med. Biol. 41, 2284–2291 (2015).
Koo, T. K., Guo, J. Y., Cohen, J. H. & Parker, K. J. Quantifying the passive stretching response of human tibialis anterior muscle using shear wave elastography. Clin. Biomech. (Bristol, Avon). 29, 33–39 (2014).
Yamakoshi, Y., Yamamoto, A., Kasahara, T., Iijima, T. & Yuminaka, Y. Shear wave mapping of skeletal muscle using shear wave wavefront reconstruction based on ultrasound color flow imaging. Jpn. J. Appl. Phys. 54, 07HC16 (2015).
Yamakoshi, Y., Yamamoto, A. & Yuminaka, Y. Novel imaging method of continuous shear wave by ultrasonic color flow mapping. Phys. Procedia. 70, 1083–1086 (2015).
Cram, J. R. Introduction to Surface Electromyography (Aspen, 1998).
Hermens, H.J. SENIAM, Sensor Locations. http://www.seniam.org/ (2020)
Glüer, C. et al. Accurate assessment of precision errors: how to measure the reproducibility of bone densitometry techniques. Osteoporos. Int. 5, 262–270 (1995).
Landis, J. R. & Koch, G. G. The measurement of observer agreement for categorical data. Biometrics 33, 159–174 (1977).
Acknowledgements
The authors are grateful to Mayuko Yamazaki (Nihon Kohden), Sena Wakano (Ogaki Municipal Hospital), Shou Ariyoshi (Osaka Medical College Hospital), Rina Terasawa (Nagoya Ekisaikai Hospital), and Hideyuki Shiga (Sanjinkai Asahi Hospital) for their technical assistance in performing the experiments. This work was supported by JSPS KAKENHI Grant Number 18K10766 (WT) from the Japan Society for the Promotion of Science (JSPS) and in part by a grant from the Public Advertisement Research Project of Nihon Fukushi University. We thank Emily Woodhouse, PhD, and Ryan Chastain-Gross, PhD, from Edanz Group (https://en-author-services.edanzgroup.com/ac) for editing a draft of this manuscript.
Author information
Authors and Affiliations
Contributions
W.T. and Y.Y. conceived the project, designed the experimental approach, conducted experiments, analyzed the data, and prepared the manuscript. M.A., K.S., T.F., and E.Y. performed the experiments and analyzed the data. S.M., Y.A., N.N., T.O., and S.S. analyzed the results and wrote the manuscript. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tsuchida, W., Yamakoshi, Y., Matsuo, S. et al. Application of the novel estimation method by shear wave elastography using vibrator to human skeletal muscle. Sci Rep 10, 22248 (2020). https://doi.org/10.1038/s41598-020-79215-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-79215-z
This article is cited by
-
Examination of rapid adjustment system based on screen score obtained using continuous shear wave elastography
Journal of Medical Ultrasonics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.