Abstract
Light-sheet microscopy enables considerable speed and phototoxicity gains, while quantitative-phase imaging confers label-free recognition of cells and organelles, and quantifies their number-density that, thermodynamically, is more representative of metabolism than size. Here, we report the fusion of these two imaging modalities onto a standard inverted microscope that retains compatibility with microfluidics and open-source software for image acquisition and processing. An accelerating Airy-beam light-sheet critically enabled imaging areas that were greater by more than one order of magnitude than a Gaussian beam illumination and matched exactly those of quantitative-phase imaging. Using this integrative imaging system, we performed a demonstrative multivariate investigation of live-cells in microfluidics that unmasked that cellular noise can affect the compartmental localization of metabolic reactions. We detail the design, assembly, and performance of the integrative imaging system, and discuss potential applications in biotechnology and evolutionary biology.
Similar content being viewed by others
Introduction
Selective plane illumination microscopy (SPIM) and light-sheet imaging (LSI), including the use of optical lattices or quasi-lattices (LLSI), have enabled substantial gains against photobleaching and toxicity in optically sectioning cellular or multicellular specimens1,2,3,4,5,6,7,8,9. Conversely, quantitative-phase imaging (QPI) retains low phototoxicity and confers label-free recognition and number-density quantification of single cells and their organelles10,11,12,13,14. These two imaging modalities offer complementary advantages. On the one hand, LSI (or LLSI) registers the 4D dynamics of fluorescent proteins with high spatiotemporal resolution and minimal physiology perturbation; QPI, on the other hand, unravels the number-density of cells (and their organelles) that is enthalpically more representative of metabolism than size, as determined by conventional, volumetric, microscopy12. Further, QPI’s capability of label-free organelle recognition (e.g., nuclei, mitochondria, lipid droplets) via direct thresholding of the innate refractive index variations11,12 or deep learning15,16,17 offers two additional advantages. First, it improves wavelength-multiplexing by freeing spectral channels that would otherwise be occupied by fluorescent reporters targeting specific organelles. Second, it can potentially improve the precision of organelle localization, given that gene-encoded fluorescent reporters can display binding bistability between organelles, such as Glycerol-3-phosphate acyltransferase 4 (GPAT4) decorating both the endoplasmic reticulum and lipid droplets (LDs)18.
Integrating QPI with LSI (or LLSI) requires configurations that: (a) are compatible with conventional sample mounting techniques; and (b) do not disrupt image acquisition in either modality. While QPI is compatible with most sample mounting techniques and microfluidics, LSI and LLSI generally require practices that are atypical to common cell culture techniques (e.g., cells embedded in agarose tubes) or are prone to contamination (e.g., objectives dipped into the sample chamber). Regarding undisrupted image acquisition, this is particularly pertinent to QPI since it relies on the interference between the transmitted field through the cell (signal) and a reference field14. Any photon losses or spatial frequency limitations to both fields would be detrimental to the fidelity and resolution of the reconstructed image.
Undisrupted QPI is challenging in most LSI (or LLSI) configurations utilizing two orthogonal objectives in close proximity due to the resulting obstructions in the signal or reference paths3,4. Single-objective configurations can potentially alleviate any spatial frequency or energy losses and enable compatibility with common sample-mounting techniques. To this end, several single-objective configurations have been recently reported, with some enabling extremely large fields-of-view (FOVs)19,20,21,22; however, approaches that enable submicron (planar/axial) resolution, such as epi-illumination SPIM or highly inclined and laminated optical sheet (HILO)6,7,8, typically achieve only a fraction of the field-of-view (FOV) endowed by QPI (for example the FOV reported in8 with an illumination beam of a 70 μm diffraction-free propagation length is approximately 5 × less than what would be possible with QPI). Inevitably, this FOV discrepancy at submicron (or subcellular) resolution levels can yield significant differences between the throughput rates of QPI and LSI (or LLSI), which can be detrimental to statistically significant investigations at the single-cell level.
Despite major recent advances in QPI and LSI (or LLSI), these two modalities rely on disparate hardware configurations and sample-mounting techniques. These limitations hinder integrative QPI and LSI imaging and, thus, key live-cell imaging investigations at the single-cell level. One such example pertains to delineating the stochastic effects in gene and metabolic networks23, where the former can be deciphered by gene-encoded fluorescent markers and the latter precisely quantified by QPI. Here, we report an integrative imaging system that acquires QPI and LSI images of the same targets (Fig. 1a,b) with identical FOVs. Further, this integrative imaging system exhibits no disruptions to the image acquisition process of either imaging modality, compatibility with conventional sample mounting techniques and microfluidics, and open access software for image acquisition and processing. We detail the design and performance of this integrative imaging system, along with a representative bioimaging application in the following section.
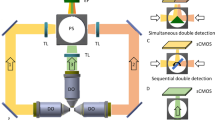
(a) A representative 3D fluorescent image of 500 nm diameter particles using Airy beam illumination after deconvolution. (b) The same particles as in (a) displayed by QPI; inset depicts the scale bar in radians. (c) Schematic illustration of the imaging set-up comprising of two objectives arranged orthogonally, one for detection (63x/0.7) and one (20x/0.42) for guiding the Airy beam to a sample enclosed in a microfluidic system; the Airy beam is generated by a spatial light modulator (SLM) and scanned in the y direction. A 0.55-NA condenser guides the white illumination on to the sample, and the transmission is encoded by a second SLM to reconstruct the optical-phase image. RDF stands for reflecting dichroic filter, which directs the fluorescent signal to sCMOS1 and the transmitted white light to a second SLM and sCMOS2.
Results
Design and assembly
The reported integrative imaging system combines spatial light interference microscopy (SLIM) for QPI with an Airy beam light-sheet for 3D fluorescent imaging on to a standard inverted microscope (Fig. 1c). Specifically, SLIM operates by illuminating the sample in a Koehler configuration through a high numerical aperture condenser (NA 0.55, 2.8 cm working distance) and guiding the sample transmission via an objective (63x/0.7) onto a spatial light modulator (Fig. 1c)24. The latter is positioned at a conjugate image plane from a standard camera port and applies additional phase-delays to the non-diffracted wavefront (background) with respect to the diffracted wavefront (see “Methods” for more details). At this configuration, SLIM reconstructs quantitative-phase images of approximately 200 × 200 μm2 areas and planar resolution of 0.641 ± 0.006 μm (mean ± standard error, n = 25 beads with a 500 nm diameter). SLIM’s sensitivity and resolution has been previously shown to effectively quantify the growth kinetics of single Escherichia coli and mammalian cells25 and nutrient allocation between growth and lipid production in single yeast cells12.
To integrate QPI with LSI of identical imaging areas and inspired by previous demonstrations5, we implemented a self-accelerating Airy beam26 for fluorescent light-sheet excitation. The set-up for generating the Airy beam (further detailed in Fig. S1 and in “Methods” ), consisted of a second spatial light modulator that exhibited an appropriate cubic phase mask (Fig. 2). This mask was imaged to the back focal plane of an illumination objective (20x/0.42) with a ~ 0.8 × overall magnification. The illumination objective was positioned orthogonally to the detection objective (Fig. 1c), with the latter being the same (63x/0.7) for both QPI and Airy-LSI.
Guided by a computational model relying on the Fast Fourier Transform Beam Propagation Method (see “Methods” for more details), we adopted an Airy beam with a cubic phase mask exhibiting a α = 5.38 mm-3 scaling parameter, thus, varying from − 84 π to + 84 π over a 10 mm range (Fig. 2). This phase mask bestowed an Airy beam with a diffraction-free path (along the x-axis in Fig. 1c) that was comparable to the dimensions of the SLIM image. Denser phase modulation further increased the diffraction-free path; however, this approach also positioned the side-lobes of the vertical structure of the Airy beam farther from each other, hindering the utility of high NA objectives.
Importantly, the set-up implemented a long working distance (20 mm) illumination objective and a custom-made 3D microscope stage. The long working distance objective enabled fluorescent excitation without obstructing QPI’s Koehler illumination. The custom stage was equipped with a piezo-electric module to vertically scan the sample with respect to the plane of illumination to enable the 3D image reconstruction. The stage was also open-ended on one side (Fig. S2), enabling complete optical access to the side-plane (yz plane in Fig. 1c) of the sample. Optical access was further facilitated by tailored microfluidic systems. These microsystems were fabricated via the combination of UV and soft lithography in a polymer that was index-matched to water and exhibited low side-wall surface roughness using (Fig. S3 and “Methods”). In essence, index matching to water rendered the microfluidics invisible to the fluorescent excitation, thus, eliminating optical aberrations at the polymer-water interface. The bottom wall of the microsystem (xy plane in Fig. 1c) and its side wall (yz plane in Fig. 1c) were 400 μm and 800 μm thick, respectively. These dimensions enabled imaging cells at the bottom surface of the microsystem without any distortion to the Airy beam27. This is because the vertical dimension of the Airy beam (i.e., the extend of the beam’s intensity along the z-axis in Fig. 1c) was significantly smaller than the thickness of the bottom wall of the microfluidic system. In turn, this enabled optical access to the sample without the illumination beam crossing the refractive index boundary at the air-polymer interface at the bottom wall of the microsystem. This finding is supported by the experimental results presented in Fig. S4.
Performance
In agreement with the computational model, the propagation invariant intensity property of the Airy beam enabled a diffraction-free path (x-axis in Fig. 1c) of approximately 200 μm, as visualized in a uniformly fluorescent polymer at a wavelength of 488 nm (Fig. 3a). This value was considerably larger than the respective path of a Gaussian beam at the same wavelength, which increased linearly in diameter by almost two orders of magnitude for the same propagation distance (Fig. 3a). To form a 2D image, the Airy beam was scanned with a MEMS mirror over a 200 μm range (y-axis in Fig. 1c). As such, we attained a 200 × 200 μm2 imaging area for LSI that matches exactly that of QPI. This imaging area surpasses previous demonstrations utilizing optical lattice configurations4 (0.37 μm axial resolution) and propagation invariant Bessel beams in an epi-illumination SPIM format (0.44 μm axial resolution by not considering the side-lobes)8, and smaller (by ~ 0.6 ×) than previous Airy beam demonstrations (0.86 μm axial resolution5). For comparison, the field-of-view using a Gaussian illumination beam in our set-up was approximately 200 × 10 μm2.
(a) Experimental data of the Airy and Gaussian beam propagation and diffraction in a uniformly fluorescent sample; dots illustrate the experimental data and solid lines the simulation results of the approximated beam diameter; the y-axis is normalized to the minimum value of each beam. (b) Full-width half maximum (FWHM) along the z-axis of 25 fluorescent particles (500 nm in diameter) denoting the axial resolution; the red data points depict the experimentally determined mean values and the blue shaded areas the 95% confidence intervals, while the legend notes the average (± s.e.) of the 25 observations; inset depicts a representative 3D view of particle before (left) and after (right) deconvolution.
To experimentally determine the resolving power of the Airy LS system along the z-axis (Fig. 1c), we employed 500 nm diameter fluorescent particles embedded in a non-scattering matrix. The full-width-at-half-maximum (FWHM) along the z-axis was 0.748 ± 0.020 μm (mean ± standard error, n = 25, Fig. 3b). We obtained this value after deconvolution to remove the transverse structure of the Airy beam, using an experimentally determined 3D point-spread-function and the Richardson-Lucy algorithm (see “Methods” for more details). This value is slightly higher than the system’s planar resolution (determined using 200 nm diameter beads at 0.523 ± 0.021 μm, mean ± standard error, n = 25, Fig. S5), enabling quasi-isotropic 3D imaging. Further, our determined lateral resolution was moderately higher than previous reports using an Airy beam light-sheet5. We attribute this improvement to the implementation of a higher NA detection objective that enabled the collection of the main Airy lobe as well as 3 side lobes (Fig. 3b, inset). Importantly, the axial resolution was more than half of the diameter of the main lobe of the Airy beam. This suggests that, in agreement with previous demonstrations5, the transverse structure of the Airy beam is accounted for by deconvolution and contributes positively to the imaging process.
Multivariate bioimaging
To demonstrate the applicability of the reported integrative system, we performed a representative live-cell, multivariate imaging investigation in microfluidics using the oleaginous yeast Yarrowia lipolytica28,29,30,31. We selected this model system for two reasons. First, Y. lipolytica cells exhibit overall dimensions (ellipsoidal volume with typically a 5.3 ± 0.4 μm major axis, mean ± standard error, Fig. S6) that are challenging for LSI. Second, Y. lipolytica represents an important tractable model system for the production of 2nd generation biofuels28. In this context, Y. lipolytica has been shown to accumulate increased amounts of triacylglycerides, a biodiesel precursor, within a cytosolic organelle termed the lipid droplet (LD)32,33,34. In addition to biotechnology applications, LDs are also central in cellular metabolism and energy homeostasis35,36,37, disease38,39,40, as well as protein, chromatin component and transcription factor trafficking41,42,43,44.
For imaging, we collected a demonstrative subpopulation of a Y. lipolytica culture expressing a GFP-tagged ergosterol 6 enzyme (erg6, YALI0F08701g45, see “Methods” for more details on the strain) growing in batch. We collected cells at 48 h and 96 h, two timepoints that correspond to low and high lipid content, respectively12. Subsequently, we introduced the cells into a microfluidic system (“Methods” ) and allowed them to sediment to the bottom surface.
Critically, QPI enabled the segmentation of single-cells without any dedicated computational approaches or staining procedures, but rather taking advantage of the cells’ higher optical-phase delay than the background46. Similarly, we segmented the LDs of individual cells in QPI by relying on their higher optical phase-delay than the cell cytosol (Fig. 4), without any additional staining12,47. Within each segmented cell, we quantified the 3D distribution of fluorescent erg6 enzymes using the Airy LSI at a 488 nm excitation wavelength (Fig. 4).
(a) Maximum projection (xy plane) of a Y. lipolytica Airy-QPI integrative image; blue denotes the QPI image (scale bar in radians), red localizes the LDs (i.e., the phase-thresholded masks), and white denotes the GFP-erg6 fluorescence; on the right, select magnified areas of erg6 are displayed in the xy and yz planes with each box size being ~ 5 × 5 × 5 μm3.
A comparison between the erg6 distribution with the LD location unmasked two unexpected forms of spatial heterogeneity. In the first, erg6 either localized in the vicinity of LDs or displayed diffusive behavior (Fig. 4). By diffusive, we specifically refer to states where erg6 does not localize in the vicinity of an LD, but potentially to the endoplasmic reticulum48 or a vacuole49. For the latter specifically, cells grown under nutrient limiting conditions can switch from growth and division to carbon storage and autophagy. The process of autophagy can consume the contents of organelles12,49,50, which can be a potential source for the dispersed erg6 signal. Further quantitative analysis revealed that the heterogeneous occupancy of diffusive and localized states occurred both at the early and late stage of lipogenesis, characterized by a statistically significant dependence on the erg6 expression levels (Fig. 5a). Specifically, cells with overall higher erg6 expression levels were more likely to exhibit localized erg6 in the vicinity of an LD.
(a) Box-plots comparing the erg6 expression levels for localized (blue) and diffusive (red) states at two different time points: 48 h (n = 61) and 96 h (n = 55); box-plots represent the 25th and 75th percentiles and whiskers the 10th and 90th percentile; asterisks denote statistically significant differences between distributions (Mann–Whitney Test, U = 100, p = 0.01 for 48 h and U = 150.5, p = 0.001 for 96 h). (b) Similar box-plots as in (a), comparing the erg6 expression levels and dry-density for cells exhibiting low (less than 10%) and high (greater than 10%) coverage of the LD surface area by erg6; the y-axis is normalized with respect to the expression and density median values of the population, while asterisks denote statistically significant differences between distributions (Mann–Whitney Test, U = 64, p = 0.03 for eg6 expression and U = 18, p = 0.07 for cellular dry-density).
The second form of spatial heterogeneity pertained particularly to erg6 localized states. Focusing on the 96 h timepoint, we observed that enzymes did not uniformly decorate the 3D surface of LDs, but rather exhibited clusters that offered only partial coverage (Fig. 4). Using the 3D resolving capability of the Airy LSI, we quantified the percentage of the LD surface area that was in contact with erg6. In this context, we observed that the low relative contact areas exhibited increased erg6 expression levels, while conversely, high contact areas exhibited lower expression levels of erg6 (Fig. 5b). In other words, cells with overall increased erg6 expression levels were statistically more likely to exhibit reduced contact areas between LDs and erg6 (Fig. 5b). Interestingly, similar statistical evidence between the cellular dry-density (determined by the cell’s optical phase, see “Methods” ) and LD coverage was not found (Fig. 5b). The latter indicates that cells stochastically overproducing biomass building blocks (e.g., proteins, ribosomes, DNA, lipids) do not regulate specifically the contact area between erg6 and LDs, and possibly the spatial heterogeneity of ergosterol biosynthesis. Critically, the increased cellular density did not correlate with erg6 expression levels, suggesting that increased production of biomass does not gratuitously lead to erg6 overexpression51.
Discussion
Single-cell biology has led to a plethora of unexpected discoveries, primarily catalyzed by advances in optical imaging52,53,54,55,56, as well as sequencing and metabolomics57,58,59. In the context of optical imaging, the advent of SPIM, LSI and LLSI has greatly advanced our ability to probe dynamic and structural cellular phenotypes at unprecedented imaging speeds and phototoxicity levels1,2,3,4,5,6,7,8,9. Low phototoxicity is also bestowed by QPI, which additionally informs about the location, size, and dry-density of cells and their organelles10,11,12,13,14,15,16,17. Importantly, dry-density offers insight that is enthalpically more pertinent to cellular physiology and metabolism than what is possible by volumetric bioimaging, including LSI 12.
Here, we reported the fusion of these two imaging modalities on to a standard inverted microscope. By relying on a self-accelerating Airy beam illumination pattern, this integrative system exhibited identical fields-of-view in each modality without any disruptions to their respective optical paths. Importantly, this design is compatible with microfluidics that alleviate some of the stringent culture and sample preparation techniques required by common LSI and LLSI configurations. Further, the described integrative design is compatible with most QPI methods, including holographic tomography and appropriate methods for thick and multiply scattering samples60,61, open-source software62,63, and alternative microscope frames, making it accessible to the broader scientific community, including non-specialists.
As a representative example, we applied the reported integrative imager to a microorganism that is challenging to image due to its small dimensions. In this context, we discovered that clonal cells can exhibit two distinct forms of spatial heterogeneity. Specifically, we observed that enzymes participating in ergosterol biosynthesis localized heterogeneously both in the cytosolic milieu and around the LDs. We also observed that, when localized, erg6 decorates heterogeneously the LDs. These two forms of spatial heterogeneity suggest that ergosterol biosynthesis (and possibly degradation) is likely also spatially heterogeneous. Such forms of heterogeneity not only indicate that LD recognition solely from the GFP signal of erg6 can be limiting, but also that cellular noise affecting the levels of erg6 expression, may also impact the compartmental localization of metabolic reactions. This observation raises further questions about the underlying metabolic costs, efficiencies, and evolutionary consequences of metabolic compartmentalization64. This live-cell imaging experiment represents one example of how the present integrative imaging system can be applied to single-cell biology investigations, namely: the application of QPI to inform about organelle location in a label-free fashion and cell metabolism via the enthalpically relevant metric of dry-density, and Airy LSI to inform about 3D protein dynamics.
Methods
Optical setup
The integrative imaging setup is detailed in Fig S1. We employed a laser source (EXLSR-488C-200-CDRH, Spectra Physics, 200 mW, 488 nm) for fluorescence excitation. The beam was expanded to a 10 mm diameter using a spatial filter (910A, Newport) comprising of a 25 μm diameter pinhole and an objective (10x/0.25 NA, Wild Heerbrugg), and subsequently collimated with a converging lens of 25 cm focal length. A half-wave plate (WPHSM05-488, Thorlabs) was installed before the Spatial Light Modulator (MSP 1920-400-800-HSP8, Meadowlark Optics). The SLM displayed a cubic phase mask that was generated in Matlab (Mathworks), with the 0 and 2π phase levels corresponding to 0 and 255 grey-levels, respectively. A 4f system (f1 = 75.6 cm and f2 = 40 cm lenses) was installed with f1 image conjugated to the SLM (i.e., the SLM was placed at the back-focal plane of f1) and f2 conjugated to a laser scanner (i.e., the laser scanner was placed at the focal plane of f2). The scanner was assembled within a 30 mm cage system, and comprised of a second 4f system (f3 = 3.5 cm and f4 = 1.2 cm), a 2D MEMS mirror (2.8 mm diameter, Mirrorcle Technologies), a scan lens (f5 = 7.5 cm), a tube lens (f6 = 30 cm), and a large working distance illumination objective (20x/0.42, Mitutoyo). The long focal-length tube lens was specifically employed to accommodate the extend of the microscope frame along the y-axis (Fig. 1c and Sup. Figure 2). The scanner was positioned on a custom-made 3D stage with a 5 cm travel range in all three axes, 1 μm resolution in the vertical axis (z-axis in Fig. 1c) and 10 μm planar resolution (xy plane in Fig. 1c). The 3D stage enabled us to precisely align the focused Airy beam with the focal planes of the detection objective (63x/0.7, PH2, Leica) and the condenser of a standard inverted microscope (DMi8, Leica). The microscope was equipped with a focus stabilization system, as well as automation in the objective turret and filter wheel position. 3D fluorescent images were captured by a scientific CMOS camera (ORCA-Flash 4.0, Hamamatsu) connected to one port of the microscope using the MicroManager ASIdiSPIM plugin. A spatial light interference microscopy (SLIM) set-up was installed on the second microscope port to relay the conjugate image plane onto a second sCMOS camera (ORCA-Flash 4.0, Hamamatsu) using a 4f system (15 cm focal lengths for both lenses), as previously described20. A second SLM (STD 512-450-850-ExtFlip, Meadowlark Optics) was positioned at the Fourier plane of the first lens of the 4f system to modulate the phase difference between the scattered and un-scattered components of light at increments of π/2, π, 3π/2 and 2π. Similar to conventional phase contrast microscopy, the scattered and un-scattered wavefronts were separated by applying hollow cone illumination using an illumination condenser (in Koehler configuration) equipped with the appropriate annulus (PH2). Under these illumination conditions, only the scattered light deviates from the illumination cone and, thus, is projected on to a different location of the SLM. Using this approach, we acquired quantitative-phase images in an automated fashion (CellVista Pro, Phi Optics) through the same detection objective, informing about the relative phase delay of the cells (scattered wavefront) with respect to the background (un-scattered wavefront). According to previous reports24, the minimum detectable phase step is less than 1 mrad with this system.
Optical alignment
Irises along the optical path (Fig. S1) ensured the excitation laser passed through the center of all optical elements, as well as enabled the selection of the first-order diffraction from the SLM and alignment inspection on a daily basis. Once installed, our optical system remained stable for months, requiring only minor mirror adjustments every few days. The active SLM pattern was aligned with the excitation beam using a CMOS camera (acA3800-14um, Basler). During installation, we ensured that the microscope stage and scanner were properly aligned by coupling the 488 nm beam to a single mode fiber (MBT613D, Thorlabs) and interfacing it with the scanner’s cage through a fiber-port collimator (PAF2P-11E, Thorlabs). By inspecting the excitation beam profile at the image plane, we made the necessary adjustments in the scanner and microscope position until the illumination and detection planes overlapped. Subsequently, we removed the fiber and aligned the free-space 488 nm beam with respect to the input and output ports of the scanner using an alignment target (CPA1, Thorlabs) and a CMOS camera mounted on the microscope stage (acA3800-14um, Basler). The Airy beam quality was inspected both with the stage-mounted CMOS camera, as well as the sCMOS camera connected to the microscope port. For the latter, we employed both a custom-made 90ο reflector on the microscope stage or a fluorescent polydimethilsiloxane (PDMS) sample.
Custom microscope stage
A custom-made microscope stage was employed to position the sample and scan it in all three directions for imaging (Fig. S2). The stage comprised of a piezoelectric system (IPZ-3150, Applied Scientific Instrumentation) with a 2.2 nm resolution and 150 μm total travel range. The piezo stage was integrated with two linear stages (LS-50, Applied Scientific Instrumentation), each exhibiting 5.5 nm encoder resolution and 50 mm total travel range. For acquisition, we synchronized the piezo stage, linear stages, and 2D MEMS mirror using a controller (TG-1000-8, Applied Scientific Instrumentation) equipped with programmable logic, and communication cards. To enable 3D imaging at a single location, the sample was scanned vertically (i.e., along the z-axis in Fig. 1c) using the piezo stage, and the Airy beam planarly (i.e., along the y-axis in Fig. 1c) using the MEMS mirror (Fig. S1).
Data acquisition and processing
Micro-Manager 1.462 and CellVista Pro (Phi Optics)24 were used for fluorescent and quantitative-phase image acquisition. A PC (Z8, Hewlett-Packard) equipped with Intel Xeon W-2123 W CPU @ 3.60 GHz processors and 128 GB RAM acquired and temporarily stored raw 3D images. For longer term storage, we transferred all data to a server. Images were analyzed using ImageJ65 on a workstation equipped with an Intel Core i7-7820X CPU @ 3.60 GHz processors and 128 GB RAM. Image deconvolution was performed using the Richardson-Lucy algorithm in the DeconvolutionLab2 ImageJ plugin63, using an experimentally determined point spread function (PSF) derived from a 3D stack of 0.2 μm diameter fluorescent particles. 3D image reconstruction was performed using the VolumeViewer plugin (ImageJ).
Optical model
To guide our experimental approach and validate our results (Fig. 3), we built a numerical model to describe the propagation of the Airy beam. The model considers a monochromatic wave with an electric field component in the \(\stackrel{\sim }{E}(x,y,z,t)=E(x,y,z){\bullet e}^{-i\omega t}\) form. This wave satisfies the Helmholtz wave equation \({\nabla }^{2}E+{k}^{2}E=0\), where \(k=\frac{2\bullet \pi \bullet n}{\lambda }\) is a wavenumber, \(\lambda\) represents the wavelength of the illumination and \(n\) the refractive index. The wave’s \(E(x,y,z)\) component can be written as a Fourier superposition of plane waves in the following form:
where \({k}_{z}=\sqrt{{k}^{2}-{k}_{x}^{2}-{k}_{y}^{2}}\) and \(A({k}_{x},{k}_{y})\) is the Fourier spectrum defined by the initial field profile at the input \(z={z}_{o}\) through a Fourier transform:
We solved Eqs. (1) and (2) via the Fast Fourier Transform Beam Propagation Method (FFT-BPM) that computes the field profile \(E(x,y,z)\) at any z for a known field distribution at \({z}_{o}=0\). As the input field (at \({z}_{o}=0\)), we considered Gaussian illumination of the SLM cubic phase, namely: \({E}_{o}=E\left(x,y,z=0\right)={Ae}^{-\frac{{x}^{2}+{y}^{2}}{{w}_{o}^{2}}} {\bullet e}^{\frac{i\bullet \alpha }{3}\left({x}^{3}+{y}^{3}\right)}\) , where \(\alpha\) is the scaling parameter of the phase, and \({w}_{o}\) and \(A\) represent the width and the amplitude of the illumination, respectively. Utilizing the FFT-BPM algorithm, we propagated the beam from \(z=0\) to all individual lenses (i.e., at distances \(z={f}_{i}\), with \({f}_{i}\) being the focal length of each lens) described in the optical set-up of Fig S1 and multiplied the field \(E\left(x,y,z={f}_{i}\right)\) with the transmission function \({T}_{i}(x,y)\) of each lens. To mimic the propagation through the lens, we used the thin lens approximation with the transmission function \({T}_{i}\left(x,y\right)= {e}^{-\frac{i\bullet \frac{2\bullet \pi }{\lambda }\bullet ({x}^{2}+{y}^{2})}{2\bullet {f}_{i}}}\). The employed algorithm is detailed as follows:
-
1.
Start from the input field at the SLM plane \(z={z}_{o}\), given by \({E}_{0}\).
-
2.
Propagate \({E}_{0}\) in free space up to the first lens, placed at \({z}_{1}={z}_{o}+{f}_{1}\):
$${E}_{01}=IFFT\left\{FFT\left\{{E}_{0}\right\}{e}^{i{k}_{z}{f}_{1}}\right\}$$ -
3.
Compute the field after the first lens as:
$${E}_{1}={E}_{01}{\bullet T}_{1}$$ -
4.
Propagate \({E}_{1}\) in free space until the second lens, placed at \({z}_{2}={z}_{1}+{f}_{1}+{f}_{2}\):
$${E}_{12}=IFFT\left\{FFT\left\{{E}_{1}\right\}{e}^{i{k}_{z}\left({f}_{1}+{f}_{2}\right)}\right\}$$ -
5.
Compute the field after the second lens as:
$${E}_{2}={E}_{12\bullet }{T}_{2}$$ -
6.
Propagate and compute beam after all experimental lenses, up until the last lens, placed at \({z}_{7}={z}_{6}+{f}_{6}+{f}_{7}\):
$${E}_{67}=IFFT\left\{FFT\left\{{E}_{6}\right\}{e}^{i{k}_{z}\left({f}_{6}+{f}_{7}\right)}\right\}$$ -
7.
Compute the field after the last lens as:
$${E}_{7}={E}_{67}{\bullet T}_{7}$$ -
8.
Propagate \({E}_{7}\) in free space for another distance \(\Delta {z}_{8}\):
$${E}_{8}=IFFT\left\{FFT\left\{{E}_{7}\right\}{e}^{i{k}_{z}\Delta {z}_{8}}\right\}$$
To overcome memory limitations while maintaining high accuracy, we simplified the model to 2D by neglecting the third dimension. The parameters used in the simulation were: \(\lambda =0.488 \mu m\), \(n=1\), \(A=1\), \({w}_{o}=4.3 mm\), \(\alpha =5.38 {mm}^{-3}\), while all focal lengths were identical to the experimental ones listed in Fig. S1 and the illumination objective set at \({f}_{7}=2 cm\). We obtained the final results at a 4 mm range around the focal length of the last lens with a grid size of \(N={2}^{20}\), as well as a transverse and longitudinal sampling of \(\Delta x=0.2 \mu m\) and \(\mathrm{\Delta z}=0.2 \mu m\).
Optical resolution and PSF characterization
To characterize the axial resolution of our optical system (Fig. 3b), we employed fluorescent particles embedded in an agarose gel. To prepare the gel sample, we mixed 1.5% agarose (Ultra-Pure, Invitrogen) with deionized water and kept the mixture in a convection oven at 80 °C for 45 min until the agarose completely dissolved. Subsequently, fluorescent micro-spheres were added to the gel and mixed thoroughly. For optimal particle density, we diluted the particle solution of 1% solids by approximately 104. The mixture was then poured into a custom holder, in-between two coverslips for 15 min to solidify prior to imaging. Specifically, we employed 0.5 μm and 0.2 μm mean diameter particles (FSDG003 and FSDG004, Bangs Laboratories) to quantify the system’s z-resolution and point spread function, respectively. For both measurements, we employed a 100 μW excitation power after the illumination objective, a 525/50 bandpass filer (Chroma) and a 0.2 μm step size on the piezo stage. To quantify the system’s axial and planar resolution, we averaged n = 25 observations. To determine the system’s PSF, we averaged n = 5 observations and subsequently used the average PSF in the deconvolution algorithms.
Propagation length and diffraction quantification
To experimentally determine the diffraction-free propagation length of the Airy and Gaussian beams (Fig. 3a), we illuminated a homogeneously fluorescent sample and quantified the beam diameter (approximated by 1/e) through the lateral intensity distribution (along the y-axis in Fig. 1c) at various propagation distances (along the x-axis in Fig. 1c). The fluorescent sample was prepared in a polydimethylsiloxane (PDMS Sylgard 184, Dow Corning) matrix mixed with the chromophore Lumogen orange (BASF). To this end, we first mixed and degassed the PDMS monomer with its catalyst (10:1 ratio), and subsequently added 10 μL of a Lumogen Orange dichloromethane (HPLC LC–MS grade, OmniSolv) solution at 0.1 mg/ml. The mixture was let to cure for 2 h at 70 °C prior to imaging. The experimental results of the Airy beam propagation shown in Fig. 3a were co-plotted with the FFT-BPM computational results, and the Gaussian results with an analytical expression for the Gaussian beam waist (w) as a function of the propagation distance z (\(w\left(z\right)={w}_{0}\sqrt{1+{(\frac{z}{{z}_{r}})}^{2}}\), with wo set at 1.2 μm).
Strain and growth conditions
The Y. lipolytica strain used in this study was generated on an auxotrophic background with decreased non-homologous end joining for targeted DNA incorporation, as previously described45. The strain was modified using a superfolder GFP plasmid to endogenously express fluorescent erg6, an enzyme in the ergosterol biosynthesis pathway. For the rich YPD medium, we mixed 20 g/L Bacto Peptone (BD), 10 g/L yeast extract (Alfa Aesar), and 20 g/L glucose (Fisher). The defined YSM medium at a C:N ratio of 150 contained 1.7 g/L yeast nitrogen base without amino acids and without ammonium sulfate (BD Difco), 0.69 g/L complete supplement mixture (CSM) without Leucine (Sunrise Science Products), and 1.1 g/L ammonium sulfate (Fisher) and 75 g/L glucose (Fisher). The erg6 expressing Y. lipolytica preculture was stored in YPD agarose (Invitrogen) plates at 4 °C and passed twice in YPD medium (5 ml round bottom polystyrene tubes) for 24 h, with the second passage performed at a 50 × dilution. Subsequently, the YPD culture was centrifuged at 490 × g, and washed in YSM three times, and transferred to 125 ml glass flasks (Corning) containing 20 ml of YSM medium. The flasks were covered with polypropylene closures (Corning) and aluminum foil. Cells were transfered from YPD to YSM at a 0.01 OD. All growth experiments were performed in a shaking incubator (180 rpm) at 28 °C. To perform integrative QPI and Airy LSI imaging, we diluted the growing Y. lipolytica culture by 25 × and transferred approximately 10 µL to the microfluidic system and allowed cells to sediment to the bottom surface. Under these conditions, no 3D motion or drift was observed for the cells during image acquisition. We imaged the cells at 48 h and 96 h, corresponding to states of high and low triacylglyceride content12.
Microfluidics
For cell imaging, we employed a polymer microfluidic system microfabricated in a polymer matrix with a refractive index matched to that of water (BIO-133-BP30, My Polymers). The microfluidic system comprised of a rectangular micro-container defined by 800 μm thick vertical sidewalls. This microsystem was first fabricated in PDMS using conventional cast-molding lithography from a patterned SU8 coated Si wafer, and subsequently transferred to BIO-133-BP30 via UV illumination in a mask-aligner (Q4000-4, Quintel Corporation). Once cells were introduced into the micro-container with a pipette, the microsystem was enclosed with a coverslip coated with a 400 μm thick film of the same polymer. Fluid exchange was possible during cell loading or alternatively via external tubes. To inspect the surface quality of the microsystem’s side-wall (Fig. S3), we positioned it on top of a coverslip and we imaged it in a backscattering geometry (similar to the principle of Fizeau interferometry) using broadband illumination (500–700 nm), a 4 × magnification objective and a sCMOS camera. This set-up enabled the visualization of the interference fringes between the polymer and the glass coverslip and, thus, the indirect assessment of surface quality.
Cell imaging
Select areas were first imaged by QPI and subsequently by the Airy beam at 488 nm. Stacks of 200 planes were acquired at a 0.2 μm step size. Single-cells were localized via maximum projection of the QPI image, and segmented to localize the cell and LD contours via direct phase-thresholding at different levels in ImageJ. Using the cell’s 2D segmented region of interest (ROI), we quantified cell area and the average optical phase (<Φ>) and subsequently the cell dry-density at a wavelength of λ = 500 nm and a refractive index increment (dn/dc) of 1.85 × 10−4 m3 kg−1 using the following equation:
The expression levels of erg6 per cell contour were quantified by subtracting the cell’s average fluorescent intensity from the extracellular background. The % coverage of the 3D LD surface by erg6 was quantified by counting the erg6 fluorescence voxels (i.e., 3D pixels with a total volume of 2 × 10–3 μm3) that were in contact with the LD, the 3D location of which was estimated from the LD diameter.
Statistics
Mann–Whitney tests were performed in OriginPro (Origin Pro 2017 64-bit, OriginLab).
References
Power, R. M. & Huisken, J. A guide to light-sheet fluorescence microscopy for multiscale imaging. Nat. Methods 14(4), 360–373 (2017).
Olarte, O. E. et al. Light-sheet microscopy: a tutorial. Adv. Opt. Photonics 10(1), 111–179 (2018).
Huisken, J. et al. Optical sectioning deep inside live embryos by selective plane illumination microscopy. Science 305(5686), 1007–1009 (2004).
Chen, B.-C. et al. Lattice light-sheet microscopy: Imaging molecules to embryos at high spatiotemporal resolution. Science 346(6208), 1257998 (2014).
Vettenburg, T. et al. Light-sheet microscopy using an Airy beam. Nat. Methods 11(5), 541–544 (2014).
Tokunaga, M., Imamoto, N. & Sakata-Sogawa, K. Highly inclined thin illumination enables clear single-molecule imaging in cells. Nat. Methods 5(2), 159–161 (2008).
Galland, R. et al. 3D high- and super-resolution imaging using single-objective SPIM. Nat. Methods 12(7), 641–644 (2015).
Yang, B. et al. Epi-illumination SPIM for volumetric imaging with high spatial-temporal resolution. Nat. Methods 16(6), 501–504 (2019).
Gustavsson, A.-K. et al. 3D single-molecule super-resolution microscopy with a tilted light sheet. Nat. Commun. 9(1), 123 (2018).
Barer, R. Interference microscopy and mass determination. Nature 169(4296), 366–367 (1952).
Choi, W. et al. Tomographic phase microscopy. Nat. Methods 4(9), 717–719 (2007).
Vasdekis, A. E. et al. Eliciting the impacts of cellular noise on metabolic trade-offs by quantitative mass imaging. Nat. Commun. 10(1), 848 (2019).
Zangle, T. A. & Teitell, M. A. Live-cell mass profiling: an emerging approach in quantitative biophysics. Nat. Methods 11(12), 1221 (2014).
Park, Y., Depeursinge, C. & Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photonics 12(10), 578–589 (2018).
Rivenson, Y. et al. PhaseStain: the digital staining of label-free quantitative phase microscopy images using deep learning. Light Sci. Appl. 8(1), 23 (2019).
Sheneman, L. and A.E. Vasdekis, Deep learning classification of lipid droplets in quantitative phase images. BioRxiv, 2020
Jo, Y. et al. Quantitative phase imaging and artificial intelligence: a review. IEEE J. Sel. Top. Quantum Electron. 25(1), 1–14 (2019).
Wilfling, F. et al. Triacylglycerol synthesis enzymes mediate lipid droplet growth by relocalizing from the ER to lipid droplets. Dev. Cell 24(4), 384–399 (2013).
Bouchard, M. B. et al. Swept confocally-aligned planar excitation (SCAPE) microscopy for high-speed volumetric imaging of behaving organisms. Nat. Photonics 9(2), 113–119 (2015).
Kumar, M. et al. Integrated one- and two-photon scanned oblique plane illumination (SOPi) microscopy for rapid volumetric imaging. Opt. Exp. 26(10), 13027–13041 (2018).
Hoffmann, M. & Judkewitz, B. Diffractive oblique plane microscopy. Diffract. Oblique Plane Microsc. 6(9), 1166–1170 (2019).
Glaser, A.K., et al., A hybrid open-top light-sheet microscope for multi-scale imaging of cleared tissues. BioRxiv, 2020
Kiviet, D. J. et al. Stochasticity of metabolism and growth at the single-cell level. Nature 514(7522), 376–379 (2014).
Wang, Z. et al. Spatial light interference microscopy (SLIM). Opt. Express 19(2), 1016–1026 (2011).
Mir, M. et al. Optical measurement of cycle-dependent cell growth. Proc. Natl. Acad. Sci. 108(32), 13124–13129 (2011).
Siviloglou, G. et al. Observation of accelerating Airy beams. Phys. Rev. Lett. 99(21), 213901 (2007).
Hedde, P. N. et al. sideSPIM - selective plane illumination based on a conventional inverted microscope. Biomed. Opt. Exp. 8(9), 3918–3937 (2017).
Qiao, K. et al. Lipid production in Yarrowialipolytica is maximized by engineering cytosolic redox metabolism. Nat. Biotechnol. 35(2), 173–177 (2017).
Blazeck, J. et al. Harnessing Yarrowialipolytica lipogenesis to create a platform for lipid and biofuel production. Nat. Commun. 5, 3131 (2014).
Ledesma-Amaro, R. & Nicaud, J.-M. Yarrowialipolytica as a biotechnological chassis to produce usual and unusual fatty acids. Prog. Lipid Res. 61, 40–50 (2016).
Kerkhoven, E. J. et al. Regulation of amino-acid metabolism controls flux to lipid accumulation in Yarrowialipolytica. NPJ Syst. Biol. Appl. 2, 16005 (2016).
Fukuda, H., Kondo, A. & Noda, H. Biodiesel fuel production by transesterification of oils. J. Biosci. Bioeng. 92(5), 405–416 (2001).
Thiam, A. R., Farese, R. V. Jr. & Walther, T. C. The biophysics and cell biology of lipid droplets. Nat. Rev. Mol. Cell Biol. 14(12), 775–786 (2013).
Hashemi, H. F. & Goodman, J. M. The life cycle of lipid droplets. Curr. Opin. Cell Biol. 33, 119–124 (2015).
Martin, S. & Parton, R. G. Lipid droplets: a unified view of a dynamic organelle. Nat. Rev. Mol. Cell Biol. 7(5), 373–378 (2006).
Wang, C. W. Lipid droplets, lipophagy, and beyond. Biochim. Biophys. Acta 1861(8 Pt B), 793–805 (2016).
Welte, M. A. Expanding roles for lipid droplets. CB 25(11), R470–R481 (2015).
Roingeard, P. and R.C. Melo, Lipid droplet hijacking by intracellular pathogens. Cell Microbiol., 2017. 19(1).
Miyanari, Y. et al. The lipid droplet is an important organelle for hepatitis C virus production. Nat. Cell Biol. 9(9), 1089–1097 (2007).
Cruz, A. L. S. et al. Lipid droplets: platforms with multiple functions in cancer hallmarks. Cell Death Dis 11(2), 105 (2020).
Li, Z. et al. Lipid droplets control the maternal histone supply of Drosophila embryos. Curr. Biol. 22(22), 2104–2113 (2012).
Cermelli, S. et al. The lipid-droplet proteome reveals that droplets are a protein-storage depot. Curr. Biol. 16(18), 1783–1795 (2006).
Ueno, M. et al. Fat-specific protein 27 modulates nuclear factor of activated T cells 5 and the cellular response to stress. J. Lipid Res. 54(3), 734–743 (2013).
Ploegh, H. L. A lipid-based model for the creation of an escape hatch from the endoplasmic reticulum. Nature 448(7152), 435–438 (2007).
Bredeweg, E. L. et al. A molecular genetic toolbox for Yarrowialipolytica. Biotechnol. Biofuels 10(1), 2 (2017).
Alanazi, H. et al. Robust microbial cell segmentation by optical-phase thresholding with minimal processing requirements. Cytometry A 91(5), 443–449 (2017).
Kim, K. et al. Three-dimensional label-free imaging and quantification of lipid droplets in live hepatocytes. Sci. Rep. 6, 36815 (2016).
Sorger, D. et al. A yeast strain lacking lipid particles bears a defect in ergosterol formation. J. Biol. Chem. 279(30), 31190–31196 (2004).
Zhang, A., Meng, Y., Li, Q. Liang, Y. The endosomal sorting complex required for transport complex negatively regulates Erg6 degradation under specific glucose restriction conditions. Traffic 21(7), 488–502 (2020).
Wang, C.-W. Stationary phase lipophagy as a cellular mechanism to recycle sterols during quiescence. Autophagy 10(11), 2075–2076 (2014).
Scott, M. et al. Interdependence of cell growth and gene expression: origins and consequences. Science 330(6007), 1099–1102 (2010).
Elowitz, M. B. et al. Stochastic gene expression in a single cell. Science 297(5584), 1183–1186 (2002).
Cai, L., Friedman, N. & Xie, X. S. Stochastic protein expression in individual cells at the single molecule level. Nature 440(7082), 358–362 (2006).
Raj, A. & van Oudenaarden, A. Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135(2), 216–226 (2008).
Kaern, M. et al. Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 6(6), 451–464 (2005).
Balaban, N. Q. et al. Bacterial persistence as a phenotypic switch. Science 305(5690), 1622–1625 (2004).
Gawad, C., Koh, W. & Quake, S. R. Single-cell genome sequencing: current state of the science. Nat. Rev. Genet. 17(3), 175 (2016).
Peterson, V. M. et al. Multiplexed quantification of proteins and transcripts in single cells. Nat. Biotechnol. 35(10), 936 (2017).
Zenobi, R. Single-cell metabolomics: analytical and biological perspectives. Science 342(6163), 1243259 (2013).
Nguyen, T. H. et al. Gradient light interference microscopy for 3D imaging of unlabeled specimens. Nat. Commun. 8(1), 210 (2017).
Lim, J. et al. High-fidelity optical diffraction tomography of multiple scattering samples. Light Sci. Appl. 8(1), 82 (2019).
Edelstein, A.D., et al., Advanced methods of microscope control using μManager software. 2014, 2014.
Sage, D. et al. DeconvolutionLab2: an open-source software for deconvolution microscopy. Methods 115, 28–41 (2017).
Dupont, S. et al. Ergosterol biosynthesis: a fungal pathway for life on land?. Evolution 66(9), 2961–2968 (2012).
Schneider, C. A., Rasband, W. S. & Eliceiri, K. W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9(7), 671–675 (2012).
Acknowledgements
We gratefully acknowledge funding from the U.S. Department of Energy, Office of Biological & Environmental Research (DE-SC0019249) for supporting this research. PSJ acknowledges funding from the Polish Ministry of Higher Education (Mobility Plus 1654/MOB/V/2017). Publication of this article was funded by the University of Idaho—Open Access Publishing Fund.
Author information
Authors and Affiliations
Contributions
N.R.S.: experiments, data analysis, contribution to manuscript preparation; P.S.J.: optical models, contribution to manuscript preparation; E.L.B.: strain construction, editing manuscript; S.N.: sample preparation and microfabrication; S.E.B.: strain construction, funding acquisition, editing manuscript; D.N.C.: optical models, editing manuscript; A.E.V.: funding acquisition, experimental design, experiments, and manuscript preparation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Subedi, N.R., Jung, P.S., Bredeweg, E.L. et al. Integrative quantitative-phase and airy light-sheet imaging. Sci Rep 10, 20150 (2020). https://doi.org/10.1038/s41598-020-76730-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-76730-x
This article is cited by
-
Artificial intelligence-enabled quantitative phase imaging methods for life sciences
Nature Methods (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.