Abstract
The quantitative evaluation of the three-dimensional (3D) morphology of porous composite materials is important for understanding mass transport phenomena, which further impact their functionalities and durability. Reactive porous paint materials are composites in nature and widely used in arts and technological applications. In artistic oil paintings, ambient moisture and water and organic solvents used in conservation treatments are known to trigger multiple physical and chemical degradation processes; however, there is no complete physical model that can quantitatively describe their transport in the paint films. In the present study, model oil paints with lead white (2PbCO3·Pb(OH)2) and zinc white (ZnO) pigments, which are frequently found in artistic oil paintings and are associated with the widespread heavy metal soap deterioration, were studied using synchrotron X-ray nano-tomography and unilateral nuclear magnetic resonance. This study aims to establish a relationship among the paints’ compositions, the 3D morphological properties and degradation. This connection is crucial for establishing reliable models that can predict transport properties of solvents used in conservation treatments and of species involved in deterioration reactions, such as soap formation.
Similar content being viewed by others
Introduction
Works of art are typically hybrid materials consisting of inorganic and/or organic components structured in complex ways. The nature of these materials used in works of art resembles many other functional composite materials. In traditional artistic oil paintings, inorganic and/or organic pigments are mixed with a drying oil binder, usually applied in multiple layers over a substrate, such as canvas, wood, or metal, with protective organic coatings on top. Deterioration processes of the oil paint films often involve interactions at the interfaces of these components, with degradations in one triggering subsequent chemical reactions and physical changes in another.
Soap formation in oil paintings is one of the most pervasive forms of deterioration which occurs when saturated fatty acids, that result from the hydrolisis of glycerides in the oil binding medium, react with heavy metals in the pigments, driers, or other addtitives to produce carboxylates, also called soaps. Among the pigments most frequently affected by saponification are lead- and zinc-based, such as lead white, lead tin yellow, and zinc white. This process may cause flaking, delamination, increased transparency, and the formation of protrusions, crater-like holes, and surface crusts1,2,3,4,5,6,7. High temperature and relative humidity, as well as aqueous solutions and organic solvents used in conservation treatments, are important factors known to trigger soap formation7,8,9,10, in addition to causing other physical and chemical degradation processes, such as paint swelling, the deformation of canvas supports, and pigment color changes11,12,13,14,15. Baij et al. reported that solvent flow enhances soap crystallization in model oil paint systems by displacing reactive molecules, such as palmitic acid8, and that the amount of water also has an effect on the rate of soaps crystallization. We hypothesize that heavy metal cations from pigments or additives and fatty acid anions or aggregates migrate through the paint matrix assisted by the diffusion of water or solvents via interconnected channels and pores of various sizes, ultimately forming soaps. Therefore, the, three-dimensional (3D) morphological parameters such as pore size, connectivity, and tortuosity will affect the diffusion of water and organic molecules in the films, and thus directly impact the deterioration.
A wide range of methods have been used to characterize the reactive species, free fatty acids and pigments, and products of soap deterioration in both microsamples removed from artistic paintings and model paint samples (See, for example1,3,5,6,16,17,18,19,20,21,22). Boon et al. utilized neutron radiography on a mesoscopic level to study water uptake by model samples of painting canvas supports and ground preparations. They reported that the canvas cellulose fibers and the glue sizing have a much stronger water uptake than the chalk ground layer bound in glue, and that the uptake rate is not uniform throughout the thickness of the sized canvas23.
Nuclear magnetic resonance (NMR) allows the measurement of the longitudinal and transverse relaxation times, T1 and T2, two important parameters can provide critical information about the physiochemical properties of cross-link polymers and water-saturated media and are used often to characterize geologic materials24,25,26.
Unilateral NMR permits the open porosity available to the diffusion of water and solvents in different materials to be determined27,28. In this article, with ‘open porosity’ we refer to the void fraction or ‘empty’ spaces that may be filled by water or organic solvents in contact with the paint film. The most common NMR methods to probe the structure of porous media are based on the measurement of relaxation times and the diffusion coefficient of water inside the porous systems. Relaxation times of fluids confined in porous media are strictly related to the geometry of the structure, as water in small pores relaxes rapidly, whereas water in large pores relaxes more slowly29,30. In many cases the properties of porous systems may be spatially resolved by means of magnetic resonance imaging (MRI)31. The development of unilateral NMR sensors, which allow one to study arbitrarily sized objects non-invasively by combining open magnets and surface RF coils to generate a sensitive volume external to the sensor and inside the object under investigation, was a breakthrough for the application of NMR to study materials relevant to cultural heritage applications32,33. Although the magnetic field of this sensor is inhomogeneous, it is possible to measure NMR parameters such as proton density, relaxation times, self-diffusion coefficients, and even to collect correlation maps34. Due to its capability to measure the hydrogen content as a function of the depth of the measurement, unilateral NMR is a very powerful method for scanning layers composed by organic substances as well as for measuring the water content absorbed by porous materials35,36,37,38.
X-ray tomography is a powerful tool for characterizing the 3D morphology of paints. For example, in a sample of a ground preparation layer composed of calcium carbonate bound by a proteinaceous medium taken from a nineteenth century painting, Gervais et al. calculated a total porosity of about 15% from X-ray micro-tomography measurements using a 370 nm pixel size39. Ma et al.22 used photothermal induced resonance in combination with IR microspectroscopy and X-ray micro-tomography to study the distribution of metal carboxylayes in a naturally aged, 23-year old Zn white oil paint containing aluminum stearate as an additive. These studies highlight the capability of X-ray micro-tomography to reveal the internal 3D structure of paints. The recent development of X-ray nano-tomography with full-field transmission X-ray microscopy (TXM) provides tens of nanometer spatial resolution with a field of view of tens of microns, making it possible to study oil paints with an even higher spatial resolution40,41,42,43.
While analyses of samples removed from works of art give in-depth information about the 3D morphological parameters22,39, the characterization of model samples prepared under controlled conditions with varying paint compositions, including different pigments, pigment-to-oil ratios and additives, permit to better understand the roles of these conditions on the morphological features that affect transport. In the present study, model paints with two pigments frequently associated with heavy metal soap deterioration in oil paintings were studied, namely lead white (2PbCO3 \(\bullet \) Pb(OH)2) and zinc white (ZnO). While lead white has been reported to form soaps in old master, modern, and contemporary works (see, for example2,3,4,44,45), zinc white, which emerged during the end of the eighteenth century46, is commonly associated with the phenomenon in paintings dating from the middle of the nineteenth century on1,5,45,47. Aluminum (Al) stearate was frequently added to twentieth century commercial paint formulations to prevent the separation of the pigment from the oil; however, it has been shown that the compound is a source of free fatty acids and that it may promote saponification1,5,47. Therefore, Al stearate was added to a set of the zinc white oil paint samples prepared for this study.
The model paint samples were characterized by novel synchrotron X-ray nano-tomography and NMR methods. Synchrotron X-ray nano-tomography enables a direct visualization of the pigment particles and Al stearate agglomerates in the polymerized oil network48. Unilateral NMR was used to measure the hydrogen content as a function of the depth in the paint films to obtain the water content absorbed by the pores36,37,38. By quantifying the volume fraction and feature size distribution of the particles, the tortuosity, and open porosity connected to the diffusion of water using these techniques, the potential effect of these properties on mass transport and the possible path for mobile materials were evaluated. This understanding is crucial to provide guidance for conservation treatments and insights into deterioration mechanisms. The knowledge of how nano- to microscale 3D morphology relevant to transport properties varies as a function of materials constituents, is also critical for a wider range of composite materials.
Experimental section
Sample preparation and preliminary characterization
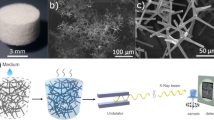
Pb white (2PbCO3 \(\bullet \) Pb(OH)2) and Al stearate (Al(OH)2C18H35O2) were purchased from Sigma-Aldrich. Zn white (ZnO) was purchased from Alfa Aesar. Pb white was mixed with standard linseed oil (LO, Kremer Pigments Inc.) with pigment-to-oil weight ratios of 1:1 and 5:1. Zn white was mixed with standard LO with a 1:1 pigment-to-oil weight ratio, with and without 10 wt.% Al stearate. The paint samples with the two pigments are labeled PbLO and ZnLO, respectively. After fully mixing, the paints were applied on Al foil, as 90 μm thick layers for PbLO and as 45 μm layers for ZnLO, using a film applicator, at room temperature (Fig. 1A). As mentioned in the main text, the resulting wet films were thinner than the applicator gap setting.
(A) Paint sample preparation process. (B) Surface morphology of Pb white and Zn white powders, and surface and cross-section morphology of the oil paints imaged: PbLO 1:1, PbLO 5:1, and ZnLO without Al stearate and with 10 wt.% Al stearate (ZnLO + AlSt). (C) X-ray nano-tomography set up and reconstruction workflow.
Additional samples were made by applying the paints on canvas supports. The PbLO 1:1 paint was deposited on a canvas support prepared with a calcite (CaCO3) layer bound in glue applied by brush, and the ZnLO 1:1 and 3:1 paints were applied directly on the canvas substrates. For all the sets of paints on canvas, the pigmented paint film was applied using a film applicator with an initial (wet) thickness of about 200 µm. For curing, all the samples were stored at room temperature under a humidity-controlled environment (ca. 52%RH) for six months.
The relative changes in the film thicknesses upon curing were determined by unilateral NMR. For this task, paint films with similar compositions as those listed in Table 1 were applied on glass slides with an approximate 200 μm initial (wet) thickness. For the X-ray nano-tomography measurements, the samples were cut with a scalpel and mounted onto tomographic sample mounting pins. To make it compatible with the field of view of the TXM and to ensure sufficient X-ray transmission, the tip of the sample was < 50 μm.
Surface and cross-section morphology
To characterize the surface morphology of the pigments and Al stearate powders, and the surface and cross-section morphology of the oil paint samples (Fig. 1B), a Hitachi S4800 SEM with a 10.0 kV accelerating voltage was used. FIB-SEM (FEI Helios) was utilized to mill the paint samples at 30.0 keV with decreasing currents in the following sequence: 21, 9.2, 6.5, 2.8 and 0.92 nA, in order to observe the entire cross-section profile, from the surface to the substrate.
Synchrotron X-ray nano-tomography
X-ray nano-tomography measurements were carried out at TXM beamline 32-ID-C, Advanced Photon Source (APS), Argonne National Laboratory (ANL)43. A beam shaping condenser was used to illuminate the sample and a Fresnel zone plate (60 nm) was used as an objective lens (Fig. 1C). The monochromatic beam energy was set at 9.76 and 8 keV for the ZnLO and PbLO samples, respectively. For each sample, 1201 projections over 180° rotation were collected with a lens-coupled 2D area detector. The field of view of the TXM was 64 µm × 54 µm for 8 keV with a pixel size of 26.16 nm, and the pixel size at 9.76 keV was 31.70 nm.
To reconstruct the 3D structures, the Gridrec algorithm with TomoPy was used49,50. Thresholding segmentation and thickness comparison were carried out on the reconstructed images of Pb-white paints in Image J51. For the Zn white samples, because the gray-scale distribution of the oil and pigment phases overlap in the histogram, the segmentation was based on visually finding possible minimum, mean, and maximum threshold values to account for the variation due to thresholding. The assessment on the effect of thresholding segmentation is presented in Supplementary Information Figures S1-5 and Supplementary Information Tables S1 and S2. The mean threshold value was used to segment the reconstructed images for the quantitative analysis of the morphological parameters. The thickness of cured paint films was measured by calculating the full-width-half-maximum of the X-ray attenuation vs. distance from the surface to the substrate of the paint films; the process was repeated at three different locations of the image to obtain the average thickness and variation. The visual comparison, specific surface area analysis, phase connectivity and 3D visualization were conducted in a commercial software AVIZO (v.9.3 FEI) and open-source software TOMVIZ software52. Further morphological analysis, including phase volume fraction, particle size distribution, and tortuosity quantification, were conducted using customized codes developed in-house with details described in prior articles53,54,55.
Unilateral NMR
1H depth profiles and spin–spin relaxation times (T2eff), were measured at 0.36 T (proton Larmor frequency of 18 MHz) with an NMR-MOUSE (Mobile Universal Surface Explorer) instrument consisting of an electronic unit manufactured by Bruker Biospin interfaced with a single-sided sensor ACT by RWTH Aachen University, Aachen, Germany35. This sensor generates an inhomogeneous magnetic field with an extremely uniform gradient to resolve the near surface structure of arbitrarily large objects. 1H depth profiles were obtained by averaging the amplitude of the first eight points of an echo train of 32 echoes with an echo time (2τ) of 41 µs, using the Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence56. The nominal spatial resolution was 50 µm.
Since the spatial resolution of unilateral NMR is lower compared to TXM, four samples with similar compositions as those listed in Table 1, but with larger thickness of ~ 200 μm, were applied on glass slides for the NMR measurements. The NMR-MOUSE sensor was re-positioned in steps of 50 and 100 µm to cover the desired spatial range, from the surface of the sample to a depth of about 600 µm, a position within the glass substrate with a zero 1H NMR signal.
Effective spin–spin relaxation times, T2eff, were measured with a CPMG pulse sequence. 1024 echoes were recorded in the center of the sample with an echo time of 41 µs. Due to the presence of an inhomogeneous magnetic field, the observed spin–spin relaxation time, T2eff, was always shorter than the T2 that would be measured in a homogeneous magnetic field. Consequently, the quantity measured by unilateral NMR is usually called effective spin–spin or transverse relaxation time, T2eff. The decay of the transverse magnetization was fit using an inverse Laplace transform (ILT) of the data to obtain the distribution of T2eff.The ILT is particularly useful when the signal is characterized by a multi-exponential decay. The ILT of the data was obtained by using the Uniform Penalty (UPEN) algorithm57. Data was first normalized by determining the mean offset and subsequently processed with the UPEN algorithm.
The effective free volume available for water diffusion was evaluated from the CPMG decays, which allows one to obtain the value of the proton spin density at t = 0 by fitting the experimental decay. To calculate the open porosity filled by water throughout the film, the samples were placed in contact with a water source following a procedure similar to that reported for measuring water capillary absorption in other porous materials58,59. Small modifications to this process were made to control the water absorption, i.e. the sample was covered with several layers of filter paper saturated with water on a glass substrate and was wrapped in a plastic film to slow down the evaporation during the measurements. After 72 h of water absorption, the T2eff was measured in the center of the film layer. The experimental data, 1H NMR normalized signal intensity (Y) was fit to the following equation:
where n is the number of components of the CPMG decay of the magnetization, 2τ is the echo time, M0i and T2i are the weight and the spin–spin relaxation time of the i-th component, respectively, and C0 is the offset value, which accounts for the noise of the measurement. The values obtained are reported in the Supporting Information file (Table S4).
Results and discussion
Distribution and mobility of proton domains and open porosity available for the diffusion of water in lead white and zinc white oil paints as determined by unilateral NMR
To evaluate how the water absorption and the open porosity of oil paints can be effected by zinc white and lead white pigments in different concentrations, and by the presence of the aluminum stearate additive, we analyzed the transverse relaxation times in the cured paint samples before and after water absorption. In all the dry samples, three components of T2eff were observed (Fig. 2a). The short component (T2A ~ 0.13–0.2 ms) that affects the majority of the protons arises from protons in the relatively rigid framework of the polymeric oil network; the intermediate component (T2B ~ 0.5–0.8 ms) reflects protons in the polymer chain portions that have some relative motional freedom (e.g. methyl groups at the ends of fatty chains); and the third component (T2C ~ 2–4 ms) is due to protons in residual unsaturated fatty acids not fully cross linked or saturated fatty acids not linked to the polymeric network (e.g. palmitic and stearic acid) that have a higher mobility that those in the rigid matrix. Interestingly, all paint samples with a higher amount of linseed oil showed a slight shift of T2eff towards higher values indicating a less rigid or less cross-linked polymeric film. This result is not surprising, since as the concentration of lead white increases, its drying action increases as well60.
After 72 h of water absorption, the distributions of T2eff have changed (Fig. 2b). All wet samples show an additional T2w long component (with a value > 10 ms) that arises from protons in a relatively free water domain. Two macro-domains of proton mobility can be identified: the first domain, with T2eff from 0.1 to 5 ms, reflects the mobility of protons in the polymerized oil with the same three components found in dry samples; the second domain, with T2eff > 10 ms, reflects the proton mobility of the water molecules.
In all samples, long and intermediate T2eff of protons in the polymerized oil are unaffected by water absorption. On the contrary, T2C, that arises from protons in not cross-linked fatty acids, shows a different behavior depending on the type and concentration of pigment and on the presence of the additive. With low pigment to oil ratios, both PbLO 1:1 and ZnLO 1:1 show an increased mobility of protons in the not cross-linked fatty acids in the presence of water (T2C increases). The presence of mobile domains in polymerized oil has been previously reported and have been suggested to have an important plasticizing role61,62. In the presence of Al stearate, ZnLO + AlSt 1:1 shows an increase in the proton population density of T2C. Since Al stearate is not part of the oil cross-linked network, it may experience a higher degree of mobility in the presence of water.
Finally, in PbLO 5:1, two types of water, one free (T2w) and one bound (Tʺ2w), were observed. These results are similar to those reported in our previous study27. Also, in this case, the appearance of a second domain of water may be due to the formation of hydrated ionic group clusters. Interestingly, the presence of bound water is not observed at low concentrations of lead white. The formation of these hydrated ionic groups in lead-based paints may be triggered by the high amount of pigment and of absorbed water. Furthermore, it was found that protons of absorbed water have a lower degree of mobility in oil paints containing zinc white (T2eff ~ 20 ms) than in paints with lead white (T2eff ~ 46 ms) with the same pigment to oil ratio (1:1). The T2eff of water may be affected by the different morphology of the porous network like in saturated rocks where a smaller pore size correlates with smaller values of T2eff. Nevertheless, in oil paints it is not possible to neglect the possible interactions of water with the polymeric oil network that might influence the relaxation of water. As a consequence, in paints, the distribution of T2eff cannot be directly associated with the distribution of porosity as is in stones and rocks30.
Carr-Purcell-Meiboom-Gill (CPMG) decay and can be used to calculate the open porosity of the samples. To calculate the effective open porosity, the amplitude of the spin proton density of water, M0w, was extrapolated and the contributions of the protons in the polymerized oil domain were neglected (for details, see the Supporting Information file). The effective open porosity was calculated by normalizing the value of the water absorbed with respect to the value obtained for bulk water (i.e., 100% of porosity)58,59.
The M0w value was normalized to the amplitude measured on bulk water M0b, which is equivalent to an effective porosity of 100%:
Using Eq. (1), values of the open porosity ΘNMR available to water were calculated to be 2.0 and 5.0% for the PbLO 1:1 and 5:1 samples, respectively. For the ZnLO samples with and without Al stearate, the values obtained were 1.7 ± 0.5 and 7.2% ± 1.0, respectively (Table 2).
Effect of the pigment to oil weight ratio on the 3D morphological properties of lead white oil paints
Figure 3A–D presents the 3D morphology and the virtual cross-sections in the xy and yz planes for the PbLO samples with two different pigment to oil weight ratios, 1:1 and 5:1. The pigment particles sedimented at the bottom of the film in the sample with the larger proportion of oil (PbLO 1:1, Fig. 3A–B), while the Pb white particles stacked homogeneously in the paint film with the higher pigment proportion (Fig. 3C–D). The film thicknesses after curing were 18.3 µm for the PbLO 1:1 sample and 30.9 µm for PbLO 5:1 sample. The change in the film thickness was calculated as the difference between the wet and the dry film thicknesses determined by unilateral NMR (see, Supporting Information file), since it is not possible to study wet paint samples by nano-tomography. The thickness difference between the dry 1:1 and 5:1 PbLO samples can be explained by the fact that the volume changes in oil paints upon polymerization/drying are mainly due to the change in the volume of the organic binder.
Figure 3E presents the volume fraction of the pigment particles along the surface-to-substrate direction. For PbLO 1:1, the volume fraction of the pigment particles increases to a value of ~ 25.0% at approximately 12 μm below the surface and then it remains approximately constant from this point to the substrate. The sedimentation of the particles could potentially occur slowly during curing of the viscous oil medium if the oil content is high enough. In contrast, for PbLO 5:1, no significant change is observed for the volume fraction of the particles along the thickness direction. The particle feature size distribution was established by quantifying the probability to find various distances from the mass center to the edge of the particle. The average particle size was then calculated based on the particle size distribution by the method developed by Munch and Holzer described elsewhere63. The feature size distributions for the Pb white pigment particles are similar for the two samples studied, with average values of 1.2 µm and 1.1 µm for PbLO 1:1 and 5:1, respectively (Fig. 3F). This similarity in the feature size distributions indicates that the particles do not aggregate when the pigment to oil weight ratio increases. The feature size calculation for the binding medium of these two samples are shown in Figure S9 (Supporting Information file).
Because the X-ray attenuation is similar for the pores and the oil phase at the tens of nm scale, empty pores cannot be differentiated from spaces occupied by the oil phase in these experiments. Nevertheless, studies in model paint systems have proposed that the transport of water, organic solvents and other species may also take place in the oil phase8,9.
Figure 4A–D shows the feature size distribution, tortuosity, and diffusion distance maps for the oil phase. The average feature sizes calculated for PbLO 1:1 and PbLO 5:1 samples are 4.9 µm and 1.3 µm, respectively (Fig. 4A) which means that when the weight fraction of pigment particles in the paint increases, the size distribution of the oil media decreases.
(A) Oil phase feature size distributions calculated for PbLO 1:1 and 5:1. (B) Tortuosity calculated for these two samples using the quasi-Euclidean method as the neighboring definition in the x, y, and z directions. (C) Visualization of connected and unconnected oil phase. The ratio of connected oil is 90.5% for PbLO 1:1 and 77.5% for PbLO 5:1. (D) Distance maps calculated by using y as the propagation direction.
The tortuosity calculated using the quasi-Euclidean method as the neighboring definition64 is presented in Fig. 4B. The tortuosity inversely correlates with the average oil phase size and is larger for the PbLO 5:1 sample in all three directions, x, y and z. As shown above, in the PbLO 1:1 sample, the pigment particles sedimented to the bottom of the film. Thus, at the top of the paint film, the size of the oil phase is larger and the diffusion path is closer to a straight path. In the PbLO 5:1 sample, the diffusion path is more tortuous because of the higher weight fraction of pigment particles. In this sample, the particles are stacked along the vertical (y) direction, leading to a larger tortuosity in the y direction, and a similar tortuosity value in the x and z directions. This particle stacking is related to the pigment-to-oil ratio as discussed above, but also due to the pigment particle shape. 2PbCO3 \(\bullet \) Pb(OH)2 belongs to the rhombohedral system (space group R \(\stackrel{-}{3}m\)), with lattice parameters \(a=5.179\mathrm{ \AA }\), b = \(8.492\mathrm{ \AA }\) and c = 23.702 \(\mathrm{\AA }\), and a particle shape that tends to be an hexagonal platelet65,66. Figure 1B presents the morphology of the Pb white pigment particles and the inset in Fig. 4B shows that the particle dimension is smaller in the y direction than in the x and z directions so the particles can stack along the y direction. It is expected that a decrease in the tortuosity of a paint film will result in an increase in the rate of solvent penetration in a conservation treatment involving surface cleaning.
Figure 4C shows the distribution of connected and unconnected oil. In PbLO 1:1, the volume fraction of connected oil is ~ 90.5%, while the fraction of connected oil is 77.5% in PbLO 5:1. The higher fraction of connected oil indicates that a smaller amount of oil is enclosed in the structure. The unconnected oil may be at the edge of the sample or exist as isolated medium. Figure 4D presents the distance maps calculated along the vertical (y) direction as the propagation direction. The 3D distance maps help to visualize the tortuosity calculated based on geometric propagation showing the actual path length of the oil medium. With a higher tortuosity in the y direction in the PbLO 5:1 sample, the diffusion path is 9.4% longer than a straight path. In contrast, the diffusion path in the PbLO 1:1 sample is only 4.0% larger than a straight path. Since the pigment particles sedimented at the bottom of the paint film in PbLO 1:1, the initial diffusion rate of the species, when moving from the surface of the paint film towards the substrate, would be faster at the beginning and would slow down as it proceeds. On the other hand, the diffusion rate for the PbLO 5:1 sample, which has a higher pigment content, would be slower overall compared with PbLO 1:1, but would remain approximately constant throughout its thickness; all this considering a pure physical process without chemical interactions.
Effect of Al stearate on the 3D morphology, tortuosity and distance maps of zinc white oil paints
It has been demonstrated that, in oil, nano-sized micelles of Al soap aggregate into jammed networks; however, over time, configuration energy is minimized by the rearrangement of the particles into more closely packed forms47,67. The morphology of the Al stearate powder is presented in Fig. 5A. As shown in the cross-sectional image in Fig. 1B, particles in the ZnLO + AlSt sample are not homogeneously distributed in the paint film as they are in the ZnLO sample. Energy-dispersive X-ray spectroscopy (EDS) mapping in ZnLO + AlSt (Fig. 5B) showed that some areas are Al-rich with no Zn, indicating that Al stearate aggregated as clusters. These Al stearate aggregates are irregular in shape (Fig. 5C,D). The two samples showed different particle distribution along the depth direction (Fig. 5E). In the ZnLO sample, the amount of pigment particles is smaller towards the bottom of the film. In the ZnLO + AlSt sample, the relative amount of pigment particles is smaller overall when compared to ZnLO because of the presence of Al stearate, as expected. Moreover, in this particular sample, the volume ratio of Al stearate increases towards the surface of the paint film in the ZnLO + AlSt sample. This can be visualized in Fig. 5C, where Al stearate agglomerates relatively larger in size are present towards the surface of the paint film.
Characterization of the effect of Al stearate. (A) Surface morphology of Al stearate powder. (B) Cross-sectional image and EDS distribution maps for Zn, Al and C in the ZnLO + AlSt sample. (C) 3D visualization of ZnLO and ZnLO + AlSt samples by X-ray nano-tomography. (D) Surface structure and shape of Al stearate agglomeration. (E) Volume ratio of particles and Al stearate in the ZnLO and ZnLO + AlSt samples. (F) Interfacial area distribution of Al stearate agglomerates at different depths.
Osmond et al. showed that the presence of Al stearate in zinc white oil paints affects zinc carboxylate formation and distribution, as they observed higher concentrations and more pronounced spatial separation of saturated C16 and C18 chain zinc carboxylates in the films47,67. Gabrieli et al. also reported that Al stearate promotes the formation of zinc soaps in zinc white-containing paints and that the amounts of soaps formed in the presence of this paint additive exceeds that expected based on an ion exchange mechanism5. These authors reported that zinc stearate soaps first form around the Al stearate agglomerates and eventually grow in the whole painting stratigraphy as irregularly shape particles. Therefore, the Al stearate-Zn white oil paint interfacial area is a parameter that should be considered when proposing a mechanism for the saponification process in these paints. Ergo, the surface areas of the Al stearate agglomerates were quantified at different depths of the paint film and normalized to a constant volume of the film (Fig. 5F). In the model samples studied, it was observed that the interfacial area of the agglomerates increases towards the bottom of the film from 0.7 to 2.7 µm−1. Since the Al stearate agglomerates have a larger surface area and the volume fraction of Al stearate is lower towards the bottom of the paint film, it is expected that saponification be more pronounced than towards the top of the film in these model samples.
Figure 6 shows the 3D morphological analysis of the ZnLO samples, with and without the Al stearate. The average size of the polymerized oil phase in the ZnLO + AlSt sample is ~ 0.3 µm which is smaller than that of the ZnLO sample at ~ 0.6 µm (Fig. 6 A). The feature size distribution of pigment particles did not show obvious differences between these two samples (Fig. 6B). Considering that X-ray nano-tomography can only resolve the agglomerated Zn white particles, not the individual particles, it may be speculated that the presence of Al stearate does not change the aggregation of the pigment particles but influences the oil curing process.
(A) Size distribution of the oil phase in the ZnLO and ZnLO + AlSt samples. (B) Size distribution of pigment particles. (C) Tortuosity values in x, y, z directions and average; y is the direction along the depth of the film. (C) Distance maps calculated using the y direction as the propagation direction.
The tortuosity of the polymerized oil phase calculated along the vertical (y) direction for the two samples was similar at ~ 1.1 (shown for ZnLO + AlSt in Fig. 6C). The distance maps for these two samples calculated using the y direction are presented in Fig. 6D. The path length for the ZnLO sample is 19.9 µm, and the theoretical value is 18.4 µm. For the ZnLO + AlSt sample, the calculated length is 18.7 µm and the theoretical length is 16.7 µm. The tortuosity values along y direction are 1.08 and 1.12 for the ZnLO and ZnLO + AlSt samples, respectively. The tortuosity of the oil medium is the ratio between the tortuous path distance and the straight distance of the phase. The Al stearate aggregated and separated from the oil medium, so the presence of Al stearate leads to a slightly more tortuous oil matrix, which would affect the diffusion of species during the saponification process and in conservation interventions.
Effects of the presence of an absorbing substrate on the 3D morphology
The 3D morphology of a paint layer in an artistic oil painting will depend on the stratigraphy of the paint passage. For example, the presence of a porous substrate which may absorb the oil binder will have an impact on the morphology of the paint films. The 3D morphology of a PbLO 1:1 sample applied on a canvas substrate with a calcium carbonate ground preparation, presented in Fig. 7A, shows that the Pb white pigment particles are relatively more densely packed when compared to the PbLO 1:1 sample applied on Al foil (Fig. 3A). The loose network of the calcium carbonate ground, which presumably consists of empty pores and pores filled with oil, can be visualized in Fig. 7A.
Pb white and Zn white oil paint samples applied on a canvas substrate. (A) 3D visualization of Pb white particles in PbLO 1:1 paint on canvas with calcium carbonate ground preparation. The virtual cross-sections on the xz and xy planes show the porous calcium carbonate layer. (B) 3D morphology of ZnLO paints applied on a canvas substrate with two different pigment-to-oil ratios. Pockets of oil phase in the sample ZnLO 1:1-canvas are indicated by red circles. The ZnLO 3:1-canvas sample showed a more homogeneous distribution of particles and oil phase.
A PbLO 1:1 sample deposited on a glass slide with an initial wet thickness of 177 ± 25 μm, as measured by unilateral NMR, has a 118 ± 25 μm dry thickness, a 33% change (Supplementary Information Table S3). The thickness of the PbLO 1:1 dry sample applied on canvas measured by X-ray nano-tomography is 6.3 ± 1.0 μm, which amounts to a ~ 96.4% shrinkage. Assuming that the initial wet thickness is consistent for both samples, the significantly larger shrinkage for the sample on canvas may be explained by the presence of the underlying calcium carbonate ground and canvas which absorb the oil binder.
To characterize the influence of the pigment-to-oil ratio on the morphology of oil paints, Zn white paint samples on canvas with pigment-to-oil ratios at 1:1 and 3:1 were compared (Table 1). In Fig. 7B, relatively larger oil pockets can be visualized for the sample with the smaller ratio, while the sample with the larger ratio shows a relatively more homogeneous distribution of oil and pigment particles. Therefore, the different pigment-to-oil ratios give rise to differences in the 3D morphology of the paint materials, which is expected to have a bearing on the diffusion of different compounds, such as organic solvents used in conservation treatments.
Conclusion
In this work, reactive porous paint films consisting of inorganic pigments and a binding oil were investigated from the nano- to the microscale, to quantify their 3D morphology relevant to transport properties. Parameters associated with the 3D morphology of lead white and zinc white oil paints, such as the pigment and oil phase volume fractions, feature size distributions, tortuosity, connectivity of the oil/pore network, diffusion paths, and open porosity available for the diffusion of water, were calculated using a combination of synchrotron X-ray nano-tomography and unilateral NMR in model paint samples. The influence of the pigment type, the presence of the aluminum stearate additive, the pigment-to-oil binder ratio, and the presence of an absorbing substrate were found to have various effects on the 3D morphology of the paints. All these parameters are crucial for establishing reliable models that can predict transport properties of water and organic solvents used in conservation treatments and of species involved in deterioration reactions, such soap formation. Because the X-ray attenuation is similar for the pores and the oil phase at the tens of nm scale, it was not possible to differentiate empty pores from spaces filled by the oil phase by synchrotron X-ray nano-tomography; however, the porosity available for the diffusion of solvents, water in our case, may be measured using unilateral NMR. In cases where relatively smaller pores need to be probed, measurements by complementary techniques, such as Brunauer–Emmett–Teller (BET), are necessary. The tortuosity in the direction from the surface to the bottom of the paint films was calculated for the model samples studied, which is an important step for evaluating the effects of solvent-induced paint swelling on transport. Overall, the understanding of materials’ 3D morphology related to transport properties is important for connecting material structures to the deterioration processes and functionalities, which are also relevant to a wider range of composite materials.
References
Osmond, G. Zinc soaps: an overview of zinc oxide reactivity and consequences of soap formation in oil-based paintings. In Metal soaps in art: Conservation and research (eds Casadio, F. et al.) 25–46 (Springer, Berlin, 2019).
Hale, C., Arslanoglu, J. & Centeno, S. A. Studying old master paintings. Technology and practice. In The National Gallery Technical Bulletin 30th Anniversary Conference Postprints (ed. Spring, M.) (Archetype Publications and the National Gallery, London, 2011).
Chen-Wiegart, Y.-C.K. et al. Elemental and molecular segregation in oil paintings due to lead soap degradation. Sci. Rep. 7, 11656. https://doi.org/10.1038/s41598-017-11525-1 (2017).
Centeno, S. A. & Mahon, D. The chemistry of aging in oil paintings: metal soaps and visual changes. Metrop Museum Art Bull 67, 12–19 (2009).
Gabrieli, F. et al. Revealing the nature and distribution of metal carboxylates in Jackson Pollock’s Alchemy (1947) by micro-attenuated total reflection FT-IR spectroscopic imaging. Anal. Chem. 89, 1283–1289. https://doi.org/10.1021/acs.analchem.6b04065 (2017).
Catalano, J. et al. 207Pb and 119Sn Solid-State NMR and relativistic density functional theory studies of the historic pigment lead-tin yellow type i and its reactivity in oil paintings. J. Phys. Chem. A 118, 7952–7958. https://doi.org/10.1021/jp505908j (2014).
Catalano, J. et al. Understanding the dynamics and structure of lead soaps in oil paintings using multinuclear NMR. In Metal Soaps in Art—Conservation & Research 69–84 (Springer, Berlin, 2019).
Baij, L., Hermans, J. J., Keune, K. & Iedema, P. Time-Dependent ATR-FTIR spectroscopic studies on fatty acid diffusion and the formation of metal soaps in oil paint model systems. Angew. Chem. Int. Ed. 57, 7351–7354. https://doi.org/10.1002/anie.201712751 (2018).
Baij, L., Hermans, J. J., Keune, K. & Iedema, P. D. Time-dependent ATR-FTIR spectroscopic studies on solvent diffusion and film swelling in oil paint model systems. Macromolecules 51, 7134–7144. https://doi.org/10.1021/acs.macromol.8b00890 (2018).
Catalano, J. et al. Molecular dynamics of palmitic acid and lead palmitate in cross-linked linseed oil films: Implications from deuterium magnetic resonance for lead soap formation in traditional oil paintings. Solid State Nucl. Magn. Reson. 89, 21–26. https://doi.org/10.1016/j.ssnmr.2017.12.003 (2018).
Saunders, D. & Kirby, J. The effect of relative humidity on artists’ pigments. Natl. Gallery Techn. Bull. 25, 62–72 (2004).
Ulrich, K., Centeno, S. A., Arslanoglu, J. & Del Federico, E. Absorption and diffusion measurements of water in acrylic paint films by single-sided NMR. Prog. Org. Coat. 71, 283–289. https://doi.org/10.1016/j.porgcoat.2011.03.019 (2011).
Tumosa, C. S. & Mecklenburg, M. F. In New Insights into the Cleaning of Paintings: Proceedings from the Cleaning 2010 International Conference, Universidad Politecnica de Valencia and Museum Conservation Institute (ed Marion F. Mecklenburg, Charola, A. Elena, and Koestler, Robert J.) 51–58 (Smithsonian Institution, 2013).
Hendrickx, R. et al. Distribution of moisture in reconstructed oil paintings on canvas during absorption and drying: A neutron radiography and NMR study. Stud. Conserv. 62, 393–409. https://doi.org/10.1080/00393630.2016.1181899 (2017).
Noble, P. Brief history of metal soaps in paintings from a conservation perspective. In Metal Soaps in Art—Conservation & Research (eds Keune, K. et al.) 1–22 (Springer, Berlin, 2019).
Higgitt, C., Spring, M. & Saunders, D. Pigment-medium interactions in oil paint films containing red lead or lead tin yellow. Natl. Gallery Tech. Bull. 75, 75–91 (2003).
Keune, K. Binding Medium, Pigments and Metal Soaps Characterised and Localised in Paint Cross-Sections PhD Thesis thesis, University of Amsterdam (2005).
Spring, M., Ricci, C., Peggie, D. & Kazarian, S. ATR-FTIR imaging for the analysis of organic materials in paint cross sections: case studies on paint samples from the National Gallery, London. Anal Bioanal. Chem. 392, 37–45. https://doi.org/10.1007/s00216-008-2092-y (2008).
Catalano, J. et al. Coordination geometry of lead carboxylates—Spectroscopic and crystallographic evidence. Dalton Trans. 44, 2340–2347. https://doi.org/10.1039/c4dt03075c (2015).
Keune, K., van Loon, A. & Boon, J. J. SEM Backscattered-electron images of paint cross sections as information source for the presence of the lead white pigment and lead-related degradation and migration phenomena in oil paintings. Microsc. Microanal. 17, 696–701. https://doi.org/10.1017/S1431927610094444 (2011).
Kobayashi, T. et al. DNP-enhanced ultrawideline 207Pb solid-state NMR spectroscopy: An application to cultural heritage science. Dalton Trans. 46, 3535–3540. https://doi.org/10.1039/c7dt00182g (2017).
Ma, X. et al. Revealing the distribution of metal carboxylates in oil paint from the micro- to nanoscale. Angew. Chem. Int. Ed. 58, 11652–11656. https://doi.org/10.1002/anie.201903553 (2019).
Boon, J. J. et al. Neutron radiography for the study of water uptake in painting canvases and preparation layers. Appl. Phys. Mater. Sci. Process. 121, 837–847. https://doi.org/10.1007/s00339-015-9381-z (2015).
Patel, J. P. & Hsu, S. L. Development of low field NMR technique for analyzing segmental mobility of crosslinked polymers. J. Polym. Sci. Part B Polym. Phys. 56, 639–642. https://doi.org/10.1002/polb.24583 (2018).
Besghini, D., Mauri, M. & Simonutti, R. Time domain NMR in polymer science: From the laboratory to the industry. Appl. Sci. Basel 9, 2. https://doi.org/10.3390/app9091801 (2019).
Behroozmand, A. A., Keating, K. & Auken, E. A review of the principles and applications of the NMR technique for near-surface characterization. Surv. Geophys. 36, 27–85. https://doi.org/10.1007/s10712-014-9304-0 (2015).
Di Tullio, V. et al. Water diffusion and transport in oil paints as studied by unilateral NMR and 1H high-resolution MAS-NMR spectroscopy. ChemPhysChem 20, 1–8. https://doi.org/10.1002/cphc.201900858 (2019).
Rehorn, C. & Blümich, B. Cultural heritage studies with mobile NMR. Angew. Chem. Int. Ed. 57, 7304–7312. https://doi.org/10.1002/anie.201713009 (2018).
Brownstein, K. R. & Tarr, C. E. Importance of classical diffusion in NMR studies of water in biological cells. Phys. Rev. A 19, 2446–2453. https://doi.org/10.1103/PhysRevA.19.2446 (1979).
Dunn, K.-J., Bergman, D. J. & LaTorraca, G. A. Nuclear Magnetic Resonance Petrophysical and Logging Applications, vol 32 (Pergamon, Bergama, 2002).
Blümich, B. NMR Imaging of Materials (Clarendon Press, Oxford, 2003).
Kleinberg, R. L., Sezginer, A., Griffin, D. D. & Fukuhara, M. Novel NMR apparatus for investigating an external sample. J. Magn. Reson. 1969(97), 466–485. https://doi.org/10.1016/0022-2364(92)90028-6 (1992).
Eidmann, G., Savelsberg, R., Blümer, P. & Blümich, B. The NMR-MOUSE, a mobile universal surface explorer. J. Magn. Reson. 122, 104–109 (1996).
Hurlimann, M. D. & Venkataramanan, L. Quantitative measurement of two-dimensional distribution functions of diffusion and relaxation in grossly inhomogeneous fields. J. Magn. Reson. 157, 31–42. https://doi.org/10.1006/jmre.2002.2567 (2002).
Perlo, J., Casanova, F. & Blümich, B. Profiles with microscopic resolution by single-sided NMR. J. Magn. Reson. 176, 64–70. https://doi.org/10.1016/j.jmr.2005.05.017 (2005).
Blümich, B. et al. Noninvasive testing of art and cultural heritage by mobile NMR. Acc. Chem. Res. 43, 761–770. https://doi.org/10.1021/ar900277h (2010).
Capitani, D., Di Tullio, V. & Proietti, N. Nuclear Magnetic Resonance to characterize and monitor cultural Heritage. Prog. Nucl. Magn. Reson. Spectrosc. 64, 29–69. https://doi.org/10.1016/j.pnmrs.2011.11.001 (2012).
Del Federico, E. et al. Unilateral NMR applied to the conservation of works of art. Anal. Bioanal. Chem. 396, 213–220. https://doi.org/10.1007/s00216-009-3128-7 (2010).
Gervais, C., Boon, J. J., Marone, F. & Ferreira, E. S. B. Characterization of porosity in a 19th century painting ground by synchrotron radiation X-ray tomography. Appl. Phys. A 111, 31–38. https://doi.org/10.1007/s00339-012-7533-y (2013).
Ge, M. Y. et al. One-minute nano-tomography using hard X-ray full-field transmission microscope. Appl. Phys. Lett. 113, 4. https://doi.org/10.1063/1.5048378 (2018).
Besli, M. M. et al. Mesoscale chemomechanical interplay of the LiNi0.8Co0.15Al0.05O2 cathode in solid-state polymer batteries. Chem. Mater. 31, 491–501. https://doi.org/10.1021/acs.chemmater.8b04418 (2019).
Liu, Y. et al. In 10th International Conference on X-ray Microscopy. 357–360 (2011).
Vicent, D. A. et al. Nano-scale 3d imaging at the advanced photon source. SPIE Newsroom. https://doi.org/10.1117/2.1201604.006461 (2016).
Mahon, D. & Centeno, S. A. A technical study of John Singer Sargent’s portrait of Madame Pierre Gautreau. Metrop. Museum J. 40, 121–129 (2005).
Rogge, C. E., Veliz Bomford, Z. & Leal, M. Seldom black and white: the works of Franz Kline. In Metal Soaps in Art—Conservation & Research (eds Casadio, K. F. et al.) 413–424 (Springer, Berlin, 2019).
Eastaugh, N., Walsh, V., Chaplin, T. & Siddall, R. Pigment compendium, a dictionary and optical microscopy historical pigments, Butterworth-Heinemann (Elsevier, Amsterdam, 2004).
Osmond, G., Boon, J. J., Puskar, L. & Drennan, J. metal stearate distributions in modern artists’ oil paints: Surface and cross-sectional investigation of reference paint films using conventional and synchrotron infrared microspectroscopy. Appl. Spectrosc. 66, 1136–1144. https://doi.org/10.1366/12-06659 (2012).
Chen-Wiegart, Y. C. K. et al. 3D morphological evolution of porous titanium by X-ray micro- and nano-tomography. J. Mater. Res. 28, 2444–2452. https://doi.org/10.1557/jmr.2013.151 (2013).
Dowd, B. A. et al. In Conference on Developments in X-Ray Tomography II. 224–236 (1999).
Gursoy, D., De Carlo, F., Xiao, X. H. & Jacobsen, C. TomoPy: A framework for the analysis of synchrotron tomographic data. J. Synchrotron Radiat. 21, 1188–1193. https://doi.org/10.1107/s1600577514013939 (2014).
Rueden, C. T. et al. Image J2: ImageJ for the next generation of scientific image data. BMC Bioinf. https://doi.org/10.1186/s12859-017-1934-z (2017).
Hanwell, D. M., Ayachit, U., Muller, A. D. & Hovden, R. Tomviz software for tomographic visualization of 3D scientific data. https://tomviz.org/ (2019).
Wang, J. J., Chen-Wiegart, Y. C. K. & Wang, J. In operando tracking phase transformation evolution of lithium iron phosphate with hard X-ray microscopy. Nat. Commun. https://doi.org/10.1038/ncomms5570 (2014).
Wang, J. J., Chen-Wiegart, Y. C. K. & Wang, J. In situ three-dimensional synchrotron X-ray nanotomography of the (De) lithiation processes in tin anodes. Angew. Chem. Int. Edit. 53, 4460–4464. https://doi.org/10.1002/anie.201310402 (2014).
Chen-Wiegart, Y. C. K., Figueroa-Santos, M. A., Petrash, S., Garcia-Miralles, J. & Wang, J. Critical factors affecting the 3D microstructural formation in hybrid conductive adhesive materials studied by X-ray nano-tomography. Nanoscale 7, 908–913. https://doi.org/10.1039/c4nr06068g (2015).
Farrar, T. C. & Becker, E. D. Pulse and Fourier Transform NMR. Introduction to Theory and Methods (Academic Press, Cambridge, 1971).
Borgia, G. C., Brown, R. J. S. & Fantazzini, P. Uniform-penalty inversion of multiexponential decay data. J. Magn. Reson. 132, 65–77. https://doi.org/10.1006/jmre.1998.1387 (1998).
Ferrara, C. et al. Comparison of GPR and unilateral NMR for water content measurements in a laboratory scale experiment. Near Surface Geophys 11, 143–153 (2013).
Dunn, K., Bergman, D. & LaTorraca, G. Nuclear Magnetic Resonance: Petrophysical and Logging Applications (Pergamon Press, Oxford, 2002).
de Viguerie, L., Payard, P. A., Portero, E., Walter, P. & Cotte, M. The drying of linseed oil investigated by Fourier transform infrared spectroscopy: Historical recipes and influence of lead compounds. Prog Organic Coat 93, 46–60. https://doi.org/10.1016/j.porgcoat.2015.12.010 (2016).
O’Neil, L. A. & Brett, R. A. Chemical reactions in paint films. J Oil Colour Chem Assoc 52, 1054–1074 (1969).
van den Berg, J. D. J., van den Berg, K. J. & Boon, J. J. Identification of non-cross-linked compounds in methanolic extracts of cured and aged linseed oil-based paint films using gas chromatography–mass spectrometry. J Chromatography A 950, 195–211. https://doi.org/10.1016/s0021-9673(02)00049-3 (2002).
Munch, B. & Holzer, L. Contradicting geometrical concepts in pore size analysis attained with electron microscopy and mercury intrusion. J. Am. Ceram. Soc. 91, 4059–4067. https://doi.org/10.1111/j.1551-2916.2008.02736.x (2008).
Chen-Wiegart, Y. C. K. et al. Tortuosity characterization of 3D microstructure at nano-scale for energy storage and conversion materials. J. Power Sources 249, 349–356. https://doi.org/10.1016/j.jpowsour.2013.10.026 (2014).
Gonzalez, V. et al. Synchrotron-based high angle resolution and high lateral resolution X-ray diffraction: Revealing lead white pigment qualities in old masters paintings. Anal. Chem. 89, 13203–13211. https://doi.org/10.1021/acs.analchem.7b02949 (2017).
Martinetto, P., Anne, M., Dooryhee, E., Walter, P. & Tsoucaris, G. Synthetic hydrocerussite, 2PbCO(3)center dot Pb(OH)(2), by X-ray powder diffraction. Acta Crystallogr. A 58, I82–I84. https://doi.org/10.1107/s0108270102006844 (2002).
Wang, X. R. & Rackaitis, M. Gelling nature of aluminum soaps in oils. J. Colloid Interface Sci. 331, 335–342. https://doi.org/10.1016/j.jcis.2008.11.032 (2009).
Acknowledgements
This research used resources of the Advanced Photon Source (APS), a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. This research used resources of the Center for Functional Nanomaterials, which is a U.S. DOE Office of Science Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704 This research used resources of the National Synchrotron Light Source II, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under Contract No. DE-SC0012704. This work was also supported by the US National Science Foundation under Grants DMR-1608594 and DMR-1608366, to The Metropolitan Museum of Art and the University of Delaware. The authors are indebted to Eleonora Del Federico and Cindie Kehlet at the Pratt Institute, New York, for sharing the unilateral NMR instrument used in this study. Karen Chen-Wiegart, Xiaoyang Liu, Chonghang Zhao, and Cheng-Hung Lin acknowledge the financial support of the Department of Materials Science and Chemical Engineering and the College of Engineering and Applied Sciences at Stony Brook University, as well as BNL Laboratory under Contract No. DESC0012704. Chen-Wiegart group members Lijie Zou and Qingkun Meng are acknowldged for their asistance during the synchrotron nano-tomography experiments. The authors acknowledge the technical support of Alex Deriy at APS.
Author information
Authors and Affiliations
Contributions
The work was developed under a larger project, which was conceived by S.A.C., N.Z., and C.D.; S.A.C. and Y.-c.K.C.-W. further developed the research idea on using X-ray nano-tomography and wrote the user proposal for the use of beamtime at APS, with inputs from V.D.T., N.Z. and C.D. X.L., V.D.T., Y.-C.L., C.-H.L., C.Z. prepared the samples under the guidance of S.A.C. and Y.-c.K.C.-W. Y.-C.L. carried out the SEM analysis on paint films. Y.-C.L. and C.Z. carried out the FIB analysis and sample preparation. X.L. and Y.-C.L. carried out the SEM and EDX analysis on Al stearate. V.D.A. advised on optimized conditions to carry out the X-ray nano-tomography experiments and set up the TXM at the APS for the experiment and provided experimental support. Y.-C.L., X.L., V.D.T., C.-H.L., C.Z. and Y.-c.K.C.-W conducted the TXM experiments at APS with advice and inputs from S.A.C and V.D.T. The NMR experiments and analysis were performed by V.D.T, with inputs from N.Z., C.D. and M.W. The X-ray nano-tomography data analysis was carried out by X.L. and Y.-C.L. in discussion with Y.-c.K.C.-W. and S.A.C. The manuscript was written by X.L., V.D.T., Y.-c.K.C.-W. and S.A.C. with inputs from M.W., N.Z. and C.D.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, X., Di Tullio, V., Lin, YC. et al. Nano- to microscale three-dimensional morphology relevant to transport properties in reactive porous composite paint films. Sci Rep 10, 18320 (2020). https://doi.org/10.1038/s41598-020-75040-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-75040-6
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.