Abstract
Arboviral infections such as dengue, Zika and chikungunya are fast spreading diseases that pose significant health problems globally. In order to control these infections, an intracellular bacterium called Wolbachia has been introduced into wild-type mosquito populations in the hopes of replacing the vector transmitting agent, Aedes aegypti with one that is incapable of transmission. In this study, we developed a Wolbachia transmission model for the novel wAu strain which possesses several favourable traits (e.g., enhanced viral blockage and maintenance at higher temperature) but not cyctoplasmic incompatibility (CI)—when a Wolbachia-infected male mosquito mates with an uninfected female mosquito, producing no viable offspring. This model describes the competitive dynamics between wAu-Wolbachia-infected and uninfected mosquitoes and the role of imperfect maternal transmission. By analysing the system via computing the basic reproduction number(s) and stability properties, the potential of the wAu strain as a viable strategy to control arboviral infections is established. The results of this work show that enhanced maintenance of Wolbachia infection at higher temperatures can overcome the lack of CI induction to support wAu-Wolbachia infected mosquito invasion. This study will support future arboviral control programs, that rely on the introduction of new Wolbachia variants.
Similar content being viewed by others
Introduction
Arthropod-borne viruses, or arboviruses, are viruses that are transmitted via blood feeding arthropods1. Arboviral infections such as dengue, Zika and chikungunya are fast spreading diseases that pose significant health problems globally2,3,4,5. These viral infections, in particular dengue, are transmitted mainly by Aedes aegypti and sometimes by Aedes albopictus (Asian Tiger) female mosquitoes when taking a blood meal from the host6,7. Approximately 390 million dengue infections are estimated to occur worldwide annually, putting 40% of the total human population at risk8. Dengue infection is the most geographically wide-spread of the arboviral infections3,8. It has different severity levels which are classified according to disease progression from dengue without warning signs to dengue with warning signs and then severe dengue9. Clinical manifestation includes sudden high-grade fever, headache, nausea, arthralgia, eye pain, muscle ache and rash in some cases10. Presently, there is no specific universal treatment for dengue infections: the vaccine envelopment targets young populations; the efficacy of the only vaccine licensed depends on prior immunity to at least one serotype of dengue; and it provides heterogeneous protection against the different serotypes11,12.
Other arboviral infections such as Zika, chikungunya and yellow fever are also of global health concern13. These arboviral infections have occurred simultaneously with dengue13,14. Some of these infections share many similar clinical manifestations with dengue infection and also allow arboviral coinfection such as dengue and chikungunya15, chikungunya and Zika16 and yellow fever and chikungunya17. Although, there are no specific treatments for Zika and chikungunya viral infections, these infections can be managed by supportive treatment of symptomatic individuals and adequate rest. This treatment includes fluid intake and administering drugs such as acetaminophen to suppress pain and fever18,19. However the prevention strategy for yellow fever infection is available i.e. vaccination20,21.
To control these infections, an intracellular bacterium called Wolbachia can be used to suppress transmission in arthropods such as mosquitoes and flies22,23,24,25. Wolbachia infection inhibits arboviral transmission in mosquitoes via four mechanisms: immune priming—preactivation of the mosquito immune system; induction of the phenoloxidase cascade—triggers immune response to viruses; competition of intracellular resources—inducing authophagy; and induction of microRNA-dependent immune pathways—essential for gene regulation and stability, immune defense, ageing and organ differentiation26. This endosymbiotic bacterium which exists naturally in more than 50% of all insect species can be found within the cytoplasm of the cells of their hosts25,27,28. Whilst Wolbachia is not naturally present in Aedes aegypti, it can be introduced via stable transinfections using microinjections29,30.
The Wolbachia-based control strategy is carried out by infecting mosquitoes with a strain of Wolbachia and then releasing them into wild mosquito populations in the hopes of replacing the vector transmitting agent Aedes aegypti with one that is incapable of transmission29,30,31. Infecting an Aedes mosquito with Wolbachia can change some of the Aedes characteristic features. In practice, Wolbachia can reduce the life-span of mosquitoes by half producing a deleterous fitness effect32. Another feature is cytoplasmic incompatibility (CI)22,33,34,35 which occurs when a Wolbachia infected male mates with an incompatible female mosquito (usually Wolbachia uninfected) producing no offspring36. Other features of Wolbachia which serve as liabilities in mosquitoes include: imperfect maternal transmission (IMT)30,37 and loss of Wolbachia infection (LWI). LWI impedes the establishment of Wolbachia-infected mosquitoes and is a result of mosquito vulnerability to high temperature38,39.
However, a novel strain of Wolbachia: wAu, has shown to produce high viral blockage whilst maintaining Wolbachia infection in Aedes mosquitoes at higher temperature23. Moreover, wAu allows superinfection to occur when wAu and other strains of Wolbachia co-exist in the vector host23. Despite these favourable features, wAu does not induce CI23. Although CI absence does not establish Wolbachia infected mosquitoes, the effect could be outweighed by LWI and IMT37.
The difference in the common Wolbachia strain features are described in Table 1 below.
In general, the introduction of mathematical models to understand infection dynamics of diseases has long been helpful in the area of disease control49. A number mathematical models of Wolbachia dynamics in a mosquito population have been formulated37,50,51,52,53,54,55,56,57,58. Some of these models introduced Wolbachia strain(s) into a mosquito population and classified them into age-sturctured Wolbachia-infected and -uninfected mosquito compartments37,53,54,57. Ndii et al.53, formulated a mathematical model for the Wolbachia interaction between the immature stages (aquatic stage), adult male and female mosquito populations to investigate the persistence of mosquitoes infected with Wolbachia when competing with the uninfected ones. They derived the steady state solutions and showed that parameters such as maternal transmission, reproductive, death and maturation rates drive the persistence of the Wolbachia-infected mosquito population. A similar model developed by Xue et al. considered the Wolbachia-induced fitness change and the CI effect57. They showed that if the basic reproduction number (\(R_0\)) of the Wolbachia-infected mosquitoes is less than one, an endemic Wolbachia infection can still occur via backward bifurcation if a sufficient number of the mosquitoes are introduced into the population. A mathematical model of Wolbachia to control dengue fever transmission52 was developed by Hughes et al. The model showed that the use of Wolbachia has high potential to control dengue where the \(R_0\) due to Wolbachia-infected Aedes mosquitoes is not too large in endemic areas. Another study of a Wolbachia invasive model incorporated IMT and LWI and showed that CI does not guarantee the establishment of Wolbachia-infected mosquitoes as the disadvantages derived from IMT and LWI in the production of Wolbachia-infected mosquitoes could outweigh CI37.
Additionally, a study conducted by O’Reilly et al combining multiple modeling methods, was used to estimate the burden of dengue and map its distribution across Indonesia59. They predicted that there was a reduction in dengue transmission after a nationwide release of wMel-Wolbachia-infected mosquitoes. In addition, they predicted about 86% of the estimated 7.8 million annual cases of symptomatic dengue in Indonesia could be averted following a complete nationwide rollout of Wolbachia-infected mosquitoes. Recently, a modeling study presented a dengue transmission model in the presence of female wild-type and wMelPop Wolbachia-infected Aedes aegypti mosquitoes. They concluded that although the wMelPop strain reduces the lifespan of infected mosquitoes, which could be challenging to achieve replacement of wild-type mosquitoes, its optimal release ensured the replacement of wild-type mosquitoes and also reduced dengue burden in the human population51. A mosquito-Wolbachia model was developed by Xue et al, to compare the potential effectiveness of two Wolbachia strains (wMel and wAlbB) to control arboviral spread60. They observed that each of the two different strains of Wolbachia can effectively decrease the rate of arboviral transmission.
Here, we develop a general Wolbachia model capable of faithfully replicating all of the strain features described in Table 1. The general transmission model is an extention of the Wolbachia transmission model introduced in Adekunle et al.37, which described the competitive dynamics between (wMel-like) Wolbachia-infected and uninfected mosquitoes. Despite the non-induction of CI in wAu-Wolbachia-infected mosquitoes, wAu infection is retained and able to block viral transmission efficiently compared to other strains even at high temperature. Therefore, we incorporated this feature to determine if the advantages (Wolbachia retainment) of the wAu strain outweigh the ineffectiveness of CI. This feature has not been considered in previous models. Furthermore, we incorporate imperfect maternal transmission into the model. By analysing the system via computing the basic reproduction number(s) and investigating the stability properties of the equilibrium points, the potential of the wAu strain as a viable strategy to control Aedes-borne infections can be established. The aim of this modeling approach is to support future Aedes-borne viral control programs, particularly with the introduction of new Wolbachia variants.
Methods
Model formation
Here, we investigate a modified Wolbachia transmission model studied in Adekunle et al.37, focusing on a novel Wolbachia strain, wAu, which has high retainment, high viral blockage and does not induce CI. The mosquito population is subdivided into two groups: the uninfected mosquitoes \((.)_u\) and the Wolbachia infected mosquitoes \((.)_w\). The term (.) can be aquatic/immature (eggs, larvae and pupae) A, male M or female F mosquitoes. In addition, we denote the aquatic/immature stages, mature male and mature female uninfected mosquitoes as \(A_u\), \(M_u\), \(F_u\), and Wolbachia-infected mosquitoes as \(A_{w}\), \(M_{w}\), \(F_{w}\) respectively. As in Adekunle et al.37 the model also incorporates the IMT of wAu-Wolbachia.
There are four possible mosquitoes’ mating pairs: \(F_uM_u\), \(F_uM_w\), \(F_wM_u\) and \(F_wM_w\). As Wolbachia infection is maternally transmitted, \(F_uM_u\) and \(F_uM_w\) will produce uninfected offspring while \(F_wM_u\) and \(F_wM_w\) will typically produce infected offspring. However if there is imperfect maternal transmission, the two latter strategies could produce some proportions of uninfected offspring23.
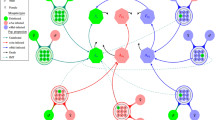
General model showing the Wolbachia infection dynamics in mosquitoes as M has been set equal to F. The green and pink compartmental polygons represent wild-type and Wolbachia-infected mosquitoes respectively. \(A_{u}\) and \(F_{u}\) represent the aquatic (eggs, larvae and pupae) and adult female mosquitoes for the uninfected mosquito population respectively while \(A_{w}\) and \(F_{w}\) represent their Wolbachia infected counterparts. The teal and red arrows illustrate the population progression of uninfected and Wolbachia-infected mosquitoes respectively. The four circles (three black and one brown) represent the mosquito mating strategies. The effect of cytoplasmic incompatibility (\(\phi \)), i.e. for wAu and wMel strains, \(\phi =0\) and \(\phi =1\) respectively, is illustrated by the brown-circled \(F_{u}\)\(F_{w}\). The dashed lines represent the proportion of uninfected offspring caused by imperfect maternal transmission (IMT). The blue lines depict mosquito mortality. If there is loss of Wolbachia infection (LWI), \(\sigma > 0\). But if there is no LWI as in wAu-Wolbachia strain, then \(\sigma =0\).
To mathematically write the system of differential equations governing the Wolbachia transmission dynamics, we express the feasible mating strategies of uninfected and Wolbachia infected mosquito populations together with their per capita egg laying rates as Eqs. (1)–(6):
where \(F=F_u +F_{w}\), \(M=M_u +M_{w}\), \(A=A_u +A_{w}\).
Here, \(\phi \) represents the CI effect which can be either 0 if there is no CI, or 1 if CI is present. \(\sigma \) is the effect of LWI, such that it can either be 0, if there is no Wolbachia loss or greater than zero otherwise. In Adekunle et al.37 where CI is assumed and LWI is considered, these quantities are set to \(\phi =1\) and \(\sigma \ge 0\). In our modified model, considering different strains with the exception of wAu strain, \(\phi =1\) and \(\sigma \) could vary from values greater than zero onwards. However, for the wAu-Wolbachia strain, CI is ineffective and high retainment of wAu-Wolbachia infection even at high temperatures23 is established, therefore we set \(\phi =0\) and \(\sigma =0\). Our model also incorporates imperfect maternal transmission generating a proportion of infected and uninfected offspring from mating of both \(F_w M_{u}\) and \(F_w M_{w}\) mosquitoes. To simplify the system, we assume that \(M=F\) in accordance with the observed ratio of male to female mosquitoes of 1.02:162. That is, we set \(\psi = 1/2\) (Fig. 1). By this, it follows that the system of ordinary differential equations (ODEs) in Eqs. (1)–(6) can be reduced to (7)–(10) which is the governing Wolbachia infection dynamics.
To mathematically express the above schematics, we have that, the feasible mating strategies of uninfected and Wolbachia infected mosquito populations together with their per capita egg laying rates are given by the following differential system:
where \(F=F_u +F_{w}\) and \(A=A_u +A_{w}\). Before proceeding, we rescale each of our state variables according to the maximum total population size, which by Adekunle et al., 201937 is set by
where \(\alpha = 1+\frac{1}{2}\left( \frac{\tau _u}{\mu _u} + \frac{\tau _w}{(\mu _w +\sigma )}\left( 1+\frac{\sigma }{\mu _u}\right) \right) \).
The closed set
which is a feasible region for the above system dynamics is positively invariant37.
Hence, we let \(\bar{A}_u = \frac{A_u}{\alpha K}\), \(\bar{A}_w = \frac{A_w}{\alpha K}\), \(\bar{F}_u = \frac{F_u}{\alpha K}\), \(\bar{F}_w = \frac{F_w}{\alpha K}\), \(\bar{A}=\bar{A}_u +\bar{A}_{w}\) and \(\bar{F}=\bar{F}_u +\bar{F}_{w}\). Also, letting \(\nu =1\), we assume a perfect maternal transmission for the reproduction outcome of \(\bar{F}_w \bar{M}_{w}\) mating. Therefore, the general Wolbachia model in terms of population proportions is given by Eqs. (12)–(14). Hereafter it is clear that we refer to the scaled values of each state variable and as such drop the overbar from our notation. The scaled model below now evolves in the feasible region \(\bar{\Omega }\), where \(\bar{\Omega } = \left\{ (\bar{A}_u, \bar{F}_u, \bar{A}_w, \bar{F}_w) \in \mathbb {R}_+^4 \, | \, \bar{A}_u + \bar{F}_u + \bar{A}_w + \bar{F}_w \le 1 \right\} \).
The modeling of wAu-Wolbachia transmission dynamics has not been done as this a distinction from other Wolbachia transmission models. Unlike the modeling work in Adekunle et al.37, apart from the non-induction of CI, we considered the loss of Wolbachia infections due to seasonal fluctuation in temperature, a key dynamics that is absent in wAu strain.
Results
Analysis of the model
The above general model (11)–(14) is parametrically adjusted to simultaneously accommodate wAu and wMel Wolbachia strains. For the wAu-Wolbachia model, we set \(\phi = \sigma = 0\) and for the wMel-Wolbachia model, we set \(\phi = 1\), \(\sigma > 0\). The wMel-Wolbachia model parameter adjustments correspond to the model studied in Adekunle et al.37.
Here, we want to analyse the general model(11)–(14) with arbitrary values of \(\phi \) and \(\sigma \) to enable comparison with wAu-Wolbachia and Adekunle et al. 201937 models. Analysing the model for wAu, we have four steady states. The first steady state \(e_1 = (0,0,0,0)\) indicates non-existence of mosquitoes. The second \(e_2 = (A_u^*,F_u^*,0,0)\) signifies the steady state for the uninfected mosquito population only. The third \(e_3 = (0,0,A_w^*,F_w^*)\) describes the equilibrium point for wAu-infected mosquitoes only. Lastly, the \(e_4 = (A_u^*,F_u^*,A_w^*,F_w^*)\) is the equilibrium point for the co-existence of both uninfected and wAu-Wolbachia-infected mosquito populations.
Non-existence mosquito population, \(e_1\)
The equilibrium point \(e_1\) is trivial and is not biologically realistic. However, we can gain some insights into the competitive model dynamics by examining the case where there is no interaction between the uninfected and Wolbachia-infected mosquitoes. In other words, we want to investigate how each population would behave in the absence of the other. In particular, we derive the reproduction number of the uninfected \(R_{0u}\) and Wolbachia-infected \(R_{0w}\) mosquito populations when they do not interact:
where the factor of \(\frac{1}{2}\) in \(R_{0u}\) and \(R_{0w}\) stems from the choice to set M = F62, i.e. \(\psi = \frac{1}{2}\).
These reproductive numbers determine if the uninfected and Wolbachia-infected mosquito populations will die out or persist when there is no interaction. Specifically, if \(R_{0u}<1\) and \(R_{0w}<1\), then the two populations will die out (Fig. 2a). We observed in the decoupled case, the expressions for \(R_{0u}\) and \(R_{0w}\) are independent of the effects of CI \((\phi )\) and LWI \((\sigma )\) and are therefore equivalent for both the wAu and wMel-Wolbachia strains (Fig. 2)37.
Graphs showing the system trajectories in the \((F_u, F_w)\) plane for (a) wAu (\(\phi = \sigma = 0\)) and (b) wMel (\(\phi = 1\), \(\sigma =0.04\)) Wolbachia models when \(\max [R_{0u}, R_{0w}] < 1\). The red ball point indicates the point of stability, that is \((F_{u}, F_{w})=(0,0)\) representing mosquito extinction. We set \(\rho _{uu}=0.01\) and \(\rho _{ww}=0.1\). Other parameters used for these model simulations are provided in Table 2.
Uninfected mosquito population, \(e_2\)
The uninfected-mosquito-only equilibrium point or Wolbachia-free equilibrium is
For \(e_2\) to exist, we require \(R_{0u}>1\). In addition to the uncoupled reproduction numbers (\(R_{0u}\) and \(R_{0w}\)) we also define the invasive reproduction number \(R_{0w|u}\) which describes the average number of secondary offspring that will become Wolbachia-infected adults after introducing a single adult Wolbachia-infected mosquito into an established Wolbachia uninfected mosquito population.
To compute \(R_{0w|u}\), we use the next generation matrix method63 to obtain
where we have substituted in the definition of \(R_{0w}\) from Eq. (16). The invasive reproduction number \(R_{0w|u}\) is the same for both wAu and wMel-Wolbachia strains as that derived in Adekunle et al.37. This is because, the expression (17) clearly shows that the invasive reproductive number \(R_{0w|u}\) is not dependent on the CI effect, \(\phi \) or LWI, \(\sigma \).
To check if the equilibrium point \(e_2\) is stable, we compute the Jacobian of the system and evaluate it at \(e_2\). In particular, letting \(z_1 = (\mu _{Au}+\tau _{u})\) and \(z_2 = (\mu _{Aw}+\tau _{w})\), yields
To obtain the characteristic equation of \(J_{e_2}\), we have
which becomes
where
Therefore, \(e_2\) is locally asymptotically stable if and only if \(R_{0w|u}<1\) and \(R_{0u}>1\) (Fig. 4). This is also consistent with the study in Adekunle et al.37 (See Table 3).
Wolbachia-infected mosquito population, \(e_3\)
The wAu-infected-only equilibrium point is \(e_3 = \left( 0,0,\frac{1}{\alpha }\left[ 1-\frac{1}{R_{0w}}\right] ,\frac{\tau _{w}}{2\mu _{w}\alpha }\left[ 1-\frac{1}{R_{0w}}\right] \right) \). This again is consistent with Adekunle et al.37.
For \(e_3\) to exist we require \(R_{0w}>1\). By computation, the invasive reproductive number \(R_{0u|w}\) with respect to uninfected mosquitoes is given as,
where \(c = (1-\phi )+\frac{\rho _{ww}}{\rho _{uu}}(1-\delta )\). Clearly, \(R_{0u|w}\) is dependent on \(\phi \). For the wMel-Wolbachia strain, i.e. \(\phi =1\), \(c = \frac{\rho _{ww}}{\rho _{uu}}(1-\delta )\) which is equivalent to that of Adekunle et al.37. However, for the wAu-Wolbachia strain, i.e. \(\phi =0\), we have a modified expression of \(c = 1+\frac{\rho _{ww}}{\rho _{uu}}(1-\delta )\) in Eq. (18) because we do not assume CI. Therefore, \(c\ge 1\) for wAu-Wolbachia strain. Computing the Jacobian at \(e_3\), we have:
The characteristic equation of \(J_{e_3}\) is then
where
Therefore, \(e_3\) is locally asymptotically stable if and only if \(R_{0u|w}<1\) and \(R_{0w}>1\) (see Fig. 4). The condition is equivalent to that found in37 with generalized expressions for \(R_{0u|w}\) used in place of the reduced version presented there (see Table 3).
Coexistent mosquito populations, \(e_4\)
The equilibrium point for which both the uninfected and Wolbachia-infected populations coexist is
\(e_4 = (\frac{2\mu _u \beta F_w^*}{\tau _{u}},\beta F_w^*,\frac{2\mu _w F_w^*}{\tau _{w}},F_w^*)\) where
\(\beta = \dfrac{R_{0w}(R_{0u|w}-1)}{R_{0u}(R_{0w|u}-1)}\) and \(\xi = \dfrac{(\beta +1)}{(\delta \beta + 1)}\). For \(e_4\) to exist, we require \(R_{0w}> \xi > 1\) and
-
(i)
\(R_{0w|u},R_{0u|w}>1\) or
-
(ii)
\(R_{0w|u},R_{0u|w}<1\).
The above conditions (i) and (ii) correspond to the cases for \(\delta >\dfrac{1}{c}\) and \(\delta < \dfrac{1}{c}\) respectively. Comparing these existence conditions with those found above for \(e_2\) and \(e_3\), we see that condition (ii) for the existence of \(e_4\) matches the combined existence and local asymptotic stability condition for \(e_2\) and \(e_3\). In other words, \(e_2\), \(e_3\) and \(e_4\) can coexist, while \(e_1\) always exists (see Fig. 4).
To establish whether \(e_4\) is stable or not, we compute the Jacobian \(J_{e_4}\) evaluated at \(e_4\) to obtain the following characteristic equation:
Let
\(z_3 = (\mu _u + \mu _w)\), \(z_4 = (\beta \rho _{uu}+\rho _{ww})\), \(z_5 = (\beta +1)\rho _{uu} +(1-\delta )\rho _{ww}\), \(z_6 = 1+\beta (2+\beta \delta )\),
\(z_7 = (\beta +1)^2\rho _{uu} +(1-\delta )\rho _{ww}\), \(z_8 = (1+\beta (2+\beta \delta ))\rho _{uu} +(1-\delta )\rho _{ww}\),
then we have:
In order to establish the nature of the equilibrium point \(e_4\), we performed numerical testing using the Monte Carlo method in50 to verify the conditions (i) and (ii) by computing the real part of the eigenvalues of the Jacobian matrix, evaluated at \(e_4\). Simulation results are illustrated in Fig. 3.
Graphs showing the numerical testing for the stability conditions (i) and (ii) and the real part of the eigenvalues’ distribution (\(\lambda _1, \lambda _2, \lambda _3\) and \(\lambda _4\)) for \(e_4\): (a,b) show that \(R_{0w|u}, R_{0u|w} >1\) always hold. (c) shows the related distribution of the real part of the eigenvalues for condition (i). (d,e) show the condition \(R_{0w|u}, R_{0u|w} <1\) always hold while (f) shows the corresponding distribution of the real part of the eigenvalues for condition (ii).
Although the conditions (i) and (ii) indicated the existence of \(e_4\), Fig. 3c showed that \(e_4\) is locally stable for condition (i) as all the eigenvalues (real part) are negative (\(\lambda _1, \lambda _2, \lambda _3,\lambda _4 <0\)). Whilst Fig. 3f showed that \(e_4\) is unstable for condition (ii) as two of the eigenvalues (real part) are positive i.e. \(\lambda _3,\lambda _4 > 0\).
Numerically, we illustrated the existence and stability regions for \(e_4\) in Fig. 4 for the two conditions (i) and (ii) relating to CI and maternal transmission (MT).
This graph shows the existence and local stability regions for the equilibrium points \(e_1\)–\(e_4\) for the Wolbachia model (11)–(14) as a function of the \(R_{0u}\) and \(R_{0w}\) relating to the cytoplasmic incompatibility (CI), \(\phi \) and maternal transmission (MT), i.e. magnitude of \(\delta \) and \(\frac{1}{c}\). The yellow shaded region indicates the local stability of \(e_1\) equilibrium. The green shaded area illustrates the local stability for the Wolbachia-free equilibrium point (\(e_2\)). \(e_3\) is locally stable at the red shaded part. The blue region indicates the coexistence local stability \(e_4\). The white region shows the existence of \(e_2, e_3\) and \(e_4\) and local stability of \(e_2\) and \(e_3\) equilibrium points. And the orange region describes the existence and local stability of \(e_1\) and \(e_3\). For \(\delta >\frac{1}{c}\); (a) describes \(\phi =0\) as the boundary \(R_{0w|u}=1\) sits above the boundary \(R_{0u|w}=1\) and the arc \(R_{0w}=\xi \) . The co-existent equilibrium \(e_4\) (blue), always sits in the region between these three boundaries because \(R_{0w|u}>1\), \(R_{0u|w}>1\) and \(R_{0w}>\xi \). If \(R_{0w}<\xi \), then \(e_1\) becomes stable (yellow). (b) describes similar conditions as in (a) but for \(\phi =1\). We observed that the boundary \(R_{0u|w}=1\) shifts up while \(R_{0w|u}=1\) remained stationary to accommodate more \(e_3\). For \(\delta <\frac{1}{c}\); (c) describes \(\phi =0\) as the relative position of \(e_4\) boundaries in (a) flips so that boundary \(R_{0u|w}=1\) sits above boundary \(R_{0w|u}=1\) and the arc \(R_{0w}=\xi \). Then, \(R_{0w|u}<1\) and \(R_{0u|w}<1\) and \(R_{0w}>\xi \) shows the co-existence of \(e_2\) and \(e_3\) (white). However, \(e_2\) and \(e_3\) are locally stable in the white region as \(R_{0w}>1\) and \(R_{01}>1\). For \(R_{0u}<1\), \(e_2\) and \(e_4\) do not exist, only \(e_1\) and \(e_3\) do and if \(R_{0w}>\xi \), \(e_1\) and \(e_3\) are locally stable (orange) and if \(R_{0w}<\xi \), only \(e_3\) becomes stable (red). (d) describes similar conditions as in (c) but for \(\phi =1\). It was observed that the boundary \(R_{0u|w}=1\) shifts up reducing the region of stability for \(e_2\).
Following a modeling study of Aedes aegypti mosquitoes and normal Wolbachia (in the presence of CI only) interaction analyzed by Ferreira et al.64, three equilibrium points: trivial (\(q_1\)); uninfected only (\(q_2\)); and coexistence (\(q_3\)), were obtained. However, the Wolbachia-only equilibrium point was not computed. The established local stability conditions for \(q_1\) and \(q_2\) correspond to that of the wMel-like Wolbachia conditions for \(e_1\) and \(e_2\) respectively. For coexistent populations to persist, the reproductive number for infected mosquitoes only, \(R_i\) must be greater than 1 and \(R_i > R_u\), where \(R_u\) is the reproductive number for wild-type mosquitoes only. The model64 also described the fitness parameter space between \(R_u\) and \(R_i\), showing the change in extinction and persistence of the three equilibria when there is an increase in the initial population proportion of the Wolbachia-infected mosquitoes. Our model showed the changes in the no-mosquito, wild-type only, Wolbachia-only and coexistence population persistence and extinction in the presence and absence of CI with high and low maternal transmission (MT).
Figure 4 illustrates the existence and local stability regions for the equilibrium points \(e_1\), \(e_2\), \(e_3\) and \(e_4\) with respect to the reproduction numbers \(R_{0u}\) and \(R_{0w}\) as well as the relative magnitude of \(\delta \) and \(\frac{1}{c}\). For \(\delta > \frac{1}{c}\) (high MT), Fig. 4a,b describe the dynamics for \(\phi =0\) (CI absent) and \(\phi =1\) (CI present) respectively. Within the subset of the yellow region of these figures bounded by \(R_{0u}=1, R_{0w}=1\), and \(R_{0w}=\xi \) we find that only \(e_1\) and \(e_3\) exist. Since \(e_3\) is unstable in this region, we expect the system trajectories to tend to the no-mosquito equilibrium \(e_1\). This was confirmed through numerical simulations shown in Fig. 5a. For the existence of \(e_4\) we require \(R_{0u|w}>1\), \(R_{0w|u}>1\) and \(R_{0w}>\xi \) for stability (within the blue region). But if \(R_{0w}<\xi \), \(e_1\) is stable (yellow).
For \(\delta < \frac{1}{c}\) (low MT), Fig. 4c,d portrayed the regions of stability for \(\phi =0\) and \(\phi =1\) respectively. The conditions \(R_{0u}<1, R_{0w}>1\), and \(R_{0u|w}>1\) project the trajectiory to tend to \(e_1\) (see Fig. 5b). In the orange region, \(e_1\) and \(e_3\) exist and are simultaneously locally stable as \(R_{0u|w}>1\) and \(R_{0w}>\xi \). In addition, we have that \(e_4\) exists where \(R_{0u|w}<1\) and \(R_{0w|u}<1\) (condition (ii)). With these conditions, \(e_4\) exists together with \(e_2\) and \(e_3\) (white region). In this white region, \(e_2\) and \(e_3\) are locally stable even as \(R_{0u}>1, R_{0w}>1\) but \(e_4\) is unstable. Also, \(e_1\) exists when \(R_{0w}>1\) and \(R_{0u}<1\) because the local stability of other equilibrium points is violated with these conditions. When \(R_{0u|w} > 1\) but \(R_{0u} < 1\) and \(R_{0w} > 1\), the only stable outcome is the mosquito-free (no-mosquito) equilibrium \(e_1\). This occurs when \(R_{0u}\) is less than but still close to one. In this region, uninfected mosquitoes are capable of dominating initially when introduced into a Wolbachia saturated equilibrium because imperfect maternal transmission achieves \(R_{0u|w} > 1\). This competitive advantage drives out the Wolbachia infected mosquitoes leaving uninfected mosquitoes only, which then are unable to sustain their population because \(R_{0u} < 1\) (Fig. 5).
With the rate of high maternal transmission (MT) in the absence of CI (like-wAu), the reproductive advantage favours the production of uninfected mosquito offspring as it tends to accommodate more coexistent mosquito populations with wild-type than wMel-like strain (presence of CI) due to the presence of CI (Fig. 4a,b). Whilst, with a low MT rate, the CI presence or absence would favour Wolbachia-infected mosquitoes or uninfected mosquitoes respectively. In other words, the coexistent equilibrium point is unstable for the two mosquito populations as these conditions are equivalent to the local stabilities of both Wolbachia-free and Wolbachia-only equilibrium points (Fig. 4c,d). If \(R_{0w} < \xi \), the system trajectories tend to the no mosquito equilibrium \(e_1\).
Graphs showing the local stability for \(e_1\) relating to the magnitude of \(\delta \) and \(\frac{1}{c}\). The initial conditions for the state variables are \(A_u(0)=0.00015\), \(F_u(0)=0.00013\), \(A_w(0)=0.013\), \(F_w(0)=0.013\). We set \(\rho _{uu}=1, \rho _{ww}=2.8571, \tau _u =\tau _w =1, \mu _{Au}=\mu _{Aw}=0.2, \mu _u=0.4630, \mu _w=0.6161\). (a) For \(\delta >\frac{1}{c}\), where \(\delta =0.4, c=2.7143, R_{0u}=0.8999, R_{0w}=1.9322, R_{0u|w}=1.2641, R_{0w|u}=0.8588\). (b) For \(\delta <\frac{1}{c}\), where \(\delta =0.2, c=3.2857, R_{0u}=0.8999, R_{0w}=1.9322, R_{0u|w}=1.5303, R_{0w|u}=0.4294\). The equilibrium point \(e_1\) is locally stable if \(R_{0u}<1, R_{0w}>1\), \(R_{0w|u}<1\) and \(R_{0u|w}>1\).
The conditions for the local stability of all equilibrium points are shown in Table 3 below.
Sensitivity analysis of Wolbachia model
To carry out the sensitivity analysis we investigate the model robustness due to uncertainties associated with parameter value estimations. In other words, we examine how senitive the invasive reproductive numbers are with respect to these parameters. This in turn, gives insight on influential parameters and their impact in reducing (or increasing) mosquito-type populations. To carry out this, we compute the normalized sensitivity indices of the invasive reproduction numbers with respect to the parameters used in the model.
Definition
The normalized forward sensitivity index of a variable v with respect to parameter w is defined as:
Using the above formular (20), we contruct the following plots in Fig. 6.
From Fig. 6 and using the baseline parameter values for the wAu-Wolbachia strain in Table 2, it is clear that the reproductive and mortality rates for both wild-type (\(\rho _{uu}, \mu _u\)) and wAu-Wolbachia-infected (\(\rho _{ww}, \mu _w\)) mosquitoes and the proportion of wAu-Wolbachia-infected offspring (\(\delta \)) have the most sensitivity in the invasive reproductive numbers \(R_{0w|u}\). Whilst for \(R_{0u|w}\), \(\mu _u\) and \(\mu _w\) are the most sensitive parameters. Hence for both invasive reproductive numbers, the most sensitive parameters are \(\mu _u\) and \(\mu _w\). This demonstrates that an increase (or decrease) in the mortality rate of wAu-Wolbachia-infected mosquitoes by 10% will decrease (or increase) \(R_{0w|u}\) by 10%.
Does CI \((\phi )\) outweigh the LWI \((\sigma )\)?
For most Wolbachia strains except wAu, the mating between uninfected female and Wolbachia-infected male mosquito crosses generates no viable offspring. However, Wolbachia-infected mosquitoes tend to lose their Wolbachia infection and lower their maternal transmission rate at high temperature (\(27{-}37^\circ {\text{C}}\))23. With the effect of climate change gradually increasing the temperature by the day, Wolbachia strains with moderate or high temperature sensitivity such as wMel may not be able to fully maintain a sufficient frequency level to invade the mosquito population.
In our general Wolbachia mathematical model, we describe a modified version of Adekunle et al.37. This modification accommodates parameter adjustments for novel wAu and wMel-Wolbachia strains. For wAu, our mathematical model showed that despite the production of mosquito offspring due to CI absence, the invasive reproduction number due to infected mosquitoes \(R_{0w|u}\) remains unchanged compared to the case where CI is present, as with the wMel-like strain37. This further strengthened the fact that CI (inclusion or exclusion) does not guarantee Wolbachia mosquitoes’ persistence. Also, the invasive reproduction number due to uninfected mosquitoes expression \(R_{0u|w}\) for wAu is similar to wMel, except that the expression depends on CI the effect. This is because, the mosquito gender crosses due to non-induction of CI for wAu, i.e. \(F_uM_w\), generates uninfected offspring with perfect maternal transmission while wMel does not. The chances of establishing Wolbachia infected mosquitoes are lower when CI is ineffective compared to when it is induced. That is, for cytoplasmic inducing wMel-Wolbachia mosquitoes, the effect of LWI outweighs CI effect as mosquitoes still lose their infections (Fig. 7). However, wAu-Wolbachia infection retainment (no LWI) in mosquitoes has shown high level of maintaining the Wolbachia frequency in the absence of CI in mosquitoes (Fig. 7). This suggests that the LWI effect outweighs CI.
The LWI rate \(\sigma (t)\) which is dependent on the seasons of the year can be modeled by a sinusoidal equation:
where \(\sigma _{max}\) is the maximum value of the seasonal variation in LWI, and \(\mathscr {C}\) is the phase shift which aligns the model with the seasonal change.
The effects of CI (\(\phi \)) and LWI (\(\sigma (t)\)) as features of wAu and wMel Wolbachia strains are shown in Fig. 7. For the total mosquito population, wAu-infected mosquitoes (\(\phi =0, \sigma _{max}=0\)) reach the maximum frequency after approximately 250 days. To see the effect of CI induction and slight LWI i.e. \(\phi =1\), \(\mathscr {C}=0.25\), for \(\sigma _{max}=0.02\) and \(\sigma _{max}=0.04\), the Wolbachia frequency level oscillates between (0.8 and 1) and (0.6 and 1) respectively. That is, there is a 20% and 40% drop in the frequency level of Wolbachia when \(\sigma (t)\) is at \(\sigma _{max}=0.02\) and \(\sigma _{max}=0.04\) respectively. This showed that, despite CI induction, LWI reduced the contribution of CI to the Wolbachia invasion (Fig. 7a). Therefore, the LWI gains highly outweigh the CI effect. By this, our analysis suggests that an increase in LWI in the presence of CI results in a drastic decrease in the Wolbachia frequency level (Fig. 7a). On the other hand, Fig. 7b showed the effect of LWI \(\sigma (t)\) and CI \(\phi \) with respect to the competitiveness between \(F_u\) and \(F_w\). We observed that the \(F_w\) population dominates the \(F_u\) when there was no CI induction and Wolbachia infection is retained, that is, \(\phi =0, \sigma _{max}=0\) (Fig. 7b). However, if CI induction occurs with loss of Wolbachia infections, then the seasonal varying effect occurs as seen in Fig. 7c.
(a) Effect of CI induction \(\phi \) and LWI \(\sigma (t)\) on the Wolbachia frequency level. The initial conditions for the state variables are \(A_u(0)=0.25\), \(F_u(0)=0.01\), \(A_w(0)=0\), \(F_w(0)=0.003\). The red line indicates Wolbachia retainment as \(\phi =0\) (no CI induction) and \(\sigma _{max}=0\) (no LWI) which are features of wAu-Wolbachia strain. The blue and black dashed lines (for wMel-Wolbachia strain) illustrate CI induction and LWI i.e \(\phi =1\) for \(\sigma _{max}=0.02\) and \(\sigma _{max}=0.04\) respectively. Parameters for \(e_3\) were used in these simulations. (b) Shows the dominance of wAu-Wolbachia infected \(F_w\) to uninfected \(F_u\) adult mosquitoes due to the retainment of Wolbachia infections (not affected by seasonal varying LWI). The wAu-Wolbachia-infected mosquitoes dominates when there is no CI \(\phi =0\) and LWI \(\sigma _{max}=0\) (red line). (c) For wMel-Wolbachia-infected mosquitoes, the effect of seasonal varying loss of Wolbachia infection is shown as infections rise and drop continuously due to LWI \(\sigma _{max}=0.04\) and CI induction \(\phi =1\).
Discussion
In this work, we modelled and investigated a general Wolbachia model that contained the transmission dynamics of wAu and wMel Wolbachia strains in Aedes mosquitoes as special cases. These transmission dynamics described the competition between the novel wAu-Wolbachia infected Aedes mosquitoes and wild-type mosquitoes and compared the dynamics with the invasive properties of the popular wMel-Wolbachia infected mosquitoes. We first derived the Wolbachia infection-status reproduction numbers for our wAu-Wolbachia model and used them to establish the conditions for the local stability of the equilibrium points for the wAu-Wolbachia invasive model. The reproduction number associated with the uninfected mosquitoes shows the reproductive advantage that the wild type has over the wAu strain. The comparison of the wAu-Wolbachia model (CI and LWI absent) and wMel-Wolbachia model (CI and LWI present) showed that the wAu strain has the potential of compensating for the undesirable features of the wMel strain.
Additionally, this study has reviewed the main features of different Wolbachia strains (Table 1) and shown that the wAu Wolbachia strain is a promising candidate for efficient Aedes-borne arboviral transmission control. Moreover, we analyzed the system dynamics of a general Wolbachia invasion model and determined the regions of local stability for each of the identified equilibrium points, highlighting the regions in parameter for which Wolbachia-infected mosquito populations persist or go extinct. This work modelled the general Wolbachia dynamics which can accommodate various Wolbachia characteristics regarding the presence or absence of CI and seasonal changes, unlike Adekunle et al.37, which considers only the presence of CI. We also investigated the advantages gained from CI and LWI. This study has demonstrated that despite the absence of CI, the Wolbachia frequency level will drop as much as tenfold of the percentage of Wolbachia infection lost. We showed that the advantage of Wolbachia retainment in mosquitoes strongly outweighed the negative impact of CI indicating wAu Wolbachia strains may be suitable for arboviral control. Therefore, this modeling work contributes to the previous studies37,54,57,64,65 and helps close the gap between ways of maintaining the Wolbachia frequency levels in the absence of LWI and CI.
One implementation question for using the wAu strain as a replacement of the wMel strain is whether the wAu strain is self-sustaining, given that it does not induce CI. In this work, the equilibrium points for the wAu-Wolbachia model are the same as that for the wMel-Wolbachia model except that stricter conditions are required to satisfy the wAu-Wolbachia model equilibrium points. These more stringent conditions translate to additional resources such as the continuous introduction of a larger scale of wAu-infected mosquitoes to ensure replacement66. Thus, the wAu strain is a promising alternative strain as it does not suffer from LWI due to high weather temperature and is highly effective in preventing the transmission of the arbovirus23,39,67. Otherwise, combining the two strains may also be a good strategy.
There are limitations associated with any mathematical modeling work, and this study is not exempted. We first assumed the same mosquito gender ratio and expected this proportion to be constant over time. This assumption may be true in a laboratory setting62, but not necessarily true in a natural mosquito habitat. However, similar conclusions are expected to be reached as the Wolbachia model reduction accurately reproduces the dynamics of the full system68. Secondly, we assumed that the absence of CI implies that cross mating resulted in offspring that are uninfected. This may not be true as a small proportion of the offspring may be Wolbachia infected23. If that is the case, then it means that lesser resources will be required to use the wAu strain as a Wolbachia-based control strategy. Lastly, we assumed the seasonality affects the associated parameters for the wMel dynamics. However, for the wAu strain, it is not affected by seasonality as wAu-Wolbachia infections are retained at high temperature.
Although several studies22,38,42,57 have demonstrated that CI drives the persistence of Wolbachia-infected Aedes mosquitoes, these studies neglected the impact of Wolbachia loss in mosquitoes. The CI drive has been shown in four mating lines (see Fig. 1) involving a Wolbachia-transinfected Aedes mosqiutoes mating with wild-type mosquitoes. One of the mating lines for which Wolbachia-infected male and uninfected female mosquitoes produced no viable offspring (via CI) truncates the uninfected offspring from being produced as infection is maternally transmitted. With the exception of the mating between the uninfected male and female mosquito line, all other mating lines produce Wolbachia-infected offspring leading to persistence. In addition, high temperature affects these Wolbachia-infected mosquitoes as they lose their infection due to the unfavourable weather conditions. However, mosquitoes infected with the wAu-Wolbachia strain have been shown to not only block arboviral transmission efficiently, but also retain the Wolbachia infection at typically unfavourable high temperatures. This retainment of infection in mosquitoes strongly outweighed the absence of CI for the wAu strain in the establishment and dominance of wAu-Wolbachia infected mosquitoes.
While vaccine implementation may have been highly effective on dengue seropositive persons in high transmission areas11,12, the introduction of Wolbachia-infected mosquitoes in low and moderate arboviral endemic areas has also effectively shown successful reduction in dengue burden43,51,59,69. Given that these two strategies could reduce the transmission of Aedes-borne diseases, in particular, dengue depending on the transmission level, a modeling study by Ndii70 proposed the use of these combined strategies and compared their effectiveness. The author showed that, Wolbachia performs better in the presence of low vaccine efficacy, but is outperformed otherwise70. Therefore combining the two strategies may be useful, however understanding both the temperature and seasonality effects on Wolbachia intervention programs, and serotypic differences relating to cross-protective immunity to investigate vaccine efficacy is necessary for the reduction and control of Aedes-borne arboviral disease transmission.
In conclusion, we have shown that the wAu-Wolbachia strain could be effective in controlling arbovirus transmission, as its advantages in terms of Wolbachia infection retention in mosquitoes may outweigh the absence of CI. This could prove even more promising, especially as the temperature increases due to climate change. Although wMel and wAlbB-Wolbachia strains only have been rolled out in natural mosquito habitats in replacement programs, combining these strains with wAu is worth exploring.
Data availability
No datasets were generated or analysed during the current study.
References
Hanley, K. A. Origin and Evolution of Viruses 351–391 (Elsevier, Amsterdam, 1998).
Ciota, A. T. & Kramer, L. D. Insights into arbovirus evolution and adaptation from experimental studies. Viruses 2, 2594–617. https://doi.org/10.3390/v2122594 (2010).
Gould, E., Pettersson, J., Higgs, S., Charrel, R. & de Lamballerie, X. Emerging arboviruses: Why today?. One Health 4, 1–13. https://doi.org/10.1016/j.onehlt.2017.06.001 (2017).
Mavian, C. et al. Islands as hotspots for emerging mosquito-borne viruses: A one-health perspective. Viruses 11, 11 (2018).
Rojas, D. P. The epidemiology and transmissibility of Zika virus in Girardot and San Andres island, Colombia, September 2015 to January 2016. Euro Surveill.https://doi.org/10.2807/1560-7917.ES.2016.21.28.30283 (2015).
Guzman, M. G. & Harris, E. Dengue. Lancet 385, 453–65. https://doi.org/10.1016/S0140-6736(14)60572-9 (2015).
Simmons, C. . P., Farrar, J. J., Nguyen, vV. & Wills, B. Dengue. Dengue. N. Engl. J. Med. 366, 1423–1432. https://doi.org/10.1056/NEJMra1110265 (2012).
Rojas, D. P. et al. Epidemiology of dengue and other arboviruses in a cohort of school children and their families in Yucatan, Mexico: Baseline and first year follow-up. PLoS Neglect. Trop. Dis. 12, e0006847 (2018).
WHO. Dengue: Guidelines for diagnosis, treatment, prevention and control. in WHO Guidelines Approved by the Guidelines Review Committee, New edition (WHO, Geneva, 2009).
Fukusumi, M. et al. Dengue sentinel taveler surveillance: Monthly and yearly notification trends among Japanese travelers, 2006–2014. PLoS Negl. Trop. Dis. 10, e0004924. https://doi.org/10.1371/journal.pntd.0004924 (2016).
Capeding, M. R. et al. Clinical efficacy and safety of a novel tetravalent dengue vaccine in healthy children in Asia: A phase 3, randomised, observer-masked, placebo-controlled trial. Lancet 384, 1358–65. https://doi.org/10.1016/S0140-6736(14)61060-6 (2014).
Villar, L. et al. Efficacy of a tetravalent dengue vaccine in children in Latin America. N. Engl. J. Med. 372, 113–23. https://doi.org/10.1056/NEJMoa1411037 (2015).
Roth, A. et al. Concurrent outbreaks of dengue, chikungunya and Zika virus infections - an unprecedented epidemic wave of mosquito-borne viruses in the Pacific 2012–2014. Euro Surveill.https://doi.org/10.2807/1560-7917.es2014.19.41.20929 (2014).
Ratsitorahina, M. et al. Outbreak of dengue and Chikungunya fevers, Toamasina, Madagascar, 2006. Emerg. Infect. Dis. 14, 1135–7. https://doi.org/10.3201/eid1407.071521 (2008).
Nayar, S. K. et al. Co-infection of dengue virus and chikungunya virus in two patients with acute febrile illness. Med. J. Malay. 62, 335–6 (2007).
Waggoner, J. J. et al. Viremia and clinical presentation in Nicaraguan patients infected With Zika virus, Chikungunya virus, and dengue virus. Clin. Infect. Dis. 63, 1584–1590. https://doi.org/10.1093/cid/ciw589 (2016).
Gould, L. H. et al. An outbreak of yellow fever with concurrent chikungunya virus transmission in South Kordofan, Sudan, 2005. Trans. R. Soc. Trop. Med. Hyg. 102, 1247–54. https://doi.org/10.1016/j.trstmh.2008.04.014 (2008).
CDC. Centers for Disease Control and Prevention: Zika Virus, Symptoms Testing & Treatment (2019). https://www.cdc.gov/zika/symptoms/treatment.html. Accessed 21 Oct 2019.
CDC. Centers for Disease Control and Prevention: Chikungunya Virus, Clinical Evaluation & Disease (2019). https://www.cdc.gov/chikungunya/hc/clinicalevaluation.html. Accessed 22 Oct 2019.
de Melo, A. B. et al. Description of a prospective 17DD yellow fever vaccine cohort in Recife. Braz. Am. J. Trop. Med. Hyg. 85, 739–47. https://doi.org/10.4269/ajtmh.2011.10-0496 (2011).
Klitting, R., Gould, E. A., Paupy, C. & de Lamballerie, X. What does the future hold for yellow fever virus? (I). Genes (Basel)https://doi.org/10.3390/genes9060291 (2018).
Hoffmann, A. A., Ross, P. A. & Rasic, G. Wolbachia strains for disease control: Ecological and evolutionary considerations. Evol. Appl. 8, 751–68. https://doi.org/10.1111/eva.12286 (2015).
Ant, T. H., Herd, C. S., Geoghegan, V., Hoffmann, A. A. & Sinkins, S. P. The Wolbachia strain wAu provides highly efficient virus transmission blocking in Aedes aegypti. PLoS Pathog. 14, e1006815. https://doi.org/10.1371/journal.ppat.1006815 (2018).
Shaw, A. E. et al. Drosophila melanogaster as a model organism for bluetongue virus replication and tropism. J. Virol. 86, 9015–24. https://doi.org/10.1128/JVI.00131-12 (2012).
Rainey, S. M., Shah, P., Kohl, A. & Dietrich, I. Understanding the Wolbachia-mediated inhibition of arboviruses in mosquitoes: Progress and challenges. J. Gen. Virol. 95, 517–30. https://doi.org/10.1099/vir.0.057422-0 (2014).
Kamtchum-Tatuene, J., Makepeace, B. L., Benjamin, L., Baylis, M. & Solomon, T. The potential role of Wolbachia in controlling the transmission of emerging human arboviral infections. Curr. Opin. Infect. Dis. 30, 108–116. https://doi.org/10.1097/QCO.0000000000000342 (2017).
Werren, J. H. Biology of Wolbachia. Annu. Rev. Entomol. 42, 587–609. https://doi.org/10.1146/annurev.ento.42.1.587 (1997).
Hilgenboecker, K., Hammerstein, P., Schlattmann, P., Telschow, A. & Werren, J. H. How many species are infected with Wolbachia?-A statistical analysis of current data. FEMS Microbiol. Lett. 281, 215–20. https://doi.org/10.1111/j.1574-6968.2008.01110.x (2008).
Moreira, L. A. et al. A Wolbachia symbiont in Aedes aegypti limits infection with dengue, Chikungunya, and Plasmodium. Cell 139, 1268–78. https://doi.org/10.1016/j.cell.2009.11.042 (2009).
Walker, T. et al. The wMel Wolbachia strain blocks dengue and invades caged Aedes aegypti populations. Nature 476, 450–3. https://doi.org/10.1038/nature10355 (2011).
Kambris, Z., Cook, P. E., Phuc, H. K. & Sinkins, S. P. Immune activation by life-shortening Wolbachia and reduced filarial competence in mosquitoes. Science 326, 134–6. https://doi.org/10.1126/science.1177531 (2009).
McMeniman, C. J. et al. Stable introduction of a life-shortening Wolbachia infection into the mosquito Aedes aegypti. Science 323, 141–4. https://doi.org/10.1126/science.1165326 (2009).
Duron, O. et al. Tracking factors modulating cytoplasmic incompatibilities in the mosquito Culex pipiens. Mol. Ecol. 15, 3061–71. https://doi.org/10.1111/j.1365-294X.2006.02996.x (2006).
Turelli, M. & Hoffmann, A. A. Cytoplasmic incompatibility in Drosophila simulans: Dynamics and parameter estimates from natural populations. Genetics 140, 1319–38 (1995).
Zhang, H. & Lui, R. Releasing Wolbachia-infected Aedes aegypti to prevent the spread of dengue virus: A mathematical study. Infect. Dis. Modell. 5, 142–160. https://doi.org/10.1016/j.idm.2019.12.004 (2020).
OConnor, L. et al. Open release of male mosquitoes infected with a wolbachia biopesticide: Field performance and infection containment. PLoS Negl. Trop. Dis. 6, e1797 (2012).
Adekunle, A. I., Meehan, M. T. & McBryde, E. S. Mathematical analysis of a Wolbachia invasive model with imperfect maternal transmission and loss of Wolbachia infection. Infect. Dis. Model 4, 265–285. https://doi.org/10.1016/j.idm.2019.10.001 (2019).
Ross, P. A., Ritchie, S. A., Axford, J. K. & Hoffmann, A. A. Loss of cytoplasmic incompatibility in Wolbachia-infected Aedes aegypti under field conditions. PLoS Negl. Trop. Dis. 13, e0007357. https://doi.org/10.1371/journal.pntd.0007357 (2019).
Ross, P. A. et al. Heatwaves cause fluctuations in wMel Wolbachia densities and frequencies in Aedes aegypti. PLoS Negl. Trop. Dis. 14, e0007958. https://doi.org/10.1371/journal.pntd.0007958 (2020).
van den Hurk, A. F. et al. Impact of Wolbachia on infection with chikungunya and yellow fever viruses in the mosquito vector Aedes aegypti. PLoS Negl. Trop. Dis. 6, e1892. https://doi.org/10.1371/journal.pntd.0001892 (2012).
Hussain, M. et al. Effect of Wolbachia on replication of West Nile virus in a mosquito cell line and adult mosquitoes. J. Virol. 87, 851–858. https://doi.org/10.1128/JVI.01837-12 (2013).
Dorigatti, I., McCormack, C., Nedjati-Gilani, G. & Ferguson, N. M. Using Wolbachia for dengue control: insights from modelling. Trends Parasitol. 34, 102–113. https://doi.org/10.1016/j.pt.2017.11.002 (2018).
Ferguson, N. M. et al. Modeling the impact on virus transmission of Wolbachia-mediated blocking of dengue virus infection of Aedes aegypti. Sci. Transl. Med. 7, 279ra37. https://doi.org/10.1126/scitranslmed.3010370 (2015).
Bian, G., Xu, Y., Lu, P., Xie, Y. & Xi, Z. The endosymbiotic bacterium Wolbachia induces resistance to dengue virus in Aedes aegypti. PLOS Pathog. 6, e1000833. https://doi.org/10.1371/journal.ppat.1000833 (2010).
Yeap, H. L. et al. Dynamics of the popcorn Wolbachia infection in outbred Aedes aegypti informs prospects for mosquito vector control. Genetics 187, 583–595. https://doi.org/10.1534/genetics.110.122390 (2011).
Xi, Z., Khoo, C. C. H. & Dobson, S. L. Wolbachia establishment and invasion in an Aedes aegypti laboratory population. Science (New York, N.Y.) 310, 326–328. https://doi.org/10.1126/science.1117607 (2005).
McMeniman, C. J. & ONeill, S. L. A virulent wolbachia infection decreases the viability of the dengue vector Aedes aegypti during Periods of Embryonic Quiescence. PLoS Negl. Trop. Dis. 4, e748. https://doi.org/10.1371/journal.pntd.0000748 (2010).
Turley, A. P., Moreira, L. A., ONeill, S. L. & McGraw, E. A. Wolbachia infection reduces blood-feeding success in the dengue fever mosquito. Aedes aegypti. PLoS Negl. Trop. Dis. 3, e516. https://doi.org/10.1371/journal.pntd.0000516 (2009).
Siettos, C. I. & Russo, L. Mathematical modeling of infectious disease dynamics. Virulence 4, 295–306. https://doi.org/10.4161/viru.24041 (2013).
Campo-Duarte, D. E., Vasilieva, O., Cardona-Salgado, D. & Svinin, M. Optimal control approach for establishing wMelPop Wolbachia infection among wild Aedes aegypti populations. J. Math. Biol. 76, 1907–1950. https://doi.org/10.1007/s00285-018-1213-2 (2018).
Cardona-Salgado, D., Campo-Duarte, D. E., Sepulveda-Salcedo, L. S. & Vasilieva, O. Wolbachia-based biocontrol for dengue reduction using dynamic optimization approach. Appl. Math. Model. 82, 125–149. https://doi.org/10.1016/j.apm.2020.01.032 (2020).
Hughes, H. & Britton, N. F. Modelling the use of Wolbachia to control dengue fever transmission. Bull. Math. Biol. 75, 796–818 (2013).
Ndii, M. Z., Hickson, R. I. & Mercer, G. N. Modelling the introduction of Wolbachia into Aedes aegypti mosquitoes to reduce dengue transmission. Anziam J.https://doi.org/10.1017/S1446181112000132 (2012).
Qu, Z. L., Xue, L. & Hyman, J. M. Modeling the transmission of Wolbachia in mosquitoes for controlling mosquito-borne diseases. Siam J. Appl. Math. 78, 826–852. https://doi.org/10.1137/17m1130800 (2018).
Schraiber, J. G. et al. Constraints on the use of lifespan-shortening Wolbachia to control dengue fever. J. Theor. Biol. 297, 26–32. https://doi.org/10.1016/j.jtbi.2011.12.006 (2012).
Telschow, A., Yamamura, N. & Werren, J. H. Bidirectional cytoplasmic incompatibility and the stable coexistence of two Wolbachia strains in parapatric host populations. J. Theor. Biol. 235, 265–74. https://doi.org/10.1016/j.jtbi.2005.01.008 (2005).
Xue, L., Manore, C. A., Thongsripong, P. & Hyman, J. M. Two-sex mosquito model for the persistence of Wolbachia. J. Biol. Dyn. 11, 216–237. https://doi.org/10.1080/17513758.2016.1229051 (2017).
Zheng, B., Tang, M., Yu, J. & Qiu, J. Wolbachia spreading dynamics in mosquitoes with imperfect maternal transmission. J. Math. Biol. 76, 235–263. https://doi.org/10.1007/s00285-017-1142-5 (2018).
OReilly, K. M. et al. Estimating the burden of dengue and the impact of release of wMel Wolbachia-infected mosquitoes in Indonesia: A modelling study. BMC Med. 17, 172. https://doi.org/10.1186/s12916-019-1396-4 (2019).
Xue, L., Fang, X. & Hyman, J. M. Comparing the effectiveness of different strains of Wolbachia for controlling chikungunya, dengue fever, and zika. PLoS Negl. Trop. Dis. 12, e0006666. https://doi.org/10.1371/journal.pntd.0006666 (2018).
Hoffmann, A. A. et al. Stability of the wMel Wolbachia Infection following invasion into Aedes aegypti populations. PLoS Negl. Trop. Dis. 8, e3115. https://doi.org/10.1371/journal.pntd.0003115 (2014).
Arrivillaga, J. & Barrera, R. Food as a limiting factor for Aedes aegypti in water-storage containers. J. Vector Ecol. 29, 11–20 (2004).
van den Driessche, P. & Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48. https://doi.org/10.1016/S0025-5564(02)00108-6 (2002).
Ferreira, C. P. Aedes aegypti and Wolbachia interaction: Population persistence in an environment changing. Theor. Ecol. 13, 137–148. https://doi.org/10.1007/s12080-019-00435-9 (2020).
Ndii, M. Z., Hickson, R. I., Allingham, D. & Mercer, G. N. Modelling the transmission dynamics of dengue in the presence of Wolbachia. Math. Biosci. 262, 157–66. https://doi.org/10.1016/j.mbs.2014.12.011 (2015).
ONeill, S. L. et al. Scaled deployment of Wolbachia to protect the community from Aedes transmitted arboviruses. Gates Open Res. 2, 36. https://doi.org/10.12688/gatesopenres.12844.1 (2018).
Ross, P. A. et al. Wolbachia infections in Aedes aegypti differ markedly in their response to cyclical heat stress. PLoS Pathog. 13, e1006006. https://doi.org/10.1371/journal.ppat.1006006 (2017).
Qu, Z. & Hyman, J. Generating a Hierarchy of Reduced Models for a System of differential equations modeling the spread of Wolbachia in mosquitoes. SIAM J. Appl. Math. 79, 1675–1699. https://doi.org/10.1137/19M1250054 (2019).
Ndii, M. Z., Allingham, D., Hickson, R. I. & Glass, K. The effect of Wolbachia on dengue dynamics in the presence of two serotypes of dengue: Symmetric and asymmetric epidemiological characteristics. Epidemiol. Infect. 144, 2874–82. https://doi.org/10.1017/S0950268816000753 (2016).
Ndii, M. Z. Modelling the use of vaccine and Wolbachia on dengue transmission dynamics. Trop. Med. Infect. Dis. 5, 78. https://doi.org/10.3390/tropicalmed5020078 (2020).
Acknowledgements
The first author was funded by the College of Medicine and Dentistry at James Cook University, Australia PhD programme.
Author information
Authors and Affiliations
Contributions
S.T.O and A.I.A. conceived the project concept; S.T.O and A.I.A. performed the model formation and interpretation. S.T.O, A.I.A. and M.T.M. analysed the results. S.T.O., A.I.A., M.T.M., D.P.R. and E.S.M. contributed in drafting the manuscript. All authors have read, reviewed and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ogunlade, S.T., Adekunle, A.I., Meehan, M.T. et al. Modeling the potential of wAu-Wolbachia strain invasion in mosquitoes to control Aedes-borne arboviral infections. Sci Rep 10, 16812 (2020). https://doi.org/10.1038/s41598-020-73819-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-73819-1
This article is cited by
-
Quantifying the impact of Wolbachia releases on dengue infection in Townsville, Australia
Scientific Reports (2023)
-
Modelling the ecological dynamics of mosquito populations with multiple co-circulating Wolbachia strains
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.