Abstract
The retina is a complex circuit of the central nervous system whose aim is to encode visual stimuli prior the higher order processing performed in the visual cortex. Due to the importance of its role, modeling the retina to advance in interpreting its spiking activity output is a well studied problem. In particular, it has been shown that latent variable models can be used to model the joint distribution of Retinal Ganglion Cells (RGCs). In this work, we validate the applicability of Restricted Boltzmann Machines to model the spiking activity responses of a large a population of RGCs recorded with high-resolution electrode arrays. In particular, we show that latent variables can encode modes in the RGC activity distribution that are closely related to the visual stimuli. In contrast to previous work, we further validate our findings by comparing results associated with recordings from retinas under normal and altered encoding conditions obtained by pharmacological manipulation. In these conditions, we observe that the model reflects well-known physiological behaviors of the retina. Finally, we show that we can also discover temporal patterns, associated with distinct dynamics of the stimuli.
Similar content being viewed by others
Introduction
Retinal Ganglion Cells (RGCs) play a key role in the visual system, being the output of the retina circuit and the connection between the retina and the areas of the brain dedicated to the high-level processing of the visual stimuli. For this reason, understanding how the visual information is encoded in the RGC population spiking activity is a very interesting problem in neuroscience, with relevant implications for retinal prostheses. Recent work1 has shown that latent factor models can encode regularities in the population spiking activity that are associated with the stimuli shown to the retina, in an unsupervised fashion. It has been further shown that a specific latent factor model, namely Restricted Boltzmann Machines2 (RBMs), can learn latent factors in a joint distribution that preserve the similarity between visual stimuli shown to the retina3. RBMs are latent variable models capable of learning the joint distribution of a set of continuous observed random variables and a set of binary unobserved random variables (often referred to as latent units). Once the model is trained, it allows to represent regularities in the observed inputs through the inferred values of the latent binary variables. A significant advantage of using RBMs is that the connections between visible units do not have to be explicitly modeled. Indeed, the hidden units independently discover the relationships between them.
In this work, we further validate the applicability of RBMs to model the joint distribution of RGC spiking activity evoked by visual stimuli. While previous work3 has shown that RBMs allow to learn a good “neural metric”, our main contribution is showing that this class of models is able to discover patterns associated with the stimuli shown to the retina, in a fully unsupervised fashion, through a series of experiments. With “unsupervised”, we intend here without giving any information about the stimuli to the model. We show that, by modeling the population distribution with RBMs, the model’s specific hidden states are activated by firing rate samples associated with specific stimuli (for example, gratings in a specific position), and different hidden units are activated by more complex activity, that resembles that of receptive fields.
The core idea behind this approach is that the joint population presents a series of modes in their behaviour, and that these modes are strongly correlated with the proposed stimuli. By “modes”, we are referring to the regularities in the population activity. We are making the assumption that the visual information is encoded in the spiking rate of the RGCs, so when we refer to “population activity” we are always referring to the firing rate of a large number of RGCs.
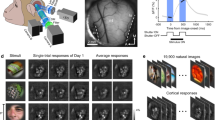
Figure 1 shows a schematic view of the pipeline we follow to carry out our analysis. New generations of Multi-Electrode Array (MEA) based on CMOS-technology4 are unique tools to study neural populations, as these devices allow to simultaneously record the activity of hundreds of RGCs activated by visual stimuli. We acquired different datasets, obtained through CMOS-MEAs with \(64\times 64\) channels, coupled with a projector presenting visual stimuli to explanted mouse retinas mounted and maintained on the chip. After recordings, we modeled the joint distribution of the firing rates with mean-covariance Restricted Boltzmann Machines5,6 (mcRBMs) , and—to detect temporal patterns—with conditional Restricted Boltzmann Machines7 (cRBMs)
We validated our hypothesis for both simple stimuli (gratings) and more complex ones (natural scenes). As a starting point, we investigate if the modes—namely, the regularities—in the firing rate distribution associated with the visual stimuli can be discovered through the latent units of RBMs. To this aim, we designed an experiment where square gratings moving in eight directions were shown to an adult mouse retina. Further, we investigated how these models respond to different levels of retina impairment induced by pharmacological manipulation of the GABA receptors of the entire retina. In particular, we investigated whether the retrieved modes reflect inner coherence in the processing of the retina, and figure out whether the decreased spatio-temporal precision of the encoding expected from physiology8,9 is captured by the model. To shed light on this question, we report results associated with a study where the RGC activity of an adult mouse retina was recorded when stimulated with different types of moving square gratings, both in normal conditions and after blocking GABA receptors (\(GABA_C\) at first, and then also \(GABA_A\) and \(GABA_B\)). As expected, the ability of the model to learn regularities in the data decreases after having increased the blockade of GABA receptors. This is because pharmacologically induced impairment leads to an unreliable population code. As a further step, we were interested in evaluating the efficiency of our models when applied to population activities recorded from a retina stimulated with more complex visual stimuli. To do so, we have chosen to use a series of natural images representing a movement of the visual field over a brick wall. Even with such more complex stimuli, the models detected stimuli-associated modes. Finally, the possibility of retrieving temporal patterns related to different dynamics of the stimuli is investigated, by modeling the RGC joint distribution. We address this task by modeling the RGC population activity with a specific type of RBM (the conditional RBM7), which allows to model also the history of the input.
Setup that characterizes our experiments. (a) The stimuli to be shown are defined: they can be simple (gratings) or more complex (natural images). (b) Such stimuli are shown to a mouse retina through a projector; the RGC signals are recorded through a High Density \(64 \times 64\) MEA chip. (c) Before being able to process the data, the firing rates need to be inferred from the spike trains; this step is carried out through log-Gaussian Cox processes. (d) Data is then processed by our models, which are trained as described in text. The visible units which define layer v take in input firing rate samples, and map those in a latent representation (layers h). (e) With a trained model, we can extract the latent representation related to each firing rate sample and analyze what different binary units/states have encoded, through the visualization technique described in text. In summary, we retrieve the stimuli associated with each firing rate sample that activate a particular unit/state and average them.
In summary, in this work we address:
-
1.
Whether RBMs are able to find modes in the RGC firing rate associated with simple and complex visual stimuli shown to the retina;
-
2.
How the impairment of the retina is reflected in the performance of the model;
-
3.
Whether temporal modes associated with the dynamics of the stimuli are detectable.
In the rest of this section, related works are detailed.
Related work
Different works address the problem of decoding RGC activity. Bialek et al.10 introduce the problem of decoding the activity of a movement-sensitive neuron in the visual system of flyes. Warland et al.11 show that stimuli (in their case, photopic, spatially uniform, temporally broadband flicker) can be decoded from spike trains, and that the decoding performance highly improves considering multiple spike trains. Pillow et al.12 evaluate a decoding approach based on correlations among different neurons’ activity. Marre et al.13 define a linear decoder trained over a population of RGCs stimulated with a moving bar, and they show that the position of the bar can be decoded from the neural activity with high accuracy. Botella-Soler et al.14 address the problem of reconstructing the stimuli proposed from RGC spike activities, reporting promising results. In summary, related works10,11,12,13,14 address the problem of understanding the relationship between RGC population activity and stimuli as a supervised task, namely, explicitly defining the connection between the stimuli shown to the retina and the corresponding RGC activity during the model training procedure.
Differently, we are interested in models able to discover patterns in an unsupervised fashion, in order to find regularities in the retina states in a fully data-driven manner. The discovered regularities can be related to the stimuli with a posterior analysis.
The application of unsupervised learning models to retinal activity is not new to this work. Trying to infer the latent structure of RGCs, Linderman et al.15 show that cell types and receptive field center locations can be unsupervisely learned from spike trains, using a Generalized Linear Model16. Tkacik et al.17 show that maximum-entropy models can be used to model the correlations among different neurons. Prentice et al.1 model the retinal population with models able to encode different modes, and show that these modes are closely correlated with the stimuli proposed to the retina. More recently, Gardella et al.3 have shown that RBMs can be used to learn a neural metric that preserves the similarity of stimuli shown to the retina.
In this work, we further validate the ability of RBMs to model the RGC population activity in a plethora of different scenarios, and by exploiting high-resolution MEAs for large-scale rerecording of light-evoked RGCs activity. In particular, while Gardella et al.3 evaluate the possibility of using RBM hidden states as a neural metric, we investigate the ability of RBMs to retrieve common patterns in the electrical activity and analyze their relationship with the stimuli showed to the retina, demonstrating that this model can retrieve activity patterns related to similar stimuli. Furthermore, we extend this analysis to the dynamic case, showing that conditional RBMs can retrieve temporal patterns associated with similar stimuli dynamics.
Finally, a novel aspect of this work is challenging the model to represent different levels of impairments of visual information encoding as obtained by pharmacological manipulation of GABA receptors. Our results show the relationship between the behavior of the model and different levels of impairment of the retina (artificially induced by blocking GABA receptors).
Materials and methods
Ethics statement
All experiments and procedures for preparing retinas from mice used in this work were approved by the IIT Animal Use Committee and by the Italian Ministry of Health (Authorization No. 110/2014-PR of the 19th of December 2014), and follow the Guide for the Care and Use of Laboratory Animals of the European Community Council Directives.
Experimental setup
All experiments were carried out with High Density MEA technology with \(64 \times 64\) channels, arranged in a square lattice and separated by 42 m. Sampling rates were in the range of 7–8 kHz and the stimuli were shown to the retina with a frequency of 30 Hz. The detailed description of the system is reported in Berdondini et al.4 and Maccione et al.18.
After every experiment, to separate the activities of the different cells, we performed spike sorting using Plexon Offline Sorter (http://www.plexon.com/products/offline-sorter) and then manually refined the results. The firing rate was inferred from the recorded spike trains via log-Gaussian Cox processes19: being doubly stochastic, we believe it represents a good model to deal with the stochasticity of RGC activity. In order to model only neurons that carry information relative to the stimuli, we only used the neurons presenting a time-varying firing rate. To this end, we removed all the neurons for which the difference between the maximum and the minimum values of the derivative of the firing rate was below a fixed threshold. In this way, we removed both silent neurons and neurons with a tonic firing rate. We dropped those neurons under the assumption that they do not carry any information to characterize the stimuli.
Restricted Boltzmann machines
Restricted Boltzmann Machines20 (RBMs) are energy-based, latent variable models capable of learning in an unsupervised fashion the joint distribution of a set of observed random variables and a set of binary unobserved random variables (often referred to as latent variables). In this model, the input variables are connected with stochastic, binary feature detectors, through symmetric weights.
The energy function associated with the joint configuration of visible and hidden variables, in case of binary input and hidden units, is defined by
where v,h are the values associated with visible and hidden units, respectively; a,b are the biases associated with those units, and W is a weight matrix. The energy is related to the probability density of visible and hidden units via
In case we want to model real-valued inputs, visible units are replaced with linear units with independent Gaussian noise, and the energy function becomes
assuming unitary standard deviation of the Gaussian noise associated with visible units.
In this work, each visible unit is associated with a different ganglion cell, and the values fed in input are the firing rate values of the RGCs at different time steps. We can train such energy-based models using an algorithm called contrastive divergence21,22. Once the model is trained, the bi-partition allows to represent regularities in the observed inputs through the inferred values of the latent binary variables. Note that we have reported only the details necessary to a basic understanding of RBMs, the technical report by Hinton2 gives more a detailed explanation
We report in the following the two particular types of RBMs used in our experimentation, namely the mean-covariance RBM5,6 (mcRBM) and the conditional RBM7 (cRBM).
Mean-covariance restricted Boltzmann machines
The mcRBM model5,6 is a modified version of the standard RBM, where the hidden units are divided in two different sets: mean units and precision units. The former is used to model the mean value of the inputs, the latter to explicitly modeling the covariance between the observed variables. The presence of this second set allows to obtain a much better fit of the data distribution than what can be achieved with simpler models like Gaussian RBMs. The mathematical detailes are reported in the Supplementary Material. An important property of mcRBMs is that, conditioning on the latent variables, the observed ones are approximately jointly Gaussian distributed6. The mean and covariance of these Gaussians are defined by the specific values of the hidden units. This means that each of the possible binary vectors representing the latent variable values is associated with one mode of the joint distribution of the inputs. This aspect makes mcRBM a very good model for our purposes of finding the regularities associated with visual stimuli shown to the retina.
Conditional restricted Boltzmann machines
RBMs and mcRBMs are not able to model the dynamics of the input, since one frame is processed at the time. The cRBM7 variant allows to model the temporal evolution of the input, by simultaneously considering different visible layers, each one associated with delayed versions of the input. The cRBM model includes two additional types of connections: autoregressive connections that link delayed input to the present one and connections between the hidden units and the history of the input. The new connections can be interpreted as a dynamic bias, and in this way the learning algorithm defined for RBMs21 does not change, it simply needs to be extended to these new weights, too. See Taylor et al.7 for a more technical explanation of the model.
Visualizing the modes
To understand which visual features the RBM states (and units) have encoded, we propose a technique closely related to spike-triggered average23 (STA), implemented as follows: (i) one binary state/unit is selected; (ii) the firing rate samples that activate that particular state/unit are retrieved; (iii) the stimuli associated with those samples are identified and averaged. Following this procedure, we can understand whether the regularities encoded by the RBM states are associated with specific stimuli or groups of stimuli.
This technique can be applied in the same way also to cRBMs. In this case, we need to average the stimuli sequences, preserving the temporal order. We obtain sequences of averages, that provide information on the time-changing input frames that are associated with specific modes in the firing rate distribution. In this way, we can visually assess the dynamics of the stimuli related to different configurations of the hidden layer.
Model evaluation
While the visualization technique described above gives a qualitative view of what the models have learned, we lack of a quantitative measure to evaluate the meaningfulness of the modes learned by the models. An objective measure is particularly useful when comparing the model performance when trained on data associated with different levels of impairment of the retina, to evaluate which model better fits the data.
We rely on information theory to evaluate whether the modes encoded by RBMs are coherently associated with particular visual stimuli. Specifically, we compute the mutual information between the stimuli proposed to the retina and the binary states learned by the RBMs. This metric provides a quantitative measure which tells us how well the model has encoded the regularities associated with the visual stimuli. The mutual information between two discrete random variables is defined by the following equation
where X and Y are the whole sets of stimuli and binary states, respectively. Since I is maximum when each state is associated with a different stimulus, we divide this term by the entropy of the stimuli, obtaining the normalized mutual information, i.e., a measure in the range 0–1.
Results
In Experiment 1, the population activity related to grating stimulation is modeled with mcRBMs5,6, to assess whether this class of models can retrieve modes associated with visual features. In Experiment 2, model performances associated with different levels of impairment are compared, to investigate if the model performances reflects the inner coherence of the retina. Experiment 3 presents the same analysis of the first one, but with more complex stimuli. In Experiments 4, the population activity is modeled with cRBMs7, to understand whether also temporal modes can be retrieved. In order to manage the complexity of the task, the MEA chip was divided in \(4\times 4\) non-overlapping regions (each patch composed by \(16\times 16\) electrodes), further referred to as \(t_{i}\), \(i = 0-15\) (as shown in Fig. 2, left). The results are discussed in the next section.
Experiment 1: heterogeneous grating stimulation
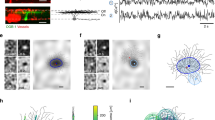
Results related to Experiment 1. Each row is associated with a different patch of the MEA chip, from which neurons were recorded during the experiments. Top-down: patches t0, t4, t7. The first two columns represent averages over stimuli associated with different binary states, the last two columns represent averages over stimuli associated with different binary units.
We stimulated a P38 stage mouse retina with gratings with different orientations. Specifically, a moving square grating with 800 m-wide bars was presented to the retina in 8 different orientations: \(0^{\circ }\), \(45^{\circ }\), \(90^{\circ }\), \(135^{\circ }\), \(180^{\circ }\), \(225^{\circ }\), \(270^{\circ }\) and \(315^{\circ }\). For each orientation, ten repetitions of the stimuli were carried out. Figure 1a shows different samples of stimuli. Totally, 3923 neurons were recorded, but only 1344 were used for the experiments, following the selection described above.
Figure 2 shows some examples of the visual representation associated with different hidden states or units, obtained through the STA-based representation described in previous section. Each row reports results related to neurons recorded from different patches of the chip. From top to bottom: t0 (114 neurons), t4 (132 neurons) and t7 (61 neurons)—see the locations of the patches in the squares reported on the left of Fig. 2. The first two columns contain images associated with different binary states, the last two columns contain images associated with different binary units.
Experiment 2: effect of GABA blockage
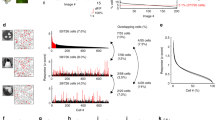
Results related to Experiment 2. Panel (a) shows the mutual information associated with (left to right) retina without GABA blockage, retina with \(GABA_C\) blockage and retina with also \(GABA_A\) and \(GABA_B\) blockage. Different colors are associated with gratings with different spatial frequency: 0.011, 0.023 and 0.045 cycles/degree in blue, red and green, respectively. Panels (b,c) show the distribution of the stimuli associated with a single latent state. While in retina without impairment a good match is found (b), blocking GABA receptors results in a mismatch (c): stimuli in counterphase are encoded in the same state.
We recorded the activity of an adult mouse retina (P45 stage) when stimulated with three different moving square gratings in three different recording conditions. At first, the retina in normal conditions was subject to three stimuli with different frequencies:
-
1.
Square grating at 0.011 cycles/degree.
-
2.
Square grating at 0.023 cycles/degree.
-
3.
Square grating at 0.045 cycles/degree.
All the stimulation protocols had temporal frequency of 1 Hz, Michelson contrast 0.5 and mean luminance \(1.36 cd/m^2\). The following stages of the experiment consisted in repeating the same stimulations under two different pharmacological treatments aimed at progressively blocking GABA receptors and hence impairing the functional behaviour of the inhibitory circuitry. For this, we rely on TPMPA and Bicuculline, which are GABA receptors antagonists, selective for \(GABA_C\) and \(GABA_A\)/\(GABA_B\) receptors, respectively. Specifically, TPMPA 150M was added first to block \(GABA_C\) receptors and Bicuculline 10M was successively added to also block \(GABA_A\) and \(GABA_B\) receptors.
To quantitatively evaluate the impairment, we calculated the normalized Mutual Information (MI) between the states learned by the model and the stimuli proposed. As expected, GABA blockage resulted in a lower MI between the states and the stimuli. Results are reported in Fig. 3a, which shows the MI scores associated with the different levels of impairment (no treatment, TPMPA and TPMPA \(+\) Bicuculline), with three different types of grating stimuli in blue, red and green. Figure 3b,c show the distributions of the stimuli associated with arbitrarily chosen states for the retina in normal conditions and after having impaired the circuitry, respectively.
We report one single example in this work, but similar behaviors were detected throughout the collection of states learned by the mcRBM.
Experiment 3: natural scenes
Results related to Experiment 3. Panel (a) shows the trajectory followed to show natural scene stimuli to the retina during Experiment 3. Panel (b) shows visual features encoded by different binary states (top) and binary units (bottom). While visual features extracted via hidden states and units appear more similar than what we could observe, e.g., in Fig. 2, it can still be observed that units reflect more generic visual features (they are more blurred, because they aggregate more stimuli).
Figure 4a reports the stimuli shown to a P38 stage mouse retina, obtained by defining a trajectory of a sliding window over an image of a brick wall. The firing rate population activity inferred from spike trains was modeled through mcRBMs following the same procedures detailed for Experiment 1.
Figure 4b shows some visual features obtained via our STA-like visualization technique. The first row shows an example of STA associated with single binary states, the second row, instead, shows an example of average stimuli associated with different binary units.
Experiment 4: modeling population dynamics
Results related to Experiment 4. Here are reported, from top to bottom, the visualizations of one hidden state and two different hidden units from a trained cRBM. As detailed in text, the visualization technique is applied in the same way as for the mcRBM, but in this case—having more visible layers, as pictured in Fig. 1—we have several averages, related to different time frames. In this case, for visualization purposes, we cut the portion of stimuli associated with the patch used to carry out our analysis (t0). The red numbers indicate the temporal evolution (1 stands for the most delayed frame)
Finally, we report results obtained by modeling data recorded for Experiment 1 analyzed with cRBMs, to understand whether also the temporal evolution of the stimuli can be decoded. The only difference in the way data are fed to the model is that a sequence of time-delayed samples from retinal activity are given in input to this particular RBM, instead of single occurrences. An additional parameter is thus the length of history modeled. We decided to design the model in such a way that the most delayed visible layer is fed with a firing rate sample associated with a stimulus which is in counterphase with respect to the present one. We arbitrarily chose to use 12 evenly spaced visible layers.
Figure 5 shows visualizations associated with two different binary units of a model trained with neurons from the patch t0. The red numbers in the squares indicate the temporal evolution (the smaller the number, the more delayed the visible layer). For visualization purposes, in this case we crop the portions of stimuli associated with the portion of retina analyzed.
Discussion
Results from Experiment 1 demonstrate that regularities in the population activity related to simple stimuli shown to the retina can be discovered by modeling the joint distribution with a mcRBM. Indeed, the interpretation of results reported in the first two columns of Fig. 2 is straightforward: latent states encode regularities in RGC joint distribution associated with different phases of the stimuli proposed to the retina. This is a key result in our study, since one goal was to figure out if such information could be recovered from the population activity in an unsupervised fashion using this class of models.
As can be observed, STA-based representations are slightly more blurred than original stimuli, due to the fact that similar stimuli are averaged. This is a positive aspect of the results, since we can expect the population activity related to one stimulus to be more similar to the activities related to comparable stimuli, rather than activities associated with very different stimuli. The consequence of this similarity is that firing rate samples associated with similar stimuli are described by the same binary states. We observed that increasing the size of the mcRBM hidden state leads to less blurred STA-based representations. This is an obvious consequence, since the machine can learn up to \(2^N\) different states, where N is the number of hidden units. If N is big, the model can learn a number of regularities big enough to learn each single input configuration.
Our interpretation of results related to hidden units (Fig. 2, columns 3 and 4) is that they encode activities associated with population receptive fields. Indeed, also Prentice et al.1 showed that latent factors of a Hidden Markov Model can model activities that are the sum of different receptive fields. It is worth noting that the worst results, in the sense of more noisy images, are the ones related to patch t7 (Fig. 2, third row): indeed, this portion of the chip is the one with less neurons recorded (61). This finding might suggest that modeling the distribution resulting from many different neurons is more informative.
Results from Experiment 3 show that even when stimulated with more complex protocols (specifically, images of a brick wall), the retinal population activity can be efficiently modeled with RBMs. Indeed, this experiment shows that single latent variables encode distinct visual features (see Fig. 4b). These results show that the joint distribution of RGC represent a reliable code also with less trivial stimuli, and the modes of the joint distribution can be retrieved using the mcRBM.
Figure 3 shows that well known physiological properties of the retina are reflected by the model (Experiment 2). Panel (a) shows that forcing an impairment in the retinal circuitry results in less informative models, namely models where the Mutual Information between the modes encoded by the binary states and the visual stimuli is reduced, in particular for stimuli with higher spatial frequency. Panels (b) and (c) show empirical proofs of this statement, reporting the distribution of the stimuli associated with a particular hidden state for both a non-impaired retina and an impaired retina, respectively. While in normal conditions the modes are associated with very precise stimuli, after the impairment the states are associated with stimuli in a pathological way. In this particular case, stimuli in counterphase are encoded in the same mode, showing that blocking GABA receptors has a dramatic effect on retinal behavior.
Finally, Fig. 5 shows results related to Experiment 4. The hidden states units of a cRBM can learn the modes in the distribution associated with temporal patterns that are related to well defined dynamics of the stimuli. In particular, in the example related to the hidden state (top), it can be observed that the mc-RBM encode the patterns associated with grating motion;in the two examples related to hidden units (middle and bottom), it can be observed that the evolution of the stimuli consists in a black-to-white or white-to-black transition – which generalizes different grating dynamics. In general, the main modes in the distribution that we could retrieve were the ones associated with color transitions. Figure 5 shows indeed that the model we used can perform this task efficiently. Finally, we report here that the single states respond to more precise dynamics of the stimuli. Summarizing, the relationship between hidden units and states of cRBMs is the same as the one we described for mcRBMs (Fig. 2).
Conclusion
We propose a new method to model RGC neuronal signals recorded from a large population of cells, and relate the stimuli shown to the retinal to a learned latent representation.
We evaluate our approach with different protocols: the first experiment, with heterogeneous gratings, shows that stimuli and their temporal evolution can be retrieved from RGC activity. The experiment on pharmacological blockage of GABA receptors shows that physiological properties of the retina are preserved by these models. Finally, the natural scene experiment demonstrates that also more complex stimuli can be retrieved from the signals.
Further investigations to better understand the applicability of Restricted Boltzmann Machines modelling in decoding large-scale spiking activity recordings in brain circuits are warranted. In perspective, this approach might support the development of new generations of brain machine interfaces for clinical applications.
Data availability
The datasets generated to carry out the experiments reported in this work are available from the corresponding author on request.
References
Prentice, J. S. et al. Error-robust modes of the retinal population code. PLoS Comput. Biol. https://doi.org/10.1371/journal.pcbi.1006057 (2016).
Hinton, G. E. A practical guide to training restricted boltzmann Machines. Tech. Rep. at https://www.cs.toronto.edu/~hinton/absps/guideTR.pdf (2010).
Gardella, C., Marre, O. & Mora, T. Blindfold learning of an accurate neural metric. PNAS 115(13), 3267–3272 (2018).
Berdondini, L. et al. Active pixel sensor array for high spatio-temporal resolution electrophysiological recordings from single cell to large scale neuronal networks. Lab Chip 9, 2644–2651 (2009).
Dahl, G., Ranzato, M., Mohamed, A. & Hinton, G. E. Phone recognition with the mean-covariance restricted Boltzmann machine. Adv. Neural Inf. Process. Syst. (NIPS) 23, 469–477 (2010).
Ranzato, M. & Hinton, G. E. Modeling pixel means and covariances using factorized third-order boltzmann machines. The IEEE Computer Society Conference on Computer Vision and Pattern Recognition 2551–2558, (2010).
Taylor, G. W., Hinton, G. E. & Roweis, S. Modeling human motion using binary latent variables. Adv. Neural Inf. Process. Syst. (NIPS) 19, 2 (2006).
Lukasiewicz, P. D., Eggers, E. D., Sagdullaev, B. T. & McCall, M. A. \(GABA_c\) receptor-mediated inhibition in the retina. Vis. Res. 44(28), 3289–3296 (2004).
Park, S. J. H., Kim, I., Looger, L. L., Demb, J. B. & Borghuis, B. G. Excitatory synaptic inputs to mouse on-off direction-selective retinal ganglion cells lack direction tuning. J. Neurosci. 34(11), 3976–3981 (2014).
Bialek, W., Rieke, F., van Steveninck, De Ruyter & Warland, R. . R. D Reading a neural code. Science 252, 1854–1857 (1991).
Warland, D. K., Reinagel, P. & Meister, M. Decoding visual information from a population of retinal ganglion cells. J. Neurophysiol. 78(5), 2336–2350 (1997).
Pillow, J. W. et al. Spatio-temporal correlations and visual signalling in a complete neural population. Nature 454, 995–999 (2008).
Marre, O. et al. High accuracy decoding of a dynamical motion from a large retinal population. PLOS Comput. Biol. https://doi.org/10.1371/journal.pcbi.1004304 (2015).
Botella-Soler, V., Deny, S., Marre, O. & Tkacik, G. Nonlinear decoding of a complex movie from the mammalian retina. PLoS Comput. Biol. https://doi.org/10.1371/journal.pcbi.1006057 (2018).
Linderman, S. W., Adams, R. P. & Pillow, J. W. Bayesian latent structure discovery from multi-neuron recordings. Adv. Neural Inf. Process. Syst. 29, 2 (2016).
Nelder, J. A. & Wedderburn, R. W. M. Generalized linear models. J. R. Stat. Soc. 135, 370–384 (1972).
Tkačik, G. et al. II Searching for collective behavior in a large network of sensory neurons. PLoS Comput. Biol. https://doi.org/10.1371/journal.pcbi.1003408 (2014).
Maccione, A. et al. Following the ontogeny of retinal waves: Pan-retinal recordings of population dynamics in the neonatal mouse. J. Physiol. 592, 1545–1563 (2014).
Møller, J., Syversveen, A. R. & Waagepetersen, R. P. Log gaussian cox processes. Scand. J. Stat. 25(3), 451–482 (1998).
Smolensky, P. Information processing in dynamical systems: Foundations of harmony theory. Parallel Distribut. Process. 1, 194–281 (1986).
Hinton, G. E. Training products of experts by minimizing contrastive divergence. Neural Comput. 14(8), 1771–1800 (2000).
Tieleman, T. Training restricted boltzmann machines using approximations to the likelihood gradient. In Proceedings of the Twenty-first International Conference on Machine Learning (ICML), (2008).
Chichilnisky, E. . J. A simple white noise analysis of neuronal light responses. Netw. Comput. Neural Syst. 12, 199–213 (2001).
Acknowledgements
This research received financial support from the 7th Framework Programme for Research of the European Commission, under Grant agreement no. 600847: RENVISION project of the Future and Emerging Technologies (FET) programme Neuro-bio-inspired systems (NBIS) FET-Proactive Initiative.
Author information
Authors and Affiliations
Contributions
R.V. wrote the manuscript. All authors are aware of the content of the manuscript and helped improving it through multiple revisions. M.Z. designed and carried out the experiments related to the mc-RBM model. R.V. designed and carried out the experiments related to the cRBM model. A.M., S.D.M. and L.B. performed the MEA data acquisition. V.M., D.S. and L.B. conceived the project. VM coordinated the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Volpi, R., Zanotto, M., Maccione, A. et al. Modeling a population of retinal ganglion cells with restricted Boltzmann machines. Sci Rep 10, 16549 (2020). https://doi.org/10.1038/s41598-020-73691-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-73691-z
This article is cited by
-
A Novel Neural Metric Based on Deep Boltzmann Machine
Neural Processing Letters (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.