Introduction

An object that is kept in equilibrium at a given temperature \(T>0\) K emits electromagnetic (EM) radiation because the charge carriers on the atomic and molecular scale oscillate due to their heat energy1. Planck’s law describes quantitatively the energy density \(u(\omega )\) of the EM radiation per unit frequency \(\omega\) for black-body radiation, which is \(u_{BB}(\omega )d\omega =\frac{\omega ^2}{\pi ^2c^3}\Theta (\omega )d\omega\), where c is the speed of light in vacuum, \(\hbar\) is the Planck constant, and \(k_B\) is the Boltzmann constant. \(\Theta (\omega ,T)=\hbar \omega /[\exp (\hbar \omega /k_BT)-1]\) is the thermal energy of a photon mode. Consequently, the energy emitted per unit surface area and per unit frequency, also called spectral radiance, of a black body into three-dimensional (3D) space is given by

$$\begin{aligned} I_{BB}(\omega )d\omega =\frac{1}{4\pi }cu(\omega )=\frac{\omega ^2}{4\pi ^3c^2} \Theta (\omega )d\omega . \end{aligned}$$
(1)

The total energy density u can then be obtained by integrating over all frequencies and angles over the half-sphere, leading to the Stefan-Boltzmann law for the energy density of black-body radiation,

$$\begin{aligned} u_{BB}=\left( \frac{8\pi ^5k_B^4}{15c^3h^3}\right) T^4=a_{BB}T^4, \end{aligned}$$
(2)

with \(a_{BB}=7.566\times 10^{-16}\) \(\hbox {Jm}^{-3}\,\hbox {K}^{-4}\). The total power emitted per unit surface area P/A of a black-body is

$$\begin{aligned} I_{BB}& = {} \frac{P}{A}=\int \limits _0^\infty I_{BB}(\omega )d\omega \int \limits _0^{2\pi }d\varphi \int \limits _0^{\pi /2} \cos \theta \sin \theta d\theta \nonumber \\& = {} \pi \int \limits _0^\infty I_{BB}(\omega )d\omega = \frac{1}{4\pi }uc \nonumber \\& = {} \frac{a_{BB}c}{4\pi }T^4=b_{BB} T^4=\left( \frac{\pi ^2k_B^4}{60c^2\hbar ^3}\right) T^4, \end{aligned}$$
(3)

where \(b_{BB}=5.67\times 10^{-8}\) \(\hbox {Wm}^{-2}\,\hbox {K}^{-4}\) is the Stefan-Boltzmann constant. The factor \(\cos \theta\) is due to the fact that black bodies are Lambertian radiators.

In recent years, several methods have been implemented for achieving a spectrally selective emittance, in particular narrowband emittance, which increases the coherence of the emitted photons. One possibility is to use a material that exhibits optical resonances due to the band structure or due to confinement of the charge carriers1. Another method is to use structural optical resonances to enhance and/or suppress the emittance. Recently, photonic crystal structures have been used to implement passive pass band filters that reflect the thermal emission at wavelengths that match the photonic bandgap2,3. Alternatively, a truncated photonic crystal can be used to enhance the emittance at resonant frequencies4,5.

Recent experiments have shown that it is possible to generate infrared (IR) emission by means of Joule heating created by means of a bias voltage applied to graphene on a \(\hbox {SiO}_2\)/Si substrate6,7. In order to avoid the breakdown of the graphene sheet at around \(T=700\) K, the graphene sheet can be encapsulated between hexagonal boron nitride (h-BN) layers, which remove efficiently the heat from graphene. The top layer protects it from oxidation8,9. In this way, the graphene sheet can be heated up to \(T=1600\) K9, or even above \(T=2000\) K8,10. Kim et al. and Luo et al. demonstrated broadband visible emission peaked around a wavelength of \(\lambda =725\) nm8,9. By using a photonic crystal substrate made of Si, Shiue et al. demonstrated narrowband near-IR emission peaked at around \(\lambda =1600\) nm with an emittance of around \(\epsilon =0.07\)10. To the best of our knowledge, there are neither theoretical nor experimental studies on spectrally selective thermal emission from graphene in the mid-IR range.

Here, we present the proof of concept of a method to tune the spectrally selective thermal emission from nanopatterned graphene (NPG) by means of a gate voltage that varies the resonance wavelength of localized surface plasmons (LSPs) around the circular holes that are arranged in a hexagonal or square lattice pattern in a single graphene sheet in the wavelength regime between 3 and 12 \(\upmu\)m. By generalizing Planck’s radiation theory to grey-body emission, we show that the thermal emission spectrum can be tuned in or out of the two main atmospheric transparency windows of 3 to 5 \(\upmu\)m and 8 to 12 \(\upmu\)m in the mid-IR regime, and also in or out of the opaque mid-IR regime between 5 and 8 \(\upmu\)m. In addition, the gate voltage can be used to tune the direction of the thermal emission due to the coherence between the localized surface plasmons (LSPs) around the holes due to the nonlocal response function in graphene, which we show by means of a nonlocal fluctuation-dissipation theorem. The main element of the nanostructure is a circular hole of diameter a in a graphene sheet. Therefore let us focus first on the optoelectronic properties of a single hole.

Figure 1
figure 1

Schematic showing our proposed ultrafast mid-IR light source based on patterned graphene placed on top of a cavity, which can be tuned by means of a gate voltage applied to the ITO layer.

Full size image

LSP of a hole in graphene

The frequency-dependent dipole moment of the hole is

$$\begin{aligned} \mathbf{p}(\mathbf{r},\omega )& = {} -\varepsilon _0\varepsilon _{||}(\mathbf{r},\omega )\mathbf{E}_{0||} \nonumber \\& = {} -\alpha _{1,2}(\mathbf{r},\omega )\mathbf{E}_{0||}, \end{aligned}$$
(4)

where the polarizabilities \(\alpha _{1,2}\) are given along the main axes x and y of the elliptic hole, and \(\mathbf{r}=\mathbf{r}_0\) is the position of the dipole moment, i.e. the hole. Graphene’s dielectric function is isotropic in the xy-plane, i.e. \(\varepsilon ''_{||}=\varepsilon ''_{xx}=\varepsilon ''_{yy}\). \(V_0\) is the volume of the graphene sheet. In the Supplementary Information we derive the general polarizabilities of an uncharged single-sheet hyperboloid with dielectric function \(\varepsilon (\omega )\) inside a medium with dielectric constant \(\varepsilon _m\) [see Eq. (163)]. The polarizabilities of an elliptical wormhole in x- and y-direction read

$$\begin{aligned} \alpha _1(\omega )& = {} \frac{2abd\pi (\pi /2-1)}{3}\frac{\varepsilon _{||}(\omega )-\varepsilon _m}{\varepsilon _m+L_1[\varepsilon _{||}(\omega )-\varepsilon _m]}, \end{aligned}$$
(5)
$$\begin{aligned} \alpha _2(\omega )& = {} \frac{2abd\pi (\pi /2-1)}{3}\frac{\varepsilon _{||}(\omega )-\varepsilon _m}{\varepsilon _m+L_2[\varepsilon _{||}(\omega )-\varepsilon _m]}. \end{aligned}$$
(6)

respectively, for which the in-plane polarizabilities lie in the plane of the graphene sheet that is parallel to the xy-plane. a and b are the length and the width of the elliptical wormhole, as shown in Fig. 11 in the Supplementary Information. \(\varepsilon _{||}(\omega )\) is the dielectric function of graphene. We assumed that the thickness d of the graphene sheet is much smaller than the size of the elliptic hole. The geometrical factors in this limit are

$$\begin{aligned} L_1\approx & {} abd\int \limits _{\eta _1}^\infty \frac{d\eta '}{(\eta '+a^2)R_{\eta '}}, \end{aligned}$$
(7)
$$\begin{aligned} L_2\approx & {} abd\int \limits _{\eta _1}^\infty \frac{d\eta '}{(\eta '+b^2)R_{\eta '}}. \end{aligned}$$
(8)

In the case of a circular hole of diameter a the polarizability simplifies to

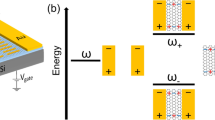
$$\begin{aligned} \alpha _{||}(\omega ) = \frac{2a^2d\pi (\pi /2-1)}{3}\frac{\varepsilon _{||}(\omega )-\varepsilon _m}{\varepsilon _m+L_{||}[\varepsilon _{||}(\omega )-\varepsilon _m]}, \end{aligned}$$
(9)

The localized surface plasmon resonance (LSP) frequency of the hole can be determined from the equation

$$\begin{aligned} \varepsilon _m+L_{||}[\varepsilon _{||}(\omega )-\varepsilon _m]=0, \end{aligned}$$
(10)

the condition for which the denominator of \(\alpha _{||}\) vanishes.

Figure 2
figure 2

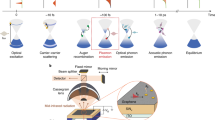
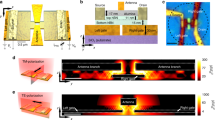
Schematic showing our proposed ultrafast mid-IR light source with the materials used in our setup. The materials from top to bottom are: one single layer of hexagonal boron nitride (h-BN), for preventing oxidation of graphene at higher temperatures, one single layer of patterned graphene, 50 nm of \(\hbox {Si}_3\,\hbox {N}_4\), for large n-doping and gating, 50 nm of ITO, metallic contact for gating, which is also transparent in mid-IR, \(\lambda /4n_{\mathrm{SU-8}}\) of SU-811, which is transparent in mid-IR, and Au back mirror. \(n_{\mathrm{SU-8}}=1.56\) is the refractive index of SU-8.

Full size image

Using the linear dispersion relation, the intraband optical conductivity is11,12

$$\begin{aligned} \sigma _{\mathrm{intra}}(\omega ) = \frac{e^2}{\pi \hbar ^2}\frac{2k_BT}{\tau ^{-1} - i\omega }\ln \left[ 2\cosh \left( \frac{\varepsilon _F}{2k_BT} \right) \right] , \end{aligned}$$
(11)

which in the case of \({\varepsilon _F} \gg {k_B}T\) is reduced to

$$\begin{aligned} \sigma _{\mathrm{intra}}(\omega ) = \frac{e^2}{\pi \hbar ^2}\frac{E_F}{\tau ^{-1} - i\omega }=\frac{2\varepsilon _m\omega _p^2}{\pi \hbar ^2(\tau ^{-1}-i\omega )}, \end{aligned}$$
(12)

where \(\tau\) is determined by impurity scattering and electron-phonon interaction \({\tau ^{ - 1}} = \tau _{imp}^{ - 1} + \tau _{e - ph}^{ - 1}\) . Using the mobility \(\mu\) of the NPG sheet, it can be presented in the form \(\tau ^{-1}=ev_F^2/(\mu E_F)\), where \(v_F=10^6\) m/s is the Fermi velocity in graphene. \(\omega _p=\sqrt{e^2E_F/2\varepsilon _m}\) is the bulk graphene plasma frequency.

It is well-known by now that hydrodynamic effects play an important role in graphene because the Coulomb interaction collision rate is dominant, i.e. \(\tau _{ee}^{ - 1}\gg \tau _{imp}^{ - 1}\) and \(\tau _{ee}^{ - 1}\gg \tau _{e - ph}^{ - 1}\), which corresponds to the hydrodynamic regime. \(\tau _{imp}^{ - 1}\) and \(\tau _{e - ph}^{ - 1}\) are the electron-impurity and electron-phonon collision rates, respectively. Since for large absorbance and emittance, we choose a large Fermi energy, we are in the Fermi liquid regime of the graphene sheet. Taking the hydrodynamic correction into account, we also consider the hydrodynamically adjusted intraband optical conductivity13,14,

$$\begin{aligned} \sigma _{\mathrm{intra}}^{\mathrm{HD}}(\omega )=\frac{\sigma _{\mathrm{intra}}(\omega )}{1-\eta ^2\frac{k_{||}^2}{\omega ^2}}, \end{aligned}$$
(13)

where \(\eta ^2=\beta ^2+D^2\omega (\gamma +i\omega )\), \(\beta ^2\approx \frac{3}{4}v_F^2\) is the intraband pressure velocity, \(D\approx 0.4\) \(\upmu\)m is the diffusion length in graphene, and \(\gamma =\tau ^{-1}\) is the relaxation rate. Interestingly, the optical conductivity becomes k-dependent and nonlocal. Also, below we will conjecture that the diffusion length D must be frequency-dependent. The effect of the hydrodynamic correction on the LSP resonances at around \(\lambda =4\) \(\upmu\)m, 7 \(\upmu\)m, and 10 \(\upmu\)m is shown in Fig. 3a–c, respectively.

Note that since \(\varepsilon =1+\chi\), where \(\chi\) is the susceptibility, it is possible to replace \(\varepsilon ''=\chi ''\). Alternatively, using the formula of the polarizability \(\alpha =\varepsilon _0\chi\) we can write \(\varepsilon ''=\alpha ''/\varepsilon _0\). The dielectric function for graphene is given by11,12

$$\begin{aligned} \varepsilon _{||}(\omega )=\varepsilon _g+\frac{i\sigma _{2D}(\omega )}{\varepsilon _0\omega d}, \end{aligned}$$
(14)

where \(\epsilon _g=2.5\) is the dielectric constant of graphite and d is the thickness of graphene. Inserting this formula into Eq. (10) gives

$$\begin{aligned} \varepsilon _m+L_{||}[\varepsilon _g+ i\frac{e^2}{\pi \hbar ^2}\frac{E_F}{\varepsilon _0\omega d(\tau ^{-1}-i\omega )}-\varepsilon _m]=0, \end{aligned}$$
(15)

Solving for the frequency and using the real part we obtain the LSP frequency,

$$\begin{aligned} \mathrm{Re}\omega _{\mathrm{LSP}} = \frac{{2L_{||}^2\varepsilon _m\omega _p^2\tau }}{{\pi \hbar ^2 \left\{ {{L^2} + d^2\varepsilon _0^2{{\left[ {L_{||}\left( {\varepsilon _g - \varepsilon _m} \right) +\varepsilon _m} \right] }^2}} \right\} }}, \end{aligned}$$
(16)

which is linear in the Fermi energy \(E_F\).

Figure 3
figure 3

Emittance \(\epsilon (\lambda )\) [equal to absorbance \(A(\lambda )\)] of the structure shown in Figs. 1 and 2 with Fermi energy \(E_F=1.0\) eV, mobility \(\mu =3000\) V/\(\hbox {cm}^2\)s, hole diameter of (a) \(a=30\) nm, (b) \(a=90\) nm, (c) \(a=300\) nm, and period (a) \({\mathcal {P}}=45\) nm, (b) \({\mathcal {P}}=150\) nm, (c) \({\mathcal {P}}=450\) nm at \(T=300\) K. The solid (black) curve represents the result of FDTD calculation. The dashed (blue) curve and the solid (black) curve are the emittances \(\epsilon _g\) and \(\epsilon _{\mathrm{FP}}\) calculated by means of Eq. (26) and Eq. (31) for the bare NPG sheet without cavity and the NPG including cavity, respectively. The dotted (green) line exhibits a blue-shift due to the hydrodynamic correction shown in Eq. (13) with \(D(\nu =30\) THz\()\approx 0\). The blue-shifted dashed (magenta) curve and the blue-shifted dot-dashed (cyan) curve are the RPA-corrected LSP peaks due to the Coulomb interaction and the Coulomb interaction including electron-phonon interaction with the optical phonons of graphene, boron nitride, and \(\hbox {Si}_3\,\hbox {N}_4\). This NPG sheet emits (a) into the atmospheric transparency window between 3 and 5 \(\upmu\)m, (b) into the atmosperic opacity window between 5 and 8 \(\upmu\)m, and (c) into the atmospheric transparency window between 8 and 12 \(\upmu\)m.

Full size image

2D array of holes in graphene

Let us now consider the 2D array of circular holes in a graphene sheet. Since the dipole moments \(p_j=\delta \mathbf{p}(\mathbf{R}_j,\omega )\) interact with each other by inducing dipole moments, we need to consider the dressed dipole moment at each site \(\mathbf{R}_j\) as source of the electric field, which is

$$\begin{aligned} {\tilde{p}}_j =p_j+ \alpha \sum \limits _{j'\ne j}{\mathcal {G}}_{jj'}{\tilde{p}}_{j'}, \end{aligned}$$
(17)

where \({\mathcal {G}}_{jj'}\) is the dipole-dipole interaction tensor. Using Bloch’s theorem \(p_j=p_0\exp (i\mathbf{k}_{||}\cdot \mathbf{R}_{||})\), the effective dipole moment becomes

$$\begin{aligned} {\tilde{p}}_0 =p_0+{\tilde{p}}_0\alpha \sum \limits _{j'\ne j}{\mathcal {G}}_{jj'}e^{i\mathbf{k}_{||}\cdot (\mathbf{R}_j-\mathbf{R}_{j'})}. \end{aligned}$$
(18)

for each site j, and thus

$$\begin{aligned} {\tilde{p}}_0=\frac{p_0}{1-\alpha {\mathcal {G}}}. \end{aligned}$$
(19)

The lattice some over the dipole-dipole interaction tensor \({\mathcal {G}}=\sum \limits _{j'\ne j}{\mathcal {G}}_{jj'}e^{i\mathbf{k}_{||}\cdot (\mathbf{R}_j-\mathbf{R}_{j'})}\) can be found in Ref.15, i.e.

$$\begin{aligned} \mathrm{Re}{\mathcal {G}}\approx & {} g/{\mathcal {P}}^3 , \end{aligned}$$
(20)
$$\begin{aligned} \mathrm{Im}{\mathcal {G}}& = {} S-2k^3/3, \end{aligned}$$
(21)

where \({\mathcal {P}}\) is the lattice period,

$$\begin{aligned} S=\frac{2\pi k}{\Omega _0}\times \left\{ \begin{array}{ll} \arccos \theta &{} \text{ for } \text{ s } \text{ polarization, } \\ \cos \theta &{} \text{ for } \text{ p } \text{ polarization. } \end{array} \right. , \end{aligned}$$
(22)

\(\Omega _0\) is the unit-cell area, and the real part is valid for periods much smaller than the wavelength. The factor \(g=5.52\) (\(g=4.52\)) for hexagonal (square) lattice. The electric field created by the effective dipole moment is determined by

$$\begin{aligned} \tilde{\mathbf{p}}_0={\tilde{\alpha }}\mathbf{E}, \end{aligned}$$
(23)

from which we obtain the effective polarizability of a hole in the coupled dipole approximation (CDA),

$$\begin{aligned} {\tilde{\alpha }}=\frac{\alpha }{1-\alpha {\mathcal {G}}}. \end{aligned}$$
(24)

This formula is the same as in Refs.15,16, where the absorption of electromagnetic waves by arrays of dipole moments and graphene disks was considered. Thus, our result corroborates Kirchhoff’s law (see below). Consequently, we obtain the same reflection and transmission amplitudes as in Ref.15, i.e.

$$\begin{aligned} r = \frac{\pm iS}{\alpha ^{-1}-{\mathcal {G}}}, \; t = 1+r, \end{aligned}$$
(25)

where the upper (lower) sign and \(S=2\pi \omega /c\Omega _0\cos \theta\) (\(S=2\pi \omega \cos \theta /c\Omega _0\)) apply to s (p) polarization. Thus, the emittance and absorbance of the bare NPG sheet are given by15,17,18

$$\begin{aligned} \epsilon _g=A_g=1-|r|^2-|t|^2. \end{aligned}$$
(26)

The coupling to the interface of the substrate with reflection and transmission amplitudes \(r_0\) and \(t_0\), respectively, which is located basically at the same position as the NPG sheet, yields the combined reflection and transmission amplitudes15

$$\begin{aligned} R=r+\frac{tt'r_0}{1-r_0r'}, \; T=\frac{tt_0}{1-r_0r'}, \end{aligned}$$
(27)

where \(r'=r\) and \(t'=1-r\) are the reflection and transmission amplitudes in backwards direction, respectively. The results for the LSP resonances at around \(\lambda =4\) \(\upmu\)m, 7 \(\upmu\)m, and 10 \(\upmu\)m are shown in Fig. 3a–c, respectively.

If we include also the whole substrate including cavity and Au mirror, we need to sum over all possible optical paths in the Fabry-Perot cavity, yielding

$$\begin{aligned} R_{\mathrm{FP}}=R+TT'r_{\mathrm{Au}}e^{i\delta }\sum \limits _{m=0}^\infty r_m^m, \end{aligned}$$
(28)

with

$$\begin{aligned} r_m= r_{\mathrm{Au}}R'e^{i\delta }, \end{aligned}$$
(29)

where \(r_{Au}\) is the complex reflection amplitude of the Au mirror in the IR regime. \(\delta =2kL\cos \theta\) is the phase accumulated by one back-and-forth scattering inside the Fabry-Perot cavity of length L. \(k\approx n_{SU-8}k_0\) is the wavenumber inside the cavity for an external EM wave with wavenumber \(k_0=2\pi /\lambda\). Since the sum is taken over a geometric series, we obtain

$$\begin{aligned} R_{\mathrm{FP}}=R+\frac{TT'r_{\mathrm{Au}}e^{i\delta }}{1- r_{\mathrm{Au}}R'e^{i\delta }}. \end{aligned}$$
(30)

Since the transmission coefficient through the Au mirror can be neglected, we obtain the emittance \(\epsilon\) and absorbance A including cavity, i.e.

$$\begin{aligned} \epsilon _{\mathrm{FP}}=A_{\mathrm{FP}}=1-|R_{\mathrm{FP}}|^2. \end{aligned}$$
(31)

The results for the LSP resonances at around \(\lambda =4\) \(\upmu\)m, 7 \(\upmu\)m, and 10 \(\upmu\)m are shown in Fig. 3a–c, respectively.

Spectral radiance of incoherent photons

Using these results, let us consider the excitation of the graphene sheet near the hole by means of thermal fluctuations, which give rise to a fluctuating EM field of a localized surface plasmon (LSP). This can be best understood by means of the fluctuation-dissipation theorem, which provides a relation between the rate of energy dissipation in a non-equilibrium system and the quantum and thermal fluctuations occuring spontaneously at different times in an equilibrium system19. The standard (local) fluctuation-dissipation theorem for fluctuating currents \(\delta {\hat{J}}_\nu (\mathbf{r},\omega )\) in three dimensions reads

$$\begin{aligned} \left<\delta {\hat{J}}_\mu (\mathbf{r},\omega )\delta {\hat{J}}_\nu (\mathbf{r}',\omega ')\right>& = {} \omega \varepsilon _0\varepsilon ''_{\mu \nu }(\mathbf{r},\omega ) \Theta (\omega ) \nonumber \\&\quad \times \delta (\omega -\omega ')\delta (\mathbf{r}-\mathbf{r}'), \end{aligned}$$
(32)

where the relative permittivity \(\varepsilon (\mathbf{r},\omega )=\varepsilon '(\mathbf{r},\omega )+i\varepsilon ''(\mathbf{r},\omega )=f(\mathbf{r})\varepsilon (\omega )\) and \(\mu ,\nu =x,y,z\) are the coordinates. Note that since \(\varepsilon =1+\chi\), where \(\chi\) is the susceptibility, it is possible to replace \(\varepsilon ''=\chi ''\). Alternatively, using the formula of the polarizability \(\alpha =\varepsilon _0\chi\) we can write \(\varepsilon ''=\alpha ''/\varepsilon _0\). \(f(\mathbf{r})=1\) on the graphene sheet and 0 otherwise. Since the fluctuating currents are contained inside the two-dimensional graphene sheet, we write the local fluctuation-dissipation theorem in its two-dimensional form, i.e.

$$\begin{aligned} \left<\delta {\hat{J}}_\mu (\mathbf{r}_{||},\omega )\delta {\hat{J}}_\nu (\mathbf{r}_{||}',\omega ')\right>& = {} {\sigma '}_{\mu \nu }^{2D}(\mathbf{r}_{||},\omega ) \Theta (\omega ) \nonumber \\&\quad \times \delta (\omega -\omega ')\delta (\mathbf{r}_{||}-\mathbf{r}_{||}'), \end{aligned}$$
(33)

where the fluctuating current densities have units of A/\(\hbox {m}^2\) and the coordinates are in-plane of the graphene sheet.

Using the method of dyadic Green’s functions, it is possible to express the fluctuating electric field generated by the fluctuating current density by

$$\begin{aligned} \delta {\hat{\mathbf{E}}}(\mathbf{r},\omega )=i\omega \mu _0\int _{\Omega }\mathbf{G}(\mathbf{r},\mathbf{r}_{0||};\omega ) \delta {\hat{\mathbf{J}}}(\mathbf{r}_{0||},\omega )d^2r_{0||}, \end{aligned}$$
(34)

where \(\Omega\) is the surface of the graphene sheet. The LSP excitation around a hole can be well approximated by a dipole field such that

$$\begin{aligned} \delta {\hat{\mathbf{J}}}(\mathbf{r}_{0||},\omega )& = {} -i\omega \sum \limits _j\delta \tilde{\mathbf{p}}(\mathbf{R}_j,\omega ) \nonumber \\& = {} -i\omega \delta \tilde{\mathbf{p}}_0(\omega )\sum \limits _{j}\delta (\mathbf{r}_{0||}-\mathbf{R}_j) , \end{aligned}$$
(35)

where \(\mathbf{R}_j=(x_j,y_j)\) are the positions of the holes in the graphene sheet.

Figure 4
figure 4

Spectral radiance of NPG including cavity, as shown in in Figs. 1 and 2, as a function of wavelength \(\lambda\) with Fermi energy \(E_F=1.0\) eV, mobility \(\mu =3000\) V/\(\hbox {cm}^2\)s, hole diameter (a) \(a=30\) nm, (b) \(a=90\) nm, (c) \(a=300\) nm, and period (a) \({\mathcal {P}}=45\) nm, (b) \({\mathcal {P}}=150\) nm, (c) \({\mathcal {P}}=450\) nm at 1300 K, 1700 K, and 2000 K.

Full size image

Consequently, we have

$$\begin{aligned} \delta {\hat{\mathbf{E}}}(\mathbf{r},\omega )=\omega ^2\mu _0\delta \tilde{\mathbf{p}}_0(\omega )\sum \limits _j\mathbf{G}(\mathbf{r},\mathbf{R}_j;\omega ). \end{aligned}$$
(36)

The dyadic Green function is defined as

$$\begin{aligned} \overleftrightarrow {\mathbf{G}}(\mathbf{r},\mathbf{r}';\omega )=\left[ \overleftrightarrow {\mathbb {1}}+\frac{1}{\mathbf{k}(\omega )^2}{\varvec{\nabla }}{\varvec{\nabla }}\right] G(\mathbf{r},\mathbf{r}';\omega ) \end{aligned}$$
(37)

with the scalar Green function given by

$$\begin{aligned} G(\mathbf{r},\mathbf{r}';\omega )=\frac{e^{-i\mathbf{k}(\omega )\cdot |\mathbf{r}-\mathbf{r}'|}}{4\pi |\mathbf{r}-\mathbf{r}'|}, \end{aligned}$$
(38)

and \(\mathbf{k}(\omega )^2=(\omega ^2/c^2)[\varepsilon _{xx}(\omega ),\varepsilon _{yy}(\omega ),\varepsilon _{zz}(\omega )]\).

Then, the fluctuation-dissipation theorem can be recast into the form

$$\begin{aligned} \left<\delta {\tilde{p}}_\mu (\mathbf{r}_{0||},\omega )\delta {\tilde{p}}_\nu ^*(\mathbf{r}_{0||}',\omega ')\right>& = {} \frac{{\sigma '}_{\mu \nu }^{2D}(\mathbf{R}_i,\omega )}{\omega ^2}\Theta (\omega )\delta (\omega -\omega ') \nonumber \\&\quad \times \delta (\mathbf{r}_{0||}-\mathbf{r}_{0||}'), \end{aligned}$$
(39)

and thus we obtain

$$\begin{aligned} \left<\delta {\hat{E}}_\mu (\mathbf{r},\omega )\delta {\hat{E}}_\nu ^*(\mathbf{r}',\omega ')\right>& = {} \omega ^4\mu _0^2\sum \limits _{m,m'}\int \limits _{\Omega }d^2r_{0||} G_{\mu m}(\mathbf{r},\mathbf{r}_{0||};\omega ) \nonumber \\&\quad \times \int \limits _{\Omega '}d^2r_{0||}'G_{m'\nu }^*(\mathbf{r}',\mathbf{r}_{0||}';\omega ')\left<\delta {\tilde{p}}_m(\mathbf{r}_0,\omega )\delta {\tilde{p}}_{m'}^*(\mathbf{r}_0',\omega )\right> \nonumber \\& = {} \frac{\omega ^2}{c^4\varepsilon _0^2}\sum \limits _{m}\int \limits _{\Omega }d^2r_{0||}G_{\mu m}(\mathbf{r},\mathbf{r}_{0||};\omega )G_{m'\nu }^*(\mathbf{r}',\mathbf{r}_{0||};\omega ') \nonumber \\&\quad \times \Theta (\omega ){\sigma '}_{mm'}^{2D}(\mathbf{r}_{0||},\omega )\delta (\omega -\omega ') \nonumber \\& = {} \frac{\omega ^2}{c^4\varepsilon _0^2}\sum \limits _{m,j}G_{\mu m}(\mathbf{r},\mathbf{R}_j;\omega )G_{m\nu }^*(\mathbf{r}',\mathbf{R}_j;\omega ') \nonumber \\&\quad \times \Theta (\omega ){\sigma '}_{mm}^{2D}(\mathbf{R}_j,\omega )\delta (\omega -\omega '), \end{aligned}$$
(40)

noting that the dielectric tensor \(\varepsilon ''(\mathbf{r},\omega )\) is diagonal.

Since the energy density of the emitted electric field at the point \(\mathbf{r}\) is

$$\begin{aligned} u(\mathbf{r},\omega )\delta (\omega -\omega ')=\varepsilon _0\sum _{i=x,y,z}\left<\delta {\hat{E}}_i^*(\mathbf{r},\omega )\delta {\hat{E}}_i(\mathbf{r},\omega ')\right>, \end{aligned}$$
(41)

we can write the spectral radiance as

$$\begin{aligned} I(\mathbf{r},\omega )& = {} \frac{\omega ^2}{4\pi c^3\varepsilon _0}\frac{1}{N}\sum \limits _{\mu ; m=x,y;j}\left| G_{\mu m}(\mathbf{r},\mathbf{R}_j;\omega )\right| ^2 \nonumber \\&\quad \times \Theta (\omega ){\sigma '}_{mm}^{2D}(\mathbf{R}_j,\omega ) \nonumber \\& = {} \frac{\omega ^2}{4\pi c^3\varepsilon _0}\Theta (\omega ){\sigma '}_{||}^{2D}(\omega ) \sum \limits _{\mu ,m}\left| G_{\mu m}(\mathbf{r},\mathbf{R}_0;\omega )\right| ^2, \end{aligned}$$
(42)

assuming that the dipole current of the LSP is in the plane of the graphene sheet, i.e. the xy-plane, and the polarizability is isotropic, ie. \({\sigma '}_{||}^{2D}={\sigma '}_{xx}^{2D}={\sigma '}_{yy}^{2D}\), and the same for all holes. N is the number of holes. In order to obtain the spectral radiance in the far field, we need to integrate over the spherical angle. Using the results from the Supplementary Information, we obtain

$$\begin{aligned} I_\infty (\omega )& = {} \frac{\omega ^2\Theta (\omega )}{3\pi ^2\varepsilon _0 c^3}{\sigma '}_{||}^{2D}(\omega ) \nonumber \\& = {} \frac{\omega ^2\Theta (\omega )}{3c^2\pi ^2} A_{||}^{2D}(\omega ), \end{aligned}$$
(43)

where we used the definition of the absorbance of a 2D material, i.e.

$$\begin{aligned} A_{2D}(\omega )=(1/\varepsilon _0 c)\mathrm{Re}\sigma _{2D}(\omega )=(1/\varepsilon _0 c)\sigma _{2D}'(\omega ), \end{aligned}$$
(44)

with 2D complex conductivity \(\sigma _{2D}(\omega )\). According to Kirchhoff’s law, emittance \(\epsilon (\omega )\), absorbance \(A(\omega )\), reflectance \(R(\omega )\), and transmittance \(T(\omega )\) are related by20

$$\begin{aligned} \epsilon (\omega )=A(\omega )=1-R(\omega )-T(\omega ), \end{aligned}$$
(45)

from which we obtain the grey-body thermal emission formula

$$\begin{aligned} I_\infty (\omega ) = \frac{\omega ^2\Theta (\omega )}{3\pi ^2c^2} \epsilon _{||}^{2D}(\omega ), \end{aligned}$$
(46)

whose prefactor bears strong similarity to Planck’s black body formula in Eq. (1).

Figure 5
figure 5

Temperature distribution inside the NPG sheet for various values of the bias voltage \(V_{\mathrm{SD}}\), calculated by means of COMSOL. As the bias voltage is increased, the maximum of temperature shifts away from the center of the NPG sheet due to the Peltier effect.

Full size image

Using FDTD to calculate the emittance \(\epsilon _{||}^{2D}(\omega )\), we evaluted the grey-body thermal emission according to Eq. (46) for the thermal emitter structure based on NPG shown in Figs. 1 and 2. Using COMSOL, we calculated the temperature distribution inside the NPG sheet, as shown in Fig. 5, when a bias voltage \(V_{\mathrm{SD}}\) is applied, which gives rise to Joule heating. The geometry of the simulated device is shown in Figs. 1 and 2. The area of the graphene channel is 10 \(\upmu\)m \(\times\) 10 \(\upmu\)m. The thickness of the graphene sheet is 0.5 nm. The size of the gold contacts is 5 \(\upmu\)m \(\times\) 10 \(\upmu\)m, with a thickness of 50 nm. Our results are shown in Fig. 4a–c for the temperatures 1300 K, 1700 K, and 2000 K of NPG. After integrating over the wavelength under the curves, we obtain the following thermal emission power per area:

Resonance wavelength

Power per area

4 \(\upmu\)m

11,221 W/\(\hbox {m}^2\)

7 \(\upmu\)m

9820 W/\(\hbox {m}^2\)

10 \(\upmu\)m

6356 W/\(\hbox {m}^2\)

Let us consider the dependence of the thermal emission of NPG on the angle \(\theta\). Integrating over \(r^2\varphi\) we obtain

$$\begin{aligned} I(\theta ,\omega )=\frac{\omega ^2}{4\pi c^2}\Theta (\omega )\frac{11+\cos (2\theta )}{16\pi }\epsilon _{||}^{2D}(\omega ), \end{aligned}$$
(47)

which is a clear deviation from a Lambert radiator. The pattern of the thermal radiation can be determined by

$$\begin{aligned} {\hat{I}}(\theta )& = {} \frac{\int _0^{2\pi }I(\mathbf{r},\omega )r^2 d\varphi }{\int _0^{2\pi }\int _0^{\pi }I(\mathbf{r},\omega )r^2\sin \theta d\theta d\varphi } \nonumber \\& = {} \frac{3}{64}\left[ 11+\cos (2\theta )\right] , \end{aligned}$$
(48)

which is shown in Fig. 6. Interestingly, since we assumed that thermal emission is completely incoherent [see Eq. (42)] the thermal emission from NPG is only weakly dependent on the emission angle \(\theta\), which can be clearly seen in Fig. 6.

Partial coherence of plasmons in graphene and the grey-body radiation

However, the assumption that thermal emission of radiation is incoherent is not always true. Since Kirchhoff’s law is valid, thermal sources can be coherent21. After theoretical calculations predicted that long-range coherence may exist for thermal emission in the case of resonant surface waves, either plasmonic or phononic in nature22,23, experiments showed that a periodic microstructure in the polar material SiC exhibits coherence over many wavelengths and radiates in well-defined and controlled directions24. Here we show that the coherence length of a graphene sheet patterned with circular holes can be as large as 150 \(\upmu\)m due to the plasmonic wave in the graphene sheet, thereby paving the way for the creation of phased arrays made of nanoantennas represented by the holes in NPG.

The coherence of thermal emission can be best understood by means of a nonlocal response function25. First, we choose the nonlocal hydrodynamic response function in Eq. (13). Using the 2D version of the fluctuation-dissipation theorem in Eq. (33), we obtain the nonlocal fluctuation-dissipation theorem in the hydrodynamic approximation,

$$\begin{aligned} \left<\delta {\hat{J}}_\mu (\mathbf{r}_{||},\omega )\delta {\hat{J}}_\nu (\mathbf{r}_{||}',\omega ')\right>& = {} \sigma _{\mu \nu }^{\mathrm{HD}}(\Delta \mathbf{r}_{||},\omega )\Theta (\omega )\delta (\omega -\omega ') \nonumber \\& = {} \frac{1}{D}\int \limits _0^\infty dk_{||} \frac{\sigma _{\mathrm{intra}}(\omega )e^{-ik_{||}\Delta \mathbf{r}_{||}}}{1-\eta ^2\frac{k_{||}^2}{\omega ^2}} \Theta (\omega )\delta (\omega -\omega ') \nonumber \\& = {} \sigma _{\mathrm{intra}}(\omega ) \frac{\omega \sqrt{\pi /2}}{D\eta }\sin \left( \frac{\omega \Delta \mathbf{r}_{||}}{\eta }\right) \Theta (\omega )\delta (\omega -\omega '), \end{aligned}$$
(49)

where \(\Delta \mathbf{r}_{||}=\mathbf{r}_{||}-\mathbf{r}_{||}'\) and \(\eta ^2=\beta ^2+D^2\omega (\gamma +i\omega )\). This result suggests that the coherence length is given approximately by D, which according to Ref.13 would be \(D\approx 0.4\) \(\upmu\)m. However, the resulting broadening of the LSP resonance peaks would be very large and therefore in complete contradiction to the experimental measurements of the LSP resonance peaks in Refs.11,26,27. Thus, we conclude that the hydrodynamic diffusion length must be frequency-dependent with \(D(\nu =0)=0.4\) \(\upmu\)m. Using the Fermi velocity of \(v_F=10^6\) m/s and a frequency of \(\nu =30\) THz, the average oscillation distance is about \(L=v_F\nu ^{-1}=0.033\) \(\upmu\)m, which is much smaller than \(D(\nu =0)\) in graphene. Thus we can approximate \(D(\nu =30\) THz\()=0\). We conjecture that there is a crossover for D into the hydrdynamic regime when the frequency is reduced below around \(\nu _0=1\) to 3 THz, below which the hydrodynamic effect leads to a strong broadening of the LSP peaks for NPG. Consequently, the viscosity of graphene should also be frequency-dependent and a crossover for the viscosity should happen at about the same frequency \(\nu _0\). We plan to elaborate this conjecture in future work. Future experiments could corroborate our conjecture by measuring the absorbance or emittance as a function of wavelength for varying scale of patterning of the graphene sheet.

Figure 6
figure 6

Spherical density plot of the normalized angular intensity distribution \({\hat{I}}(\theta )\) of the thermal emission from NPG in the case of incoherent photons.

Full size image

Next, let us consider the coherence of thermal emission by means of the nonlocal optical conductivity in the RPA approximation. Using the general formula

$$\begin{aligned} \sigma (q,\omega )=\frac{ie^2\omega }{q^2}\chi ^0(q,\omega ), \end{aligned}$$
(50)

with

$$\begin{aligned} \chi ^0(q,\omega )\approx \frac{E_F q^2}{\pi \hbar ^2\omega (\omega +i\tau ^{-1})} \end{aligned}$$
(51)

in the low-temperature and low-frequency approximation, one obtains Eq. (12). Now, let us use the full polarization in RPA approximation including only the Coulomb interaction,

$$\begin{aligned} \chi ^{\mathrm{RPA}}(q,\omega )=\frac{\chi ^0(q,\omega )}{1- v_c(q){\chi ^0}(q,\omega ) }, \end{aligned}$$
(52)

from which we obtain

$$\begin{aligned} \sigma ^{\mathrm{RPA}}(q,\omega )& = {} \frac{ie^2\omega }{q^2}\chi (q,\omega ) \nonumber \\& = {} \frac{ie^2\omega E_F}{\pi \hbar ^2\omega (\omega +i\tau ^{-1})-\frac{e^2E_F}{2\epsilon _0} q}, \end{aligned}$$
(53)

which introduces the nonlocal response via the Coulomb interaction in the denominator. The effect of the RPA correction on the LSP resonances at around \(\lambda =4\) \(\upmu\)m, 7 \(\upmu\)m, and 10 \(\upmu\)m is shown in Fig. 3a–c, respectively. After taking the Fourier transform, we obtain the nonlocal fluctuation-dissipation theorem in RPA approximation,

$$\begin{aligned} & \left \langle \delta {\hat{J}}_\mu (\mathbf{r}_{||},\omega )\delta {\hat{J}}_\nu (\mathbf{r}_{||}',\omega ')\right\rangle = \sigma _{\mu \nu }^{\mathrm{RPA}}(\Delta \mathbf{r}_{||},\omega )\Theta (\omega )\delta (\omega -\omega ') \nonumber \\&\quad =\frac{\sqrt{2\pi }\epsilon _0\omega }{C_{RPA}} e^{iK_{RPA}\Delta \mathbf{r}_{||}-\frac{\Delta {\mathbf{r}}_{||}}{C_{RPA}}} \Theta (\omega )\delta (\omega -\omega '), \end{aligned}$$
(54)

where the coherence length in RPA approximation is

$$\begin{aligned} C_{RPA}=\frac{e^2|E_F|}{2\pi \hbar ^2\epsilon _0\gamma \omega }, \end{aligned}$$
(55)

and the coherence wavenumber is given by

$$\begin{aligned} K_{RPA}=\frac{2\pi \hbar ^2\epsilon _0\omega ^2}{e^2|E_F|}. \end{aligned}$$
(56)

For simplicity, we switch now to a square lattice of holes. In the case of the LSP resonance for a square lattice of holes at \(\lambda =10\) \(\upmu\)m, corresponding to \(\nu =30\) THz, \(E_F=1.0\) eV, \(\omega =2\pi \nu\), and \(\gamma =ev_F^2/(\mu E_F)=0.3\) THz for \(\mu =3000\) \(\hbox {cm}^2\,\hbox {V}^{-1}\,\hbox {s}^{-1}\), which results in a coherence length of \(C_{RPA}=3\) \(\upmu\)m. This result is in reasonable agreement with the full width at half maximum (FWHM) values of the widths of the LSP resonance peaks in Refs.11,26,27. This coherence length would allow to preserve coherence for a linear array of period \({\mathcal {P}}=300\) nm and \(C_{RPA}/{\mathcal {P}}=10\) holes. In order to show the coherence length that can be achieved with graphene, we can consider a suspended graphene sheet with a mobility of \(\mu =150{,}00\) \(\hbox {cm}^2\,\hbox {V}^{-1}\,\hbox {s}^{-1}\). Then the coherence length increases to a value of \(C_{RPA}=13\) \(\upmu\)m, which would allow for coherence over a linear array with \(C_{RPA}/{\mathcal {P}}=43\) holes.

Figure 7
figure 7

Coherence length \(C_{\mathrm{FDTD}}\) and coherence time \(\tau _{\mathrm{FDTD}}\) of emitted photons, extracted from the full-width half-maximum (FWHM) of the spectral radiances shown in Fig. 4a–c.

Full size image

In the case of the LSP resonance for a square lattice of holes at \(\lambda =5\) \(\upmu\)m, corresponding to \(\nu =60\) THz, \(E_F=1.0\) eV, \(\omega =2\pi \nu\), and \(\gamma =ev_F^2/(\mu E_F)=0.3\) THz for \(\mu =3000\) \(\hbox {cm}^2\,\hbox {V}^{-1}\,\hbox {s}^{-1}\) , which results in a coherence length of \(C_{RPA}=1.5\) \(\upmu\)m. Considering again a suspended graphene sheet, the coherence length can be increased to \(C_{RPA}=6.7\) \(\upmu\)m. Since the period in this case is \({\mathcal {P}}=45\) nm, the coherence for \(\mu =3000\) \(\hbox {cm}^2\,\hbox {V}^{-1}\,\hbox {s}^{-1}\) and \(\mu =150{,}00\) \(\hbox {cm}^2\,\hbox {V}^{-1}\,\hbox {s}^{-1}\) can be preserved for a linear array of \(C_{RPA}/{\mathcal {P}}=33\) and 148 holes, respectively.

The coherence length and time of thermally emitted photons is larger because the photons travel mostly in vacuum. Taking advantage of the Wiener-Kinchine theorem21, we can extract the coherence length \(C_{\mathrm{FDTD}}\) and coherence time \(\tau _{\mathrm{FDTD}}\) of thermally emitted photons by means of the full-width half-maximum (FWHM) of the spectral radiances shown in Fig. 4a–c. Our results are shown in Fig. 7. The coherence length of the thermally emitted photons can reach up to \(C_{\mathrm{FDTD}}=150\) \(\upmu\)m at a resonance wavelength of \(\lambda =4\) \(\upmu\)m. This means that the coherence length of the thermally emitted photons is about 37 times larger than the wavelength.

Phased array of LSPs in graphene

Thus, the latter large coherence length allows for the coherent control of a 150x150 square array of holes with period \({\mathcal {P}}=45\) nm, individually acting as nanoantennas, that can be used to create a phased array of nanoantennas. One of the intriguing properties of a phased array is that it allows to control the directivity of the emission of photons, which is currently being implemented for large 5G antennas in the 3 to 30 GHz range. The beamsteering capability of our NPG sheet is shown in Fig. 8. In contrast, our proposed phased array based on NPG can operate in the 10 to 100 THz range.

The temporal control of the individual phases of the holes requires an extraordinary fast switching time of around 1 ps, which is not feasible with current electronics. However, the nonlocal response function reveals a spatial phase shift determined by the coherence wavenumber \(K_{RPA}\), which is independent of the mobility of graphene. In the case of the LSP resonance at \(\lambda =4\) \(\upmu\)m, we obtain \(\lambda _{RPA}=2\pi /K_{RPA}=6\) \(\upmu\)m, resulting in a minimum phase shift of \(2\pi {\mathcal {P}}/\lambda _{RPA}=0.042=2.4^{\circ }\) between neighboring holes, which can be increased to a phase shift of \(9.7^{\circ }\) by decreasing the Fermi energy to \(E_F=0.25\) eV. Thus, the phase shift between neighboring holes can be tuned arbitrarily between \(2.4^{\circ }\) and \(9.7^{\circ }\) by varying the Fermi energy between \(E_F=1.0\) eV and \(E_F=0.25\) eV. Fig. 8 shows the capability of beamsteering for our proposed structure by means of directional thermal emission, which is tunable by means of the gate voltage applied to the NPG sheet.

Due to the full control of directivity with angle of emission between \(\theta =12^\circ\) and \(\theta =80^\circ\) by tuning the Fermi energy in the range between \(E_F=1.0\) eV and \(E_F=0.25\) eV, thereby achieving beamsteering by means of the gate voltage, our proposed mid-IR light source based on NPG can be used not only in a vertical setup for surface emission, but also in a horizontal setup for edge emission, which is essential for nanophotonics applications.

Figure 8
figure 8

Directivity of the thermal emission from NPG where the holes act as nanoantennas in a phased array. This emission pattern for \(E_F=1.0\) eV can be used for surface-emitting mid-IR sources. In the case of a 150x150, 75x75, 56x56, 37x37 square lattice of holes (size of lattice matches coherence length) with period \({\mathcal {P}}=45\) nm and hole diameter of 30 nm, introducing a relative phase of \(2.43^\circ\), \(4.86^\circ\), \(7.28^\circ\), \(9.71^\circ\) between the nanoantennas allows for beamsteering in the range between \(\theta =12^\circ\) and \(\theta =80^\circ\) by tuning the Fermi energy in the range between \(E_F=1.0\) eV and \(E_F=0.25\) eV.

Full size image

Conclusion

In conclusion, we have demonstrated in our theoretical study that NPG can be used to develop a plasmonically enhanced mid-IR light source with spectrally tunable selective thermal emission. Most importantly, the LSPs along with an optical cavity increase substantially the emittance of graphene from about 2% for pristine graphene to 80% for NPG, thereby outperforming state-of-the-art graphene light sources working in the visible and NIR by at least a factor of 100. Combining our proposed mid-IR light source based on patterned graphene with our demonstrated mid-IR detector based on NPG27, we are going to develop a mid-IR spectroscopy and detection platform based on patterned graphene that will be able to detect a variety of molecules that have mid-IR vibrational resonances, such as CO, \(\hbox {CO}_2\), NO, \(\hbox {NO}_2\), \(\hbox {CH}_4\), TNT, \(\hbox {H}_2\,\hbox {O}_2\), acetone, TATP, Sarin, VX, etc. In particular, a recent study showed that it is possible to detect the hepatitis B and C viruses label-free at a wavelength of around 6 \(\upmu\)m28. Therefore, we will make great effort to demonstrate that our platform will be able to detect with high sensitivity and selectivity the COVID-19 virus and other viruses that pose a threat to humanity.