Abstract
The approximate analytical solutions of the three-dimensional radial Schrödinger wave equation with a multiple potential function has been studied using a suitable approximation scheme to the centrifugal term in the framework of parametric Nikiforov–Uvarov method. The energy equation and the wave function were obtained. The calculated wave function was used to study Shannon entropy and variance via expectation values. The behaviour of Shannon entropy and variance respectively with the equilibrium bond length were examined in detail. A special case of the multiple potential (pseudoharmonic-like potential) was equally examined under Shannon entropy and variance. For further application of the study, some diatomic molecules were examined under variance and Shannon entropy. Finally, some variance inequalities were derived using Cramer-Rao uncertainty relation and these were justified by numerical results.
Similar content being viewed by others
Introduction
The essential reason for the probabilistic character of the quantum theory of physical system relies upon the uncertainty relation. This relation may be mathematically expressed by means of the Boltzmann-Shannon information entropy (entropic uncertainty relation) in a much more appropriate and accurate way than the standard deviation1. The information entropy is a superior measure of a spread and then of quantum uncertainty, a property of fundamental relevance for adequate characterization of position and momentum of single-particle densities2. These entropies have been used for various practical purposes such as the measurement of squeezing of quantum fluctuation3, reconstruction of charge and momentum densities of atomic and molecular systems4. In physical sciences, Shannon entropy measures the spread of the electron density. The concentration of the wave function of the state is higher when Shannon entropy is small5. Thus, Shannon entropy is used to determine the stability of a given system. A system is conceived to be more stable when Shannon entropy is small and becomes unstable when Shannon entropy is higher. Shannon entropy is related to fundamental and experimentally measurable quantities such as the kinetic energy and magnetic susceptibility which makes them useful in the study of the structure and dynamics of atomic and molecular systems6. It is noted that Shannon entropy has drawn many attentions due to its usefulness in different areas. Despite the various studies on Shannon entropy by different authors, Dehesa et al.7, stated that the analytical determination of the information entropies of physical systems is in its infancy. Recently, Yahya et al.8 and Onate et al.9 separately studied the Shannon entropy for some potential models using different traditional techniques. Motivated by this, we intend to investigate the analytical determination of Shannon entropy and Variance for a multiple potential which is proposed in the concept of the work. Another objective of this study is to derive some variance inequalities using the basic Cramer-Rao uncertainty relation of Fisher information.
The multiple potential is a combination of pseudoharmonic-like potential, double pure Coulomb potential and constant potential. The modification of the potential is to enable the potential fits in the study of some theoretic quantities with both spectroscopic and non-spectroscopic parameters. According to Sage and Goodisman10, the Pseudoharmonic potential is a useful potential. The authors pointed out that the harmonic oscillator potential (one of the most important potential model), is unrealistic in several aspect when compared to a real molecular vibrational potential, hence the suggestion for the Pseudoharmonic potential. According to them, the Pseudoharmonic potential maintains the availability of explicit solutions. This necessitate the inclusion of the Pseudoharmonic-like potential in this work. The multiple potential has a physical form
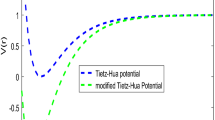
where \(D_{e}\) is the dissociation energy, \(r_{e}\) is the equilibrium bond length, \(r\) is the internuclear separation, \(C\) and \(\lambda\) characterized the strengths of the potential. The change in their numerical values changes the shape of the potential. The multiple potential is a diatomic potential with the diatomic spectroscopic parameter given in Eq. (1). The Shape of the multiple potential and the Pseudoharmonic-like potential respectively, are shown in Fig. 1. The scheme of our presentation is as follows: “Method” section gives the solution of the radial equation with multiple potential. In “Some theoretic quantities and the multiple potential” section, we present the theoretic quantities. The discussion and conclusion are given in “Discussion of results” and “Conclusion” sections respectively.
Method
The radial Schrödinger equation and the multiple potential
In a spherical potential model \(V(r),\) the time independent Schrödinger equation is given by11,12,13
where \(\ell\) and \(n\) are orbital angular momentum and radial quantum number respectively, \(R_{n,\ell } (r)\) is the wave function, \(\mu\) and \(\hbar\) are reduced mass and Planck constant respectively, and \(E_{n\ell }\) is the non-relativistic energy. Substituting Eq. (1) into Eq. (2), we have
Using the following transformation, \(s = r^{2} ,\) Eq. (3) turns to
Comparing Eq. (4) with equation (A1), have the values for the parametric constants in equation (A4) as follows
Substituting Eq. (5) into equation (A2) and equation (A3) respectively, we have the energy equation and the corresponding wave function as
where \(N_{n,\ell }\) is a normalization constant which can be determine using normalization condition below
The normalization constant is thus obtain as
Some theoretic quantities and the multiple potential
In this section, we calculate some theoretic quantities such as Shannon entropy and Variance. The quantities are calculated using the probability density function which is the square of the wave function.
Expectation values
In this section, we calculate the expectation values of the multiple potential. To obtain the radial expectation values, we use the Hellmann Feynman theory14,15,16,17,18. If the Hamiltonian for a particular quantum system is a function of the parameter \(V\), then, taking the eigenvalues as \(E_{n,\ell } (V)\) and eigenfunction as \(R_{n,\ell } (V)\) of the Hamiltonian, we can write from Hellmann Feynman Theory that
provided that \(R_{n,\ell }\) is continuous with respect to \(V.\) In terms of our potential, the effective Hamiltonian is given as
When \(V = D_{e}\) and \(V = \mu ,\) then the expectation values of \(r^{2}\) and \(p^{2}\) for multiple potential are obtain as follows
Shannon entropy
Shannon entropy measures the spread of electron density and as such, it is used to determine the system’s stability. As pointed out earlier, the smaller the Shannon entropy, the more concentration of the wave function of the state. In this work, Shannon entropy will be considered in both position space and momentum space. In the position space, Shannon entropy is given as 9,19,20,21,22
where \(\rho (r)\) is the probability density function that can be obtained from the radial wave function. For the position space, the radial wave function given in Eq. (6) can be written as
where
The probability density function is the squared of the radial wave function. Thus, the probability density is given
Thus, with Eq. (17), Eq. (14) becomes
where
In the momentum space, Shannon entropy is given as
where \(\gamma (p)\) is the probability density function for the momentum space, the radial wave function given in Eq. (7) can be written as
The probability density then becomes
With the probability density in Eq. (23), the Shannon entropy for momentum space in Eq. (21) becomes
From the work of Dehesa et al.22, it can be shown for an accurate result that at the ground state,
This will be verified later in the numerical results.
Variance
In this section, we calculate the variance of a multiple potential. Given a normalized-to-unity (probability) density \(\rho (r)\), there are several functional quantities for measuring the uncertainty or information content associated with the density. Among the three popular ones is the variance which is given as23,24
Equation (26) above can be solved using expectation values. However, Dehesa et al.19, showed that a relationship exist between Fisher Information and Variance. These authors pointed out that the Fisher Information in momentum space is equal to four times the variance in position space. Thus,
These authors also showed the relationship between the expectation values and Fisher Information as
Comparing Eqs. (27) and (28), we can write the variance for position space as
Following the work of Dehesa et al.19, the variance for momentum space can be written as
At this juncture, we want to derive some uncertainty inequalities for variance based on Eqs. (27), (28), (29) and (30). To begin the derivation, we first considered the upper bound. For any \(n\) and \(\ell ,\) the upper bound for the position and momentum spaces of the variance is given as
From Cramer-Rao inequalities,
From Eqs. (32) and (33), we can now establish the inequality
Combining Eqs. (31) and (34) leads to another inequality of the form
The authenticity of Eqs. (34) and (35) will be verified in the numerical results as will be seen in subsequent tables.
Discussion of results
Table 1 showed the spectroscopic parameters for some diatomic molecules studied in this work. In Table 2, we presented the numerical values of the explicit bound state energies. The numerical results of our calculation showed that the results obtained with \(- C = \lambda ,\) \(C = 0\) and \(\lambda = 0,\) are equivalent. The results of the analytical determination of information entropies calculated for the ground state in both position space and momentum space are shown in various Tables. In Table 3, we numerically verify the uncertainty relation in Eq. (25). The Shannon entropy in the position space is bounded while in the momentum space the Shannon entropy is unbounded for the various values of the dissociation energy of multiple potential. The physical meaning of the inequality is that a decrease in Shannon entropy for position space corresponds to an increase in Shannon entropy for momentum space. This indicates that a diffused density distribution \(\gamma (p)\) in momentum space is associated with a localized density distribution \(\rho (r)\) in the position space or configuration space. It can be seen that the lower bound for the sum of the Shannon entropy is 13.18210163 which is greater than \((1 + log\pi )\) that is equal to 1.497206180. However, the position space Shannon entropy exhibit squeezing effect in Table 3. However, the numerical results in this Table satisfied Bialynick-Birula, Mycielski inequality.
In Table 4, we presented numerical values for variance in position space and momentum space for ground state and the first excited state. The position and momentum spaces for the variance have an inverse relationship with each other. A strongly localized distribution in the momentum space corresponds to widely delocalized distribution in the position space. The results obtained in each case, followed the same trend and obeyed Heisenberg Uncertainty Principle. To test the variance-inequalities presented in Eqs. (34) and (35) respectively, we generated numerical results in Table 5. Following Eq. (34), it can be seen that sixteen multiplied by the product of variance cannot go lower than eight one divided by the product of the expectation values. The lower bound for \(16V(\rho )V(\gamma )\) is 36.66666667 while the upper bound for \(81/\left\langle {p^{2} } \right\rangle \left\langle {r^{2} } \right\rangle\) is 35.34545454. Hence, Eq. (34) is justified. Similarly, Eq. (35) shows that the product of variance cannot go lower than nine divided by four. The lower bound for the product of variance is 2.291666667 while nine divided by four is 2.250000000. This also justified the variance inequality in Eq. (35).
Finally, we presented numerical values of variance both in momentum space and position space in Tables 6 and 7 respectively for some selected diatomic molecules using the spectroscopic parameters in Table 1. These Tables showed that the increase in both the quantum number and angular momentum quantum number for the multiple potential do not satisfied uncertainty principle in terms of variance. In Tables 8 and 9, we numerically presented the Shannon entropy for position space and momentum space respectively of four molecules with various \(\lambda .\) The position space and momentum space information entropies have an inverse relationship with each other. A strongly localized distribution in the momentum space corresponds to widely delocalized distribution in the position space. However, an entropy squeezing is noted for the position space. In the two Tables, there is a change in position space and momentum space Shannon entropies as the parameter \(\lambda ,\) goes up but the sum is bounded above the inequality for BBM. In Table 10, we numerically studied Shannon entropy in position space and momentum space for different values of \(C\) for \(\ell = 0\) and \(\ell = 1.\) For the two values of \(\ell ,\) the Shannon entropy in the position space is bounded while in the momentum space the Shannon entropy is unbounded for multiple potential. It can be seen that the lower bound for the sum of the Shannon entropy with \(\ell = 0\) is 4.916111226 while the lower bound for \(\ell = 1\) is 11.49671887. In each case, the lower bound for the sum of the entropies is greater than \((1 + log\pi )\) that is equal to 1.497206180. Thus, a general formulation of information theoretic uncertainty relations for the different conjugate pair of observables is described for some parameters and all dimensions for multiple potential as the inequality satisfied Bialynick-Birula, Mycielski inequality. It is observed that the Shannon entropy in position space exhibit entropy squeezing which is contrary to the behaviour of Shannon entropy in momentum space. In Table 11, we examined the variation of variance with various values of \(\lambda\) and \(C\) respectively. It is seen that the variance in momentum space for both cases exhibit squeezing effect. However, the position space and momentum space variance obeyed uncertainty relation.
The shape of multiple potential and pseudoharmonic-like potential respectively are shown in Fig. 1. In Figs. 2 and 3, we plotted Shannon entropy for momentum space and position space respectively against the equilibrium bond length for the multiple potential functions. In the momentum space, as the equilibrium bond length increases linearly, there is a sharp monotonic decrease in the Shannon entropy while in position space, there is a sharp increase in the Shannon entropy as the equilibrium bond length increases. However, Shannon entropy experience more squeezing in Fig. 3. As the value of the equilibrium bond length increases, the Shannon entropies tends towards a constant value. In Figs. 4 and 5, we plotted Shannon entropy for position space and momentum space respectively against the equilibrium bond length for a pseudoharmonic-like potential. The results obtained is equivalent to the results of the multiple potential. Figures 6 and 7 showed the variation of variance for both position space and momentum space respectively against the equilibrium bond length for multiple potential. In the position space, variance increases as the equilibrium bond length increases while in the momentum space, an increase in the equilibrium bond length results to a monotonic decrease in variance. There is more squeezing effect in the momentum space as the equilibrium bond length increases. The same results were observed in Figs. 8 and 9 for pseudoharmonic-like potential. In Fig. 9, the variance for momentum space becomes squeezing. The Shannon entropy for position space and momentum space respectively, are plotted against the dissociation energy in Figs. 10 and 11. In Fig. 10, as the dissociation energy increases from zero, there is more concentration of the wave function of the state which results to more stability of the system. In this Fig, the Shannon entropy for position space becomes squeezing as the dissociation energy increases linearly. In Fig. 11 however, there is less concentration of the wave function of the state as the dissociation energy goes up. This brings about less stability of the system.
Conclusion
We have used the parametric Nikiforv-Uvarov method to obtain the analytic solutions of the the radial Schrödinger equation for multiple potential. Our results showed that the numerical values of the multiple potential are equivalent to the numerical values of the two subset potentials studied. Some expectation values were calculated using Hellmann–Feynman theorem. A new variance uncertainty relation established has been justified by numerical results. Finally, a Shannon entropy uncertainty and inequality relation was also confirmed by generating numerical values using MATLAB 9.2.0.538062. Our results revealed that the Shannon entropy for various \(\lambda\) with \(\ell = 0\) do not satisfied Bialynick-Birula, Mycielski inequality while with \(\ell = 1\) satisfied it.
References
Uffink, J. & Hilgewoord, J. Uncertainty principle and uncertainty relations. Found. Phys. 15, 925–944 (1985).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. A 136, 864–871 (1964).
Orlowski, A. Information entropy and squeezing of quantum fluctuations. Phys. Rev. A 56, 2545 (1997).
Galindo, A. & Pascual, P. Quantum Mechanics (Springer, Berlin, 1978).
Romera, E. & Dehesa, J. S. The Fisher–Shannon information plane, an electron correlation tool. J. Chem. Phys. 120, 8906 (2004).
Angulo, J. C., Antolin, J., Zarzo, A. & Cuchi, J. C. Maximum entropy technique with estimation of atomic radial densities. Eur. Phys. J. D 7, 479 (1999).
Dehesa, J. S., Martinez-Finkelshtein, A. & Sorokin, V. N. Quantum-information entropies for highly excited states of single-particle systems with power-type potentials. Phys. Rev. A 66, 062109 (2002).
Yahya, W. A., Oyewumi, K. J. & Sen, K. D. Position and momentum information-theoretic measures of the pseudoharmonic potential. Int. J. Quant. Chem. 115, 1543 (2015).
Onate, C. A., Onyeaju, M. C., Ikot, A. N. & Ebomwonyi, O. Eigen solutions and entropic system for Hellmann potential in the presence of the Schrödinger equation. Eur. Phys. J. Plus 132, 462 (2017).
Sage, M. & Goodisman, J. Improving on the conventional presentation of molecular vibrations: advantages of the pseudoharmonic potential and the direct construction of potential energy curves. Am. J. Phys. 53, 350–355 (1985).
Ikhdair, S. M. On the bound-state solutions of the Manning–Rosen potential including an improved approximation to the orbital centrifugal term. Phys. Scr. 83, 015010 (2011).
Bayrak, O. & Boztosun, I. Bound state solutions of the Hulthén potential by using the asymptotic iteration method. Phys. Scr. 76, 92 (2007).
Ikot, A. N., Abbey, T. M., Chukwuocha, E. O. & Onyeaju, M. C. Solutions of the Schrödinger equation for pseudo-Coulomb potential plus a new improved ring-shaped potential in the cosmic string space–time. Can. J. Phys. 94, 517–521 (2016).
Feynman, R. P. Forces in molecules. Phys. Rev. 56, 340–343 (1939).
Hellmann, G. Introduction to Quantum Chemistry, German, (1937)
Agboola, D. The Hulthén potential in D-dimensions. Phys. Scr. 80, 065304 (2009).
Oyewumi, K. J. & Sen, K. D. Exact solutions of the Schrödinger equation for the pseudoharmonic potential: an application to some diatomic molecules. J. Math. Chem. 50, 1039–1059 (2012).
Onate, C. A. Relativistic and non-relativistic solutions of the inversely quadratic Yukawa potential. Afri. Rev. Phys. 8, 325–329 (2013).
Dehesa, J. S., Toranzo, I. V. & Puertas-Centeno, D. Entropic measures of Rydberg-like harmonic states. Int. J. Quant. Chem. 117, 48–56 (2017).
Yahya, W. A., Oyewumi, K. J. & Sen, K. D. Quantum information entropies for the—state Pöschl–Teller-type potential. J. Math. Chem. 54, 1810–1821 (2016).
Najafizade, S. A., Hassanabadi, H. & Zarrinkamar, S. Nonrelativistic Shannon information entropy for Kratzer potential. Chin. Phys. B 25, 040301 (2016).
Dehesa, J. S., Assche, W. V. & Yáñez, R. J. Information entropy of classical orthogonal polynomials and their application to the harmonic oscillator and Coulomb potentials. Methods Appl. Anal. 4, 91–110 (1997).
Idiodi, J. O. A. & Onate, C. A. Entropy, Fisher information and variance with Frost–Musulin potenial. Commun. Theor. Phys. 66, 296–274 (2016).
Dehesa, J. S., Martinez-Finkelshtein, A. & Sorokin, V. N. Information-theoretic measures for Morse and Pӧschl–Teller potentials. Mol. Phys. 104, 613–622 (2006).
Falaye, B. J., Oyewumi, K. J., Ikhdair, S. M. & Hamzavi, M. Eigensolution techniques, their applications and Fisherʼs information entropy of the Tietz–Wei diatomic molecular model. Phys. Scr. 89, 115204 (2014).
Author information
Authors and Affiliations
Contributions
C.A. Onate designed and wrote the paper M.C. Onyeaju discussed result and wrote the paper A. Abolarinwa edit the work and wrote the paper A.F. Lukman type set and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Onate, C.A., Onyeaju, M.C., Abolarinwa, A. et al. Analytical determination of theoretic quantities for multiple potential. Sci Rep 10, 17542 (2020). https://doi.org/10.1038/s41598-020-73372-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-73372-x
This article is cited by
-
Bound state solutions and thermodynamic properties of modified exponential screened plus Yukawa potential
Journal of the Egyptian Mathematical Society (2022)
-
Few generalized entropic relations related to Rydberg atoms
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.